初中数学北师大版(2024)七年级下册期中质量检测卷(含答案)
文档属性
| 名称 | 初中数学北师大版(2024)七年级下册期中质量检测卷(含答案) | 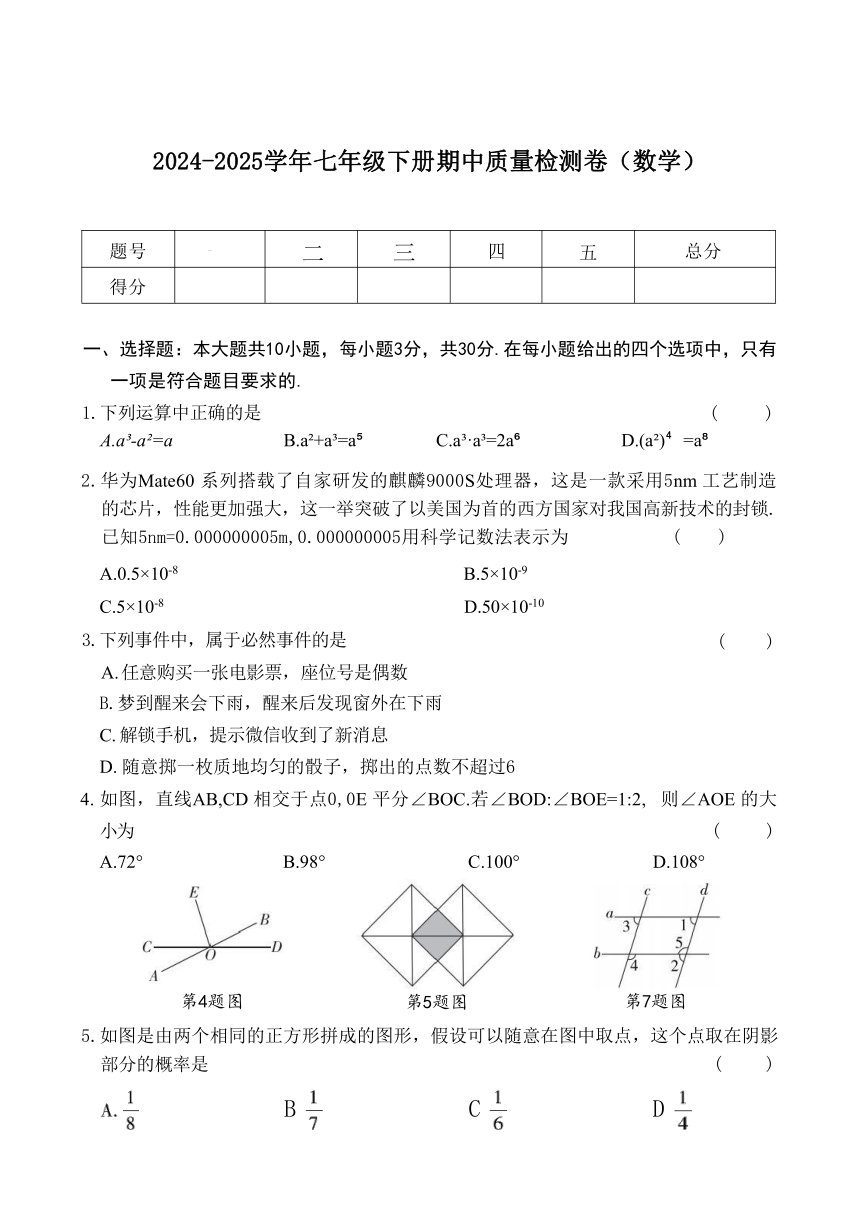 | |
| 格式 | docx | ||
| 文件大小 | 202.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-08 12:01:17 | ||
图片预览




文档简介
2024-2025学年七年级下册期中质量检测卷(数学)
题号 一 二 三 四 五 总分
得分
一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有 一项是符合题目要求的.
1.下列运算中正确的是 ( ) A.a -a =a B.a +a =a C.a ·a =2a D.(a ) =a
2.华为Mate60 系列搭载了自家研发的麒麟9000S处理器,这是一款采用5nm 工艺制造 的芯片,性能更加强大,这一举突破了以美国为首的西方国家对我国高新技术的封锁. 已知5nm=0.000000005m,0.000000005用科学记数法表示为 ( )
A.0.5×10-8 B.5×10-9
C.5×10-8 D.50×10-10
3.下列事件中,属于必然事件的是 ( )
A. 任意购买一张电影票,座位号是偶数
B.梦到醒来会下雨,醒来后发现窗外在下雨
C. 解锁手机,提示微信收到了新消息
D. 随意掷一枚质地均匀的骰子,掷出的点数不超过6
4. 如图,直线AB,CD 相交于点0,0E 平分∠BOC.若∠BOD:∠BOE=1:2, 则∠AOE 的大 小为 ( ) A.72° B.98° C.100° D.108°
第4题图
第5题图
第7题图
5.如图是由两个相同的正方形拼成的图形,假设可以随意在图中取点,这个点取在阴影 部分的概率是 ( )
B
C
D
6.已知a,b,c 是△ABC的三条边长,化简|a-b-c|-|c-a+b| 的结果为 A.2a-2b-2c B.2a+2b C.-2c
7.如图,直线c,d 被直线a,b 所截.下列条件不能判定c//d的是
D.0
( )
( )
A. ∠4=∠5 B. ∠2+∠4=180°
C. ∠1=∠3 D. ∠1=∠2
8.下列说法正确的是 ( )
A. 三角形的三条中线交于一点
B. 三角形的角平分线是射线
C.三角形的三条高所在的直线交于一点,且这一点不在三角形内就在三角形外
D.三角形的一条角平分线能把三角形分成两个面积相等的三角形
9.如图是四张全等的长方形纸片拼成的图形,利用图中空白部分面积的不同表示方法,写出 一个关于a,b 的恒等式是 ( )
A.(a+b) =a +2ab+b
B.(a+b)(a-b)=a -b
C.(a+b) -4ab=(a-b)
D.(a+b) +(a-b) =2a +2b
10. 如图,△AOB≌△ADC,∠O=90°,∠ABC=∠ACB, 记∠ OAD=α,∠ABO=β. 当 BC//OA
时,α与β之间的数量关系为 ( )
A.α=β B.α=2β
C.α+β=90° D.α+2β=180°
二、填空题:本大题共5小题,每小题3分,共15分.
11.己知3"=4,3”=5,则3"+2n=
12.如图,计划把河中的水引到水池 M 中,可以先过点M 作 MC⊥AB,垂足为 C, 然后沿 MC 开渠,则能使所开的渠最短,这种设计方案的根据是
第 1 2 题 图
第 1 3 题 图
第 1 5 题 图
13.如图,若AB//CD,AB⊥AE,∠CAE=42°, 则∠ACD 的度数为
14.在一个不透明的盒子里装有2个红球和 n 个白球,这些球除颜色外其余完全相同,摇 匀后随机摸出一个,摸出红球的概率是0.2,则n 的值为
15.如 图 ,AD 是 △ABC 中 BC 边上的中线,若 AB=6,AC =8,则 AD 的 取 值 范 围是
三、解答题(一):本大题共3小题,每小题7分,共21分.
16.计算:
(1)2025 -1025 ;
(2)98 +4×98+4(用乘法公式求解).
17. 先化简,再求值:[(x+3y)(x-3y)-(x-y) ]÷(-2y), 其中|x+1|+(y-2) =0.
18. 如图,AB=AC,BD=CD,∠B=26°, 求∠C 的度数.
四、解答题(二):本大题共3小题,每小题9分,共27分.
19.在一个不透明的布袋中装有8个红球和16个白球,它们除颜色不同外其余都相同.
(1)从布袋中任意摸出一个球,摸到白球是 事件(填“必然”“不可能”或“随 机”).
(2)求从布袋中任意摸出一个球是红球的概率.
(3)现从布袋中取走若干个白球,并放入相同数目的红球,搅拌均匀后,再从布袋中任 意摸出一个球是红球的概率是 ,问取走了多少个白球
20.如图,已知DF//AB, 且∠1=∠B.
(1)试说明 EF//BC;
(2)若 CE 平分∠ACB, 且∠ CEF=40°, 求∠AFE 的度数.
21.从边长为a 的正方形中剪掉一个边长为b 的正方形(如图①),然后将剩余部分
拼成一个长方形(如图②).
(1)上述操作能验证的等式是 A.a -2ab+b =(a-b)
B.a -b =(a+b)(a-b)
(
图
②
)C.a +ab=a(a+b)
(2)计算:(2a+b-c)(2a-b+c).
(3)计算:
五、解答题(三):本大题共2小题,第22题13分,第23题14分,共27分.
22.【问题发现】(1)如图①,△ABC与△CDE 中,∠B=∠E=∠ACD=90°,AC=CD,B,C,E 三点在同一直线上,AB=3,ED=4, 则 BE=
【问题解决】(2)如图②,在 Rt△ABC 中,∠ABC=90°,BC=4, 过 点C 作 CD⊥AC, 且 CD=AC,求△BCD的面积.
图①
图②
23. 如图①,E 是直线 AB,CD内部一 点,AB//CD,连接 EA,ED.
(1)探究猜想:
若∠A=20°,∠D=50°, 则∠AED= ° ; 若∠A=35°,∠D=45°, 则∠AED=
猜想图①中∠ AED,∠EAB,∠EDC 之间的数量关系并说明理由.
(2)拓展应用:
如图②,射线 FE 与长方形ABCD的边AB 交于点E, 与边 CD 交于点F,I,Ⅱ,Ⅲ,IV
分别是被射线FE 隔开的4个区域(不含边界,其中区域Ⅲ,IV位于直线 AB 上方) ,P 是位于以上四个区域内的点,猜想∠PEB,∠PFC,∠EPF 间的数量关系(直接写出 结论).
(
图
①
)图②
期中质量检测卷
1.D 2.B 3.D 4.D 5.B 6.D 7.D 8.A 9.C
10.B【 解析】因为△AOB≌△ADC, 所以AB=AC,∠BAO=∠CAD.
所以∠BAC=∠OAD=α.
在△ABC中 , 因为BC//OA,
所以∠OBC=180°-∠0=180°-90°=90° .
所以
整理,得α=2β.
11.100 12.垂线段最短 13.132°14.8
15.1因为AD是 BC 边上的中线,
所以 BD=CD.
在△ABD 和△ECD中 ,
所以△ ABD≌△ECD(SAS).
所以AB=EC.
因为AB=6, 所以 CE=6.
因为AC=8, 所以8-6所以2<2AD<14.所以116.解:(1)原式=(2025+1025)(2025-1025) =3050000.
(2)原式=(98+2) =10000.
17. 解:原式=(x -9y -x +2xy-y )÷(-2y) =(-10y +2xy)÷(-2y)
=5y-x.
因为 |x+1|+(y-2) =0,
所以x+1=0,y-2=0. 解得x=-1,y=2.
所以原式=5×2-(-1)=11.
18. 解:在△ABD和△ACD中 , 所以△ABD≌△ACD(SSS).所以∠C=∠B. 因为∠B=26°, 所以∠C=26° .
19.解:(1)随机
(2)因为从布袋中摸出一个球,有16+8=24(种)情况, 摸到红球的情况有8种,都是等可能的,
所以P(从布袋中任意摸出一个球是红球 (3)设取走了x 个白球,则放入了x 个红球,共有(x+8) 个 红球.
根据题意,得 .解得x=1.
答:取走了1个白球.
20. 解:(1)因为DF//AB, 所以∠1=∠AEF.
又因为∠1=∠B, 所以∠ B=∠AEF. 所以 EF//BC.
(2)因为 EF//BC,
所以∠ECB=∠CEF=40°,∠AFE=∠ACB.
因为 CE 平分∠ACB, 所以∠ACB=2∠ECB=80°.
所以∠AFE=∠ACB=80°.
21.解:(1)B
(2)原式=[2a+(b-c)][2a-(b-c)] =(2a) -(b-c)
=4a -b +2bc-c .
22.解:(1)7
(2)过点D 作 DE⊥BC,交BC 的延长线于点E, 如图②. 因为DE⊥BC,CD⊥AC,
所以∠E=∠ACD=90°.
所以∠ACB=90°-∠DCE=∠CDE.
在△ABC和△CED 中 , 图②
所以△ABC≌△CED(AAS). 所以 BC=ED=4.
所以
23.解:(1)7080
∠AED=∠EAB+∠EDC. 理由如下:
过点E 作 EF//CD, 如图①. 所以∠2=∠EDC.
因为AB//CD,所以EF//AB. 所以∠1=∠EAB.
所以∠AED=∠1+∠2=∠EAB+∠EDC.
(2)当点 P 在区域 I 时,如图,∠EPF+∠PEB+∠PFC=360°.
当点P 在区域Ⅱ时,如图,∠ EPF= ∠PEB+∠PFC.
当点P 在区域Ⅲ时,如图,∠EPF=∠PFC-∠PEB.
当点P 在区域IV 时,如图,∠ EPF=∠PEB-∠PFC.
题号 一 二 三 四 五 总分
得分
一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有 一项是符合题目要求的.
1.下列运算中正确的是 ( ) A.a -a =a B.a +a =a C.a ·a =2a D.(a ) =a
2.华为Mate60 系列搭载了自家研发的麒麟9000S处理器,这是一款采用5nm 工艺制造 的芯片,性能更加强大,这一举突破了以美国为首的西方国家对我国高新技术的封锁. 已知5nm=0.000000005m,0.000000005用科学记数法表示为 ( )
A.0.5×10-8 B.5×10-9
C.5×10-8 D.50×10-10
3.下列事件中,属于必然事件的是 ( )
A. 任意购买一张电影票,座位号是偶数
B.梦到醒来会下雨,醒来后发现窗外在下雨
C. 解锁手机,提示微信收到了新消息
D. 随意掷一枚质地均匀的骰子,掷出的点数不超过6
4. 如图,直线AB,CD 相交于点0,0E 平分∠BOC.若∠BOD:∠BOE=1:2, 则∠AOE 的大 小为 ( ) A.72° B.98° C.100° D.108°
第4题图
第5题图
第7题图
5.如图是由两个相同的正方形拼成的图形,假设可以随意在图中取点,这个点取在阴影 部分的概率是 ( )
B
C
D
6.已知a,b,c 是△ABC的三条边长,化简|a-b-c|-|c-a+b| 的结果为 A.2a-2b-2c B.2a+2b C.-2c
7.如图,直线c,d 被直线a,b 所截.下列条件不能判定c//d的是
D.0
( )
( )
A. ∠4=∠5 B. ∠2+∠4=180°
C. ∠1=∠3 D. ∠1=∠2
8.下列说法正确的是 ( )
A. 三角形的三条中线交于一点
B. 三角形的角平分线是射线
C.三角形的三条高所在的直线交于一点,且这一点不在三角形内就在三角形外
D.三角形的一条角平分线能把三角形分成两个面积相等的三角形
9.如图是四张全等的长方形纸片拼成的图形,利用图中空白部分面积的不同表示方法,写出 一个关于a,b 的恒等式是 ( )
A.(a+b) =a +2ab+b
B.(a+b)(a-b)=a -b
C.(a+b) -4ab=(a-b)
D.(a+b) +(a-b) =2a +2b
10. 如图,△AOB≌△ADC,∠O=90°,∠ABC=∠ACB, 记∠ OAD=α,∠ABO=β. 当 BC//OA
时,α与β之间的数量关系为 ( )
A.α=β B.α=2β
C.α+β=90° D.α+2β=180°
二、填空题:本大题共5小题,每小题3分,共15分.
11.己知3"=4,3”=5,则3"+2n=
12.如图,计划把河中的水引到水池 M 中,可以先过点M 作 MC⊥AB,垂足为 C, 然后沿 MC 开渠,则能使所开的渠最短,这种设计方案的根据是
第 1 2 题 图
第 1 3 题 图
第 1 5 题 图
13.如图,若AB//CD,AB⊥AE,∠CAE=42°, 则∠ACD 的度数为
14.在一个不透明的盒子里装有2个红球和 n 个白球,这些球除颜色外其余完全相同,摇 匀后随机摸出一个,摸出红球的概率是0.2,则n 的值为
15.如 图 ,AD 是 △ABC 中 BC 边上的中线,若 AB=6,AC =8,则 AD 的 取 值 范 围是
三、解答题(一):本大题共3小题,每小题7分,共21分.
16.计算:
(1)2025 -1025 ;
(2)98 +4×98+4(用乘法公式求解).
17. 先化简,再求值:[(x+3y)(x-3y)-(x-y) ]÷(-2y), 其中|x+1|+(y-2) =0.
18. 如图,AB=AC,BD=CD,∠B=26°, 求∠C 的度数.
四、解答题(二):本大题共3小题,每小题9分,共27分.
19.在一个不透明的布袋中装有8个红球和16个白球,它们除颜色不同外其余都相同.
(1)从布袋中任意摸出一个球,摸到白球是 事件(填“必然”“不可能”或“随 机”).
(2)求从布袋中任意摸出一个球是红球的概率.
(3)现从布袋中取走若干个白球,并放入相同数目的红球,搅拌均匀后,再从布袋中任 意摸出一个球是红球的概率是 ,问取走了多少个白球
20.如图,已知DF//AB, 且∠1=∠B.
(1)试说明 EF//BC;
(2)若 CE 平分∠ACB, 且∠ CEF=40°, 求∠AFE 的度数.
21.从边长为a 的正方形中剪掉一个边长为b 的正方形(如图①),然后将剩余部分
拼成一个长方形(如图②).
(1)上述操作能验证的等式是 A.a -2ab+b =(a-b)
B.a -b =(a+b)(a-b)
(
图
②
)C.a +ab=a(a+b)
(2)计算:(2a+b-c)(2a-b+c).
(3)计算:
五、解答题(三):本大题共2小题,第22题13分,第23题14分,共27分.
22.【问题发现】(1)如图①,△ABC与△CDE 中,∠B=∠E=∠ACD=90°,AC=CD,B,C,E 三点在同一直线上,AB=3,ED=4, 则 BE=
【问题解决】(2)如图②,在 Rt△ABC 中,∠ABC=90°,BC=4, 过 点C 作 CD⊥AC, 且 CD=AC,求△BCD的面积.
图①
图②
23. 如图①,E 是直线 AB,CD内部一 点,AB//CD,连接 EA,ED.
(1)探究猜想:
若∠A=20°,∠D=50°, 则∠AED= ° ; 若∠A=35°,∠D=45°, 则∠AED=
猜想图①中∠ AED,∠EAB,∠EDC 之间的数量关系并说明理由.
(2)拓展应用:
如图②,射线 FE 与长方形ABCD的边AB 交于点E, 与边 CD 交于点F,I,Ⅱ,Ⅲ,IV
分别是被射线FE 隔开的4个区域(不含边界,其中区域Ⅲ,IV位于直线 AB 上方) ,P 是位于以上四个区域内的点,猜想∠PEB,∠PFC,∠EPF 间的数量关系(直接写出 结论).
(
图
①
)图②
期中质量检测卷
1.D 2.B 3.D 4.D 5.B 6.D 7.D 8.A 9.C
10.B【 解析】因为△AOB≌△ADC, 所以AB=AC,∠BAO=∠CAD.
所以∠BAC=∠OAD=α.
在△ABC中 , 因为BC//OA,
所以∠OBC=180°-∠0=180°-90°=90° .
所以
整理,得α=2β.
11.100 12.垂线段最短 13.132°14.8
15.1
所以 BD=CD.
在△ABD 和△ECD中 ,
所以△ ABD≌△ECD(SAS).
所以AB=EC.
因为AB=6, 所以 CE=6.
因为AC=8, 所以8-6
(2)原式=(98+2) =10000.
17. 解:原式=(x -9y -x +2xy-y )÷(-2y) =(-10y +2xy)÷(-2y)
=5y-x.
因为 |x+1|+(y-2) =0,
所以x+1=0,y-2=0. 解得x=-1,y=2.
所以原式=5×2-(-1)=11.
18. 解:在△ABD和△ACD中 , 所以△ABD≌△ACD(SSS).所以∠C=∠B. 因为∠B=26°, 所以∠C=26° .
19.解:(1)随机
(2)因为从布袋中摸出一个球,有16+8=24(种)情况, 摸到红球的情况有8种,都是等可能的,
所以P(从布袋中任意摸出一个球是红球 (3)设取走了x 个白球,则放入了x 个红球,共有(x+8) 个 红球.
根据题意,得 .解得x=1.
答:取走了1个白球.
20. 解:(1)因为DF//AB, 所以∠1=∠AEF.
又因为∠1=∠B, 所以∠ B=∠AEF. 所以 EF//BC.
(2)因为 EF//BC,
所以∠ECB=∠CEF=40°,∠AFE=∠ACB.
因为 CE 平分∠ACB, 所以∠ACB=2∠ECB=80°.
所以∠AFE=∠ACB=80°.
21.解:(1)B
(2)原式=[2a+(b-c)][2a-(b-c)] =(2a) -(b-c)
=4a -b +2bc-c .
22.解:(1)7
(2)过点D 作 DE⊥BC,交BC 的延长线于点E, 如图②. 因为DE⊥BC,CD⊥AC,
所以∠E=∠ACD=90°.
所以∠ACB=90°-∠DCE=∠CDE.
在△ABC和△CED 中 , 图②
所以△ABC≌△CED(AAS). 所以 BC=ED=4.
所以
23.解:(1)7080
∠AED=∠EAB+∠EDC. 理由如下:
过点E 作 EF//CD, 如图①. 所以∠2=∠EDC.
因为AB//CD,所以EF//AB. 所以∠1=∠EAB.
所以∠AED=∠1+∠2=∠EAB+∠EDC.
(2)当点 P 在区域 I 时,如图,∠EPF+∠PEB+∠PFC=360°.
当点P 在区域Ⅱ时,如图,∠ EPF= ∠PEB+∠PFC.
当点P 在区域Ⅲ时,如图,∠EPF=∠PFC-∠PEB.
当点P 在区域IV 时,如图,∠ EPF=∠PEB-∠PFC.
同课章节目录
