初中数学北师大版(2024)七年级下册 期末质量测试卷二(含答案)
文档属性
| 名称 | 初中数学北师大版(2024)七年级下册 期末质量测试卷二(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 313.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-08 12:08:07 | ||
图片预览

文档简介
2024-2025学年七年级下册期末质量测试卷二(数学)
题号 一 二 三 四 五 总分
得分
一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有 一项是符合题目要求的.
1.“谁知盘中餐,粒粒皆辛苦”.已知一粒米的质量约0.000021kg,则数据0.000021用 科学记数法表示为 ( ) A.0.21×10-4 B.2.1×10-4 C.21×10-8 D.2.1×10-5
2.我国新能源汽车发展势头迅猛,以下汽车车标融入了数学几何元素,其中是轴对称图 形的是 ( )
A B C D
3.如图,直线AD//BC,BA⊥AC 于点A.若∠2=55°,则∠1为 ( )
A.35° B.45° C.55° D.25°
第3题图 第6题图
4.计算 的结果是 ( )
B D
5.一个不透明的袋子里装有2个白球、3个红球,除颜色外,其余如材料、大小、质量等完 全相同.随机从中抽出一个球,抽到红球的概率是 ( )
B. D
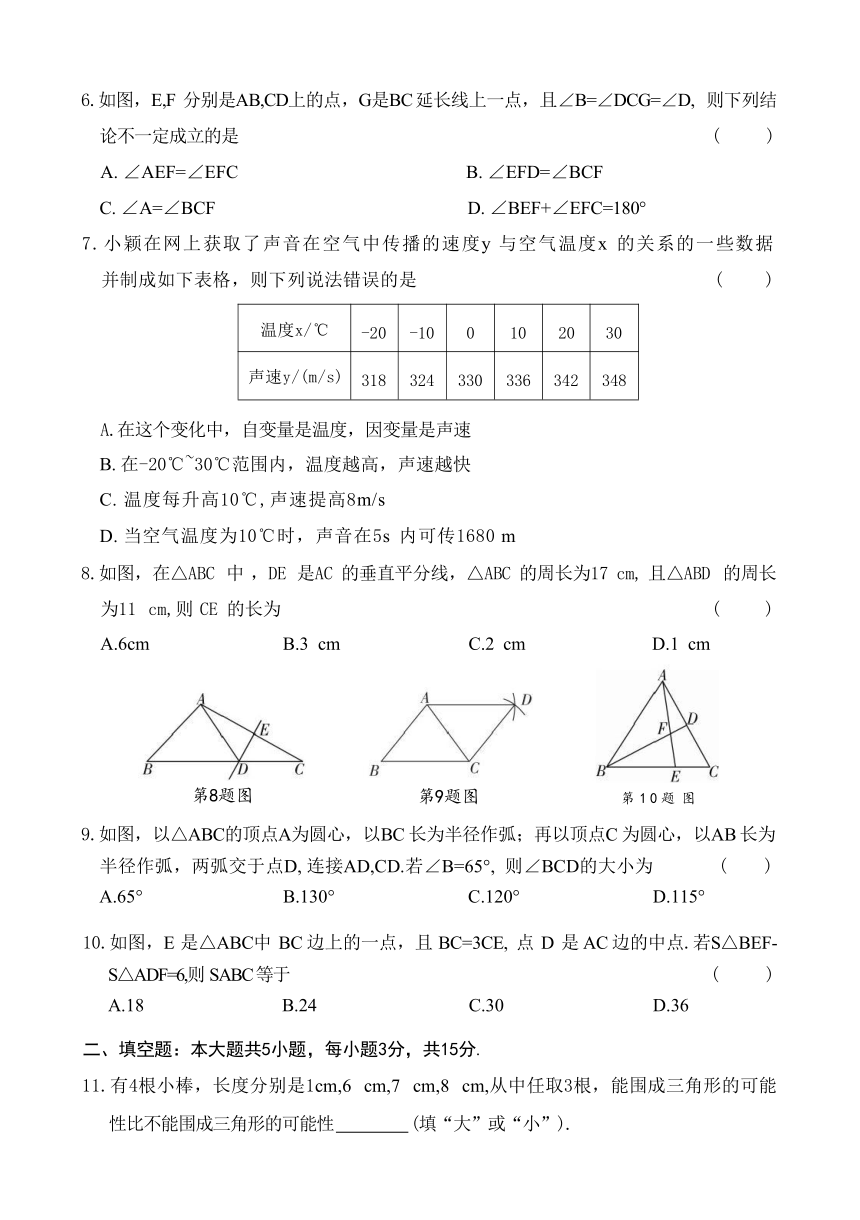
6.如图,E,F 分别是AB,CD上的点,G是BC 延长线上一点,且∠B=∠DCG=∠D, 则下列结 论不一定成立的是 ( )
A. ∠AEF=∠EFC B. ∠EFD=∠BCF
C. ∠A=∠BCF D. ∠BEF+∠EFC=180°
7.小颖在网上获取了声音在空气中传播的速度y 与空气温度x 的关系的一些数据 并制成如下表格,则下列说法错误的是 ( )
温度x/℃ -20 -10 0 10 20 30
声速y/(m/s) 318 324 330 336 342 348
A.在这个变化中,自变量是温度,因变量是声速
B. 在-20℃~30℃范围内,温度越高,声速越快
C. 温度每升高10℃,声速提高8m/s
D. 当空气温度为10℃时,声音在5s 内可传1680 m
8.如图,在△ABC 中 ,DE 是AC 的垂直平分线,△ABC 的周长为17 cm, 且△ABD 的周长 为11 cm,则 CE 的长为 ( ) A.6cm B.3 cm C.2 cm D.1 cm
第8题图 第9题图 第 1 0 题 图
9.如图,以△ABC的顶点A为圆心,以BC 长为半径作弧;再以顶点C 为圆心,以AB 长为 半径作弧,两弧交于点D, 连接AD,CD.若∠B=65°, 则∠BCD的大小为 ( ) A.65° B.130° C.120° D.115°
10.如图,E 是△ABC中 BC 边上的一点,且 BC=3CE, 点 D 是 AC 边的中点.若S△BEF- S△ADF=6,则 SABC 等于 ( ) A.18 B.24 C.30 D.36
二、填空题:本大题共5小题,每小题3分,共15分.
11.有4根小棒,长度分别是1cm,6 cm,7 cm,8 cm,从中任取3根,能围成三角形的可能 性比不能围成三角形的可能性 (填“大”或“小”).
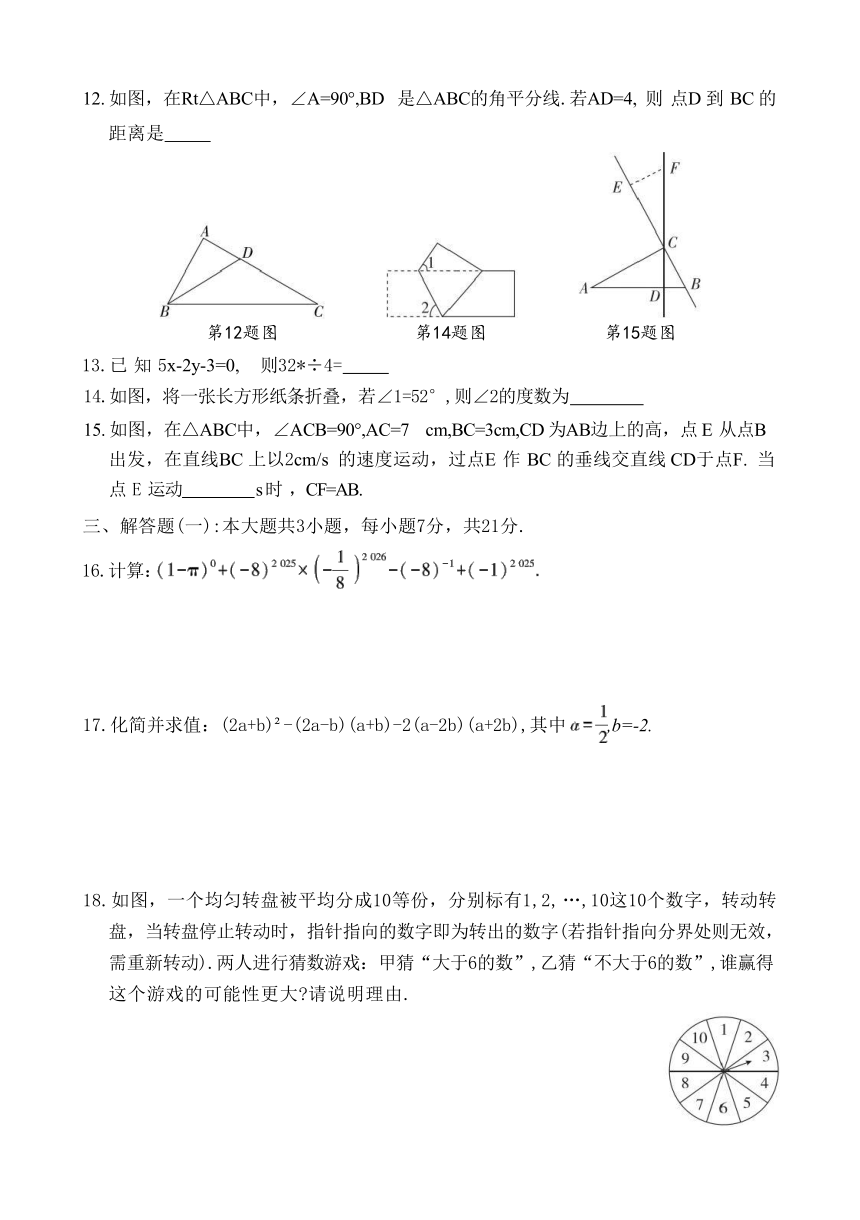
12. 如图,在Rt△ABC中,∠A=90°,BD 是△ABC的角平分线.若AD=4, 则 点D 到 BC 的
距离是
第12题图 第14题图 第15题图
13.已 知 5x-2y-3=0, 则32*÷4=
14.如图,将一张长方形纸条折叠,若∠1=52°,则∠2的度数为
15. 如图,在△ABC中,∠ACB=90°,AC=7 cm,BC=3cm,CD 为AB边上的高,点 E 从点B 出发,在直线BC 上以2cm/s 的速度运动,过点E 作 BC 的垂线交直线 CD于点F. 当 点 E 运动 s 时 ,CF=AB.
三、解答题(一):本大题共3小题,每小题7分,共21分.
16.计算:
17.化简并求值:(2a+b) -(2a-b)(a+b)-2(a-2b)(a+2b),其中 ,b=-2.
18.如图,一个均匀转盘被平均分成10等份,分别标有1,2, …,10这10个数字,转动转 盘,当转盘停止转动时,指针指向的数字即为转出的数字(若指针指向分界处则无效, 需重新转动).两人进行猜数游戏:甲猜“大于6的数”,乙猜“不大于6的数”,谁赢得 这个游戏的可能性更大 请说明理由.
四、解答题(二):本大题共3小题,每小题9分,共27分.
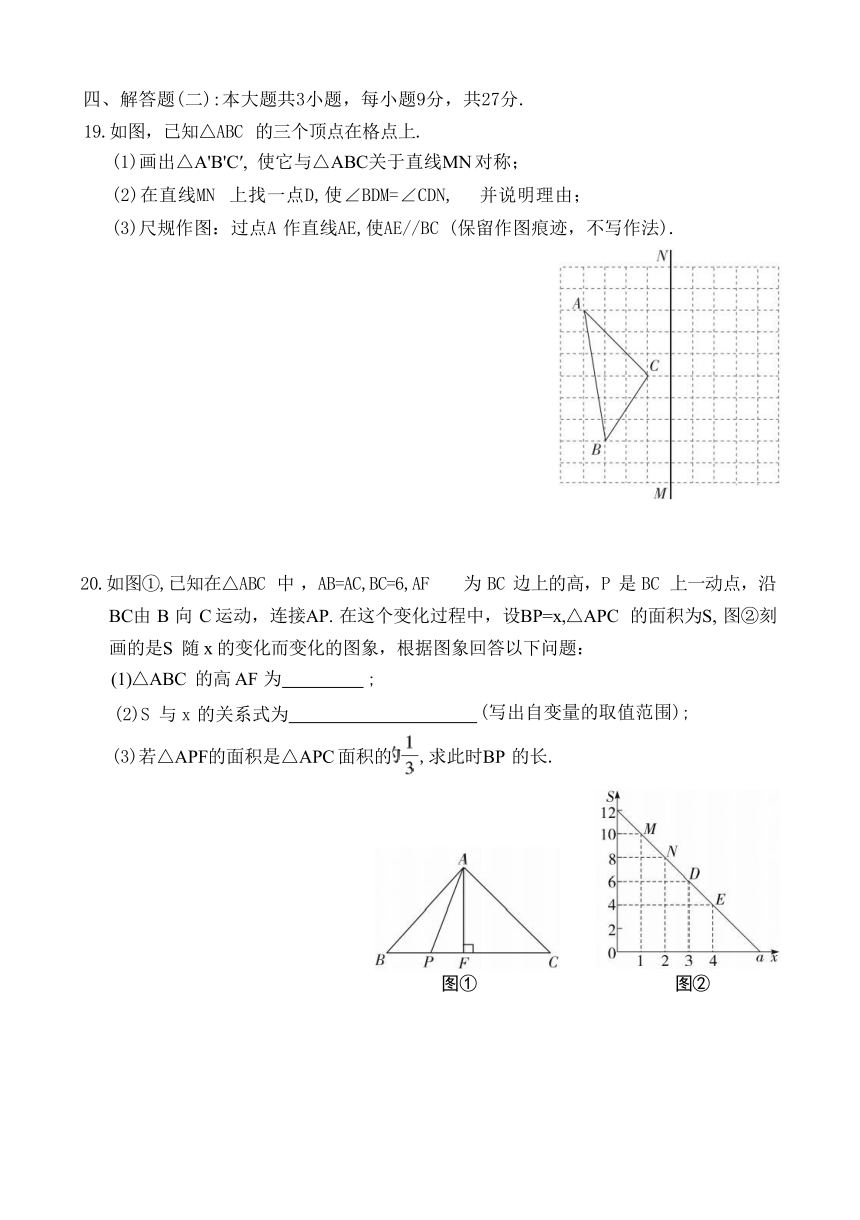
19.如图,已知△ABC 的三个顶点在格点上.
(1)画出△A'B'C′, 使它与△ABC关于直线MN 对称;
(2)在直线MN 上找一点D,使∠BDM=∠CDN, 并说明理由;
(3)尺规作图:过点A 作直线AE,使AE//BC (保留作图痕迹,不写作法).
20.如图①,已知在△ABC 中 ,AB=AC,BC=6,AF 为 BC 边上的高,P 是 BC 上一动点,沿 BC由 B 向 C 运动,连接AP. 在这个变化过程中,设BP=x,△APC 的面积为S, 图②刻 画的是S 随 x 的变化而变化的图象,根据图象回答以下问题:
(1)△ABC 的高 AF 为 ;
(2)S 与 x 的关系式为 (写出自变量的取值范围);
(3)若△APF的面积是△APC 面积的,求此时BP 的长.
图①
图②
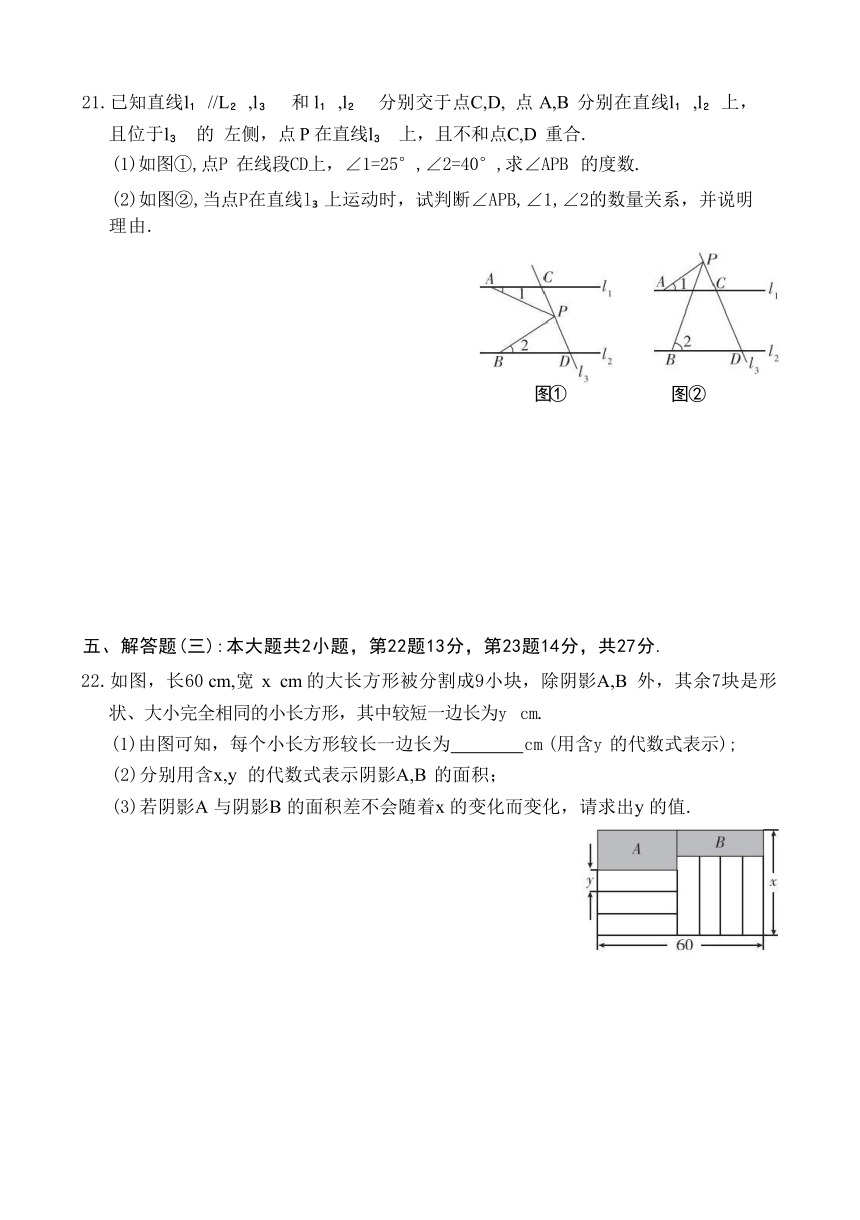
21.已知直线l //L ,l 和 l ,l 分别交于点C,D, 点 A,B 分别在直线l ,l 上,且位于l 的 左侧,点 P 在直线l 上,且不和点C,D 重合.
(1)如图①,点P 在线段CD上,∠1=25°,∠2=40°,求∠APB 的度数.
(2)如图②,当点P在直线l 上运动时,试判断∠APB,∠1,∠2的数量关系,并说明 理由.
(
图
①
)图②
五、解答题(三):本大题共2小题,第22题13分,第23题14分,共27分.
22.如图,长60 cm,宽 x cm 的大长方形被分割成9小块,除阴影A,B 外,其余7块是形 状、大小完全相同的小长方形,其中较短一边长为y cm.
(1)由图可知,每个小长方形较长一边长为 cm (用含y 的代数式表示);
(2)分别用含x,y 的代数式表示阴影A,B 的面积;
(3)若阴影A 与阴影B 的面积差不会随着x 的变化而变化,请求出y 的值.
23. (1)如图①,△ACB 和△DCE均为等边三角形,当△DCE 旋转至点A,D,E 在同一直线上 时,连接BE.填空:∠AEB的度数为 ;线段AD,BE 之间的数量关系为
(2)如图②,△ACB 和△DCE 均为等腰三角形,∠ACB=∠DCE=90°, 点 A,D,E 在同 一直线上,CM 为△DCE 中 DE 边上的高,连接 BE. 请判断∠AEB 的度数及线段 CM, AE,BE 之间的数量关系,并说明理由.
(3)若图①中的△DCE 绕点 C 旋转,点A,D,E 不在同一直线上时,设AD 与 BE 相交 于点0,∠ACD=∠BCE=θ(0°<θ<180°), 尝试在图中探索∠AOE的度数,直接写出结 果,不必说明理由.
图① 图②
期末质量检测卷(二)
1.D 2.D 3.A 4.D 5.C 6.B 7.C 8.B 9.D
10.D【 解析】设△ABC 的面积为x. 因为点D 是AC 边的中点,
所以
因为BC=3CE, 所以
因为S△BEP-S△ADr=6,S△BEP=S△BCD-S四边形DCEP,
S△ADF=S△AEc-S 四边形DCEF,
所以S△BEF-SADF=(S△BCD-S四边形DCe)-(S△AEC-S四边形DCEF)= S△BCD-S△AEc=6.
所以解得 x=36.
所以△ABC的面积为36.
11.小 12.4 13.8 14.64°
15.2或5【解析】因为∠ACB=90°, 所以∠A+∠CBD=90° . 因为CD 为AB边上的高,所以∠CDB=90° .
所以∠ BCD+∠CBD=90°.所以∠A=∠BCD.
因为∠ BCD=∠ECF, 所以∠ECF=∠A.
因为过点E 作 BC 的垂线交直线CD于点F,
所以∠CEF=90°=∠ACB.
在△CEF 和△ACB中 ,
所以△CEF≌△ACB(AAS).所以 CE=AC=7cm.
①如图,当点 E 在射线BC 上运动时, BE=CE+BC=7+3=10(cm),
因为点E 在直线 BC 上以2cm/s 的速 度运动,
所以点 E 运动了10÷2=5(s);
②如图,当点E 在射线 CB 上运动时,
BE'=CE'-BC=7-3=4(cm),
因为点E 在直线 BC 上以2cm/s 的速度运动, 所以点 E 运动了4÷2=2(s).
综上所述,当点E 运动5s 或 2s 时 ,CF=AB.
16.解:原
=0.
17.解:原式=4a +4ab+b -(2a +2ab-ab-b )-2(a -4b )
=4a +4ab+b -2a -ab+b -2a +8b
=3ab+10b .
当 ,b=-2 时,原式=-3+40=37.
18.解:乙赢得这个游戏的可能性更大.理由如下:
因为共有10种等可能的结果,其中“大于6的数”的有 4种,“不大于6的数”的有6种,
所以 P(甲赢),P (乙赢)
因为
所以乙赢得这个游戏的可能性更大.
19.解:(1)如图,△A'B'C′ 即为所求.
(2)如图,点D 即为所求.
因为点B 与点B'关于MN对称,
所以∠BDM=∠B'DM
因为∠ CDN=∠B'DM,
所以∠ BDM=∠CDN.
(3)如图,AE即为所求.
20.解:(1)4
(2)S=12-2x(0≤x≤6)
(3)因为 AB=AC,AF⊥BC,BC=6, 所以
因为 , 所 由题意可知,当0≤x<3 时 ,PF=3-x,
则- ,解得: 当3≤x≤6 时 ,PF=x-3,
),解得:
综上所述,当△APF的面积是△APC 面积的时,BP 的长
或
21.解:(1)如图①,过点P 作 PE//L, 则∠1=∠APE.
因为l //L , 所以 PE//L .
所以∠2=∠BPE.
因为∠ APB=∠APE+∠BPE, 所以∠APB=∠1+∠2.
因为∠1=25°,∠2=40°, 所以∠APB=25°+40°=65° .
(2)①当点P 在 l 的上方时,∠2=∠1+∠APB.理由 如下:
过点 P 作PE//L , 如图②,则∠1=∠APE.
因为l //L , 所以 PE//L . 所以∠2=∠ BPE,
因为∠ BPE=∠APE+∠APB, 所以∠2=∠1+∠APB.
图②
②当点P 在线段 CD上时,由(1),可得∠APB=∠1+∠2.
③当点P 在l 的下方时,∠1=∠2+∠APB.理由如下:
过点 P 作PE//L , 如图③,则∠1=∠APE 因为LI //L ,所以PE//L .
所以∠2=∠BPE.
因为∠ APE=∠BPE+∠APB,
所以∠1=∠2+∠APB. 图③
22.解:(1)(60-4y)
(2)根据题意,可得阴影 A 的长为(60-4y)cm, 宽 为 (x-3y)cm,
阴影 B 的长为4y cm,宽为[x-(60-4y)]cm,
所以S =(60-4y)(x-3y)=12y -4xy-180y+60x(cm ), S =4y[x-(60-4y)]=4xy-240y+16y (cm ).
(3)由(2),得 S -S =(12y -4xy-180y+60x)-(4xy- 240y+16y )
=12y -4xy-180y+60x-4xy+
240y-16y
=-4y -8xy+60y+60x =(60x-8xy)+60y-4y =x(60-8y)+60y-4y .
因为它们的面积差不会随着x 的变化而变化,
所以60-8y=0. 解得
23. 解:(1)60° AD=BE
(2)∠AEB=90°,AE=BE+2CM. 理由如下:
因为△ACB 和△DCE均为等腰直角三角形, 所以 CA=CB,CD=CE, ∠ACB=∠DCE=90°.
所以∠ ACD=∠BCE.
所以△ACD≌△BCE(SAS).
所以 AD=BE,∠ADC=∠BEC.
因为△DCE为等腰直角三角形,
所以∠ CDE=∠CED=45°.
因为点A,D,E 在同一直线上,
所以∠ADC=135°. 所以∠BEC=135°.
所以∠AEB=∠BEC-∠CED=90°.
因为 CM为△DCE 中DE 边上的高,
所以∠ CDM=∠ECM=∠DCM=∠CEM=45°,DM=EM. 因为DC=CE, 所以△DCM≌△CEM(SAS).
所以 DM=CM=EM.
所以AE=AD+DE=BE+2CM.
(3)∠AOE 的度数是60°或120°. [提示]如图③ .
由(1)知△ACD≌△BCE, 所以∠CAD=∠CBE.
因为∠ CAB=∠CBA=60°, 所以∠OAB+∠OBA=120° .
所以∠AOE=180°-120°=60° . 如图④.
同理求得∠AOB=60°, 所以∠AOE=120° .
所以∠AOE的度数是60°或120°.
题号 一 二 三 四 五 总分
得分
一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有 一项是符合题目要求的.
1.“谁知盘中餐,粒粒皆辛苦”.已知一粒米的质量约0.000021kg,则数据0.000021用 科学记数法表示为 ( ) A.0.21×10-4 B.2.1×10-4 C.21×10-8 D.2.1×10-5
2.我国新能源汽车发展势头迅猛,以下汽车车标融入了数学几何元素,其中是轴对称图 形的是 ( )
A B C D
3.如图,直线AD//BC,BA⊥AC 于点A.若∠2=55°,则∠1为 ( )
A.35° B.45° C.55° D.25°
第3题图 第6题图
4.计算 的结果是 ( )
B D
5.一个不透明的袋子里装有2个白球、3个红球,除颜色外,其余如材料、大小、质量等完 全相同.随机从中抽出一个球,抽到红球的概率是 ( )
B. D
6.如图,E,F 分别是AB,CD上的点,G是BC 延长线上一点,且∠B=∠DCG=∠D, 则下列结 论不一定成立的是 ( )
A. ∠AEF=∠EFC B. ∠EFD=∠BCF
C. ∠A=∠BCF D. ∠BEF+∠EFC=180°
7.小颖在网上获取了声音在空气中传播的速度y 与空气温度x 的关系的一些数据 并制成如下表格,则下列说法错误的是 ( )
温度x/℃ -20 -10 0 10 20 30
声速y/(m/s) 318 324 330 336 342 348
A.在这个变化中,自变量是温度,因变量是声速
B. 在-20℃~30℃范围内,温度越高,声速越快
C. 温度每升高10℃,声速提高8m/s
D. 当空气温度为10℃时,声音在5s 内可传1680 m
8.如图,在△ABC 中 ,DE 是AC 的垂直平分线,△ABC 的周长为17 cm, 且△ABD 的周长 为11 cm,则 CE 的长为 ( ) A.6cm B.3 cm C.2 cm D.1 cm
第8题图 第9题图 第 1 0 题 图
9.如图,以△ABC的顶点A为圆心,以BC 长为半径作弧;再以顶点C 为圆心,以AB 长为 半径作弧,两弧交于点D, 连接AD,CD.若∠B=65°, 则∠BCD的大小为 ( ) A.65° B.130° C.120° D.115°
10.如图,E 是△ABC中 BC 边上的一点,且 BC=3CE, 点 D 是 AC 边的中点.若S△BEF- S△ADF=6,则 SABC 等于 ( ) A.18 B.24 C.30 D.36
二、填空题:本大题共5小题,每小题3分,共15分.
11.有4根小棒,长度分别是1cm,6 cm,7 cm,8 cm,从中任取3根,能围成三角形的可能 性比不能围成三角形的可能性 (填“大”或“小”).
12. 如图,在Rt△ABC中,∠A=90°,BD 是△ABC的角平分线.若AD=4, 则 点D 到 BC 的
距离是
第12题图 第14题图 第15题图
13.已 知 5x-2y-3=0, 则32*÷4=
14.如图,将一张长方形纸条折叠,若∠1=52°,则∠2的度数为
15. 如图,在△ABC中,∠ACB=90°,AC=7 cm,BC=3cm,CD 为AB边上的高,点 E 从点B 出发,在直线BC 上以2cm/s 的速度运动,过点E 作 BC 的垂线交直线 CD于点F. 当 点 E 运动 s 时 ,CF=AB.
三、解答题(一):本大题共3小题,每小题7分,共21分.
16.计算:
17.化简并求值:(2a+b) -(2a-b)(a+b)-2(a-2b)(a+2b),其中 ,b=-2.
18.如图,一个均匀转盘被平均分成10等份,分别标有1,2, …,10这10个数字,转动转 盘,当转盘停止转动时,指针指向的数字即为转出的数字(若指针指向分界处则无效, 需重新转动).两人进行猜数游戏:甲猜“大于6的数”,乙猜“不大于6的数”,谁赢得 这个游戏的可能性更大 请说明理由.
四、解答题(二):本大题共3小题,每小题9分,共27分.
19.如图,已知△ABC 的三个顶点在格点上.
(1)画出△A'B'C′, 使它与△ABC关于直线MN 对称;
(2)在直线MN 上找一点D,使∠BDM=∠CDN, 并说明理由;
(3)尺规作图:过点A 作直线AE,使AE//BC (保留作图痕迹,不写作法).
20.如图①,已知在△ABC 中 ,AB=AC,BC=6,AF 为 BC 边上的高,P 是 BC 上一动点,沿 BC由 B 向 C 运动,连接AP. 在这个变化过程中,设BP=x,△APC 的面积为S, 图②刻 画的是S 随 x 的变化而变化的图象,根据图象回答以下问题:
(1)△ABC 的高 AF 为 ;
(2)S 与 x 的关系式为 (写出自变量的取值范围);
(3)若△APF的面积是△APC 面积的,求此时BP 的长.
图①
图②
21.已知直线l //L ,l 和 l ,l 分别交于点C,D, 点 A,B 分别在直线l ,l 上,且位于l 的 左侧,点 P 在直线l 上,且不和点C,D 重合.
(1)如图①,点P 在线段CD上,∠1=25°,∠2=40°,求∠APB 的度数.
(2)如图②,当点P在直线l 上运动时,试判断∠APB,∠1,∠2的数量关系,并说明 理由.
(
图
①
)图②
五、解答题(三):本大题共2小题,第22题13分,第23题14分,共27分.
22.如图,长60 cm,宽 x cm 的大长方形被分割成9小块,除阴影A,B 外,其余7块是形 状、大小完全相同的小长方形,其中较短一边长为y cm.
(1)由图可知,每个小长方形较长一边长为 cm (用含y 的代数式表示);
(2)分别用含x,y 的代数式表示阴影A,B 的面积;
(3)若阴影A 与阴影B 的面积差不会随着x 的变化而变化,请求出y 的值.
23. (1)如图①,△ACB 和△DCE均为等边三角形,当△DCE 旋转至点A,D,E 在同一直线上 时,连接BE.填空:∠AEB的度数为 ;线段AD,BE 之间的数量关系为
(2)如图②,△ACB 和△DCE 均为等腰三角形,∠ACB=∠DCE=90°, 点 A,D,E 在同 一直线上,CM 为△DCE 中 DE 边上的高,连接 BE. 请判断∠AEB 的度数及线段 CM, AE,BE 之间的数量关系,并说明理由.
(3)若图①中的△DCE 绕点 C 旋转,点A,D,E 不在同一直线上时,设AD 与 BE 相交 于点0,∠ACD=∠BCE=θ(0°<θ<180°), 尝试在图中探索∠AOE的度数,直接写出结 果,不必说明理由.
图① 图②
期末质量检测卷(二)
1.D 2.D 3.A 4.D 5.C 6.B 7.C 8.B 9.D
10.D【 解析】设△ABC 的面积为x. 因为点D 是AC 边的中点,
所以
因为BC=3CE, 所以
因为S△BEP-S△ADr=6,S△BEP=S△BCD-S四边形DCEP,
S△ADF=S△AEc-S 四边形DCEF,
所以S△BEF-SADF=(S△BCD-S四边形DCe)-(S△AEC-S四边形DCEF)= S△BCD-S△AEc=6.
所以解得 x=36.
所以△ABC的面积为36.
11.小 12.4 13.8 14.64°
15.2或5【解析】因为∠ACB=90°, 所以∠A+∠CBD=90° . 因为CD 为AB边上的高,所以∠CDB=90° .
所以∠ BCD+∠CBD=90°.所以∠A=∠BCD.
因为∠ BCD=∠ECF, 所以∠ECF=∠A.
因为过点E 作 BC 的垂线交直线CD于点F,
所以∠CEF=90°=∠ACB.
在△CEF 和△ACB中 ,
所以△CEF≌△ACB(AAS).所以 CE=AC=7cm.
①如图,当点 E 在射线BC 上运动时, BE=CE+BC=7+3=10(cm),
因为点E 在直线 BC 上以2cm/s 的速 度运动,
所以点 E 运动了10÷2=5(s);
②如图,当点E 在射线 CB 上运动时,
BE'=CE'-BC=7-3=4(cm),
因为点E 在直线 BC 上以2cm/s 的速度运动, 所以点 E 运动了4÷2=2(s).
综上所述,当点E 运动5s 或 2s 时 ,CF=AB.
16.解:原
=0.
17.解:原式=4a +4ab+b -(2a +2ab-ab-b )-2(a -4b )
=4a +4ab+b -2a -ab+b -2a +8b
=3ab+10b .
当 ,b=-2 时,原式=-3+40=37.
18.解:乙赢得这个游戏的可能性更大.理由如下:
因为共有10种等可能的结果,其中“大于6的数”的有 4种,“不大于6的数”的有6种,
所以 P(甲赢),P (乙赢)
因为
所以乙赢得这个游戏的可能性更大.
19.解:(1)如图,△A'B'C′ 即为所求.
(2)如图,点D 即为所求.
因为点B 与点B'关于MN对称,
所以∠BDM=∠B'DM
因为∠ CDN=∠B'DM,
所以∠ BDM=∠CDN.
(3)如图,AE即为所求.
20.解:(1)4
(2)S=12-2x(0≤x≤6)
(3)因为 AB=AC,AF⊥BC,BC=6, 所以
因为 , 所 由题意可知,当0≤x<3 时 ,PF=3-x,
则- ,解得: 当3≤x≤6 时 ,PF=x-3,
),解得:
综上所述,当△APF的面积是△APC 面积的时,BP 的长
或
21.解:(1)如图①,过点P 作 PE//L, 则∠1=∠APE.
因为l //L , 所以 PE//L .
所以∠2=∠BPE.
因为∠ APB=∠APE+∠BPE, 所以∠APB=∠1+∠2.
因为∠1=25°,∠2=40°, 所以∠APB=25°+40°=65° .
(2)①当点P 在 l 的上方时,∠2=∠1+∠APB.理由 如下:
过点 P 作PE//L , 如图②,则∠1=∠APE.
因为l //L , 所以 PE//L . 所以∠2=∠ BPE,
因为∠ BPE=∠APE+∠APB, 所以∠2=∠1+∠APB.
图②
②当点P 在线段 CD上时,由(1),可得∠APB=∠1+∠2.
③当点P 在l 的下方时,∠1=∠2+∠APB.理由如下:
过点 P 作PE//L , 如图③,则∠1=∠APE 因为LI //L ,所以PE//L .
所以∠2=∠BPE.
因为∠ APE=∠BPE+∠APB,
所以∠1=∠2+∠APB. 图③
22.解:(1)(60-4y)
(2)根据题意,可得阴影 A 的长为(60-4y)cm, 宽 为 (x-3y)cm,
阴影 B 的长为4y cm,宽为[x-(60-4y)]cm,
所以S =(60-4y)(x-3y)=12y -4xy-180y+60x(cm ), S =4y[x-(60-4y)]=4xy-240y+16y (cm ).
(3)由(2),得 S -S =(12y -4xy-180y+60x)-(4xy- 240y+16y )
=12y -4xy-180y+60x-4xy+
240y-16y
=-4y -8xy+60y+60x =(60x-8xy)+60y-4y =x(60-8y)+60y-4y .
因为它们的面积差不会随着x 的变化而变化,
所以60-8y=0. 解得
23. 解:(1)60° AD=BE
(2)∠AEB=90°,AE=BE+2CM. 理由如下:
因为△ACB 和△DCE均为等腰直角三角形, 所以 CA=CB,CD=CE, ∠ACB=∠DCE=90°.
所以∠ ACD=∠BCE.
所以△ACD≌△BCE(SAS).
所以 AD=BE,∠ADC=∠BEC.
因为△DCE为等腰直角三角形,
所以∠ CDE=∠CED=45°.
因为点A,D,E 在同一直线上,
所以∠ADC=135°. 所以∠BEC=135°.
所以∠AEB=∠BEC-∠CED=90°.
因为 CM为△DCE 中DE 边上的高,
所以∠ CDM=∠ECM=∠DCM=∠CEM=45°,DM=EM. 因为DC=CE, 所以△DCM≌△CEM(SAS).
所以 DM=CM=EM.
所以AE=AD+DE=BE+2CM.
(3)∠AOE 的度数是60°或120°. [提示]如图③ .
由(1)知△ACD≌△BCE, 所以∠CAD=∠CBE.
因为∠ CAB=∠CBA=60°, 所以∠OAB+∠OBA=120° .
所以∠AOE=180°-120°=60° . 如图④.
同理求得∠AOB=60°, 所以∠AOE=120° .
所以∠AOE的度数是60°或120°.
同课章节目录
