江苏省淮阴中学、丹阳中学等G4联盟2025届高三下学期4月阶段检测数学试卷(PDF版,含答案)
文档属性
| 名称 | 江苏省淮阴中学、丹阳中学等G4联盟2025届高三下学期4月阶段检测数学试卷(PDF版,含答案) |  | |
| 格式 | |||
| 文件大小 | 435.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-09 15:52:59 | ||
图片预览



文档简介
2025年数学学科调研测试试卷
注意事项:
1.答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考生号,试室号,座位号填写在答题
卡上。用 2B铅笔将试卷类型和考生号填涂在答题卡相应位置上。
2.选择题每小题选出答案后,用 2B铅笔把答题卡上对应的题目选项的答案信息点涂黑;如需改动,用
橡皮擦干净后,再填涂其他答案。答案不能答在试卷上。
3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置
上;如需改动,先划掉原来的答案,然后再写上新的答案,公众号:MST数学聚集地MathHUB不准使用铅笔和
涂改液。不按以上要求作答的答案无效。
一、单选题:本题共 8小题,每小题 5分,共 40分,每小题只有一个选项符合要求
1.已知集合U= -2,-1,0,1,2,3 ,A= -1,0,1 ,B= 1,2 ,则CU A∪B = ( )
A. -2,3 B. -2,2,3 C. -2,-1,0,3 D. -2,-1,0,2,3
2.在复平面内, 2+ i -1+ i 对应的点位于= ( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
3. 1+ sin2θ已知 θ为第四象限角,sinθ+ 2cosθ= 0,则 ( )
sinθ+cosθ
A. 5 B. - 5 C. 2 5 D. - 2 55 5 5 5
2
4. x若双曲线C1与双曲线C2: 4 - y
2= 1的渐近线相同,且过点 2, 2 ,则双曲线C1的方程为 ( )
y2 2 2 y2
A. 24 - x = 1 B. y
2- x4 = 1 C.
x
2 - 2 = 1 D. x
2- 32 y
2= 1
a +a
5.已知 p:数列 an 满足:对任意的 k∈N *,n∈N *,n> k,都有 an= n+k n-k2 ,q:数列 an 是等差数列.
则 p是 q的 ( )
A. 充分不必要条件 B. .必要不充分条件 C. 充要条件 D. 既不充分也不必要条件
6.已知 α,β为平面 a,b为直线,下列说法四确的是 ( )
A. 若直线 a,b与平面 α所成角相等,则 a b
B. 若 a,b α,且 a β,b β,则 α β
C. 若 α⊥ β,α∩ β= l,a α,b β,若 a,b均不垂直于 l,则 a,b不垂直
D. 若 α⊥ β,a α,b β,b⊥ a,则 b β
7.如图,平面内有A,B,C,D 4个区域,可以对任意两个区域进行连线,(任意两个区域只能连一条线),现随
机连 3条线,则从A,B,C,D任何一个区域都可以到达其它区域的概率为 ( )
A. 15 B.
3
4
C. 3
A B
5 D.
4
5
C D
8.若函数 f(x) = ax- 21-x+ 1(a> 0)存在两个不同的零点,则实数 a的取值范围为 ( )
A. 0, 1 1 1 1 1 1 1 14 ∪ 4 , 2 B. 0, 4 ∪ 2 ,1 C. 4 , 2 D. 2 ,1
二、多选题:本题共 3小题,每小题 6分,共 18分。在每小题给出的四个选项中,有多项符合题目要求。全
部选对的得 6分,部分选对的得部分分,有选错的得 0分。
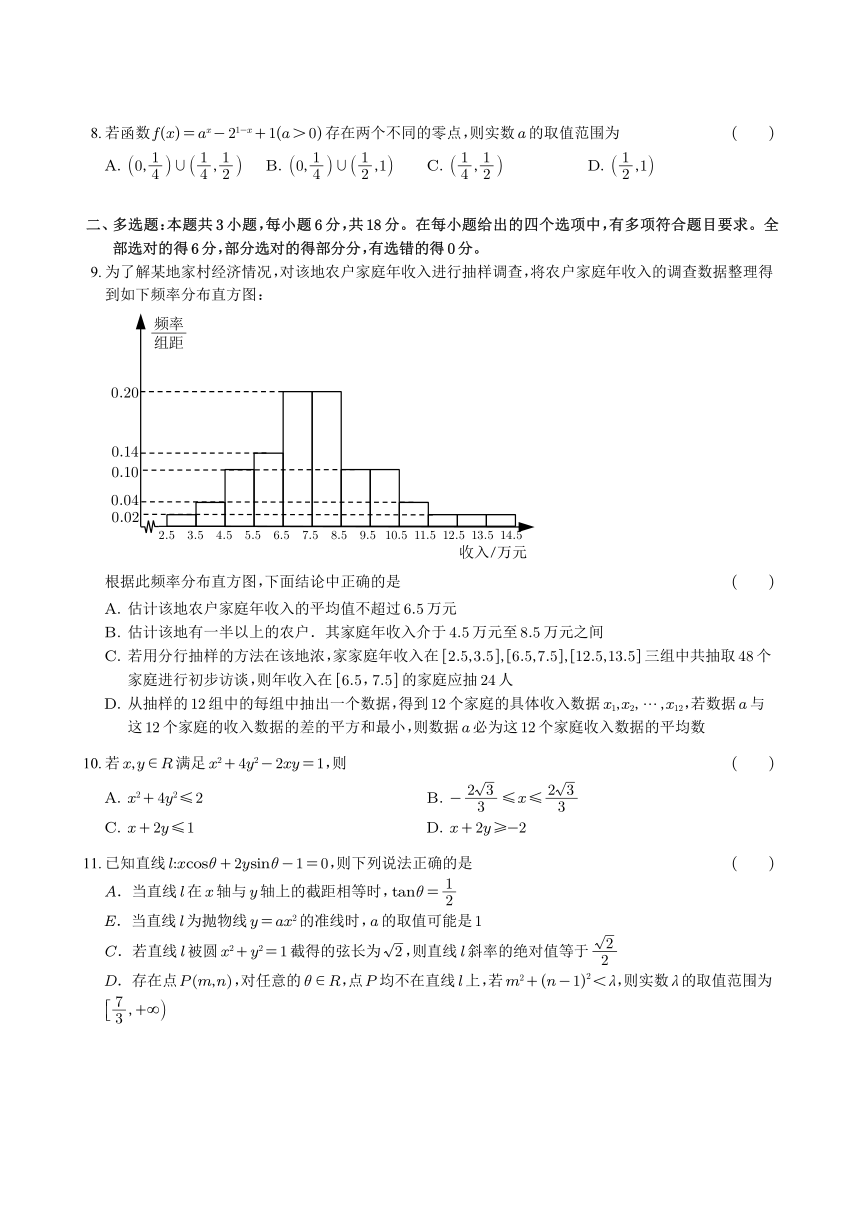
9.为了解某地家村经济情况,对该地农户家庭年收入进行抽样调查,将农户家庭年收入的调查数据整理得
到如下频率分布直方图:
频率
组距
0.20
0.14
0.10
0.04
0.02
2.5 3.5 4.5 5.5 6.5 7.5 8.5 9.5 10.5 11.5 12.5 13.5 14.5
收入 /万元
根据此频率分布直方图,下面结论中正确的是 ( )
A. 估计该地农户家庭年收入的平均值不超过 6.5万元
B. 估计该地有一半以上的农户.其家庭年收入介于 4.5万元至 8.5万元之间
C. 若用分行抽样的方法在该地浓,家家庭年收入在 [2.5,3.5], 6.5,7.5 , 12.5,13.5 三组中共抽取 48个
家庭进行初步访谈,则年收入在 [6.5,7.5]的家庭应抽 24人
D. 从抽样的 12组中的每组中抽出一个数据,得到 12个家庭的具体收入数据 x1,x2, ,x12,若数据 a与
这 12个家庭的收入数据的差的平方和最小,则数据 a必为这 12个家庭收入数据的平均数
10.若 x,y∈R满足 x2+ 4y2- 2xy= 1,则 ( )
A. x2+ 4y2≤ 2 B. - 2 33 ≤ x≤
2 3
3
C. x+ 2y≤ 1 D. x+ 2y≥-2
11.已知直线 l:xcosθ+ 2ysinθ- 1= 0,则下列说法正确的是 ( )
A.当直线 l在 x轴与 y 1轴上的截距相等时,tanθ= 2
E.当直线 l为抛物线 y= ax2的准线时,a的取值可能是 1
C.若直线 l被圆 x2+ y2= 1 2截得的弦长为 2,则直线 l斜率的绝对值等于 2
D.存在点P m,n ,对任意的 θ∈R,点P均不在直线 l上,若m2+ (n- 1)2< λ,则实数 λ的取值范围为
7 3 ,+∞
三、填空题:本题共 3小题,每小题 5分,共 15分
4
12.在 x3+ 1x 的展开式中,常数项为 .
13.已知正三棱柱所有棱长都相等,它的六个顶点都在半径为 7的球面上,则此正三棱柱的体积为 .
14.已知函数 f x 为R上的奇函数,f x 在 0,+∞ 上单调递增, x> 0 f(x) + 2都有 x > 0且
f x f f x + 2x = 1,则 f sinx 的值域为 .
四、解答题:本题共 5小题,共 77分,解答应写出文字说明,证明过程或演算步骤
15. (本题满分 13分)
斜三棱柱ABC-A1B1C1中,所有棱长都为 2,∠A1AC= 60°,平面AA1C1C⊥平面ABC.
(1)若D为CC1中点,E点在线段BC上,且BE= 2EC,求证:A1B 平面ADE;
(2)求二面角A1-AB-C的正弦值.
A1 C1
B1
D
A C
E
B
16. (本题满分 15分)
已知在ΔABC中,角A,B,C的对边分别为 a,b,c,满足 2a-b tanB= btanC,2sin A-C = sinB.
(1)求角C的大小及 sinA的值;
(2)设AB= 5,求ΔABC的面积.
17. (本题满分 15分)
= ln(2x+1), x≥0已知 f x ax2+2x-1, x<0
(1)设函数 f x 在原点处的切线方程为 y= g x ,当 x< 0时,f x ≤ 2g x ,求实数 a的取值范围;
(2)若函数 f x 的图象上存在两点关于原点对称,求实数 a的取值范围.
18. (本题满分 17分)
2 y2
E: x - = 1(a> b> 0) 2 , 3 2椭圆 2 2 过点 2 2 ,离心率为 2 .过原点的直线 l交椭圆于A,B两点,a b
点C,D在椭圆E上,且满足AB= 2CD,设直线AC与BD交于点F.
(1)求椭圆E的方 ;
(2)求点F的轨迹方程;
(3)设直线AB与点F的轨迹交于M ,N两点,求证:ΔMNF的面积为定值.
19. (本题满分 17分)
已知一个袋子中有 x个红球,y个黑球, x,y∈N *,y≥2 ,这些球除颜色外完全相同.
(1)当 x= 1,y= 2时,甲乙两人进行摸球比赛,某人摸球时,从袋子中摸出一个球,记下颜色后放回袋中;
摸到红球得一分,否则对方得一分 (记为一次摸球);甲乙轮流依次摸球,甲先摸,规定当一方比另外一方
多 2分时胜出,比赛结束.
①求第 6次摸球后比赛结束,且甲乙共摸到 3次红球的概率;
②若规定甲乙摸球次数的总和达到 2n n≥2,n∈N * 时也停止比赛,设随机变量X为比赛结束时的摸
球次数,写出随机变量X的分布列,并求E X .
(2)将口袋中的球随机逐个取出,并放入编号为 1,2,3, ,x+ y的盆子中,其中第 k次取出的球放入编号
为 k k=1,2,3, ,x+y 的盒子,随机变量X表示最后一个取出的黑球所在的编号的倒数,当 x> y时,
E(X)< 1求证: .
2(y-1)
参考答案
1.A 2.B 3.B 4.B 5.C 6.C 7.D 8.A
9.BD 10.ABD 11.ACD
12. 4 13. 18 14. 0 1,+∞
15. (1)连结A1C,交AD于F,连结EF,因为棱柱中AA1 CC1,AA1=CC1,且D是CC1中点,所以
CD AA1,且AA1= 2CD,所以A1F= 2FC
A1 C1
B1
F D
A C
E
B
又因为BE= 2EC CF CE,所以 =
FA1 EB
= 2,所以EF A1B
又因为A1B不在平面ADE内,EF在平面ADE内,所以A1B 面ADE.
(2)法一:公众号:MST数学聚集地MathHUB
取A的中点H,因为AA1=AC,∠A1AC= 60°,所以A1C= 2,所以A1H⊥AC,BH⊥AC,
所以A1H⊥平ABC
以 HB,HC,HA1 为正交基底建立如图所示空间直角坐标系,设二面角A1-AB-C的平面角为 α
z
A1 C1
B1
F D
C
A
E y
B
x
则A 0,-1,1 ,B 3,0,0 ,A1 0,0, 3 ,所以AB= 3,1,0 ,AA1= 0,1, 3 ,
3x+y=0
设平面A1AB的法向量为n= x,y,z ,则 + = ,取 x= 1,y=- 3 ,z= 1,则n=y 3z 0 1,- 3,1
平面ABC的一个法向量为n0= 0,0,1
1 2 5
则 cos n,n0 = ,所以 sinα= 1-cos2 n,n5 0 = 5
法二:作A1H⊥AC于H,作HG⊥AB于G
因为平面AA1C1C⊥平面ABC,且交线为AC,A1H⊥AC,A1H在平面ABC内
所以A1H⊥平面ABC
又因为AB在平面ABC内,所以A1H⊥AB
因为AB⊥HG,A1H⊥AB,A1H∩HG=H,A1H,HG都在平面A1GH内
所以AB⊥平面A1GH,所以AB⊥A1G,因为AB⊥A1G,HG⊥AB,所以∠A1GH是所求二面角的平面角
A1H⊥AC,∠A1AH= 60°,则AH= 1,A1H= 3
AG⊥GH,∠HAG≡ 60°,AH= 1,所以GH= 32
A H
所以 tan∠A 11GH= = 2 2 5,所以所求二面角的正弦值为 .GH 5
16. (1)因为 2a-b tanB= btanC sinB sinC,所以 2sinA-sinB cosB = sinB cosC
所以 2sinAcosC- sinBcosC = cosB sinC,所以 2 sinAcosC = sinA
因为 sinA≠ 0,所以 cosC= 22 ,因为C∈ 0,π
1
,所以C= 4
因为 2sin A-C = sinB,所以 2sin A-C = sin A+C ,
所以 sinAcosC= 3cosAsinC,所以 tanA= 3tanC= 3.
又因为 sin2A+ cos2A= 1,且A∈ 0,π sinA= 3 10 ,所以 10 .
(2) 1 sinA= 3 10 ,cosA= 10 sinB = sin 3π -A = 2 5由 10 10 ,所以 4 5
AB = AC因为 sinB ,所以AC= 2 10.sinC
1
所以面积为 2 bcsinA= 15.
17. (1)f ' 2 x = 2x+1 ,f ' 0 = 2,f 0 = 0
所以 g x = 2x.公众号:MST数学聚集地MathHUB
所以 ax2+ 2x- 1≤ 4x对任意 x< 0成立, ax2- 2x- 1≤ 0
a≤ 1 + 22 x (x< 0),求得 a≤-1.x
2 问题等价于 ln 2x+1 + ax2- 2x- 1= 0在 x> 0上有解
2 2x= + + - - ' =
2ax+a-2
令 h x ln 2x 1 ax 2x 1,h x 2x+1
① a≤ 0时,h' x ≤ 0,h x 单调递减,h 0 =-1,所以 h x < 0,不符合题意
② a≥ 2时,h' x ≥ 0,h x 单调递增,h 0 =-1< 0,h 10 = ln21+ 100a- 21> 0,所以 h x 在 x> 0上
有一个零点,符合题意
③ 0< a< 2 2-a 2-a时,h x 在 0, 2a 递减, 2a ,+∞ 递增,
h 0 =-1< 0 h 1+ 1+a, a +e > 0,所以 h x 在 x> 0上有一个零点,符合题意
综上 a> 0
18.
1
1 2 +
3
2 = 1,
c = 2 2 2 2a 2 ,则 a= 2c,b = a - c = c
2
2a 4b
1 + 3 = 1 c= 1 E x
2
所以 2 2 ,则 ,所以 :
2
4c 4c 2
+ y = 1
( ) , , , x+x0 , y+y0 , x-x0 , y-y2 设A x 00 y0 F x y ,则C 2 2 D 2 2
x-x 2 y-y 2 x+x 2 y+y 20
所以 8 +
0 = , 0 + 0 4 1① 8 4 = 1②
由①②得 x2+ 2y2+ x2+ 2y2= 8,又因为 x20 0 0+ 2y20= 2
2 2
所以 x2+ 2y2= 6 x + y6 3 = 1为轨迹F点的方程.
3 设CD:y= kx+ b k存在时
y=kx+b
2 22+ 2= 1+2k x + 4kbx+ 2 b
2-1
x 2y 2
= 0
Δ= 16k2b2- 8(1+ 2k2) (b2- 1)> 0得 b2< 1+ 2k2
2 b2-1
x1+ x2= -4kb ,
x
1+2k2 1
x2= 1+2k2
2
则 CD = 1+k2 x1-x = 2 2 1+k2 2 2k
2+1-b2
1+2k
AB= 2 2 1+k
2
所以 2 2k
2+1,因为 |AB| = 2|CD|
1+2k
所以 2k2+1= 2 2k2+1-b2,则 4b2= 6k2+ 13 ,所以 |b| =
3 1+2k22
b 2
设直线AB与CD 3 1+2k之间的距离为 d0= =
1+k2 2 1+k2
2
所以F点设直线的距离 d= 2d0= 3 1+2k
1+k2
AB:y= y=kxkx 6, x2+ 2= x =2y 0 1+2k2
所以 |MN | = 2 1+k2 |x| = 2 1+k2 6 1,所以S△MNF= 2 AB d= 3 21+2k2
k不存在时,|MN | = 2 3 ,|FO| = 6,所以ΔMNF的面积也为 3 2
19. 1 ①设A为第 6次摸球后比赛结束,且甲乙共摸到 3次红球
P A = 4 1
3
则 3
2 32
3 = 729
②
X 2 4 6 2 n-1 2n
2 n-2 n-1
P 4 5 4 5 4 5 4 59 9 9 9 9 9 9 9
P 4 5 4 5
2 4 5 n-2 4 5 n-1
9 9 9 9 9 9 9 9 7分
2 n-2 n-1
所以E X = 8 9 1+2×
5
9 +3×
5
9 + +
5
n-1 9 + 2n
5
9 .
5 5 2 5 n-2
设Sn= 1+ 2× 9 + 3× 9 + + n-1 9
5 s = 5 + 2× 5
2 n-2 n-1
9 n 9 9 + + n-2
5
9 + n-1
5
9
4 2 n-2 n-1 n-1 n-1
所以 9 Sn= 1+
5
9 +
5 + + 5 - 5 9 5 59 9 n-1 = 1- 9 4 9 - n-1 9
8 9 9 5 n-1 5 n-1
所以 9 Sn= 2 - 2 9 - 2 n-1 9
E X = 9 - 5
n-1
所以 2 2
5
9 , n≥2,n∈N
*
(3)
1 1 1 1
X y y+1 y+t y+x
Cy-1 Cy-1 Cy-1 y-1y-1 y y+1-1
C
P y y y
x+y-1
C yx+y Cx+y Cx+y Cx+y
x Cy-11 x= x+y-1E X 1 1 y-1y+t Cy = y Cx+y-1t=0 x+y Cx+y t=0 y+t
1 y-1 = 1 (y+t-1)! = y+t-1 (y+t-2)! (y+t-2)!因为 y+t Cy+t-1 y+t ( y+t-2 != = 1 y-2
y-1 !t! y-1
C y+t-2
x
所以E(X)< 1 Cy-2 = 1 y-2 y-2 y-2y y+1-2 y (Cy-2+Cy-1 + +Cy+x-2) =(y-1)Cx+y t=0 (y-1)Cx+y
1
Cy-1+Cy-2 y-2 1 y-1 y-2 y-2- y y-1 y-1
+ +Cy+x-2 = y C +C + +C- y-1 y-1 y+x-2 y 1 C x+y y 1 C x+y
= = 1 1 y-1 y-2 1 y-1
y-1 Cy
=
- y
C
y 1 C y+X-2
+Cy+x-2 = C
x+y x+y y-1
x+y-1
Cyx+y
= y ,又因为 x> y所以E(X)< 1
x+y y-1 2(y-1)
注意事项:
1.答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考生号,试室号,座位号填写在答题
卡上。用 2B铅笔将试卷类型和考生号填涂在答题卡相应位置上。
2.选择题每小题选出答案后,用 2B铅笔把答题卡上对应的题目选项的答案信息点涂黑;如需改动,用
橡皮擦干净后,再填涂其他答案。答案不能答在试卷上。
3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置
上;如需改动,先划掉原来的答案,然后再写上新的答案,公众号:MST数学聚集地MathHUB不准使用铅笔和
涂改液。不按以上要求作答的答案无效。
一、单选题:本题共 8小题,每小题 5分,共 40分,每小题只有一个选项符合要求
1.已知集合U= -2,-1,0,1,2,3 ,A= -1,0,1 ,B= 1,2 ,则CU A∪B = ( )
A. -2,3 B. -2,2,3 C. -2,-1,0,3 D. -2,-1,0,2,3
2.在复平面内, 2+ i -1+ i 对应的点位于= ( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
3. 1+ sin2θ已知 θ为第四象限角,sinθ+ 2cosθ= 0,则 ( )
sinθ+cosθ
A. 5 B. - 5 C. 2 5 D. - 2 55 5 5 5
2
4. x若双曲线C1与双曲线C2: 4 - y
2= 1的渐近线相同,且过点 2, 2 ,则双曲线C1的方程为 ( )
y2 2 2 y2
A. 24 - x = 1 B. y
2- x4 = 1 C.
x
2 - 2 = 1 D. x
2- 32 y
2= 1
a +a
5.已知 p:数列 an 满足:对任意的 k∈N *,n∈N *,n> k,都有 an= n+k n-k2 ,q:数列 an 是等差数列.
则 p是 q的 ( )
A. 充分不必要条件 B. .必要不充分条件 C. 充要条件 D. 既不充分也不必要条件
6.已知 α,β为平面 a,b为直线,下列说法四确的是 ( )
A. 若直线 a,b与平面 α所成角相等,则 a b
B. 若 a,b α,且 a β,b β,则 α β
C. 若 α⊥ β,α∩ β= l,a α,b β,若 a,b均不垂直于 l,则 a,b不垂直
D. 若 α⊥ β,a α,b β,b⊥ a,则 b β
7.如图,平面内有A,B,C,D 4个区域,可以对任意两个区域进行连线,(任意两个区域只能连一条线),现随
机连 3条线,则从A,B,C,D任何一个区域都可以到达其它区域的概率为 ( )
A. 15 B.
3
4
C. 3
A B
5 D.
4
5
C D
8.若函数 f(x) = ax- 21-x+ 1(a> 0)存在两个不同的零点,则实数 a的取值范围为 ( )
A. 0, 1 1 1 1 1 1 1 14 ∪ 4 , 2 B. 0, 4 ∪ 2 ,1 C. 4 , 2 D. 2 ,1
二、多选题:本题共 3小题,每小题 6分,共 18分。在每小题给出的四个选项中,有多项符合题目要求。全
部选对的得 6分,部分选对的得部分分,有选错的得 0分。
9.为了解某地家村经济情况,对该地农户家庭年收入进行抽样调查,将农户家庭年收入的调查数据整理得
到如下频率分布直方图:
频率
组距
0.20
0.14
0.10
0.04
0.02
2.5 3.5 4.5 5.5 6.5 7.5 8.5 9.5 10.5 11.5 12.5 13.5 14.5
收入 /万元
根据此频率分布直方图,下面结论中正确的是 ( )
A. 估计该地农户家庭年收入的平均值不超过 6.5万元
B. 估计该地有一半以上的农户.其家庭年收入介于 4.5万元至 8.5万元之间
C. 若用分行抽样的方法在该地浓,家家庭年收入在 [2.5,3.5], 6.5,7.5 , 12.5,13.5 三组中共抽取 48个
家庭进行初步访谈,则年收入在 [6.5,7.5]的家庭应抽 24人
D. 从抽样的 12组中的每组中抽出一个数据,得到 12个家庭的具体收入数据 x1,x2, ,x12,若数据 a与
这 12个家庭的收入数据的差的平方和最小,则数据 a必为这 12个家庭收入数据的平均数
10.若 x,y∈R满足 x2+ 4y2- 2xy= 1,则 ( )
A. x2+ 4y2≤ 2 B. - 2 33 ≤ x≤
2 3
3
C. x+ 2y≤ 1 D. x+ 2y≥-2
11.已知直线 l:xcosθ+ 2ysinθ- 1= 0,则下列说法正确的是 ( )
A.当直线 l在 x轴与 y 1轴上的截距相等时,tanθ= 2
E.当直线 l为抛物线 y= ax2的准线时,a的取值可能是 1
C.若直线 l被圆 x2+ y2= 1 2截得的弦长为 2,则直线 l斜率的绝对值等于 2
D.存在点P m,n ,对任意的 θ∈R,点P均不在直线 l上,若m2+ (n- 1)2< λ,则实数 λ的取值范围为
7 3 ,+∞
三、填空题:本题共 3小题,每小题 5分,共 15分
4
12.在 x3+ 1x 的展开式中,常数项为 .
13.已知正三棱柱所有棱长都相等,它的六个顶点都在半径为 7的球面上,则此正三棱柱的体积为 .
14.已知函数 f x 为R上的奇函数,f x 在 0,+∞ 上单调递增, x> 0 f(x) + 2都有 x > 0且
f x f f x + 2x = 1,则 f sinx 的值域为 .
四、解答题:本题共 5小题,共 77分,解答应写出文字说明,证明过程或演算步骤
15. (本题满分 13分)
斜三棱柱ABC-A1B1C1中,所有棱长都为 2,∠A1AC= 60°,平面AA1C1C⊥平面ABC.
(1)若D为CC1中点,E点在线段BC上,且BE= 2EC,求证:A1B 平面ADE;
(2)求二面角A1-AB-C的正弦值.
A1 C1
B1
D
A C
E
B
16. (本题满分 15分)
已知在ΔABC中,角A,B,C的对边分别为 a,b,c,满足 2a-b tanB= btanC,2sin A-C = sinB.
(1)求角C的大小及 sinA的值;
(2)设AB= 5,求ΔABC的面积.
17. (本题满分 15分)
= ln(2x+1), x≥0已知 f x ax2+2x-1, x<0
(1)设函数 f x 在原点处的切线方程为 y= g x ,当 x< 0时,f x ≤ 2g x ,求实数 a的取值范围;
(2)若函数 f x 的图象上存在两点关于原点对称,求实数 a的取值范围.
18. (本题满分 17分)
2 y2
E: x - = 1(a> b> 0) 2 , 3 2椭圆 2 2 过点 2 2 ,离心率为 2 .过原点的直线 l交椭圆于A,B两点,a b
点C,D在椭圆E上,且满足AB= 2CD,设直线AC与BD交于点F.
(1)求椭圆E的方 ;
(2)求点F的轨迹方程;
(3)设直线AB与点F的轨迹交于M ,N两点,求证:ΔMNF的面积为定值.
19. (本题满分 17分)
已知一个袋子中有 x个红球,y个黑球, x,y∈N *,y≥2 ,这些球除颜色外完全相同.
(1)当 x= 1,y= 2时,甲乙两人进行摸球比赛,某人摸球时,从袋子中摸出一个球,记下颜色后放回袋中;
摸到红球得一分,否则对方得一分 (记为一次摸球);甲乙轮流依次摸球,甲先摸,规定当一方比另外一方
多 2分时胜出,比赛结束.
①求第 6次摸球后比赛结束,且甲乙共摸到 3次红球的概率;
②若规定甲乙摸球次数的总和达到 2n n≥2,n∈N * 时也停止比赛,设随机变量X为比赛结束时的摸
球次数,写出随机变量X的分布列,并求E X .
(2)将口袋中的球随机逐个取出,并放入编号为 1,2,3, ,x+ y的盆子中,其中第 k次取出的球放入编号
为 k k=1,2,3, ,x+y 的盒子,随机变量X表示最后一个取出的黑球所在的编号的倒数,当 x> y时,
E(X)< 1求证: .
2(y-1)
参考答案
1.A 2.B 3.B 4.B 5.C 6.C 7.D 8.A
9.BD 10.ABD 11.ACD
12. 4 13. 18 14. 0 1,+∞
15. (1)连结A1C,交AD于F,连结EF,因为棱柱中AA1 CC1,AA1=CC1,且D是CC1中点,所以
CD AA1,且AA1= 2CD,所以A1F= 2FC
A1 C1
B1
F D
A C
E
B
又因为BE= 2EC CF CE,所以 =
FA1 EB
= 2,所以EF A1B
又因为A1B不在平面ADE内,EF在平面ADE内,所以A1B 面ADE.
(2)法一:公众号:MST数学聚集地MathHUB
取A的中点H,因为AA1=AC,∠A1AC= 60°,所以A1C= 2,所以A1H⊥AC,BH⊥AC,
所以A1H⊥平ABC
以 HB,HC,HA1 为正交基底建立如图所示空间直角坐标系,设二面角A1-AB-C的平面角为 α
z
A1 C1
B1
F D
C
A
E y
B
x
则A 0,-1,1 ,B 3,0,0 ,A1 0,0, 3 ,所以AB= 3,1,0 ,AA1= 0,1, 3 ,
3x+y=0
设平面A1AB的法向量为n= x,y,z ,则 + = ,取 x= 1,y=- 3 ,z= 1,则n=y 3z 0 1,- 3,1
平面ABC的一个法向量为n0= 0,0,1
1 2 5
则 cos n,n0 = ,所以 sinα= 1-cos2 n,n5 0 = 5
法二:作A1H⊥AC于H,作HG⊥AB于G
因为平面AA1C1C⊥平面ABC,且交线为AC,A1H⊥AC,A1H在平面ABC内
所以A1H⊥平面ABC
又因为AB在平面ABC内,所以A1H⊥AB
因为AB⊥HG,A1H⊥AB,A1H∩HG=H,A1H,HG都在平面A1GH内
所以AB⊥平面A1GH,所以AB⊥A1G,因为AB⊥A1G,HG⊥AB,所以∠A1GH是所求二面角的平面角
A1H⊥AC,∠A1AH= 60°,则AH= 1,A1H= 3
AG⊥GH,∠HAG≡ 60°,AH= 1,所以GH= 32
A H
所以 tan∠A 11GH= = 2 2 5,所以所求二面角的正弦值为 .GH 5
16. (1)因为 2a-b tanB= btanC sinB sinC,所以 2sinA-sinB cosB = sinB cosC
所以 2sinAcosC- sinBcosC = cosB sinC,所以 2 sinAcosC = sinA
因为 sinA≠ 0,所以 cosC= 22 ,因为C∈ 0,π
1
,所以C= 4
因为 2sin A-C = sinB,所以 2sin A-C = sin A+C ,
所以 sinAcosC= 3cosAsinC,所以 tanA= 3tanC= 3.
又因为 sin2A+ cos2A= 1,且A∈ 0,π sinA= 3 10 ,所以 10 .
(2) 1 sinA= 3 10 ,cosA= 10 sinB = sin 3π -A = 2 5由 10 10 ,所以 4 5
AB = AC因为 sinB ,所以AC= 2 10.sinC
1
所以面积为 2 bcsinA= 15.
17. (1)f ' 2 x = 2x+1 ,f ' 0 = 2,f 0 = 0
所以 g x = 2x.公众号:MST数学聚集地MathHUB
所以 ax2+ 2x- 1≤ 4x对任意 x< 0成立, ax2- 2x- 1≤ 0
a≤ 1 + 22 x (x< 0),求得 a≤-1.x
2 问题等价于 ln 2x+1 + ax2- 2x- 1= 0在 x> 0上有解
2 2x= + + - - ' =
2ax+a-2
令 h x ln 2x 1 ax 2x 1,h x 2x+1
① a≤ 0时,h' x ≤ 0,h x 单调递减,h 0 =-1,所以 h x < 0,不符合题意
② a≥ 2时,h' x ≥ 0,h x 单调递增,h 0 =-1< 0,h 10 = ln21+ 100a- 21> 0,所以 h x 在 x> 0上
有一个零点,符合题意
③ 0< a< 2 2-a 2-a时,h x 在 0, 2a 递减, 2a ,+∞ 递增,
h 0 =-1< 0 h 1+ 1+a, a +e > 0,所以 h x 在 x> 0上有一个零点,符合题意
综上 a> 0
18.
1
1 2 +
3
2 = 1,
c = 2 2 2 2a 2 ,则 a= 2c,b = a - c = c
2
2a 4b
1 + 3 = 1 c= 1 E x
2
所以 2 2 ,则 ,所以 :
2
4c 4c 2
+ y = 1
( ) , , , x+x0 , y+y0 , x-x0 , y-y2 设A x 00 y0 F x y ,则C 2 2 D 2 2
x-x 2 y-y 2 x+x 2 y+y 20
所以 8 +
0 = , 0 + 0 4 1① 8 4 = 1②
由①②得 x2+ 2y2+ x2+ 2y2= 8,又因为 x20 0 0+ 2y20= 2
2 2
所以 x2+ 2y2= 6 x + y6 3 = 1为轨迹F点的方程.
3 设CD:y= kx+ b k存在时
y=kx+b
2 22+ 2= 1+2k x + 4kbx+ 2 b
2-1
x 2y 2
= 0
Δ= 16k2b2- 8(1+ 2k2) (b2- 1)> 0得 b2< 1+ 2k2
2 b2-1
x1+ x2= -4kb ,
x
1+2k2 1
x2= 1+2k2
2
则 CD = 1+k2 x1-x = 2 2 1+k2 2 2k
2+1-b2
1+2k
AB= 2 2 1+k
2
所以 2 2k
2+1,因为 |AB| = 2|CD|
1+2k
所以 2k2+1= 2 2k2+1-b2,则 4b2= 6k2+ 13 ,所以 |b| =
3 1+2k22
b 2
设直线AB与CD 3 1+2k之间的距离为 d0= =
1+k2 2 1+k2
2
所以F点设直线的距离 d= 2d0= 3 1+2k
1+k2
AB:y= y=kxkx 6, x2+ 2= x =2y 0 1+2k2
所以 |MN | = 2 1+k2 |x| = 2 1+k2 6 1,所以S△MNF= 2 AB d= 3 21+2k2
k不存在时,|MN | = 2 3 ,|FO| = 6,所以ΔMNF的面积也为 3 2
19. 1 ①设A为第 6次摸球后比赛结束,且甲乙共摸到 3次红球
P A = 4 1
3
则 3
2 32
3 = 729
②
X 2 4 6 2 n-1 2n
2 n-2 n-1
P 4 5 4 5 4 5 4 59 9 9 9 9 9 9 9
P 4 5 4 5
2 4 5 n-2 4 5 n-1
9 9 9 9 9 9 9 9 7分
2 n-2 n-1
所以E X = 8 9 1+2×
5
9 +3×
5
9 + +
5
n-1 9 + 2n
5
9 .
5 5 2 5 n-2
设Sn= 1+ 2× 9 + 3× 9 + + n-1 9
5 s = 5 + 2× 5
2 n-2 n-1
9 n 9 9 + + n-2
5
9 + n-1
5
9
4 2 n-2 n-1 n-1 n-1
所以 9 Sn= 1+
5
9 +
5 + + 5 - 5 9 5 59 9 n-1 = 1- 9 4 9 - n-1 9
8 9 9 5 n-1 5 n-1
所以 9 Sn= 2 - 2 9 - 2 n-1 9
E X = 9 - 5
n-1
所以 2 2
5
9 , n≥2,n∈N
*
(3)
1 1 1 1
X y y+1 y+t y+x
Cy-1 Cy-1 Cy-1 y-1y-1 y y+1-1
C
P y y y
x+y-1
C yx+y Cx+y Cx+y Cx+y
x Cy-11 x= x+y-1E X 1 1 y-1y+t Cy = y Cx+y-1t=0 x+y Cx+y t=0 y+t
1 y-1 = 1 (y+t-1)! = y+t-1 (y+t-2)! (y+t-2)!因为 y+t Cy+t-1 y+t (
y-1 !t! y-1
C y+t-2
x
所以E(X)< 1 Cy-2 = 1 y-2 y-2 y-2y y+1-2 y (Cy-2+Cy-1 + +Cy+x-2) =(y-1)Cx+y t=0 (y-1)Cx+y
1
Cy-1+Cy-2 y-2 1 y-1 y-2 y-2- y y-1 y-1
+ +Cy+x-2 = y C +C + +C- y-1 y-1 y+x-2 y 1 C x+y y 1 C x+y
= = 1 1 y-1 y-2 1 y-1
y-1 Cy
=
- y
C
y 1 C y+X-2
+Cy+x-2 = C
x+y x+y y-1
x+y-1
Cyx+y
= y ,又因为 x> y所以E(X)< 1
x+y y-1 2(y-1)
同课章节目录
