人教版(2025)数学八年级上册16.3.2 完全平方公式-第1课时 课件(共39张PPT)
文档属性
| 名称 | 人教版(2025)数学八年级上册16.3.2 完全平方公式-第1课时 课件(共39张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-08 00:00:00 | ||
图片预览






文档简介
(共39张PPT)
16.3.2 完全平方公式-第1课时
第十六章 整式的乘法
【2025新教材】人教版数学 八年级上册
授课教师:********
班 级:********
时 间:********
16.3.2 完全平方公式 - 第 1 课时教案
一、教学目标
(一)知识与技能目标
学生能够准确推导并理解完全平方公式,即\((a + b)^2 = a^2 + 2ab + b^2\)和\((a - b)^2 = a^2 - 2ab + b^2\),清晰掌握公式的结构特征。
熟练运用完全平方公式进行简单的整式乘法运算,包括底数为数字、字母、单项式等不同形式的运算。
能利用完全平方公式解决与整式乘法相关的简单实际问题,如在代数式化简、求值等场景中的应用。
(二)过程与方法目标
通过创设实际问题情境和数学问题,引导学生经历探索完全平方公式的过程,培养学生从特殊到一般的归纳推理能力以及符号感。
组织学生开展小组合作学习,共同探讨完全平方公式的推导方法和应用技巧,提高学生的合作交流能力和解决问题的能力。
在公式推导和应用过程中,让学生体会数形结合、类比、转化等数学思想方法,提升学生的数学思维能力。
(三)情感态度与价值观目标
激发学生对完全平方公式学习的兴趣,在自主探索和合作交流中体验成功的喜悦,增强学习数学的自信心。
培养学生严谨认真的学习态度和一丝不苟的计算习惯,在公式应用中注重每一个步骤的准确性和逻辑性。
让学生感受数学知识之间的内在联系和相互转化,体会数学的简洁美和应用价值,提高学生学习数学的积极性和主动性。
二、学情分析
学生在学习本节课之前,已经掌握了整式的加减、单项式乘单项式、单项式乘多项式、多项式乘多项式以及平方差公式等知识,具备了一定的整式运算基础和数学思维能力。然而,完全平方公式的推导和理解对于学生来说可能存在一定难度,尤其是公式中\(2ab\)这一项的由来以及公式结构特征的准确把握。在学习过程中,学生可能会出现以下困难:在公式推导时,对多项式乘法法则的运用不够熟练,导致推导过程出错;在公式应用时,容易混淆\((a + b)^2\)与\(a^2 + b^2\)、\((a - b)^2\)与\(a^2 - b^2\),出现漏乘\(2\)倍项、符号处理不当等问题。此外,将实际问题转化为数学问题并运用完全平方公式解决,对学生的数学建模能力也提出了较高要求。因此,在教学过程中,要充分利用学生已有的知识经验,通过大量具体的实例,引导学生逐步理解和掌握完全平方公式,加强对易错点和难点的讲解与练习,关注学生的个体差异,及时给予指导和帮助。
三、教学重难点
(一)教学重点
完全平方公式的推导过程,让学生理解公式的来源和本质。
熟练掌握完全平方公式的结构特征,能准确运用公式进行整式乘法运算。
(二)教学难点
深入理解完全平方公式的结构特征,特别是\(2ab\)这一项在公式中的意义和作用,避免与其他公式混淆。
在实际问题中,能够准确识别并运用完全平方公式解决问题,提高学生的数学应用能力。
四、教学方法
讲授法:通过清晰、准确的语言,向学生讲解完全平方公式的推导过程、结构特征和应用方法,使学生对知识有系统的认识。重点讲解公式推导的关键步骤和易错之处,帮助学生理解和掌握。
探究法:创设问题情境,引导学生自主探究完全平方公式,让学生在探究过程中发现问题、提出问题并解决问题,培养学生的探究能力和创新思维。
讨论法:组织学生进行小组讨论,共同探讨完全平方公式的推导思路和应用技巧,促进学生之间的思想交流与合作,让学生在讨论中相互学习、共同进步。
练习法:设计有针对性的练习题,让学生在练习中巩固所学的完全平方公式知识,提高学生的运算能力和解题技巧。通过练习,及时发现学生存在的问题,进行有针对性的辅导和纠正。
五、教学过程
(一)复习导入(5 分钟)
回顾多项式与多项式相乘的法则:
提问学生多项式与多项式相乘的运算法则,让学生回答并举例说明。
如\((x + 2)(x + 3) = x^2 + 3x + 2x + 6 = x^2 + 5x + 6\) 。
复习平方差公式:
请学生说出平方差公式的内容和符号表示。
平方差公式:\((a + b)(a - b) = a^2 - b^2\) 。
进行简单的多项式乘法计算练习:
在黑板上写出题目,如\((x + 1)(x + 4)\)、\((2x - 3)(3x + 1)\),请几位学生到黑板上板演,其他学生在练习本上完成,然后集体订正答案,复习巩固多项式乘法知识,为学习完全平方公式做好铺垫。
(二)探索新知(15 分钟)
两数和的完全平方公式推导
情境引入:提出问题 “若一个正方形的边长为\(a + b\),那么它的面积是多少?” 引导学生根据正方形面积公式列出式子\((a + b)^2\),从而引出对\((a + b)^2\)展开形式的探究。
推导过程:利用多项式与多项式相乘的法则,将\((a + b)^2\)展开,即\((a + b)^2 = (a + b)(a + b) = a^2 + ab + ab + b^2 = a^2 + 2ab + b^2\) 。
归纳法则:总结两数和的完全平方公式为\((a + b)^2 = a^2 + 2ab + b^2\),用文字叙述为:两个数的和的平方,等于它们的平方和,加上它们的积的\(2\)倍。强调公式中\(a\)、\(b\)可以表示任意数、单项式或多项式。
几何解释:展示一个边长为\(a + b\)的大正方形,将其分割为一个边长为\(a\)的小正方形、一个边长为\(b\)的小正方形和两个长为\(a\)宽为\(b\)的长方形。大正方形面积为\((a + b)^2\),四个小图形面积和为\(a^2 + ab + ab + b^2\),从图形面积角度直观验证\((a + b)^2 = a^2 + 2ab + b^2\) 。
两数差的完全平方公式推导
类比探究:引导学生思考,若把\((a + b)^2\)中的\(b\)换成\(-b\),会得到怎样的式子。让学生自己尝试运用多项式乘法法则展开\((a - b)^2\) 。
推导过程:\((a - b)^2 = [a + (-b)]^2 = a^2 + 2a(-b) + (-b)^2 = a^2 - 2ab + b^2\) 。
归纳法则:总结两数差的完全平方公式为\((a - b)^2 = a^2 - 2ab + b^2\),用文字叙述为:两个数的差的平方,等于它们的平方和,减去它们的积的\(2\)倍。
对比分析:将两数和的完全平方公式与两数差的完全平方公式进行对比,让学生观察它们的相同点和不同点,强调公式中符号的变化规律。
(三)例题讲解(15 分钟)
例 1:运用完全平方公式计算
(1) \((x + 5)^2\)
分析:这里\(a = x\),\(b = 5\),根据两数和的完全平方公式\((a + b)^2 = a^2 + 2ab + b^2\)进行计算。
解:\((x + 5)^2 = x^2 + 2 \cdot x \cdot 5 + 5^2 = x^2 + 10x + 25\)
(2) \((2m + n)^2\)
分析:\(a = 2m\),\(b = n\),运用公式计算。
解:\((2m + n)^2 = (2m)^2 + 2 \cdot (2m) \cdot n + n^2 = 4m^2 + 4mn + n^2\)
例 2:运用完全平方公式计算
(1) \((x - 3)^2\)
分析:这里\(a = x\),\(b = 3\),根据两数差的完全平方公式\((a - b)^2 = a^2 - 2ab + b^2\)进行计算。
解:\((x - 3)^2 = x^2 - 2 \cdot x \cdot 3 + 3^2 = x^2 - 6x + 9\)
(2) \((3a - 2b)^2\)
分析:\(a = 3a\),\(b = 2b\),运用公式计算。
解:\((3a - 2b)^2 = (3a)^2 - 2 \cdot (3a) \cdot (2b) + (2b)^2 = 9a^2 - 12ab + 4b^2\)
例 3:运用完全平方公式进行简便计算
(1) \(101^2\)
分析:把\(101\)写成\(100 + 1\),然后利用两数和的完全平方公式计算。
解:\(101^2 = (100 + 1)^2 = 100^2 + 2 \times 100 \times 1 + 1^2 = 10000 + 200 + 1 = 10201\)
(2) \(98^2\)
分析:把\(98\)写成\(100 - 2\),利用两数差的完全平方公式计算。
解:\(98^2 = (100 - 2)^2 = 100^2 - 2 \times 100 \times 2 + 2^2 = 10000 - 400 + 4 = 9604\)
(四)课堂练习(10 分钟)
运用完全平方公式计算:
(1) \((y + 7)^2\)
(2) \((3x + 2y)^2\)
(3) \((a - 10)^2\)
(4) \((4m - 3n)^2\)
下面的计算是否正确?如果错误,请改正。
(1) \((x + 2)^2 = x^2 + 4\) ( )
(2) \((2a - 1)^2 = 4a^2 - 2a + 1\) ( )
(3) \((-x - y)^2 = x^2 - 2xy + y^2\) ( )
教师巡视学生的练习情况,及时发现问题并给予指导,选取部分学生的答案进行展示和点评,纠正学生出现的错误。
(五)课堂小结(3 分钟)
与学生一起回顾完全平方公式,包括两数和的完全平方公式\((a + b)^2 = a^2 + 2ab + b^2\)和两数差的完全平方公式\((a - b)^2 = a^2 - 2ab + b^2\),强调公式的结构特征和符号规律。
总结运用完全平方公式进行计算的关键步骤和注意事项,如准确确定\(a\)、\(b\)的值,注意\(2ab\)项的系数和符号等。
引导学生回顾完全平方公式的推导过程,体会从特殊到一般的数学思想方法以及数形结合的思想。
(六)作业布置(2 分钟)
基础作业:教材课后练习题中关于完全平方公式的相关题目,巩固本节课所学的基础知识和运算技能。
拓展作业:
已知\(x + y = 5\),\(xy = 3\),求\(x^2 + y^2\)的值。
利用完全平方公式计算\((2 + 1)(2^2 + 1)(2^4 + 1)(2^8 + 1) + 1\) 。
六、教学反思
在教学过程中,关注学生对完全平方公式的推导和应用的掌握情况。通过学生在课堂练习和回答问题中出现的错误,分析学生在学习过程中存在的困难和问题,如对公式结构理解不清晰、计算粗心等。针对这些问题,在后续教学中加强对公式结构的讲解和练习,增加一些易错点的专项训练,同时注重培养学生良好的学习习惯和计算习惯。此外,还要关注不同层次学生的学习情况,对学习困难的学生进行个别辅导,确保每个学生都能在本节课中有所收获和提高。同时,在教学方法上,思考是否可以进一步优化,让学生更加主动地参与到公式的探索和应用中,提高课堂教学的效率和质量。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
1. 通过学生自主探究理解完全平方公式,掌握公式的结构特征,了解公式的几何意义,并能熟练运用公式进行简单计算,提高学生解决问题的能力.
2.利用去括号法则得到添括号法则,培养学生的逆向思维能力.
3.让学生经历探索完全平方公式的过程,进一步发展学生的符号感和推理能力.
4.通过探究过程,使学生了解“特殊—一般”的认识规律,体会数形结合、类比、转化的数学思想.
重点
难点
旧识回顾
1.a2可以表示成什么?
2.多项式与多项式相乘的法则是什么?
a×a
一般地,多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加
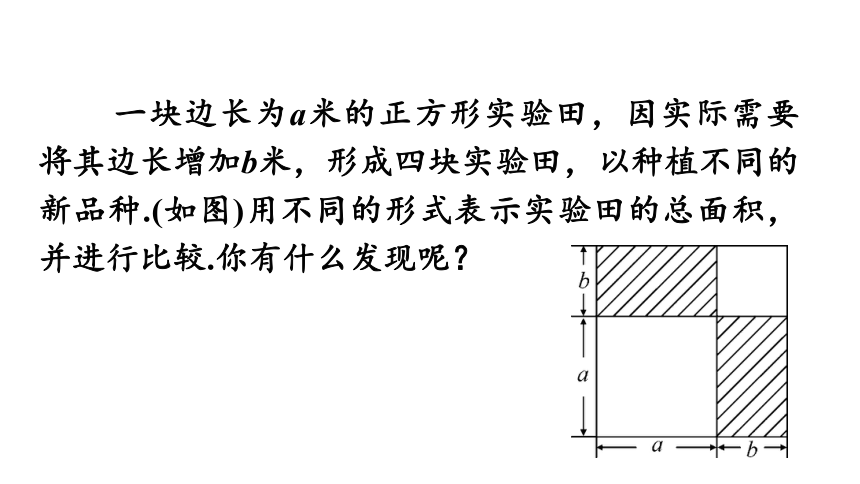
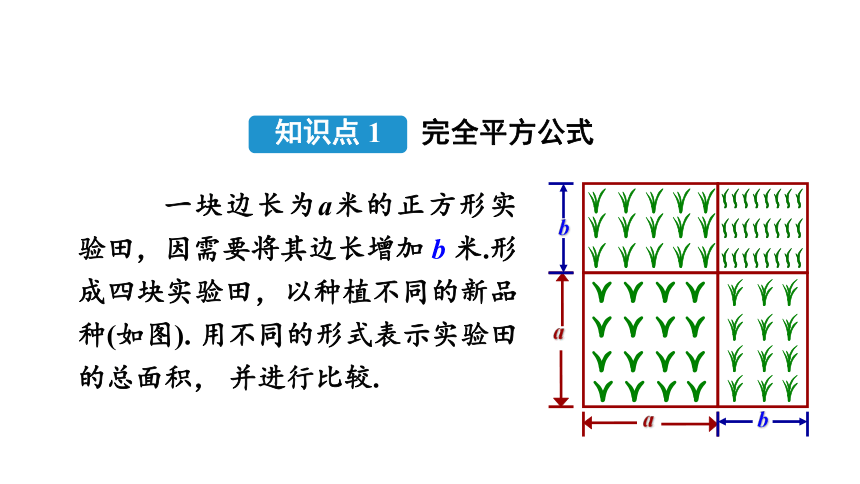
一块边长为a米的正方形实验田,因实际需要将其边长增加b米,形成四块实验田,以种植不同的新品种.(如图)用不同的形式表示实验田的总面积,并进行比较.你有什么发现呢?
一块边长为a米的正方形实验田,因需要将其边长增加 b 米.形成四块实验田,以种植不同的新品种(如图). 用不同的形式表示实验田的总面积, 并进行比较.
a
a
b
b
知识点 1
完全平方公式
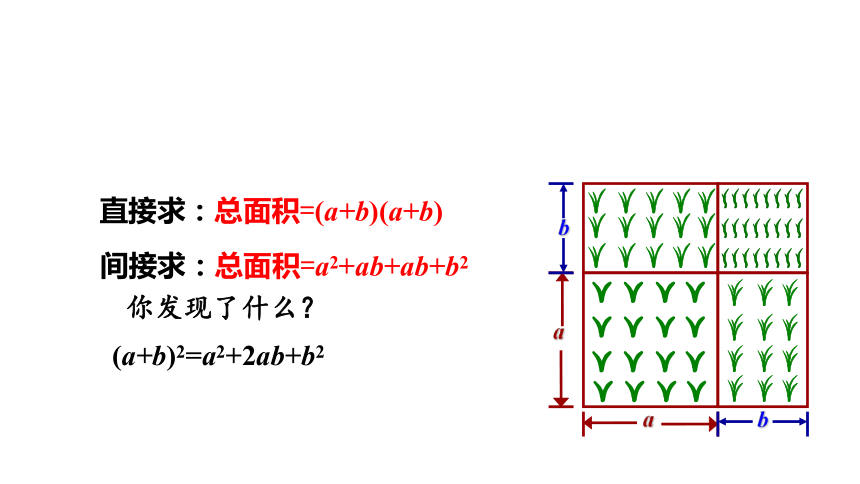
直接求:总面积=(a+b)(a+b)
间接求:总面积=a2+ab+ab+b2
你发现了什么?
(a+b)2=a2+2ab+b2
a
a
b
b
计算下列多项式的积,你能发现什么规律?
(1) (p+1)2=(p+1)(p+1)= .
p2+2p+1
(2) (m+2)2=(m+2)(m+2)= .
m2+4m+4
(3) (p–1)2=(p–1)(p–1)= .
p2–2p+1
(4) (m–2)2=(m–2)(m–2)= .
m2–4m+4
问题1:
学生活动 【一起探究】
根据你发现的规律,你能写出下列式子的答案吗?
(a+b)2= .
a2+2ab+b2
(a–b)2= .
a2–2ab+b2
问题2:
(a+b)2= .
a2+2ab+b2
(a–b)2= .
a2–2ab+b2
也就是说,两个数的和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍.这两个公式叫做(乘法的)完全平方公式.
简记为:“首平方,尾平方,积的2倍放中央”
完全平方公式
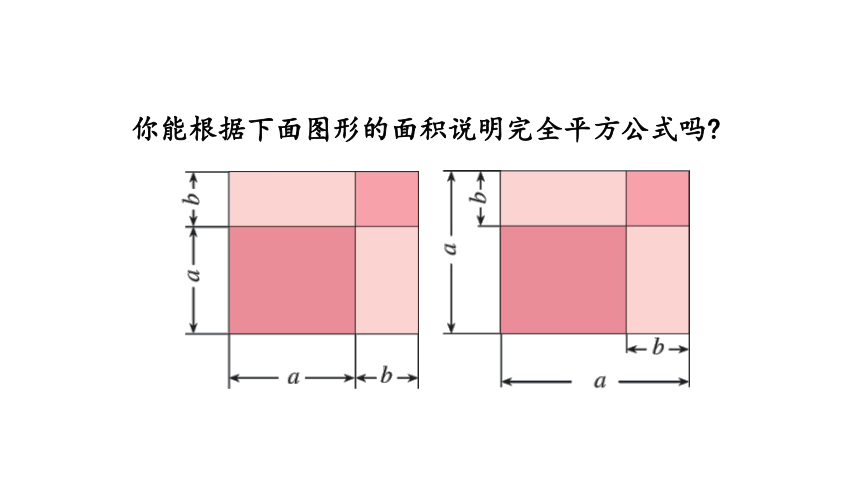
你能根据下面图形的面积说明完全平方公式吗
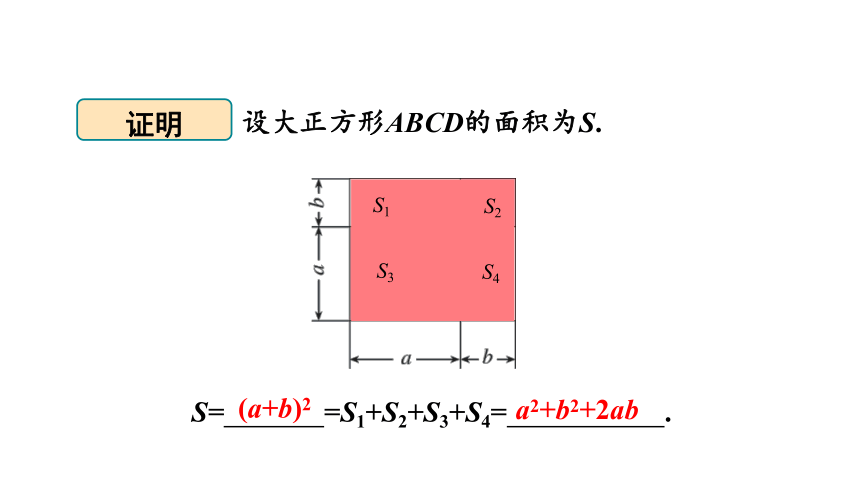
设大正方形ABCD的面积为S.
S= =S1+S2+S3+S4= .
(a+b)2
a2+b2+2ab
S1
S2
S3
S4
证明
a
a
b
b
=
+
+
+
a2
ab
ab
b2
(a+b)2= .
a2+2ab+b2
和的完全平方公式:
几何解释
a2
ab
b(a b)
=
a2 2ab+b2 .
=
(a b)2
a b
a b
a
a
ab
b(a b)
b
b
(a b)2
(a–b)2= .
a2–2ab+b2
差的完全平方公式:
几何解释
(a+b)2= a2+2ab+b2.
(a–b)2= a2–2ab+b2.
观察下面两个完全平方式,比一比,回答下列问题:
(1) 说一说积的次数和项数.
(2) 两个完全平方式的积有相同的项吗?与a,b有什么关系?
(3) 两个完全平方式的积中不同的是哪一项?与a, b有什么关系?它的符号与什么有关?
问题4:
公式特征:
公式中的字母a,b可以表示数、单项式和多项式.
积为二次三项式;
积中两项为两数的平方和;
另一项是两数积的2倍,且与两数中间的符号相同.
例1 运用完全平方公式计算:
解: (4m+n)2=
=16m2
(1)(4m+n)2;
(a + b)2= a2 + 2ab + b2
(4m)2
+2 (4m) n
+n2
+8mn
+n2;
素养考点 1
利用完全平方公式进行计算
(2)
(a – b)2 = a2– 2ab + b2
y2
=y2
–y
+
解: =
+
–2 y
(1) 1022;
= (100 –1)2
=10000 –200+1
解: 1022
= (100+2)2
=10000+400+4
=10404.
(2) 992.
992
=9801.
例2 运用完全平方公式计算:
素养考点 2
利用完全平方公式进行简便计算
方法总结:当一个数具备与整十、整百相差一个正整数时求它的平方,我们可以通过变形运用完全平方公式进行运算较简便.
利用乘法公式计算:
(1)982–101×99; (2)20162–2016×4030+20152.
=(2016–2015)2=1.
解:(1)原式=(100–2)2–(100+1)(100–1)
=1002–400+4–1002+1=–395;
(2)原式=20162–2×2016×2015+20152
例3 已知x–y=6,xy=–8.
求:(1) x2+y2的值; (2)(x+y)2的值.
=36 –16=20;
解:(1)∵x–y=6,xy=–8,
(x–y)2=x2+y2–2xy,
∴x2+y2=(x–y)2+2xy
(2)∵x2+y2=20,xy=–8,
∴(x+y)2=x2+y2+2xy
=20 –16=4.
素养考点 3
利用完全平方公式的变形求整式的值
方法总结:本题要熟练掌握完全平方公式的变式:
x2+y2=(x–y)2+2xy=(x+y)2–2xy,(x–y)2=(x+y)2–4xy.
添括号法则
a+(b+c) = a+b+c;
a– (b+c) = a – b – c.
a + b + c = a + ( b + c) ;
a – b – c = a – ( b + c ) .
去括号:
把上面两个等式的左右两边反过来,也就是添括号:
知识点 2
添括号时,如果括号前面是正号,括到括号里的各项都不变号;如果括号前面是负号,括到括号里的各项都改变符号(简记为“负变正不变”).
添括号法则
例 运用乘法公式计算:
(1) (x+2y–3)(x–2y+3) ; (2) (a+b+c)2.
原式=[x+(2y–3)][x–(2y–3)]
解: (1)
(2)原式= [(a+b)+c]2
= x2–(2y–3)2
= x2–(4y2–12y+9)
= x2–4y2+12y–9.
= (a+b)2+2(a+b)c+c2
=a2+2ab+b2+2ac+2bc+c2.
素养考点
添括号法则的应用
计算:(1)(a–b+c)2; (2)(1–2x+y)(1+2x–y).
=1–4x2+4xy–y2.
解:(1)原式=[(a–b)+c]2
=(a–b)2+c2+2(a–b)c
=a2–2ab+b2+c2+2ac–2bc;
(2)原式=[1– (2x–y)][1+(2x–y)]
=12–(2x–y)2
1. 给出下列算式: ;
; ;
.其中错误的
有( )
C
A. 1个 B. 2个 C. 3个 D. 4个
返回
2. 如果,则 的值是( )
A. 4 B. 或4 C. 8 D. 或8
【点拨】 ,
, ,
.
D
返回
3. 如图,可验证的乘法公式是( )
A
A.
B.
C.
D.
返回
4.若,则 的值为____.
5.若,则代数式 为______.
6.[2025广州越秀区期中]若 ,那么多项式
的值是___.
8
返回
7.母题教材P115例4 利用完全平方公式计算:
(1) ;
【解】原式 .
(2) ;
原式 .
利用完全平方公式进行数值运算时,可以将底数拆
成两个数的和或差,拆分时主要有两种形式:
一是将与整十、整百或整千接近的数拆分成整十、整百或整
千的数与相差的数的和或差;二是将带分数拆分成整数与真
分数的和或差.
. .
. .
. .
返回
8.(1)解方程: ;
【解】 ,
,
,
,
.
(2)计算: .
.
返回
9. 母题教材P117习题 一个正方形的边长少了 ,它的
面积就减少了 ,那么这个正方形的边长为( )
B
A. B.
C. D.
返回
10. 母题母题 若,,则
( )
A. 52 B. 50 C. 45 D. 60
【点拨】, .
A
返回
11.设,, ,若
,则 的值是____.
16
【点拨】,,,.又, .
返回
完全平方公式
法则
注意
(a±b)2= a2±2ab+b2
1.项数、符号、字母及其指数
2.不能直接应用公式进行计算的式子,可能需要先添括号变形成符合公式的要求才行
常用
结论
3.弄清完全平方公式和平方差公式不同(从公式结构特点及结果两方面)
a2+b2=(a+b)2–2ab=(a–b)2+2ab;
4ab=(a+b)2–(a–b)2.
谢谢观看!
16.3.2 完全平方公式-第1课时
第十六章 整式的乘法
【2025新教材】人教版数学 八年级上册
授课教师:********
班 级:********
时 间:********
16.3.2 完全平方公式 - 第 1 课时教案
一、教学目标
(一)知识与技能目标
学生能够准确推导并理解完全平方公式,即\((a + b)^2 = a^2 + 2ab + b^2\)和\((a - b)^2 = a^2 - 2ab + b^2\),清晰掌握公式的结构特征。
熟练运用完全平方公式进行简单的整式乘法运算,包括底数为数字、字母、单项式等不同形式的运算。
能利用完全平方公式解决与整式乘法相关的简单实际问题,如在代数式化简、求值等场景中的应用。
(二)过程与方法目标
通过创设实际问题情境和数学问题,引导学生经历探索完全平方公式的过程,培养学生从特殊到一般的归纳推理能力以及符号感。
组织学生开展小组合作学习,共同探讨完全平方公式的推导方法和应用技巧,提高学生的合作交流能力和解决问题的能力。
在公式推导和应用过程中,让学生体会数形结合、类比、转化等数学思想方法,提升学生的数学思维能力。
(三)情感态度与价值观目标
激发学生对完全平方公式学习的兴趣,在自主探索和合作交流中体验成功的喜悦,增强学习数学的自信心。
培养学生严谨认真的学习态度和一丝不苟的计算习惯,在公式应用中注重每一个步骤的准确性和逻辑性。
让学生感受数学知识之间的内在联系和相互转化,体会数学的简洁美和应用价值,提高学生学习数学的积极性和主动性。
二、学情分析
学生在学习本节课之前,已经掌握了整式的加减、单项式乘单项式、单项式乘多项式、多项式乘多项式以及平方差公式等知识,具备了一定的整式运算基础和数学思维能力。然而,完全平方公式的推导和理解对于学生来说可能存在一定难度,尤其是公式中\(2ab\)这一项的由来以及公式结构特征的准确把握。在学习过程中,学生可能会出现以下困难:在公式推导时,对多项式乘法法则的运用不够熟练,导致推导过程出错;在公式应用时,容易混淆\((a + b)^2\)与\(a^2 + b^2\)、\((a - b)^2\)与\(a^2 - b^2\),出现漏乘\(2\)倍项、符号处理不当等问题。此外,将实际问题转化为数学问题并运用完全平方公式解决,对学生的数学建模能力也提出了较高要求。因此,在教学过程中,要充分利用学生已有的知识经验,通过大量具体的实例,引导学生逐步理解和掌握完全平方公式,加强对易错点和难点的讲解与练习,关注学生的个体差异,及时给予指导和帮助。
三、教学重难点
(一)教学重点
完全平方公式的推导过程,让学生理解公式的来源和本质。
熟练掌握完全平方公式的结构特征,能准确运用公式进行整式乘法运算。
(二)教学难点
深入理解完全平方公式的结构特征,特别是\(2ab\)这一项在公式中的意义和作用,避免与其他公式混淆。
在实际问题中,能够准确识别并运用完全平方公式解决问题,提高学生的数学应用能力。
四、教学方法
讲授法:通过清晰、准确的语言,向学生讲解完全平方公式的推导过程、结构特征和应用方法,使学生对知识有系统的认识。重点讲解公式推导的关键步骤和易错之处,帮助学生理解和掌握。
探究法:创设问题情境,引导学生自主探究完全平方公式,让学生在探究过程中发现问题、提出问题并解决问题,培养学生的探究能力和创新思维。
讨论法:组织学生进行小组讨论,共同探讨完全平方公式的推导思路和应用技巧,促进学生之间的思想交流与合作,让学生在讨论中相互学习、共同进步。
练习法:设计有针对性的练习题,让学生在练习中巩固所学的完全平方公式知识,提高学生的运算能力和解题技巧。通过练习,及时发现学生存在的问题,进行有针对性的辅导和纠正。
五、教学过程
(一)复习导入(5 分钟)
回顾多项式与多项式相乘的法则:
提问学生多项式与多项式相乘的运算法则,让学生回答并举例说明。
如\((x + 2)(x + 3) = x^2 + 3x + 2x + 6 = x^2 + 5x + 6\) 。
复习平方差公式:
请学生说出平方差公式的内容和符号表示。
平方差公式:\((a + b)(a - b) = a^2 - b^2\) 。
进行简单的多项式乘法计算练习:
在黑板上写出题目,如\((x + 1)(x + 4)\)、\((2x - 3)(3x + 1)\),请几位学生到黑板上板演,其他学生在练习本上完成,然后集体订正答案,复习巩固多项式乘法知识,为学习完全平方公式做好铺垫。
(二)探索新知(15 分钟)
两数和的完全平方公式推导
情境引入:提出问题 “若一个正方形的边长为\(a + b\),那么它的面积是多少?” 引导学生根据正方形面积公式列出式子\((a + b)^2\),从而引出对\((a + b)^2\)展开形式的探究。
推导过程:利用多项式与多项式相乘的法则,将\((a + b)^2\)展开,即\((a + b)^2 = (a + b)(a + b) = a^2 + ab + ab + b^2 = a^2 + 2ab + b^2\) 。
归纳法则:总结两数和的完全平方公式为\((a + b)^2 = a^2 + 2ab + b^2\),用文字叙述为:两个数的和的平方,等于它们的平方和,加上它们的积的\(2\)倍。强调公式中\(a\)、\(b\)可以表示任意数、单项式或多项式。
几何解释:展示一个边长为\(a + b\)的大正方形,将其分割为一个边长为\(a\)的小正方形、一个边长为\(b\)的小正方形和两个长为\(a\)宽为\(b\)的长方形。大正方形面积为\((a + b)^2\),四个小图形面积和为\(a^2 + ab + ab + b^2\),从图形面积角度直观验证\((a + b)^2 = a^2 + 2ab + b^2\) 。
两数差的完全平方公式推导
类比探究:引导学生思考,若把\((a + b)^2\)中的\(b\)换成\(-b\),会得到怎样的式子。让学生自己尝试运用多项式乘法法则展开\((a - b)^2\) 。
推导过程:\((a - b)^2 = [a + (-b)]^2 = a^2 + 2a(-b) + (-b)^2 = a^2 - 2ab + b^2\) 。
归纳法则:总结两数差的完全平方公式为\((a - b)^2 = a^2 - 2ab + b^2\),用文字叙述为:两个数的差的平方,等于它们的平方和,减去它们的积的\(2\)倍。
对比分析:将两数和的完全平方公式与两数差的完全平方公式进行对比,让学生观察它们的相同点和不同点,强调公式中符号的变化规律。
(三)例题讲解(15 分钟)
例 1:运用完全平方公式计算
(1) \((x + 5)^2\)
分析:这里\(a = x\),\(b = 5\),根据两数和的完全平方公式\((a + b)^2 = a^2 + 2ab + b^2\)进行计算。
解:\((x + 5)^2 = x^2 + 2 \cdot x \cdot 5 + 5^2 = x^2 + 10x + 25\)
(2) \((2m + n)^2\)
分析:\(a = 2m\),\(b = n\),运用公式计算。
解:\((2m + n)^2 = (2m)^2 + 2 \cdot (2m) \cdot n + n^2 = 4m^2 + 4mn + n^2\)
例 2:运用完全平方公式计算
(1) \((x - 3)^2\)
分析:这里\(a = x\),\(b = 3\),根据两数差的完全平方公式\((a - b)^2 = a^2 - 2ab + b^2\)进行计算。
解:\((x - 3)^2 = x^2 - 2 \cdot x \cdot 3 + 3^2 = x^2 - 6x + 9\)
(2) \((3a - 2b)^2\)
分析:\(a = 3a\),\(b = 2b\),运用公式计算。
解:\((3a - 2b)^2 = (3a)^2 - 2 \cdot (3a) \cdot (2b) + (2b)^2 = 9a^2 - 12ab + 4b^2\)
例 3:运用完全平方公式进行简便计算
(1) \(101^2\)
分析:把\(101\)写成\(100 + 1\),然后利用两数和的完全平方公式计算。
解:\(101^2 = (100 + 1)^2 = 100^2 + 2 \times 100 \times 1 + 1^2 = 10000 + 200 + 1 = 10201\)
(2) \(98^2\)
分析:把\(98\)写成\(100 - 2\),利用两数差的完全平方公式计算。
解:\(98^2 = (100 - 2)^2 = 100^2 - 2 \times 100 \times 2 + 2^2 = 10000 - 400 + 4 = 9604\)
(四)课堂练习(10 分钟)
运用完全平方公式计算:
(1) \((y + 7)^2\)
(2) \((3x + 2y)^2\)
(3) \((a - 10)^2\)
(4) \((4m - 3n)^2\)
下面的计算是否正确?如果错误,请改正。
(1) \((x + 2)^2 = x^2 + 4\) ( )
(2) \((2a - 1)^2 = 4a^2 - 2a + 1\) ( )
(3) \((-x - y)^2 = x^2 - 2xy + y^2\) ( )
教师巡视学生的练习情况,及时发现问题并给予指导,选取部分学生的答案进行展示和点评,纠正学生出现的错误。
(五)课堂小结(3 分钟)
与学生一起回顾完全平方公式,包括两数和的完全平方公式\((a + b)^2 = a^2 + 2ab + b^2\)和两数差的完全平方公式\((a - b)^2 = a^2 - 2ab + b^2\),强调公式的结构特征和符号规律。
总结运用完全平方公式进行计算的关键步骤和注意事项,如准确确定\(a\)、\(b\)的值,注意\(2ab\)项的系数和符号等。
引导学生回顾完全平方公式的推导过程,体会从特殊到一般的数学思想方法以及数形结合的思想。
(六)作业布置(2 分钟)
基础作业:教材课后练习题中关于完全平方公式的相关题目,巩固本节课所学的基础知识和运算技能。
拓展作业:
已知\(x + y = 5\),\(xy = 3\),求\(x^2 + y^2\)的值。
利用完全平方公式计算\((2 + 1)(2^2 + 1)(2^4 + 1)(2^8 + 1) + 1\) 。
六、教学反思
在教学过程中,关注学生对完全平方公式的推导和应用的掌握情况。通过学生在课堂练习和回答问题中出现的错误,分析学生在学习过程中存在的困难和问题,如对公式结构理解不清晰、计算粗心等。针对这些问题,在后续教学中加强对公式结构的讲解和练习,增加一些易错点的专项训练,同时注重培养学生良好的学习习惯和计算习惯。此外,还要关注不同层次学生的学习情况,对学习困难的学生进行个别辅导,确保每个学生都能在本节课中有所收获和提高。同时,在教学方法上,思考是否可以进一步优化,让学生更加主动地参与到公式的探索和应用中,提高课堂教学的效率和质量。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
1. 通过学生自主探究理解完全平方公式,掌握公式的结构特征,了解公式的几何意义,并能熟练运用公式进行简单计算,提高学生解决问题的能力.
2.利用去括号法则得到添括号法则,培养学生的逆向思维能力.
3.让学生经历探索完全平方公式的过程,进一步发展学生的符号感和推理能力.
4.通过探究过程,使学生了解“特殊—一般”的认识规律,体会数形结合、类比、转化的数学思想.
重点
难点
旧识回顾
1.a2可以表示成什么?
2.多项式与多项式相乘的法则是什么?
a×a
一般地,多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加
一块边长为a米的正方形实验田,因实际需要将其边长增加b米,形成四块实验田,以种植不同的新品种.(如图)用不同的形式表示实验田的总面积,并进行比较.你有什么发现呢?
一块边长为a米的正方形实验田,因需要将其边长增加 b 米.形成四块实验田,以种植不同的新品种(如图). 用不同的形式表示实验田的总面积, 并进行比较.
a
a
b
b
知识点 1
完全平方公式
直接求:总面积=(a+b)(a+b)
间接求:总面积=a2+ab+ab+b2
你发现了什么?
(a+b)2=a2+2ab+b2
a
a
b
b
计算下列多项式的积,你能发现什么规律?
(1) (p+1)2=(p+1)(p+1)= .
p2+2p+1
(2) (m+2)2=(m+2)(m+2)= .
m2+4m+4
(3) (p–1)2=(p–1)(p–1)= .
p2–2p+1
(4) (m–2)2=(m–2)(m–2)= .
m2–4m+4
问题1:
学生活动 【一起探究】
根据你发现的规律,你能写出下列式子的答案吗?
(a+b)2= .
a2+2ab+b2
(a–b)2= .
a2–2ab+b2
问题2:
(a+b)2= .
a2+2ab+b2
(a–b)2= .
a2–2ab+b2
也就是说,两个数的和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍.这两个公式叫做(乘法的)完全平方公式.
简记为:“首平方,尾平方,积的2倍放中央”
完全平方公式
你能根据下面图形的面积说明完全平方公式吗
设大正方形ABCD的面积为S.
S= =S1+S2+S3+S4= .
(a+b)2
a2+b2+2ab
S1
S2
S3
S4
证明
a
a
b
b
=
+
+
+
a2
ab
ab
b2
(a+b)2= .
a2+2ab+b2
和的完全平方公式:
几何解释
a2
ab
b(a b)
=
a2 2ab+b2 .
=
(a b)2
a b
a b
a
a
ab
b(a b)
b
b
(a b)2
(a–b)2= .
a2–2ab+b2
差的完全平方公式:
几何解释
(a+b)2= a2+2ab+b2.
(a–b)2= a2–2ab+b2.
观察下面两个完全平方式,比一比,回答下列问题:
(1) 说一说积的次数和项数.
(2) 两个完全平方式的积有相同的项吗?与a,b有什么关系?
(3) 两个完全平方式的积中不同的是哪一项?与a, b有什么关系?它的符号与什么有关?
问题4:
公式特征:
公式中的字母a,b可以表示数、单项式和多项式.
积为二次三项式;
积中两项为两数的平方和;
另一项是两数积的2倍,且与两数中间的符号相同.
例1 运用完全平方公式计算:
解: (4m+n)2=
=16m2
(1)(4m+n)2;
(a + b)2= a2 + 2ab + b2
(4m)2
+2 (4m) n
+n2
+8mn
+n2;
素养考点 1
利用完全平方公式进行计算
(2)
(a – b)2 = a2– 2ab + b2
y2
=y2
–y
+
解: =
+
–2 y
(1) 1022;
= (100 –1)2
=10000 –200+1
解: 1022
= (100+2)2
=10000+400+4
=10404.
(2) 992.
992
=9801.
例2 运用完全平方公式计算:
素养考点 2
利用完全平方公式进行简便计算
方法总结:当一个数具备与整十、整百相差一个正整数时求它的平方,我们可以通过变形运用完全平方公式进行运算较简便.
利用乘法公式计算:
(1)982–101×99; (2)20162–2016×4030+20152.
=(2016–2015)2=1.
解:(1)原式=(100–2)2–(100+1)(100–1)
=1002–400+4–1002+1=–395;
(2)原式=20162–2×2016×2015+20152
例3 已知x–y=6,xy=–8.
求:(1) x2+y2的值; (2)(x+y)2的值.
=36 –16=20;
解:(1)∵x–y=6,xy=–8,
(x–y)2=x2+y2–2xy,
∴x2+y2=(x–y)2+2xy
(2)∵x2+y2=20,xy=–8,
∴(x+y)2=x2+y2+2xy
=20 –16=4.
素养考点 3
利用完全平方公式的变形求整式的值
方法总结:本题要熟练掌握完全平方公式的变式:
x2+y2=(x–y)2+2xy=(x+y)2–2xy,(x–y)2=(x+y)2–4xy.
添括号法则
a+(b+c) = a+b+c;
a– (b+c) = a – b – c.
a + b + c = a + ( b + c) ;
a – b – c = a – ( b + c ) .
去括号:
把上面两个等式的左右两边反过来,也就是添括号:
知识点 2
添括号时,如果括号前面是正号,括到括号里的各项都不变号;如果括号前面是负号,括到括号里的各项都改变符号(简记为“负变正不变”).
添括号法则
例 运用乘法公式计算:
(1) (x+2y–3)(x–2y+3) ; (2) (a+b+c)2.
原式=[x+(2y–3)][x–(2y–3)]
解: (1)
(2)原式= [(a+b)+c]2
= x2–(2y–3)2
= x2–(4y2–12y+9)
= x2–4y2+12y–9.
= (a+b)2+2(a+b)c+c2
=a2+2ab+b2+2ac+2bc+c2.
素养考点
添括号法则的应用
计算:(1)(a–b+c)2; (2)(1–2x+y)(1+2x–y).
=1–4x2+4xy–y2.
解:(1)原式=[(a–b)+c]2
=(a–b)2+c2+2(a–b)c
=a2–2ab+b2+c2+2ac–2bc;
(2)原式=[1– (2x–y)][1+(2x–y)]
=12–(2x–y)2
1. 给出下列算式: ;
; ;
.其中错误的
有( )
C
A. 1个 B. 2个 C. 3个 D. 4个
返回
2. 如果,则 的值是( )
A. 4 B. 或4 C. 8 D. 或8
【点拨】 ,
, ,
.
D
返回
3. 如图,可验证的乘法公式是( )
A
A.
B.
C.
D.
返回
4.若,则 的值为____.
5.若,则代数式 为______.
6.[2025广州越秀区期中]若 ,那么多项式
的值是___.
8
返回
7.母题教材P115例4 利用完全平方公式计算:
(1) ;
【解】原式 .
(2) ;
原式 .
利用完全平方公式进行数值运算时,可以将底数拆
成两个数的和或差,拆分时主要有两种形式:
一是将与整十、整百或整千接近的数拆分成整十、整百或整
千的数与相差的数的和或差;二是将带分数拆分成整数与真
分数的和或差.
. .
. .
. .
返回
8.(1)解方程: ;
【解】 ,
,
,
,
.
(2)计算: .
.
返回
9. 母题教材P117习题 一个正方形的边长少了 ,它的
面积就减少了 ,那么这个正方形的边长为( )
B
A. B.
C. D.
返回
10. 母题母题 若,,则
( )
A. 52 B. 50 C. 45 D. 60
【点拨】, .
A
返回
11.设,, ,若
,则 的值是____.
16
【点拨】,,,.又, .
返回
完全平方公式
法则
注意
(a±b)2= a2±2ab+b2
1.项数、符号、字母及其指数
2.不能直接应用公式进行计算的式子,可能需要先添括号变形成符合公式的要求才行
常用
结论
3.弄清完全平方公式和平方差公式不同(从公式结构特点及结果两方面)
a2+b2=(a+b)2–2ab=(a–b)2+2ab;
4ab=(a+b)2–(a–b)2.
谢谢观看!
同课章节目录
