2.3 匀变速直线运动的位移与时间的关系课件(2)35页ppt
文档属性
| 名称 | 2.3 匀变速直线运动的位移与时间的关系课件(2)35页ppt |  | |
| 格式 | pptx | ||
| 文件大小 | 947.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-06-09 00:23:20 | ||
图片预览







文档简介
(共35张PPT)
人教2019版 必修第一册
2.3 匀变速直线运动的位移与时间的关系
第二章 匀变速直线运动的研究
【新课导入】
由做匀速直线运动物体的 v-t 图像可以看出,在时间 t 内的位移 x 对应图中着色部分的矩形面积。
那么,做匀变速直线运动的物体,在时间 t 内的位移与时间会有怎样的关系?
匀速直线运动的位移
x=vt
v
t
结论:
匀速直线运动的位移就是v – t 图线与t轴所夹的矩形“面积”。
公式法
图象法
v/m·s-1
t/s
2
6
4
10
8
3
4
5
6
0
2
1
甲
-2
-4
x
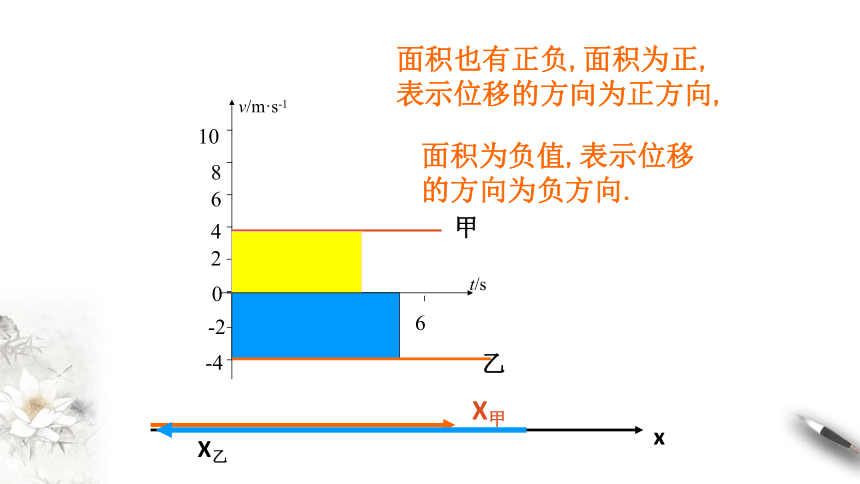
面积也有正负,面积为正,表示位移的方向为正方向,
面积为负值,表示位移的方向为负方向.
乙
X甲
X乙
匀变速直线运动的位移是否也对应 v-t 图象一定的面积?
t
v
v0
t
vt
0
…
我们需要研究匀变速直线运动的位移规律!
问题
解决
一、匀变速直线运动的位移
怎样求解匀变速直线运动的位移?
将运动进行分割,在很短时间(⊿t)内,将变速直线运动近似为匀速直线运动,利用 x=v t 计算每一段的位移,各段位移之和即为变速运动的位移。
问题
解决
将复杂问题抽象成一个我们熟悉的简单模型,利用这个模型的规律进行近似研究,能得到接近真实值的研究结果。这是物理思想方法之一。
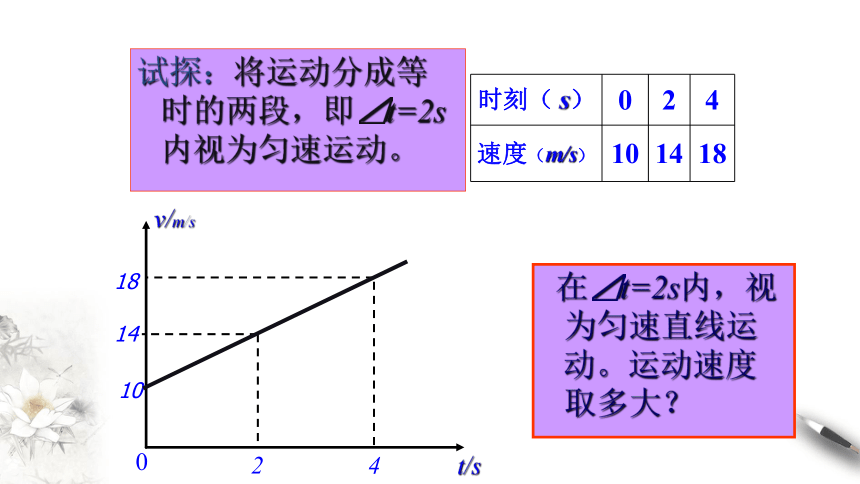
试探:将运动分成等时的两段,即⊿t=2s内视为匀速运动。
在⊿t=2s内,视为匀速直线运动。运动速度取多大?
时刻( s) 0 2 4
速度(m/s) 10 14 18
t/s
v/m/s
10
4
18
0
14
2
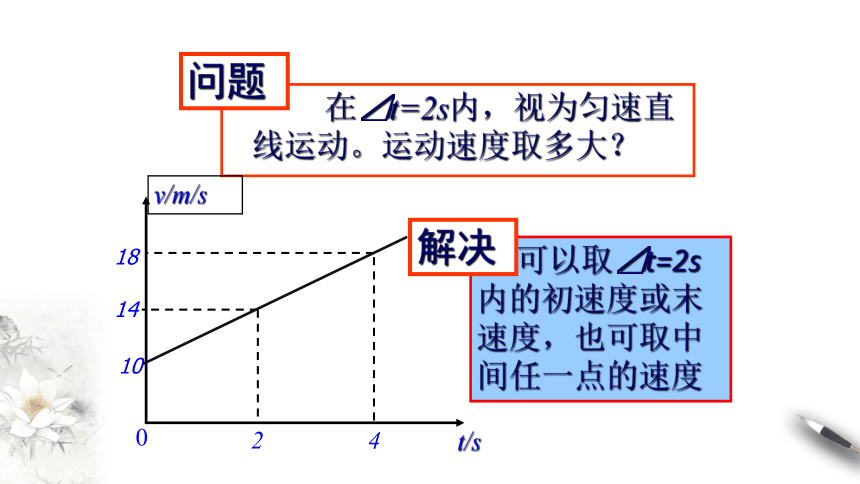
在⊿t=2s内,视为匀速直线运动。运动速度取多大?
问题
t/s
v/m/s
10
4
18
0
14
2
可以取⊿t=2s内的初速度或末速度,也可取中间任一点的速度
解决
t/s
v/m/s
10
4
18
0
14
2
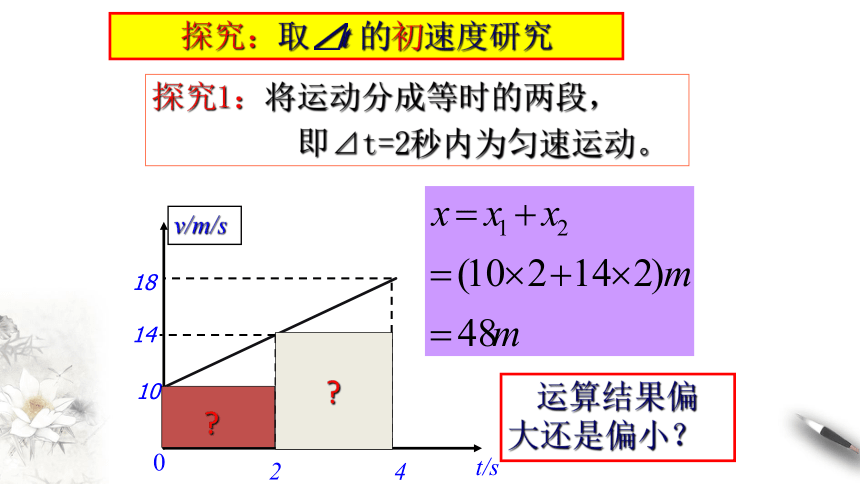
探究1:将运动分成等时的两段,
即⊿t=2秒内为匀速运动。
探究:取⊿t 的初速度研究
运算结果偏大还是偏小?
探究2:将运动分成等时的四段,
即⊿t=1秒内为匀速运动。
时刻( s) 0 1 2 3 4
速度(m/s) 10 12 14 16 18
t/s
v/m/s
10
4
18
0
14
2
3
1
探究:取⊿t 的初速度研究
运算结果偏大还是偏小?
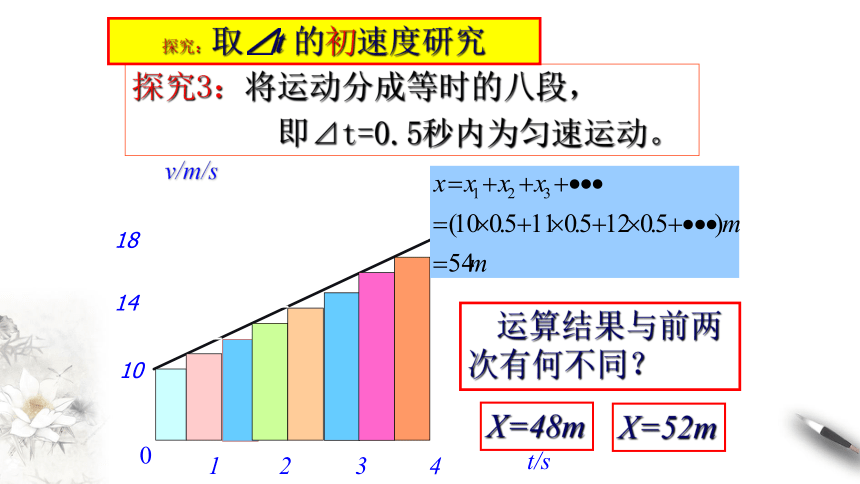
探究3:将运动分成等时的八段,
即⊿t=0.5秒内为匀速运动。
t/s
v/m/s
10
4
18
0
14
2
3
1
运算结果与前两次有何不同?
X=48m
X=52m
探究:取⊿t 的初速度研究
探究小结----图象分析
t/s
v/m/s
10
4
18
0
14
2
t/s
v/m/s
10
4
18
0
14
2
3
1
3
1
t/s
v/m/s
10
4
18
0
14
2
⊿t 越小,估算值就越接近真实值!
X=48m
X=52m
X=54m
结论
(大于54m)
v/m/s
0
2
4
2
4
6
3
t/s
5
1
v/m/s
0
2
4
2
4
6
3
t/s
5
1
从v-t图象中探究匀变速直线运动的位移
分割
粗略地表示位移
较精确地表示位移
假如把时间轴无限分割,情况又会怎么样呢?
通过v-t图象推导出匀变速直线运动的位移规律
t
v
v0
t
vt
0
位移=梯形“面积”
X与t成正比吗?
vt = v0+ at
匀变速直线运动的位移是时间的二次函数。
匀变速直线运动的位移与时间的关系
这就是匀变速直线运动的位移公式。
匀变速直线运动的位移
1.位移公式:
2.对位移公式的理解:
⑴反映了位移随时间的变化规律。
⑵因为υ0、α、x均为矢量,使用公式时应先规定正方向。(一般以υ0的方向为正方向)若物体做匀加速运动,a取正值,若物体做匀减速运动,则a取负值。
(3)若v0=0,
x1=v0t
位移公式的再认识
v
t
v0
t
vt
0
x=x1+x2
如图乙所示,在 v-t 图像中,各段位移可以用一个又窄又高的小矩形的面积代表。5 个小矩形的面积之和近似地代表物体在整个运动过程中的位移。如果以这5个小矩形的面积之和算出的位移代表物体在整个过程中的位移,显然位移就少算了。
拓展学习
为了精确一些,可以把运动过程划分为更多的小段,如图丙所示,用所有这些小段的位移之和,近似代表物体在整个过程中的位移。小矩形越窄,多个小矩形的面积之和越接近物体的位移。
拓展学习
可以想象,如果把整个运动过程分割得非常非常细,很多很多小矩形的面积之和就能非常精确地代表物体的位移了。这时,很多很多小矩形顶端的“锯齿形”就看不出来了,这些小矩形合在一起成了一个梯形 OABC(图 丁)。这个梯形的面积就代表做匀变速直线运动的物体从开始(此时速度是 v0)到 t 时刻(此时速度是 v)这段时间间隔的位移。
拓展学习
上面这种分析问题的方法具有一般意义,原则上对于处理任意形状的 v-t 图像都适用。对于图 所示的运动物体的位移,可用其 v-t 图像着色部分图形的面积来表示。
在处理较复杂的变化量问题时,常常先把整个区间化为若干个小区间,认为每一小区间内研究的量不变,再求和。这是物理学中常用的一种方法。
拓展学习
【例题 1】航空母舰的舰载机既要在航母上起飞,也要在航母上降落。
(1)某舰载机起飞时,采用弹射装置使飞机获得 10 m/s 的速度后,由机上发动机使飞机获得 25 m/s2 的加速度在航母跑道上匀加速前进,2.4 s 后离舰升空。飞机匀加速滑行的距离是多少?
(2)飞机在航母上降落时,需用阻拦索使飞机迅速停下来。若某次飞机着舰时的速度为 80 m/s,飞机钩住阻拦索后经过 2.5 s 停下来。将这段运动视为匀减速直线运动,此过程中飞机加速度的大小及滑行的距离各是多少?
【分析 】两个问题都是已知匀变速直线运动的时间来计算位移。
第(1)问需要用匀变速直线运动的位移与时间的关系式计算。
第(2)问中,飞机着舰做匀减速直线运动的加速度需要根据速度与时间的关系式计算。匀减速运动各矢量的方向较为复杂,因此需要建立一维坐标系来确定它们的正负。
【解 析】(1)根据匀变速直线运动的位移与时间的关系式,有
(2)沿飞机滑行方向建立一维坐标系,飞机初速度 v0 = 80 m/s,末速度 v = 0,根据匀变速直线运动的速度与时间的关系式,有
加速度为负值表示方向与 x 轴正方向相反。再根据匀变速直线运动的位移与时间的关系式,有
【答案】(1)飞机起飞时滑行距离为 96 m。(2)着舰过程中加速度的大小为 32 m/s2,滑行距离为100 m。
二、速度与位移的关系
速度—时间公式
位移—时间公式
①
②
由①式有
可得
③
将③式代入②式,有
公式的推导
速度--位移公式
说明:
1、v-x公式适用于已知量和未知量均不涉及时间的问题
2、v-x公式中包含的4个物理量均为矢量,需建立坐标系以确定其正负
【特别提醒】匀变速直线运动的速度与位移的关系式。如果在所研究的问题中,已知量和未知量都不涉及时间,利用这个公式求解,往往会更简便。
【例题2】动车铁轨旁两相邻里程碑之间的距离是1km。某同学乘坐动车时,通过观察里程碑和车厢内电子屏上显示的动车速度来估算动车减速进站时的加速度大小。当他身边的窗户经过某一里程碑时,屏幕显示的动车速度是126km/h。动车又前进了 3 个里程碑时,速度变为 54 km/h。把动车进站过程视为匀减速直线运动。
那么动车进站的加速度是多少?
它还要行驶多远才能停下来?
【分析】 由于把动车进站过程视为匀减速直线运动,因此可以应用匀变速直线运动的速度与位移关系式计算动车的加速度。本题加速度方向跟速度方向相反,因此需要建立一维坐标系来处理相关物理量的正负号。
【解析】 沿动车运动方向为正方向建立一维坐标系。把动车通过 3 000 m 的运动称为前一过程,之后到停下来称为后一过程。
设在前一过程中的末位置为 M 点。 初速度 v0 = 126 km/h = 35 m/s,末速度 vM = 54 km/h = 15 m/s,位移 x1 = 3 000 m。
对前一过程,根据匀变速直线运动的速度与位移的关系式,有
对后一过程,末速度 v = 0,初速度 vM = 15 m/s。
由 v2 = vM2 + 2ax2,有
【答案】动车进站的加速度大小为 0.167 m/s2,方向与动车运动方向相反;还要行驶 674 m 才能停下来。
人教2019版 必修第一册
2.3 匀变速直线运动的位移与时间的关系
第二章 匀变速直线运动的研究
【新课导入】
由做匀速直线运动物体的 v-t 图像可以看出,在时间 t 内的位移 x 对应图中着色部分的矩形面积。
那么,做匀变速直线运动的物体,在时间 t 内的位移与时间会有怎样的关系?
匀速直线运动的位移
x=vt
v
t
结论:
匀速直线运动的位移就是v – t 图线与t轴所夹的矩形“面积”。
公式法
图象法
v/m·s-1
t/s
2
6
4
10
8
3
4
5
6
0
2
1
甲
-2
-4
x
面积也有正负,面积为正,表示位移的方向为正方向,
面积为负值,表示位移的方向为负方向.
乙
X甲
X乙
匀变速直线运动的位移是否也对应 v-t 图象一定的面积?
t
v
v0
t
vt
0
…
我们需要研究匀变速直线运动的位移规律!
问题
解决
一、匀变速直线运动的位移
怎样求解匀变速直线运动的位移?
将运动进行分割,在很短时间(⊿t)内,将变速直线运动近似为匀速直线运动,利用 x=v t 计算每一段的位移,各段位移之和即为变速运动的位移。
问题
解决
将复杂问题抽象成一个我们熟悉的简单模型,利用这个模型的规律进行近似研究,能得到接近真实值的研究结果。这是物理思想方法之一。
试探:将运动分成等时的两段,即⊿t=2s内视为匀速运动。
在⊿t=2s内,视为匀速直线运动。运动速度取多大?
时刻( s) 0 2 4
速度(m/s) 10 14 18
t/s
v/m/s
10
4
18
0
14
2
在⊿t=2s内,视为匀速直线运动。运动速度取多大?
问题
t/s
v/m/s
10
4
18
0
14
2
可以取⊿t=2s内的初速度或末速度,也可取中间任一点的速度
解决
t/s
v/m/s
10
4
18
0
14
2
探究1:将运动分成等时的两段,
即⊿t=2秒内为匀速运动。
探究:取⊿t 的初速度研究
运算结果偏大还是偏小?
探究2:将运动分成等时的四段,
即⊿t=1秒内为匀速运动。
时刻( s) 0 1 2 3 4
速度(m/s) 10 12 14 16 18
t/s
v/m/s
10
4
18
0
14
2
3
1
探究:取⊿t 的初速度研究
运算结果偏大还是偏小?
探究3:将运动分成等时的八段,
即⊿t=0.5秒内为匀速运动。
t/s
v/m/s
10
4
18
0
14
2
3
1
运算结果与前两次有何不同?
X=48m
X=52m
探究:取⊿t 的初速度研究
探究小结----图象分析
t/s
v/m/s
10
4
18
0
14
2
t/s
v/m/s
10
4
18
0
14
2
3
1
3
1
t/s
v/m/s
10
4
18
0
14
2
⊿t 越小,估算值就越接近真实值!
X=48m
X=52m
X=54m
结论
(大于54m)
v/m/s
0
2
4
2
4
6
3
t/s
5
1
v/m/s
0
2
4
2
4
6
3
t/s
5
1
从v-t图象中探究匀变速直线运动的位移
分割
粗略地表示位移
较精确地表示位移
假如把时间轴无限分割,情况又会怎么样呢?
通过v-t图象推导出匀变速直线运动的位移规律
t
v
v0
t
vt
0
位移=梯形“面积”
X与t成正比吗?
vt = v0+ at
匀变速直线运动的位移是时间的二次函数。
匀变速直线运动的位移与时间的关系
这就是匀变速直线运动的位移公式。
匀变速直线运动的位移
1.位移公式:
2.对位移公式的理解:
⑴反映了位移随时间的变化规律。
⑵因为υ0、α、x均为矢量,使用公式时应先规定正方向。(一般以υ0的方向为正方向)若物体做匀加速运动,a取正值,若物体做匀减速运动,则a取负值。
(3)若v0=0,
x1=v0t
位移公式的再认识
v
t
v0
t
vt
0
x=x1+x2
如图乙所示,在 v-t 图像中,各段位移可以用一个又窄又高的小矩形的面积代表。5 个小矩形的面积之和近似地代表物体在整个运动过程中的位移。如果以这5个小矩形的面积之和算出的位移代表物体在整个过程中的位移,显然位移就少算了。
拓展学习
为了精确一些,可以把运动过程划分为更多的小段,如图丙所示,用所有这些小段的位移之和,近似代表物体在整个过程中的位移。小矩形越窄,多个小矩形的面积之和越接近物体的位移。
拓展学习
可以想象,如果把整个运动过程分割得非常非常细,很多很多小矩形的面积之和就能非常精确地代表物体的位移了。这时,很多很多小矩形顶端的“锯齿形”就看不出来了,这些小矩形合在一起成了一个梯形 OABC(图 丁)。这个梯形的面积就代表做匀变速直线运动的物体从开始(此时速度是 v0)到 t 时刻(此时速度是 v)这段时间间隔的位移。
拓展学习
上面这种分析问题的方法具有一般意义,原则上对于处理任意形状的 v-t 图像都适用。对于图 所示的运动物体的位移,可用其 v-t 图像着色部分图形的面积来表示。
在处理较复杂的变化量问题时,常常先把整个区间化为若干个小区间,认为每一小区间内研究的量不变,再求和。这是物理学中常用的一种方法。
拓展学习
【例题 1】航空母舰的舰载机既要在航母上起飞,也要在航母上降落。
(1)某舰载机起飞时,采用弹射装置使飞机获得 10 m/s 的速度后,由机上发动机使飞机获得 25 m/s2 的加速度在航母跑道上匀加速前进,2.4 s 后离舰升空。飞机匀加速滑行的距离是多少?
(2)飞机在航母上降落时,需用阻拦索使飞机迅速停下来。若某次飞机着舰时的速度为 80 m/s,飞机钩住阻拦索后经过 2.5 s 停下来。将这段运动视为匀减速直线运动,此过程中飞机加速度的大小及滑行的距离各是多少?
【分析 】两个问题都是已知匀变速直线运动的时间来计算位移。
第(1)问需要用匀变速直线运动的位移与时间的关系式计算。
第(2)问中,飞机着舰做匀减速直线运动的加速度需要根据速度与时间的关系式计算。匀减速运动各矢量的方向较为复杂,因此需要建立一维坐标系来确定它们的正负。
【解 析】(1)根据匀变速直线运动的位移与时间的关系式,有
(2)沿飞机滑行方向建立一维坐标系,飞机初速度 v0 = 80 m/s,末速度 v = 0,根据匀变速直线运动的速度与时间的关系式,有
加速度为负值表示方向与 x 轴正方向相反。再根据匀变速直线运动的位移与时间的关系式,有
【答案】(1)飞机起飞时滑行距离为 96 m。(2)着舰过程中加速度的大小为 32 m/s2,滑行距离为100 m。
二、速度与位移的关系
速度—时间公式
位移—时间公式
①
②
由①式有
可得
③
将③式代入②式,有
公式的推导
速度--位移公式
说明:
1、v-x公式适用于已知量和未知量均不涉及时间的问题
2、v-x公式中包含的4个物理量均为矢量,需建立坐标系以确定其正负
【特别提醒】匀变速直线运动的速度与位移的关系式。如果在所研究的问题中,已知量和未知量都不涉及时间,利用这个公式求解,往往会更简便。
【例题2】动车铁轨旁两相邻里程碑之间的距离是1km。某同学乘坐动车时,通过观察里程碑和车厢内电子屏上显示的动车速度来估算动车减速进站时的加速度大小。当他身边的窗户经过某一里程碑时,屏幕显示的动车速度是126km/h。动车又前进了 3 个里程碑时,速度变为 54 km/h。把动车进站过程视为匀减速直线运动。
那么动车进站的加速度是多少?
它还要行驶多远才能停下来?
【分析】 由于把动车进站过程视为匀减速直线运动,因此可以应用匀变速直线运动的速度与位移关系式计算动车的加速度。本题加速度方向跟速度方向相反,因此需要建立一维坐标系来处理相关物理量的正负号。
【解析】 沿动车运动方向为正方向建立一维坐标系。把动车通过 3 000 m 的运动称为前一过程,之后到停下来称为后一过程。
设在前一过程中的末位置为 M 点。 初速度 v0 = 126 km/h = 35 m/s,末速度 vM = 54 km/h = 15 m/s,位移 x1 = 3 000 m。
对前一过程,根据匀变速直线运动的速度与位移的关系式,有
对后一过程,末速度 v = 0,初速度 vM = 15 m/s。
由 v2 = vM2 + 2ax2,有
【答案】动车进站的加速度大小为 0.167 m/s2,方向与动车运动方向相反;还要行驶 674 m 才能停下来。
