【期末押题预测】期末核心考点 圆周运动(含解析)2024-2025学年高一下学期物理 人教版(2019)
文档属性
| 名称 | 【期末押题预测】期末核心考点 圆周运动(含解析)2024-2025学年高一下学期物理 人教版(2019) |  | |
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-06-08 23:33:31 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
期末核心考点 圆周运动
一.选择题(共7小题)
1.(2025春 成华区期中)如图甲所示,修正带是通过两个齿轮的相互咬合进行工作的,其原理可简化为图乙所示,其中A、B两点是两个齿轮的啮合点,则齿轮上A、B两点具有相同的( )
A.线速度的大小 B.角速度
C.周期 D.向心加速度的大小
2.(2025春 城关区校级期中)中国选手邓雅文在2024年巴黎奥运会女子自由式小轮车公园赛决赛中获得金牌。如图所示,几位运动员正在倾斜的弯道上做匀速圆周运动,圆周运动的半径为r,车相对弯道无侧向滑动。若邓雅文连同小轮车(可视为质点)的总质量为m,倾斜弯道可视为倾角为θ的斜面,不计摩擦阻力和空气阻力,重力加速度大小为g。下列说法正确的是( )
A.邓雅文和小轮车所受支持力竖直向上
B.邓雅文和小轮车对弯道的压力大小为
C.邓雅文和小轮车的线速度大小为
D.邓雅文和小轮车运动的半径越大,其线速度就越小
3.(2025春 西城区校级期中)如图是宇航员在“天宫课堂”中利用旋转的方法进行水油分离的实验装置,在空间站中快速摇转该装置就可以实现水油分离。关于这个实验,下列说法正确的是( )
A.不旋转时,由于水和油受重力会自然分层
B.旋转时,转速越小越容易实现水油分离
C.水油分离时靠近试管底部的是密度较大的水
D.在天宫中利用此装置进行实验,装置必须水平放置才能实现水油分离
4.(2025春 农安县期中)小物块紧贴粗糙圆筒内壁,随圆筒一起绕竖直中心轴线做匀速圆周运动(物块与圆筒保持相对静止),如图所示。关于小物块受力情况下列说法正确的是( )
A.物块不受摩擦力
B.摩擦力提供向心力
C.弹力和摩擦力的合力提供向心力
D.弹力提供向心力
5.(2025春 南京期中)如图所示,某同学坐在摩天轮的座椅上随座舱在竖直平面内做匀速圆周运动,座椅始终保持水平。图中M、N与圆心O等高,P位于最低点,Q位于最高点。下列说法中正确的是( )
A.M处座椅对人的支持力大于人的重力
B.N处座椅对人的作用力大于人的重力
C.P处座椅对人的支持力小于人的重力
D.Q处座椅对人的摩擦力方向水平向右
6.(2025春 西城区校级期中)如图所示,长L的轻杆一端与一小球相连,另一端连在光滑固定轴上,在最高点给小球一个向右的水平初速度v0,小球在竖直平面内做顺时针方向的圆周运动,重力加速度为g。下列判断正确的是( )
A.最高点处轻杆对小球作用力一定指向圆心
B.小球运动到与圆心等高的位置时,其加速度大小可能为g
C.在小球从最高点到最低点的过程中,重力做功的功率一直增大
D.如果增大v0,在最低点与圆心等高位置处轻杆对小球拉力的差值不变
7.(2025春 香坊区校级期中)如图甲所示是哈尔滨红博广场转盘道的俯视图,A、B两车(同种型号可认为质量相等)正在绕环岛做线速度大小相等的匀速圆周运动,如图乙所示。已知A、B两车做匀速圆周运动的半径之比满足rA:rB=3:4,下列说法正确的是( )
A.A、B两车的角速度之比ωA:ωB=4:3
B.A、B两车的向心加速度之比aA:aB=3:4
C.A、B两车所受的合力大小之比FA:FB=1:1
D.A、B两车所需的向心力大小之比FnA:FnB=9:16
二.多选题(共3小题)
(多选)8.(2025春 成华区期中)如图所示的四幅图表示的是有关圆周运动的基本模型,下列说法正确的是( )
A.图a中轻杆长为l,若小球在最高点的速率小于,则杆对小球的作用力向上
B.图b中若火车转弯速率小于设计转弯速率,则轮缘对外轨道有横向挤压作用
C.图c中静置于圆盘上的A和B材料相同,质量mA=2mB,到转轴的距离满足RA=2RB,若从零开始逐渐增大圆盘转速,则物体B先相对圆盘滑动
D.图d中两个小球在相同高度的水平面内做匀速圆周运动,它们的角速度大小相同
(多选)9.(2025春 西安校级月考)如图所示,A、B两个材料相同的物体放在水平旋转的圆盘上,A的质量为m,B的质量为2m,B离轴距离为R,A离轴距离为2R,两物体始终相对盘静止,则( )
A.A与B的线速度大小之比为2:1
B.A与B的角速度之比为1:1
C.A与B的向心加速度大小之比为1:1
D.在转盘转速增加时,A比B先开始滑动
(多选)10.(2025春 东城区校级期中)如图所示,在光滑的水平面上放一个原长为L的轻质弹簧,劲度系数为k,它的一端固定,另一端系一个质量为m的小球。当小球在该平面上做半径为4L的匀速圆周运动时( )
A.小球做圆周运动的向心力为3kL
B.小球做圆周运动的线速度为2kL
C.小球做圆周运动的角速度为
D.小球做圆运动的周期为2π
三.填空题(共3小题)
11.(2025春 泉州期中)如图所示,一皮带传动装置,A、B、C三点到各自转轴的距离分别为RA、RB、RC,已知RB=RC,若在传动过程中,皮带不打滑。则A点与C点的角速度之比 ,A、B、C三点线速度之比为 。
12.(2025春 鼓楼区校级期中)如图,小程同学购买的变速自行车有3级链轮和6级飞轮,踏板与链轮固接,后轮与飞轮固接,链轮和飞轮的齿数如表所示。骑行时通过选择不同的链轮和飞轮,可以获得合理的变速。假设踏板的转速不变,选择链轮的齿数为48,为使自行车行进的速度最大,应选择的飞轮的齿数为 ;此时链轮与后轮的转速之比为 。
名称 链轮
齿数 48 38 28
名称 飞轮
齿数 14 16 18 22 24 28
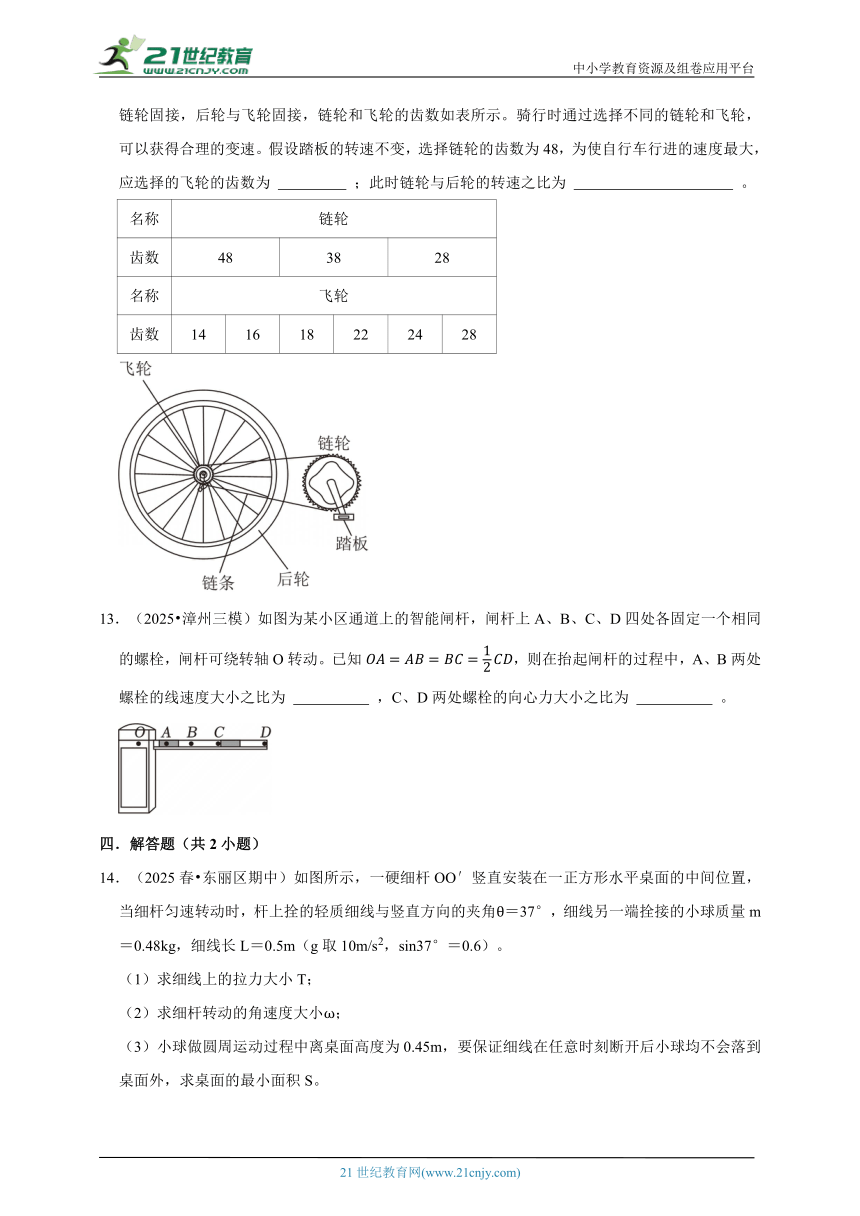
13.(2025 漳州三模)如图为某小区通道上的智能闸杆,闸杆上A、B、C、D四处各固定一个相同的螺栓,闸杆可绕转轴O转动。已知,则在抬起闸杆的过程中,A、B两处螺栓的线速度大小之比为 ,C、D两处螺栓的向心力大小之比为 。
四.解答题(共2小题)
14.(2025春 东丽区期中)如图所示,一硬细杆OO′竖直安装在一正方形水平桌面的中间位置,当细杆匀速转动时,杆上拴的轻质细线与竖直方向的夹角θ=37°,细线另一端拴接的小球质量m=0.48kg,细线长L=0.5m(g取10m/s2,sin37°=0.6)。
(1)求细线上的拉力大小T;
(2)求细杆转动的角速度大小ω;
(3)小球做圆周运动过程中离桌面高度为0.45m,要保证细线在任意时刻断开后小球均不会落到桌面外,求桌面的最小面积S。
15.(2025春 云岩区校级期中)如图所示,半径R=0.20m的光滑半圆环轨道处于竖直平面内,半圆环与水平地面相切于圆环的端点A。一质量为m的小球从A点冲上竖直半圆环轨道,沿轨道运动到B点飞出,最后落在水平地面上的C点(图上未画),已知小球在B点时对轨道的压力恰为mg,g取10m/s2,求:
(1)小球在B点的速度;
(2)A、C间的距离。
期末核心考点 圆周运动
参考答案与试题解析
一.选择题(共7小题)
1.(2025春 成华区期中)如图甲所示,修正带是通过两个齿轮的相互咬合进行工作的,其原理可简化为图乙所示,其中A、B两点是两个齿轮的啮合点,则齿轮上A、B两点具有相同的( )
A.线速度的大小 B.角速度
C.周期 D.向心加速度的大小
【考点】向心加速度的表达式及影响向心加速度大小的因素;线速度与角速度的关系;传动问题.
【专题】定性思想;推理法;匀速圆周运动专题;推理论证能力.
【答案】A
【分析】修正带的传动属于齿轮传动,A与B的线速度大小相等,由v=ωr研究A与B角速度的关系,由向心加速度公式研究向心加速度的关系,由研究周期关系。
【解答】解:AB、修正带的传动属于齿轮传动,A与B的线速度大小相等;二者的半径不同,由v=ωr可知A与B角速度的不相等,故A正确,B错误;
C、二者角速度不相等,根据可知,二者的周期不相等,故C错误;
D、由向心加速度公式,A的半径大于B的半径,可知,A的向心加速度小于B的向心加速度,故D错误。
故选:A。
【点评】本题考查灵活选择物理规律的能力.对于圆周运动,公式较多,要根据不同的条件灵活选择公式。
2.(2025春 城关区校级期中)中国选手邓雅文在2024年巴黎奥运会女子自由式小轮车公园赛决赛中获得金牌。如图所示,几位运动员正在倾斜的弯道上做匀速圆周运动,圆周运动的半径为r,车相对弯道无侧向滑动。若邓雅文连同小轮车(可视为质点)的总质量为m,倾斜弯道可视为倾角为θ的斜面,不计摩擦阻力和空气阻力,重力加速度大小为g。下列说法正确的是( )
A.邓雅文和小轮车所受支持力竖直向上
B.邓雅文和小轮车对弯道的压力大小为
C.邓雅文和小轮车的线速度大小为
D.邓雅文和小轮车运动的半径越大,其线速度就越小
【考点】车辆在道路上的转弯问题;牛顿第二定律与向心力结合解决问题.
【专题】定量思想;推理法;牛顿运动定律综合专题;推理论证能力.
【答案】B
【分析】邓雅文和小轮车所受支持力垂直于轨道向上;受力分析再根据牛顿第三定律求解;根据牛顿第二定律列式求解,分析判断。
【解答】解:A、邓雅文和小轮车所受支持力垂直于轨道向上,而不是竖直向上,故A错误;
B、如图所示
对邓雅文和小轮车受力分析,根据几何关系可得
根据牛顿第三定律,车对弯道的压力大小为,故B正确;
CD、根据牛顿第二定律可得
解得邓雅文和小轮车的线速度大小
可知邓雅文和小轮车运动的半径越大,其线速度越大,故CD错误。
故选:B。
【点评】本题以实际运动场景为背景,综合考查了匀速圆周运动的向心力来源、斜面上的受力分析、正交分解法、牛顿第三定律以及物理量的函数关系,要求考生能将实际问题抽象为物理模型,并熟练运用力学规律进行推导和判断。
3.(2025春 西城区校级期中)如图是宇航员在“天宫课堂”中利用旋转的方法进行水油分离的实验装置,在空间站中快速摇转该装置就可以实现水油分离。关于这个实验,下列说法正确的是( )
A.不旋转时,由于水和油受重力会自然分层
B.旋转时,转速越小越容易实现水油分离
C.水油分离时靠近试管底部的是密度较大的水
D.在天宫中利用此装置进行实验,装置必须水平放置才能实现水油分离
【考点】离心运动的应用和防止.
【专题】定性思想;推理法;匀速圆周运动专题;推理论证能力.
【答案】C
【分析】根据完全失重状态运用离心运动的知识,结合不同物质的密度差异在圆周运动中的表现进行分析解答。
【解答】解:A.太空中处于完全失重状态,不旋转时水和油不能分离自然分层,故A错误;
B.旋转时,转速越大越容易发生离心运动,所以更容易实现水油分离,故B错误;
C.水油分离是因为水的密度较大更容易离心而分离的,则靠近试管底部的是密度较大的水,故C正确;
D.在天宫中利用此装置进行实验,处于完全失重状态,则装置竖直放置也能实现水油分离,故D错误。
故选:C。
【点评】考查离心运动的知识和离心现象的理解,会根据题意进行准确的分析解答。
4.(2025春 农安县期中)小物块紧贴粗糙圆筒内壁,随圆筒一起绕竖直中心轴线做匀速圆周运动(物块与圆筒保持相对静止),如图所示。关于小物块受力情况下列说法正确的是( )
A.物块不受摩擦力
B.摩擦力提供向心力
C.弹力和摩擦力的合力提供向心力
D.弹力提供向心力
【考点】向心力的来源分析.
【专题】定性思想;推理法;弹力的存在及方向的判定专题;摩擦力专题;理解能力.
【答案】D
【分析】根据小物块在随圆筒做匀速圆周运动时,其受力情况。考虑到圆筒内壁粗糙,物块可能会受到摩擦力的作用。提供向心力的是指向圆心的力,即圆筒内壁对物块的弹力。
【解答】解:根据受力分析可知,竖直方向物块受重力和摩擦力作用而平衡,水平方向受筒壁的弹力作用,其中弹力提供物块做圆周运动的向心力,故D正确,ABC错误;
故选:D。
【点评】此题的关键在于理解向心力的来源及物块与圆筒之间的摩擦力作用。
5.(2025春 南京期中)如图所示,某同学坐在摩天轮的座椅上随座舱在竖直平面内做匀速圆周运动,座椅始终保持水平。图中M、N与圆心O等高,P位于最低点,Q位于最高点。下列说法中正确的是( )
A.M处座椅对人的支持力大于人的重力
B.N处座椅对人的作用力大于人的重力
C.P处座椅对人的支持力小于人的重力
D.Q处座椅对人的摩擦力方向水平向右
【考点】向心力的定义及物理意义(受力分析方面);匀速圆周运动.
【专题】定性思想;推理法;匀速圆周运动专题;推理论证能力.
【答案】B
【分析】匀速圆周运动向心力合力提供向心力,方向指向圆心。
【解答】解:A.在M点,由于摩天轮在做匀速圆周运动,支持力等于人的重力,故A错误;
B.在N点座椅对人的作用力指人受到的支持力与摩擦力的合力,其中支持力等于重力,方向向上,摩擦力提供向心力,方向向左,故座椅对人的作用力一定大于人的重力,故B正确;
C.在P点,重力与支持力的合力提供向心力,方向向上,故支持力大于重力,故C错误;
D.在Q点由支持力与重力提供向心力,方向向下,摩擦力等于零,故D错误。
故选:B。
【点评】考查对匀速圆周运动的理解,清楚向心力的含义。
6.(2025春 西城区校级期中)如图所示,长L的轻杆一端与一小球相连,另一端连在光滑固定轴上,在最高点给小球一个向右的水平初速度v0,小球在竖直平面内做顺时针方向的圆周运动,重力加速度为g。下列判断正确的是( )
A.最高点处轻杆对小球作用力一定指向圆心
B.小球运动到与圆心等高的位置时,其加速度大小可能为g
C.在小球从最高点到最低点的过程中,重力做功的功率一直增大
D.如果增大v0,在最低点与圆心等高位置处轻杆对小球拉力的差值不变
【考点】杆球类模型及其临界条件;功率的定义、物理意义和计算式的推导;牛顿第二定律的简单应用;牛顿第二定律与向心力结合解决问题.
【专题】定量思想;推理法;匀速圆周运动专题;推理论证能力.
【答案】D
【分析】根据向心力公式、竖直面内圆周运动杆模型和合加速度知识,功率公式和机械能守恒定律结合牛顿第二定律列式求解。
【解答】解:A.根据向心力的公式,最高点处速度较小时,小球的重力可能大于小球做圆周运动的向心力,此时轻杆会对小球施加背向圆心的支持力,故A错误;
B.小球运动到与圆心等高的位置时,向心加速度水平,重力加速度竖直向下,则合加速度大小一定大于g,故B错误;
C.小球从最高点到最低点的过程中,速度方向逐渐由水平向左变成水平向右,竖直方向的分速度先增大后减小,根据功率的定义式,可知小球受到的重力的功率先变大后变小,故C错误;
D.如果增大v0小球从最高点运动到水平位置的过程,根据机械能守恒定律,有,在水平位置受到拉力提供向心力,根据牛顿第二定律,有,在最低点,再对小球受力分析,同理根据牛顿第二定律,有,从最高点到最低点的过程,根据机械能守恒定律,有,联立解得F2﹣F1=3mg,根据表达式可知如果增大v0,轻杆在最低点与水平位置处对小球拉力的差值不会变化,故D正确。
故选:D。
【点评】考查向心力公式、竖直面内圆周运动杆模型和合加速度知识,功率公式和机械能守恒定律结合牛顿第二定律,会根据题意进行准确分析解答。
7.(2025春 香坊区校级期中)如图甲所示是哈尔滨红博广场转盘道的俯视图,A、B两车(同种型号可认为质量相等)正在绕环岛做线速度大小相等的匀速圆周运动,如图乙所示。已知A、B两车做匀速圆周运动的半径之比满足rA:rB=3:4,下列说法正确的是( )
A.A、B两车的角速度之比ωA:ωB=4:3
B.A、B两车的向心加速度之比aA:aB=3:4
C.A、B两车所受的合力大小之比FA:FB=1:1
D.A、B两车所需的向心力大小之比FnA:FnB=9:16
【考点】车辆在道路上的转弯问题;线速度与角速度的关系;牛顿第二定律与向心力结合解决问题.
【专题】定量思想;控制变量法;牛顿第二定律在圆周运动中的应用;分析综合能力.
【答案】A
【分析】A、B两车做匀速圆周运动的线速度大小相等,根据ω求角速度之比;根据求向心加速度之比;根据F合=Fn=m求两车所受的合力大小之比以及两车所需的向心力大小之比。
【解答】解:A、A、B两车正在绕环岛做线速度大小相等的匀速圆周运动,根据可得,A、B两车的角速度之比ωA:ωB=rB:rA=4:3,故A正确;
B、根据可得,A、B两车的向心加速度之比aA:aB=rB:rA=4:3,故B错误;
CD、两车做匀速圆周运动,由合力提供向心力,则有,则A、B两车所受的合力大小之比FA:FB=rB:rA=4:3,A、B两车所需的向心力大小之比FnA:FnB=rB:rA=4:3,故CD错误。
故选:A。
【点评】解答本题时,要明确物体做匀速圆周运动时,由合力提供所需要的向心力,并能灵活选择向心力公式。
二.多选题(共3小题)
(多选)8.(2025春 成华区期中)如图所示的四幅图表示的是有关圆周运动的基本模型,下列说法正确的是( )
A.图a中轻杆长为l,若小球在最高点的速率小于,则杆对小球的作用力向上
B.图b中若火车转弯速率小于设计转弯速率,则轮缘对外轨道有横向挤压作用
C.图c中静置于圆盘上的A和B材料相同,质量mA=2mB,到转轴的距离满足RA=2RB,若从零开始逐渐增大圆盘转速,则物体B先相对圆盘滑动
D.图d中两个小球在相同高度的水平面内做匀速圆周运动,它们的角速度大小相同
【考点】拱桥和凹桥类模型分析;水平转盘上物体的圆周运动;火车的轨道转弯问题.
【专题】定量思想;推理法;匀速圆周运动专题;推理论证能力.
【答案】AD
【分析】根据竖直面内圆周运动杆模型、火车转弯和向心力表达式,以及圆锥摆物体的受力情况,向心力表达式进行分析解答。
【解答】解:A.图a中若轻杆上的小球在最高点时,杆受作用力为零,此时,解得,若线速度小于,杆对小球的作用力向上,故A正确;
B.图b中若火车转弯未达规定速度行驶时,此时重力和轨道的支持力的合力大于火车所需的向心力,此时火车有做向心运动的趋势,轮缘对内侧轨道有作用,故B错误;
C.根据f=mω2r,若半径RA=2RB,质量mA=2mB,则A更容易达到最大静摩擦力,发生相对滑动,故C错误;
D.根据mgtanθ=mω2htanθ,可得,则两个小球在相同的高度做匀速圆周运动,它们的角速度相同,故D正确。
故选:AD。
【点评】考查竖直面内圆周运动杆模型、火车转弯和向心力表达式,以及圆锥摆物体的受力情况,向心力表达式,会根据题意进行准确分析解答。
(多选)9.(2025春 西安校级月考)如图所示,A、B两个材料相同的物体放在水平旋转的圆盘上,A的质量为m,B的质量为2m,B离轴距离为R,A离轴距离为2R,两物体始终相对盘静止,则( )
A.A与B的线速度大小之比为2:1
B.A与B的角速度之比为1:1
C.A与B的向心加速度大小之比为1:1
D.在转盘转速增加时,A比B先开始滑动
【考点】水平转盘上物体的圆周运动;角速度、周期、频率与转速的关系及计算;向心加速度的计算.
【专题】比较思想;临界法;牛顿第二定律在圆周运动中的应用;分析综合能力.
【答案】ABD
【分析】A、B同轴转动,角速度相同,根据v=ωr求线速度之比;由向心加速度公式a=rω2求向心加速度之比;谁先达到最大静摩擦力谁先滑动。
【解答】解:AB、A与B两物体始终相对盘静止,则A与B的角速度相同,均等于圆盘的角速度,则有
ωA:ωB=1:1
根据v=ωr可得,vA:vB=rA:rB=2R:R=2:1,故AB正确;
C、根据a=ω2r可得,aA:aB=rA:rB=2R:R=2:1,故C错误;
D、根据静摩擦力提供向心力可得
f=ma
可得A与B所受摩擦力大小相等
最大静摩擦力为
fm=μmg
A的质量小,最大静摩擦力小,所以在转盘转速增加时,A与B所受摩擦力都增大,A静摩擦力先达到最大值,则A比B先滑动,故D正确。
故选:ABD。
【点评】解决本题的关键要知道共轴转动的物体角速度相等,掌握线速度、角速度、向心加速度的关系,并能灵活运用。
(多选)10.(2025春 东城区校级期中)如图所示,在光滑的水平面上放一个原长为L的轻质弹簧,劲度系数为k,它的一端固定,另一端系一个质量为m的小球。当小球在该平面上做半径为4L的匀速圆周运动时( )
A.小球做圆周运动的向心力为3kL
B.小球做圆周运动的线速度为2kL
C.小球做圆周运动的角速度为
D.小球做圆运动的周期为2π
【考点】水平转盘上物体的圆周运动.
【专题】定量思想;推理法;匀速圆周运动专题;推理论证能力.
【答案】AD
【分析】由胡克定律可求得弹簧的弹力,受力分析知弹力提供向心力,由向心力公式逐个分析即可。
【解答】解:由胡克定律得弹簧的弹力F=k 3L
A、弹簧的弹力提供小球做圆周运动的向心力,所以向心力为3kL,故A正确;
B、由向心力公式得,解得:,故B错误;
C、由向心力公式得F=m 4Lω2,解得:,故C错误;
D、由向心力公式得,解得:,故D正确。
故选:AD。
【点评】本题考查了胡克定律、向心力公式,要求熟练掌握向心力公式的不同表达式,根据题目要求灵活选择。
三.填空题(共3小题)
11.(2025春 泉州期中)如图所示,一皮带传动装置,A、B、C三点到各自转轴的距离分别为RA、RB、RC,已知RB=RC,若在传动过程中,皮带不打滑。则A点与C点的角速度之比 1:2 ,A、B、C三点线速度之比为 2:1:2 。
【考点】传动问题;线速度与角速度的关系.
【专题】应用题;定量思想;推理法;匀速圆周运动专题;分析综合能力.
【答案】1:2;2:1:2。
【分析】同轴转动物体的角速度相等,同缘传动的线速度大小相等,根据图示情景,应用线速度与角速度的关系分析答题。
【解答】解:A、C同缘传动,线速度v大小相等,由v=ωr可知,,
A、B同轴转动,它们的角速度ω相等,由v=ωr可知vA:vB=RA:RB=2:1,
又由于vA=vC,则vA:vB:vC=2:1:2;
故答案为:1:2;2:1:2。
【点评】本题考查了传动问题,知道同轴转动物体的角速度相等,同缘传动的线速度大小相等是解题的前提,根据线速度与角速度的关系即可解题。
12.(2025春 鼓楼区校级期中)如图,小程同学购买的变速自行车有3级链轮和6级飞轮,踏板与链轮固接,后轮与飞轮固接,链轮和飞轮的齿数如表所示。骑行时通过选择不同的链轮和飞轮,可以获得合理的变速。假设踏板的转速不变,选择链轮的齿数为48,为使自行车行进的速度最大,应选择的飞轮的齿数为 14 ;此时链轮与后轮的转速之比为 。
名称 链轮
齿数 48 38 28
名称 飞轮
齿数 14 16 18 22 24 28
【考点】角速度、周期、频率与转速的关系及计算.
【专题】定量思想;推理法;匀速圆周运动专题;推理论证能力.
【答案】14,。
【分析】根据共轴转动链轮传动的知识进行分析解答。
【解答】解:链轮和飞轮的线速度相同,飞轮和后轮为共轴转动角速度相同,自行车的行驶速度为后轮的线速度。v飞=v链,ω飞 r飞=ω链 r链,飞轮的角速度,后轮线速度,所以当链轮的齿数最多、飞轮的齿数最少时,自行车速度最大,所以为使自行车行进的速度最大,应选择的飞轮的齿数为14,此时链轮与后轮的转速之比为。
故答案为:14,。
【点评】考查共轴转动链轮传动的知识,会根据题意进行准确分析解答。
13.(2025 漳州三模)如图为某小区通道上的智能闸杆,闸杆上A、B、C、D四处各固定一个相同的螺栓,闸杆可绕转轴O转动。已知,则在抬起闸杆的过程中,A、B两处螺栓的线速度大小之比为 1:2 ,C、D两处螺栓的向心力大小之比为 3:5 。
【考点】探究圆周运动的相关参数问题.
【专题】定量思想;推理法;匀速圆周运动专题;推理论证能力.
【答案】1:2;3:5。
【分析】根据线速度、角速度与半径的关系式计算;根据向心力公式计算。
【解答】解:在抬起闸杆的过程中,杆上各点做圆周运动的角速度ω相等,根据线速度、角速度与半径的关系式v=ωr可得
根据
可得
故答案为:1:2;3:5。
【点评】本题关键掌握在抬起闸杆的过程中,杆上各点做圆周运动的角速度ω相等。
四.解答题(共2小题)
14.(2025春 东丽区期中)如图所示,一硬细杆OO′竖直安装在一正方形水平桌面的中间位置,当细杆匀速转动时,杆上拴的轻质细线与竖直方向的夹角θ=37°,细线另一端拴接的小球质量m=0.48kg,细线长L=0.5m(g取10m/s2,sin37°=0.6)。
(1)求细线上的拉力大小T;
(2)求细杆转动的角速度大小ω;
(3)小球做圆周运动过程中离桌面高度为0.45m,要保证细线在任意时刻断开后小球均不会落到桌面外,求桌面的最小面积S。
【考点】牛顿第二定律与向心力结合解决问题;共点力的平衡问题及求解.
【专题】定量思想;推理法;共点力作用下物体平衡专题;推理论证能力.
【答案】(1)求细线上的拉力大小T为6N;
(2)求细杆转动的角速度大小ω为5rad/s;
(3)桌面的最小面积S为0.81m2。
【分析】第一问利用小球在竖直方向上的受力平衡求解细线拉力。第二问利用小球在水平方向上的向心力公式求解角速度。第三问分析细线断开后小球的运动轨迹,结合平抛运动规律和几何关系求解桌面的最小面积。
【解答】解:(1)小球受到重力mg和细线拉力T的作用。由于小球在竖直方向上受力平衡,因此有:Tcosθ=mg
可得:T=6N
因此,细线上的拉力大小为:T=6N
(2)小球在水平方向上做匀速圆周运动,向心力由细线拉力的水平分量提供,即:Tsinθ=mω2r
其中,小球做圆周运动的半径为:r=Lsinθ
解得:r=0.3m
联立解得:ω=5rad/s。
因此,细线转动的角速度大小为:ω=5rad/s。
(3)当细线断开时,小球以水平速度做平抛运动。小球做圆周运动时的水平速度为:
v=ωr
解得:v=1.5m/s
小球做平抛运动时,竖直方向上做自由落体运动,下落高度为:
h=Lcos45°﹣0.45
解得:h=0.05m
根据自由落体运动公式:
解得:t=0.1s
在水平方向上,小球的水平位移为:x=vt
解得:x=0.15m
小球做圆周运动时的水平半径为0.3m,因此小球在细线断开后水平方向上的最大位移为:
为了保证小球在任意时刻断开后均不会落到桌面外,桌面的最小面积为:S=(πR2)最大
解得:
但是,考虑到小球在细线断开后水平方向上的最大位移为0.3m+0.15m=0.45m,因此桌面的最小面积为:
S=(2×0.45)2m2= 0.81m2,因此,桌面的最小面积为:S= 0.81m2
答:(1)求细线上的拉力大小T为6N;
(2)求细杆转动的角速度大小ω为5rad/s;
(3)桌面的最小面积S为0.81m2。
【点评】该试题涉及圆周运动、牛顿第二定律以及平抛运动的相关知识。
15.(2025春 云岩区校级期中)如图所示,半径R=0.20m的光滑半圆环轨道处于竖直平面内,半圆环与水平地面相切于圆环的端点A。一质量为m的小球从A点冲上竖直半圆环轨道,沿轨道运动到B点飞出,最后落在水平地面上的C点(图上未画),已知小球在B点时对轨道的压力恰为mg,g取10m/s2,求:
(1)小球在B点的速度;
(2)A、C间的距离。
【考点】圆周运动与平抛运动相结合的问题;牛顿第三定律的理解与应用;物体在圆形竖直轨道内的圆周运动.
【专题】计算题;定量思想;模型法;动能定理的应用专题;分析综合能力.
【答案】(1)小球在B点的速度为2m/s;
(2)A、C间的距离为m。
【分析】(1)小球在B点时,由合力提供向心力,根据牛顿第二定律求小球在B点的速度;
(2)从B到C小球做平抛运动,根据分位移公式求解A、C间的距离。
【解答】解:(1)根据牛顿第三定律,小球在B点时轨道对小球的压力为FN=mg,方向竖直向下。
根据牛顿第二定律得
mg+FN=m
解得vB=2m/s
(2)从B到C小球做平抛运动,则有
2R
x=vBt
解得A、C间的距离为xm
答:(1)小球在B点的速度为2m/s;
(2)A、C间的距离为m。
【点评】本题是圆周运动与平抛运动的综合,对于圆周运动,要明确向心力来源。对于平抛运动,要掌握分运动的规律。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末核心考点 圆周运动
一.选择题(共7小题)
1.(2025春 成华区期中)如图甲所示,修正带是通过两个齿轮的相互咬合进行工作的,其原理可简化为图乙所示,其中A、B两点是两个齿轮的啮合点,则齿轮上A、B两点具有相同的( )
A.线速度的大小 B.角速度
C.周期 D.向心加速度的大小
2.(2025春 城关区校级期中)中国选手邓雅文在2024年巴黎奥运会女子自由式小轮车公园赛决赛中获得金牌。如图所示,几位运动员正在倾斜的弯道上做匀速圆周运动,圆周运动的半径为r,车相对弯道无侧向滑动。若邓雅文连同小轮车(可视为质点)的总质量为m,倾斜弯道可视为倾角为θ的斜面,不计摩擦阻力和空气阻力,重力加速度大小为g。下列说法正确的是( )
A.邓雅文和小轮车所受支持力竖直向上
B.邓雅文和小轮车对弯道的压力大小为
C.邓雅文和小轮车的线速度大小为
D.邓雅文和小轮车运动的半径越大,其线速度就越小
3.(2025春 西城区校级期中)如图是宇航员在“天宫课堂”中利用旋转的方法进行水油分离的实验装置,在空间站中快速摇转该装置就可以实现水油分离。关于这个实验,下列说法正确的是( )
A.不旋转时,由于水和油受重力会自然分层
B.旋转时,转速越小越容易实现水油分离
C.水油分离时靠近试管底部的是密度较大的水
D.在天宫中利用此装置进行实验,装置必须水平放置才能实现水油分离
4.(2025春 农安县期中)小物块紧贴粗糙圆筒内壁,随圆筒一起绕竖直中心轴线做匀速圆周运动(物块与圆筒保持相对静止),如图所示。关于小物块受力情况下列说法正确的是( )
A.物块不受摩擦力
B.摩擦力提供向心力
C.弹力和摩擦力的合力提供向心力
D.弹力提供向心力
5.(2025春 南京期中)如图所示,某同学坐在摩天轮的座椅上随座舱在竖直平面内做匀速圆周运动,座椅始终保持水平。图中M、N与圆心O等高,P位于最低点,Q位于最高点。下列说法中正确的是( )
A.M处座椅对人的支持力大于人的重力
B.N处座椅对人的作用力大于人的重力
C.P处座椅对人的支持力小于人的重力
D.Q处座椅对人的摩擦力方向水平向右
6.(2025春 西城区校级期中)如图所示,长L的轻杆一端与一小球相连,另一端连在光滑固定轴上,在最高点给小球一个向右的水平初速度v0,小球在竖直平面内做顺时针方向的圆周运动,重力加速度为g。下列判断正确的是( )
A.最高点处轻杆对小球作用力一定指向圆心
B.小球运动到与圆心等高的位置时,其加速度大小可能为g
C.在小球从最高点到最低点的过程中,重力做功的功率一直增大
D.如果增大v0,在最低点与圆心等高位置处轻杆对小球拉力的差值不变
7.(2025春 香坊区校级期中)如图甲所示是哈尔滨红博广场转盘道的俯视图,A、B两车(同种型号可认为质量相等)正在绕环岛做线速度大小相等的匀速圆周运动,如图乙所示。已知A、B两车做匀速圆周运动的半径之比满足rA:rB=3:4,下列说法正确的是( )
A.A、B两车的角速度之比ωA:ωB=4:3
B.A、B两车的向心加速度之比aA:aB=3:4
C.A、B两车所受的合力大小之比FA:FB=1:1
D.A、B两车所需的向心力大小之比FnA:FnB=9:16
二.多选题(共3小题)
(多选)8.(2025春 成华区期中)如图所示的四幅图表示的是有关圆周运动的基本模型,下列说法正确的是( )
A.图a中轻杆长为l,若小球在最高点的速率小于,则杆对小球的作用力向上
B.图b中若火车转弯速率小于设计转弯速率,则轮缘对外轨道有横向挤压作用
C.图c中静置于圆盘上的A和B材料相同,质量mA=2mB,到转轴的距离满足RA=2RB,若从零开始逐渐增大圆盘转速,则物体B先相对圆盘滑动
D.图d中两个小球在相同高度的水平面内做匀速圆周运动,它们的角速度大小相同
(多选)9.(2025春 西安校级月考)如图所示,A、B两个材料相同的物体放在水平旋转的圆盘上,A的质量为m,B的质量为2m,B离轴距离为R,A离轴距离为2R,两物体始终相对盘静止,则( )
A.A与B的线速度大小之比为2:1
B.A与B的角速度之比为1:1
C.A与B的向心加速度大小之比为1:1
D.在转盘转速增加时,A比B先开始滑动
(多选)10.(2025春 东城区校级期中)如图所示,在光滑的水平面上放一个原长为L的轻质弹簧,劲度系数为k,它的一端固定,另一端系一个质量为m的小球。当小球在该平面上做半径为4L的匀速圆周运动时( )
A.小球做圆周运动的向心力为3kL
B.小球做圆周运动的线速度为2kL
C.小球做圆周运动的角速度为
D.小球做圆运动的周期为2π
三.填空题(共3小题)
11.(2025春 泉州期中)如图所示,一皮带传动装置,A、B、C三点到各自转轴的距离分别为RA、RB、RC,已知RB=RC,若在传动过程中,皮带不打滑。则A点与C点的角速度之比 ,A、B、C三点线速度之比为 。
12.(2025春 鼓楼区校级期中)如图,小程同学购买的变速自行车有3级链轮和6级飞轮,踏板与链轮固接,后轮与飞轮固接,链轮和飞轮的齿数如表所示。骑行时通过选择不同的链轮和飞轮,可以获得合理的变速。假设踏板的转速不变,选择链轮的齿数为48,为使自行车行进的速度最大,应选择的飞轮的齿数为 ;此时链轮与后轮的转速之比为 。
名称 链轮
齿数 48 38 28
名称 飞轮
齿数 14 16 18 22 24 28
13.(2025 漳州三模)如图为某小区通道上的智能闸杆,闸杆上A、B、C、D四处各固定一个相同的螺栓,闸杆可绕转轴O转动。已知,则在抬起闸杆的过程中,A、B两处螺栓的线速度大小之比为 ,C、D两处螺栓的向心力大小之比为 。
四.解答题(共2小题)
14.(2025春 东丽区期中)如图所示,一硬细杆OO′竖直安装在一正方形水平桌面的中间位置,当细杆匀速转动时,杆上拴的轻质细线与竖直方向的夹角θ=37°,细线另一端拴接的小球质量m=0.48kg,细线长L=0.5m(g取10m/s2,sin37°=0.6)。
(1)求细线上的拉力大小T;
(2)求细杆转动的角速度大小ω;
(3)小球做圆周运动过程中离桌面高度为0.45m,要保证细线在任意时刻断开后小球均不会落到桌面外,求桌面的最小面积S。
15.(2025春 云岩区校级期中)如图所示,半径R=0.20m的光滑半圆环轨道处于竖直平面内,半圆环与水平地面相切于圆环的端点A。一质量为m的小球从A点冲上竖直半圆环轨道,沿轨道运动到B点飞出,最后落在水平地面上的C点(图上未画),已知小球在B点时对轨道的压力恰为mg,g取10m/s2,求:
(1)小球在B点的速度;
(2)A、C间的距离。
期末核心考点 圆周运动
参考答案与试题解析
一.选择题(共7小题)
1.(2025春 成华区期中)如图甲所示,修正带是通过两个齿轮的相互咬合进行工作的,其原理可简化为图乙所示,其中A、B两点是两个齿轮的啮合点,则齿轮上A、B两点具有相同的( )
A.线速度的大小 B.角速度
C.周期 D.向心加速度的大小
【考点】向心加速度的表达式及影响向心加速度大小的因素;线速度与角速度的关系;传动问题.
【专题】定性思想;推理法;匀速圆周运动专题;推理论证能力.
【答案】A
【分析】修正带的传动属于齿轮传动,A与B的线速度大小相等,由v=ωr研究A与B角速度的关系,由向心加速度公式研究向心加速度的关系,由研究周期关系。
【解答】解:AB、修正带的传动属于齿轮传动,A与B的线速度大小相等;二者的半径不同,由v=ωr可知A与B角速度的不相等,故A正确,B错误;
C、二者角速度不相等,根据可知,二者的周期不相等,故C错误;
D、由向心加速度公式,A的半径大于B的半径,可知,A的向心加速度小于B的向心加速度,故D错误。
故选:A。
【点评】本题考查灵活选择物理规律的能力.对于圆周运动,公式较多,要根据不同的条件灵活选择公式。
2.(2025春 城关区校级期中)中国选手邓雅文在2024年巴黎奥运会女子自由式小轮车公园赛决赛中获得金牌。如图所示,几位运动员正在倾斜的弯道上做匀速圆周运动,圆周运动的半径为r,车相对弯道无侧向滑动。若邓雅文连同小轮车(可视为质点)的总质量为m,倾斜弯道可视为倾角为θ的斜面,不计摩擦阻力和空气阻力,重力加速度大小为g。下列说法正确的是( )
A.邓雅文和小轮车所受支持力竖直向上
B.邓雅文和小轮车对弯道的压力大小为
C.邓雅文和小轮车的线速度大小为
D.邓雅文和小轮车运动的半径越大,其线速度就越小
【考点】车辆在道路上的转弯问题;牛顿第二定律与向心力结合解决问题.
【专题】定量思想;推理法;牛顿运动定律综合专题;推理论证能力.
【答案】B
【分析】邓雅文和小轮车所受支持力垂直于轨道向上;受力分析再根据牛顿第三定律求解;根据牛顿第二定律列式求解,分析判断。
【解答】解:A、邓雅文和小轮车所受支持力垂直于轨道向上,而不是竖直向上,故A错误;
B、如图所示
对邓雅文和小轮车受力分析,根据几何关系可得
根据牛顿第三定律,车对弯道的压力大小为,故B正确;
CD、根据牛顿第二定律可得
解得邓雅文和小轮车的线速度大小
可知邓雅文和小轮车运动的半径越大,其线速度越大,故CD错误。
故选:B。
【点评】本题以实际运动场景为背景,综合考查了匀速圆周运动的向心力来源、斜面上的受力分析、正交分解法、牛顿第三定律以及物理量的函数关系,要求考生能将实际问题抽象为物理模型,并熟练运用力学规律进行推导和判断。
3.(2025春 西城区校级期中)如图是宇航员在“天宫课堂”中利用旋转的方法进行水油分离的实验装置,在空间站中快速摇转该装置就可以实现水油分离。关于这个实验,下列说法正确的是( )
A.不旋转时,由于水和油受重力会自然分层
B.旋转时,转速越小越容易实现水油分离
C.水油分离时靠近试管底部的是密度较大的水
D.在天宫中利用此装置进行实验,装置必须水平放置才能实现水油分离
【考点】离心运动的应用和防止.
【专题】定性思想;推理法;匀速圆周运动专题;推理论证能力.
【答案】C
【分析】根据完全失重状态运用离心运动的知识,结合不同物质的密度差异在圆周运动中的表现进行分析解答。
【解答】解:A.太空中处于完全失重状态,不旋转时水和油不能分离自然分层,故A错误;
B.旋转时,转速越大越容易发生离心运动,所以更容易实现水油分离,故B错误;
C.水油分离是因为水的密度较大更容易离心而分离的,则靠近试管底部的是密度较大的水,故C正确;
D.在天宫中利用此装置进行实验,处于完全失重状态,则装置竖直放置也能实现水油分离,故D错误。
故选:C。
【点评】考查离心运动的知识和离心现象的理解,会根据题意进行准确的分析解答。
4.(2025春 农安县期中)小物块紧贴粗糙圆筒内壁,随圆筒一起绕竖直中心轴线做匀速圆周运动(物块与圆筒保持相对静止),如图所示。关于小物块受力情况下列说法正确的是( )
A.物块不受摩擦力
B.摩擦力提供向心力
C.弹力和摩擦力的合力提供向心力
D.弹力提供向心力
【考点】向心力的来源分析.
【专题】定性思想;推理法;弹力的存在及方向的判定专题;摩擦力专题;理解能力.
【答案】D
【分析】根据小物块在随圆筒做匀速圆周运动时,其受力情况。考虑到圆筒内壁粗糙,物块可能会受到摩擦力的作用。提供向心力的是指向圆心的力,即圆筒内壁对物块的弹力。
【解答】解:根据受力分析可知,竖直方向物块受重力和摩擦力作用而平衡,水平方向受筒壁的弹力作用,其中弹力提供物块做圆周运动的向心力,故D正确,ABC错误;
故选:D。
【点评】此题的关键在于理解向心力的来源及物块与圆筒之间的摩擦力作用。
5.(2025春 南京期中)如图所示,某同学坐在摩天轮的座椅上随座舱在竖直平面内做匀速圆周运动,座椅始终保持水平。图中M、N与圆心O等高,P位于最低点,Q位于最高点。下列说法中正确的是( )
A.M处座椅对人的支持力大于人的重力
B.N处座椅对人的作用力大于人的重力
C.P处座椅对人的支持力小于人的重力
D.Q处座椅对人的摩擦力方向水平向右
【考点】向心力的定义及物理意义(受力分析方面);匀速圆周运动.
【专题】定性思想;推理法;匀速圆周运动专题;推理论证能力.
【答案】B
【分析】匀速圆周运动向心力合力提供向心力,方向指向圆心。
【解答】解:A.在M点,由于摩天轮在做匀速圆周运动,支持力等于人的重力,故A错误;
B.在N点座椅对人的作用力指人受到的支持力与摩擦力的合力,其中支持力等于重力,方向向上,摩擦力提供向心力,方向向左,故座椅对人的作用力一定大于人的重力,故B正确;
C.在P点,重力与支持力的合力提供向心力,方向向上,故支持力大于重力,故C错误;
D.在Q点由支持力与重力提供向心力,方向向下,摩擦力等于零,故D错误。
故选:B。
【点评】考查对匀速圆周运动的理解,清楚向心力的含义。
6.(2025春 西城区校级期中)如图所示,长L的轻杆一端与一小球相连,另一端连在光滑固定轴上,在最高点给小球一个向右的水平初速度v0,小球在竖直平面内做顺时针方向的圆周运动,重力加速度为g。下列判断正确的是( )
A.最高点处轻杆对小球作用力一定指向圆心
B.小球运动到与圆心等高的位置时,其加速度大小可能为g
C.在小球从最高点到最低点的过程中,重力做功的功率一直增大
D.如果增大v0,在最低点与圆心等高位置处轻杆对小球拉力的差值不变
【考点】杆球类模型及其临界条件;功率的定义、物理意义和计算式的推导;牛顿第二定律的简单应用;牛顿第二定律与向心力结合解决问题.
【专题】定量思想;推理法;匀速圆周运动专题;推理论证能力.
【答案】D
【分析】根据向心力公式、竖直面内圆周运动杆模型和合加速度知识,功率公式和机械能守恒定律结合牛顿第二定律列式求解。
【解答】解:A.根据向心力的公式,最高点处速度较小时,小球的重力可能大于小球做圆周运动的向心力,此时轻杆会对小球施加背向圆心的支持力,故A错误;
B.小球运动到与圆心等高的位置时,向心加速度水平,重力加速度竖直向下,则合加速度大小一定大于g,故B错误;
C.小球从最高点到最低点的过程中,速度方向逐渐由水平向左变成水平向右,竖直方向的分速度先增大后减小,根据功率的定义式,可知小球受到的重力的功率先变大后变小,故C错误;
D.如果增大v0小球从最高点运动到水平位置的过程,根据机械能守恒定律,有,在水平位置受到拉力提供向心力,根据牛顿第二定律,有,在最低点,再对小球受力分析,同理根据牛顿第二定律,有,从最高点到最低点的过程,根据机械能守恒定律,有,联立解得F2﹣F1=3mg,根据表达式可知如果增大v0,轻杆在最低点与水平位置处对小球拉力的差值不会变化,故D正确。
故选:D。
【点评】考查向心力公式、竖直面内圆周运动杆模型和合加速度知识,功率公式和机械能守恒定律结合牛顿第二定律,会根据题意进行准确分析解答。
7.(2025春 香坊区校级期中)如图甲所示是哈尔滨红博广场转盘道的俯视图,A、B两车(同种型号可认为质量相等)正在绕环岛做线速度大小相等的匀速圆周运动,如图乙所示。已知A、B两车做匀速圆周运动的半径之比满足rA:rB=3:4,下列说法正确的是( )
A.A、B两车的角速度之比ωA:ωB=4:3
B.A、B两车的向心加速度之比aA:aB=3:4
C.A、B两车所受的合力大小之比FA:FB=1:1
D.A、B两车所需的向心力大小之比FnA:FnB=9:16
【考点】车辆在道路上的转弯问题;线速度与角速度的关系;牛顿第二定律与向心力结合解决问题.
【专题】定量思想;控制变量法;牛顿第二定律在圆周运动中的应用;分析综合能力.
【答案】A
【分析】A、B两车做匀速圆周运动的线速度大小相等,根据ω求角速度之比;根据求向心加速度之比;根据F合=Fn=m求两车所受的合力大小之比以及两车所需的向心力大小之比。
【解答】解:A、A、B两车正在绕环岛做线速度大小相等的匀速圆周运动,根据可得,A、B两车的角速度之比ωA:ωB=rB:rA=4:3,故A正确;
B、根据可得,A、B两车的向心加速度之比aA:aB=rB:rA=4:3,故B错误;
CD、两车做匀速圆周运动,由合力提供向心力,则有,则A、B两车所受的合力大小之比FA:FB=rB:rA=4:3,A、B两车所需的向心力大小之比FnA:FnB=rB:rA=4:3,故CD错误。
故选:A。
【点评】解答本题时,要明确物体做匀速圆周运动时,由合力提供所需要的向心力,并能灵活选择向心力公式。
二.多选题(共3小题)
(多选)8.(2025春 成华区期中)如图所示的四幅图表示的是有关圆周运动的基本模型,下列说法正确的是( )
A.图a中轻杆长为l,若小球在最高点的速率小于,则杆对小球的作用力向上
B.图b中若火车转弯速率小于设计转弯速率,则轮缘对外轨道有横向挤压作用
C.图c中静置于圆盘上的A和B材料相同,质量mA=2mB,到转轴的距离满足RA=2RB,若从零开始逐渐增大圆盘转速,则物体B先相对圆盘滑动
D.图d中两个小球在相同高度的水平面内做匀速圆周运动,它们的角速度大小相同
【考点】拱桥和凹桥类模型分析;水平转盘上物体的圆周运动;火车的轨道转弯问题.
【专题】定量思想;推理法;匀速圆周运动专题;推理论证能力.
【答案】AD
【分析】根据竖直面内圆周运动杆模型、火车转弯和向心力表达式,以及圆锥摆物体的受力情况,向心力表达式进行分析解答。
【解答】解:A.图a中若轻杆上的小球在最高点时,杆受作用力为零,此时,解得,若线速度小于,杆对小球的作用力向上,故A正确;
B.图b中若火车转弯未达规定速度行驶时,此时重力和轨道的支持力的合力大于火车所需的向心力,此时火车有做向心运动的趋势,轮缘对内侧轨道有作用,故B错误;
C.根据f=mω2r,若半径RA=2RB,质量mA=2mB,则A更容易达到最大静摩擦力,发生相对滑动,故C错误;
D.根据mgtanθ=mω2htanθ,可得,则两个小球在相同的高度做匀速圆周运动,它们的角速度相同,故D正确。
故选:AD。
【点评】考查竖直面内圆周运动杆模型、火车转弯和向心力表达式,以及圆锥摆物体的受力情况,向心力表达式,会根据题意进行准确分析解答。
(多选)9.(2025春 西安校级月考)如图所示,A、B两个材料相同的物体放在水平旋转的圆盘上,A的质量为m,B的质量为2m,B离轴距离为R,A离轴距离为2R,两物体始终相对盘静止,则( )
A.A与B的线速度大小之比为2:1
B.A与B的角速度之比为1:1
C.A与B的向心加速度大小之比为1:1
D.在转盘转速增加时,A比B先开始滑动
【考点】水平转盘上物体的圆周运动;角速度、周期、频率与转速的关系及计算;向心加速度的计算.
【专题】比较思想;临界法;牛顿第二定律在圆周运动中的应用;分析综合能力.
【答案】ABD
【分析】A、B同轴转动,角速度相同,根据v=ωr求线速度之比;由向心加速度公式a=rω2求向心加速度之比;谁先达到最大静摩擦力谁先滑动。
【解答】解:AB、A与B两物体始终相对盘静止,则A与B的角速度相同,均等于圆盘的角速度,则有
ωA:ωB=1:1
根据v=ωr可得,vA:vB=rA:rB=2R:R=2:1,故AB正确;
C、根据a=ω2r可得,aA:aB=rA:rB=2R:R=2:1,故C错误;
D、根据静摩擦力提供向心力可得
f=ma
可得A与B所受摩擦力大小相等
最大静摩擦力为
fm=μmg
A的质量小,最大静摩擦力小,所以在转盘转速增加时,A与B所受摩擦力都增大,A静摩擦力先达到最大值,则A比B先滑动,故D正确。
故选:ABD。
【点评】解决本题的关键要知道共轴转动的物体角速度相等,掌握线速度、角速度、向心加速度的关系,并能灵活运用。
(多选)10.(2025春 东城区校级期中)如图所示,在光滑的水平面上放一个原长为L的轻质弹簧,劲度系数为k,它的一端固定,另一端系一个质量为m的小球。当小球在该平面上做半径为4L的匀速圆周运动时( )
A.小球做圆周运动的向心力为3kL
B.小球做圆周运动的线速度为2kL
C.小球做圆周运动的角速度为
D.小球做圆运动的周期为2π
【考点】水平转盘上物体的圆周运动.
【专题】定量思想;推理法;匀速圆周运动专题;推理论证能力.
【答案】AD
【分析】由胡克定律可求得弹簧的弹力,受力分析知弹力提供向心力,由向心力公式逐个分析即可。
【解答】解:由胡克定律得弹簧的弹力F=k 3L
A、弹簧的弹力提供小球做圆周运动的向心力,所以向心力为3kL,故A正确;
B、由向心力公式得,解得:,故B错误;
C、由向心力公式得F=m 4Lω2,解得:,故C错误;
D、由向心力公式得,解得:,故D正确。
故选:AD。
【点评】本题考查了胡克定律、向心力公式,要求熟练掌握向心力公式的不同表达式,根据题目要求灵活选择。
三.填空题(共3小题)
11.(2025春 泉州期中)如图所示,一皮带传动装置,A、B、C三点到各自转轴的距离分别为RA、RB、RC,已知RB=RC,若在传动过程中,皮带不打滑。则A点与C点的角速度之比 1:2 ,A、B、C三点线速度之比为 2:1:2 。
【考点】传动问题;线速度与角速度的关系.
【专题】应用题;定量思想;推理法;匀速圆周运动专题;分析综合能力.
【答案】1:2;2:1:2。
【分析】同轴转动物体的角速度相等,同缘传动的线速度大小相等,根据图示情景,应用线速度与角速度的关系分析答题。
【解答】解:A、C同缘传动,线速度v大小相等,由v=ωr可知,,
A、B同轴转动,它们的角速度ω相等,由v=ωr可知vA:vB=RA:RB=2:1,
又由于vA=vC,则vA:vB:vC=2:1:2;
故答案为:1:2;2:1:2。
【点评】本题考查了传动问题,知道同轴转动物体的角速度相等,同缘传动的线速度大小相等是解题的前提,根据线速度与角速度的关系即可解题。
12.(2025春 鼓楼区校级期中)如图,小程同学购买的变速自行车有3级链轮和6级飞轮,踏板与链轮固接,后轮与飞轮固接,链轮和飞轮的齿数如表所示。骑行时通过选择不同的链轮和飞轮,可以获得合理的变速。假设踏板的转速不变,选择链轮的齿数为48,为使自行车行进的速度最大,应选择的飞轮的齿数为 14 ;此时链轮与后轮的转速之比为 。
名称 链轮
齿数 48 38 28
名称 飞轮
齿数 14 16 18 22 24 28
【考点】角速度、周期、频率与转速的关系及计算.
【专题】定量思想;推理法;匀速圆周运动专题;推理论证能力.
【答案】14,。
【分析】根据共轴转动链轮传动的知识进行分析解答。
【解答】解:链轮和飞轮的线速度相同,飞轮和后轮为共轴转动角速度相同,自行车的行驶速度为后轮的线速度。v飞=v链,ω飞 r飞=ω链 r链,飞轮的角速度,后轮线速度,所以当链轮的齿数最多、飞轮的齿数最少时,自行车速度最大,所以为使自行车行进的速度最大,应选择的飞轮的齿数为14,此时链轮与后轮的转速之比为。
故答案为:14,。
【点评】考查共轴转动链轮传动的知识,会根据题意进行准确分析解答。
13.(2025 漳州三模)如图为某小区通道上的智能闸杆,闸杆上A、B、C、D四处各固定一个相同的螺栓,闸杆可绕转轴O转动。已知,则在抬起闸杆的过程中,A、B两处螺栓的线速度大小之比为 1:2 ,C、D两处螺栓的向心力大小之比为 3:5 。
【考点】探究圆周运动的相关参数问题.
【专题】定量思想;推理法;匀速圆周运动专题;推理论证能力.
【答案】1:2;3:5。
【分析】根据线速度、角速度与半径的关系式计算;根据向心力公式计算。
【解答】解:在抬起闸杆的过程中,杆上各点做圆周运动的角速度ω相等,根据线速度、角速度与半径的关系式v=ωr可得
根据
可得
故答案为:1:2;3:5。
【点评】本题关键掌握在抬起闸杆的过程中,杆上各点做圆周运动的角速度ω相等。
四.解答题(共2小题)
14.(2025春 东丽区期中)如图所示,一硬细杆OO′竖直安装在一正方形水平桌面的中间位置,当细杆匀速转动时,杆上拴的轻质细线与竖直方向的夹角θ=37°,细线另一端拴接的小球质量m=0.48kg,细线长L=0.5m(g取10m/s2,sin37°=0.6)。
(1)求细线上的拉力大小T;
(2)求细杆转动的角速度大小ω;
(3)小球做圆周运动过程中离桌面高度为0.45m,要保证细线在任意时刻断开后小球均不会落到桌面外,求桌面的最小面积S。
【考点】牛顿第二定律与向心力结合解决问题;共点力的平衡问题及求解.
【专题】定量思想;推理法;共点力作用下物体平衡专题;推理论证能力.
【答案】(1)求细线上的拉力大小T为6N;
(2)求细杆转动的角速度大小ω为5rad/s;
(3)桌面的最小面积S为0.81m2。
【分析】第一问利用小球在竖直方向上的受力平衡求解细线拉力。第二问利用小球在水平方向上的向心力公式求解角速度。第三问分析细线断开后小球的运动轨迹,结合平抛运动规律和几何关系求解桌面的最小面积。
【解答】解:(1)小球受到重力mg和细线拉力T的作用。由于小球在竖直方向上受力平衡,因此有:Tcosθ=mg
可得:T=6N
因此,细线上的拉力大小为:T=6N
(2)小球在水平方向上做匀速圆周运动,向心力由细线拉力的水平分量提供,即:Tsinθ=mω2r
其中,小球做圆周运动的半径为:r=Lsinθ
解得:r=0.3m
联立解得:ω=5rad/s。
因此,细线转动的角速度大小为:ω=5rad/s。
(3)当细线断开时,小球以水平速度做平抛运动。小球做圆周运动时的水平速度为:
v=ωr
解得:v=1.5m/s
小球做平抛运动时,竖直方向上做自由落体运动,下落高度为:
h=Lcos45°﹣0.45
解得:h=0.05m
根据自由落体运动公式:
解得:t=0.1s
在水平方向上,小球的水平位移为:x=vt
解得:x=0.15m
小球做圆周运动时的水平半径为0.3m,因此小球在细线断开后水平方向上的最大位移为:
为了保证小球在任意时刻断开后均不会落到桌面外,桌面的最小面积为:S=(πR2)最大
解得:
但是,考虑到小球在细线断开后水平方向上的最大位移为0.3m+0.15m=0.45m,因此桌面的最小面积为:
S=(2×0.45)2m2= 0.81m2,因此,桌面的最小面积为:S= 0.81m2
答:(1)求细线上的拉力大小T为6N;
(2)求细杆转动的角速度大小ω为5rad/s;
(3)桌面的最小面积S为0.81m2。
【点评】该试题涉及圆周运动、牛顿第二定律以及平抛运动的相关知识。
15.(2025春 云岩区校级期中)如图所示,半径R=0.20m的光滑半圆环轨道处于竖直平面内,半圆环与水平地面相切于圆环的端点A。一质量为m的小球从A点冲上竖直半圆环轨道,沿轨道运动到B点飞出,最后落在水平地面上的C点(图上未画),已知小球在B点时对轨道的压力恰为mg,g取10m/s2,求:
(1)小球在B点的速度;
(2)A、C间的距离。
【考点】圆周运动与平抛运动相结合的问题;牛顿第三定律的理解与应用;物体在圆形竖直轨道内的圆周运动.
【专题】计算题;定量思想;模型法;动能定理的应用专题;分析综合能力.
【答案】(1)小球在B点的速度为2m/s;
(2)A、C间的距离为m。
【分析】(1)小球在B点时,由合力提供向心力,根据牛顿第二定律求小球在B点的速度;
(2)从B到C小球做平抛运动,根据分位移公式求解A、C间的距离。
【解答】解:(1)根据牛顿第三定律,小球在B点时轨道对小球的压力为FN=mg,方向竖直向下。
根据牛顿第二定律得
mg+FN=m
解得vB=2m/s
(2)从B到C小球做平抛运动,则有
2R
x=vBt
解得A、C间的距离为xm
答:(1)小球在B点的速度为2m/s;
(2)A、C间的距离为m。
【点评】本题是圆周运动与平抛运动的综合,对于圆周运动,要明确向心力来源。对于平抛运动,要掌握分运动的规律。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
