人教版高一数学必修四(课件)1.1任意角和弧度制 (共33张PPT)
文档属性
| 名称 | 人教版高一数学必修四(课件)1.1任意角和弧度制 (共33张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-06-19 21:53:17 | ||
图片预览









文档简介
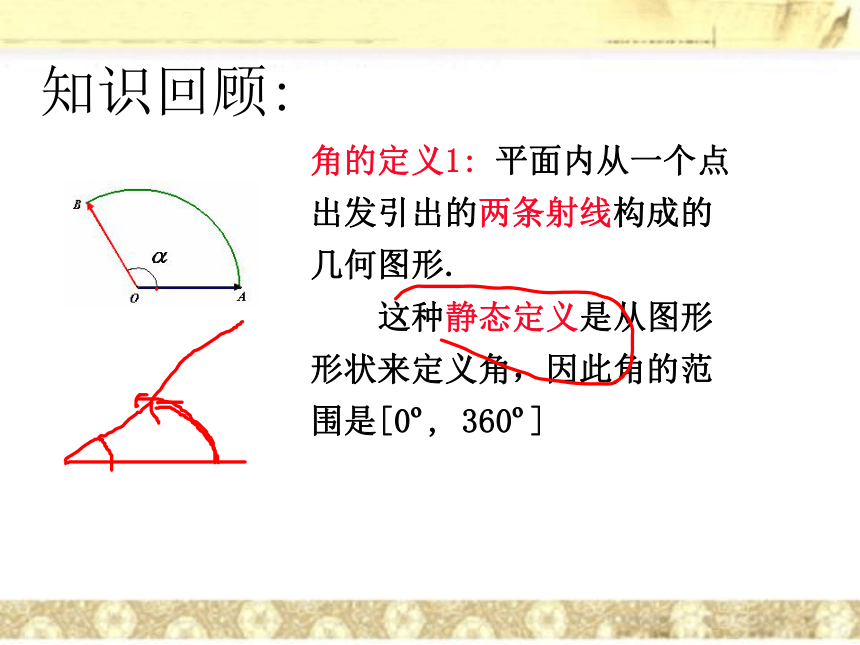
课件33张PPT。必修四第一章 三角函数 1.1任意角和弧度制任意角和弧度制知识回顾: 同学们,我们回顾一下学过的这些角:知识回顾:角的定义1: 平面内从一个点出发引出的两条射线构成的几何图形.
这种静态定义是从图形形状来定义角,因此角的范围是[0o, 360o]同学们见过不在0°~360°范围的角吗?我们来看一些实例。同学们现实生活中确定有存在不在学过范围的角现状生活中:体操、跳水、滑冰、转体720度的高难度动作,直体后空翻转体900度及以上的旋转
时钟的时针、分针转动和调准时间时顺时针、逆时针拨转角度
主从动轮转动角
车的轮子的转动角
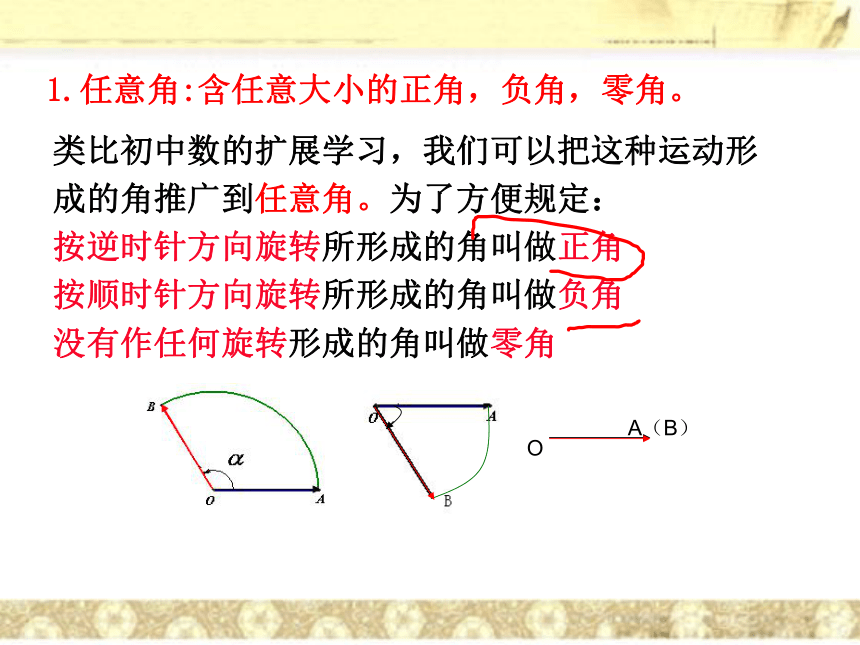
风车,风扇叶片等转动定义2:平面内一条射线绕着端点从一个位置旋转到另一个位置所成的图形.射线OA、OB分别是角的始边和终边,端点O为角的顶点。思考:这些旋转形成的角该如何表示和区分?引入新的角定义:类比初中数的扩展学习,我们可以把这种运动形成的角推广到任意角。为了方便规定:
按逆时针方向旋转所形成的角叫做正角
按顺时针方向旋转所形成的角叫做负角
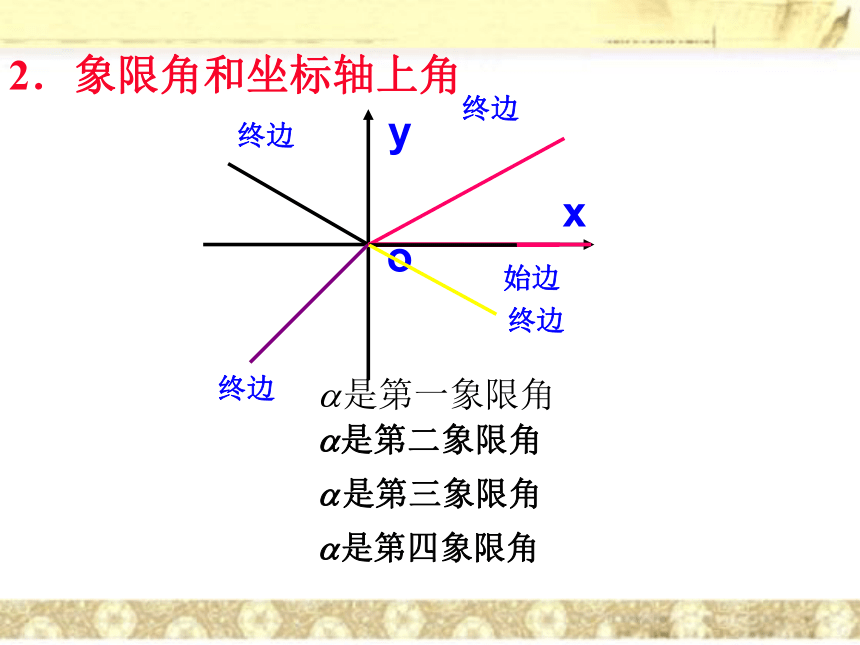
没有作任何旋转形成的角叫做零角1.任意角:含任意大小的正角,负角,零角。在初中我们研究了锐角三角函数,为了研究任意角的三角函数,用角和长度定位点,实现几何问题代数化。我们常在直角坐标系内讨论角。把角的顶点重合于坐标原点,角的始边重合于x轴的正半轴。角的终边落在第几象限,就说这个角是第几象限的角(包含第一、 二、三、 四象限角)角的终边落在哪坐标轴上,就说这个角是哪坐标轴上角(包含x,y正负半轴上的角) 2.象限角和坐标轴上角用旋转定义的任意角,需要注意三个要素:旋转中心、旋转方向和旋转量 (当旋转超过一周时,旋转量即超过360o,角度的绝对值可大于360o 。于是就有720o , - 540o,第一象限的角也已经超越原来锐角的范畴.)角3.终边相同的角 ⑴ 观察:?330? ,750?角,它们的终边与30?角的终边有何关系?⑵探究:与30 ?终边相同的角(含30 ?角本身)集合用描述法如何表示?
?330?=30?+(?1)×360? (k=-1) , 30?=30?+0×360? (k=0), 750?=30?+2×360?(k=2)
(3)结论:
思考:从终边相同的角集合表示中可以悟出什么?与 终边相同的角(含 本身)集合用描述法又将如何表示?例1:写出终边落在y轴上的角的集合。解:终边落在y轴正半轴上的角的集合为S1={β| β=900+K?3600,K∈Z} ={β| β=900+2K?1800,K∈Z}={β| β=900+1800 的偶数倍}终边落在y轴负半轴上的角的集合为S2={β| β=2700+K?3600,K∈Z}={β| β=900+1800+2K?1800,K∈Z}={β| β=900+(2K+1)1800 ,K∈Z}={β| β=900+1800 的奇数倍}S=S1∪S2所以 终边落在y轴上的角的集合为={β| β=900+1800 的偶数倍}∪{β| β=900+1800 的奇数倍}={β| β=900+1800 的整数倍} ={β| β=900+K?1800 ,K∈Z} 根据角的动态定义:角是由射线绕它的端点旋转而成的,在旋转的过程中射线上的点必然形成一条圆弧。
思考:不同的点所形成的圆弧的长度是不同的,但都对应同一个圆心角,探索弧长与其半径之比有什么关系? 1 ?的角是周角的
用1o角作单位来度量角的制度叫做角度制
但角的度量单位如同长度,面积,体积等有不同单位一样,也由于数据大,书写不便等有引入不同单位的需要。设α=no,AB弧长为l,半径OA为r,
则可以看出,等式右端不含
半径,表示弧长与半径的
比值跟半径无关,只与α的
大小有关。 3.弧度3.弧度 弧长等于半径长(l=r)的圆弧所对的圆心角叫做1弧度的角,弧度记作rad.角 的弧度数的绝对值规定等于 .
的正负由 的终边的旋转方向决定。
这种以弧度为单位来度量角的制度叫做弧度制。∵ 360?= ,∴ 180?=? rad, 用弧度来度量角,实际上角的集合与实数集R之间建立一一对应的关系:正实数零负实数请运用转换公式,填写下表:60°90°-150°270°3.弧度对比记忆:初中弧长和面积公式:思考:扇形的弧长和面积共含几个变量,已知几个量,才能求出另外的量呢?例2. 已知一半径为R的扇形,它的周长等于所在圆的周长,那么扇形的中心角是多少弧度?合多少度?扇形的面积是多少? 解:周长=2πR=2R+l,所以l=2(π-1)R.所以扇形的中心角是2(π-1) rad.合作探究练习1: 用角度和弧度分别表示:终边在x轴上的角的集合
终边在坐标轴上的角的集合
终边在第一象限角的集合
终边在y=x直线上的角的集合1.{β| β=k?1800 ,k∈Z} {β| β=kπ ,k∈Z}2.{β| β=k?900 ,k∈Z} {β| β=k? ,k∈Z}3.{β| k ? 3600 <β方法是:用所给角除以3600(2π)
所给角是正的:按通常的除法进行;
所给角是负的:度数除以3600(2π),商是负数,它的绝对值应比被除数为其相反数时相应的商大1,以便使余数为正值。2.判断一个角是第几象限角,
方法是:把所给角 改写成 : 0+k ·3600 ( K∈Z,00≤ 0<3600) 的形式, 0在第几象限, 就是第几象限角。0 +k·2π ( K∈Z, 0≤ 0<2π ) 合作探究练习3:
(1)在半径为R的圆中,240o的中心角所对的弧长为 ,面积为2R 2的扇形的中心角等于 弧度。
(2)一手表现发现走慢十五分钟需调正,分针要转多少弧度?(2)需顺时针转90度,即为所以 α=4.课堂小结:
1.任意角:
角的不同分类:正角、负角和零角
象限角和坐标轴上的角
终边相同的角集合表示:
2.角度制和弧度制的转化:
1?=1 rad3.扇形的弧长和面积公式.(角度和弧度制)作业课后作业:
见本节校本作业一张谢谢同学们配合!
欢迎各位专家和老师提出宝贵意见!在直角坐标系中任取象限的一个角 ,其 和
角所在象限怎样变化?已知α,β角的终边相同,那么α-β的终边在( )
A x轴的非负半轴上 B y轴的非负半轴上
C x轴的非正半轴上 D y轴的非正半轴上A在直角坐标系中,若α与β终边互相垂直,那么α与β之间的关系是( )
A. β=α+90o
B β=α±90o
C β=k·360o+90o+α,k∈Z
D β=k·360o±90o+α, k∈ZD若α是第四象限角,则180o-α是( )
A 第一象限角 B 第二象限角
C 第三象限角 D 第四象限角C1)已知扇形的周长为10cm,面积为4cm,求扇形的圆心角的弧度数。
(2)已知一扇形的周长为40cm,当它的半径和圆心角取什么值时,才能使扇形的面积取得最大?最大面积是多少?课堂小结:
1.任意角:
角的不同分类:正角、负角和零角
象限角和坐标轴上的角
终边相同的角集合表示:
2.角度制和弧度制的转化:
1?=1 rad3.扇形的弧长和面积公式.(角度和弧度制)
这种静态定义是从图形形状来定义角,因此角的范围是[0o, 360o]同学们见过不在0°~360°范围的角吗?我们来看一些实例。同学们现实生活中确定有存在不在学过范围的角现状生活中:体操、跳水、滑冰、转体720度的高难度动作,直体后空翻转体900度及以上的旋转
时钟的时针、分针转动和调准时间时顺时针、逆时针拨转角度
主从动轮转动角
车的轮子的转动角
风车,风扇叶片等转动定义2:平面内一条射线绕着端点从一个位置旋转到另一个位置所成的图形.射线OA、OB分别是角的始边和终边,端点O为角的顶点。思考:这些旋转形成的角该如何表示和区分?引入新的角定义:类比初中数的扩展学习,我们可以把这种运动形成的角推广到任意角。为了方便规定:
按逆时针方向旋转所形成的角叫做正角
按顺时针方向旋转所形成的角叫做负角
没有作任何旋转形成的角叫做零角1.任意角:含任意大小的正角,负角,零角。在初中我们研究了锐角三角函数,为了研究任意角的三角函数,用角和长度定位点,实现几何问题代数化。我们常在直角坐标系内讨论角。把角的顶点重合于坐标原点,角的始边重合于x轴的正半轴。角的终边落在第几象限,就说这个角是第几象限的角(包含第一、 二、三、 四象限角)角的终边落在哪坐标轴上,就说这个角是哪坐标轴上角(包含x,y正负半轴上的角) 2.象限角和坐标轴上角用旋转定义的任意角,需要注意三个要素:旋转中心、旋转方向和旋转量 (当旋转超过一周时,旋转量即超过360o,角度的绝对值可大于360o 。于是就有720o , - 540o,第一象限的角也已经超越原来锐角的范畴.)角3.终边相同的角 ⑴ 观察:?330? ,750?角,它们的终边与30?角的终边有何关系?⑵探究:与30 ?终边相同的角(含30 ?角本身)集合用描述法如何表示?
?330?=30?+(?1)×360? (k=-1) , 30?=30?+0×360? (k=0), 750?=30?+2×360?(k=2)
(3)结论:
思考:从终边相同的角集合表示中可以悟出什么?与 终边相同的角(含 本身)集合用描述法又将如何表示?例1:写出终边落在y轴上的角的集合。解:终边落在y轴正半轴上的角的集合为S1={β| β=900+K?3600,K∈Z} ={β| β=900+2K?1800,K∈Z}={β| β=900+1800 的偶数倍}终边落在y轴负半轴上的角的集合为S2={β| β=2700+K?3600,K∈Z}={β| β=900+1800+2K?1800,K∈Z}={β| β=900+(2K+1)1800 ,K∈Z}={β| β=900+1800 的奇数倍}S=S1∪S2所以 终边落在y轴上的角的集合为={β| β=900+1800 的偶数倍}∪{β| β=900+1800 的奇数倍}={β| β=900+1800 的整数倍} ={β| β=900+K?1800 ,K∈Z} 根据角的动态定义:角是由射线绕它的端点旋转而成的,在旋转的过程中射线上的点必然形成一条圆弧。
思考:不同的点所形成的圆弧的长度是不同的,但都对应同一个圆心角,探索弧长与其半径之比有什么关系? 1 ?的角是周角的
用1o角作单位来度量角的制度叫做角度制
但角的度量单位如同长度,面积,体积等有不同单位一样,也由于数据大,书写不便等有引入不同单位的需要。设α=no,AB弧长为l,半径OA为r,
则可以看出,等式右端不含
半径,表示弧长与半径的
比值跟半径无关,只与α的
大小有关。 3.弧度3.弧度 弧长等于半径长(l=r)的圆弧所对的圆心角叫做1弧度的角,弧度记作rad.角 的弧度数的绝对值规定等于 .
的正负由 的终边的旋转方向决定。
这种以弧度为单位来度量角的制度叫做弧度制。∵ 360?= ,∴ 180?=? rad, 用弧度来度量角,实际上角的集合与实数集R之间建立一一对应的关系:正实数零负实数请运用转换公式,填写下表:60°90°-150°270°3.弧度对比记忆:初中弧长和面积公式:思考:扇形的弧长和面积共含几个变量,已知几个量,才能求出另外的量呢?例2. 已知一半径为R的扇形,它的周长等于所在圆的周长,那么扇形的中心角是多少弧度?合多少度?扇形的面积是多少? 解:周长=2πR=2R+l,所以l=2(π-1)R.所以扇形的中心角是2(π-1) rad.合作探究练习1: 用角度和弧度分别表示:终边在x轴上的角的集合
终边在坐标轴上的角的集合
终边在第一象限角的集合
终边在y=x直线上的角的集合1.{β| β=k?1800 ,k∈Z} {β| β=kπ ,k∈Z}2.{β| β=k?900 ,k∈Z} {β| β=k? ,k∈Z}3.{β| k ? 3600 <β
所给角是正的:按通常的除法进行;
所给角是负的:度数除以3600(2π),商是负数,它的绝对值应比被除数为其相反数时相应的商大1,以便使余数为正值。2.判断一个角是第几象限角,
方法是:把所给角 改写成 : 0+k ·3600 ( K∈Z,00≤ 0<3600) 的形式, 0在第几象限, 就是第几象限角。0 +k·2π ( K∈Z, 0≤ 0<2π ) 合作探究练习3:
(1)在半径为R的圆中,240o的中心角所对的弧长为 ,面积为2R 2的扇形的中心角等于 弧度。
(2)一手表现发现走慢十五分钟需调正,分针要转多少弧度?(2)需顺时针转90度,即为所以 α=4.课堂小结:
1.任意角:
角的不同分类:正角、负角和零角
象限角和坐标轴上的角
终边相同的角集合表示:
2.角度制和弧度制的转化:
1?=1 rad3.扇形的弧长和面积公式.(角度和弧度制)作业课后作业:
见本节校本作业一张谢谢同学们配合!
欢迎各位专家和老师提出宝贵意见!在直角坐标系中任取象限的一个角 ,其 和
角所在象限怎样变化?已知α,β角的终边相同,那么α-β的终边在( )
A x轴的非负半轴上 B y轴的非负半轴上
C x轴的非正半轴上 D y轴的非正半轴上A在直角坐标系中,若α与β终边互相垂直,那么α与β之间的关系是( )
A. β=α+90o
B β=α±90o
C β=k·360o+90o+α,k∈Z
D β=k·360o±90o+α, k∈ZD若α是第四象限角,则180o-α是( )
A 第一象限角 B 第二象限角
C 第三象限角 D 第四象限角C1)已知扇形的周长为10cm,面积为4cm,求扇形的圆心角的弧度数。
(2)已知一扇形的周长为40cm,当它的半径和圆心角取什么值时,才能使扇形的面积取得最大?最大面积是多少?课堂小结:
1.任意角:
角的不同分类:正角、负角和零角
象限角和坐标轴上的角
终边相同的角集合表示:
2.角度制和弧度制的转化:
1?=1 rad3.扇形的弧长和面积公式.(角度和弧度制)
