人教版高一数学必修四 1.4.2正弦函数、余弦函数的性质 (共18张PPT)
文档属性
| 名称 | 人教版高一数学必修四 1.4.2正弦函数、余弦函数的性质 (共18张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 625.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-06-20 13:52:15 | ||
图片预览






文档简介
课件18张PPT。课题: 正弦函数 余弦函数的性质1.4.2 正弦函数、余弦函数的性质 问题提出1.周期函数是怎样定义的? 对于函数f(x),如果存在一个非零常数T,使得当x取定义域内的每一个值时,都有f(x +T)=f(x), 那么函数f(x)就叫做周期函数,非零常数T就叫做这个函数的周期.2.正、余弦函数的最小正周期是多少?函数 和
的最小正周期是多少?3.周期性是正、余弦函数所具有的一个基本性质,此外,正、余弦函数还具有哪些性质呢?我们将对此作进一步探究.函数的奇偶性、
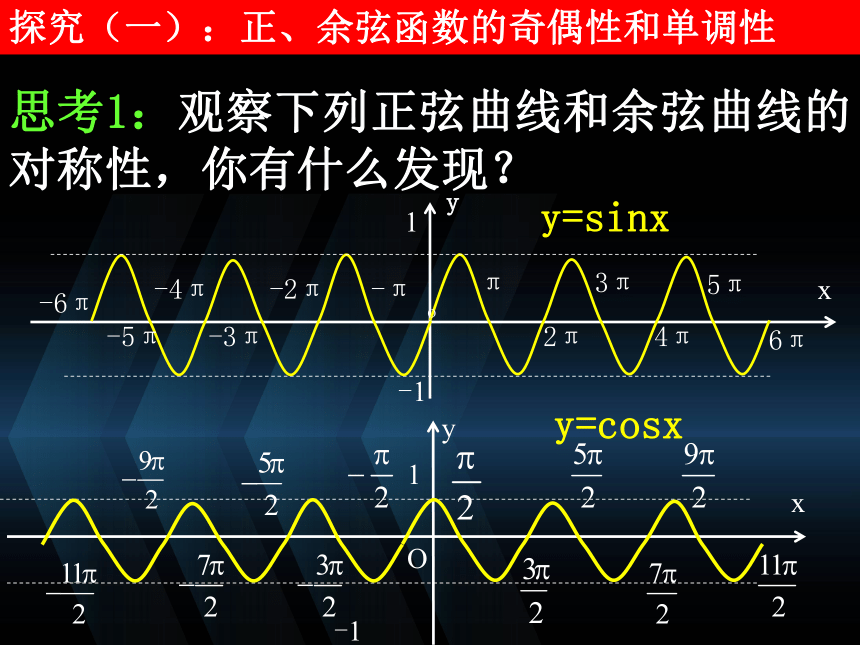
单调性与最值探究(一):正、余弦函数的奇偶性和单调性思考1:观察下列正弦曲线和余弦曲线的对称性,你有什么发现?思考2:上述对称性反映出正、余弦函数分别具有什么性质?如何从理论上加以验证?正弦函数是奇函数,余弦函数是偶函数.思考3:观察正弦曲线,正弦函数在哪些区间上是增函数?在哪些区间上是减函数?如何将这些单调区间进行整合?正弦函数在每一个闭区间
上都是增函数;在每一个闭区间
上都是减函数.思考4:类似地,余弦函数在哪些区间上是增函数?在哪些区间上是减函数?余弦函数在每一个闭区间
上都是增函数;在每一个闭区间
上都是减函数.思考5:正弦函数在每一个开区间(2kπ, +2kπ) (k∈Z)上都是增函数,能否认为正弦函数在第一象限是增函数?探究(二):正、余弦函数的最值与对称性 思考1:观察正弦曲线和余弦曲线,正、余弦函数是否存在最大值和最小值?若存在,其最大值和最小值分别为多少?思考2:当自变量x分别取何值时,正弦函数y=sinx取得最大值1和最小值-1?正弦函数当且仅当 时取最大值1, 当且仅当 时取最小值-1 思考3:当自变量x分别取何值时,余弦函数y=cosx取得最大值1和最小值-1?余弦函数当且仅当 时取最大值1, 当且仅当 时取最小值-1. 思考4:根据上述结论,正、余弦函数的值域是什么?函数y=Asinωx(Aω≠0)的值域是什么?思考5:正弦曲线除了关于原点对称外,是否还关于其它的点和直线对称? 正弦曲线关于点(kπ,0)和直线
对称.[-|A|,|A|]思考6:余弦曲线除了关于y轴对称外,是否还关于其它的点和直线对称?余弦曲线关于点 和直线x=kπ对称.理论迁移 例3 求函数 ,
x∈[-2π,2π]的单调递增区间. 例2 比较下列各组数的大小:小结作业 1. 正、余弦函数的基本性质主要指周期性、奇偶性、单调性、对称性和最值,它们都是结合图象得出来的,要求熟练掌握.2.正弦函数是奇函数,余弦函数是偶函数.一般地,y=Asinωx是奇函数,y=Acosωx(Aω≠0)是偶函数.作业:P40-41练习:1,2,3,5,6.3.正、余弦函数有无数个单调区间和无数个最值点,简单复合函数的性质应转化为基本函数处理.
的最小正周期是多少?3.周期性是正、余弦函数所具有的一个基本性质,此外,正、余弦函数还具有哪些性质呢?我们将对此作进一步探究.函数的奇偶性、
单调性与最值探究(一):正、余弦函数的奇偶性和单调性思考1:观察下列正弦曲线和余弦曲线的对称性,你有什么发现?思考2:上述对称性反映出正、余弦函数分别具有什么性质?如何从理论上加以验证?正弦函数是奇函数,余弦函数是偶函数.思考3:观察正弦曲线,正弦函数在哪些区间上是增函数?在哪些区间上是减函数?如何将这些单调区间进行整合?正弦函数在每一个闭区间
上都是增函数;在每一个闭区间
上都是减函数.思考4:类似地,余弦函数在哪些区间上是增函数?在哪些区间上是减函数?余弦函数在每一个闭区间
上都是增函数;在每一个闭区间
上都是减函数.思考5:正弦函数在每一个开区间(2kπ, +2kπ) (k∈Z)上都是增函数,能否认为正弦函数在第一象限是增函数?探究(二):正、余弦函数的最值与对称性 思考1:观察正弦曲线和余弦曲线,正、余弦函数是否存在最大值和最小值?若存在,其最大值和最小值分别为多少?思考2:当自变量x分别取何值时,正弦函数y=sinx取得最大值1和最小值-1?正弦函数当且仅当 时取最大值1, 当且仅当 时取最小值-1 思考3:当自变量x分别取何值时,余弦函数y=cosx取得最大值1和最小值-1?余弦函数当且仅当 时取最大值1, 当且仅当 时取最小值-1. 思考4:根据上述结论,正、余弦函数的值域是什么?函数y=Asinωx(Aω≠0)的值域是什么?思考5:正弦曲线除了关于原点对称外,是否还关于其它的点和直线对称? 正弦曲线关于点(kπ,0)和直线
对称.[-|A|,|A|]思考6:余弦曲线除了关于y轴对称外,是否还关于其它的点和直线对称?余弦曲线关于点 和直线x=kπ对称.理论迁移 例3 求函数 ,
x∈[-2π,2π]的单调递增区间. 例2 比较下列各组数的大小:小结作业 1. 正、余弦函数的基本性质主要指周期性、奇偶性、单调性、对称性和最值,它们都是结合图象得出来的,要求熟练掌握.2.正弦函数是奇函数,余弦函数是偶函数.一般地,y=Asinωx是奇函数,y=Acosωx(Aω≠0)是偶函数.作业:P40-41练习:1,2,3,5,6.3.正、余弦函数有无数个单调区间和无数个最值点,简单复合函数的性质应转化为基本函数处理.
