人教版高中物理必修二 课件5.5 :向心加速度 (共13张PPT)
文档属性
| 名称 | 人教版高中物理必修二 课件5.5 :向心加速度 (共13张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 128.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2016-06-20 00:00:00 | ||
图片预览





文档简介
课件13张PPT。5.5 向心加速度一、复习提问 什么是匀速圆周运动?“匀速”的含义是什么?那么做匀速圆周运动的物体其加速度有什么样的特点呢?它的方向怎样?大小如何计算?匀速圆周运动是变速运动变速运动运动状态改变一定存在加速度二、向心加速度请同学们阅读教材“速度变化量”部分,同时在练习本上画出物体加速运动和减速运动时速度变化量△v的图示,思考并回答问题:
1.速度变化量①速度的变化量△v是矢量还是标量?
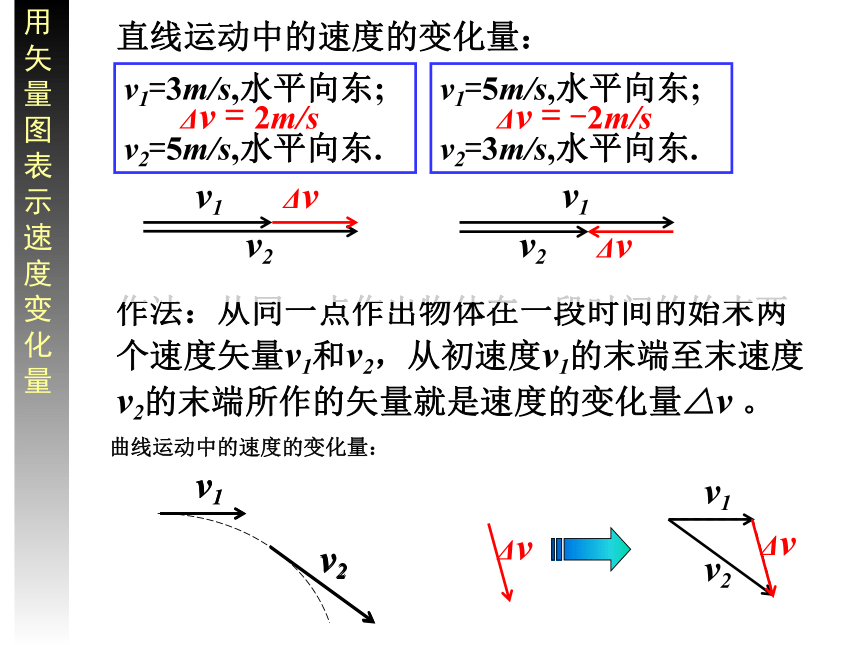
②如果出速度v1和末速度v2不在同一直线上,如何表示速度的变化量△v?加速度方向的一般性讨论 a 的方向与Δv 的方向相同如何确定Δv的方向?速度的变化量Δv用矢量图表示速度变化量作法:从同一点作出物体在一段时间的始末两个速度矢量v1和v2,从初速度v1的末端至末速度v2的末端所作的矢量就是速度的变化量△v 。直线运动中的速度的变化量:
v1=3m/s,水平向东;
v2=5m/s,水平向东.v1=5m/s,水平向东;
v2=3m/s,水平向东.v1Δvv2Δv = 2m/sΔv = -2m/s曲线运动中的速度的变化量:向心加速度1、定义:做匀速圆周运动的物体加速度指向圆心,这个加速度称为向心加速度4、物理意义:描述速度方向变化的快慢2、符号:an3、方向:始终指向圆心5、说明:匀速圆周运动加速度的大小不变,方向时刻改变,所以匀速圆周运动不是匀变速运动,是变加速运动指向圆心vAOABvB△vvARR由△OAB与
△BvAvB相似得出:向心加速度的表达式向心加速度的表达式向心加速度的表达式:v不变时,an与r 成反比ω不变时,an与r 成正比 自行车的大齿轮、小齿轮、后轮三个轮子的半径不一样,它们的边缘上有三个点A、B、C。其中哪两点向心加速度的关系适用于“向心加速度与半径成正比”,哪两点适用于“向心加速度与半径成反比”? 做出解释。
思考与讨论:分析:A、B两点所在轮子用同一根铁链相连,线速度V大小相等,适用于“向心加速度与半径成反比”;B、C两点围绕同一个轴心转动,角速度ω相等,适用于“向心加速度与半径成正比”。小结1、向心加速度的定义、物理意义3、向心加速度的大小:2、向心加速度的方向:指向圆心4、向心加速度的方向时刻改变由a = v2/r 知,做匀速圆周运动的物体,其线速度大小一定时,向心加速度与半径成反比由a = rω2 知,做匀速圆周运动的物体,角速度一定时,向心加速度与半径成正比匀速圆周运动是变加速运动
1、一物体在水平面内沿半径 R=20cm的圆形轨道做匀速圆周运动,线速度v=0.2m/s,则它的向心加速度为______m/s2,角速度为_____ rad/s,周期为_____s。0.212π练习2.关于北京和广州随地球自转的向心加速度,下列说法中正确的是( )
A、它们的方向都沿半径指向地心
B、它们的方向都平行于赤道平面指向地轴
C、北京的向心加速度比广州的向心加速度大
D、北京的向心加速度比广州的向心加速度小
BD练习3、如图所示装置中,三个轮的半径分别为r、2r、4r,b点到圆心的距离为r,求图中a、b、c、d各点的加速度之比。 练习
1.速度变化量①速度的变化量△v是矢量还是标量?
②如果出速度v1和末速度v2不在同一直线上,如何表示速度的变化量△v?加速度方向的一般性讨论 a 的方向与Δv 的方向相同如何确定Δv的方向?速度的变化量Δv用矢量图表示速度变化量作法:从同一点作出物体在一段时间的始末两个速度矢量v1和v2,从初速度v1的末端至末速度v2的末端所作的矢量就是速度的变化量△v 。直线运动中的速度的变化量:
v1=3m/s,水平向东;
v2=5m/s,水平向东.v1=5m/s,水平向东;
v2=3m/s,水平向东.v1Δvv2Δv = 2m/sΔv = -2m/s曲线运动中的速度的变化量:向心加速度1、定义:做匀速圆周运动的物体加速度指向圆心,这个加速度称为向心加速度4、物理意义:描述速度方向变化的快慢2、符号:an3、方向:始终指向圆心5、说明:匀速圆周运动加速度的大小不变,方向时刻改变,所以匀速圆周运动不是匀变速运动,是变加速运动指向圆心vAOABvB△vvARR由△OAB与
△BvAvB相似得出:向心加速度的表达式向心加速度的表达式向心加速度的表达式:v不变时,an与r 成反比ω不变时,an与r 成正比 自行车的大齿轮、小齿轮、后轮三个轮子的半径不一样,它们的边缘上有三个点A、B、C。其中哪两点向心加速度的关系适用于“向心加速度与半径成正比”,哪两点适用于“向心加速度与半径成反比”? 做出解释。
思考与讨论:分析:A、B两点所在轮子用同一根铁链相连,线速度V大小相等,适用于“向心加速度与半径成反比”;B、C两点围绕同一个轴心转动,角速度ω相等,适用于“向心加速度与半径成正比”。小结1、向心加速度的定义、物理意义3、向心加速度的大小:2、向心加速度的方向:指向圆心4、向心加速度的方向时刻改变由a = v2/r 知,做匀速圆周运动的物体,其线速度大小一定时,向心加速度与半径成反比由a = rω2 知,做匀速圆周运动的物体,角速度一定时,向心加速度与半径成正比匀速圆周运动是变加速运动
1、一物体在水平面内沿半径 R=20cm的圆形轨道做匀速圆周运动,线速度v=0.2m/s,则它的向心加速度为______m/s2,角速度为_____ rad/s,周期为_____s。0.212π练习2.关于北京和广州随地球自转的向心加速度,下列说法中正确的是( )
A、它们的方向都沿半径指向地心
B、它们的方向都平行于赤道平面指向地轴
C、北京的向心加速度比广州的向心加速度大
D、北京的向心加速度比广州的向心加速度小
BD练习3、如图所示装置中,三个轮的半径分别为r、2r、4r,b点到圆心的距离为r,求图中a、b、c、d各点的加速度之比。 练习
