【专项押题预测】临考查漏补缺:解答题(二)(含解析)-2025年各地区中考数学模拟题汇编
文档属性
| 名称 | 【专项押题预测】临考查漏补缺:解答题(二)(含解析)-2025年各地区中考数学模拟题汇编 |  | |
| 格式 | docx | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-09 05:26:40 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
【专项押题预测】临考查漏补缺:解答题(二)-2025年各地区中考数学模拟题汇编
1.(2025·福建福州·三模)在平面直角坐标系中,已知二次函数是常数,.
(1)若,函数图象经过点和,求函数图象的顶点坐标.
(2)若函数图象经过点,当时,;当时,,求的值.
2.(2025·北京密云·一模)如图,在菱形中,对角线相交于点O,点E为的中点,连接并延长至点F,使,连接.
(1)求证:四边形是矩形;
(2)若,菱形的周长为40,求的值.
3.(2025·辽宁抚顺·模拟预测)如图,是以为直径的上的任意一点,平分交于点,连接,过点作交的延长线于点,延长交的延长线于点.
(1)求证:.
(2)若,求的长.
4.(2025·山东临沂·一模)如图,一次函数的图象与反比例函数的图象交于点A、B,点A在第一象限,过点A作轴于点C,轴于点D,点B的纵坐标为,一次函数的图象分别交x轴、y轴于点E、F,连接、,已知,.
(1)求一次函数与反比例函数的解析式;
(2)求的面积.
5.(2025·重庆·模拟预测)列方程解应用题:为发展农业新质生产力,重庆农科院研发的智能采茶机器人正式上岗作业.经测试,每分钟一名工人采茶的数量比一台机器人采茶的数量少5片,若一名工人采茶6分钟、一台机器人采茶10分钟,共采茶450片.
(1)分别求出一名工人和一台机器人每分钟采茶的片数;
(2)经科研人员研发指导,工人和机器人的采茶速度都得以提高,机器人每分钟比之前多采片茶叶,工人每分钟比之前多采a片茶叶,这样,一台机器人采1200片茶叶所用的时间是一名工人采600片茶叶所用时间的1.5倍,求出a的值.
6.(2025·河南驻马店·三模)在平面直角坐标系中,平行四边形如图所示,点A的坐标为,点C的坐标为,反比例函数的图象经过点B,作直线.
(1)求反比例函数和一次函数的解析式;
(2)在反比例函数图象上取点P(点P位于点B左侧),过点P作轴,交于点Q,连接,,请问是否存在最大值,若存在请求出最大值及点P坐标,若不存在请说明理由.
7.(2025·辽宁抚顺·模拟预测)开展丰富多样的教育活动是教育强国的一项重要措施,为了增强学生的社会责任感和公民意识,某市组织全市初中部分学生参加“环保小卫士”知识竞赛活动.随机抽取部分学生的测试成绩进行整理和分析(测试满分为100分,成绩得分用表示,共分为四组:A.,B.,C.,D.).下面给出了部分信息:
信息一:
信息二:学生竞赛成绩在C组的数据(单位:分)如下:
80,82,83,83,84,85,86,87,87,89.
请根据以上信息,解答下列问题:
(1)求本次抽取的学生人数,并补全频数分布直方图;
(2)求所抽取的学生成绩的中位数;
(3)该市共有3000名初中学生,请估计该市初中学生成绩在A组的人数.
8.(2025·四川资阳·二模)某旅游度假村有甲种风格客房20间,乙种风格客房30间.按现有定价:若全部入住,一天的营业额为12000元;若甲、乙两种风格客房均有10间入住,一天的营业额为5000元.
(1)求甲、乙两种客房每间现有定价分别是多少元?
(2)度假村以乙种风格客房为例,市场情况调研发现:若每个房间每天按现有定价,房间会全部住满;当每个房间每天的定价每增加20元时,就会增加2个房间空闲.如果游客居住房间,度假村需对每个居住的房间每天支出60元的各种费用.当每间房间定价为多少元时,乙种风格客房每天的利润最大,最大利润是多少元?
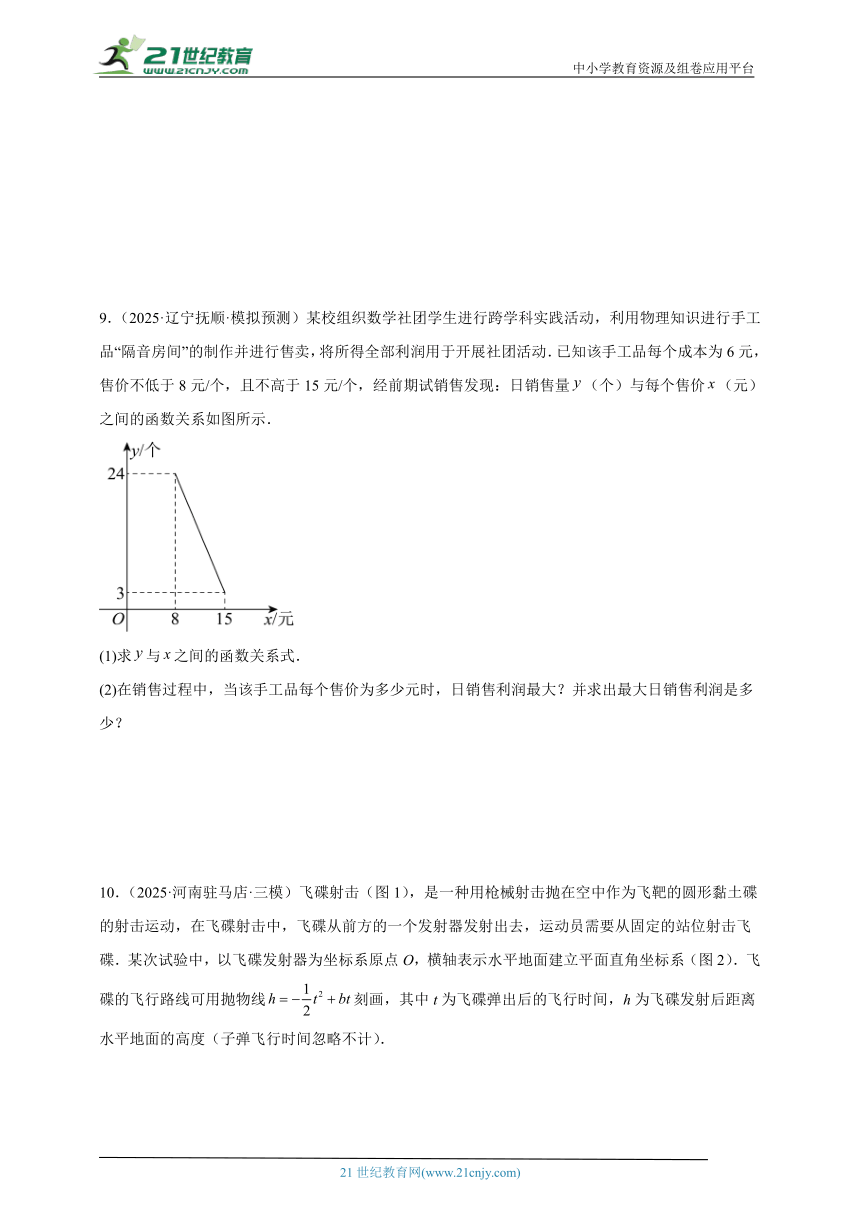
9.(2025·辽宁抚顺·模拟预测)某校组织数学社团学生进行跨学科实践活动,利用物理知识进行手工品“隔音房间”的制作并进行售卖,将所得全部利润用于开展社团活动.已知该手工品每个成本为6元,售价不低于8元/个,且不高于15元/个,经前期试销售发现:日销售量(个)与每个售价(元)之间的函数关系如图所示.
(1)求与之间的函数关系式.
(2)在销售过程中,当该手工品每个售价为多少元时,日销售利润最大?并求出最大日销售利润是多少?
10.(2025·河南驻马店·三模)飞碟射击(图1),是一种用枪械射击抛在空中作为飞靶的圆形黏土碟的射击运动,在飞碟射击中,飞碟从前方的一个发射器发射出去,运动员需要从固定的站位射击飞碟.某次试验中,以飞碟发射器为坐标系原点O,横轴表示水平地面建立平面直角坐标系(图2).飞碟的飞行路线可用抛物线刻画,其中t为飞碟弹出后的飞行时间,h为飞碟发射后距离水平地面的高度(子弹飞行时间忽略不计).
(1)飞碟发射________秒后能达到最大高度(用含有b的代数式表示);
(2)若飞碟发射1秒之后,飞行高度为,求抛物线的解析式;
(3)在(2)的基础上,若规定运动员要在飞碟距离地面96米处将其击落,第一次瞄准后没有击发,该运动员说“我4秒后射击仍然可以将其击落”,请判断她的说法是否正确?
11.(2025·河南驻马店·三模)盆栽是一种美学文化,展现了人与自然的和谐共生,盆栽的美不仅在于其形态和色彩,更在于其背后所蕴含的丰富的文化意义.某花卉店计划购进一批盆栽尝试进行销售,据了解1盆甲盆栽、3盆乙盆栽的进价共计元;3盆甲盆栽、1盆乙盆栽的进价共计元.
(1)求甲、乙两种盆栽每盆进价分别为多少元?
(2)若该店计划用元购进以上两种盆栽(两种盆栽均购买)试销,请你计算一下有几种购买方案?
(3)若该花卉店销售1盆甲盆栽可获利8元,销售1盆乙盆栽可获利3元,在(2)的购买方案中,假如这些盆栽全部售出,哪种方案获利最大?最大利润是多少元?
12.(2025·江苏镇江·二模)我国快递市场繁荣活跃,某快递公司为提高服务质量,对公司的业务量、公众满意度等数据进行统计分析.公司随机抽取了某日发往相邻城市的快递中的1000件,称重并记录每件快递的重量(单位:,精确到),下面给出了部分信息:
.每件快递重量的频数分布直方图(数据分成11组:,,,,,,,,,,);
.在这一组的数据如下:
.这1000件快递重量的平均数、中位数、众数如表:
平均数 中位数 众数
快递重量(单位:)
根据以上信息,回答下列问题:
(1)补全频数分布直方图;
(2) ;
(3)下面四个结论中:①的值一定在这一组;②的值可能在这一组;③的值不可能在这一组:④的值不可能在这一组,所有正确结论的序号是 ;
(4)该日快递公司在全市揽收的快递包裹中有4000件发往相邻城市,估计这批快递的重量.
13.(2025·河南驻马店·三模)在一次数学实践活动中,王林同学要测量古塔的高度,他从古塔底部点B处前行到达斜坡的底部点C处,然后沿斜坡前行到达最佳测量点D处,在点D处测得塔顶A的仰角为,已知斜坡的斜面坡度,且点A,B,C,D,E在同一平面内.求古塔的高度.
(结果精确到0.1米,参考数据:,,)
14.(2025·河南驻马店·三模)如图1所示,在,,,,D为斜边上不与端点重合的一动点,过点D作,垂足为E,将沿翻折,点A的对应点为点F,连接.
【初步探究】
(1)在点D的移动过程中,的度数发生变化吗?请说明理由.
【尝试应用】
(2)如图2所示,若为等腰三角形,请求出线段的长.
【深度求索】
(3)在(1)的基础上,若为直角三角形,请直接写出线段的长.
15.(2025·河南驻马店·三模)2025年初,河南全省共发生电动自行车火灾96起,从已调查完毕起火原因看,绝大部分的火灾源于电动车夜间充电导致的电路故障;广大初中生作为电动车的使用群体之一,教会他们安全充电成为校园消防的重要任务.驻马店某中学制作了时长100分钟的电动车安全充电以及普及消防知识的教育视频并组织学生周末观看,政教处随机抽查了部分学生观看视频的时长,并绘制如下不完整的统计图表.
部分学生观看教育视频时长频数分布表
组别 时长x/分钟 频数
A 20
B 40
C ▲
D 60
E 10
部分学生观看教育视频时长扇形统计图
结合以上信息,回答下列问题:
(1)本次调查属于________调查,本次调查的样本容量为________;
(2)样本数据的中位数落在________组;
(3)根据调查结果,请你对类似自行观看教育视频的活动提出一条合理化建议.
16.(2025·河南安阳·三模)如图所示,某城市中心的科技大厦楼顶安装了一座新型5G信号塔,用于提升周边区域的网络覆盖.为了确保信号塔的稳定性和安全性,信号塔主设备的高度需要精确计算,某数学活动小组受邀前往现场进行测量计算.测量小组在科技大厦附近的空地上选择了四个测量点,,,,这些点位于同一条直线上.测量过程中,小组成员使用测角仪和皮尺进行了实地测量.在点时,他们刚好能看到信号塔的最高点,测得仰角,并测得的长度为9米,接着他们移动到点,刚好能看到信号塔主设备的最低点,测得仰角,并测得的长度为1.8米.求信号塔主设备的长度.(结果精确到0.01米参考数据:)
17.(2025·山东临沂·一模)“当你背单词时,阿拉斯加的鳕鱼正跃出水面;当你算数学时,南太平洋的海鸥正掠过海岸当你晚自习时,地球的极圈正五彩斑斓;但少年,梦要你亲自实现,那些你觉得看不到的人和遇不到的风景都终将在你生命里出现.”这是直播带货新平台“东方甄选”货王董宇辉在推销鳕鱼时的台词.所推销鳕鱼的成本为每袋50元,当售价为每袋90元时,每分钟可销售100袋.为了吸引更多顾客,“东方甄选”采取降价措施.据市场调查反映:销售单价每降1元,则每分钟可多销售10袋.
(1)每袋鳕鱼的售价为多少元时,每分钟的销量为150袋?
(2)“东方甄选”不忘公益初心,热心教育事业,其决定从每分钟利润中捐出500元帮助留守儿童,为了保证捐款后每分钟利润达到5500元,且要最大限度让利消费者,求此时鳕鱼的销售单价为多少元?
(3)当销售售价为多少元时,每分钟的利润最大,最大利润是多少?
18.(2025·重庆·二模)如图,在中,,点为线段上一动点,以为边向左作等边.
(1)如图1,当为边中点时,若,,求的周长;
(2)若,点在线段上,且满足,线段交线段于点,连接.
①如图2,若,用等式表示线段和之间的数量关系,并证明;
②如图3,连接,,点运动过程中,当为直角三角形时,请直接写出的值.
19.(2025·辽宁抚顺·模拟预测)若函数的图象上至少存在一个点,该点关于轴的对称点落在函数的图象上,则称函数为函数和函数的“关联函数”,这两个点称为函数和函数的一对“关联点”.例如:如图,点在函数的图象上,点在函数的图象上,点关于轴对称,此时函数为函数和函数的“关联函数”,点和点是一对“关联点”.
【基础练习】
(1)请直接写出函数与函数的“关联函数”和“关联点”的坐标.
(2)若函数与函数的“关联函数”的顶点在轴上,求的值.
【灵活应用】
(3)当函数与函数的自变量满足时,其“关联函数”的最大值为,最小值为,若,求的值.
【深度探究】
(4)在(3)的条件下,当直线与“关联函数”的交点从左到右依次为,则以点与一对“关联点”构成四边形,此四边形能否成为平行四边形?若能,请直接写出的值;若不能,请说明理由.(参考数据:,,)
20.(2025·辽宁抚顺·模拟预测)综合与实践:
【提出问题】
辽宁省沈阳市地处中国东北地区,地势平坦,位于北纬,东经之间,这里四季分明,夏季炎热多雨,冬季寒冷干燥,春季和秋季温度适中.沈阳某小区一居民楼落地窗户朝南,窗户的高度为2米,此地一年中冬至这一天的正午时刻太阳光与地面的夹角最小为,夏至这一天正午时刻太阳光与地面的夹角最大为.某居民想为自己家的落地窗户设计一个直角形遮阳篷,要求它既能最大限度地遮挡夏天炎热的阳光,又能最大限度地使冬天温暖的阳光射入室内.请帮该居民完成设计方案.
【设计方案】
根据商家提供的如图1所示的直角形遮阳棚样品图,抽象数学模型,画出如图2所示的示意图.代表窗户的高,三点共线,代表遮阳棚的宽,,为一年中正午时刻太阳光线与地面产生最大夹角时的光线,为一年中正午时刻太阳光线与地面产生最小夹角时的光线.
【解决方案】
请求出此居民楼需要设计的遮阳棚的宽.(结果精确到0.1米)
【改进方案】
为防止雨水聚积遮阳棚,综合实践小组又把直角形遮阳棚进行升级改造成能够收缩的圆弧形遮阳棚,如图3.经改造设计成以点为圆心,图2中的长为半径的伸缩圆弧形遮阳棚,如图4.在圆弧形遮阳棚点处牵引绳子(其中点是的中点),绳子由图4中和两部分组成,.该居民购买2.5米长的绳子,问绳子是否够用?请说明理由.
(参考数据:,,,)
21.(2025·四川资阳·二模)如图,在平面直角坐标系中,点在抛物线上,且横坐标为1,点与点关于抛物线的对称轴对称,直线与轴交于点,点为抛物线的顶点,点的坐标为.
(1)求线段的长;
(2)点为线段上方抛物线上的任意一点,当的面积最大时,求此时点坐标,并求出最大面积;
(3)在(2)的情况下,过点作的垂线交于点,点在轴上一点,求的最小值.
22.(2025·河北保定·三模)如图是某位同学设计的电脑动画,随着音乐节奏起伏变化,屏幕上就会闪现不同的抛物线,抛物线的统一形式为,且顶点始终在直线上.
(1)当,时,求抛物线的顶点坐标和的值;
(2)试推断与之间的数量关系,并说明理由;
(3)已知,且符合题干的抛物线顶点的横坐标为1,将抛物线向右平移个单位长度,再向上平移个单位长度得到抛物线,且抛物线的顶点恰好也在直线上.
①求的值;
②该同学发现电脑屏幕上有一个黑点(位置固定),刚好落在平面直角坐标系中点的位置,该同学通过电脑放大功能,将抛物线横向、纵向同时放大倍得到抛物线,使点落在抛物线上(放大过程中不改变坐标原点的位置),直接写出符合条件的的值.
《【专项押题预测】临考查漏补缺:解答题(二)-2025年各地区中考数学模拟题汇编》参考答案
1.(1)
(2)
【分析】本题考查了二次函数的图象和性质,待定系数法求二次函数解析式,二次函数的顶点式等知识,熟练掌握二次函数的图象和性质并准确计算是解题的关键.
(1)根据,函数图象经过点和,利用待定系数法求解,即可解题;
(2)根据题意得到,函数图象在时取得最小值,即,以及,联立这三个式子求解,即可解题.
【详解】(1)解:,函数图象经过点和,
,
解得,
二次函数解析式为,
函数图象的顶点坐标为.
(2)解:函数图象经过点,
①,
当时,;当时,,
函数在时取得最小值,即②,
,
,在的左侧,
当时,,即③,
由①②③解得.
2.(1)见详解
(2)
【分析】本题主要考查了菱形的性质、矩形的判定与性质、勾股定理等知识,熟练掌握菱形的性质、矩形的判定与性质是解题关键.
(1)首先根据菱形的性质可得,结合“对角线相互平分的四边形为平行四边形”可证明四边形为平行四边形,然后根据“有一个角为直角的平行四边形为矩形”,即可证明结论;
(2)过点作于点,首先确定菱形的边长,在中利用勾股定理解得的长度,在由矩形的性质可得,,,,利用面积法求得的值,然后在中,由正弦的定义求解即可.
【详解】(1)证明:∵四边形为菱形,
∴,即,
∵点E为的中点,
∴,
又∵,
∴四边形为平行四边形,
∵,
∴四边形是矩形;
(2)如下图,过点作于点,
∵四边形为菱形,且周长为40,
∴,
∵,
∴,
∴在中,可有,
∵四边形是矩形,
∴,,,,
∵,
∴,解得,
∴在中,可有.
3.(1)见解析
(2)的长为
【分析】(1)角平分线的性质得出,而,可得从而;
(2)如图,过点作于点,连接;可得,设的半径为,在中,由勾股定理可得,由可得,即,从而可得四边形是矩形,则,由此可求出.
【详解】(1)解:证明:平分,
.
.
.
(2)如图,过点作于点,连接.
.
,
.
,
.
设的半径为.
.
在中,,
由勾股定理,得,即.
.
,即.
,
四边形是矩形.
.
在中,,
由勾股定理.得.
.
的长为.
【点睛】本题考查的是圆的基本性质,圆周角定理,切线的判定,同时考查了勾股定理、相似三角形的判定与性质,矩形的判定和性质,解题关键在于熟练掌握各个知识点的关联和运用.
4.(1)反比例函数表达式,一次函数表达式为;
(2)
【分析】(1)利用,求出点的坐标,再用待定系数法求出两个函数表达式即可;
(2)首先求出,然后利用的面积,即可求解;
【详解】(1)解:对于,令,则,
故点,则,
而,故点,
的纵坐标为3,点在反比例函数上,故点,
,
解得,故点,
反比例函数表达式为,
将点的纵坐标代入上式得,,
解得,故,
将点的坐标代入得,,解得,
故一次函数表达式为;
(2)对于,令,则,
解得,故点,
的面积.
【点睛】本题考查了反比例函数与一次函数的交点,当有两个函数的时候,着重使用一次函数,体现了方程思想,综合性较强.
5.(1)一台机器人每分钟采茶的片数为30,则一名工人每分钟采茶的片数为25
(2)
【分析】此题考查了一元一次方程和分式方程的应用,
(1)设一台机器人每分钟采茶的片数为x,则一名工人每分钟采茶的片数为,根据题意列出一元一次方程求解即可;
(2)根据题意列出分式方程求解即可.
【详解】(1)设一台机器人每分钟采茶的片数为x,则一名工人每分钟采茶的片数为
根据题意得,
解得
∴
∴一台机器人每分钟采茶的片数为30,则一名工人每分钟采茶的片数为25;
(2)根据题意得,
解得
经检验,是原方程的解.
6.(1),
(2)存在,的最大值为,此时点P的坐标为
【分析】本题考查了平行四边形的性质,二次函数的应用,待定系数法等知识,解题的关键是:
(1)根据平行四边形的性质求出点B的坐标,然后根据待定系数法求解即可;
(2)设,则,则,根据三角形的公式可求出
,然后根据二次函数的性质求解即可.
【详解】(1)解:∵四边形是平行四边形,
∴,,
∵,
∴,
∵,
∴,
代入,得,
解得,
∴反比例函数的解析式为,
设一次函数的解析式为,
∴,
解得,
∴;
(2)解:设,则,
∴,
∴
,
∵,
∴抛物线开口向下,
∴当时,有最大值为,
此时点P的坐标为
7.(1)本次抽取的学生人数为50人,见解析
(2)中位数为分
(3)估计该市初中学生成绩在A组的人数约为300人
【分析】本题主要考查了扇形统计图与条形统计图信息相关联,用样本估计总体,求中位数,正确读懂统计图是解题的关键.
(1)用D组的人数除以其人数占比可求出参与调查的人数,再求出B组的人数即可补全统计图;
(2)根据中位数的定义求解即可;
(3)用3000乘以样本中A组的人数占比即可得到答案.
【详解】(1)解:(人).
∴本次抽取的学生人数为50人.
∴B组的人数为(人).
补全频数分布直方图如下:
(2)解:共抽取了50人,
所抽取的学生成绩的中位数是第25,26个数的平均值(把50人成绩按照从低到高排列).
成绩在组的有5人,组的有15人,组的有10人,
中位数在组.
中位数为(分).
(3)解:(人).
答:估计该市初中学生成绩在A组的人数约为300人.
8.(1)甲、乙两种客房每间现有定价分别是300元、200元
(2)当每间房间定价为280元时,乙种风格客房每天的利润最大,最大利润是4840元
【分析】本题考查了二次函数的应用、二元一次方程组的应用,解答本题的关键是明确题意,正确列出方程组和二次函数关系式,利用二次函数的性质解答.
(1)设甲、乙两种客房每间现有定价分别是元、元,根据题意列方程组并解方程组解决;
(2)设每天的定价增加了个20元,则有个房间空闲,根据题意列出函数关系式并根据二次函数性质求最值即可;
【详解】(1)解:设甲、乙两种客房每间现有定价分别是元、元,
根据题意,得:,
解得,
答:甲、乙两种客房每间现有定价分别是300元、200元;
(2)解:设每天的定价增加了个20元,则有个房间空闲,
根据题意有:
,
,
当时,取得最大值,最大值为4840,此时房间的定价为元,
答:当每间房间定价为280元时,乙种风格客房每天的利润最大,最大利润是4840元.
9.(1)
(2)当该手工品每个售价为11元时,日销售利润最大,最大日销售利润是75元
【分析】本题考查了求一次函数解析式,二次函数的应用.
(1)设与之间的函数关系式为,根据题意求解析式即可;
(2)设销售该手工品日销售利润为元,根据题意得到,再由二次函数的性质计算即可.
【详解】(1)设与之间的函数关系式为.
根据题意,得解得
与之间的函数关系式为.
(2)设销售该手工品日销售利润为元.
根据题意,得.
抛物线的开口向下.
,
当时,取最大值,最大值为75.
答:当该手工品每个售价为11元时,日销售利润最大,最大日销售利润是75元.
10.(1)
(2)
(3)正确,见解析
【分析】本题考查了二次函数的实际应用,正确理解题意,求出函数解析式是解题的关键.
(1)根据二次函数的性质即可求解;
(2)将代入,求出即可;
(3)将代入,求出,即可求出时间间隔.
【详解】(1)解:∵,
∴时,离地面的高度最大,
故答案为:;
(2)解:由题意得,将代入,得,
解得:,
故函数解析式为:;
(3)解:正确,理由如下:
由(2)得,
当时,,
解得:,
∵,间隔时间为4秒,
∴她的说法正确.
11.(1)甲盆栽每盆进价为元,乙盆栽每盆进价为元.
(2)共有三种购买方案,分别为购买甲盆栽盆,乙盆栽盆;购买甲盆栽盆,乙盆栽盆;购买甲盆栽盆,乙盆栽盆;
(3)购买甲盆栽盆,乙盆栽盆时,获利最大,为元.
【分析】本题考查了二元一次方程组以及一次函数的应用,正确理解题意是解题关键.
(1)设甲、乙两种盆栽每盆进价分别为元,由题意得:,据此即可求解;
(2)设甲、乙两种盆栽分别购进盆,由题意得:,即:;根据均为正整数,即可求解;
(3)设利润为,则,可推出随着的增大而增大,据此即可求解;
【详解】(1)解:设甲、乙两种盆栽每盆进价分别为元,由题意得:
,解得:,
∴甲盆栽每盆进价为元,乙盆栽每盆进价为元.
(2)解:设甲、乙两种盆栽分别购进盆,由题意得:
,
即:
∵均为正整数,
∴当时,;
当时,;
当时,;
∴共有三种购买方案,分别为购买甲盆栽盆,乙盆栽盆;购买甲盆栽盆,乙盆栽盆;购买甲盆栽盆,乙盆栽盆;
(3)解:设利润为,
则,
∴随着的增大而增大,
故当时,元;
即:购买甲盆栽盆,乙盆栽盆时,获利最大,为元.
12.(1)见解析
(2)
(3)②④
(4)
【分析】本题主要考查的是频数分布直方图、用样本估计总体、加权平均数、中位数和众数等知识点,熟练掌握上述知识点是解题的关键.
(1)用数据总数减去其他组数据求出这一组的数据,然后补全统计图即可;
(2)结合中位数的定义进行求解即可;
(3)根据众数的定义并结合频数分布直方图可知:在的频数是,的频数是336,相对其他来说,都是远多于其他区间(的频数为15)的频数的,而众数是出现次数最多的一组数据,这是区间,不是具体数值,因此众数出现在这两个区间,的可能性都有的,且可能性较大,出现在,可能性还是有的,但可能性不大,自然众数不可能出现在,其频数都太小了,由此逐一判断各选项即可;
(4)用样本估计整体即可.
【详解】(1)解:解:(件),
补全的频数分布直方图如图所示:
(2)解:把这1000件快递按照重量从低到高排列,中位数为第500件和第501件重量的平均重量,
∵前三组,即中的快递件数为:,前四组中的快递件数为
∴中位数在这一组,
根据这一组的数据如下:;
∴.
(3)解:结合频数分布直方图可知:在的频数是,的频数是336,
相对其他来说,都是远多于其他区间(的频数为15)的频数的,
而众数是出现次数最多的一组数据,
∴众数出现在,这两个区间的可能性都有的,且可能性较大,
出现在,可能性还是有的,但可能性不大,
自然众数不可能出现在,其频数都太小了,
∴①n一定在,说法太绝对,错误;
②n可能在,正确;
③n不可能出现,说法太绝对,错误;
④n不可能出现,正确;
故选:②④.
(4)解:.
答:估计这批快递的重量为.
13.古塔的高度为.
【分析】本题考查解三角形的实际应用.利用坡度比,在中,设,,由勾股定理列方程求解即可得到和,在中,由三角函数定义求出,数形结合,由代值求解即可得到答案.
【详解】解:如图所示:作于点,作交的延长线于点,
则四边形是矩形,
在中,斜坡的斜面坡度,,
设,,
由勾股定理可得,
即,
解得(负值已舍),
,,
,
,
在中,,,
则,即,
解得,
,
答:古塔的高度为.
14.(1)的度数不会发生变化,理由见解析;(2);(3)
【分析】本题主要查了折叠的性质,三角形外角的性质,等腰三角形的性质,勾股定理以及锐角三角函数,利用分类讨论思想解答是解题的关键.
(1)由折叠的性质以及三角形外角的性质解答即可;
(2)根据等腰三角形的性质可得,从而得到,再由折叠的性质可得,即可解答;
(3)根据勾股定理以及锐角三角函数可得,,从而得到,设,则,,然后分两种情况:当时,当时,解答即可.
【详解】解:(1)在点D的移动过程中,的度数不会发生变化,理由如下:
由折叠的性质得:,
∴,
∴在点D的移动过程中,的度数不会发生变化.
(2)∵为等腰三角形,
∴,
∵,
∴,
由折叠的性质得:,
∴;
(3)∵在,,,,
∴,,
∴,
∴,
设,则,
∴,
当时,此时,
∴,
∵,
∴,
解得:或0(舍去),
此时;
当时,此时,
∴,
∵,
∴,
此时方程无解;
综上所述,线段的长为.
15.(1)抽样;200
(2)C
(3)见解析
【分析】本题考查了数据的统计与分析,中位线等知识,解题的关键是:
(1)根据抽样调查和普查的区别即可得出答案,根据B组频数除以B组所占百分比即可求解;
(2)根据中位数的定义求解即可;
(3)提出一个合理建议即可.
【详解】(1)解:本次调查属于抽样调查,本次调查的样本容量为,
故答案为:抽样;200;
(2)解:C组的频数为,
∵样本数据的中位数为第100和101个数的平均数,,,
∴样本数据的中位数落在C组,
故答案为:C;
(3)解:从以上信息可看出,估计全校有的学生观看时间低于40分钟,说明学生的思想上还不够重视,要加强教育.(答案不唯一)
16.2.7米
【分析】本题考查了三角函数的实际应用.先根据等腰三角形的性质得到米,进而求出米,再根据计算即可.
【详解】解:在中,,
∴是等腰直角三角形,
.
米,
米.
米,
(米).
在中,,,
(米).
(米).
答:信号塔主设备的长度约为2.7米.
17.(1)每袋鳕鱼的售价为85元时,每分钟销量为150袋;
(2)此时鳕鱼的销售单价为70元
(3)当销售单价为75元时,能获得最大利润,最大利润为6250元
【分析】本题考查一元一次方程、一元二次方程和二次函数的应用,解题的关键是根据题意,找到等量关系,列出方程,列函数式,进行解答.
(1)设每袋鳕鱼的售价为x元,根据题意,则,解出x,即可;
(2)设此时鳕鱼的销售单价为y元,根据题意,则方程为,解出方程,根据最大限度让利消费者,取值即可.
(3)设鳕鱼的销售单价为a元,每分钟的利润为w,根据题意得,
根据,得当时,w取得最大值,最大值为6250.
【详解】(1)解:设每袋鳕鱼的售价为x元时,每分钟的销量为150袋,
,
∴,
答:每袋鳕鱼的售价为85元时,每分钟销量为150袋;
(2)解:设鳕鱼的销售单价为y元,根据题意得:
,
解得
∵让消费者获得最大的利益,
∴,
答:此时鳕鱼的销售单价为70元.
(3)解:设鳕鱼的销售单价为a元,每分钟的利润为w,根据题意得:
,
∵,
∴当时,w取得最大值,
最大值为6250.
故当销售单价为75元时,能获得最大利润,最大利润为6250元.
18.(1)
(2)①,理由见解析;②或
【分析】本题考查全等三角形的判定与性质,等边三角形的判定与性质,等腰三角形的判定与性质,三角函数,含角的直角三角形的性质,直角三角形斜边中线的性质,熟练掌握这些性质与判定是解题的关键.
(1)在中,利用三角函数求得,由勾股定理得,再利用直角三角形斜边中线的性质得,最后利用等边三角形性质求解;
(2)①在上取一点,使,连接,,延长交于点,利用倒角得,可得是等边三角形,结合等边,利用手拉手模型证明,可得,,通过倒角可得,则,,则可证,则,,得,,再证明,,,易得,利用,倒角可得,则,即可证明;
②同①在上取一点,使,连接,,延长交于点,同①可得,,设,则,分两种情况:当时和当时,分别作图计算即可 .
【详解】(1)解:在中,
∵,,,
∴,
∴,
∵为边中点,
∴,
∵是等边三角形,
∴的周长;
(2)解:①,理由如下:
在上取一点,使,连接,,延长交于点,
∵是等边三角形,
∴,,
∵,
∴,
即,
∴是等边三角形,
∴,
∴,
∴,
∴,
∴,,
∴,
∵,,
∴,
∴,
∴,
∴,,
∴,
∴,
∴,
又∵,
∴,,
∴,
∵,,
∴,,,
∴,,
∴,
∴,
∵,
∴,
∴,
∴,,
∴,
∴,
∴,
∴;
②同①在上取一点,使,连接,,延长交于点,
同①可得,,
设,
∴,
当时,如图,
∵,
∴,,
∴,
∵,,
∴,
∴,
∴;
当时,如图,
∵,
∴,,
∴,
∵, ,
∴,
∴,
∴;
综上,或.
19.()“关联函数”为 ,“关联点”的坐标为和或和;
();
()的值为或-1;
()能,的值为或
【分析】根据“关联函数”的定义可得“关联函数”的解析式是,设函数的一个点的坐标为,则关于轴的对称点的坐标为,根据“关联点”之间的关系得到方程,解方程求出“关联点”即可;
根据“关联函数”的定义可得“关联函数”的解析式是,“关联函数”的顶点在轴上,可得:,解方程求出值即可;
根据题意可得:“关联函数”的解析式为,根据解析式可以求出顶点坐标为,当时,,当时,,根据与“关联函数”的对称轴的关系分四种情况求解;
分别写出当的值为或时“关联函数”的解析式,根据平行四边形的性质表示出“关联点”的坐标,根据“关联点”的定义得到关于的方程,从而求出点 的坐标,再根据直线与“关联函数”的图象交于点,确定的值即可.
【详解】解:函数中,,
函数中,
“关联函数”为;
设函数的一个点的坐标为,则关于轴的对称点的坐标为,
点在函数的图象上,
,
解得:,,
点的坐标为或,
点的坐标为或,
“关联点”的坐标为和或和;
解:根据题意,得“关联函数”为,
“关联函数”的顶点在轴上,
,
解得:,,
,
;
解:根据题意,得“关联函数”为,
函数的对称轴为直线,顶点坐标为,
当时,,
当时,,
,
抛物线的开口向下,
,即时,
可得:,,
,
解得:;
直线关于直线的对称直线为,
当时,
解得:时,
可得:,,
,
解得:,(不合题意,舍去);
当,
解得:时,
可得:,,
,
解得:,(不合题意,舍去);
当,即时,
,
,
此时,,
,
解得:.
综上所述,的值为或;
解:能,的值为或.
当时,一次函数的表达式为,
反比例函数的表达式为,
“关联函数”的表达式为.
设一次函数的一个点的坐标为,
则点关于轴对称的点的坐标为,
点在函数的图象上,
,
解得:,
点,,
轴,
,
点在“关联函数”的图象上,
点的坐标为,
,
当时,以为顶点的四边形是平行四边形,
点.
点也在“关联函数”的图象上,
,
解得:,
点,
直线与“关联函数”的图象交于点,,
;
当时,一次函数的表达式为,
反比例函数的表达式为,
“关联函数”的表达式为,
设一次函数的一个点的坐标为,
则点关于轴对称的点的坐标为,
点在函数的图象上,
,
整理得:,
解得:,,
点的横坐标为或,
点的横坐标为或,
点,关于轴对称,
轴,
的长为或.
点在“关联函数”的图象上,
设点的坐标为,
,
有以下两种情况:
当时,
以为顶点的四边形是平行四边形,
点,
点也在“关联函数”的图象上,
,
解得:,
点,
直线与“关联函数”的图象交于点,,
,
当时,以为顶点的四边形是平行四边形,
点,
点也在“关联函数”的图象上,
,
解得:,
点,
直线与“关联函数”的图象交于点,,
(不符合题意,舍去),
综上所述,的值为或.
【点睛】本题考查了新定义、反比例函数与一次函数交点问题、轴对称的性质、二次函数的性质、平行四边形的判定与性质,解决本题的关键是根据二次函数的性质确定点的坐标.
20.解决方案:遮阳棚的宽约为0.7米;改进方案:绳子不够用,理由见解析
【分析】(1)在,可设米,则米,可得,再在中,,由此可证;
(2)在中可得,由为的中点,可得,最后在,,,可得,由此可证绳子不够.
【详解】解:【解决方案】由题意,知米,.
.
在中,,
.
设米,则米.
米.
在中,,
,即.
解得.
答:遮阳棚的宽约为0.7米.
【改进方案】绳子不够用.理由如下:
由【解决方案】,得在中,,
(米).
如图,连接.
米.
由题意,得.
为的中点.
.
.
,
,
在中,,,
(米)
(米).
米.
(米).
绳子不够用.
【点睛】本题主要考查锐角三角函数值的应用,圆弧的相关知识点,掌握锐角三角函数和圆相关知识是解题的关键.
21.(1)
(2),
(3)
【分析】本题考查二次函数综合,涉及二次函数图象与性质、二次函数与面积综合、二次函数求最值等问题,数形结合是解决问题的关键.
(1)根据题意,令,代入表达式求出即可得到,再根据点与点关于抛物线的对称轴对称,即可求出,从而得到答案;
(2)作轴交于,如图所示,设,数形结合,在平面直角坐标系中表示出的面积,由二次函数图象与性质分析即可得到答案;
(3)作直线交于,使得,作于交于,如图所示,数形结合得,利用等面积法求解即可得到答案.
【详解】(1)解:点在抛物线上,且横坐标为1,
令,则,则,
点与点关于抛物线的对称轴对称,
,
;
(2)解:作轴交于,如图所示:
设,
直线的解析式为,
,
,
,
抛物线开口向下,有最大值,当时,的面积最大为,此时;
(3)解:作直线交于,使得,作于交于,如图所示:
由(2)知点,,
,
,
,此时的值最小,
,
,
的最小值为.
22.(1)抛物线的顶点坐标为,
(2)
(3)①;②的值为或
【分析】本题主要考查了二次函数应用,位似图形的性质,解题时要熟练掌握并能灵活运用二次函数的性质是关键.
(1)根据抛物线的顶点坐标公式,求得顶点坐标为,再将代入正比例函数解析式,即可求解;
(2)根据题意可得,可得顶点坐标,再设抛物线的解析式为,从而可得抛物线 的解析式,结合顶点在上,即可得解;
(3)依据题意,由①得抛物线的顶点坐标为,又将抛物线横向、纵向同时放大倍后,可得顶点坐标为,从而抛物线将点代入,即可求解.
【详解】(1)解:,
,
抛物线的顶点坐标为,
将代入得
;
(2)与之间的数量关系为.理由如下:
由题意,顶点始终在直线上,
∴
,
.
与之间的数量关系为.
(3)①由题意,,
.
抛物线顶点的横坐标为,
顶点的纵坐标为.
设抛物线的解析式为
抛物线 的解析式为
抛物线 的顶点坐标为
在上
.
②由①得抛物线的顶点坐标为.
将抛物线横向、纵向同时放大倍后,
顶点坐标为.
抛物线
将点代入得
解得:
∴的值为或.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
【专项押题预测】临考查漏补缺:解答题(二)-2025年各地区中考数学模拟题汇编
1.(2025·福建福州·三模)在平面直角坐标系中,已知二次函数是常数,.
(1)若,函数图象经过点和,求函数图象的顶点坐标.
(2)若函数图象经过点,当时,;当时,,求的值.
2.(2025·北京密云·一模)如图,在菱形中,对角线相交于点O,点E为的中点,连接并延长至点F,使,连接.
(1)求证:四边形是矩形;
(2)若,菱形的周长为40,求的值.
3.(2025·辽宁抚顺·模拟预测)如图,是以为直径的上的任意一点,平分交于点,连接,过点作交的延长线于点,延长交的延长线于点.
(1)求证:.
(2)若,求的长.
4.(2025·山东临沂·一模)如图,一次函数的图象与反比例函数的图象交于点A、B,点A在第一象限,过点A作轴于点C,轴于点D,点B的纵坐标为,一次函数的图象分别交x轴、y轴于点E、F,连接、,已知,.
(1)求一次函数与反比例函数的解析式;
(2)求的面积.
5.(2025·重庆·模拟预测)列方程解应用题:为发展农业新质生产力,重庆农科院研发的智能采茶机器人正式上岗作业.经测试,每分钟一名工人采茶的数量比一台机器人采茶的数量少5片,若一名工人采茶6分钟、一台机器人采茶10分钟,共采茶450片.
(1)分别求出一名工人和一台机器人每分钟采茶的片数;
(2)经科研人员研发指导,工人和机器人的采茶速度都得以提高,机器人每分钟比之前多采片茶叶,工人每分钟比之前多采a片茶叶,这样,一台机器人采1200片茶叶所用的时间是一名工人采600片茶叶所用时间的1.5倍,求出a的值.
6.(2025·河南驻马店·三模)在平面直角坐标系中,平行四边形如图所示,点A的坐标为,点C的坐标为,反比例函数的图象经过点B,作直线.
(1)求反比例函数和一次函数的解析式;
(2)在反比例函数图象上取点P(点P位于点B左侧),过点P作轴,交于点Q,连接,,请问是否存在最大值,若存在请求出最大值及点P坐标,若不存在请说明理由.
7.(2025·辽宁抚顺·模拟预测)开展丰富多样的教育活动是教育强国的一项重要措施,为了增强学生的社会责任感和公民意识,某市组织全市初中部分学生参加“环保小卫士”知识竞赛活动.随机抽取部分学生的测试成绩进行整理和分析(测试满分为100分,成绩得分用表示,共分为四组:A.,B.,C.,D.).下面给出了部分信息:
信息一:
信息二:学生竞赛成绩在C组的数据(单位:分)如下:
80,82,83,83,84,85,86,87,87,89.
请根据以上信息,解答下列问题:
(1)求本次抽取的学生人数,并补全频数分布直方图;
(2)求所抽取的学生成绩的中位数;
(3)该市共有3000名初中学生,请估计该市初中学生成绩在A组的人数.
8.(2025·四川资阳·二模)某旅游度假村有甲种风格客房20间,乙种风格客房30间.按现有定价:若全部入住,一天的营业额为12000元;若甲、乙两种风格客房均有10间入住,一天的营业额为5000元.
(1)求甲、乙两种客房每间现有定价分别是多少元?
(2)度假村以乙种风格客房为例,市场情况调研发现:若每个房间每天按现有定价,房间会全部住满;当每个房间每天的定价每增加20元时,就会增加2个房间空闲.如果游客居住房间,度假村需对每个居住的房间每天支出60元的各种费用.当每间房间定价为多少元时,乙种风格客房每天的利润最大,最大利润是多少元?
9.(2025·辽宁抚顺·模拟预测)某校组织数学社团学生进行跨学科实践活动,利用物理知识进行手工品“隔音房间”的制作并进行售卖,将所得全部利润用于开展社团活动.已知该手工品每个成本为6元,售价不低于8元/个,且不高于15元/个,经前期试销售发现:日销售量(个)与每个售价(元)之间的函数关系如图所示.
(1)求与之间的函数关系式.
(2)在销售过程中,当该手工品每个售价为多少元时,日销售利润最大?并求出最大日销售利润是多少?
10.(2025·河南驻马店·三模)飞碟射击(图1),是一种用枪械射击抛在空中作为飞靶的圆形黏土碟的射击运动,在飞碟射击中,飞碟从前方的一个发射器发射出去,运动员需要从固定的站位射击飞碟.某次试验中,以飞碟发射器为坐标系原点O,横轴表示水平地面建立平面直角坐标系(图2).飞碟的飞行路线可用抛物线刻画,其中t为飞碟弹出后的飞行时间,h为飞碟发射后距离水平地面的高度(子弹飞行时间忽略不计).
(1)飞碟发射________秒后能达到最大高度(用含有b的代数式表示);
(2)若飞碟发射1秒之后,飞行高度为,求抛物线的解析式;
(3)在(2)的基础上,若规定运动员要在飞碟距离地面96米处将其击落,第一次瞄准后没有击发,该运动员说“我4秒后射击仍然可以将其击落”,请判断她的说法是否正确?
11.(2025·河南驻马店·三模)盆栽是一种美学文化,展现了人与自然的和谐共生,盆栽的美不仅在于其形态和色彩,更在于其背后所蕴含的丰富的文化意义.某花卉店计划购进一批盆栽尝试进行销售,据了解1盆甲盆栽、3盆乙盆栽的进价共计元;3盆甲盆栽、1盆乙盆栽的进价共计元.
(1)求甲、乙两种盆栽每盆进价分别为多少元?
(2)若该店计划用元购进以上两种盆栽(两种盆栽均购买)试销,请你计算一下有几种购买方案?
(3)若该花卉店销售1盆甲盆栽可获利8元,销售1盆乙盆栽可获利3元,在(2)的购买方案中,假如这些盆栽全部售出,哪种方案获利最大?最大利润是多少元?
12.(2025·江苏镇江·二模)我国快递市场繁荣活跃,某快递公司为提高服务质量,对公司的业务量、公众满意度等数据进行统计分析.公司随机抽取了某日发往相邻城市的快递中的1000件,称重并记录每件快递的重量(单位:,精确到),下面给出了部分信息:
.每件快递重量的频数分布直方图(数据分成11组:,,,,,,,,,,);
.在这一组的数据如下:
.这1000件快递重量的平均数、中位数、众数如表:
平均数 中位数 众数
快递重量(单位:)
根据以上信息,回答下列问题:
(1)补全频数分布直方图;
(2) ;
(3)下面四个结论中:①的值一定在这一组;②的值可能在这一组;③的值不可能在这一组:④的值不可能在这一组,所有正确结论的序号是 ;
(4)该日快递公司在全市揽收的快递包裹中有4000件发往相邻城市,估计这批快递的重量.
13.(2025·河南驻马店·三模)在一次数学实践活动中,王林同学要测量古塔的高度,他从古塔底部点B处前行到达斜坡的底部点C处,然后沿斜坡前行到达最佳测量点D处,在点D处测得塔顶A的仰角为,已知斜坡的斜面坡度,且点A,B,C,D,E在同一平面内.求古塔的高度.
(结果精确到0.1米,参考数据:,,)
14.(2025·河南驻马店·三模)如图1所示,在,,,,D为斜边上不与端点重合的一动点,过点D作,垂足为E,将沿翻折,点A的对应点为点F,连接.
【初步探究】
(1)在点D的移动过程中,的度数发生变化吗?请说明理由.
【尝试应用】
(2)如图2所示,若为等腰三角形,请求出线段的长.
【深度求索】
(3)在(1)的基础上,若为直角三角形,请直接写出线段的长.
15.(2025·河南驻马店·三模)2025年初,河南全省共发生电动自行车火灾96起,从已调查完毕起火原因看,绝大部分的火灾源于电动车夜间充电导致的电路故障;广大初中生作为电动车的使用群体之一,教会他们安全充电成为校园消防的重要任务.驻马店某中学制作了时长100分钟的电动车安全充电以及普及消防知识的教育视频并组织学生周末观看,政教处随机抽查了部分学生观看视频的时长,并绘制如下不完整的统计图表.
部分学生观看教育视频时长频数分布表
组别 时长x/分钟 频数
A 20
B 40
C ▲
D 60
E 10
部分学生观看教育视频时长扇形统计图
结合以上信息,回答下列问题:
(1)本次调查属于________调查,本次调查的样本容量为________;
(2)样本数据的中位数落在________组;
(3)根据调查结果,请你对类似自行观看教育视频的活动提出一条合理化建议.
16.(2025·河南安阳·三模)如图所示,某城市中心的科技大厦楼顶安装了一座新型5G信号塔,用于提升周边区域的网络覆盖.为了确保信号塔的稳定性和安全性,信号塔主设备的高度需要精确计算,某数学活动小组受邀前往现场进行测量计算.测量小组在科技大厦附近的空地上选择了四个测量点,,,,这些点位于同一条直线上.测量过程中,小组成员使用测角仪和皮尺进行了实地测量.在点时,他们刚好能看到信号塔的最高点,测得仰角,并测得的长度为9米,接着他们移动到点,刚好能看到信号塔主设备的最低点,测得仰角,并测得的长度为1.8米.求信号塔主设备的长度.(结果精确到0.01米参考数据:)
17.(2025·山东临沂·一模)“当你背单词时,阿拉斯加的鳕鱼正跃出水面;当你算数学时,南太平洋的海鸥正掠过海岸当你晚自习时,地球的极圈正五彩斑斓;但少年,梦要你亲自实现,那些你觉得看不到的人和遇不到的风景都终将在你生命里出现.”这是直播带货新平台“东方甄选”货王董宇辉在推销鳕鱼时的台词.所推销鳕鱼的成本为每袋50元,当售价为每袋90元时,每分钟可销售100袋.为了吸引更多顾客,“东方甄选”采取降价措施.据市场调查反映:销售单价每降1元,则每分钟可多销售10袋.
(1)每袋鳕鱼的售价为多少元时,每分钟的销量为150袋?
(2)“东方甄选”不忘公益初心,热心教育事业,其决定从每分钟利润中捐出500元帮助留守儿童,为了保证捐款后每分钟利润达到5500元,且要最大限度让利消费者,求此时鳕鱼的销售单价为多少元?
(3)当销售售价为多少元时,每分钟的利润最大,最大利润是多少?
18.(2025·重庆·二模)如图,在中,,点为线段上一动点,以为边向左作等边.
(1)如图1,当为边中点时,若,,求的周长;
(2)若,点在线段上,且满足,线段交线段于点,连接.
①如图2,若,用等式表示线段和之间的数量关系,并证明;
②如图3,连接,,点运动过程中,当为直角三角形时,请直接写出的值.
19.(2025·辽宁抚顺·模拟预测)若函数的图象上至少存在一个点,该点关于轴的对称点落在函数的图象上,则称函数为函数和函数的“关联函数”,这两个点称为函数和函数的一对“关联点”.例如:如图,点在函数的图象上,点在函数的图象上,点关于轴对称,此时函数为函数和函数的“关联函数”,点和点是一对“关联点”.
【基础练习】
(1)请直接写出函数与函数的“关联函数”和“关联点”的坐标.
(2)若函数与函数的“关联函数”的顶点在轴上,求的值.
【灵活应用】
(3)当函数与函数的自变量满足时,其“关联函数”的最大值为,最小值为,若,求的值.
【深度探究】
(4)在(3)的条件下,当直线与“关联函数”的交点从左到右依次为,则以点与一对“关联点”构成四边形,此四边形能否成为平行四边形?若能,请直接写出的值;若不能,请说明理由.(参考数据:,,)
20.(2025·辽宁抚顺·模拟预测)综合与实践:
【提出问题】
辽宁省沈阳市地处中国东北地区,地势平坦,位于北纬,东经之间,这里四季分明,夏季炎热多雨,冬季寒冷干燥,春季和秋季温度适中.沈阳某小区一居民楼落地窗户朝南,窗户的高度为2米,此地一年中冬至这一天的正午时刻太阳光与地面的夹角最小为,夏至这一天正午时刻太阳光与地面的夹角最大为.某居民想为自己家的落地窗户设计一个直角形遮阳篷,要求它既能最大限度地遮挡夏天炎热的阳光,又能最大限度地使冬天温暖的阳光射入室内.请帮该居民完成设计方案.
【设计方案】
根据商家提供的如图1所示的直角形遮阳棚样品图,抽象数学模型,画出如图2所示的示意图.代表窗户的高,三点共线,代表遮阳棚的宽,,为一年中正午时刻太阳光线与地面产生最大夹角时的光线,为一年中正午时刻太阳光线与地面产生最小夹角时的光线.
【解决方案】
请求出此居民楼需要设计的遮阳棚的宽.(结果精确到0.1米)
【改进方案】
为防止雨水聚积遮阳棚,综合实践小组又把直角形遮阳棚进行升级改造成能够收缩的圆弧形遮阳棚,如图3.经改造设计成以点为圆心,图2中的长为半径的伸缩圆弧形遮阳棚,如图4.在圆弧形遮阳棚点处牵引绳子(其中点是的中点),绳子由图4中和两部分组成,.该居民购买2.5米长的绳子,问绳子是否够用?请说明理由.
(参考数据:,,,)
21.(2025·四川资阳·二模)如图,在平面直角坐标系中,点在抛物线上,且横坐标为1,点与点关于抛物线的对称轴对称,直线与轴交于点,点为抛物线的顶点,点的坐标为.
(1)求线段的长;
(2)点为线段上方抛物线上的任意一点,当的面积最大时,求此时点坐标,并求出最大面积;
(3)在(2)的情况下,过点作的垂线交于点,点在轴上一点,求的最小值.
22.(2025·河北保定·三模)如图是某位同学设计的电脑动画,随着音乐节奏起伏变化,屏幕上就会闪现不同的抛物线,抛物线的统一形式为,且顶点始终在直线上.
(1)当,时,求抛物线的顶点坐标和的值;
(2)试推断与之间的数量关系,并说明理由;
(3)已知,且符合题干的抛物线顶点的横坐标为1,将抛物线向右平移个单位长度,再向上平移个单位长度得到抛物线,且抛物线的顶点恰好也在直线上.
①求的值;
②该同学发现电脑屏幕上有一个黑点(位置固定),刚好落在平面直角坐标系中点的位置,该同学通过电脑放大功能,将抛物线横向、纵向同时放大倍得到抛物线,使点落在抛物线上(放大过程中不改变坐标原点的位置),直接写出符合条件的的值.
《【专项押题预测】临考查漏补缺:解答题(二)-2025年各地区中考数学模拟题汇编》参考答案
1.(1)
(2)
【分析】本题考查了二次函数的图象和性质,待定系数法求二次函数解析式,二次函数的顶点式等知识,熟练掌握二次函数的图象和性质并准确计算是解题的关键.
(1)根据,函数图象经过点和,利用待定系数法求解,即可解题;
(2)根据题意得到,函数图象在时取得最小值,即,以及,联立这三个式子求解,即可解题.
【详解】(1)解:,函数图象经过点和,
,
解得,
二次函数解析式为,
函数图象的顶点坐标为.
(2)解:函数图象经过点,
①,
当时,;当时,,
函数在时取得最小值,即②,
,
,在的左侧,
当时,,即③,
由①②③解得.
2.(1)见详解
(2)
【分析】本题主要考查了菱形的性质、矩形的判定与性质、勾股定理等知识,熟练掌握菱形的性质、矩形的判定与性质是解题关键.
(1)首先根据菱形的性质可得,结合“对角线相互平分的四边形为平行四边形”可证明四边形为平行四边形,然后根据“有一个角为直角的平行四边形为矩形”,即可证明结论;
(2)过点作于点,首先确定菱形的边长,在中利用勾股定理解得的长度,在由矩形的性质可得,,,,利用面积法求得的值,然后在中,由正弦的定义求解即可.
【详解】(1)证明:∵四边形为菱形,
∴,即,
∵点E为的中点,
∴,
又∵,
∴四边形为平行四边形,
∵,
∴四边形是矩形;
(2)如下图,过点作于点,
∵四边形为菱形,且周长为40,
∴,
∵,
∴,
∴在中,可有,
∵四边形是矩形,
∴,,,,
∵,
∴,解得,
∴在中,可有.
3.(1)见解析
(2)的长为
【分析】(1)角平分线的性质得出,而,可得从而;
(2)如图,过点作于点,连接;可得,设的半径为,在中,由勾股定理可得,由可得,即,从而可得四边形是矩形,则,由此可求出.
【详解】(1)解:证明:平分,
.
.
.
(2)如图,过点作于点,连接.
.
,
.
,
.
设的半径为.
.
在中,,
由勾股定理,得,即.
.
,即.
,
四边形是矩形.
.
在中,,
由勾股定理.得.
.
的长为.
【点睛】本题考查的是圆的基本性质,圆周角定理,切线的判定,同时考查了勾股定理、相似三角形的判定与性质,矩形的判定和性质,解题关键在于熟练掌握各个知识点的关联和运用.
4.(1)反比例函数表达式,一次函数表达式为;
(2)
【分析】(1)利用,求出点的坐标,再用待定系数法求出两个函数表达式即可;
(2)首先求出,然后利用的面积,即可求解;
【详解】(1)解:对于,令,则,
故点,则,
而,故点,
的纵坐标为3,点在反比例函数上,故点,
,
解得,故点,
反比例函数表达式为,
将点的纵坐标代入上式得,,
解得,故,
将点的坐标代入得,,解得,
故一次函数表达式为;
(2)对于,令,则,
解得,故点,
的面积.
【点睛】本题考查了反比例函数与一次函数的交点,当有两个函数的时候,着重使用一次函数,体现了方程思想,综合性较强.
5.(1)一台机器人每分钟采茶的片数为30,则一名工人每分钟采茶的片数为25
(2)
【分析】此题考查了一元一次方程和分式方程的应用,
(1)设一台机器人每分钟采茶的片数为x,则一名工人每分钟采茶的片数为,根据题意列出一元一次方程求解即可;
(2)根据题意列出分式方程求解即可.
【详解】(1)设一台机器人每分钟采茶的片数为x,则一名工人每分钟采茶的片数为
根据题意得,
解得
∴
∴一台机器人每分钟采茶的片数为30,则一名工人每分钟采茶的片数为25;
(2)根据题意得,
解得
经检验,是原方程的解.
6.(1),
(2)存在,的最大值为,此时点P的坐标为
【分析】本题考查了平行四边形的性质,二次函数的应用,待定系数法等知识,解题的关键是:
(1)根据平行四边形的性质求出点B的坐标,然后根据待定系数法求解即可;
(2)设,则,则,根据三角形的公式可求出
,然后根据二次函数的性质求解即可.
【详解】(1)解:∵四边形是平行四边形,
∴,,
∵,
∴,
∵,
∴,
代入,得,
解得,
∴反比例函数的解析式为,
设一次函数的解析式为,
∴,
解得,
∴;
(2)解:设,则,
∴,
∴
,
∵,
∴抛物线开口向下,
∴当时,有最大值为,
此时点P的坐标为
7.(1)本次抽取的学生人数为50人,见解析
(2)中位数为分
(3)估计该市初中学生成绩在A组的人数约为300人
【分析】本题主要考查了扇形统计图与条形统计图信息相关联,用样本估计总体,求中位数,正确读懂统计图是解题的关键.
(1)用D组的人数除以其人数占比可求出参与调查的人数,再求出B组的人数即可补全统计图;
(2)根据中位数的定义求解即可;
(3)用3000乘以样本中A组的人数占比即可得到答案.
【详解】(1)解:(人).
∴本次抽取的学生人数为50人.
∴B组的人数为(人).
补全频数分布直方图如下:
(2)解:共抽取了50人,
所抽取的学生成绩的中位数是第25,26个数的平均值(把50人成绩按照从低到高排列).
成绩在组的有5人,组的有15人,组的有10人,
中位数在组.
中位数为(分).
(3)解:(人).
答:估计该市初中学生成绩在A组的人数约为300人.
8.(1)甲、乙两种客房每间现有定价分别是300元、200元
(2)当每间房间定价为280元时,乙种风格客房每天的利润最大,最大利润是4840元
【分析】本题考查了二次函数的应用、二元一次方程组的应用,解答本题的关键是明确题意,正确列出方程组和二次函数关系式,利用二次函数的性质解答.
(1)设甲、乙两种客房每间现有定价分别是元、元,根据题意列方程组并解方程组解决;
(2)设每天的定价增加了个20元,则有个房间空闲,根据题意列出函数关系式并根据二次函数性质求最值即可;
【详解】(1)解:设甲、乙两种客房每间现有定价分别是元、元,
根据题意,得:,
解得,
答:甲、乙两种客房每间现有定价分别是300元、200元;
(2)解:设每天的定价增加了个20元,则有个房间空闲,
根据题意有:
,
,
当时,取得最大值,最大值为4840,此时房间的定价为元,
答:当每间房间定价为280元时,乙种风格客房每天的利润最大,最大利润是4840元.
9.(1)
(2)当该手工品每个售价为11元时,日销售利润最大,最大日销售利润是75元
【分析】本题考查了求一次函数解析式,二次函数的应用.
(1)设与之间的函数关系式为,根据题意求解析式即可;
(2)设销售该手工品日销售利润为元,根据题意得到,再由二次函数的性质计算即可.
【详解】(1)设与之间的函数关系式为.
根据题意,得解得
与之间的函数关系式为.
(2)设销售该手工品日销售利润为元.
根据题意,得.
抛物线的开口向下.
,
当时,取最大值,最大值为75.
答:当该手工品每个售价为11元时,日销售利润最大,最大日销售利润是75元.
10.(1)
(2)
(3)正确,见解析
【分析】本题考查了二次函数的实际应用,正确理解题意,求出函数解析式是解题的关键.
(1)根据二次函数的性质即可求解;
(2)将代入,求出即可;
(3)将代入,求出,即可求出时间间隔.
【详解】(1)解:∵,
∴时,离地面的高度最大,
故答案为:;
(2)解:由题意得,将代入,得,
解得:,
故函数解析式为:;
(3)解:正确,理由如下:
由(2)得,
当时,,
解得:,
∵,间隔时间为4秒,
∴她的说法正确.
11.(1)甲盆栽每盆进价为元,乙盆栽每盆进价为元.
(2)共有三种购买方案,分别为购买甲盆栽盆,乙盆栽盆;购买甲盆栽盆,乙盆栽盆;购买甲盆栽盆,乙盆栽盆;
(3)购买甲盆栽盆,乙盆栽盆时,获利最大,为元.
【分析】本题考查了二元一次方程组以及一次函数的应用,正确理解题意是解题关键.
(1)设甲、乙两种盆栽每盆进价分别为元,由题意得:,据此即可求解;
(2)设甲、乙两种盆栽分别购进盆,由题意得:,即:;根据均为正整数,即可求解;
(3)设利润为,则,可推出随着的增大而增大,据此即可求解;
【详解】(1)解:设甲、乙两种盆栽每盆进价分别为元,由题意得:
,解得:,
∴甲盆栽每盆进价为元,乙盆栽每盆进价为元.
(2)解:设甲、乙两种盆栽分别购进盆,由题意得:
,
即:
∵均为正整数,
∴当时,;
当时,;
当时,;
∴共有三种购买方案,分别为购买甲盆栽盆,乙盆栽盆;购买甲盆栽盆,乙盆栽盆;购买甲盆栽盆,乙盆栽盆;
(3)解:设利润为,
则,
∴随着的增大而增大,
故当时,元;
即:购买甲盆栽盆,乙盆栽盆时,获利最大,为元.
12.(1)见解析
(2)
(3)②④
(4)
【分析】本题主要考查的是频数分布直方图、用样本估计总体、加权平均数、中位数和众数等知识点,熟练掌握上述知识点是解题的关键.
(1)用数据总数减去其他组数据求出这一组的数据,然后补全统计图即可;
(2)结合中位数的定义进行求解即可;
(3)根据众数的定义并结合频数分布直方图可知:在的频数是,的频数是336,相对其他来说,都是远多于其他区间(的频数为15)的频数的,而众数是出现次数最多的一组数据,这是区间,不是具体数值,因此众数出现在这两个区间,的可能性都有的,且可能性较大,出现在,可能性还是有的,但可能性不大,自然众数不可能出现在,其频数都太小了,由此逐一判断各选项即可;
(4)用样本估计整体即可.
【详解】(1)解:解:(件),
补全的频数分布直方图如图所示:
(2)解:把这1000件快递按照重量从低到高排列,中位数为第500件和第501件重量的平均重量,
∵前三组,即中的快递件数为:,前四组中的快递件数为
∴中位数在这一组,
根据这一组的数据如下:;
∴.
(3)解:结合频数分布直方图可知:在的频数是,的频数是336,
相对其他来说,都是远多于其他区间(的频数为15)的频数的,
而众数是出现次数最多的一组数据,
∴众数出现在,这两个区间的可能性都有的,且可能性较大,
出现在,可能性还是有的,但可能性不大,
自然众数不可能出现在,其频数都太小了,
∴①n一定在,说法太绝对,错误;
②n可能在,正确;
③n不可能出现,说法太绝对,错误;
④n不可能出现,正确;
故选:②④.
(4)解:.
答:估计这批快递的重量为.
13.古塔的高度为.
【分析】本题考查解三角形的实际应用.利用坡度比,在中,设,,由勾股定理列方程求解即可得到和,在中,由三角函数定义求出,数形结合,由代值求解即可得到答案.
【详解】解:如图所示:作于点,作交的延长线于点,
则四边形是矩形,
在中,斜坡的斜面坡度,,
设,,
由勾股定理可得,
即,
解得(负值已舍),
,,
,
,
在中,,,
则,即,
解得,
,
答:古塔的高度为.
14.(1)的度数不会发生变化,理由见解析;(2);(3)
【分析】本题主要查了折叠的性质,三角形外角的性质,等腰三角形的性质,勾股定理以及锐角三角函数,利用分类讨论思想解答是解题的关键.
(1)由折叠的性质以及三角形外角的性质解答即可;
(2)根据等腰三角形的性质可得,从而得到,再由折叠的性质可得,即可解答;
(3)根据勾股定理以及锐角三角函数可得,,从而得到,设,则,,然后分两种情况:当时,当时,解答即可.
【详解】解:(1)在点D的移动过程中,的度数不会发生变化,理由如下:
由折叠的性质得:,
∴,
∴在点D的移动过程中,的度数不会发生变化.
(2)∵为等腰三角形,
∴,
∵,
∴,
由折叠的性质得:,
∴;
(3)∵在,,,,
∴,,
∴,
∴,
设,则,
∴,
当时,此时,
∴,
∵,
∴,
解得:或0(舍去),
此时;
当时,此时,
∴,
∵,
∴,
此时方程无解;
综上所述,线段的长为.
15.(1)抽样;200
(2)C
(3)见解析
【分析】本题考查了数据的统计与分析,中位线等知识,解题的关键是:
(1)根据抽样调查和普查的区别即可得出答案,根据B组频数除以B组所占百分比即可求解;
(2)根据中位数的定义求解即可;
(3)提出一个合理建议即可.
【详解】(1)解:本次调查属于抽样调查,本次调查的样本容量为,
故答案为:抽样;200;
(2)解:C组的频数为,
∵样本数据的中位数为第100和101个数的平均数,,,
∴样本数据的中位数落在C组,
故答案为:C;
(3)解:从以上信息可看出,估计全校有的学生观看时间低于40分钟,说明学生的思想上还不够重视,要加强教育.(答案不唯一)
16.2.7米
【分析】本题考查了三角函数的实际应用.先根据等腰三角形的性质得到米,进而求出米,再根据计算即可.
【详解】解:在中,,
∴是等腰直角三角形,
.
米,
米.
米,
(米).
在中,,,
(米).
(米).
答:信号塔主设备的长度约为2.7米.
17.(1)每袋鳕鱼的售价为85元时,每分钟销量为150袋;
(2)此时鳕鱼的销售单价为70元
(3)当销售单价为75元时,能获得最大利润,最大利润为6250元
【分析】本题考查一元一次方程、一元二次方程和二次函数的应用,解题的关键是根据题意,找到等量关系,列出方程,列函数式,进行解答.
(1)设每袋鳕鱼的售价为x元,根据题意,则,解出x,即可;
(2)设此时鳕鱼的销售单价为y元,根据题意,则方程为,解出方程,根据最大限度让利消费者,取值即可.
(3)设鳕鱼的销售单价为a元,每分钟的利润为w,根据题意得,
根据,得当时,w取得最大值,最大值为6250.
【详解】(1)解:设每袋鳕鱼的售价为x元时,每分钟的销量为150袋,
,
∴,
答:每袋鳕鱼的售价为85元时,每分钟销量为150袋;
(2)解:设鳕鱼的销售单价为y元,根据题意得:
,
解得
∵让消费者获得最大的利益,
∴,
答:此时鳕鱼的销售单价为70元.
(3)解:设鳕鱼的销售单价为a元,每分钟的利润为w,根据题意得:
,
∵,
∴当时,w取得最大值,
最大值为6250.
故当销售单价为75元时,能获得最大利润,最大利润为6250元.
18.(1)
(2)①,理由见解析;②或
【分析】本题考查全等三角形的判定与性质,等边三角形的判定与性质,等腰三角形的判定与性质,三角函数,含角的直角三角形的性质,直角三角形斜边中线的性质,熟练掌握这些性质与判定是解题的关键.
(1)在中,利用三角函数求得,由勾股定理得,再利用直角三角形斜边中线的性质得,最后利用等边三角形性质求解;
(2)①在上取一点,使,连接,,延长交于点,利用倒角得,可得是等边三角形,结合等边,利用手拉手模型证明,可得,,通过倒角可得,则,,则可证,则,,得,,再证明,,,易得,利用,倒角可得,则,即可证明;
②同①在上取一点,使,连接,,延长交于点,同①可得,,设,则,分两种情况:当时和当时,分别作图计算即可 .
【详解】(1)解:在中,
∵,,,
∴,
∴,
∵为边中点,
∴,
∵是等边三角形,
∴的周长;
(2)解:①,理由如下:
在上取一点,使,连接,,延长交于点,
∵是等边三角形,
∴,,
∵,
∴,
即,
∴是等边三角形,
∴,
∴,
∴,
∴,
∴,,
∴,
∵,,
∴,
∴,
∴,
∴,,
∴,
∴,
∴,
又∵,
∴,,
∴,
∵,,
∴,,,
∴,,
∴,
∴,
∵,
∴,
∴,
∴,,
∴,
∴,
∴,
∴;
②同①在上取一点,使,连接,,延长交于点,
同①可得,,
设,
∴,
当时,如图,
∵,
∴,,
∴,
∵,,
∴,
∴,
∴;
当时,如图,
∵,
∴,,
∴,
∵, ,
∴,
∴,
∴;
综上,或.
19.()“关联函数”为 ,“关联点”的坐标为和或和;
();
()的值为或-1;
()能,的值为或
【分析】根据“关联函数”的定义可得“关联函数”的解析式是,设函数的一个点的坐标为,则关于轴的对称点的坐标为,根据“关联点”之间的关系得到方程,解方程求出“关联点”即可;
根据“关联函数”的定义可得“关联函数”的解析式是,“关联函数”的顶点在轴上,可得:,解方程求出值即可;
根据题意可得:“关联函数”的解析式为,根据解析式可以求出顶点坐标为,当时,,当时,,根据与“关联函数”的对称轴的关系分四种情况求解;
分别写出当的值为或时“关联函数”的解析式,根据平行四边形的性质表示出“关联点”的坐标,根据“关联点”的定义得到关于的方程,从而求出点 的坐标,再根据直线与“关联函数”的图象交于点,确定的值即可.
【详解】解:函数中,,
函数中,
“关联函数”为;
设函数的一个点的坐标为,则关于轴的对称点的坐标为,
点在函数的图象上,
,
解得:,,
点的坐标为或,
点的坐标为或,
“关联点”的坐标为和或和;
解:根据题意,得“关联函数”为,
“关联函数”的顶点在轴上,
,
解得:,,
,
;
解:根据题意,得“关联函数”为,
函数的对称轴为直线,顶点坐标为,
当时,,
当时,,
,
抛物线的开口向下,
,即时,
可得:,,
,
解得:;
直线关于直线的对称直线为,
当时,
解得:时,
可得:,,
,
解得:,(不合题意,舍去);
当,
解得:时,
可得:,,
,
解得:,(不合题意,舍去);
当,即时,
,
,
此时,,
,
解得:.
综上所述,的值为或;
解:能,的值为或.
当时,一次函数的表达式为,
反比例函数的表达式为,
“关联函数”的表达式为.
设一次函数的一个点的坐标为,
则点关于轴对称的点的坐标为,
点在函数的图象上,
,
解得:,
点,,
轴,
,
点在“关联函数”的图象上,
点的坐标为,
,
当时,以为顶点的四边形是平行四边形,
点.
点也在“关联函数”的图象上,
,
解得:,
点,
直线与“关联函数”的图象交于点,,
;
当时,一次函数的表达式为,
反比例函数的表达式为,
“关联函数”的表达式为,
设一次函数的一个点的坐标为,
则点关于轴对称的点的坐标为,
点在函数的图象上,
,
整理得:,
解得:,,
点的横坐标为或,
点的横坐标为或,
点,关于轴对称,
轴,
的长为或.
点在“关联函数”的图象上,
设点的坐标为,
,
有以下两种情况:
当时,
以为顶点的四边形是平行四边形,
点,
点也在“关联函数”的图象上,
,
解得:,
点,
直线与“关联函数”的图象交于点,,
,
当时,以为顶点的四边形是平行四边形,
点,
点也在“关联函数”的图象上,
,
解得:,
点,
直线与“关联函数”的图象交于点,,
(不符合题意,舍去),
综上所述,的值为或.
【点睛】本题考查了新定义、反比例函数与一次函数交点问题、轴对称的性质、二次函数的性质、平行四边形的判定与性质,解决本题的关键是根据二次函数的性质确定点的坐标.
20.解决方案:遮阳棚的宽约为0.7米;改进方案:绳子不够用,理由见解析
【分析】(1)在,可设米,则米,可得,再在中,,由此可证;
(2)在中可得,由为的中点,可得,最后在,,,可得,由此可证绳子不够.
【详解】解:【解决方案】由题意,知米,.
.
在中,,
.
设米,则米.
米.
在中,,
,即.
解得.
答:遮阳棚的宽约为0.7米.
【改进方案】绳子不够用.理由如下:
由【解决方案】,得在中,,
(米).
如图,连接.
米.
由题意,得.
为的中点.
.
.
,
,
在中,,,
(米)
(米).
米.
(米).
绳子不够用.
【点睛】本题主要考查锐角三角函数值的应用,圆弧的相关知识点,掌握锐角三角函数和圆相关知识是解题的关键.
21.(1)
(2),
(3)
【分析】本题考查二次函数综合,涉及二次函数图象与性质、二次函数与面积综合、二次函数求最值等问题,数形结合是解决问题的关键.
(1)根据题意,令,代入表达式求出即可得到,再根据点与点关于抛物线的对称轴对称,即可求出,从而得到答案;
(2)作轴交于,如图所示,设,数形结合,在平面直角坐标系中表示出的面积,由二次函数图象与性质分析即可得到答案;
(3)作直线交于,使得,作于交于,如图所示,数形结合得,利用等面积法求解即可得到答案.
【详解】(1)解:点在抛物线上,且横坐标为1,
令,则,则,
点与点关于抛物线的对称轴对称,
,
;
(2)解:作轴交于,如图所示:
设,
直线的解析式为,
,
,
,
抛物线开口向下,有最大值,当时,的面积最大为,此时;
(3)解:作直线交于,使得,作于交于,如图所示:
由(2)知点,,
,
,
,此时的值最小,
,
,
的最小值为.
22.(1)抛物线的顶点坐标为,
(2)
(3)①;②的值为或
【分析】本题主要考查了二次函数应用,位似图形的性质,解题时要熟练掌握并能灵活运用二次函数的性质是关键.
(1)根据抛物线的顶点坐标公式,求得顶点坐标为,再将代入正比例函数解析式,即可求解;
(2)根据题意可得,可得顶点坐标,再设抛物线的解析式为,从而可得抛物线 的解析式,结合顶点在上,即可得解;
(3)依据题意,由①得抛物线的顶点坐标为,又将抛物线横向、纵向同时放大倍后,可得顶点坐标为,从而抛物线将点代入,即可求解.
【详解】(1)解:,
,
抛物线的顶点坐标为,
将代入得
;
(2)与之间的数量关系为.理由如下:
由题意,顶点始终在直线上,
∴
,
.
与之间的数量关系为.
(3)①由题意,,
.
抛物线顶点的横坐标为,
顶点的纵坐标为.
设抛物线的解析式为
抛物线 的解析式为
抛物线 的顶点坐标为
在上
.
②由①得抛物线的顶点坐标为.
将抛物线横向、纵向同时放大倍后,
顶点坐标为.
抛物线
将点代入得
解得:
∴的值为或.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
