【专项押题预测】临考查漏补缺:填空题(含解析)-2025年各地区中考数学模拟题汇编
文档属性
| 名称 | 【专项押题预测】临考查漏补缺:填空题(含解析)-2025年各地区中考数学模拟题汇编 |  | |
| 格式 | docx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-09 05:26:20 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
【专项押题预测】临考查漏补缺:填空题-2025年各地区中考数学模拟题汇编
1.(2025·黑龙江哈尔滨·三模)一个不透明的袋子中装有2个黑球,3个白球,这些球除颜色外无其它差别,从袋子中随机摸出两个球,则摸出的两个球都是黑球的概率为 .
2.(2025·黑龙江哈尔滨·三模)分式方程的解为 .
3.(2025·黑龙江哈尔滨·三模)在函数中,自变量的取值范围是 .
4.(2025·黑龙江哈尔滨·三模)对于实数m、n,定义一种新运算“※”为,这里等式右边是实数运算,例如:,则方程的解为 .
5.(2025·湖北武汉·模拟预测)如图,拦水坝的横断面为梯形,迎水坡的斜面坡度是指坡面的铅直高度与水平宽度的比,背水坡的斜面坡度是指坡面的铅直高度与水平宽度的比.若,则的长度是 .(参考数据:.)
6.(2025·湖北武汉·模拟预测)已知两个不同点,都在反比例函数的图象上,请写出一个满足条件的点坐标是 .
7.(2025·四川成都·二模)若关于的一元二次方程两根为、,且,则的值为 .
8.(2025·四川成都·二模)如图,在中,,按以下步骤作图:①以点为圆心、适当长为半径作弧,分别交,于点,;②分别以点,为圆心、大于的长为半径作弧,两弧在的内部相交于点;③作射线交于点.若,,则的长为 .
9.(2025·四川成都·二模)已知反比例函数的图象经过点,,则 .(填“”或“”或“”)
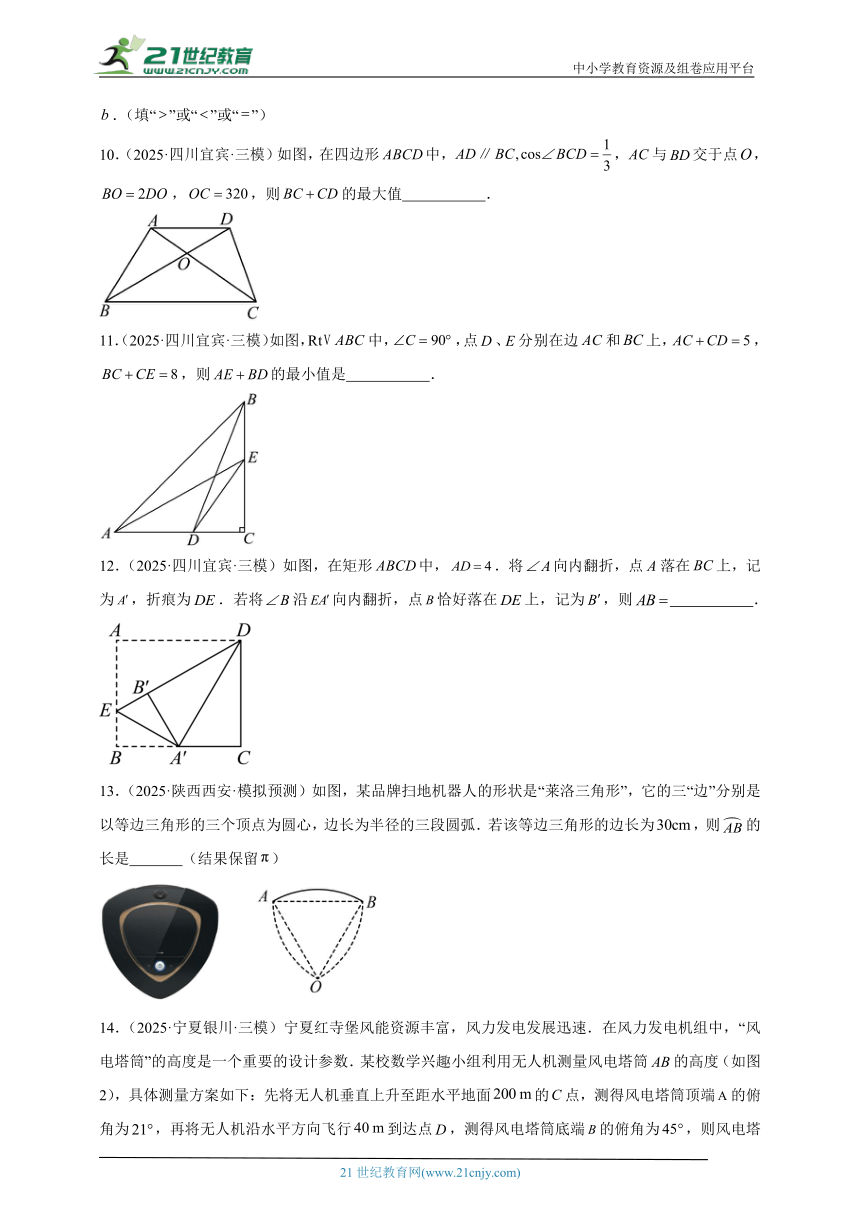
10.(2025·四川宜宾·三模)如图,在四边形中,,与交于点,,,则的最大值 .
11.(2025·四川宜宾·三模)如图,Rt中,,点、分别在边和上,,,则的最小值是 .
12.(2025·四川宜宾·三模)如图,在矩形中,.将向内翻折,点A落在上,记为,折痕为.若将沿向内翻折,点恰好落在上,记为,则 .
13.(2025·陕西西安·模拟预测)如图,某品牌扫地机器人的形状是“莱洛三角形”,它的三“边”分别是以等边三角形的三个顶点为圆心,边长为半径的三段圆弧.若该等边三角形的边长为,则的长是 (结果保留)
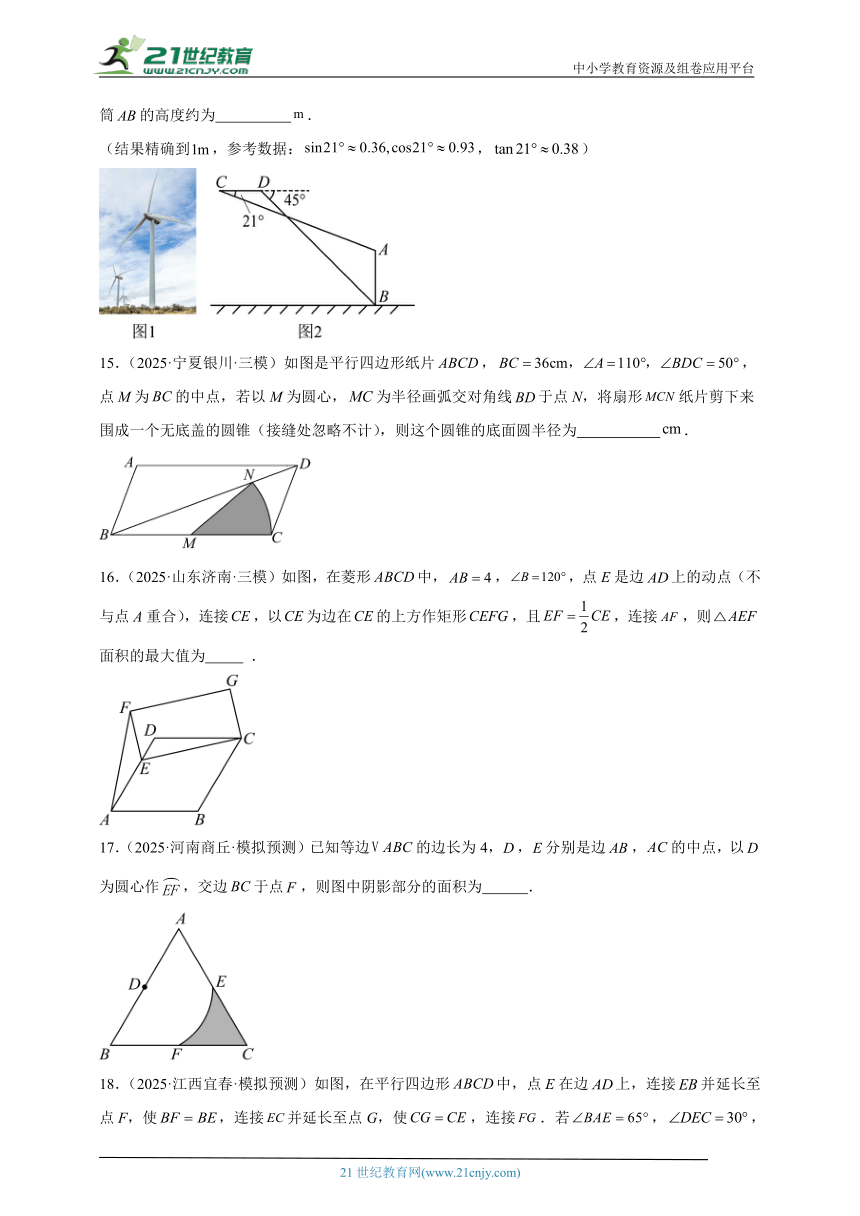
14.(2025·宁夏银川·三模)宁夏红寺堡风能资源丰富,风力发电发展迅速.在风力发电机组中,“风电塔筒”的高度是一个重要的设计参数.某校数学兴趣小组利用无人机测量风电塔筒的高度(如图2),具体测量方案如下:先将无人机垂直上升至距水平地面的点,测得风电塔筒顶端的俯角为,再将无人机沿水平方向飞行到达点,测得风电塔筒底端的俯角为,则风电塔筒的高度约为 .
(结果精确到,参考数据:,)
15.(2025·宁夏银川·三模)如图是平行四边形纸片,,点M为的中点,若以M为圆心,为半径画弧交对角线于点N,将扇形纸片剪下来围成一个无底盖的圆锥(接缝处忽略不计),则这个圆锥的底面圆半径为 .
16.(2025·山东济南·三模)如图,在菱形中,,,点E是边上的动点(不与点A重合),连接,以为边在的上方作矩形,且,连接,则面积的最大值为 .
17.(2025·河南商丘·模拟预测)已知等边的边长为4,,分别是边,的中点,以为圆心作,交边于点,则图中阴影部分的面积为 .
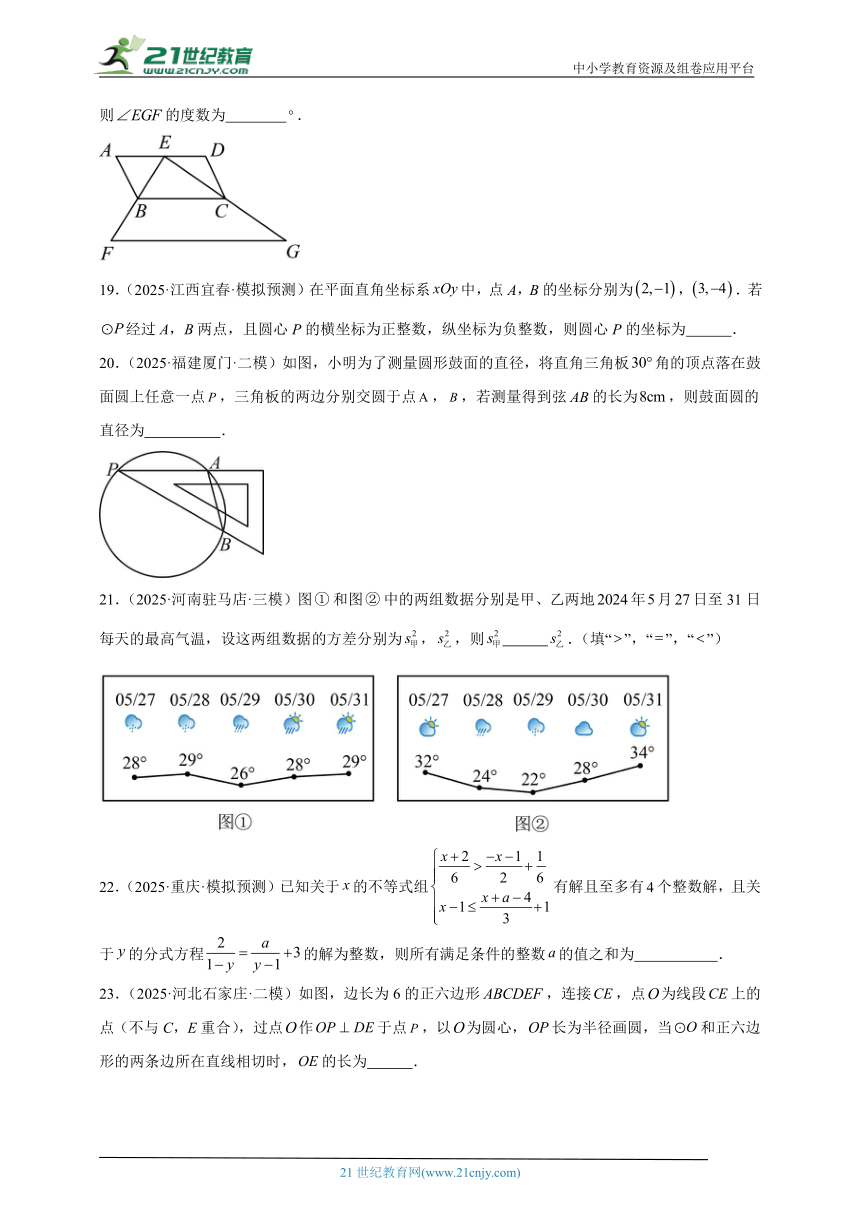
18.(2025·江西宜春·模拟预测)如图,在平行四边形中,点E在边上,连接并延长至点F,使,连接并延长至点G,使,连接.若,,则的度数为 .
19.(2025·江西宜春·模拟预测)在平面直角坐标系中,点A,B的坐标分别为,.若经过A,B两点,且圆心P的横坐标为正整数,纵坐标为负整数,则圆心P的坐标为 .
20.(2025·福建厦门·二模)如图,小明为了测量圆形鼓面的直径,将直角三角板角的顶点落在鼓面圆上任意一点,三角板的两边分别交圆于点,,若测量得到弦的长为,则鼓面圆的直径为 .
21.(2025·河南驻马店·三模)图和图中的两组数据分别是甲、乙两地年月日至31日每天的最高气温,设这两组数据的方差分别为,,则 .(填“”,“”,“”)
22.(2025·重庆·模拟预测)已知关于的不等式组有解且至多有个整数解,且关于的分式方程的解为整数,则所有满足条件的整数的值之和为 .
23.(2025·河北石家庄·二模)如图,边长为6的正六边形,连接,点为线段上的点(不与C,E重合),过点作于点,以为圆心,长为半径画圆,当和正六边形的两条边所在直线相切时,的长为 .
24.(2025·浙江杭州·一模)如图,在正方形中,点、分别在边、上,且,点关于直线的对称点在线段的延长线上,与交于点.
(1)若点与点关于直线对称,则 ;
(2)若,则 .
25.(2025·河南平顶山·模拟预测)如图,在中,,过点作于点,点是延长线上一点,线段,的延长线交于点,若,,,则的长为 .
26.(2025·福建厦门·二模)如图,直线经过点,则关于x的不等式的解集是 .
27.(2025·甘肃酒泉·三模)如图,平行四边形中,E是的延长线上一点,与交于点.若的面积为3,则的面积为 .
28.(2025·湖北武汉·模拟预测)为了研究函数的性质,小广用描点法画它的图象,列出了如下表格:
x … 0 2 3 …
… m …
下列五个结论:①;②该函数图象在x轴上方;③该函数图象与直线有2个交点;④当时,该函数图象有最低点;⑤点和是该函数图象上两点,若,则或或.其中正确的结论是 (填序号).
29.(2025·湖北武汉·模拟预测)图①中的吉林省广播电视塔,又称“吉塔”.某直升飞机于空中A处探测到吉塔,此时飞行高度,如图②.从直升飞机上看塔尖C的俯角,看塔底D的俯角,则吉塔的高度为 .(结果精确到).
(参考数据:)
30.(2025·湖北武汉·模拟预测)在压力不变的情况下,某物体承受的压强P(单位:)与它的受力面积S(单位:)是反比例函数关系,其函数图象如图所示.当.时,P= .
《【专项押题预测】临考查漏补缺:填空题-2025年各地区中考数学模拟题汇编》参考答案
1.
【分析】利用画树状图法计算概率.
本题考查了画树状图法求概率,熟练运用画树状图法求概率是解题的关键.
【详解】解:设黑色的球分别,,白球分别为,,,画树状图如下:
一共有20种等可能性的结果,其中摸出的两个球都是黑球的有2种等可能性,
故摸出的两个球都是黑球的概率为.
故答案为:.
2.
【分析】本题考查解分式方程,利用去分母将原方程化为整式方程,解得的值后进行检验即可.熟练掌握解方程的方法是解题的关键.
【详解】解:,
去分母得:,
解得:,
经检验,是分式方程的解,
故答案为:.
3.
【分析】本题考查了函数自变量的取值范围,分式有意义的条件.
根据分式有意义的条件分母不为零,分析原式,即可得出答案.
【详解】解:有意义,
,
,
故答案为:.
4.
【分析】本题是新定义题型,主要考查了解分式方程,正确理解新定义法则是关键;
根据新定义的法则可得关于x的方程,解方程并检验后即得答案.
【详解】解:根据题意:方程即为:,
即,
去分母得:,
解得:,
经检验:是原方程的解;
故答案为:.
5.31.6
【分析】本题主要考查了解直角三角形的应用坡度问题和勾股定理,准确计算是解题的关键.
首先由迎水坡的斜面坡度求出,然后得到,然后由背水坡的斜面坡度求出,然后利用勾股定理求解即可.
【详解】∵迎水坡的斜面坡度
∴,即
∴
根据题意得,四边形是矩形
∴
∵背水坡的斜面坡度
∴,即
∴
∴.
故答案为:31.6.
6.(答案不唯一)
【分析】本题考查了反比例函数图象上点的坐标,根据点的坐标求出反比例函数解析式,再给出点的横坐标一个值,代入求出解析式求出的值,就可以写出点的坐标,理解题意,正确求出反比例函数解析式是解题的关键.
【详解】解:∵是反比例函数图象上的点,
∴,
取时,,
∴点的坐标是,
故答案为:(答案不唯一).
7.
【分析】本题考查了一元二次方程根和系数的关系,由一元二次方程根和系数的关系可得,,进而可得,据此即可求解,掌握一元二次方程根和系数的关系是解题的关键.
【详解】解:∵关于的一元二次方程两根为、,
∴,,
∴,
∴,
故答案为:.
8.
【分析】本题考查了角平分线作图及其性质,全等三角形的判定与性质,勾股定理,熟练掌握以上知识点是解题的关键.作于点,根据角平分线的性质可知,可证,得到,然后利用勾股定理在中求得,在中建立方程求得,最后在中,根据勾股定理即可求得答案.
【详解】解:作于点,如图所示,
根据作图可知,是的角平分线,
,,
,
,
,
,
,
,
,
在中,,
在中,,即
,
解得(负值已舍去),
在中,.
故答案为:.
9.
【分析】本题考查反比例函数的图象与性质,根据反比例函数图象所在象限以及增减性判断即可.
【详解】解:由题意,反比例函数的图象位于第二、四象限,且在每一象限内,y随x的增大而增大,
∵反比例函数的图象经过点,,,
∴,
故答案为:.
10.
【分析】证明,得出,,根据是定值,是定长,进而求得的最大值,过点作交的延长于点,延长至,使得,求得,根据当为过点的圆的直径时,取得最大值,得出,解,即可求解.
【详解】解:∵,
∴,
∴,
∵,
∴,
∴,
又∵,
∴,
∴,
∵,
∴,
∵,
∴是定值,则也是定值,
根据“定弦定角”模型可知,当为圆的直径时,取得最大值,
如图所示,过点作交的延长于点,延长至,使得,
设,则,,
∴,
在中,,
在中,,
∴,
∴当为过点的圆的直径时,取得最大值,
此时,如图所示,
∵为直径,
∴,
∴,
∴,
∴的最大值为.
故答案为:.
【点睛】本题考查了圆周角定理,相似三角形的性质与判定,勾股定理,解直角三角形,熟练掌握以上知识是解题的关键.
11.
【分析】本题考查了勾股定理,将问题进行转化是解题的关键;设,得出,,勾股定理表示出,转化为平面内一点到和点的距离的和,则当在线段上时,取得最小值,最小值为的长,即可求解.
【详解】解:设,
∵,,
∴,,
∴,,
∴,
即表示的点到和点的距离的和,
如图
∴当在线段上时,取得最小值,最小值为的长为;
故答案为:.
12.
【分析】本题主要考查矩形中的折叠问题、解直角三角形等知识点,灵活运用解直角三角形求线段的长度成为解题的关键.
根据题意可得,即,解得出,进而求得,再根据即可求解.
【详解】解:如图:
∵将向内翻折,点A落在上,记为,折痕为.若将沿向内翻折,点恰好落在上,记为,
∴,,
∵,
∴,
在中,,
,解得:,
∴,
在中,,
∴,
∴,
.
故答案为:.
13.
【分析】本题主要考查了求弧长,等边三角形的性质,根据等边三角形的性质得到,再根据弧长公式计算求解即可.
【详解】解:∵是正三角形,
∴,
∴的长是,
故答案为:.
14.109
【分析】本题考查解直角三角形的实际应用,正确构造直角三角形是解题的关键.
延长交的延长线于点E,在中,根据,得出为等腰直角三角形,说明,在中根据,,进而求出结果即可.
【详解】解:延长交的延长线于点E,则,.
在中,,
∴为等腰直角三角形,
∴,
,
在中,,,
,
,
故答案为:109.
15.2
【分析】本题考查了平行四边形的性质、弧长公式、圆锥等知识,熟练掌握弧长公式是解题关键.先根据平行四边形的性质可得,再根据三角形的内角和定理可得,然后根据等腰三角形的性质可得,最后根据三角形的外角性质可得的度数;先利用弧长公式求出扇形的弧长,再根据圆锥的底面圆的周长等于扇形的弧长求解即可得.
【详解】解:∵四边形是平行四边形,,
∴,
∵,
∴,
由圆的性质可知,,
∴,
∴,
∴扇形的弧长为,
∴圆锥的底面圆半径为,
故答案为: 2.
16.
【分析】本题考查了相似三角形的判定和性质,菱形的性质,二次函数的应用.作点关于点的对称点,连接,,则,作于点,作交延长线于点,设,证明,求得,求得,则,利用二次函数的性质求解即可.
【详解】解:作点关于点的对称点,连接,,则面积等于面积,
∵菱形,,,
∴,
∴,
∵矩形,
∴,
∵,
∴,
作于点,作交延长线于点,设,
∵,
∴,
∴,
∴,
∴,
∵,
∴,
∴,
∵,
∴,
∴,
∴,
∴,
,
∵,
∴当时,有最大值,最大值为,
故答案为:.
17.
【分析】本题考查了等边三角形判定与性质和扇形的面积公式的知识,掌握以上知识是解答本题的关键;
连接,,证得和是等边三角形,求得,,然后根据阴影部分面积等于面积减去扇形面积减去面积减去面积进行计算,即可求解;
【详解】解:连接,,如图:
∵、是、中点,是等边三角形,
∴,,,,,,
∴,
∴是等边三角形,
∴,,
∵以为圆心作,交边于点,
∴,
∵,
∴是等边三角形,
∴,
∴,
∴阴影部分面积等于面积减去扇形面积减去面积减去面积,
即面积为,面积为,
面积为,
∴扇形面积为,
∴阴影部分面积为:;
故答案为:
18.30
【分析】本题考查了平行四边形的性质,三角形中位线的性质;熟练掌握平行四边形的性质,并能进行推理计算是解决问题的关键.
由平行四边形的性质可得,根据中位线性质可得,进而根据平行线的性质得出答案即可.
【详解】解:∵四边形是平行四边形,
∴,
∴,
∵,,
∴是是中位线,
∴,
∴.
故答案为:30.
19.或或
【分析】题目主要考查中垂线的性质,圆的基本性质,根据题意得出经过A,B两点圆的圆心在的中垂线上,然后作出图形求解即可.
【详解】解:经过A,B两点圆的圆心在的中垂线上,由条件“圆心O的横坐标为正整数、纵坐标为负整数”所限,
如图所示:
只有或或三点.
20. /厘米
【分析】此题考查圆周角定理、等边三角形的判定与性质等知识;设鼓面圆的圆心为,连接、,则,因为,所以是等边三角形,则,所以的直径为,于是得到问题的答案.
【详解】解:设鼓面圆的圆心为,连接、,则,
,,
,
是等边三角形,
,
的半径为,
的直径为,
故答案为:.
21.
【分析】本题考查了平均数,方差,分别计算甲乙两地的平均数和方差,然后比较即可,掌握平均数和方差的计算是解题的关键.
【详解】解:甲地平均数为:,
∴,
乙地平均数为:,
∴,
∴,
故答案为:.
22.
【分析】本题主要考查了解一元一次不等式组,解分式方程,熟练掌握解一元一次不等式组和分式方程的步骤是解题关键.
解关于的不等式组,得,根据不等式组有解且至多有个整数解,得,再解关于的分式方程得,根据分式方程的解为整数且分母不为可得符合条件的的值,再求和即可.
【详解】解:
由①解得:,
由②解得:,
.
关于x的不等式组有解且至多有个整数解,
,
当时,解得:,
当时,解得:,
,
关于的分式方程,
化简,得:,
关于的分式方程的解为整数,且,
,
或,
所有满足条件的整数的值之和.
故答案为:.
23.或/或
【分析】先由正六边形得到,则判断出与相切于点,当与边相切时,记切点为点,连接,根据圆的切线的性质可得平分,则,解,即可求解;记与的左交点为点,连接,当点与点重合时,可得到点重合,再解即可.
【详解】∵正六边形,
∴,
∴,
∵,长为半径画圆,
∴与相切于点,
当与边相切时,记切点为点,连接,如图:
则,,而,
∴平分,
∵,
∴,
∴在中,;
记与的左交点为点,连接,
∵,
∴,
∵,
∴,
当点与点重合时,如图:
∴,
∴点重合,
∴,
∴与相切于点,而与相切于点,故符合题意,
∴,
综上:当和正六边形的两条边所在直线相切时,的长为或,
故答案为:或.
【点睛】本题考查了圆的切线的判定与性质,解直角三角形的相关计算,等腰三角形的性质,正多边形的内角问题等知识点,熟练掌握各知识点并灵活运用是解题的关键.
24.
【分析】(1)由轴对称可得到,从而,即可解答;
(2)延长,,交于点M,设与交于点N,由得到,设,.证明,根据“三线合一”得到,设,则,,,,,由得到,即,求得,即可解答.
【详解】解:(1)∵点与点关于直线对称,
∴,
∵点与点关于对称,
∴,
∵在正方形中,,
∴,
∴,
∵,
∴,
∵在正方形中,,
∴,
∴.
故答案为:.
(2)延长,,交于点,设与交于点,
∵在正方形中,,
∴,
∴,
∴设,,
点与点关于对称,
∴,
∴,
∴,
∴,
∵在正方形中,,
∴,
∴在正方形中,.
设,
∴,,
,
∵点与点关于对称,
∴,
∵在正方形中,,
∴四边形是矩形,
∴,
∴,
∴,
∵,
∴,
∴,即,
解得:,(不合题意,舍去)
∴,
∴.
故答案为:.
【点睛】本题考查正方形的性质,轴对称图形的性质,求锐角三角函数值,相似三角形的判定及性质,等腰三角形的判定与性质,矩形的判定与性质,解一元二次方程,综合运用相关知识是解题的关键.
25./
【分析】过点分别作的垂线,垂足为,在中利用正切的定义得到,利用勾股定理列出方程,求出,,得到,利用勾股定理求出,通过证明得到,由得,则,得到,根据列出方程,求出,再利用勾股定理以及线段的和差即可求出的长.
【详解】解:如图,过点分别作的垂线,垂足为,
,
,
在中,,
,
,
,
解得:或(负值舍去),
,
,
,
,
,,
是的高,,
,
,
,,
,
,
,
,
,
,即,
,
在中,,
,
,即,
,
,
,
.
故答案为:.
【点睛】本题考查了解直角三角形、一元二次方程的应用、相似三角形的性质与判定、勾股定理、等边对等角、二次根式的混合运算,结合图形作垂线构造直角三角形是解题的关键.
26.
【分析】本题考查了一次函数与一元一次不等式的关系,写出函数图象在下方所对应的自变量的范围即可.
【详解】解:根据函数图象,直线经过点,则关于x的不等式的解集是
故答案为:.
27.12
【分析】根据, ,即可判定,根据,得,即可求得的面积.本题考查了相似三角形的判定与性质.
【详解】解:∵四边形是平行四边形
∴, ,
,
∴
,
∵
∴
∴,
∴
又的面积为3 ,
∴的面积为,
故答案为:12
28.①②④
【分析】将代入即可判断①;根据题意判断出即可判断②;将代入得到或,然后根据判别式即可判断③;首先求出抛物线与x轴的交点坐标为和,得到当时,,然后得出,得出中,有最大值,进而可判断④;由表格得到,当时,,然后根据得到,进而求解即可.
【详解】解:①将代入,故①正确;
②∵,
∴,
∴该函数图象在x轴上方,故②正确;
③当时,,
∴或,
∴或,
∴或,
∴或,
∴该函数图像与直线有4个交点,故③错误;
④设,
当时,,
解得或,
∴抛物线与x轴的交点坐标为和,
∵,
∴抛物线开口向上,
∴当时,,
∴此时,
∵中,
∴此抛物线开口向下,
∴它有最大值,
∴有最小值,即函数有最低点,故④正确;
⑤∵点和是该函数图象上两点,
∴由表格得,当时,,
当时,,
∵若,
∴,
∴,
∴,
解得或,故⑤错误.
综上所述,其中正确的结论是①②④.
故答案为:①②④.
【点睛】此题考查二次函数的图象和性质,二次函数与x轴交点问题,解题的关键是掌握二次函数的图象和性质.
29.218.3
【分析】本题考查了解直角三角形的应用,过点C作,垂足为F,先说明四边形是矩形,再在中,利用直角三角形的边角间关系求出的长,最后利用线段的和差关系得结论.
【详解】解:过点C作,垂足为F,
∵,,,
∴,
∴四边形是矩形,
∴,,
∵,
∴,,
∴,
在中,
∵,
∴,
∴.
答:吉塔的高度约为.
故答案为:218.3.
30.
【分析】本题考查反比例函数的应用,正确进行计算是解题关键.
先求出反比例函数的解析式,再代入数据求解即可.
【详解】解:设函数的解析式为,
将代入可得:,
解得:,
当,
,
故答案为:.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
【专项押题预测】临考查漏补缺:填空题-2025年各地区中考数学模拟题汇编
1.(2025·黑龙江哈尔滨·三模)一个不透明的袋子中装有2个黑球,3个白球,这些球除颜色外无其它差别,从袋子中随机摸出两个球,则摸出的两个球都是黑球的概率为 .
2.(2025·黑龙江哈尔滨·三模)分式方程的解为 .
3.(2025·黑龙江哈尔滨·三模)在函数中,自变量的取值范围是 .
4.(2025·黑龙江哈尔滨·三模)对于实数m、n,定义一种新运算“※”为,这里等式右边是实数运算,例如:,则方程的解为 .
5.(2025·湖北武汉·模拟预测)如图,拦水坝的横断面为梯形,迎水坡的斜面坡度是指坡面的铅直高度与水平宽度的比,背水坡的斜面坡度是指坡面的铅直高度与水平宽度的比.若,则的长度是 .(参考数据:.)
6.(2025·湖北武汉·模拟预测)已知两个不同点,都在反比例函数的图象上,请写出一个满足条件的点坐标是 .
7.(2025·四川成都·二模)若关于的一元二次方程两根为、,且,则的值为 .
8.(2025·四川成都·二模)如图,在中,,按以下步骤作图:①以点为圆心、适当长为半径作弧,分别交,于点,;②分别以点,为圆心、大于的长为半径作弧,两弧在的内部相交于点;③作射线交于点.若,,则的长为 .
9.(2025·四川成都·二模)已知反比例函数的图象经过点,,则 .(填“”或“”或“”)
10.(2025·四川宜宾·三模)如图,在四边形中,,与交于点,,,则的最大值 .
11.(2025·四川宜宾·三模)如图,Rt中,,点、分别在边和上,,,则的最小值是 .
12.(2025·四川宜宾·三模)如图,在矩形中,.将向内翻折,点A落在上,记为,折痕为.若将沿向内翻折,点恰好落在上,记为,则 .
13.(2025·陕西西安·模拟预测)如图,某品牌扫地机器人的形状是“莱洛三角形”,它的三“边”分别是以等边三角形的三个顶点为圆心,边长为半径的三段圆弧.若该等边三角形的边长为,则的长是 (结果保留)
14.(2025·宁夏银川·三模)宁夏红寺堡风能资源丰富,风力发电发展迅速.在风力发电机组中,“风电塔筒”的高度是一个重要的设计参数.某校数学兴趣小组利用无人机测量风电塔筒的高度(如图2),具体测量方案如下:先将无人机垂直上升至距水平地面的点,测得风电塔筒顶端的俯角为,再将无人机沿水平方向飞行到达点,测得风电塔筒底端的俯角为,则风电塔筒的高度约为 .
(结果精确到,参考数据:,)
15.(2025·宁夏银川·三模)如图是平行四边形纸片,,点M为的中点,若以M为圆心,为半径画弧交对角线于点N,将扇形纸片剪下来围成一个无底盖的圆锥(接缝处忽略不计),则这个圆锥的底面圆半径为 .
16.(2025·山东济南·三模)如图,在菱形中,,,点E是边上的动点(不与点A重合),连接,以为边在的上方作矩形,且,连接,则面积的最大值为 .
17.(2025·河南商丘·模拟预测)已知等边的边长为4,,分别是边,的中点,以为圆心作,交边于点,则图中阴影部分的面积为 .
18.(2025·江西宜春·模拟预测)如图,在平行四边形中,点E在边上,连接并延长至点F,使,连接并延长至点G,使,连接.若,,则的度数为 .
19.(2025·江西宜春·模拟预测)在平面直角坐标系中,点A,B的坐标分别为,.若经过A,B两点,且圆心P的横坐标为正整数,纵坐标为负整数,则圆心P的坐标为 .
20.(2025·福建厦门·二模)如图,小明为了测量圆形鼓面的直径,将直角三角板角的顶点落在鼓面圆上任意一点,三角板的两边分别交圆于点,,若测量得到弦的长为,则鼓面圆的直径为 .
21.(2025·河南驻马店·三模)图和图中的两组数据分别是甲、乙两地年月日至31日每天的最高气温,设这两组数据的方差分别为,,则 .(填“”,“”,“”)
22.(2025·重庆·模拟预测)已知关于的不等式组有解且至多有个整数解,且关于的分式方程的解为整数,则所有满足条件的整数的值之和为 .
23.(2025·河北石家庄·二模)如图,边长为6的正六边形,连接,点为线段上的点(不与C,E重合),过点作于点,以为圆心,长为半径画圆,当和正六边形的两条边所在直线相切时,的长为 .
24.(2025·浙江杭州·一模)如图,在正方形中,点、分别在边、上,且,点关于直线的对称点在线段的延长线上,与交于点.
(1)若点与点关于直线对称,则 ;
(2)若,则 .
25.(2025·河南平顶山·模拟预测)如图,在中,,过点作于点,点是延长线上一点,线段,的延长线交于点,若,,,则的长为 .
26.(2025·福建厦门·二模)如图,直线经过点,则关于x的不等式的解集是 .
27.(2025·甘肃酒泉·三模)如图,平行四边形中,E是的延长线上一点,与交于点.若的面积为3,则的面积为 .
28.(2025·湖北武汉·模拟预测)为了研究函数的性质,小广用描点法画它的图象,列出了如下表格:
x … 0 2 3 …
… m …
下列五个结论:①;②该函数图象在x轴上方;③该函数图象与直线有2个交点;④当时,该函数图象有最低点;⑤点和是该函数图象上两点,若,则或或.其中正确的结论是 (填序号).
29.(2025·湖北武汉·模拟预测)图①中的吉林省广播电视塔,又称“吉塔”.某直升飞机于空中A处探测到吉塔,此时飞行高度,如图②.从直升飞机上看塔尖C的俯角,看塔底D的俯角,则吉塔的高度为 .(结果精确到).
(参考数据:)
30.(2025·湖北武汉·模拟预测)在压力不变的情况下,某物体承受的压强P(单位:)与它的受力面积S(单位:)是反比例函数关系,其函数图象如图所示.当.时,P= .
《【专项押题预测】临考查漏补缺:填空题-2025年各地区中考数学模拟题汇编》参考答案
1.
【分析】利用画树状图法计算概率.
本题考查了画树状图法求概率,熟练运用画树状图法求概率是解题的关键.
【详解】解:设黑色的球分别,,白球分别为,,,画树状图如下:
一共有20种等可能性的结果,其中摸出的两个球都是黑球的有2种等可能性,
故摸出的两个球都是黑球的概率为.
故答案为:.
2.
【分析】本题考查解分式方程,利用去分母将原方程化为整式方程,解得的值后进行检验即可.熟练掌握解方程的方法是解题的关键.
【详解】解:,
去分母得:,
解得:,
经检验,是分式方程的解,
故答案为:.
3.
【分析】本题考查了函数自变量的取值范围,分式有意义的条件.
根据分式有意义的条件分母不为零,分析原式,即可得出答案.
【详解】解:有意义,
,
,
故答案为:.
4.
【分析】本题是新定义题型,主要考查了解分式方程,正确理解新定义法则是关键;
根据新定义的法则可得关于x的方程,解方程并检验后即得答案.
【详解】解:根据题意:方程即为:,
即,
去分母得:,
解得:,
经检验:是原方程的解;
故答案为:.
5.31.6
【分析】本题主要考查了解直角三角形的应用坡度问题和勾股定理,准确计算是解题的关键.
首先由迎水坡的斜面坡度求出,然后得到,然后由背水坡的斜面坡度求出,然后利用勾股定理求解即可.
【详解】∵迎水坡的斜面坡度
∴,即
∴
根据题意得,四边形是矩形
∴
∵背水坡的斜面坡度
∴,即
∴
∴.
故答案为:31.6.
6.(答案不唯一)
【分析】本题考查了反比例函数图象上点的坐标,根据点的坐标求出反比例函数解析式,再给出点的横坐标一个值,代入求出解析式求出的值,就可以写出点的坐标,理解题意,正确求出反比例函数解析式是解题的关键.
【详解】解:∵是反比例函数图象上的点,
∴,
取时,,
∴点的坐标是,
故答案为:(答案不唯一).
7.
【分析】本题考查了一元二次方程根和系数的关系,由一元二次方程根和系数的关系可得,,进而可得,据此即可求解,掌握一元二次方程根和系数的关系是解题的关键.
【详解】解:∵关于的一元二次方程两根为、,
∴,,
∴,
∴,
故答案为:.
8.
【分析】本题考查了角平分线作图及其性质,全等三角形的判定与性质,勾股定理,熟练掌握以上知识点是解题的关键.作于点,根据角平分线的性质可知,可证,得到,然后利用勾股定理在中求得,在中建立方程求得,最后在中,根据勾股定理即可求得答案.
【详解】解:作于点,如图所示,
根据作图可知,是的角平分线,
,,
,
,
,
,
,
,
,
在中,,
在中,,即
,
解得(负值已舍去),
在中,.
故答案为:.
9.
【分析】本题考查反比例函数的图象与性质,根据反比例函数图象所在象限以及增减性判断即可.
【详解】解:由题意,反比例函数的图象位于第二、四象限,且在每一象限内,y随x的增大而增大,
∵反比例函数的图象经过点,,,
∴,
故答案为:.
10.
【分析】证明,得出,,根据是定值,是定长,进而求得的最大值,过点作交的延长于点,延长至,使得,求得,根据当为过点的圆的直径时,取得最大值,得出,解,即可求解.
【详解】解:∵,
∴,
∴,
∵,
∴,
∴,
又∵,
∴,
∴,
∵,
∴,
∵,
∴是定值,则也是定值,
根据“定弦定角”模型可知,当为圆的直径时,取得最大值,
如图所示,过点作交的延长于点,延长至,使得,
设,则,,
∴,
在中,,
在中,,
∴,
∴当为过点的圆的直径时,取得最大值,
此时,如图所示,
∵为直径,
∴,
∴,
∴,
∴的最大值为.
故答案为:.
【点睛】本题考查了圆周角定理,相似三角形的性质与判定,勾股定理,解直角三角形,熟练掌握以上知识是解题的关键.
11.
【分析】本题考查了勾股定理,将问题进行转化是解题的关键;设,得出,,勾股定理表示出,转化为平面内一点到和点的距离的和,则当在线段上时,取得最小值,最小值为的长,即可求解.
【详解】解:设,
∵,,
∴,,
∴,,
∴,
即表示的点到和点的距离的和,
如图
∴当在线段上时,取得最小值,最小值为的长为;
故答案为:.
12.
【分析】本题主要考查矩形中的折叠问题、解直角三角形等知识点,灵活运用解直角三角形求线段的长度成为解题的关键.
根据题意可得,即,解得出,进而求得,再根据即可求解.
【详解】解:如图:
∵将向内翻折,点A落在上,记为,折痕为.若将沿向内翻折,点恰好落在上,记为,
∴,,
∵,
∴,
在中,,
,解得:,
∴,
在中,,
∴,
∴,
.
故答案为:.
13.
【分析】本题主要考查了求弧长,等边三角形的性质,根据等边三角形的性质得到,再根据弧长公式计算求解即可.
【详解】解:∵是正三角形,
∴,
∴的长是,
故答案为:.
14.109
【分析】本题考查解直角三角形的实际应用,正确构造直角三角形是解题的关键.
延长交的延长线于点E,在中,根据,得出为等腰直角三角形,说明,在中根据,,进而求出结果即可.
【详解】解:延长交的延长线于点E,则,.
在中,,
∴为等腰直角三角形,
∴,
,
在中,,,
,
,
故答案为:109.
15.2
【分析】本题考查了平行四边形的性质、弧长公式、圆锥等知识,熟练掌握弧长公式是解题关键.先根据平行四边形的性质可得,再根据三角形的内角和定理可得,然后根据等腰三角形的性质可得,最后根据三角形的外角性质可得的度数;先利用弧长公式求出扇形的弧长,再根据圆锥的底面圆的周长等于扇形的弧长求解即可得.
【详解】解:∵四边形是平行四边形,,
∴,
∵,
∴,
由圆的性质可知,,
∴,
∴,
∴扇形的弧长为,
∴圆锥的底面圆半径为,
故答案为: 2.
16.
【分析】本题考查了相似三角形的判定和性质,菱形的性质,二次函数的应用.作点关于点的对称点,连接,,则,作于点,作交延长线于点,设,证明,求得,求得,则,利用二次函数的性质求解即可.
【详解】解:作点关于点的对称点,连接,,则面积等于面积,
∵菱形,,,
∴,
∴,
∵矩形,
∴,
∵,
∴,
作于点,作交延长线于点,设,
∵,
∴,
∴,
∴,
∴,
∵,
∴,
∴,
∵,
∴,
∴,
∴,
∴,
,
∵,
∴当时,有最大值,最大值为,
故答案为:.
17.
【分析】本题考查了等边三角形判定与性质和扇形的面积公式的知识,掌握以上知识是解答本题的关键;
连接,,证得和是等边三角形,求得,,然后根据阴影部分面积等于面积减去扇形面积减去面积减去面积进行计算,即可求解;
【详解】解:连接,,如图:
∵、是、中点,是等边三角形,
∴,,,,,,
∴,
∴是等边三角形,
∴,,
∵以为圆心作,交边于点,
∴,
∵,
∴是等边三角形,
∴,
∴,
∴阴影部分面积等于面积减去扇形面积减去面积减去面积,
即面积为,面积为,
面积为,
∴扇形面积为,
∴阴影部分面积为:;
故答案为:
18.30
【分析】本题考查了平行四边形的性质,三角形中位线的性质;熟练掌握平行四边形的性质,并能进行推理计算是解决问题的关键.
由平行四边形的性质可得,根据中位线性质可得,进而根据平行线的性质得出答案即可.
【详解】解:∵四边形是平行四边形,
∴,
∴,
∵,,
∴是是中位线,
∴,
∴.
故答案为:30.
19.或或
【分析】题目主要考查中垂线的性质,圆的基本性质,根据题意得出经过A,B两点圆的圆心在的中垂线上,然后作出图形求解即可.
【详解】解:经过A,B两点圆的圆心在的中垂线上,由条件“圆心O的横坐标为正整数、纵坐标为负整数”所限,
如图所示:
只有或或三点.
20. /厘米
【分析】此题考查圆周角定理、等边三角形的判定与性质等知识;设鼓面圆的圆心为,连接、,则,因为,所以是等边三角形,则,所以的直径为,于是得到问题的答案.
【详解】解:设鼓面圆的圆心为,连接、,则,
,,
,
是等边三角形,
,
的半径为,
的直径为,
故答案为:.
21.
【分析】本题考查了平均数,方差,分别计算甲乙两地的平均数和方差,然后比较即可,掌握平均数和方差的计算是解题的关键.
【详解】解:甲地平均数为:,
∴,
乙地平均数为:,
∴,
∴,
故答案为:.
22.
【分析】本题主要考查了解一元一次不等式组,解分式方程,熟练掌握解一元一次不等式组和分式方程的步骤是解题关键.
解关于的不等式组,得,根据不等式组有解且至多有个整数解,得,再解关于的分式方程得,根据分式方程的解为整数且分母不为可得符合条件的的值,再求和即可.
【详解】解:
由①解得:,
由②解得:,
.
关于x的不等式组有解且至多有个整数解,
,
当时,解得:,
当时,解得:,
,
关于的分式方程,
化简,得:,
关于的分式方程的解为整数,且,
,
或,
所有满足条件的整数的值之和.
故答案为:.
23.或/或
【分析】先由正六边形得到,则判断出与相切于点,当与边相切时,记切点为点,连接,根据圆的切线的性质可得平分,则,解,即可求解;记与的左交点为点,连接,当点与点重合时,可得到点重合,再解即可.
【详解】∵正六边形,
∴,
∴,
∵,长为半径画圆,
∴与相切于点,
当与边相切时,记切点为点,连接,如图:
则,,而,
∴平分,
∵,
∴,
∴在中,;
记与的左交点为点,连接,
∵,
∴,
∵,
∴,
当点与点重合时,如图:
∴,
∴点重合,
∴,
∴与相切于点,而与相切于点,故符合题意,
∴,
综上:当和正六边形的两条边所在直线相切时,的长为或,
故答案为:或.
【点睛】本题考查了圆的切线的判定与性质,解直角三角形的相关计算,等腰三角形的性质,正多边形的内角问题等知识点,熟练掌握各知识点并灵活运用是解题的关键.
24.
【分析】(1)由轴对称可得到,从而,即可解答;
(2)延长,,交于点M,设与交于点N,由得到,设,.证明,根据“三线合一”得到,设,则,,,,,由得到,即,求得,即可解答.
【详解】解:(1)∵点与点关于直线对称,
∴,
∵点与点关于对称,
∴,
∵在正方形中,,
∴,
∴,
∵,
∴,
∵在正方形中,,
∴,
∴.
故答案为:.
(2)延长,,交于点,设与交于点,
∵在正方形中,,
∴,
∴,
∴设,,
点与点关于对称,
∴,
∴,
∴,
∴,
∵在正方形中,,
∴,
∴在正方形中,.
设,
∴,,
,
∵点与点关于对称,
∴,
∵在正方形中,,
∴四边形是矩形,
∴,
∴,
∴,
∵,
∴,
∴,即,
解得:,(不合题意,舍去)
∴,
∴.
故答案为:.
【点睛】本题考查正方形的性质,轴对称图形的性质,求锐角三角函数值,相似三角形的判定及性质,等腰三角形的判定与性质,矩形的判定与性质,解一元二次方程,综合运用相关知识是解题的关键.
25./
【分析】过点分别作的垂线,垂足为,在中利用正切的定义得到,利用勾股定理列出方程,求出,,得到,利用勾股定理求出,通过证明得到,由得,则,得到,根据列出方程,求出,再利用勾股定理以及线段的和差即可求出的长.
【详解】解:如图,过点分别作的垂线,垂足为,
,
,
在中,,
,
,
,
解得:或(负值舍去),
,
,
,
,
,,
是的高,,
,
,
,,
,
,
,
,
,
,即,
,
在中,,
,
,即,
,
,
,
.
故答案为:.
【点睛】本题考查了解直角三角形、一元二次方程的应用、相似三角形的性质与判定、勾股定理、等边对等角、二次根式的混合运算,结合图形作垂线构造直角三角形是解题的关键.
26.
【分析】本题考查了一次函数与一元一次不等式的关系,写出函数图象在下方所对应的自变量的范围即可.
【详解】解:根据函数图象,直线经过点,则关于x的不等式的解集是
故答案为:.
27.12
【分析】根据, ,即可判定,根据,得,即可求得的面积.本题考查了相似三角形的判定与性质.
【详解】解:∵四边形是平行四边形
∴, ,
,
∴
,
∵
∴
∴,
∴
又的面积为3 ,
∴的面积为,
故答案为:12
28.①②④
【分析】将代入即可判断①;根据题意判断出即可判断②;将代入得到或,然后根据判别式即可判断③;首先求出抛物线与x轴的交点坐标为和,得到当时,,然后得出,得出中,有最大值,进而可判断④;由表格得到,当时,,然后根据得到,进而求解即可.
【详解】解:①将代入,故①正确;
②∵,
∴,
∴该函数图象在x轴上方,故②正确;
③当时,,
∴或,
∴或,
∴或,
∴或,
∴该函数图像与直线有4个交点,故③错误;
④设,
当时,,
解得或,
∴抛物线与x轴的交点坐标为和,
∵,
∴抛物线开口向上,
∴当时,,
∴此时,
∵中,
∴此抛物线开口向下,
∴它有最大值,
∴有最小值,即函数有最低点,故④正确;
⑤∵点和是该函数图象上两点,
∴由表格得,当时,,
当时,,
∵若,
∴,
∴,
∴,
解得或,故⑤错误.
综上所述,其中正确的结论是①②④.
故答案为:①②④.
【点睛】此题考查二次函数的图象和性质,二次函数与x轴交点问题,解题的关键是掌握二次函数的图象和性质.
29.218.3
【分析】本题考查了解直角三角形的应用,过点C作,垂足为F,先说明四边形是矩形,再在中,利用直角三角形的边角间关系求出的长,最后利用线段的和差关系得结论.
【详解】解:过点C作,垂足为F,
∵,,,
∴,
∴四边形是矩形,
∴,,
∵,
∴,,
∴,
在中,
∵,
∴,
∴.
答:吉塔的高度约为.
故答案为:218.3.
30.
【分析】本题考查反比例函数的应用,正确进行计算是解题关键.
先求出反比例函数的解析式,再代入数据求解即可.
【详解】解:设函数的解析式为,
将代入可得:,
解得:,
当,
,
故答案为:.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
