【专项押题预测】临考查漏补缺:解答题(一)(含解析)-2025年各地区中考数学模拟题汇编
文档属性
| 名称 | 【专项押题预测】临考查漏补缺:解答题(一)(含解析)-2025年各地区中考数学模拟题汇编 |  | |
| 格式 | docx | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-09 05:53:20 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
【专项押题预测】临考查漏补缺:解答题(一)-2025年各地区中考数学模拟题汇编
1.(2025·广东·二模)为出行方便,越来越多的市民使用起了共享单车,图1为单车实物图,图2为单车示意图,与地面平行,坐垫可沿射线方向调节.已知,车轮半径为,当时,小明体验后觉得骑着比较舒适,此时坐垫离地面高度约为?(结果精确到,参考数据:,,)
2.(24-25九年级下·安徽六安·阶段练习)在2025年春节联欢晚会上,新年吉祥物“巳升升”特别惹人注目,其设计灵感源于中华传统文化,整体造型参考甲骨文中的“巳”字,采用青绿色为主色调,外形愁态可掬,寓意“福从头起,尾随如意”,我们在电商平台和实体店了解其销售情况.
(1)统计某电商平台,2024年12月份吉祥物一月的销售量是5万件,2025年2月份吉祥物一月的销售量是7.2万件,若近三个月月平均增长率相同,求月平均增长率;
(2)对某实体店的销售情况进行了解,该店吉祥物的进价为每件60元,若售价定为每件100元,则每天能销售量20件.通过市场调查发现,售价每降价1元,每天可多售出2件,为了进一步推广宣传,商家决定降价促销,要求尽量减少库存,且使每天销售获利1200元,请你分析售价应降低多少元?
3.(2025·安徽合肥·三模)如图,已知内接于,为直径,过点作的切线交延长线于,为上的一点,连接,交于,且.
(1)求证:;
(2)若的半径为,求的长.
4.(2025·安徽合肥·三模)观察下列等式:
①
②
③
④
(1)请按以上规律写出第⑥个等式:___________;
(2)猜想并写出符合上述规律的第个等式:___________;并证明猜想的正确性.
5.(2025·安徽合肥·三模)在如图所示的平面直角坐标系中,已知.
(1)将绕点逆时针旋转得到,请画出;
(2)以坐标原点为位似中心,在轴下方,画出的位似图形,使它与的位似比为.
(3)在轴上找一点,使得,并直接写出点的坐标.
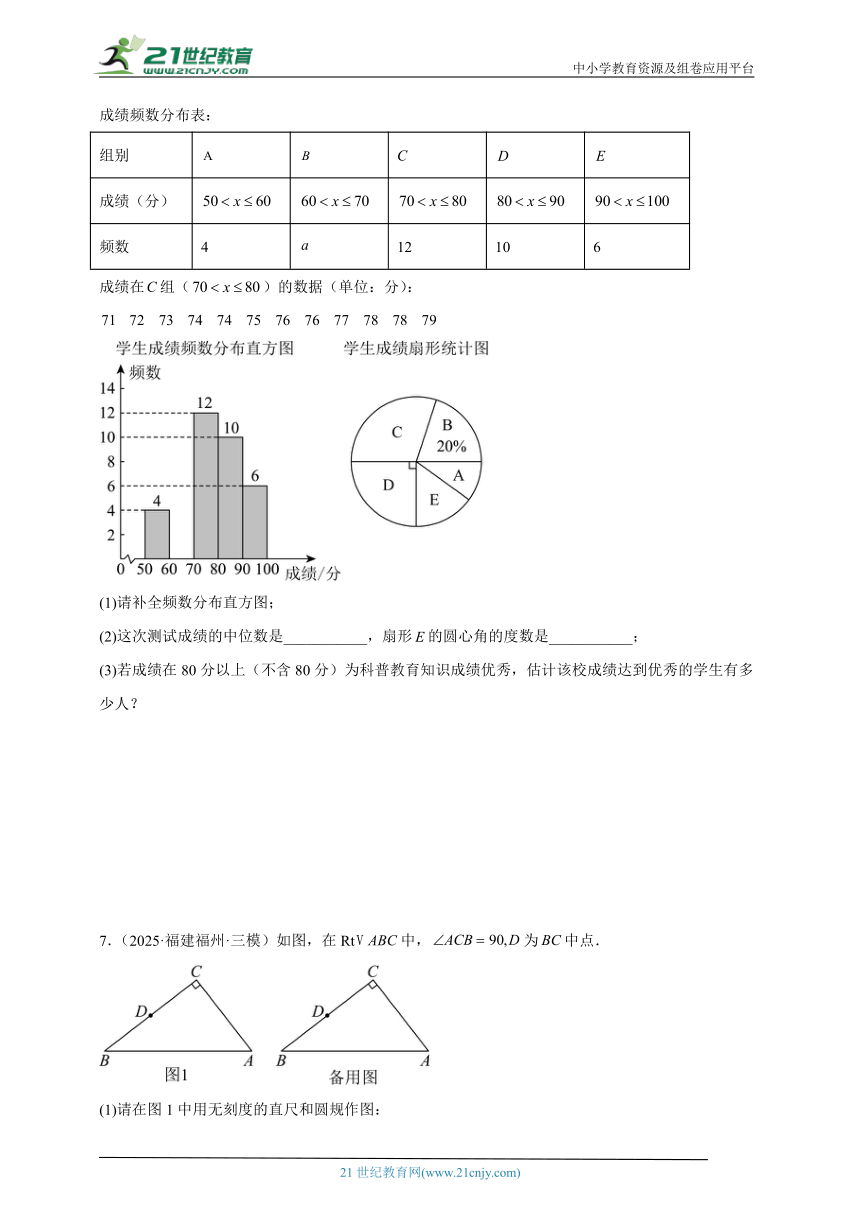
6.(2025·陕西榆林·三模)2025年3月9日,国家卫生健康委员会相关负责人宣布,将正式实施为期三年的“体重管理年”行动,普及健康生活方式,帮助居民科学管理体重.为推进“体重管理年”,某中学举行了“健康体重,一起行动”科普教育,并组织1500名学生参加了知识答卷,为了解科普效果,从中随机抽取了部分学生的成绩进行统计,并对收集到的数据进行了整理、描述和分析.信息如下:
成绩频数分布表:
组别 C
成绩(分)
频数 4 12 10 6
成绩在组()的数据(单位:分):
(1)请补全频数分布直方图;
(2)这次测试成绩的中位数是___________,扇形的圆心角的度数是___________;
(3)若成绩在80分以上(不含80分)为科普教育知识成绩优秀,估计该校成绩达到优秀的学生有多少人?
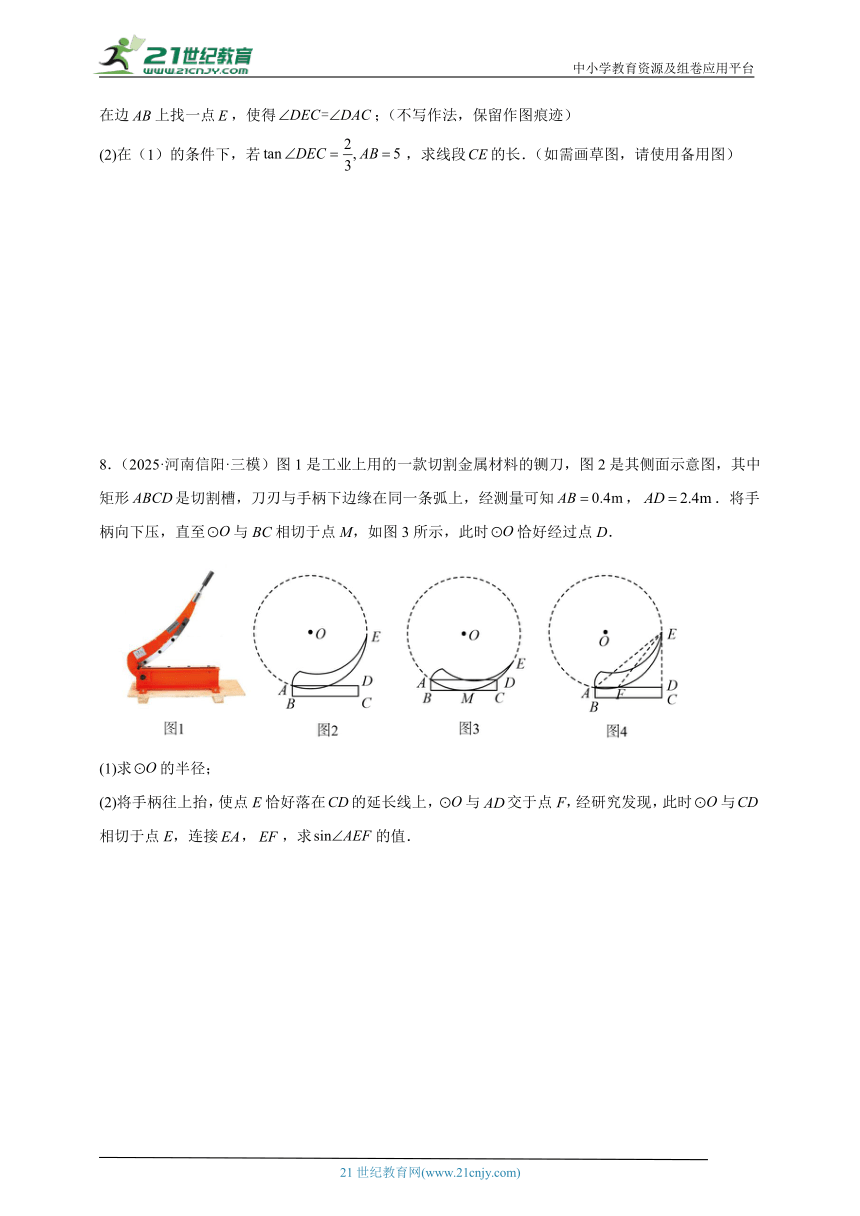
7.(2025·福建福州·三模)如图,在Rt中,为中点.
(1)请在图1中用无刻度的直尺和圆规作图:
在边上找一点,使得;(不写作法,保留作图痕迹)
(2)在(1)的条件下,若,求线段的长.(如需画草图,请使用备用图)
8.(2025·河南信阳·三模)图1是工业上用的一款切割金属材料的铡刀,图2是其侧面示意图,其中矩形是切割槽,刀刃与手柄下边缘在同一条弧上,经测量可知,.将手柄向下压,直至与BC相切于点M,如图3所示,此时恰好经过点D.
(1)求的半径;
(2)将手柄往上抬,使点E恰好落在的延长线上,与交于点F,经研究发现,此时与相切于点E,连接,,求的值.
9.(2025·福建泉州·模拟预测)如图1,在中,,,垂足为,点,分别在边,上,,,与相交于点.
(1)求证:;
(2)如图2,点在的延长线上,且,交的延长线于点,求证:
;
.
10.(2025·甘肃平凉·二模)随着中考的临近,为了给即将参加中考的学生加油鼓励,九年级(1)班的班长制作了一个如图所示质地均匀的转盘(转盘被平均分成四等份),再将“中考加油”四个字分别写在每个扇形上,让班上的每个同学自由转动两次转盘,转盘停止后,指针所指扇形区域内的字即为转出的字(若指针指向分割线,则不计次数,重新转动,直至指针指向某一扇形区域为止).
(1)该班的小敏同学转动一次转盘,转出的字为“考”属于______事件;(选填“必然”“随机”或“不可能”)
(2)该班的小凡同学转动转盘两次,利用列表或画树状图的方法求小凡同学两次转出的字可以组成词语“中考”或“加油”的概率.
11.(2025·北京房山·二模)如图,已知为的外接圆,为的直径,是的中点,弦于点,是上一点,连接.
(1)求证:;
(2)若,求.
12.(2025·吉林白城·模拟预测)如图,在矩形中,,.为中点,连接.动点从点出发,沿射线以的速度运动.过作,过作于点,当经过点时,点停止运动.设点的运动时间为.与四边形重叠部分图形的面积为.
(1)当点落在边上时,的值为________;
(2)当经过点时,的值为________;
(3)求关于的函数解析式,并直接写出自变量的取值范围.
13.(2025·四川成都·模拟预测)如图,是的外接圆,点在的延长线上,连接,作于点,交于点,且,连接.
(1)求证:是的切线;
(2),,求线段的长.
14.(2025·四川成都·模拟预测)成都某中学准备每年组织开展“风筝节”“我运动,我快乐”“跳蚤书市”“校园十佳歌手大赛”“元旦文艺晚会”等课余活动,让学生劳逸结合.该校采用随机抽样调查的方式对部分学生个人最喜爱的一项课余活动进行了调查,并根据收集到的信息分为:风筝节;:我运动,我快乐;:跳蚤书市;:校园十佳歌手大赛;:元旦文艺晚会共五组进行统计,并根据调查结果绘制成如下两幅不完整的统计图.
(1)本次调查的学生共有________人,并补全条形统计图;
(2)扇形统计图中“”对应的扇形圆心角的度数为________;
(3)本次调查中,最喜爱“我运动,我快乐”中有品学兼优的两男和三女共5名学生,若从中随机抽取两名学生作为该活动的主持人,请利用画树状图或列表的方法,求恰好抽到一名男生和一名女生的概率.
15.(2025·江苏盐城·二模)如图,已知轮船甲位于港口A西南方向的点B处,轮船乙位于港口A正南方向的点C处,点C位于点B南偏东方向.轮船甲向正东航行10 nmile到点D,轮船乙向正北航20 nmile到点E,测得点D位于点E北偏西方向.
(1)求此时轮船甲乙之间的距离.
(2)求此时轮船乙到港口A的距离.(结果精确到1 nmile,参考数据:,,,,,)
16.(2025·四川成都·模拟预测)如图,在平面直角坐标系中,直线与反比例函数的图象交于两点,与轴和轴分别交于点和点,其中点坐标为,点在反比例函数图象上.
(1)求点的坐标及反比例函数的表达式;
(2)若点在点的右侧,过点作轴,垂足为,若,求的长;
(3)是否存在一点,使得,若存在,求出点的坐标;若不存在,请说明理由.
17.(2025·江苏盐城·二模)某公司需向甲地紧急运送的货物,决定使用、两种型号的无人机运送.已知每台型无人机的单次最高载货量比每台型无人机的单次最高载货量多;在满载情况下,某次用相同数量的无人机一次性运送货物,型无人机共载货,型无人机共载货.
(1)每台型无人机和型无人机的单次最高载货量分别是多少?
(2)该公司决定使用台型无人机()和台型无人机载货,在每台无人机都满载的情况下,刚好一次性完成的货物运送:
①求满足条件的、值;
②若型无人机单次运费为型无人机单次运费的倍.为了节省成本,该公司应使用两种型号的无人机各多少台?
18.(2025·河南信阳·三模)2025年3月23日,歼-10首飞成功27年,近年来,歼-10家族不断突破、不断壮大.小明和小亮到一家科技体验馆购买航模,已知该体验馆有两种优惠方案可以选择,且两种方案只能参加其中一种.
方案一:科技体验馆推出70元抵100元的代金券,付费时可以抵扣100元.
方案二:购买航模的费用一律打八折.
(1)若小明选中的航模的价格为元,方案一需付费元,方案二需付费元.
①请写出,关于x的函数表达式;
②通过计算,小明发现参加两种方案所需费用相差8元,求m的值.
(2)小亮也选中了一个航模,价格为元,发现参加方案一更划算,求n的取值范围.
19.(2025·四川资阳·二模)如图,在矩形中,,,是上的一个动点.
(1)如图,连接,是对角线的中点,连结.当时,求的长.
(2)如图,连接、,过点作交于点,连结,与交于点.当平分时,求的长.
(3)如图,连接,点在上,将矩形沿直线折叠,折叠后点落在上的点处,过点作于点,与交于点,且.
①求的值;
②连接,与是否相似?请说明理由.
20.(2025·重庆·模拟预测)如图,已知在中,,点E在直线上,连接.过点C作于点D,交于点E
(1)如图1,若点E在线段上,平分,,,求的长度;
(2)如图2,若点E在线段上,,延长至点G,连接,满足,请用等式表示线段、之间的数量关系,并证明;
(3)如图3,若,将沿翻折至所在平面得,连接,点P为的中点,连接,在E点运动过程中,当取最小值时,直接写出此时的值.
21.(2025·黑龙江哈尔滨·三模)已知抛物线交轴于点、,交轴于点,顶点的纵坐标为.
(1)如图,求抛物线的解析式;
(2)如图,点为第一象限的抛物线对称轴上一点,连接,将绕点逆时针旋转后得到线段(点在第一象限内),过点作直线轴,交轴于点,交抛物线于点,设点的纵坐标为,线段的长为,求与的函数关系式,并写出自变量的取值范围;
(3)如图,在()的条件下,连接,过点作,射线交过点且与垂直的直线于点,过点作于点,点为上一点,过点作,交于点,交于点,连接,若,,求点的坐标.
《【专项押题预测】临考查漏补缺:解答题(一)-2025年各地区中考数学模拟题汇编》参考答案
1.
【分析】本题考查了解直角三角形的应用,作出适当的辅助线,构造出直角三角形是解题的关键;作于H,作地面于P,利用三角函数求出即可.
【详解】解:如图,作于H,作地面于P,
由题知,,
∴,
∴坐垫C离地面高度约为.
2.(1)月平均增长率为
(2)售价应降低20元
【分析】本题考查了一元二次方程实际应用问题,根据题意找到相等关系是解题的关键.
(1)设月平均增长率为,根据题意列出方程即可;
(2)设售价应降低元,则可卖出件,利用每件获利乘以销售数量等于每天销售获利,列方程即可解答.
【详解】(1)解:设月平均增长率为,
由题意得,,
解得:(不合题意,舍去),
答:月平均增长率为;
(2)解:设售价应降低元,
由题意得,,
整理得:,
解得:,
尽量减少库存,
,
答:售价应降低20元.
3.(1)见解析
(2).
【分析】(1)根据圆周角定理和切线的性质得到,利用等角的余角相等求得,即可证明;
(2)作于点,利用角平分线的性质求得,证明,求得,设,在中,由勾股定理列式计算即可求解.
【详解】(1)证明:∵为的直径,为的切线,
∴,
∴,
∵,
∴,
∵,,
∴,
∴;
(2)解:作于点,
∵为的直径,的半径为5,
∴,,
∵,
∴,
由(1)得,
∴,
∵,
∴,
∴,
设,
∴,,
在中,由勾股定理得,即,
解得,
∴.
【点睛】本题考查切线的性质,圆周角定理,勾股定理,角平分线的性质,全等三角形的判定和性质.正确引出辅助线解决问题是解题的关键.
4.(1);
(2),证明见解析.
【分析】本题主要考查根据规律运算、完全平方公式应用、整式的混合运算法则等知识点,根据题干得到式子之间存在的规律是解题的关键.
(1)根据题干规律直接写出答案即可;
(2)找出分子两个数之间关系直接写出答案,利用完全平方公式以及整式的相关运算法则即可证明.
【详解】(1)解:由题意可得,第⑥个等式为:.
故答案为:.
(2)解:第个:,证明如下:
∵左边,右边,
∴左边右边,
∴.
5.(1)见解析
(2)见解析
(3)
【分析】本题主要考查了位似变换、旋转变换、等腰三角形的性质等知识点,掌握位似变换和旋转变换的定义是解题的关键.
(1)先利用旋转的性质确定的对应点的位置,然后再顺次连接即可;
(2)先利用旋转的性质确定的对应点的位置,然后再顺次连接即可;
(3)先根据等腰三角形的性质求得点M的位置,然后再写出坐标即可.
【详解】(1)解:如图:即为所求.
(2)解:如图:即为所求.
(3)解:如图:轴上的点,使得,此时M的坐标为.
6.(1)图见解析
(2);
(3)该校成绩达到优秀的学生约有600人
【分析】本题考查读频数分布直方图,频数(率分布表和扇形统计图的能力和利用统计图获取信息的能力.
(1)根据频数分布直方图可得到的值,然后补全频数分布直方图;
(2)将样本中成绩从低到高排列,排在中间的两个数是76,77,可得中位数,用乘以组的百分比即可得到扇形的圆心角的度数;
(3)用学生总人数乘以成绩在80分以上(不含80分)的百分比,计算即可得解.
【详解】(1)解: 被抽取的学生人数为,
,
补全频数分布直方图,如图所示.
;
(2)解:将样本中成绩从低到高排列,排在中间的两个数是76,77,故中位数是,
扇形的圆心角的度数是.
∴估计这次测试成绩的中位数是,扇形的圆心角的度数是.
(3)解:(人),
答:该校成绩达到优秀的学生约有600人.
7.(1)见解析
(2)
【分析】(1)尺规作边的垂直平分线,得出中点点,以点为圆心,为直径作圆,圆交边于点,连接,则.
(2)根据,得出,设,则,根据和勾股定理求出,得,过作,根据等面积法得出,勾股定理求出,即可得,根据圆周角定理得出,即可得,根据平行线分线段成比例得出.再根据勾股定理即可求解.
【详解】(1)解:如图,点即为所求;
理由,∵,为圆的直径,
∴点在圆上,
∵,
∴.
(2)解:∵,
∴,
设,则,
∵,
∴,解得:,
∴,
过作,
则,
∴,
∴,
∴,
∵为圆的直径,
∴,
∴,
∴.
∴.
【点睛】该题考查了勾股定理,圆周角定理,平行线分线段成比例,解直角三角形等知识点,解题的关键是正确作出图形.
8.(1)的半径为
(2)
【分析】本题考查了解直角三角形的应用,切线的性质,勾股定理,圆周角定理.
(1)连接交于点N,则,得,连接,设的半径为,则,根据勾股定理得,解方程即可解答;
(2)连接,则,过点作于点,由矩形的判定与性质得到,连接,则,再根据圆周角定理得到即可解答.
【详解】(1)解:如图1,连接交于点N,则,
,
,
连接,设的半径为,则,
由勾股定理,得,
,
解得,
故的半径为;
(2)解:如图2,连接,则,
过点作AI于点,
又,
四边形是矩形,
,
,
连接,则,
,
又,
,
.
9.(1)见解析
(2)见解析 见解析
【分析】本题考查了全等三角形的判定与性质,等边三角形的判定与性质,同弧或等弧所对的圆周角相等,熟练掌握以上知识点是解答本题的关键.
(1)利用“”证明即可;
(2)证明为等边三角形得,又,进而求得,延长至点,使得,连接,,则有,证明为等边三角形得,又,所以;
证明得,,由得,,所以,,,四点共圆,证明得,又,所以.
【详解】(1)证明:在中,,
.
在和中,,
;
(2)证明:由(1)可知,,
,
,
为等边三角形,
.
,
,
延长至点,使得,连接,,则有,
,
,
,
为等边三角形,
,
,
;
由得,,
,
,
在和中,,
,
,,
由得,,
,,,四点共圆,
,
在和中,,
,
,
,
.
10.(1)随机
(2)
【分析】本题主要考查了事件的分类,利用列表或画树状图求概率等知识点,解题的关键是熟练掌握事件的分类和求概率的方法.
(1)根据事件的分类进行判断即可;
(2)画树状图进行求概率即可.
【详解】(1)解:该事件属于随机事件,
故答案为:随机;
(2)解:画树状图如下:
由树状图可知共有16种等可能的结果,其中两次转出的字可以组成词语“中考”或“加油”的结果有4种,
∴P(小凡同学两次转出的字可以组成词语“中考”或“加油”.
11.(1)证明见解析
(2)
【分析】本题考查了相似三角形的性质与判定,垂径定理,圆周角定理,以及解直角三角形,熟练掌握以上知识是解题的关键;
(1)根据题意可得,根据垂径定理可得进而可得,则;
(2)连接,证明得出,进而得出,根据,即可求解.
【详解】(1)解:∵D是的中点,
∴,
∵且为的直径,
∴,
∴,
∴;
(2)解:连接,
∵,
∴,
∵为的直径,
∴,
∵,
∴,
∴,
∴,
设的半径为,则,
解得,
∴,
∴,
∴,
∵,
∴.
12.(1)
(2)
(3)当时,;当时,;当时,
【分析】(1)首先根据题意画图,勾股定理求出,证明出,得到,,然后利用,得到,然后代数求解即可;
(2)首先根据题意画图,得出,然后根据代数求出,进而求解即可;
(3)根据题意分3种情况讨论,然后解直角三角形求出相应线段的长,然后根据割补法求解即可.
【详解】(1)解:如图所示,
∵在矩形中,,.
∴,,
∵为中点,
∴,
∵,
∴,
∵,,
∴四边形是平行四边形,
∴,
∵,
∴,
∴
∴,即,
∴;
(2)解:如图所示,
∵,
∴
由(1)可得,,,
∴,即,
∴,
∴,
∴;
(3)解:当时,,如图①,
此时,
∵,
∴,
∴,
∴,.
.
.
当时,如图②,过作交于点,设交于N,
∴,
为中点,
,,
,
又∵,
∴四边形是平行四边形,
∴平行四边形是矩形.
在中,,.
.
同理可得,
∴,
;
③当时,如图③,设交于F、G,交于H,
∴;
∵,
∴,
在中,,
∴;
同理可得,
∴,
∵,
∴,
∴,
∴,
∴
.
综上所述,当时,;当时,;当时,.
【点睛】此题考查了矩形的性质,解直角三角形,勾股定理,平行四边形的性质与判定等知识,解题的关键是掌握以上知识点.
13.(1)见解析
(2)
【分析】(1)连接,,利用垂径定理,圆周角定理和切线的判定定理解答即可;
(2)利用直角三角形的边角关系定理和勾股定理求得,,利用相似三角形的判定与性质求得线段,利用勾股定理即可求得结论.
【详解】(1)证明:连接,,如图,
,,
,
,
.
,
.
,
,
是的半径,
是的切线;
(2)解:由(1)知:,
,
,
.
.
.
.
,,
,
.
.
.
【点睛】本题主要考查了圆的切线的判定,圆周角定理,直角三角形的性质,三角形的内角和定理,勾股定理,相似三角形的判定与性质,直角三角形的边角关系定理,连接经过切点的半径是解决此类问题常添加的辅助线.
14.(1)300,图见解析
(2)
(3)
【分析】本题考查了条形统计图与扇形统计图综合,列表法求概率,熟练掌握以上知识是解题的关键;
(1)根据选择“”的人数与占比求得接受调查的学生人数,进而求得选择“”的人数,即可补全统计图;
(2)根据的人数占比乘以,即可求解;
(3)根据列表法求概率,即可求解.
【详解】(1)解: 选择“”的人数有75人,在扇形统计图中的占比为
∴接受调查的学生共有(人).
选择“”的人数为(人).
补全条形统计图如图;
故答案为:.
(2)选择“”的人数为66人,
“”在扇形统计图中的占比为
扇形统计图中“”对应的扇形圆心角的度数为.
故答案为:.
(3)将该5名学生分别记作:男1、男2、女1、女2、女3,根据题意,列表如下:
第二次 第一次
男1 男2 女1 女2 女3
男1 (男2,男1) (女1,男1) (女2,男1) (女3,男1)
男2 (男1,男2) (女1,男2) (女2,男2) (女3,男2)
女1 (男1,女1) (男2,女1) (女2,女1) (女3,女1)
女2 (男1,女2) (男2,女2) (女1,女2) (女3,女2)
女3 (男1,女3) (男2,女3) (女1,女3) (女2,女3)
由列表可知,共有20种等可能的结果,其中恰好抽到一男一女的结果有12种,
∴P(恰好抽到一名男生和一名女生)
15.(1)26nmile
(2)40nmile
【分析】本题考查了解直角三角形的应用,正确理解题意、熟练掌握锐角三角函数的定义是解题的关键;
(1)延长交于点F,则,根据题意可得,设,利用直角三角形的边角关系结合锐角三角函数列方程求出x,然后再求出即可;
(2)利用(1)的结果计算即可.
【详解】(1)解:延长交于点F,则,
由题意可得:,
∴,
∴,
设,则,
在直角三角形中,,
∴,
∴,
在直角三角形中,∵,
∴,即,
解得:,
∴,
∴,
即此时轮船甲乙之间的距离约为;
(2)解:,
∴,
答:此时轮船乙到港口A的距离是.
16.(1),
(2)
(3)存在满足条件的点,其坐标为或
【分析】本题考查了反比例函数与一次函数综合,
(1)根据待定系数法求出一次函数和反比例函数的表达式,然后联立方程组求解即可得出点A的坐标;
(2)过点作轴,垂足为.根据已知可得,设,根据图形面积建立方程,求出点M的坐标,然后勾股定理,即可求解.
(3)根据角的2倍关系,考虑分类画出图形(点在直线下方,点在直线上方),由于是直线与轴相交得到的,利用平行线转换到以为顶点的等角,再结合等腰三角形的三线合一,求出直线的表达式,联立反比例函数的表达式求解.
【详解】(1)解: 在直线上,
,解得,
点的坐标为,直线的表达式为.
将点代入反比例函数中,得,
反比例函数的表达式为.
联立,
解得或,
点的坐标为;
(2)如解图①,过点作轴,垂足为.
在一次函数中,令,得,
.
轴,
.
点在反比例函数的图象上,轴,轴,
.
,
.
设,
则,
解得或,
经检验,或是所列方程的解,
点在点的右侧,
,
,
;
(3)如解图②,若点在直线AB下方,过点作轴于点,延长CE至点,使得.
,
.
由(1)(2)得,
,
,
联立,
解得或,
;
若点在直线上方,过点作交的延长线于点,延长至点,使得,连接并延长交反比例函数的图象于点,即为所求的点.
,
联立,
解得,
.
此时,
是GH的中点,
,
,
联立,
解得或,
.
综上所述,存在满足条件的点,其坐标为或.
17.(1)每台型号无人机单次最高载货量为,每台型号无人机单次最高载货量为;
(2)①或;②该公司应使用4台A型号无人机,5台B型号无人机.
【分析】本题考查了分式方程的应用,二元一次方程的应用.
(1)设每台A型号无人机的单次最高载货量为,则B型无人机的单次最高载货量为,根据“用相同数量的无人机一次性运送货物,A型无人机共载货,B型无人机共载货”列出分式方程求解即可;
(2)①根据题意得,,再根据m的取值范围求解即可;
②根据①的结论,分别求出两种方案的总费用进行比较即可.
【详解】(1)解:设每台A型号无人机的单次最高载货量为,则每台B型号无人机的单次最高载货量为,
根据题意得,
解得,
经检验,是所列方程的根,且符合题意,
∴,
答:每台A型号无人机单次最高载货量为,每台B型号无人机单次最高载货量为;
(2)解:①∵,
∴,
∵,m、n为整数,
∴或;
②设B型无人机单次运费为元,则A型无人机单次运费为元,
当,时,(元),
当,时,(元),
∵,
∴该公司应使用4台A型号无人机,5台B型号无人机.
18.(1)①,;②260
(2)或
【分析】题目主要考查一次函数的实际应用,不等式的应用,理解题意是解题关键.
(1)①根据题意,直接列出函数关系式即可;②分两种情况分析令,令,分别求解即可;
(2)分四种情况分别分析两种方案的优惠价格,即可得出结果.
【详解】(1)解:(1)①根据题意得:,即.
.
②令,
解得(不符合题意,舍去).
令,
解得(符合题意).
故的值为260.
(2)根据题意得:当时,
方案一购买需n元,方案二购买需0.8n元,,不符合题意.
当时,令,
得,
.
当时,方案一购买优惠的价格为元,
方案二购买优惠的价格小于元,符合题意.
当时,方案一购买优惠的价格为元,
方案二购买优惠的价格不超过元,符合题意.
综上,n的取值范围为或.
19.(1)
(2)
(3)①;②相似,理由见解析
【分析】()先求出,进而求出,再推出,利用相似三角形的性质解答即可求解;
()先证明,进而求出,再证明,进而求出,最后用勾股定理解答即可求解;
()①先求出,再求出,根据勾股定理求出,,再证明,得出,得出,即可得,即得到,即可求解;②先推出,进而得出,再推导出,即可求证.
【详解】(1)解:如图,连接,
∵矩形,
∴,,,
∴,
∵是中点,
∴,
∴,
∵,
∴,
∴,
∴,
∴,
设,则,
∴,
解得,
∴;
(2)解:如图,
∵矩形,平分,
∴,,
∴,
∴,
∴,
∴,
∵,
∴,
∴,
∵,
∴,
∴,
∵,
∴,
∴,
∴,
过点作于,
∴,
∴,,
∵,
∴,
∴,
设,则,
∴,
解得,
∴,
∴;
(3)解:①∵矩形,
∴,
∵,,
∴,
∵,
∴,
由折叠知,,,,
∴,
设,则,
∵,
∴,
解得,
∴,,
∵,
∴,
∴,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
∴,
∴;
②相似,理由如下:
由折叠知,,,
∴,
∵,
∴,
∴,
∵,
∴,
∴,
∴,
∵,
∴,
∴,
∴,
∴,
∵,
∴,
∴.
【点睛】此题考查了矩形的性质,折叠的性质,直角三角形的性质,相似三角形的判定和性质,全等三角形的判定和性质,勾股定理,等腰三角形的判定和性质等,正确作出辅助线是解题的关键.
20.(1)3
(2),理由见解析
(3)
【分析】(1)利用同角的余角相等得到,利用角平分线的定义和三角形的外角的性质得到,从而得到,从而得解;
(2)根据题意可知是等腰三角形,,,再利用三角形的外角的性质证明,过点E作交的延长线于点H,从而证明,,得到,继而得到;
(3)由,设,则,,取的中点O,连接,,利用直角三角形斜边上的中线等于斜边的一半可得,根据是的中位线,得到,,故当点O、C、P三点共线且点P在O、C之间时,取最小值,此时,画出图形,延长和交于点D,由证明,得到,从而得到,,,设,则,由折叠得到,运用勾股定理得到,从而列出方程,解出x,即,从而求出,从而得解.
【详解】(1)解:∵,,
∴,
又∵平分,
∴,
∴,
∴,
又∵,
∴;
(2),理由如下:
由(1)得:,
∵,,
∴,,
又∵,即,
∴,
过点E作交的延长线于点H,
则,,
在与中,
,
∴,
∴,
在与中,
,
∴,
∴,
∴,
∴,
即;
(3)∵在中,,
∴,
设,则,,
取的中点O,连接,,则,
由折叠可知:,,
∵点P为的中点,点O是的中点,
∴是的中位线,
∴,,
∴当点O、C、P三点共线且点P在O、C之间时,取最小值,
此时,
此时,如下图所示,延长和交于点D,
∵,
∴,
∴,
∴,,
∴,
设,则,
由折叠可知:,
∴,
∴,即,
解得:,
∴,
∴,
∴.
即当取最小值时,的值为.
【点睛】本题考查三角形的外角的性质,三角形的中位线,勾股定理,相似三角形的判定与性质,全等三角形的性质,折叠的性质,综合性非常大,正确作出辅助线把握图形的变化规律是解题的关键.
21.(1)
(2)
(3)
【分析】()把二次函数解析式转化为顶点式,进而根据顶点的纵坐标列出方程解答即可;
()过点作直线轴,交轴于点,交于点,设对称轴交轴于点,可证,得到,再求出点,得到,进而由四边形为矩形得,即得,得到点的横坐标为,最后代入二次函数解析式求出点的纵坐标即可求解;
()过点作,过点作,可得,,进而得到,,即得,设,可得,过点作交的延长线于点,由得,设,则,又由得,即得,利用可得,即到,即得到,求出即可求解;
本题考查了待定系数法求二次函数解析式,二次函数的几何应用,锐角三角函数,正确作出辅助线是解题的关键.
【详解】(1)解:∵ ,
∴顶点的坐标为,
∵顶点的纵坐标为,
∴,
∴,
∴抛物线的解析式为.
(2)解:过点作直线轴,交轴于点,交于点,设对称轴交轴于点,
∴,,
∵轴,
∴,
∴,
∵,,
∴,
由旋转得,,
∴,
∴,
当时,代入,得,
∴,
∴,
∵,
∴四边形为矩形,
∴,
∴,
∴点的横坐标为,
∵点在抛物线上,
∴点的纵坐标为,
即;
(3)解:过点作,过点作,
∵顶点,,
∴,
,
在中和中,
,,
∴,
∴,
设,
∵,,
∴,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
∴,
过点作交的延长线于点,
∵,,,
∴,
∴,
设,则,
∵,,
∴,
∵,
∴,
∴,
∴,
∴,
∵,
∴,
∴,
∴,
∴,
∴,
解得,
∴,,
∴点的坐标为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
【专项押题预测】临考查漏补缺:解答题(一)-2025年各地区中考数学模拟题汇编
1.(2025·广东·二模)为出行方便,越来越多的市民使用起了共享单车,图1为单车实物图,图2为单车示意图,与地面平行,坐垫可沿射线方向调节.已知,车轮半径为,当时,小明体验后觉得骑着比较舒适,此时坐垫离地面高度约为?(结果精确到,参考数据:,,)
2.(24-25九年级下·安徽六安·阶段练习)在2025年春节联欢晚会上,新年吉祥物“巳升升”特别惹人注目,其设计灵感源于中华传统文化,整体造型参考甲骨文中的“巳”字,采用青绿色为主色调,外形愁态可掬,寓意“福从头起,尾随如意”,我们在电商平台和实体店了解其销售情况.
(1)统计某电商平台,2024年12月份吉祥物一月的销售量是5万件,2025年2月份吉祥物一月的销售量是7.2万件,若近三个月月平均增长率相同,求月平均增长率;
(2)对某实体店的销售情况进行了解,该店吉祥物的进价为每件60元,若售价定为每件100元,则每天能销售量20件.通过市场调查发现,售价每降价1元,每天可多售出2件,为了进一步推广宣传,商家决定降价促销,要求尽量减少库存,且使每天销售获利1200元,请你分析售价应降低多少元?
3.(2025·安徽合肥·三模)如图,已知内接于,为直径,过点作的切线交延长线于,为上的一点,连接,交于,且.
(1)求证:;
(2)若的半径为,求的长.
4.(2025·安徽合肥·三模)观察下列等式:
①
②
③
④
(1)请按以上规律写出第⑥个等式:___________;
(2)猜想并写出符合上述规律的第个等式:___________;并证明猜想的正确性.
5.(2025·安徽合肥·三模)在如图所示的平面直角坐标系中,已知.
(1)将绕点逆时针旋转得到,请画出;
(2)以坐标原点为位似中心,在轴下方,画出的位似图形,使它与的位似比为.
(3)在轴上找一点,使得,并直接写出点的坐标.
6.(2025·陕西榆林·三模)2025年3月9日,国家卫生健康委员会相关负责人宣布,将正式实施为期三年的“体重管理年”行动,普及健康生活方式,帮助居民科学管理体重.为推进“体重管理年”,某中学举行了“健康体重,一起行动”科普教育,并组织1500名学生参加了知识答卷,为了解科普效果,从中随机抽取了部分学生的成绩进行统计,并对收集到的数据进行了整理、描述和分析.信息如下:
成绩频数分布表:
组别 C
成绩(分)
频数 4 12 10 6
成绩在组()的数据(单位:分):
(1)请补全频数分布直方图;
(2)这次测试成绩的中位数是___________,扇形的圆心角的度数是___________;
(3)若成绩在80分以上(不含80分)为科普教育知识成绩优秀,估计该校成绩达到优秀的学生有多少人?
7.(2025·福建福州·三模)如图,在Rt中,为中点.
(1)请在图1中用无刻度的直尺和圆规作图:
在边上找一点,使得;(不写作法,保留作图痕迹)
(2)在(1)的条件下,若,求线段的长.(如需画草图,请使用备用图)
8.(2025·河南信阳·三模)图1是工业上用的一款切割金属材料的铡刀,图2是其侧面示意图,其中矩形是切割槽,刀刃与手柄下边缘在同一条弧上,经测量可知,.将手柄向下压,直至与BC相切于点M,如图3所示,此时恰好经过点D.
(1)求的半径;
(2)将手柄往上抬,使点E恰好落在的延长线上,与交于点F,经研究发现,此时与相切于点E,连接,,求的值.
9.(2025·福建泉州·模拟预测)如图1,在中,,,垂足为,点,分别在边,上,,,与相交于点.
(1)求证:;
(2)如图2,点在的延长线上,且,交的延长线于点,求证:
;
.
10.(2025·甘肃平凉·二模)随着中考的临近,为了给即将参加中考的学生加油鼓励,九年级(1)班的班长制作了一个如图所示质地均匀的转盘(转盘被平均分成四等份),再将“中考加油”四个字分别写在每个扇形上,让班上的每个同学自由转动两次转盘,转盘停止后,指针所指扇形区域内的字即为转出的字(若指针指向分割线,则不计次数,重新转动,直至指针指向某一扇形区域为止).
(1)该班的小敏同学转动一次转盘,转出的字为“考”属于______事件;(选填“必然”“随机”或“不可能”)
(2)该班的小凡同学转动转盘两次,利用列表或画树状图的方法求小凡同学两次转出的字可以组成词语“中考”或“加油”的概率.
11.(2025·北京房山·二模)如图,已知为的外接圆,为的直径,是的中点,弦于点,是上一点,连接.
(1)求证:;
(2)若,求.
12.(2025·吉林白城·模拟预测)如图,在矩形中,,.为中点,连接.动点从点出发,沿射线以的速度运动.过作,过作于点,当经过点时,点停止运动.设点的运动时间为.与四边形重叠部分图形的面积为.
(1)当点落在边上时,的值为________;
(2)当经过点时,的值为________;
(3)求关于的函数解析式,并直接写出自变量的取值范围.
13.(2025·四川成都·模拟预测)如图,是的外接圆,点在的延长线上,连接,作于点,交于点,且,连接.
(1)求证:是的切线;
(2),,求线段的长.
14.(2025·四川成都·模拟预测)成都某中学准备每年组织开展“风筝节”“我运动,我快乐”“跳蚤书市”“校园十佳歌手大赛”“元旦文艺晚会”等课余活动,让学生劳逸结合.该校采用随机抽样调查的方式对部分学生个人最喜爱的一项课余活动进行了调查,并根据收集到的信息分为:风筝节;:我运动,我快乐;:跳蚤书市;:校园十佳歌手大赛;:元旦文艺晚会共五组进行统计,并根据调查结果绘制成如下两幅不完整的统计图.
(1)本次调查的学生共有________人,并补全条形统计图;
(2)扇形统计图中“”对应的扇形圆心角的度数为________;
(3)本次调查中,最喜爱“我运动,我快乐”中有品学兼优的两男和三女共5名学生,若从中随机抽取两名学生作为该活动的主持人,请利用画树状图或列表的方法,求恰好抽到一名男生和一名女生的概率.
15.(2025·江苏盐城·二模)如图,已知轮船甲位于港口A西南方向的点B处,轮船乙位于港口A正南方向的点C处,点C位于点B南偏东方向.轮船甲向正东航行10 nmile到点D,轮船乙向正北航20 nmile到点E,测得点D位于点E北偏西方向.
(1)求此时轮船甲乙之间的距离.
(2)求此时轮船乙到港口A的距离.(结果精确到1 nmile,参考数据:,,,,,)
16.(2025·四川成都·模拟预测)如图,在平面直角坐标系中,直线与反比例函数的图象交于两点,与轴和轴分别交于点和点,其中点坐标为,点在反比例函数图象上.
(1)求点的坐标及反比例函数的表达式;
(2)若点在点的右侧,过点作轴,垂足为,若,求的长;
(3)是否存在一点,使得,若存在,求出点的坐标;若不存在,请说明理由.
17.(2025·江苏盐城·二模)某公司需向甲地紧急运送的货物,决定使用、两种型号的无人机运送.已知每台型无人机的单次最高载货量比每台型无人机的单次最高载货量多;在满载情况下,某次用相同数量的无人机一次性运送货物,型无人机共载货,型无人机共载货.
(1)每台型无人机和型无人机的单次最高载货量分别是多少?
(2)该公司决定使用台型无人机()和台型无人机载货,在每台无人机都满载的情况下,刚好一次性完成的货物运送:
①求满足条件的、值;
②若型无人机单次运费为型无人机单次运费的倍.为了节省成本,该公司应使用两种型号的无人机各多少台?
18.(2025·河南信阳·三模)2025年3月23日,歼-10首飞成功27年,近年来,歼-10家族不断突破、不断壮大.小明和小亮到一家科技体验馆购买航模,已知该体验馆有两种优惠方案可以选择,且两种方案只能参加其中一种.
方案一:科技体验馆推出70元抵100元的代金券,付费时可以抵扣100元.
方案二:购买航模的费用一律打八折.
(1)若小明选中的航模的价格为元,方案一需付费元,方案二需付费元.
①请写出,关于x的函数表达式;
②通过计算,小明发现参加两种方案所需费用相差8元,求m的值.
(2)小亮也选中了一个航模,价格为元,发现参加方案一更划算,求n的取值范围.
19.(2025·四川资阳·二模)如图,在矩形中,,,是上的一个动点.
(1)如图,连接,是对角线的中点,连结.当时,求的长.
(2)如图,连接、,过点作交于点,连结,与交于点.当平分时,求的长.
(3)如图,连接,点在上,将矩形沿直线折叠,折叠后点落在上的点处,过点作于点,与交于点,且.
①求的值;
②连接,与是否相似?请说明理由.
20.(2025·重庆·模拟预测)如图,已知在中,,点E在直线上,连接.过点C作于点D,交于点E
(1)如图1,若点E在线段上,平分,,,求的长度;
(2)如图2,若点E在线段上,,延长至点G,连接,满足,请用等式表示线段、之间的数量关系,并证明;
(3)如图3,若,将沿翻折至所在平面得,连接,点P为的中点,连接,在E点运动过程中,当取最小值时,直接写出此时的值.
21.(2025·黑龙江哈尔滨·三模)已知抛物线交轴于点、,交轴于点,顶点的纵坐标为.
(1)如图,求抛物线的解析式;
(2)如图,点为第一象限的抛物线对称轴上一点,连接,将绕点逆时针旋转后得到线段(点在第一象限内),过点作直线轴,交轴于点,交抛物线于点,设点的纵坐标为,线段的长为,求与的函数关系式,并写出自变量的取值范围;
(3)如图,在()的条件下,连接,过点作,射线交过点且与垂直的直线于点,过点作于点,点为上一点,过点作,交于点,交于点,连接,若,,求点的坐标.
《【专项押题预测】临考查漏补缺:解答题(一)-2025年各地区中考数学模拟题汇编》参考答案
1.
【分析】本题考查了解直角三角形的应用,作出适当的辅助线,构造出直角三角形是解题的关键;作于H,作地面于P,利用三角函数求出即可.
【详解】解:如图,作于H,作地面于P,
由题知,,
∴,
∴坐垫C离地面高度约为.
2.(1)月平均增长率为
(2)售价应降低20元
【分析】本题考查了一元二次方程实际应用问题,根据题意找到相等关系是解题的关键.
(1)设月平均增长率为,根据题意列出方程即可;
(2)设售价应降低元,则可卖出件,利用每件获利乘以销售数量等于每天销售获利,列方程即可解答.
【详解】(1)解:设月平均增长率为,
由题意得,,
解得:(不合题意,舍去),
答:月平均增长率为;
(2)解:设售价应降低元,
由题意得,,
整理得:,
解得:,
尽量减少库存,
,
答:售价应降低20元.
3.(1)见解析
(2).
【分析】(1)根据圆周角定理和切线的性质得到,利用等角的余角相等求得,即可证明;
(2)作于点,利用角平分线的性质求得,证明,求得,设,在中,由勾股定理列式计算即可求解.
【详解】(1)证明:∵为的直径,为的切线,
∴,
∴,
∵,
∴,
∵,,
∴,
∴;
(2)解:作于点,
∵为的直径,的半径为5,
∴,,
∵,
∴,
由(1)得,
∴,
∵,
∴,
∴,
设,
∴,,
在中,由勾股定理得,即,
解得,
∴.
【点睛】本题考查切线的性质,圆周角定理,勾股定理,角平分线的性质,全等三角形的判定和性质.正确引出辅助线解决问题是解题的关键.
4.(1);
(2),证明见解析.
【分析】本题主要考查根据规律运算、完全平方公式应用、整式的混合运算法则等知识点,根据题干得到式子之间存在的规律是解题的关键.
(1)根据题干规律直接写出答案即可;
(2)找出分子两个数之间关系直接写出答案,利用完全平方公式以及整式的相关运算法则即可证明.
【详解】(1)解:由题意可得,第⑥个等式为:.
故答案为:.
(2)解:第个:,证明如下:
∵左边,右边,
∴左边右边,
∴.
5.(1)见解析
(2)见解析
(3)
【分析】本题主要考查了位似变换、旋转变换、等腰三角形的性质等知识点,掌握位似变换和旋转变换的定义是解题的关键.
(1)先利用旋转的性质确定的对应点的位置,然后再顺次连接即可;
(2)先利用旋转的性质确定的对应点的位置,然后再顺次连接即可;
(3)先根据等腰三角形的性质求得点M的位置,然后再写出坐标即可.
【详解】(1)解:如图:即为所求.
(2)解:如图:即为所求.
(3)解:如图:轴上的点,使得,此时M的坐标为.
6.(1)图见解析
(2);
(3)该校成绩达到优秀的学生约有600人
【分析】本题考查读频数分布直方图,频数(率分布表和扇形统计图的能力和利用统计图获取信息的能力.
(1)根据频数分布直方图可得到的值,然后补全频数分布直方图;
(2)将样本中成绩从低到高排列,排在中间的两个数是76,77,可得中位数,用乘以组的百分比即可得到扇形的圆心角的度数;
(3)用学生总人数乘以成绩在80分以上(不含80分)的百分比,计算即可得解.
【详解】(1)解: 被抽取的学生人数为,
,
补全频数分布直方图,如图所示.
;
(2)解:将样本中成绩从低到高排列,排在中间的两个数是76,77,故中位数是,
扇形的圆心角的度数是.
∴估计这次测试成绩的中位数是,扇形的圆心角的度数是.
(3)解:(人),
答:该校成绩达到优秀的学生约有600人.
7.(1)见解析
(2)
【分析】(1)尺规作边的垂直平分线,得出中点点,以点为圆心,为直径作圆,圆交边于点,连接,则.
(2)根据,得出,设,则,根据和勾股定理求出,得,过作,根据等面积法得出,勾股定理求出,即可得,根据圆周角定理得出,即可得,根据平行线分线段成比例得出.再根据勾股定理即可求解.
【详解】(1)解:如图,点即为所求;
理由,∵,为圆的直径,
∴点在圆上,
∵,
∴.
(2)解:∵,
∴,
设,则,
∵,
∴,解得:,
∴,
过作,
则,
∴,
∴,
∴,
∵为圆的直径,
∴,
∴,
∴.
∴.
【点睛】该题考查了勾股定理,圆周角定理,平行线分线段成比例,解直角三角形等知识点,解题的关键是正确作出图形.
8.(1)的半径为
(2)
【分析】本题考查了解直角三角形的应用,切线的性质,勾股定理,圆周角定理.
(1)连接交于点N,则,得,连接,设的半径为,则,根据勾股定理得,解方程即可解答;
(2)连接,则,过点作于点,由矩形的判定与性质得到,连接,则,再根据圆周角定理得到即可解答.
【详解】(1)解:如图1,连接交于点N,则,
,
,
连接,设的半径为,则,
由勾股定理,得,
,
解得,
故的半径为;
(2)解:如图2,连接,则,
过点作AI于点,
又,
四边形是矩形,
,
,
连接,则,
,
又,
,
.
9.(1)见解析
(2)见解析 见解析
【分析】本题考查了全等三角形的判定与性质,等边三角形的判定与性质,同弧或等弧所对的圆周角相等,熟练掌握以上知识点是解答本题的关键.
(1)利用“”证明即可;
(2)证明为等边三角形得,又,进而求得,延长至点,使得,连接,,则有,证明为等边三角形得,又,所以;
证明得,,由得,,所以,,,四点共圆,证明得,又,所以.
【详解】(1)证明:在中,,
.
在和中,,
;
(2)证明:由(1)可知,,
,
,
为等边三角形,
.
,
,
延长至点,使得,连接,,则有,
,
,
,
为等边三角形,
,
,
;
由得,,
,
,
在和中,,
,
,,
由得,,
,,,四点共圆,
,
在和中,,
,
,
,
.
10.(1)随机
(2)
【分析】本题主要考查了事件的分类,利用列表或画树状图求概率等知识点,解题的关键是熟练掌握事件的分类和求概率的方法.
(1)根据事件的分类进行判断即可;
(2)画树状图进行求概率即可.
【详解】(1)解:该事件属于随机事件,
故答案为:随机;
(2)解:画树状图如下:
由树状图可知共有16种等可能的结果,其中两次转出的字可以组成词语“中考”或“加油”的结果有4种,
∴P(小凡同学两次转出的字可以组成词语“中考”或“加油”.
11.(1)证明见解析
(2)
【分析】本题考查了相似三角形的性质与判定,垂径定理,圆周角定理,以及解直角三角形,熟练掌握以上知识是解题的关键;
(1)根据题意可得,根据垂径定理可得进而可得,则;
(2)连接,证明得出,进而得出,根据,即可求解.
【详解】(1)解:∵D是的中点,
∴,
∵且为的直径,
∴,
∴,
∴;
(2)解:连接,
∵,
∴,
∵为的直径,
∴,
∵,
∴,
∴,
∴,
设的半径为,则,
解得,
∴,
∴,
∴,
∵,
∴.
12.(1)
(2)
(3)当时,;当时,;当时,
【分析】(1)首先根据题意画图,勾股定理求出,证明出,得到,,然后利用,得到,然后代数求解即可;
(2)首先根据题意画图,得出,然后根据代数求出,进而求解即可;
(3)根据题意分3种情况讨论,然后解直角三角形求出相应线段的长,然后根据割补法求解即可.
【详解】(1)解:如图所示,
∵在矩形中,,.
∴,,
∵为中点,
∴,
∵,
∴,
∵,,
∴四边形是平行四边形,
∴,
∵,
∴,
∴
∴,即,
∴;
(2)解:如图所示,
∵,
∴
由(1)可得,,,
∴,即,
∴,
∴,
∴;
(3)解:当时,,如图①,
此时,
∵,
∴,
∴,
∴,.
.
.
当时,如图②,过作交于点,设交于N,
∴,
为中点,
,,
,
又∵,
∴四边形是平行四边形,
∴平行四边形是矩形.
在中,,.
.
同理可得,
∴,
;
③当时,如图③,设交于F、G,交于H,
∴;
∵,
∴,
在中,,
∴;
同理可得,
∴,
∵,
∴,
∴,
∴,
∴
.
综上所述,当时,;当时,;当时,.
【点睛】此题考查了矩形的性质,解直角三角形,勾股定理,平行四边形的性质与判定等知识,解题的关键是掌握以上知识点.
13.(1)见解析
(2)
【分析】(1)连接,,利用垂径定理,圆周角定理和切线的判定定理解答即可;
(2)利用直角三角形的边角关系定理和勾股定理求得,,利用相似三角形的判定与性质求得线段,利用勾股定理即可求得结论.
【详解】(1)证明:连接,,如图,
,,
,
,
.
,
.
,
,
是的半径,
是的切线;
(2)解:由(1)知:,
,
,
.
.
.
.
,,
,
.
.
.
【点睛】本题主要考查了圆的切线的判定,圆周角定理,直角三角形的性质,三角形的内角和定理,勾股定理,相似三角形的判定与性质,直角三角形的边角关系定理,连接经过切点的半径是解决此类问题常添加的辅助线.
14.(1)300,图见解析
(2)
(3)
【分析】本题考查了条形统计图与扇形统计图综合,列表法求概率,熟练掌握以上知识是解题的关键;
(1)根据选择“”的人数与占比求得接受调查的学生人数,进而求得选择“”的人数,即可补全统计图;
(2)根据的人数占比乘以,即可求解;
(3)根据列表法求概率,即可求解.
【详解】(1)解: 选择“”的人数有75人,在扇形统计图中的占比为
∴接受调查的学生共有(人).
选择“”的人数为(人).
补全条形统计图如图;
故答案为:.
(2)选择“”的人数为66人,
“”在扇形统计图中的占比为
扇形统计图中“”对应的扇形圆心角的度数为.
故答案为:.
(3)将该5名学生分别记作:男1、男2、女1、女2、女3,根据题意,列表如下:
第二次 第一次
男1 男2 女1 女2 女3
男1 (男2,男1) (女1,男1) (女2,男1) (女3,男1)
男2 (男1,男2) (女1,男2) (女2,男2) (女3,男2)
女1 (男1,女1) (男2,女1) (女2,女1) (女3,女1)
女2 (男1,女2) (男2,女2) (女1,女2) (女3,女2)
女3 (男1,女3) (男2,女3) (女1,女3) (女2,女3)
由列表可知,共有20种等可能的结果,其中恰好抽到一男一女的结果有12种,
∴P(恰好抽到一名男生和一名女生)
15.(1)26nmile
(2)40nmile
【分析】本题考查了解直角三角形的应用,正确理解题意、熟练掌握锐角三角函数的定义是解题的关键;
(1)延长交于点F,则,根据题意可得,设,利用直角三角形的边角关系结合锐角三角函数列方程求出x,然后再求出即可;
(2)利用(1)的结果计算即可.
【详解】(1)解:延长交于点F,则,
由题意可得:,
∴,
∴,
设,则,
在直角三角形中,,
∴,
∴,
在直角三角形中,∵,
∴,即,
解得:,
∴,
∴,
即此时轮船甲乙之间的距离约为;
(2)解:,
∴,
答:此时轮船乙到港口A的距离是.
16.(1),
(2)
(3)存在满足条件的点,其坐标为或
【分析】本题考查了反比例函数与一次函数综合,
(1)根据待定系数法求出一次函数和反比例函数的表达式,然后联立方程组求解即可得出点A的坐标;
(2)过点作轴,垂足为.根据已知可得,设,根据图形面积建立方程,求出点M的坐标,然后勾股定理,即可求解.
(3)根据角的2倍关系,考虑分类画出图形(点在直线下方,点在直线上方),由于是直线与轴相交得到的,利用平行线转换到以为顶点的等角,再结合等腰三角形的三线合一,求出直线的表达式,联立反比例函数的表达式求解.
【详解】(1)解: 在直线上,
,解得,
点的坐标为,直线的表达式为.
将点代入反比例函数中,得,
反比例函数的表达式为.
联立,
解得或,
点的坐标为;
(2)如解图①,过点作轴,垂足为.
在一次函数中,令,得,
.
轴,
.
点在反比例函数的图象上,轴,轴,
.
,
.
设,
则,
解得或,
经检验,或是所列方程的解,
点在点的右侧,
,
,
;
(3)如解图②,若点在直线AB下方,过点作轴于点,延长CE至点,使得.
,
.
由(1)(2)得,
,
,
联立,
解得或,
;
若点在直线上方,过点作交的延长线于点,延长至点,使得,连接并延长交反比例函数的图象于点,即为所求的点.
,
联立,
解得,
.
此时,
是GH的中点,
,
,
联立,
解得或,
.
综上所述,存在满足条件的点,其坐标为或.
17.(1)每台型号无人机单次最高载货量为,每台型号无人机单次最高载货量为;
(2)①或;②该公司应使用4台A型号无人机,5台B型号无人机.
【分析】本题考查了分式方程的应用,二元一次方程的应用.
(1)设每台A型号无人机的单次最高载货量为,则B型无人机的单次最高载货量为,根据“用相同数量的无人机一次性运送货物,A型无人机共载货,B型无人机共载货”列出分式方程求解即可;
(2)①根据题意得,,再根据m的取值范围求解即可;
②根据①的结论,分别求出两种方案的总费用进行比较即可.
【详解】(1)解:设每台A型号无人机的单次最高载货量为,则每台B型号无人机的单次最高载货量为,
根据题意得,
解得,
经检验,是所列方程的根,且符合题意,
∴,
答:每台A型号无人机单次最高载货量为,每台B型号无人机单次最高载货量为;
(2)解:①∵,
∴,
∵,m、n为整数,
∴或;
②设B型无人机单次运费为元,则A型无人机单次运费为元,
当,时,(元),
当,时,(元),
∵,
∴该公司应使用4台A型号无人机,5台B型号无人机.
18.(1)①,;②260
(2)或
【分析】题目主要考查一次函数的实际应用,不等式的应用,理解题意是解题关键.
(1)①根据题意,直接列出函数关系式即可;②分两种情况分析令,令,分别求解即可;
(2)分四种情况分别分析两种方案的优惠价格,即可得出结果.
【详解】(1)解:(1)①根据题意得:,即.
.
②令,
解得(不符合题意,舍去).
令,
解得(符合题意).
故的值为260.
(2)根据题意得:当时,
方案一购买需n元,方案二购买需0.8n元,,不符合题意.
当时,令,
得,
.
当时,方案一购买优惠的价格为元,
方案二购买优惠的价格小于元,符合题意.
当时,方案一购买优惠的价格为元,
方案二购买优惠的价格不超过元,符合题意.
综上,n的取值范围为或.
19.(1)
(2)
(3)①;②相似,理由见解析
【分析】()先求出,进而求出,再推出,利用相似三角形的性质解答即可求解;
()先证明,进而求出,再证明,进而求出,最后用勾股定理解答即可求解;
()①先求出,再求出,根据勾股定理求出,,再证明,得出,得出,即可得,即得到,即可求解;②先推出,进而得出,再推导出,即可求证.
【详解】(1)解:如图,连接,
∵矩形,
∴,,,
∴,
∵是中点,
∴,
∴,
∵,
∴,
∴,
∴,
∴,
设,则,
∴,
解得,
∴;
(2)解:如图,
∵矩形,平分,
∴,,
∴,
∴,
∴,
∴,
∵,
∴,
∴,
∵,
∴,
∴,
∵,
∴,
∴,
∴,
过点作于,
∴,
∴,,
∵,
∴,
∴,
设,则,
∴,
解得,
∴,
∴;
(3)解:①∵矩形,
∴,
∵,,
∴,
∵,
∴,
由折叠知,,,,
∴,
设,则,
∵,
∴,
解得,
∴,,
∵,
∴,
∴,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
∴,
∴;
②相似,理由如下:
由折叠知,,,
∴,
∵,
∴,
∴,
∵,
∴,
∴,
∴,
∵,
∴,
∴,
∴,
∴,
∵,
∴,
∴.
【点睛】此题考查了矩形的性质,折叠的性质,直角三角形的性质,相似三角形的判定和性质,全等三角形的判定和性质,勾股定理,等腰三角形的判定和性质等,正确作出辅助线是解题的关键.
20.(1)3
(2),理由见解析
(3)
【分析】(1)利用同角的余角相等得到,利用角平分线的定义和三角形的外角的性质得到,从而得到,从而得解;
(2)根据题意可知是等腰三角形,,,再利用三角形的外角的性质证明,过点E作交的延长线于点H,从而证明,,得到,继而得到;
(3)由,设,则,,取的中点O,连接,,利用直角三角形斜边上的中线等于斜边的一半可得,根据是的中位线,得到,,故当点O、C、P三点共线且点P在O、C之间时,取最小值,此时,画出图形,延长和交于点D,由证明,得到,从而得到,,,设,则,由折叠得到,运用勾股定理得到,从而列出方程,解出x,即,从而求出,从而得解.
【详解】(1)解:∵,,
∴,
又∵平分,
∴,
∴,
∴,
又∵,
∴;
(2),理由如下:
由(1)得:,
∵,,
∴,,
又∵,即,
∴,
过点E作交的延长线于点H,
则,,
在与中,
,
∴,
∴,
在与中,
,
∴,
∴,
∴,
∴,
即;
(3)∵在中,,
∴,
设,则,,
取的中点O,连接,,则,
由折叠可知:,,
∵点P为的中点,点O是的中点,
∴是的中位线,
∴,,
∴当点O、C、P三点共线且点P在O、C之间时,取最小值,
此时,
此时,如下图所示,延长和交于点D,
∵,
∴,
∴,
∴,,
∴,
设,则,
由折叠可知:,
∴,
∴,即,
解得:,
∴,
∴,
∴.
即当取最小值时,的值为.
【点睛】本题考查三角形的外角的性质,三角形的中位线,勾股定理,相似三角形的判定与性质,全等三角形的性质,折叠的性质,综合性非常大,正确作出辅助线把握图形的变化规律是解题的关键.
21.(1)
(2)
(3)
【分析】()把二次函数解析式转化为顶点式,进而根据顶点的纵坐标列出方程解答即可;
()过点作直线轴,交轴于点,交于点,设对称轴交轴于点,可证,得到,再求出点,得到,进而由四边形为矩形得,即得,得到点的横坐标为,最后代入二次函数解析式求出点的纵坐标即可求解;
()过点作,过点作,可得,,进而得到,,即得,设,可得,过点作交的延长线于点,由得,设,则,又由得,即得,利用可得,即到,即得到,求出即可求解;
本题考查了待定系数法求二次函数解析式,二次函数的几何应用,锐角三角函数,正确作出辅助线是解题的关键.
【详解】(1)解:∵ ,
∴顶点的坐标为,
∵顶点的纵坐标为,
∴,
∴,
∴抛物线的解析式为.
(2)解:过点作直线轴,交轴于点,交于点,设对称轴交轴于点,
∴,,
∵轴,
∴,
∴,
∵,,
∴,
由旋转得,,
∴,
∴,
当时,代入,得,
∴,
∴,
∵,
∴四边形为矩形,
∴,
∴,
∴点的横坐标为,
∵点在抛物线上,
∴点的纵坐标为,
即;
(3)解:过点作,过点作,
∵顶点,,
∴,
,
在中和中,
,,
∴,
∴,
设,
∵,,
∴,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
∴,
过点作交的延长线于点,
∵,,,
∴,
∴,
设,则,
∵,,
∴,
∵,
∴,
∴,
∴,
∴,
∵,
∴,
∴,
∴,
∴,
∴,
解得,
∴,,
∴点的坐标为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
