2025鲁教版八年级数学下册期末综合素质评价试卷(含答案)
文档属性
| 名称 | 2025鲁教版八年级数学下册期末综合素质评价试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 276.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-09 07:36:38 | ||
图片预览




文档简介
2025鲁教版八年级数学下册期末综合素质评价试卷
限时:120分钟 满分:120分
一、选择题(每题3分,共36分)
1.下列计算正确的是( )
A. B.
C. D.
2.函数的自变量的取值范围是( )
A. B. C. D.
3.若,,则的值为( )
A.8 B. C. D.4
4.若关于的一元二次方程有一个根为,则另一个根为( )
A. B. C. D.
5.如图,在菱形中,对角线,相交于点,若,,则的长是( )
(第5题)
A.8 B.7 C.4 D.3
6.如果一个三角形的三边长分别为1,,4.则化简的结果是( )
A. B. C.1 D.
7.若,则的值是( )
A.3 B. C. D.
8.如图,在矩形中,,,将长等于宽2倍的可变矩形如图放置,使,,三点在同一直线上,则阴影部分的面积为( )
(第8题)
A.8 B.9 C. D.
9.如图①是装了液体的高脚杯示意图(数据如图),用去一部分液体后如图②所示,此时液面直径( )
(第9题)
A. B. C. D.
10.如图,在边长为2的菱形中, ,是边的中点,是边上一动点,将沿所在的直线翻折得到 ,连接 ,则长度的最小值是( )
(第10题)
A.7 B. C. D.
11.如图,学校为举办文艺汇演搭建了舞台及登台的台阶,台阶总高度,台阶部分铺红地毯,地毯长度为,支撑钢梁,且为的中点,则钢梁的长为( )
(第11题)
A. B. C. D.
12.如图,在等边三角形中,,分别是边,的中点,为线段上任意一点,,的延长线分别交,于点,,且,则的边长为( )
(第12题)
A.12 B.9 C.6 D.3
二、填空题(每题 3 分,共 18 分)
13.已知,,则代数式的值为______.
14.若一元二次方程的两根为,,则的值为______.
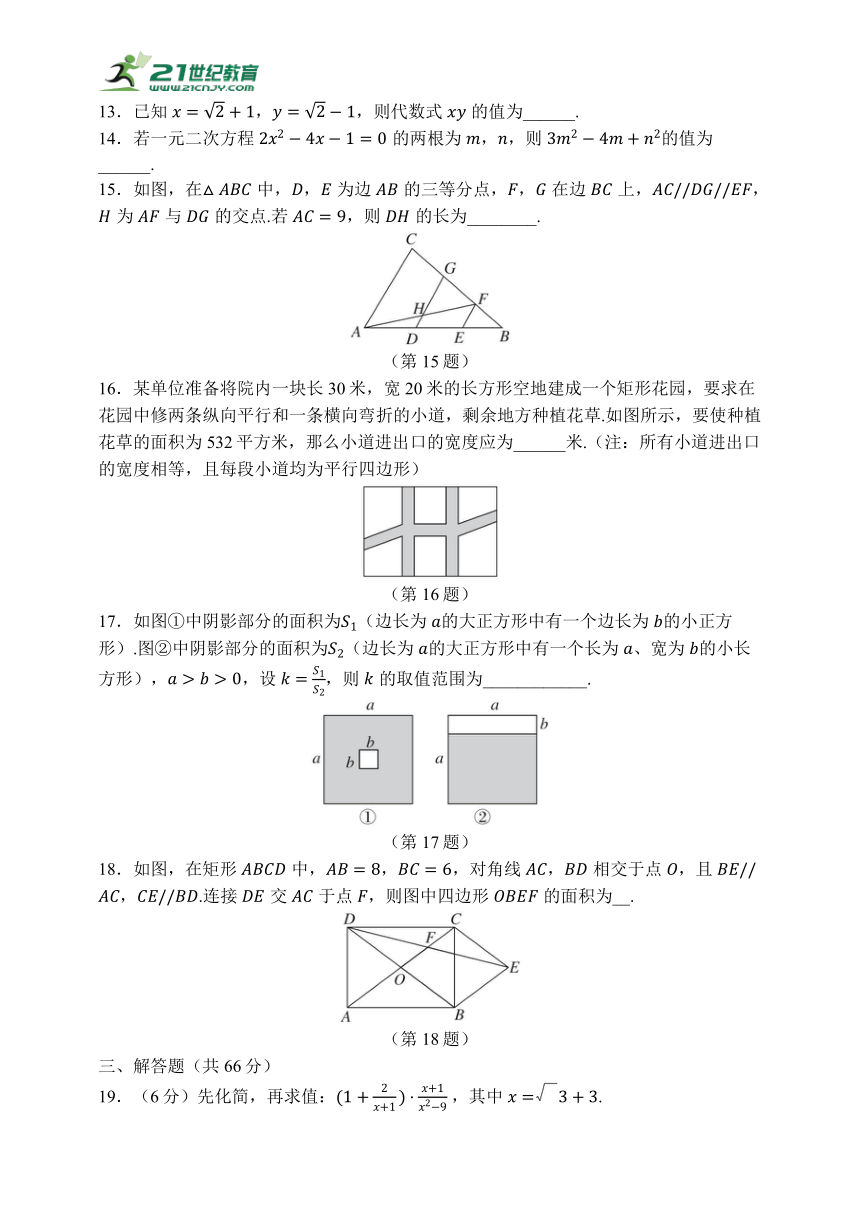
15.如图,在中,,为边的三等分点,,在边上,,为与的交点.若,则的长为________.
(第15题)
16.某单位准备将院内一块长30米,宽20米的长方形空地建成一个矩形花园,要求在花园中修两条纵向平行和一条横向弯折的小道,剩余地方种植花草.如图所示,要使种植花草的面积为532平方米,那么小道进出口的宽度应为______米.(注:所有小道进出口的宽度相等,且每段小道均为平行四边形)
(第16题)
17.如图①中阴影部分的面积为(边长为 的大正方形中有一个边长为 的小正方形).图②中阴影部分的面积为(边长为 的大正方形中有一个长为、宽为 的小长方形),,设,则的取值范围为____________.
(第17题)
18.如图,在矩形中,,,对角线,相交于点,且,.连接交于点,则图中四边形的面积为__.
(第18题)
三、解答题(共66分)
19.(6分)先化简,再求值: ,其中.
20.(8分)如图,在由边长为1的小正方形组成的网格图中有,建立平面直角坐标系后,点的坐标是.
(1) 以为位似中心,作,与相似比为,且在第二象限;
(2) 在上面所画的图形中,若线段上有一点,它的横坐标为,点在上的对应点的横坐标为,则______.
21.(9分)如图所示,在矩形中,为边上一点,且.
(1) 求证:;
(2) 为线段延长线上一点,且满足,求证:.
22.(8分)某数学兴趣小组测量校园内一棵树的高度.采用以下方法:如图,把支架放在离树适当距离的水平地面上的点处,再把镜子水平放在支架上的点处,然后沿着直线后退至点处,这时恰好在镜子里看到树的顶端.再用皮尺分别测量,,,观测者目高的长.利用测得的数据可以求出这棵树的高度.已知于点,于点,于点,米.米,米,米,求这棵树的高度(的长).
23.(10分)阅读下列材料,并解决问题:
【观察发现】
,
.
,
.
【建立模型】
形如的化简(其中,为正整数),只要找到两个正整数,,使,,那么.
【问题解决】
(1)
① 化简:________;
② ________;
(2) 已知正方形的边长为,现有一个长为,宽为的长方形,当它们的面积相等时,求正方形的边长;
(3) 已知,,求代数式的值.
24.(10分)某工厂拥有两条不同的护目镜加工生产线,.原计划生产线每小时生产护目镜 400 个,生产线每小时生产护目镜 500 个.
(1) 若生产线,共工作12小时,且生产护目镜的总数量不少于5 500个,则生产线至少生产护目镜多少小时?
(2) 原计划,生产线每天平均工作8小时,但现在为了尽快满足我市护目镜的需求,两条生产线每天均比原计划多工作了相同的小时数,但因为机器损耗及人员不足的原因,生产线每增加1小时,该生产线实际工作时每小时的产量均减少10个,生产线每增加1小时,该生产线每小时的产量均减少15个,这样一天生产的护目镜将比原计划多3 300 个,求该厂实际每天生产护目镜的时间.
25.(15分)在矩形中,点,分别在边,上,将矩形沿所在的直线折叠,使点的对应点落在边上,点的对应点为点,交于点.
(1) 如图①,求证:;
(2) 如图②,当为的中点,,时,求的长;
(3) 如图③,连接,当,分别为,的中点时,探究与的数量关系,并说明理由.
【参考答案】
一、选择题(每题3分,共36分)
1.A
2.C
3.D
4.D
5.A
6.A
7.B
【解析】,即,
.故选B.
8.B
【解析】设,则,.故选B.
9.C
【解析】如图①,过点作,垂足为.
如图②,过点作,垂足为.
,
易知,
.
,
,
,解得.故选C.
10.B
【解析】根据题意可知,是定值,的长度取最小值时,点应在上.如图,
过点作,交的延长线于点 在边长为2的菱形中, ,为中点,, . ,.
.
在中,.
在中,.
易知,
.故选B.
11.B
【解析】由题意得, .
,,
.
在中,.
是的中点,.
, .
.
又,.
,即,解得.
钢梁的长为.故选B.
12.B
【解析】如图,过点A作直线,延长交于点,延长交于点.
,,,
.
由题知点D在的中位线上,
易知中边上的高与中边上的高相等.
与的相似比为.
,,,
…①;
同理可得,…②.
由,得,
整理,得.
又,,
易得.
的边长为9.故选B.
二、填空题(每题 3 分,共 18 分)
13.1
14.6
15.
16.1
17.
【解析】由题意,得,,.,,即.
18.18
【解析】 四边形是矩形,对角线,相交于点, ,,, 四边形是平行四边形., 易得 ,,, 易知 易知, 易得..
三、解答题(共66分)
19.【解】
.
当时,原式.
20.(1) 【解】如图,即为所求.
(2) 2
21.(1) 【证明】 四边形是矩形,
,.
.
, ..
,
,
即.
,.
(2) 连接,交于点.
, .
又 ,.
,.
易知.
,.
,.
.
在和中,
.
22.【解】如图,过点作水平线交于点,交于点是水平线,,,都是铅垂线,
米,米,米.(米).
易知 ,,
.
,即,
解得米.
(米).
这棵树的高度为3.85米.
23.(1) ①
②
(2) 【解】由题意,得.
,
令,,,
解得,.
.
.
(3) ,,
,.
.
24.(1) 【解】设生产线生产护目镜小时,则生产线生产护目镜小时,
根据题意,得,解得,
的最小值为生产线至少生产护目镜7小时.
(2) 设该厂实际每天生产护目镜的时间为小时,则生产线实际每小时生产护目镜个,生产线实际每小时生产护目镜个.
根据题意,得,整理,得,
解得,(不符合题意,舍去).
该厂实际每天生产护目镜的时间为14小时.
25.(1) 【证明】如图. 四边形是矩形,
.
.
由折叠的性质,可知 ,
.
.
(2) 【解】 四边形是矩形,
,.
为的中点,.
由折叠的性质,可知.
设,.
在中,,即,解得,..
,,即,
解得.
易知,.
(3) 【解】.理由:如图,延长,交于点,连接.
由折叠性质,可知,, 直线,.
,.
易得.
为的中点,
设.
.
为的中点,.
四边形是矩形,
, .
..
又,.
,.
.
在中,.
.
在中,.
, 易得.
..
..
限时:120分钟 满分:120分
一、选择题(每题3分,共36分)
1.下列计算正确的是( )
A. B.
C. D.
2.函数的自变量的取值范围是( )
A. B. C. D.
3.若,,则的值为( )
A.8 B. C. D.4
4.若关于的一元二次方程有一个根为,则另一个根为( )
A. B. C. D.
5.如图,在菱形中,对角线,相交于点,若,,则的长是( )
(第5题)
A.8 B.7 C.4 D.3
6.如果一个三角形的三边长分别为1,,4.则化简的结果是( )
A. B. C.1 D.
7.若,则的值是( )
A.3 B. C. D.
8.如图,在矩形中,,,将长等于宽2倍的可变矩形如图放置,使,,三点在同一直线上,则阴影部分的面积为( )
(第8题)
A.8 B.9 C. D.
9.如图①是装了液体的高脚杯示意图(数据如图),用去一部分液体后如图②所示,此时液面直径( )
(第9题)
A. B. C. D.
10.如图,在边长为2的菱形中, ,是边的中点,是边上一动点,将沿所在的直线翻折得到 ,连接 ,则长度的最小值是( )
(第10题)
A.7 B. C. D.
11.如图,学校为举办文艺汇演搭建了舞台及登台的台阶,台阶总高度,台阶部分铺红地毯,地毯长度为,支撑钢梁,且为的中点,则钢梁的长为( )
(第11题)
A. B. C. D.
12.如图,在等边三角形中,,分别是边,的中点,为线段上任意一点,,的延长线分别交,于点,,且,则的边长为( )
(第12题)
A.12 B.9 C.6 D.3
二、填空题(每题 3 分,共 18 分)
13.已知,,则代数式的值为______.
14.若一元二次方程的两根为,,则的值为______.
15.如图,在中,,为边的三等分点,,在边上,,为与的交点.若,则的长为________.
(第15题)
16.某单位准备将院内一块长30米,宽20米的长方形空地建成一个矩形花园,要求在花园中修两条纵向平行和一条横向弯折的小道,剩余地方种植花草.如图所示,要使种植花草的面积为532平方米,那么小道进出口的宽度应为______米.(注:所有小道进出口的宽度相等,且每段小道均为平行四边形)
(第16题)
17.如图①中阴影部分的面积为(边长为 的大正方形中有一个边长为 的小正方形).图②中阴影部分的面积为(边长为 的大正方形中有一个长为、宽为 的小长方形),,设,则的取值范围为____________.
(第17题)
18.如图,在矩形中,,,对角线,相交于点,且,.连接交于点,则图中四边形的面积为__.
(第18题)
三、解答题(共66分)
19.(6分)先化简,再求值: ,其中.
20.(8分)如图,在由边长为1的小正方形组成的网格图中有,建立平面直角坐标系后,点的坐标是.
(1) 以为位似中心,作,与相似比为,且在第二象限;
(2) 在上面所画的图形中,若线段上有一点,它的横坐标为,点在上的对应点的横坐标为,则______.
21.(9分)如图所示,在矩形中,为边上一点,且.
(1) 求证:;
(2) 为线段延长线上一点,且满足,求证:.
22.(8分)某数学兴趣小组测量校园内一棵树的高度.采用以下方法:如图,把支架放在离树适当距离的水平地面上的点处,再把镜子水平放在支架上的点处,然后沿着直线后退至点处,这时恰好在镜子里看到树的顶端.再用皮尺分别测量,,,观测者目高的长.利用测得的数据可以求出这棵树的高度.已知于点,于点,于点,米.米,米,米,求这棵树的高度(的长).
23.(10分)阅读下列材料,并解决问题:
【观察发现】
,
.
,
.
【建立模型】
形如的化简(其中,为正整数),只要找到两个正整数,,使,,那么.
【问题解决】
(1)
① 化简:________;
② ________;
(2) 已知正方形的边长为,现有一个长为,宽为的长方形,当它们的面积相等时,求正方形的边长;
(3) 已知,,求代数式的值.
24.(10分)某工厂拥有两条不同的护目镜加工生产线,.原计划生产线每小时生产护目镜 400 个,生产线每小时生产护目镜 500 个.
(1) 若生产线,共工作12小时,且生产护目镜的总数量不少于5 500个,则生产线至少生产护目镜多少小时?
(2) 原计划,生产线每天平均工作8小时,但现在为了尽快满足我市护目镜的需求,两条生产线每天均比原计划多工作了相同的小时数,但因为机器损耗及人员不足的原因,生产线每增加1小时,该生产线实际工作时每小时的产量均减少10个,生产线每增加1小时,该生产线每小时的产量均减少15个,这样一天生产的护目镜将比原计划多3 300 个,求该厂实际每天生产护目镜的时间.
25.(15分)在矩形中,点,分别在边,上,将矩形沿所在的直线折叠,使点的对应点落在边上,点的对应点为点,交于点.
(1) 如图①,求证:;
(2) 如图②,当为的中点,,时,求的长;
(3) 如图③,连接,当,分别为,的中点时,探究与的数量关系,并说明理由.
【参考答案】
一、选择题(每题3分,共36分)
1.A
2.C
3.D
4.D
5.A
6.A
7.B
【解析】,即,
.故选B.
8.B
【解析】设,则,.故选B.
9.C
【解析】如图①,过点作,垂足为.
如图②,过点作,垂足为.
,
易知,
.
,
,
,解得.故选C.
10.B
【解析】根据题意可知,是定值,的长度取最小值时,点应在上.如图,
过点作,交的延长线于点 在边长为2的菱形中, ,为中点,, . ,.
.
在中,.
在中,.
易知,
.故选B.
11.B
【解析】由题意得, .
,,
.
在中,.
是的中点,.
, .
.
又,.
,即,解得.
钢梁的长为.故选B.
12.B
【解析】如图,过点A作直线,延长交于点,延长交于点.
,,,
.
由题知点D在的中位线上,
易知中边上的高与中边上的高相等.
与的相似比为.
,,,
…①;
同理可得,…②.
由,得,
整理,得.
又,,
易得.
的边长为9.故选B.
二、填空题(每题 3 分,共 18 分)
13.1
14.6
15.
16.1
17.
【解析】由题意,得,,.,,即.
18.18
【解析】 四边形是矩形,对角线,相交于点, ,,, 四边形是平行四边形., 易得 ,,, 易知 易知, 易得..
三、解答题(共66分)
19.【解】
.
当时,原式.
20.(1) 【解】如图,即为所求.
(2) 2
21.(1) 【证明】 四边形是矩形,
,.
.
, ..
,
,
即.
,.
(2) 连接,交于点.
, .
又 ,.
,.
易知.
,.
,.
.
在和中,
.
22.【解】如图,过点作水平线交于点,交于点是水平线,,,都是铅垂线,
米,米,米.(米).
易知 ,,
.
,即,
解得米.
(米).
这棵树的高度为3.85米.
23.(1) ①
②
(2) 【解】由题意,得.
,
令,,,
解得,.
.
.
(3) ,,
,.
.
24.(1) 【解】设生产线生产护目镜小时,则生产线生产护目镜小时,
根据题意,得,解得,
的最小值为生产线至少生产护目镜7小时.
(2) 设该厂实际每天生产护目镜的时间为小时,则生产线实际每小时生产护目镜个,生产线实际每小时生产护目镜个.
根据题意,得,整理,得,
解得,(不符合题意,舍去).
该厂实际每天生产护目镜的时间为14小时.
25.(1) 【证明】如图. 四边形是矩形,
.
.
由折叠的性质,可知 ,
.
.
(2) 【解】 四边形是矩形,
,.
为的中点,.
由折叠的性质,可知.
设,.
在中,,即,解得,..
,,即,
解得.
易知,.
(3) 【解】.理由:如图,延长,交于点,连接.
由折叠性质,可知,, 直线,.
,.
易得.
为的中点,
设.
.
为的中点,.
四边形是矩形,
, .
..
又,.
,.
.
在中,.
.
在中,.
, 易得.
..
..
同课章节目录
