【期末押题预测】题型专项培优 应用题(含解析)-2024-2025学年苏教版数学六年级下册
文档属性
| 名称 | 【期末押题预测】题型专项培优 应用题(含解析)-2024-2025学年苏教版数学六年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 736.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-09 07:27:40 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
题型专项培优 应用题(含解析)-2024-2025学年苏教版数学六年级下册
1.某商店销售一种电器,他们先将成本提高百分之三十之后才标价,后来又按照标价的八折优惠卖出,结果每销售一件该电器仍获得80元的利润;那么这种电器的成本价是多少元?
2. 六⑴班举行联欢活动,老师买了很多礼物。小涛将一些写有成语的卡片(如下)反面朝上放在桌子上,两个小组分别派一人摸卡片。每人任意摸出一张,然后放回,并打乱顺序,摸到含有数字的成语,“勤学”组先选礼物,摸到含有颜色的成语,“团结”组先选礼物。
(1)这个游戏规则公平吗?为什么?
(2)如果是你,你会制定怎样的游戏规则?
3.有3个自然数,两两相加得到3个和,分别是36、41、43,你知道这三个数的平均数是多少吗?
4.桌上有8个球,编号分别是①至⑧,其中6个球一样重,另外两个球都轻一些,是次品。为了找出次品,丽丽用天平称了三次,结果如下。
第一次:①+②比③+④轻;
第二次:⑤+⑥比⑦+⑧轻;
第三次:①+③+⑤与②+④+⑧一样重。
两个次品的编号分别是几?
5.小明家有1g、2g、4g和8g的钢块各1个,后来丢失了其中一个钢块,所以无法称出12g和7 g的质量。丢失的钢块是几克重的?(钢块只能放一边)
6.五一期间,商场开展促销活动:佳佳商场所有商品一律七折;华美商场每满1000元减300元。李叔叔想买一台液晶电视,两商场原价都是4500元,李叔叔在哪家商场购买更优惠?
7.甲、乙两城之间的铁路长927千米,一列火车于6月22日上午10时从甲城开往乙城,当天晚上7时到达。这列火车平均每小时行驶多少千米?
8.外卖送餐为我们生活带来了许多便利,某学习小组调查了一名外卖小哥一周的送餐情况,规定送餐量超过40单(送一次外卖称为一单)的部分记为“+”,低于40单的部分记为“﹣”。如表是该外卖小哥一周的送餐量:
星期 一 二 三 四 五 六 日
送餐量(单位:单) ﹣3 +4 ﹣5 +14 ﹣1 +7 +19
(1)求该外卖小哥这一周平均每天送餐多少单?
(2)外卖小哥每天的工资由底薪30元加上送单补贴构成,送单补贴的方案如下:每天送餐量不超过40单的部分,每单补贴4元;超过40单但不超过50单的部分,每单补贴6元;超过50单的部分,每单补贴8元.求该外卖小哥这一周工资收入多少元?
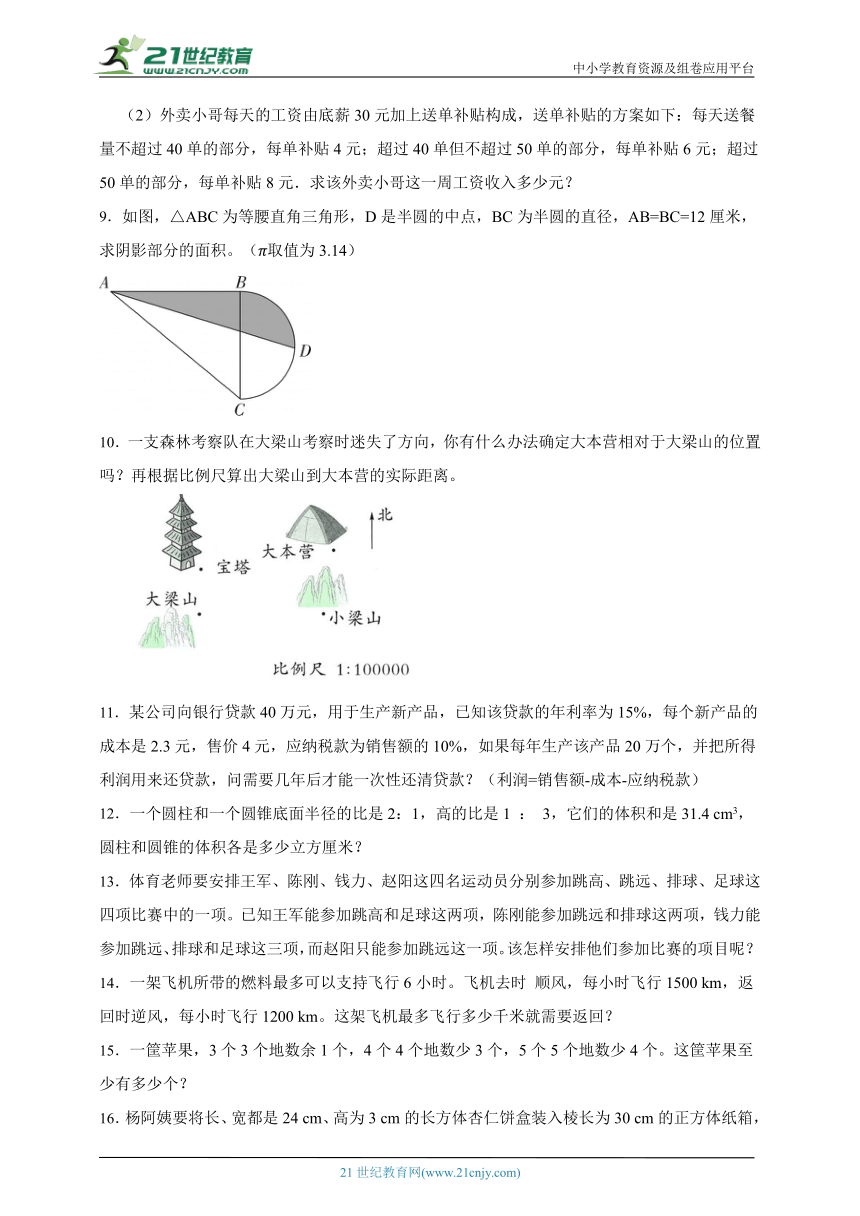
9.如图,△ABC为等腰直角三角形,D是半圆的中点,BC为半圆的直径,AB=BC=12厘米,求阴影部分的面积。(取值为3.14)
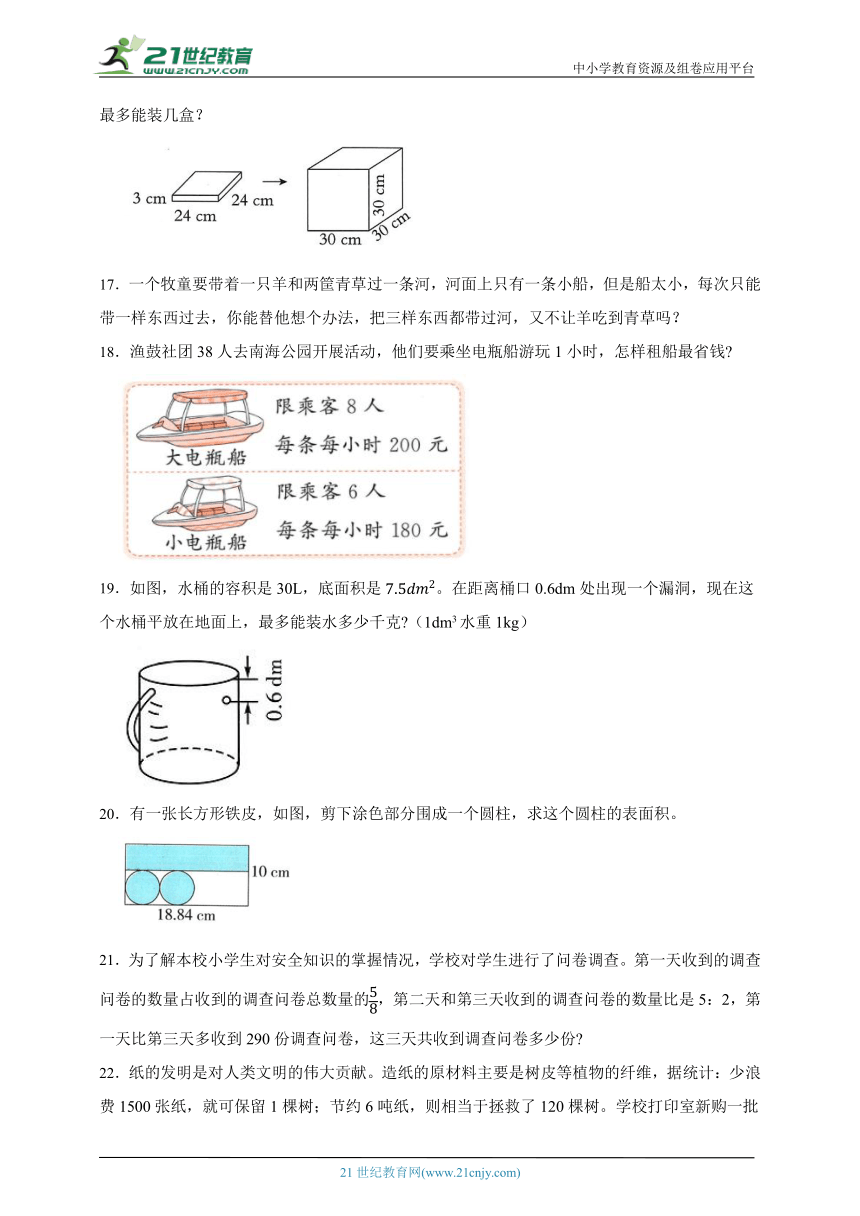
10.一支森林考察队在大梁山考察时迷失了方向,你有什么办法确定大本营相对于大梁山的位置吗?再根据比例尺算出大梁山到大本营的实际距离。
11.某公司向银行贷款40万元,用于生产新产品,已知该贷款的年利率为15%,每个新产品的成本是2.3元,售价4元,应纳税款为销售额的10%,如果每年生产该产品20万个,并把所得利润用来还贷款,问需要几年后才能一次性还清贷款?(利润=销售额-成本-应纳税款)
12.一个圆柱和一个圆锥底面半径的比是2:1,高的比是1 : 3,它们的体积和是31.4 cm3,圆柱和圆锥的体积各是多少立方厘米?
13.体育老师要安排王军、陈刚、钱力、赵阳这四名运动员分别参加跳高、跳远、排球、足球这四项比赛中的一项。已知王军能参加跳高和足球这两项,陈刚能参加跳远和排球这两项,钱力能参加跳远、排球和足球这三项,而赵阳只能参加跳远这一项。该怎样安排他们参加比赛的项目呢?
14.一架飞机所带的燃料最多可以支持飞行6小时。飞机去时 顺风,每小时飞行1500 km,返回时逆风,每小时飞行1200 km。这架飞机最多飞行多少千米就需要返回?
15.一筐苹果,3个3个地数余1个,4个4个地数少3个,5个5个地数少4个。这筐苹果至少有多少个?
16.杨阿姨要将长、宽都是24 cm、高为3 cm的长方体杏仁饼盒装入棱长为30 cm的正方体纸箱,最多能装几盒?
17.一个牧童要带着一只羊和两筐青草过一条河,河面上只有一条小船,但是船太小,每次只能带一样东西过去,你能替他想个办法,把三样东西都带过河,又不让羊吃到青草吗?
18.渔鼓社团38人去南海公园开展活动,他们要乘坐电瓶船游玩1小时,怎样租船最省钱
19.如图,水桶的容积是30L,底面积是。在距离桶口0.6dm处出现一个漏洞,现在这个水桶平放在地面上,最多能装水多少千克 (1dm3水重1kg)
20.有一张长方形铁皮,如图,剪下涂色部分围成一个圆柱,求这个圆柱的表面积。
21.为了解本校小学生对安全知识的掌握情况,学校对学生进行了问卷调查。第一天收到的调查问卷的数量占收到的调查问卷总数量的,第二天和第三天收到的调查问卷的数量比是5:2,第一天比第三天多收到290份调查问卷,这三天共收到调查问卷多少份
22.纸的发明是对人类文明的伟大贡献。造纸的原材料主要是树皮等植物的纤维,据统计:少浪费1500张纸,就可保留1棵树;节约6吨纸,则相当于拯救了120棵树。学校打印室新购一批白纸,计划每天用90张,可以用20天。由于注意了节约用纸,实际每天只用60张,这批白纸实际用了多少天?
23.只列式,不用计算。
琪琪把2000元压岁钱存入银行,定期3年,年利率是1.95%,到期后准备将利息捐赠给贫困地区,琪琪可以捐出多少元?
24.国家税收是公共财政的重要来源,用于提供基础设施、医疗保健、教育和社会保障等公共服务。这有助于满足社会的公共需求并促进社会发展与繁荣。交税是个人履行公民责任的方式,保障个人基本权益的同时维护了公共利益。我县某企业3月份的营业额是200万元。按规定,应按营业额的5%缴纳营业税。该企业3月份应缴纳营业税多少万元
25.表中的M和N是两个相关联的量,并且成正比例关系,试着填写表格。
M 2 3
6
……
N
15 20 25
35 ……
26.一个运动场如右图,两端是半圆形,中间是长方形。
(1)这个运动场的周长是多少米?
(2)这个运动场的面积是多少平方米?(得数保留整数)
27.王叔叔买了15张成人票和儿童票,一共用去265元。已知每张成人票20元,每张儿童票15元。王叔叔买成人票和儿童票各多少张?
28.一个长方体玻璃水缸,长8分米,宽5分米,高5分米,水深4分米。如果竖直放入一块棱长为4分米的正方体铁块,缸里的水会溢出多少升?
29.一个棱长为20cm的正方体容器里装了一半的水,现将一块石头完全浸没在水中,水面上升到14 cm。这块石头的体积是多少立方厘米?
30.一只狗被拴在底座为边长的等边三角形建筑物的墙角上(如图),绳长是,求狗所能到的地方的总面积.(圆周率按计算)
31.同同先用橡皮泥做了一个圆柱,再在圆柱中凿了四个相同的圆柱形孔,剩余部分的体积是多少立方厘米?(大圆柱的底面直径为24cm,小圆柱的底面直径为8cm,高都是15 cm)
32.小华的爸爸、妈妈都在医院上班,爸爸每上班3天休息1天,妈妈每上班4天休息1天。如果9月1日这一天爸爸、妈妈同时在家休息,那么下一次爸爸、妈妈同时在家休息是哪一天?
33.一张长方形纸长48厘米,宽40厘米。如果把它剪成大小相同的正方形(正方形的边长是整厘米数)且没有剩余,正方形边长可能是多少厘米?当正方形边长最长时,可以剪多少个?
34.如下图,已知,是真角三角形。AC=4cm,BC=2cm,求阴影部分的面积。
35.下面正方形的边长是6厘米,求涂色部分的周长。
36.有28人去郊游,每辆大车限乘8人,每辆小车限乘4人。
(1)如果都坐大车,至少需要几辆大车?
(2)如果都坐小车,至少需要几辆小车?
(3)如果大车、小车搭配坐,请你给出一个合适的乘车方案?
37.一次数学竞赛共有20道题,做对一道题得5分,做错一道题倒扣3分。刘冬得了52分,你知道刘冬做对了几道题吗?
38.在下面一个边长为4厘米的正方形中画一个最大的圆。如果将这个圆剪去,剩下图形的面积是多少平方厘米?
39.福建山清水秀,有很多著名的景点。下面是武夷山和东山两地的月平均气温统计图。
(1)东山这一年的月平均气温最高是 ℃,最低是 ℃。
(2)武夷山和东山在 月的月平均气温相差最大。
(3)武夷山这一年的月平均气温是如何变化的?
(4)来自东北地区的一家人准备到福建旅游。结合上图,你建议他们去武夷山还是东山?写出你的理由。
40.如下图,空地上有一栋房屋,房屋的墙角拴着一只羊,这座房屋长6 m,宽4 m。
(1)拴羊的绳长4m,羊在空地上的活动范围是多少平方米?
(2)如果拴羊的绳长换成6m,那么羊的活动范围增加了多少平方米?
41.甲、乙两人在10年前的年龄比为2:3,现在他俩的年龄比为3:4,那么10年后他俩的年龄比为多少?
42.如图,ABCD是长方形,BC=6cm,AB=10cm,对角线AC、BD相交O点。E、F分别是AD与BC的中点,图中的阴影部分以EF为轴旋转一周。
(1)则阴影部AOD绕EF旋转后的立体图形的底面面积是多少 (π取3)
(2)则白色部分扫出的立体图形的体积是多少立方厘米 (π取3)
43.某公司订购400根方木,每根方木横截面的面积是25平方分米,长是4米,这些木料一共有多少方?(1方=1立方米)
答案解析
1.【答案】解:设那么每辆电动自行车的成本价为x元.
根据题意,得0.8×(1+30%)x-x=80
解得,x=2000.
答:这种电器的成本价是2000元
【解析】【分析】 把这种服装的成本价看作单位“1”,按成本价提高30%后标价相当于原价的1+30%,又以8折优惠卖出,此时相当于原价的(1+30%)×80%,比原价还多(1+30%)×80%﹣1,即获利部分,正好是80元,因此列出方程解决问题.
2.【答案】(1)解:不公平。因为含有颜色的成语卡片比含有数字的成语卡片多,即摸到的可能性不相等,所以这个游戏规则不公平。
(2)解:摸到含有两种颜色或两个数字的成语卡片,“勤学”组先选礼物;摸到含有一种颜色或一个数字的成语卡片,“团结”组先选礼物。(答案不唯一)
【解析】【分析】(1)数含有数字成语,有“六神无主”“十年寒窗”“五湖四海”,共3个。数含有颜色成语,有“绿水青山"“花红柳绿””白发苍颜"“"蓝田种玉”"青黄不接”,共5个。卡片总数固定,数是不同导致摸到可能性不同,所以游戏不公平
(2)新规则要让两组摸到对应成语可能性相等。
3.【答案】解:(36 +41+43)÷2÷3
=60÷6
=20
答:这三个数的平均数是20。
【解析】【分析】假设这三个数分别是甲、乙、丙,可以列式:甲+乙=36,甲+丙=41,乙+丙=43。观察这三个等式的左边,出现了两个甲、两个乙、两个丙,(36+41+ 43)就是(甲+乙+丙)×2,所以这三个数的平均数=它们的和÷2÷数的个数。
4.【答案】解:由第一次知,①②中有一个次品; 由第二次知,⑤6中有一个次品;所以次品可能是①⑤、①⑥、②⑤或②⑥.
当①⑤都是次品时,第三次称的一样重不成立;
当①⑥都是次品时,第三次称的一样重不成立;
当②⑤都是次品时,第三次称重成立;
当②⑥都是次晶时,第三次称的一样重不成立。
所以两个次品的编号分别是②和⑤.
【解析】【分析】 首先,根据第一次称重结果,①+②比③+④轻,可以推断出轻球在③和④中。
其次,根据第二次称重结果,⑤+⑥比⑦+⑧轻,可以推断出轻球在⑤和⑥中。
然后,通过第三次称重结果,①+③+⑤与②+④+⑧一样重,结合前两次称重的结果,我们可以确定④和⑤是轻球。因为如果③是轻球,那么①+③+⑤的重量应该比②+④+⑧轻,这与第三次称重的结果不符。因此可以确定④和⑤是轻球。
5.【答案】解:因为12=4+8,7-4+1+2,所以只有丢失4g的钢块,才能使12g和7g的质量无法称出。
【解析】【分析】 12克可以由4克和8克的钢块组合得到( 12 = 4 + 8 ),而7克可以由1克、2克和4克的钢块组合得到( 7 = 1 + 2 + 4 )。如果小明能够称出这两个重量,那么他的钢块中必须包含4克的钢块。但是,题目明确指出小明无法称出这两个重量,这意味着他的钢块中缺少了能够使这两个组合成立的关键钢块——即4克的钢块。
6.【答案】解:佳佳商场:4500×70%=3150(元)
华美商场:4500-300×4=3300(元)
3150<3300
答:李叔叔在佳佳商场购买更优惠。
【解析】【分析】佳佳商场:七折即现价是原价的70%,原价×70%=现价;
华美商场:每满1000元减300元,原价4500元满了4个1000元,所以原价-300×4=现价,最后比较两个商场的现价即可判断。
7.【答案】解:晚上7时化为24时计时法是19:00
19-7=9(小时)
927÷9= 103(千米)
答:这列火车平均每小时行驶103千米。
【解析】【分析】把普通计时法改写成24时计时法,上午的时刻不变,下午或晚上时刻加12时,把上午、下午、晚上这些汉字去掉;
9小时行驶的路程÷9=平均每小时行驶的路程。
8.【答案】(1)解:40+(-3+4-5+14-1+7+19)÷7
=40+35÷7
=40+5
=45(单)
答: 该外卖小哥这一周平均每天送餐45单 。
(2)解:(40×7-3-5-1)×4+(4+7+10×2)×6+(4+9)×8+30×7
=1084+186+104+210
=1584(元)
答: 该外卖小哥这一周工资收入1584元。
【解析】【分析】(1)求出表中数据的平均数,再加上标准数40即可;
(2)根据工资的计算方法列式计算即可。
9.【答案】解:
=72+28.26-54
=46.26(平方厘米)
答:阴影部分的面积是46.26平方厘米。
【解析】【分析】如图,
找出BC线上的中点,用字母EG表示,连接DE,延长DE,使DE垂直AF;阴影部分的面积=长为12厘米、宽为(12÷2)厘米的长方形的面积+直径为12厘米的圆的面积-底为(12÷2)厘米、高为(12+12÷2)厘米的三角形的面积,然后再根据长方形的面积公式S=ab,圆的面积公式S = πr2,三角形的面积公式S =ah÷2进行解答。
10.【答案】解:如上图,大本营在大梁山的东偏北25°方向上。
3.5÷= 350000(厘米)
350000厘米= 3500米
答:大梁山到大本营的实际距离为3500米。
【解析】【分析】先测量出大梁山到大本营的图上距离,再根据实际距离=图上距离÷比例尺,求出实际距离。
11.【答案】解:每年利润=(4-2.3)×20-4×20×10%=26(万元),
设需要x年才能一次性还清贷款,则
26x=40×15%x+40
26x=6x+40
20x=40
x=2
答: 需要2年后才能一次性还清贷款。
【解析】【分析】本题需要先计算出一年的利润是多少;可以设需要x年才能一次性还清贷款,然后根据“利息=贷款本金×利率×时间”,列出方程等式,最终求得答案。
12.【答案】解:22 :12=4:1
(4×1): (1×3÷3)=4: 1
31.4×=25.12( cm3)
31.4×= 6.28( cm3 )
答:圆柱和圆锥的体积各是25.12立方厘、6.28立方厘米。
【解析】【分析】依据“圆柱和圆锥底面半径的比是2: 1”可以得到,圆柱和圆锥底面积的比是22:12=4:1。然后结合圆柱和圆锥底面积的比和高的比,求出它们的体积比。圆柱、圆锥分别的体积=它们的体积和÷总份数×各自分别占的份数。
13.【答案】根据给出的条件列出下表:
跳高 跳远 排球 足球
王军 √ √
陈刚 √ √
钱力 √ √ √
赵阳 √
可以看出,应安排赵阳参加跳远,陈刚参加排球,钱力参加足球,王军参加跳高
【解析】【分析】将条件列在一张表格内,借助于表格进行分析、推理
14.【答案】解:设飞机去时用了x小时。
1500x= 1200×(6-x)
x=
1500 ×= 4000 ( km)
答:这架飞机最多飞行4000 km就需要返回。
【解析】【分析】顺风飞行的时间+逆风飞行时间=最多飞行时间,根据速度×时间=路程,都是同一架飞机所以往返的路程相同,据此列出反比例方程,求解。
15.【答案】解:3,4和5的最小公倍数是3×4×5=60
60+1=61 (个)
答:这筐苹果至少有61个。
【解析】【分析】这筐苹果的个数比3、4、5的最小公倍数多1,先找出3、4、5的最小公倍数,3、4、5是互质数,他们的最小公倍数就是他们的乘积。这筐苹果的个数=3、4、5的最小公倍数+1.
16.【答案】解:有两种装法:
方法一:以长为24 cm,寬为3 cm的面为底面放人纸箱,可以装12盒,然后剩下的部分还能以长为24 cm、宽为24 cm的面为底面装2盒。
方法二:以长为24 cm、宽为24 cm的面为底面放人纸箱,可以装10盒,然后剩下的部分还能以长为24cm宽为3cm的面为底面装4盒。
答:最多可以装14盒。
【解析】【分析】 为了求出最多能装几盒,需要分别考虑正方体纸箱不同的摆放方式,从而确定装盒数量。
17.【答案】解:第一次将羊带到河对岸,牧童空船返回;第二次将一筐青草带到河对岸,放下青草带羊返回;第三次将另一筐青草带到河对岸,牧童空船返回;第四次将羊带到河对岸。
【解析】【分析】由于羊和青草不能让它们单独在一起,因此牧童需要将羊最后带过河。
第一次带羊过河,空手返回;第二次带一筐青草过河,返回时带羊返回;第三次再带一筐青草过河,空手返回;第四次带羊过河。
18.【答案】解:200÷8=25(元)
180÷6=30(元)
①8×5=40(人)
200×5=1000(元)
②8×4+6=38(人)
200×4+180
=800+180
=980(元)
1000>980
答:租4条大电瓶船和1条小电瓶船最省钱。
【解析】【分析】分别计算出大、小电瓶船的单价,选择单价便宜的,并且尽量使空余座位最少时,最省钱,最少需要的钱数=大电瓶船的单价×大电瓶船的条数+小电瓶船的单价×小电瓶船的条数。
19.【答案】解:7.5×(30÷7.5-0.6)×1
=7.5×(4-0.6)×1
=7.5×3.4
=25.5(千克)
答:最多能装水25.5千克。
【解析】【分析】根据题意可知,先求出水桶能装水的高度,水桶的容积÷底面积-漏洞离桶口的距离=装水的高度,然后用水桶的底面积×装水的高度=能装水的体积,根据1dm3的水重1kg,水的体积×1=装水的质量,据此列式解答。
20.【答案】解:18.84÷3.14÷2
=6÷2
=3(cm)
3.14×32×2+18.84×( 10-3×2)
=56.52+75.36
=131.88(cm2)
答:这个圆柱的表面积是131.88平方厘米。
【解析】【分析】这个圆柱的表面积=底面积×2+侧面积;其中,底面积=π×半径2,侧面积=长×宽,长=18.84,宽=10-直径×2。
21.【答案】解:第三天收到的调查问卷的数量占调查问卷总数量的
收到的调查问卷总数量为(份)
答:这三天共收到调查问卷 560份。
【解析】【分析】先根据第一天收到问卷占比求出第三天收到问卷占比,即,再利用第一天比第三天多收290份这一条件,用多的份数除以第一天与第三天占比之差,得出问卷总数。
22.【答案】30天
23.【答案】2000×1.95%×3
24.【答案】解:200×5%=10(万元)
答:该企业3月份应缴纳营业税10万元。
【解析】【分析】税额=营业额×税率,据此解答。
25.【答案】
M 2 3 4 5 6 7 ……
N 10 15 20 25 30 35 ……
【解析】【解答】解:15÷3=5
2×5=10
20÷5=4
25÷5=5
6×5=30
35÷5=7
M 2 3 4 5 6 7 ……
N 10 15 20 25 30 35 ……
【分析】表中的M和N成正比例关系,则N÷M=15÷3=5;据此计算出得数。
26.【答案】(1)解: 3.14×42×2+100×2
=131.88×2+200
=263.76+200
=463.76(米)
答:这个运动场的周长是463.76米。
(2)解: 100×42×2+3.14×
=4200×2+3.14×1764
=8400+5538.96
=13938.96
≈13939(平方米)
答:这个运动场的面积是13939平方米。
【解析】【分析】(1)由图形可知,这个运动场的周长由一个半径是42米的圆的周长+长方形的两条长(100×2),根据2πr+100×2,代入数据求解即可;
(2)这个运动场的面积为半径为42米的圆的面积+中间长方形的面积,且长方形的长是100米,宽是42×2米,根据+100×(42×2),代入数据解答即可。
27.【答案】解:假设都是儿童票,则成人票有:
(265-15×15)÷(20-15)
=(265-225)÷5
=40÷5
=8(张)
15-8=7(张)
答:李叔叔买成人票8张,儿童票7张。
【解析】【分析】假设都是儿童票,则用的钱数比265少40元,是因为把成人票也按照15元一张来计算了,这样每张就少算了5元。因此用一共少算的钱数除以每张成人票少算的钱数即可求出成人票的张数,进而求出儿童票的张数。
28.【答案】24升
29.【答案】解:20×20×(14-20÷2)
=400×4
=1600(立方厘米)
答:这块石头的体积是1600立方厘米。
【解析】【分析】根据题意,容器内水面上升的部分的体积就是石头的体积。由于容器是一个正方体,其棱长为20cm,因此根据正方体底面积=棱长×棱长,得出该正方体容器的底面积为20×20cm。水面上升了(14-10)=4cm,根据长方体体积=长×宽×高,得出石头的体积等于容器底面积乘以水面上升的高度,据此解答即可。
30.【答案】解: 狗的活动范围由三部分组成。
第一部分面积 :=
第二部分和第三部分面积: 每部分为=, 两部分面积和为2×
总面积 =+2×=43.96
答: 狗所能到的地方的总面积为43.96 平方米。
【解析】【分析】扇形面积公式S=,狗活动范围由三部分组成:半径4米、圆心角300 的扇形,以及两个半径1米、圆心角120 的扇形。根据扇形面积公式分别算出各部分面积,再求和,得到总面积。
31.【答案】解:3.14×(24÷2)2×15 -3.14×(8÷2)2×15×4
=3.14×144×15-3.14×16×15×4
=452.16×15-753.6×4
=6782.4-3014.4
=3768( cm3 )
答:剩余部分的体积是3768cm3。
【解析】【分析】圆柱的体积=底面积×高,大圆柱的体积-小圆柱的体积×4=剩余部分的体积。
32.【答案】解:3+1=4(天)
4+1=5(天)
4和5的最小公倍数是20
1+20=21(日)
答:下一次爸爸、妈妈同时在家休息是9月21日。
【解析】【分析】爸爸每上班3天休息1天,即每4天休息1天;妈妈每上班4天休息1天,即每5天休息1天。求出4和5的最小公倍数是20,也就是每20天爸爸、妈妈同时在家休息1天,所以下一次爸爸、妈妈同时在家休息是9月21日。
33.【答案】解:48的因数有:1、2、3、4、6、8、12、24、48;
40的因数有1、2、4、5、8、10、20、40;
48和40的公因数有:1、2、4、8;最大公因数是8,
(48÷8)×(40÷8)=30(个)。
答:正方形的边长可能是1厘米、2厘米、4厘米、8厘米,边长最大时,可以剪30个。
【解析】【分析】把一个大长方形剪成若干个小正方形,就是求大长方形长和宽的公因数,当正方形边长最大时,它为长和宽的最大公因数。
34.【答案】解:如图,阴影部分的面积分别为①、③、⑤
3.14×(4÷2)×2÷2+3.14×(2÷2)×1÷2-①-③-⑤-③=4×2÷2-③
3.14×2+3.14÷2-①-③-⑤=4
①+③+⑤
=3.14×2+3.14÷2-4
=6.28+1.57-4
=7.85-4
=3.85(平方厘米)
答:阴影部分的面积为3.85平方厘米
【解析】【分析】阴影部分的面积分别为①、③、⑤,则空白部分的面积等于直径是4厘米的半圆的面积与直径是2厘米的半圆的面积减去①、⑤,2个③的面积,而空白部分的面积还等于三角形ABC的面积减去③的面积,由此即可求出阴影部分的面积
35.【答案】解:圆的直径=6÷2=3(厘米)
6×4+3.14×3×4
=24+37.68
=61.68(厘米)
答:阴影部分的周长是61.68厘米。
【解析】【分析】正方形的周长=正方形的边长×4,4个圆的周长=π×圆的直径×4;涂色部分的周长=正方形的周长+4个圆的周长,据此解答。
36.【答案】(1)解: 28÷8=3(辆)......4(人)
3+1=4(辆)
答:至少需要4辆大车。
(2)解:如果都坐小车,至少需要几辆小车?
28÷4=7(辆)
答:至少需要租7辆小车。
(3)解:如果大车、小车搭配坐,请你给出一个合适的乘车方案?
方法一:
8×1=8(人)
4×5=20(人)
8+20=28(人)
方法二:
8×2=16(人)
4×3=12(人)
16+12=28(人)
方法三:
8×3=24(人)
4×1=4(人)
24+4=28(人)
答:大车1辆、小车5辆;大车2辆、小车3辆;大车3辆、小车1辆。
【解析】【分析】(1)去郊游的总人数÷每辆大车限乘的人数, 有余数,那么至少需要的大车辆数=商+1。
(2)去郊游的总人数÷每辆小车限乘的人数,没有余数,那么至少需要的小车辆数=商。
(3)合适的乘车方案就是搭配着坐,可以全部坐满,没有空座。
方法一:先搭配1辆大车,那就是坐8人,剩下的人数就是28-8,再搭配坐小车,刚好坐满。
方法二:先搭配2辆大车,那就是已经坐了16人了,剩下的人数就是28-16,再搭配坐小车,刚好坐满。
方法三:先搭配3辆大车,那就是已经坐了24人,剩下的人数就是28-24,再搭配坐小车,刚好坐满。
37.【答案】解:(20×3+52)÷(5+3)
=112÷8
=14(道)
答:刘冬做对了14道题。
【解析】【分析】假设都做错了,则会扣分20×3,不仅不得分还会扣分。用一共扣的分数加上本来得的分数就是分数差,用分数差除以做对和做错一道题的分数差(5+3)即可求出做对的题数。
38.【答案】解:4×4-3.14×(4÷2)2
=16-3.14×4
=16-12.56
=3.44(平方厘米)
答: 剩下图形的面积是3.44平方厘米 。
【解析】【分析】正方形的面积-圆的面积=剩余图形的面积。
39.【答案】(1)31;16
(2)3
(3)答:武夷山这一年中,1~7月的月平均气温呈上升趋势,7~12月的月平均气温呈下降趋势。
(4)答:我建议他们去东山。因为两地夏季气温相差不大,而东山冬季气温更高,温度更适宜游玩。
【解析】【解答】解:(1)31最大,16最小,
东山这一年的月平均气温最高是31℃,最低是16℃。
(2)23-9=14
武夷山和东山在3月的月平均气温相差最大。
故答案为:(1)31;16;(2)3。
【分析】(1)数最大的,月平均气温最高,数最小的,月平均气温最低;
(2)两个度数之间相差的格数最多,说明月平均气温相差最大;
(3)折线的走势是向上,说明月平均气温呈上升趋势,走势是下降,月平均气温呈下降趋势;
(4)答案合理即可,不唯一。
40.【答案】(1)解:如图:
3.14×4×4×
=50.24×
=37.68(平方米)
答:羊在空地上的活动范围是37.68平方米。
(2)解:如图:
9-4=2(米)
3.14×6×6×+3.14×2×2×-37.68
=113.04×+12.56×-37.68
=84.78+3.14-37.68
=87.92-37.68
=50.24(平方米)
答:羊的活动范围增加了50.24平方米。
【解析】【分析】(1)半径是4米的圆的面积×=羊在空地上的活动范围;
(2)半径是6米的圆的面积×+半径是2米的圆的面积×-原来羊在空地上的活动范围=羊的活动范围增加的面积。
41.【答案】解:设10年前甲的年龄为2x岁,则当时乙的年龄为3x岁。
3(3x+10)=4(2x+10)
9x+30=8x+40
9x-8x=40-30
x=10
所以10年前甲的年龄为10×2=20(岁),乙的年龄为10×3=30(岁),10年后两人分别是40岁、50岁,10年后两人的年龄比为4:5。
答:10年后他俩的年龄比是4:5。
【解析】【分析】设10年前甲的年龄为2x岁,则当时乙的年龄为3x岁。则现在甲的年龄是(2x+10)岁,乙的年龄是(3x+10)岁,根据此时两人的年龄比是3:4列出比例,解比例求出x的值,进而分别求出10年前两人的年龄,再求出10年后两人的年龄,写出10年后两人的年龄比即可。
42.【答案】(1)解:6÷2=3(厘米)
(平方厘米)
答:阴影部AOD绕EF旋转后的立体图形的底面面积是27平方厘米。
(2)解:圆柱体积:(立方厘米)
圆锥体积:(立方厘米)
空白体积:270-90=180(立方厘米)
答:白色部分扫出的立体图形的体积是180立方厘米
【解析】【分析】(1)由题意可知,BC=6cm,AB=10cm,则阴影部AOD绕EF旋转后的立体图形(圆锥)的底面半径为6÷2=3(厘米),圆锥的底面积公式为:S=πr2,代入数值计算即可。
(2)圆柱的体积公式为:V=πr2h,代入数值计算出圆柱的体积,圆锥的体积公式为:V=πr2h,代入数值计算出圆锥的体积,则白色部分扫出的立体图形的体积=圆柱的体积-圆锥的体积,计算出结果即可。
43.【答案】25平方分米=0.25平方米
0.25×4×400=400(立方米)=400(方)
答:这些木料一共有400方。
【解析】【分析】1根方木体积=方木横截面的面积×长,1根方木体积×400根=400根方木体积。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
题型专项培优 应用题(含解析)-2024-2025学年苏教版数学六年级下册
1.某商店销售一种电器,他们先将成本提高百分之三十之后才标价,后来又按照标价的八折优惠卖出,结果每销售一件该电器仍获得80元的利润;那么这种电器的成本价是多少元?
2. 六⑴班举行联欢活动,老师买了很多礼物。小涛将一些写有成语的卡片(如下)反面朝上放在桌子上,两个小组分别派一人摸卡片。每人任意摸出一张,然后放回,并打乱顺序,摸到含有数字的成语,“勤学”组先选礼物,摸到含有颜色的成语,“团结”组先选礼物。
(1)这个游戏规则公平吗?为什么?
(2)如果是你,你会制定怎样的游戏规则?
3.有3个自然数,两两相加得到3个和,分别是36、41、43,你知道这三个数的平均数是多少吗?
4.桌上有8个球,编号分别是①至⑧,其中6个球一样重,另外两个球都轻一些,是次品。为了找出次品,丽丽用天平称了三次,结果如下。
第一次:①+②比③+④轻;
第二次:⑤+⑥比⑦+⑧轻;
第三次:①+③+⑤与②+④+⑧一样重。
两个次品的编号分别是几?
5.小明家有1g、2g、4g和8g的钢块各1个,后来丢失了其中一个钢块,所以无法称出12g和7 g的质量。丢失的钢块是几克重的?(钢块只能放一边)
6.五一期间,商场开展促销活动:佳佳商场所有商品一律七折;华美商场每满1000元减300元。李叔叔想买一台液晶电视,两商场原价都是4500元,李叔叔在哪家商场购买更优惠?
7.甲、乙两城之间的铁路长927千米,一列火车于6月22日上午10时从甲城开往乙城,当天晚上7时到达。这列火车平均每小时行驶多少千米?
8.外卖送餐为我们生活带来了许多便利,某学习小组调查了一名外卖小哥一周的送餐情况,规定送餐量超过40单(送一次外卖称为一单)的部分记为“+”,低于40单的部分记为“﹣”。如表是该外卖小哥一周的送餐量:
星期 一 二 三 四 五 六 日
送餐量(单位:单) ﹣3 +4 ﹣5 +14 ﹣1 +7 +19
(1)求该外卖小哥这一周平均每天送餐多少单?
(2)外卖小哥每天的工资由底薪30元加上送单补贴构成,送单补贴的方案如下:每天送餐量不超过40单的部分,每单补贴4元;超过40单但不超过50单的部分,每单补贴6元;超过50单的部分,每单补贴8元.求该外卖小哥这一周工资收入多少元?
9.如图,△ABC为等腰直角三角形,D是半圆的中点,BC为半圆的直径,AB=BC=12厘米,求阴影部分的面积。(取值为3.14)
10.一支森林考察队在大梁山考察时迷失了方向,你有什么办法确定大本营相对于大梁山的位置吗?再根据比例尺算出大梁山到大本营的实际距离。
11.某公司向银行贷款40万元,用于生产新产品,已知该贷款的年利率为15%,每个新产品的成本是2.3元,售价4元,应纳税款为销售额的10%,如果每年生产该产品20万个,并把所得利润用来还贷款,问需要几年后才能一次性还清贷款?(利润=销售额-成本-应纳税款)
12.一个圆柱和一个圆锥底面半径的比是2:1,高的比是1 : 3,它们的体积和是31.4 cm3,圆柱和圆锥的体积各是多少立方厘米?
13.体育老师要安排王军、陈刚、钱力、赵阳这四名运动员分别参加跳高、跳远、排球、足球这四项比赛中的一项。已知王军能参加跳高和足球这两项,陈刚能参加跳远和排球这两项,钱力能参加跳远、排球和足球这三项,而赵阳只能参加跳远这一项。该怎样安排他们参加比赛的项目呢?
14.一架飞机所带的燃料最多可以支持飞行6小时。飞机去时 顺风,每小时飞行1500 km,返回时逆风,每小时飞行1200 km。这架飞机最多飞行多少千米就需要返回?
15.一筐苹果,3个3个地数余1个,4个4个地数少3个,5个5个地数少4个。这筐苹果至少有多少个?
16.杨阿姨要将长、宽都是24 cm、高为3 cm的长方体杏仁饼盒装入棱长为30 cm的正方体纸箱,最多能装几盒?
17.一个牧童要带着一只羊和两筐青草过一条河,河面上只有一条小船,但是船太小,每次只能带一样东西过去,你能替他想个办法,把三样东西都带过河,又不让羊吃到青草吗?
18.渔鼓社团38人去南海公园开展活动,他们要乘坐电瓶船游玩1小时,怎样租船最省钱
19.如图,水桶的容积是30L,底面积是。在距离桶口0.6dm处出现一个漏洞,现在这个水桶平放在地面上,最多能装水多少千克 (1dm3水重1kg)
20.有一张长方形铁皮,如图,剪下涂色部分围成一个圆柱,求这个圆柱的表面积。
21.为了解本校小学生对安全知识的掌握情况,学校对学生进行了问卷调查。第一天收到的调查问卷的数量占收到的调查问卷总数量的,第二天和第三天收到的调查问卷的数量比是5:2,第一天比第三天多收到290份调查问卷,这三天共收到调查问卷多少份
22.纸的发明是对人类文明的伟大贡献。造纸的原材料主要是树皮等植物的纤维,据统计:少浪费1500张纸,就可保留1棵树;节约6吨纸,则相当于拯救了120棵树。学校打印室新购一批白纸,计划每天用90张,可以用20天。由于注意了节约用纸,实际每天只用60张,这批白纸实际用了多少天?
23.只列式,不用计算。
琪琪把2000元压岁钱存入银行,定期3年,年利率是1.95%,到期后准备将利息捐赠给贫困地区,琪琪可以捐出多少元?
24.国家税收是公共财政的重要来源,用于提供基础设施、医疗保健、教育和社会保障等公共服务。这有助于满足社会的公共需求并促进社会发展与繁荣。交税是个人履行公民责任的方式,保障个人基本权益的同时维护了公共利益。我县某企业3月份的营业额是200万元。按规定,应按营业额的5%缴纳营业税。该企业3月份应缴纳营业税多少万元
25.表中的M和N是两个相关联的量,并且成正比例关系,试着填写表格。
M 2 3
6
……
N
15 20 25
35 ……
26.一个运动场如右图,两端是半圆形,中间是长方形。
(1)这个运动场的周长是多少米?
(2)这个运动场的面积是多少平方米?(得数保留整数)
27.王叔叔买了15张成人票和儿童票,一共用去265元。已知每张成人票20元,每张儿童票15元。王叔叔买成人票和儿童票各多少张?
28.一个长方体玻璃水缸,长8分米,宽5分米,高5分米,水深4分米。如果竖直放入一块棱长为4分米的正方体铁块,缸里的水会溢出多少升?
29.一个棱长为20cm的正方体容器里装了一半的水,现将一块石头完全浸没在水中,水面上升到14 cm。这块石头的体积是多少立方厘米?
30.一只狗被拴在底座为边长的等边三角形建筑物的墙角上(如图),绳长是,求狗所能到的地方的总面积.(圆周率按计算)
31.同同先用橡皮泥做了一个圆柱,再在圆柱中凿了四个相同的圆柱形孔,剩余部分的体积是多少立方厘米?(大圆柱的底面直径为24cm,小圆柱的底面直径为8cm,高都是15 cm)
32.小华的爸爸、妈妈都在医院上班,爸爸每上班3天休息1天,妈妈每上班4天休息1天。如果9月1日这一天爸爸、妈妈同时在家休息,那么下一次爸爸、妈妈同时在家休息是哪一天?
33.一张长方形纸长48厘米,宽40厘米。如果把它剪成大小相同的正方形(正方形的边长是整厘米数)且没有剩余,正方形边长可能是多少厘米?当正方形边长最长时,可以剪多少个?
34.如下图,已知,是真角三角形。AC=4cm,BC=2cm,求阴影部分的面积。
35.下面正方形的边长是6厘米,求涂色部分的周长。
36.有28人去郊游,每辆大车限乘8人,每辆小车限乘4人。
(1)如果都坐大车,至少需要几辆大车?
(2)如果都坐小车,至少需要几辆小车?
(3)如果大车、小车搭配坐,请你给出一个合适的乘车方案?
37.一次数学竞赛共有20道题,做对一道题得5分,做错一道题倒扣3分。刘冬得了52分,你知道刘冬做对了几道题吗?
38.在下面一个边长为4厘米的正方形中画一个最大的圆。如果将这个圆剪去,剩下图形的面积是多少平方厘米?
39.福建山清水秀,有很多著名的景点。下面是武夷山和东山两地的月平均气温统计图。
(1)东山这一年的月平均气温最高是 ℃,最低是 ℃。
(2)武夷山和东山在 月的月平均气温相差最大。
(3)武夷山这一年的月平均气温是如何变化的?
(4)来自东北地区的一家人准备到福建旅游。结合上图,你建议他们去武夷山还是东山?写出你的理由。
40.如下图,空地上有一栋房屋,房屋的墙角拴着一只羊,这座房屋长6 m,宽4 m。
(1)拴羊的绳长4m,羊在空地上的活动范围是多少平方米?
(2)如果拴羊的绳长换成6m,那么羊的活动范围增加了多少平方米?
41.甲、乙两人在10年前的年龄比为2:3,现在他俩的年龄比为3:4,那么10年后他俩的年龄比为多少?
42.如图,ABCD是长方形,BC=6cm,AB=10cm,对角线AC、BD相交O点。E、F分别是AD与BC的中点,图中的阴影部分以EF为轴旋转一周。
(1)则阴影部AOD绕EF旋转后的立体图形的底面面积是多少 (π取3)
(2)则白色部分扫出的立体图形的体积是多少立方厘米 (π取3)
43.某公司订购400根方木,每根方木横截面的面积是25平方分米,长是4米,这些木料一共有多少方?(1方=1立方米)
答案解析
1.【答案】解:设那么每辆电动自行车的成本价为x元.
根据题意,得0.8×(1+30%)x-x=80
解得,x=2000.
答:这种电器的成本价是2000元
【解析】【分析】 把这种服装的成本价看作单位“1”,按成本价提高30%后标价相当于原价的1+30%,又以8折优惠卖出,此时相当于原价的(1+30%)×80%,比原价还多(1+30%)×80%﹣1,即获利部分,正好是80元,因此列出方程解决问题.
2.【答案】(1)解:不公平。因为含有颜色的成语卡片比含有数字的成语卡片多,即摸到的可能性不相等,所以这个游戏规则不公平。
(2)解:摸到含有两种颜色或两个数字的成语卡片,“勤学”组先选礼物;摸到含有一种颜色或一个数字的成语卡片,“团结”组先选礼物。(答案不唯一)
【解析】【分析】(1)数含有数字成语,有“六神无主”“十年寒窗”“五湖四海”,共3个。数含有颜色成语,有“绿水青山"“花红柳绿””白发苍颜"“"蓝田种玉”"青黄不接”,共5个。卡片总数固定,数是不同导致摸到可能性不同,所以游戏不公平
(2)新规则要让两组摸到对应成语可能性相等。
3.【答案】解:(36 +41+43)÷2÷3
=60÷6
=20
答:这三个数的平均数是20。
【解析】【分析】假设这三个数分别是甲、乙、丙,可以列式:甲+乙=36,甲+丙=41,乙+丙=43。观察这三个等式的左边,出现了两个甲、两个乙、两个丙,(36+41+ 43)就是(甲+乙+丙)×2,所以这三个数的平均数=它们的和÷2÷数的个数。
4.【答案】解:由第一次知,①②中有一个次品; 由第二次知,⑤6中有一个次品;所以次品可能是①⑤、①⑥、②⑤或②⑥.
当①⑤都是次品时,第三次称的一样重不成立;
当①⑥都是次品时,第三次称的一样重不成立;
当②⑤都是次品时,第三次称重成立;
当②⑥都是次晶时,第三次称的一样重不成立。
所以两个次品的编号分别是②和⑤.
【解析】【分析】 首先,根据第一次称重结果,①+②比③+④轻,可以推断出轻球在③和④中。
其次,根据第二次称重结果,⑤+⑥比⑦+⑧轻,可以推断出轻球在⑤和⑥中。
然后,通过第三次称重结果,①+③+⑤与②+④+⑧一样重,结合前两次称重的结果,我们可以确定④和⑤是轻球。因为如果③是轻球,那么①+③+⑤的重量应该比②+④+⑧轻,这与第三次称重的结果不符。因此可以确定④和⑤是轻球。
5.【答案】解:因为12=4+8,7-4+1+2,所以只有丢失4g的钢块,才能使12g和7g的质量无法称出。
【解析】【分析】 12克可以由4克和8克的钢块组合得到( 12 = 4 + 8 ),而7克可以由1克、2克和4克的钢块组合得到( 7 = 1 + 2 + 4 )。如果小明能够称出这两个重量,那么他的钢块中必须包含4克的钢块。但是,题目明确指出小明无法称出这两个重量,这意味着他的钢块中缺少了能够使这两个组合成立的关键钢块——即4克的钢块。
6.【答案】解:佳佳商场:4500×70%=3150(元)
华美商场:4500-300×4=3300(元)
3150<3300
答:李叔叔在佳佳商场购买更优惠。
【解析】【分析】佳佳商场:七折即现价是原价的70%,原价×70%=现价;
华美商场:每满1000元减300元,原价4500元满了4个1000元,所以原价-300×4=现价,最后比较两个商场的现价即可判断。
7.【答案】解:晚上7时化为24时计时法是19:00
19-7=9(小时)
927÷9= 103(千米)
答:这列火车平均每小时行驶103千米。
【解析】【分析】把普通计时法改写成24时计时法,上午的时刻不变,下午或晚上时刻加12时,把上午、下午、晚上这些汉字去掉;
9小时行驶的路程÷9=平均每小时行驶的路程。
8.【答案】(1)解:40+(-3+4-5+14-1+7+19)÷7
=40+35÷7
=40+5
=45(单)
答: 该外卖小哥这一周平均每天送餐45单 。
(2)解:(40×7-3-5-1)×4+(4+7+10×2)×6+(4+9)×8+30×7
=1084+186+104+210
=1584(元)
答: 该外卖小哥这一周工资收入1584元。
【解析】【分析】(1)求出表中数据的平均数,再加上标准数40即可;
(2)根据工资的计算方法列式计算即可。
9.【答案】解:
=72+28.26-54
=46.26(平方厘米)
答:阴影部分的面积是46.26平方厘米。
【解析】【分析】如图,
找出BC线上的中点,用字母EG表示,连接DE,延长DE,使DE垂直AF;阴影部分的面积=长为12厘米、宽为(12÷2)厘米的长方形的面积+直径为12厘米的圆的面积-底为(12÷2)厘米、高为(12+12÷2)厘米的三角形的面积,然后再根据长方形的面积公式S=ab,圆的面积公式S = πr2,三角形的面积公式S =ah÷2进行解答。
10.【答案】解:如上图,大本营在大梁山的东偏北25°方向上。
3.5÷= 350000(厘米)
350000厘米= 3500米
答:大梁山到大本营的实际距离为3500米。
【解析】【分析】先测量出大梁山到大本营的图上距离,再根据实际距离=图上距离÷比例尺,求出实际距离。
11.【答案】解:每年利润=(4-2.3)×20-4×20×10%=26(万元),
设需要x年才能一次性还清贷款,则
26x=40×15%x+40
26x=6x+40
20x=40
x=2
答: 需要2年后才能一次性还清贷款。
【解析】【分析】本题需要先计算出一年的利润是多少;可以设需要x年才能一次性还清贷款,然后根据“利息=贷款本金×利率×时间”,列出方程等式,最终求得答案。
12.【答案】解:22 :12=4:1
(4×1): (1×3÷3)=4: 1
31.4×=25.12( cm3)
31.4×= 6.28( cm3 )
答:圆柱和圆锥的体积各是25.12立方厘、6.28立方厘米。
【解析】【分析】依据“圆柱和圆锥底面半径的比是2: 1”可以得到,圆柱和圆锥底面积的比是22:12=4:1。然后结合圆柱和圆锥底面积的比和高的比,求出它们的体积比。圆柱、圆锥分别的体积=它们的体积和÷总份数×各自分别占的份数。
13.【答案】根据给出的条件列出下表:
跳高 跳远 排球 足球
王军 √ √
陈刚 √ √
钱力 √ √ √
赵阳 √
可以看出,应安排赵阳参加跳远,陈刚参加排球,钱力参加足球,王军参加跳高
【解析】【分析】将条件列在一张表格内,借助于表格进行分析、推理
14.【答案】解:设飞机去时用了x小时。
1500x= 1200×(6-x)
x=
1500 ×= 4000 ( km)
答:这架飞机最多飞行4000 km就需要返回。
【解析】【分析】顺风飞行的时间+逆风飞行时间=最多飞行时间,根据速度×时间=路程,都是同一架飞机所以往返的路程相同,据此列出反比例方程,求解。
15.【答案】解:3,4和5的最小公倍数是3×4×5=60
60+1=61 (个)
答:这筐苹果至少有61个。
【解析】【分析】这筐苹果的个数比3、4、5的最小公倍数多1,先找出3、4、5的最小公倍数,3、4、5是互质数,他们的最小公倍数就是他们的乘积。这筐苹果的个数=3、4、5的最小公倍数+1.
16.【答案】解:有两种装法:
方法一:以长为24 cm,寬为3 cm的面为底面放人纸箱,可以装12盒,然后剩下的部分还能以长为24 cm、宽为24 cm的面为底面装2盒。
方法二:以长为24 cm、宽为24 cm的面为底面放人纸箱,可以装10盒,然后剩下的部分还能以长为24cm宽为3cm的面为底面装4盒。
答:最多可以装14盒。
【解析】【分析】 为了求出最多能装几盒,需要分别考虑正方体纸箱不同的摆放方式,从而确定装盒数量。
17.【答案】解:第一次将羊带到河对岸,牧童空船返回;第二次将一筐青草带到河对岸,放下青草带羊返回;第三次将另一筐青草带到河对岸,牧童空船返回;第四次将羊带到河对岸。
【解析】【分析】由于羊和青草不能让它们单独在一起,因此牧童需要将羊最后带过河。
第一次带羊过河,空手返回;第二次带一筐青草过河,返回时带羊返回;第三次再带一筐青草过河,空手返回;第四次带羊过河。
18.【答案】解:200÷8=25(元)
180÷6=30(元)
①8×5=40(人)
200×5=1000(元)
②8×4+6=38(人)
200×4+180
=800+180
=980(元)
1000>980
答:租4条大电瓶船和1条小电瓶船最省钱。
【解析】【分析】分别计算出大、小电瓶船的单价,选择单价便宜的,并且尽量使空余座位最少时,最省钱,最少需要的钱数=大电瓶船的单价×大电瓶船的条数+小电瓶船的单价×小电瓶船的条数。
19.【答案】解:7.5×(30÷7.5-0.6)×1
=7.5×(4-0.6)×1
=7.5×3.4
=25.5(千克)
答:最多能装水25.5千克。
【解析】【分析】根据题意可知,先求出水桶能装水的高度,水桶的容积÷底面积-漏洞离桶口的距离=装水的高度,然后用水桶的底面积×装水的高度=能装水的体积,根据1dm3的水重1kg,水的体积×1=装水的质量,据此列式解答。
20.【答案】解:18.84÷3.14÷2
=6÷2
=3(cm)
3.14×32×2+18.84×( 10-3×2)
=56.52+75.36
=131.88(cm2)
答:这个圆柱的表面积是131.88平方厘米。
【解析】【分析】这个圆柱的表面积=底面积×2+侧面积;其中,底面积=π×半径2,侧面积=长×宽,长=18.84,宽=10-直径×2。
21.【答案】解:第三天收到的调查问卷的数量占调查问卷总数量的
收到的调查问卷总数量为(份)
答:这三天共收到调查问卷 560份。
【解析】【分析】先根据第一天收到问卷占比求出第三天收到问卷占比,即,再利用第一天比第三天多收290份这一条件,用多的份数除以第一天与第三天占比之差,得出问卷总数。
22.【答案】30天
23.【答案】2000×1.95%×3
24.【答案】解:200×5%=10(万元)
答:该企业3月份应缴纳营业税10万元。
【解析】【分析】税额=营业额×税率,据此解答。
25.【答案】
M 2 3 4 5 6 7 ……
N 10 15 20 25 30 35 ……
【解析】【解答】解:15÷3=5
2×5=10
20÷5=4
25÷5=5
6×5=30
35÷5=7
M 2 3 4 5 6 7 ……
N 10 15 20 25 30 35 ……
【分析】表中的M和N成正比例关系,则N÷M=15÷3=5;据此计算出得数。
26.【答案】(1)解: 3.14×42×2+100×2
=131.88×2+200
=263.76+200
=463.76(米)
答:这个运动场的周长是463.76米。
(2)解: 100×42×2+3.14×
=4200×2+3.14×1764
=8400+5538.96
=13938.96
≈13939(平方米)
答:这个运动场的面积是13939平方米。
【解析】【分析】(1)由图形可知,这个运动场的周长由一个半径是42米的圆的周长+长方形的两条长(100×2),根据2πr+100×2,代入数据求解即可;
(2)这个运动场的面积为半径为42米的圆的面积+中间长方形的面积,且长方形的长是100米,宽是42×2米,根据+100×(42×2),代入数据解答即可。
27.【答案】解:假设都是儿童票,则成人票有:
(265-15×15)÷(20-15)
=(265-225)÷5
=40÷5
=8(张)
15-8=7(张)
答:李叔叔买成人票8张,儿童票7张。
【解析】【分析】假设都是儿童票,则用的钱数比265少40元,是因为把成人票也按照15元一张来计算了,这样每张就少算了5元。因此用一共少算的钱数除以每张成人票少算的钱数即可求出成人票的张数,进而求出儿童票的张数。
28.【答案】24升
29.【答案】解:20×20×(14-20÷2)
=400×4
=1600(立方厘米)
答:这块石头的体积是1600立方厘米。
【解析】【分析】根据题意,容器内水面上升的部分的体积就是石头的体积。由于容器是一个正方体,其棱长为20cm,因此根据正方体底面积=棱长×棱长,得出该正方体容器的底面积为20×20cm。水面上升了(14-10)=4cm,根据长方体体积=长×宽×高,得出石头的体积等于容器底面积乘以水面上升的高度,据此解答即可。
30.【答案】解: 狗的活动范围由三部分组成。
第一部分面积 :=
第二部分和第三部分面积: 每部分为=, 两部分面积和为2×
总面积 =+2×=43.96
答: 狗所能到的地方的总面积为43.96 平方米。
【解析】【分析】扇形面积公式S=,狗活动范围由三部分组成:半径4米、圆心角300 的扇形,以及两个半径1米、圆心角120 的扇形。根据扇形面积公式分别算出各部分面积,再求和,得到总面积。
31.【答案】解:3.14×(24÷2)2×15 -3.14×(8÷2)2×15×4
=3.14×144×15-3.14×16×15×4
=452.16×15-753.6×4
=6782.4-3014.4
=3768( cm3 )
答:剩余部分的体积是3768cm3。
【解析】【分析】圆柱的体积=底面积×高,大圆柱的体积-小圆柱的体积×4=剩余部分的体积。
32.【答案】解:3+1=4(天)
4+1=5(天)
4和5的最小公倍数是20
1+20=21(日)
答:下一次爸爸、妈妈同时在家休息是9月21日。
【解析】【分析】爸爸每上班3天休息1天,即每4天休息1天;妈妈每上班4天休息1天,即每5天休息1天。求出4和5的最小公倍数是20,也就是每20天爸爸、妈妈同时在家休息1天,所以下一次爸爸、妈妈同时在家休息是9月21日。
33.【答案】解:48的因数有:1、2、3、4、6、8、12、24、48;
40的因数有1、2、4、5、8、10、20、40;
48和40的公因数有:1、2、4、8;最大公因数是8,
(48÷8)×(40÷8)=30(个)。
答:正方形的边长可能是1厘米、2厘米、4厘米、8厘米,边长最大时,可以剪30个。
【解析】【分析】把一个大长方形剪成若干个小正方形,就是求大长方形长和宽的公因数,当正方形边长最大时,它为长和宽的最大公因数。
34.【答案】解:如图,阴影部分的面积分别为①、③、⑤
3.14×(4÷2)×2÷2+3.14×(2÷2)×1÷2-①-③-⑤-③=4×2÷2-③
3.14×2+3.14÷2-①-③-⑤=4
①+③+⑤
=3.14×2+3.14÷2-4
=6.28+1.57-4
=7.85-4
=3.85(平方厘米)
答:阴影部分的面积为3.85平方厘米
【解析】【分析】阴影部分的面积分别为①、③、⑤,则空白部分的面积等于直径是4厘米的半圆的面积与直径是2厘米的半圆的面积减去①、⑤,2个③的面积,而空白部分的面积还等于三角形ABC的面积减去③的面积,由此即可求出阴影部分的面积
35.【答案】解:圆的直径=6÷2=3(厘米)
6×4+3.14×3×4
=24+37.68
=61.68(厘米)
答:阴影部分的周长是61.68厘米。
【解析】【分析】正方形的周长=正方形的边长×4,4个圆的周长=π×圆的直径×4;涂色部分的周长=正方形的周长+4个圆的周长,据此解答。
36.【答案】(1)解: 28÷8=3(辆)......4(人)
3+1=4(辆)
答:至少需要4辆大车。
(2)解:如果都坐小车,至少需要几辆小车?
28÷4=7(辆)
答:至少需要租7辆小车。
(3)解:如果大车、小车搭配坐,请你给出一个合适的乘车方案?
方法一:
8×1=8(人)
4×5=20(人)
8+20=28(人)
方法二:
8×2=16(人)
4×3=12(人)
16+12=28(人)
方法三:
8×3=24(人)
4×1=4(人)
24+4=28(人)
答:大车1辆、小车5辆;大车2辆、小车3辆;大车3辆、小车1辆。
【解析】【分析】(1)去郊游的总人数÷每辆大车限乘的人数, 有余数,那么至少需要的大车辆数=商+1。
(2)去郊游的总人数÷每辆小车限乘的人数,没有余数,那么至少需要的小车辆数=商。
(3)合适的乘车方案就是搭配着坐,可以全部坐满,没有空座。
方法一:先搭配1辆大车,那就是坐8人,剩下的人数就是28-8,再搭配坐小车,刚好坐满。
方法二:先搭配2辆大车,那就是已经坐了16人了,剩下的人数就是28-16,再搭配坐小车,刚好坐满。
方法三:先搭配3辆大车,那就是已经坐了24人,剩下的人数就是28-24,再搭配坐小车,刚好坐满。
37.【答案】解:(20×3+52)÷(5+3)
=112÷8
=14(道)
答:刘冬做对了14道题。
【解析】【分析】假设都做错了,则会扣分20×3,不仅不得分还会扣分。用一共扣的分数加上本来得的分数就是分数差,用分数差除以做对和做错一道题的分数差(5+3)即可求出做对的题数。
38.【答案】解:4×4-3.14×(4÷2)2
=16-3.14×4
=16-12.56
=3.44(平方厘米)
答: 剩下图形的面积是3.44平方厘米 。
【解析】【分析】正方形的面积-圆的面积=剩余图形的面积。
39.【答案】(1)31;16
(2)3
(3)答:武夷山这一年中,1~7月的月平均气温呈上升趋势,7~12月的月平均气温呈下降趋势。
(4)答:我建议他们去东山。因为两地夏季气温相差不大,而东山冬季气温更高,温度更适宜游玩。
【解析】【解答】解:(1)31最大,16最小,
东山这一年的月平均气温最高是31℃,最低是16℃。
(2)23-9=14
武夷山和东山在3月的月平均气温相差最大。
故答案为:(1)31;16;(2)3。
【分析】(1)数最大的,月平均气温最高,数最小的,月平均气温最低;
(2)两个度数之间相差的格数最多,说明月平均气温相差最大;
(3)折线的走势是向上,说明月平均气温呈上升趋势,走势是下降,月平均气温呈下降趋势;
(4)答案合理即可,不唯一。
40.【答案】(1)解:如图:
3.14×4×4×
=50.24×
=37.68(平方米)
答:羊在空地上的活动范围是37.68平方米。
(2)解:如图:
9-4=2(米)
3.14×6×6×+3.14×2×2×-37.68
=113.04×+12.56×-37.68
=84.78+3.14-37.68
=87.92-37.68
=50.24(平方米)
答:羊的活动范围增加了50.24平方米。
【解析】【分析】(1)半径是4米的圆的面积×=羊在空地上的活动范围;
(2)半径是6米的圆的面积×+半径是2米的圆的面积×-原来羊在空地上的活动范围=羊的活动范围增加的面积。
41.【答案】解:设10年前甲的年龄为2x岁,则当时乙的年龄为3x岁。
3(3x+10)=4(2x+10)
9x+30=8x+40
9x-8x=40-30
x=10
所以10年前甲的年龄为10×2=20(岁),乙的年龄为10×3=30(岁),10年后两人分别是40岁、50岁,10年后两人的年龄比为4:5。
答:10年后他俩的年龄比是4:5。
【解析】【分析】设10年前甲的年龄为2x岁,则当时乙的年龄为3x岁。则现在甲的年龄是(2x+10)岁,乙的年龄是(3x+10)岁,根据此时两人的年龄比是3:4列出比例,解比例求出x的值,进而分别求出10年前两人的年龄,再求出10年后两人的年龄,写出10年后两人的年龄比即可。
42.【答案】(1)解:6÷2=3(厘米)
(平方厘米)
答:阴影部AOD绕EF旋转后的立体图形的底面面积是27平方厘米。
(2)解:圆柱体积:(立方厘米)
圆锥体积:(立方厘米)
空白体积:270-90=180(立方厘米)
答:白色部分扫出的立体图形的体积是180立方厘米
【解析】【分析】(1)由题意可知,BC=6cm,AB=10cm,则阴影部AOD绕EF旋转后的立体图形(圆锥)的底面半径为6÷2=3(厘米),圆锥的底面积公式为:S=πr2,代入数值计算即可。
(2)圆柱的体积公式为:V=πr2h,代入数值计算出圆柱的体积,圆锥的体积公式为:V=πr2h,代入数值计算出圆锥的体积,则白色部分扫出的立体图形的体积=圆柱的体积-圆锥的体积,计算出结果即可。
43.【答案】25平方分米=0.25平方米
0.25×4×400=400(立方米)=400(方)
答:这些木料一共有400方。
【解析】【分析】1根方木体积=方木横截面的面积×长,1根方木体积×400根=400根方木体积。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
