2016年5月海南省琼中中学 优质课教学比赛高中数学(新课标人教A版)必修四2.3.4平面向量共线的坐标表示 教学课件 (共17张PPT)
文档属性
| 名称 | 2016年5月海南省琼中中学 优质课教学比赛高中数学(新课标人教A版)必修四2.3.4平面向量共线的坐标表示 教学课件 (共17张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-06-20 13:51:36 | ||
图片预览






文档简介
课件17张PPT。
2.3.4平面向量共线的
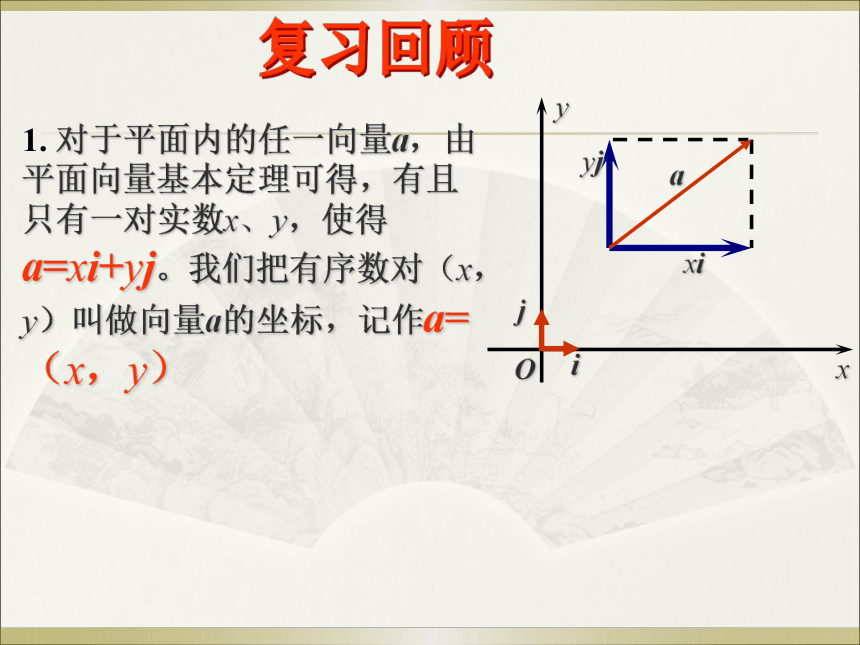
坐标表示1. 对于平面内的任一向量a,由平面向量基本定理可得,有且只有一对实数x、y,使得a=xi+yj。我们把有序数对(x,y)叫做向量a的坐标,记作a=(x,y)复习回顾2. 向量的坐标运算:3.平面向量共线定理:问题: 如果向量 , 共线(其中 ≠ ),那么 , 满足什么关系?思考: 设 =(x1,y1), =(x2,y2),若向量 , 共线(其中 ≠ ),则这两个向量的坐标应满足什么关系?结论: 设 =(x1,y1), =(x2,y2),(其中 ),当且仅当向量 与向量 共线。 探究:例6.练习:典例精析变式训练C4. 已知a=(1, 0), b=(2, 1), 当实数k为何值时,向量ka-b与a+3b平行? 并确定它们是同向还是反向. 解:ka-b=(k-2, -1), a+3b=(7, 3),
∵ka-b与a+3b平行这两个向量是反向。解法1:已知A(-1, -1), B(1,3), C(1,5) ,D(2,7) ,变式训练例8.设点P是线段P1P2上的一点,P1、P2的坐标分别是
。
(1)当点P是线段P1P2的中点时,求点P的坐标;
(2)当点P是线段P1P2的一个三等分点时,求点P的坐标。xyOP1P2P(1)M解:(1)所以,点P的坐标为例8.设点P是线段P1P2上的一点,P1、P2的坐标分别是
(2)当点P是线段P1P2的一个三等分点时,求点P的坐标。解:(2)①解法二: ②若点p靠近P2点 时向量平行(共线)等价条件的两种形式:小结:探究: 解:
∵ka-b与a+3b平行这两个向量是反向。解法1:已知A(-1, -1), B(1,3), C(1,5) ,D(2,7) ,变式训练例8.设点P是线段P1P2上的一点,P1、P2的坐标分别是
。
(1)当点P是线段P1P2的中点时,求点P的坐标;
(2)当点P是线段P1P2的一个三等分点时,求点P的坐标。xyOP1P2P(1)M解:(1)所以,点P的坐标为例8.设点P是线段P1P2上的一点,P1、P2的坐标分别是
(2)当点P是线段P1P2的一个三等分点时,求点P的坐标。解:(2)①解法二: ②若点p靠近P2点 时向量平行(共线)等价条件的两种形式:小结:探究: 解:
