期末必考专题:三角形、平行四边形和梯形(真题汇编)(含答案)-2024-2025学年数学四年级下册苏教版
文档属性
| 名称 | 期末必考专题:三角形、平行四边形和梯形(真题汇编)(含答案)-2024-2025学年数学四年级下册苏教版 |  | |
| 格式 | docx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-09 12:47:46 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
期末必考专题:三角形、平行四边形和梯形(真题汇编)-2024-2025学年数学四年级下册苏教版
1.(2025春 忠县期末)(1)在点子图中画一个钝角三角形,再把它分成两个直角三角形。
(2)在点子图中画一个等腰直角三角形,并画出斜边上的高。
2.(2025春 龙华区期末)已知∠1=120°,三角形ABC是直角三角形,三角形ABD是等腰三角形,求∠2和∠3的度数。
3.(2025春 奉化区期末)用18根1厘米长的小棒摆成一个等腰三角形,有几种不同的摆法?请列表说明。
腰/cm
腰/cm
底/cm
能否围成三角形
答:有 种不同的摆法。
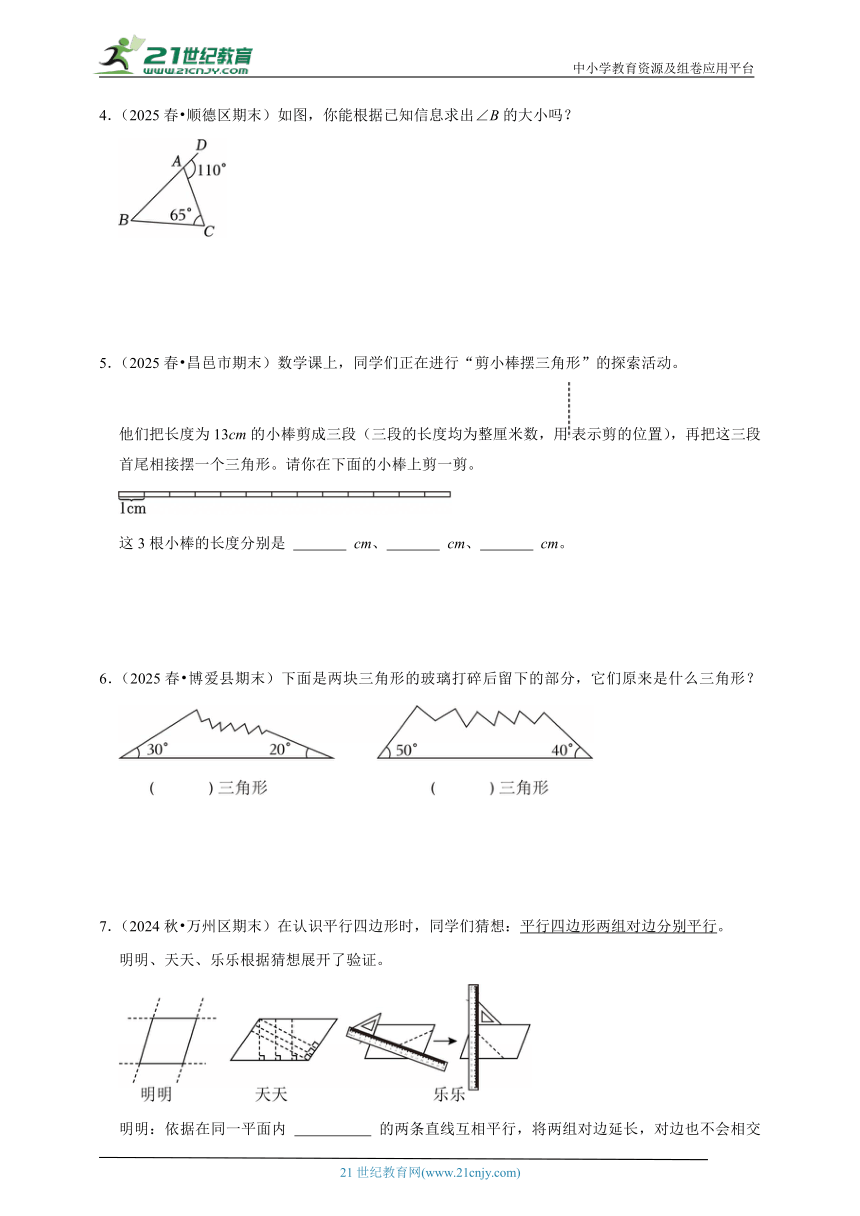
4.(2025春 顺德区期末)如图,你能根据已知信息求出∠B的大小吗?
5.(2025春 昌邑市期末)数学课上,同学们正在进行“剪小棒摆三角形”的探索活动。
他们把长度为13cm的小棒剪成三段(三段的长度均为整厘米数,用表示剪的位置),再把这三段首尾相接摆一个三角形。请你在下面的小棒上剪一剪。
这3根小棒的长度分别是 cm、 cm、 cm。
6.(2025春 博爱县期末)下面是两块三角形的玻璃打碎后留下的部分,它们原来是什么三角形?
7.(2024秋 万州区期末)在认识平行四边形时,同学们猜想:平行四边形两组对边分别平行。
明明、天天、乐乐根据猜想展开了验证。
明明:依据在同一平面内 的两条直线互相平行,将两组对边延长,对边也不会相交的方法进行验证。
天天:依据端点分别在两条平行线上,且与平行线 的所有线段的长度都 来验证。
乐乐:依据平移三角尺的方法验证了两组对边分别平行。
最后,三人得出相同的结论:平行四边形两组对边分别平行。
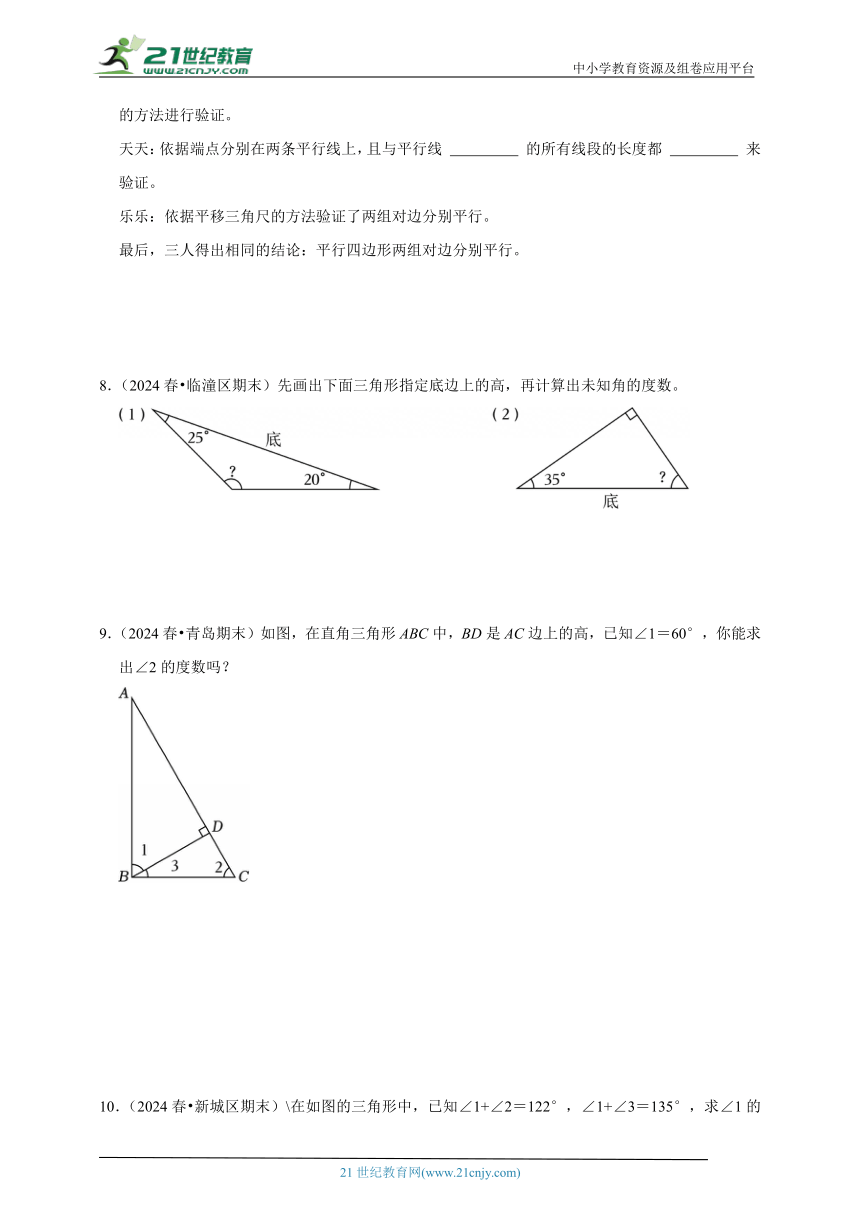
8.(2024春 临潼区期末)先画出下面三角形指定底边上的高,再计算出未知角的度数。
9.(2024春 青岛期末)如图,在直角三角形ABC中,BD是AC边上的高,已知∠1=60°,你能求出∠2的度数吗?
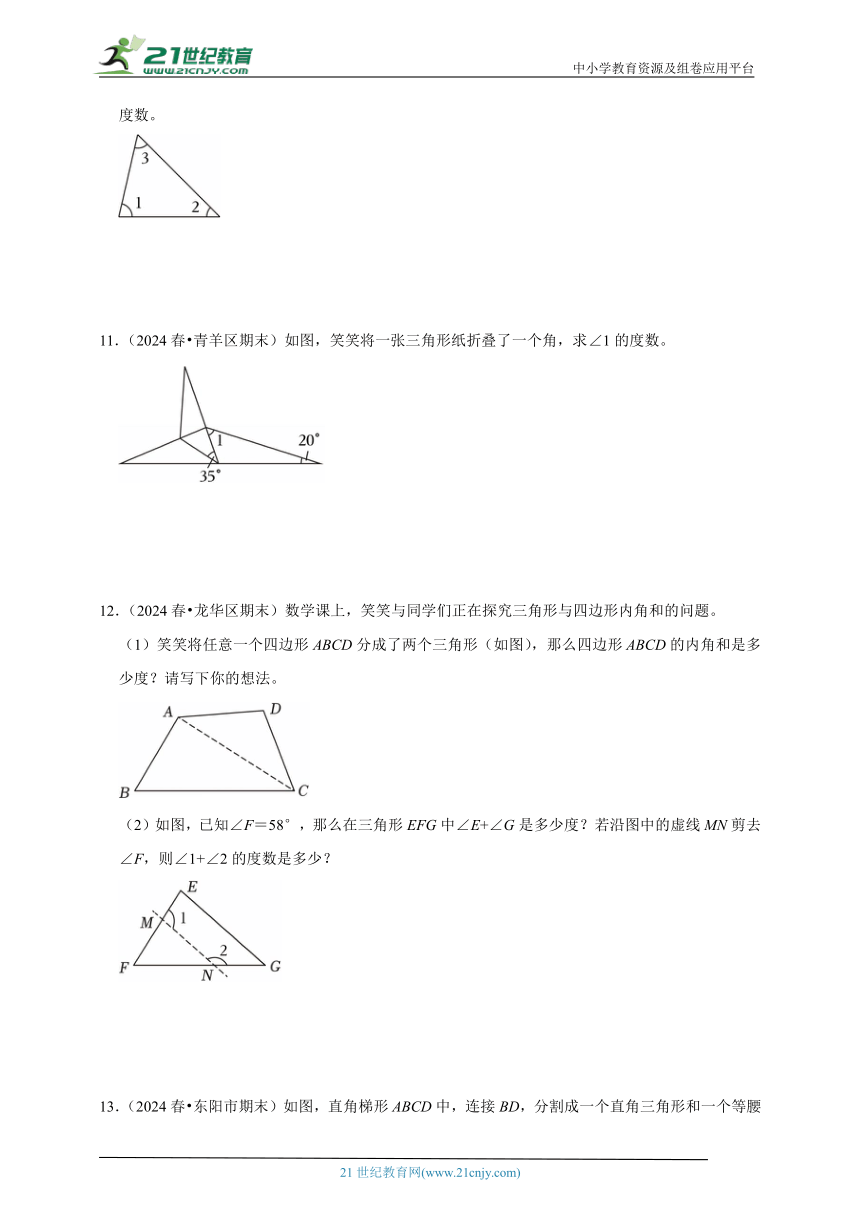
10.(2024春 新城区期末)\在如图的三角形中,已知∠1+∠2=122°,∠1+∠3=135°,求∠1的度数。
11.(2024春 青羊区期末)如图,笑笑将一张三角形纸折叠了一个角,求∠1的度数。
12.(2024春 龙华区期末)数学课上,笑笑与同学们正在探究三角形与四边形内角和的问题。
(1)笑笑将任意一个四边形ABCD分成了两个三角形(如图),那么四边形ABCD的内角和是多少度?请写下你的想法。
(2)如图,已知∠F=58°,那么在三角形EFG中∠E+∠G是多少度?若沿图中的虚线MN剪去∠F,则∠1+∠2的度数是多少?
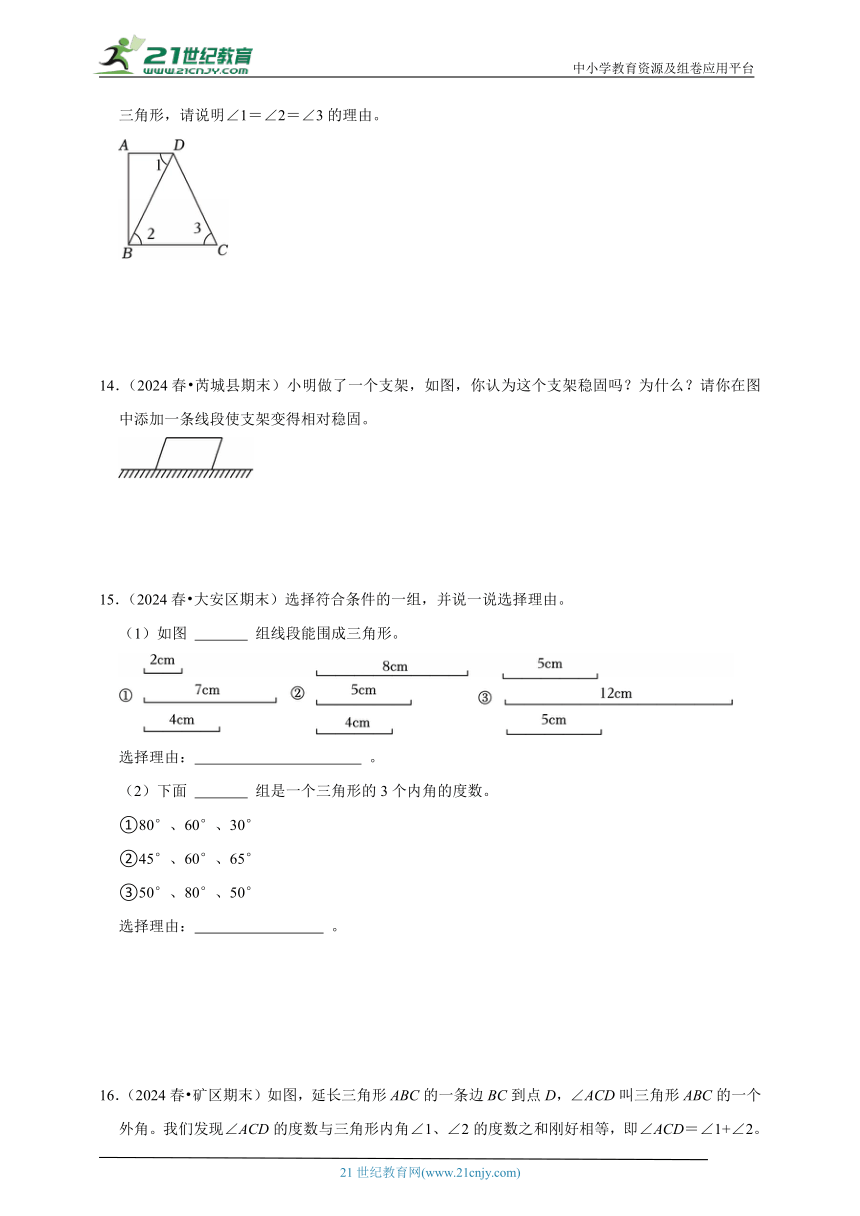
13.(2024春 东阳市期末)如图,直角梯形ABCD中,连接BD,分割成一个直角三角形和一个等腰三角形,请说明∠1=∠2=∠3的理由。
14.(2024春 芮城县期末)小明做了一个支架,如图,你认为这个支架稳固吗?为什么?请你在图中添加一条线段使支架变得相对稳固。
15.(2024春 大安区期末)选择符合条件的一组,并说一说选择理由。
(1)如图 组线段能围成三角形。
选择理由: 。
(2)下面 组是一个三角形的3个内角的度数。
①80°、60°、30°
②45°、60°、65°
③50°、80°、50°
选择理由: 。
16.(2024春 矿区期末)如图,延长三角形ABC的一条边BC到点D,∠ACD叫三角形ABC的一个外角。我们发现∠ACD的度数与三角形内角∠1、∠2的度数之和刚好相等,即∠ACD=∠1+∠2。
你能用所学知识解释这个结论吗?试着说一说。
17.(2024春 惠来县期末)一个三角形中,两个较小角的度数和是80°,两个较大角的度数和是155°。这个三角形三个内角分别是多少度?
18.(2024 江北区)如图1,∠1、∠2、∠3是三角形ABC的三个内角.现将三角形的三条边AB、BC、CA分别延长,形成了∠4、∠5、∠6三个角,这三个角叫三角形的外角,如图2.
不测量,你能推理得出∠4、∠5和∠6这三个外角的和是几度吗?请写出你的思考过程.
19.(2024春 郑州期末)奇奇小组在数学课上用“剪小棒摆三角形”探究三角形有关知识:
他们首先尝试把长度为14厘米的小棒剪成3段(3段的长度均为整厘米数),再把这3段首尾相接摆成一个三角形。(如图,图中每个一样长)
(1)奇奇想到了两种剪法,如图(“”表示剪的位置)。按这两种剪法剪开后的小棒能分别摆成三角形吗?如果能,请在括号里画“√”,如果不能,请在括号里画“×”。
①第一种剪法:
②第二种剪法:
(2)如果先从小棒左边剪下4厘米长的一段作为三角形的一条边,如图(“”表示剪的位置),要想摆成一个三角形,接下来应该从哪里剪开才能得到三角形的另外两条边?请你在图中画“”表示出接下来要剪的位置,并写出你的思考过程。
思考过程: 。
期末必考专题:三角形、平行四边形和梯形(真题汇编)-2024-2025学年数学四年级下册苏教版
参考答案与试题解析
一.解答题(共19小题)
1.(2025春 忠县期末)(1)在点子图中画一个钝角三角形,再把它分成两个直角三角形。
(2)在点子图中画一个等腰直角三角形,并画出斜边上的高。
【解答】解:(1)在点子图中画一个钝角三角形,再把它分成两个直角三角形。如图:
(2)在点子图中画一个等腰直角三角形,并画出斜边上的高。如图:
(画法不唯一)
2.(2025春 龙华区期末)已知∠1=120°,三角形ABC是直角三角形,三角形ABD是等腰三角形,求∠2和∠3的度数。
【解答】解:∠2=( 180°﹣120°)÷2
=60°÷2
=30°
∠3=180°﹣90°﹣30°
=90°﹣30°
=60°
答:∠2是30°,∠3是60°。
3.(2025春 奉化区期末)用18根1厘米长的小棒摆成一个等腰三角形,有几种不同的摆法?请列表说明。
腰/cm
腰/cm
底/cm
能否围成三角形
答:有 4 种不同的摆法。
【解答】解:
腰/cm 5 6 7 8
腰/cm 5 6 7 8
底/cm 8 6 4 3
能否围成三角形 能 能 能 能
因此有4种不同的摆法。
故答案为:4。
4.(2025春 顺德区期末)如图,你能根据已知信息求出∠B的大小吗?
【解答】解:180°﹣110°=70°
180°﹣70°﹣65°=45°
答:∠B的度数是45°。
5.(2025春 昌邑市期末)数学课上,同学们正在进行“剪小棒摆三角形”的探索活动。
他们把长度为13cm的小棒剪成三段(三段的长度均为整厘米数,用表示剪的位置),再把这三段首尾相接摆一个三角形。请你在下面的小棒上剪一剪。
这3根小棒的长度分别是 3 cm、 4 cm、 6 cm。
【解答】解:当三条边为3cm、4cm、6cm时:3+4=7cm,7>6,4﹣3=1cm,1<6,能组成三角形。(答案不唯一)
这3根小棒的长度分别是3cm、4cm、6cm。(答案不唯一)
故答案为:3;4;6。
6.(2025春 博爱县期末)下面是两块三角形的玻璃打碎后留下的部分,它们原来是什么三角形?
【解答】解:180°﹣30°﹣20°=130°
180°﹣50°﹣40°=90°
故答案为:
7.(2024秋 万州区期末)在认识平行四边形时,同学们猜想:平行四边形两组对边分别平行。
明明、天天、乐乐根据猜想展开了验证。
明明:依据在同一平面内 不相交 的两条直线互相平行,将两组对边延长,对边也不会相交的方法进行验证。
天天:依据端点分别在两条平行线上,且与平行线 垂直 的所有线段的长度都 相等 来验证。
乐乐:依据平移三角尺的方法验证了两组对边分别平行。
最后,三人得出相同的结论:平行四边形两组对边分别平行。
【解答】解:明明:依据在同一平面内不相交的两条直线互相平行,将两组对边延长,对边也不会相交的方法进行验证。
天天:依据端点分别在两条平行线上,且与平行线垂直的所有线段的长度都相等来验证。
乐乐:依据平移三角尺的方法验证了两组对边分别平行。
最后,三人得出相同的结论:平行四边形两组对边分别平行。
故答案为:不相交;垂直,相等。
8.(2024春 临潼区期末)先画出下面三角形指定底边上的高,再计算出未知角的度数。
【解答】解:根据分析,作图如下:
(1)180°﹣25°﹣20°
=155°﹣20°
=135°
(2)90°﹣35°=55°
9.(2024春 青岛期末)如图,在直角三角形ABC中,BD是AC边上的高,已知∠1=60°,你能求出∠2的度数吗?
【解答】解:结合图形可知:∠3=90°﹣∠1。
由三角形内角和为180° 可知:
∠2=180°﹣90°﹣∠3。
=90°﹣(90°﹣∠1)
=∠1
=60°
答:∠2的度数是60°。
10.(2024春 新城区期末)\在如图的三角形中,已知∠1+∠2=122°,∠1+∠3=135°,求∠1的度数。
【解答】解:∠3=180°﹣122°
=58°
∠2=180°﹣135°
=45°
则∠1=180°﹣∠2﹣∠3
=180°﹣58°﹣45°
=122°﹣45°
=77°
答:∠1的度数是77°。
11.(2024春 青羊区期末)如图,笑笑将一张三角形纸折叠了一个角,求∠1的度数。
【解答】解:如下图所示:
∠2=180°﹣∠3﹣35°=180°﹣70°=110°
∠1=180°﹣∠2﹣20°=180°﹣110°﹣20°=50°
答:∠1的度数是50°。
12.(2024春 龙华区期末)数学课上,笑笑与同学们正在探究三角形与四边形内角和的问题。
(1)笑笑将任意一个四边形ABCD分成了两个三角形(如图),那么四边形ABCD的内角和是多少度?请写下你的想法。
(2)如图,已知∠F=58°,那么在三角形EFG中∠E+∠G是多少度?若沿图中的虚线MN剪去∠F,则∠1+∠2的度数是多少?
【解答】解:(1)因为三角形的内角和等于180°,四边形分成两个三角形,所以四边形的内角和=180°×2=360°。
(2)因为∠F=58°
所以∠E+∠G=180°﹣58°=122°
∠1+∠2=360°﹣122°=238°
13.(2024春 东阳市期末)如图,直角梯形ABCD中,连接BD,分割成一个直角三角形和一个等腰三角形,请说明∠1=∠2=∠3的理由。
【解答】解:∠BAD=90°,∠ABC=90°
180°﹣∠BAD=90°,∠1+∠ABD=90°,∠2+∠ABD=∠ABC=90°
∠1=∠2
等腰三角形中两个底角相等,所以在三角形BDC中∠2=∠3。
所以∠1=∠2=∠3。
14.(2024春 芮城县期末)小明做了一个支架,如图,你认为这个支架稳固吗?为什么?请你在图中添加一条线段使支架变得相对稳固。
【解答】解:这个支架不稳固,因为平行四边形易变形,不具有稳定性。在图中添加一条线段使支架变得相对稳固。如图:
(画法不唯一,合理即可)
15.(2024春 大安区期末)选择符合条件的一组,并说一说选择理由。
(1)如图 ② 组线段能围成三角形。
选择理由: 符合三角形三边的关系,任意两边之和大于第三边 。
(2)下面 ③ 组是一个三角形的3个内角的度数。
①80°、60°、30°
②45°、60°、65°
③50°、80°、50°
选择理由: 三个角的和是180° 。
【解答】解:(1)①2+4=6(厘米),6厘米<7厘米,所以不能围成三角形;
②4+5=9(厘米);9厘米>8厘米,5+8=13(厘米),13厘米>4厘米,4+8=12(厘米),12厘米>5厘米,能围成三角形;
③5+5=10(厘米),10厘米<12厘米,所以不能围成三角形。
所以②组线段能围成三角形,选择理由:符合三角形三边的关系,任意两边之和大于第三边。
(2)①80°+60°+30°=170°,不满足三角形内角和是180°,所以不是三角形的3个内角;
②45°+60°+65°=170°,不满足三角形内角和是180°,所以不是三角形的3个内角;
③50°+80°+50°=180°,满足三角形内角和定理,所以是三角形的3个内角;
所以③组是一个三角形的3个内角的度数,选择理由:三个角的和是180°。
故答案为:(1)②,符合三角形三边的关系,任意两边之和大于第三边;(2)③,三个角的和是180°。
16.(2024春 矿区期末)如图,延长三角形ABC的一条边BC到点D,∠ACD叫三角形ABC的一个外角。我们发现∠ACD的度数与三角形内角∠1、∠2的度数之和刚好相等,即∠ACD=∠1+∠2。
你能用所学知识解释这个结论吗?试着说一说。
【解答】解:根据图示,结合三角形的内角和是180度,可知∠1+∠2+∠ACB=180°,结合∠ACB和∠ACD是一个平角可知,∠ACB+∠ACD=180°,比较可知∠ACD=∠1+∠2。(合理即可。)
17.(2024春 惠来县期末)一个三角形中,两个较小角的度数和是80°,两个较大角的度数和是155°。这个三角形三个内角分别是多少度?
【解答】解:中间角的度数:80°+155°﹣180°=55°
最小角:80°﹣55°=25°
最大角:155°﹣55°=100°
答:这个三角形三个内角分别是25°,55°,100°。
18.(2024 江北区)如图1,∠1、∠2、∠3是三角形ABC的三个内角.现将三角形的三条边AB、BC、CA分别延长,形成了∠4、∠5、∠6三个角,这三个角叫三角形的外角,如图2.
不测量,你能推理得出∠4、∠5和∠6这三个外角的和是几度吗?请写出你的思考过程.
【解答】解:能推理得出∠4、∠5和∠6这三个外角的和是360°,理由如下:
因为∠1+∠6=180°,∠2+∠4=180°,∠3+∠5=180°
所以∠1+∠2+∠3+∠4+∠5+∠6
=180°×3
=540°
又因为,∠1+∠2+∠3=180°
所以∠4+∠5+∠6
=540°﹣180°
=360°.
19.(2024春 郑州期末)奇奇小组在数学课上用“剪小棒摆三角形”探究三角形有关知识:
他们首先尝试把长度为14厘米的小棒剪成3段(3段的长度均为整厘米数),再把这3段首尾相接摆成一个三角形。(如图,图中每个一样长)
(1)奇奇想到了两种剪法,如图(“”表示剪的位置)。按这两种剪法剪开后的小棒能分别摆成三角形吗?如果能,请在括号里画“√”,如果不能,请在括号里画“×”。
①第一种剪法:
②第二种剪法:
(2)如果先从小棒左边剪下4厘米长的一段作为三角形的一条边,如图(“”表示剪的位置),要想摆成一个三角形,接下来应该从哪里剪开才能得到三角形的另外两条边?请你在图中画“”表示出接下来要剪的位置,并写出你的思考过程。
思考过程: 三角形任意两边之和大于第三边 。
【解答】解:(1)①剪成的三段为7厘米,6厘米,1厘米,6+1=7,所以此种剪法错误,如下图所示:
②剪成的三段为3厘米,5厘米,6厘米,3+5>6,所以此种剪法正确,如下图所示:
(2)14﹣4=10(厘米)
10÷2=5(厘米)
因为4+5>5,所以在9厘米处剪开即可。如下图所示(答案不唯一):
思考过程:三角形任意两边之和大于第三边。
故答案为:三角形任意两边之和大于第三边。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末必考专题:三角形、平行四边形和梯形(真题汇编)-2024-2025学年数学四年级下册苏教版
1.(2025春 忠县期末)(1)在点子图中画一个钝角三角形,再把它分成两个直角三角形。
(2)在点子图中画一个等腰直角三角形,并画出斜边上的高。
2.(2025春 龙华区期末)已知∠1=120°,三角形ABC是直角三角形,三角形ABD是等腰三角形,求∠2和∠3的度数。
3.(2025春 奉化区期末)用18根1厘米长的小棒摆成一个等腰三角形,有几种不同的摆法?请列表说明。
腰/cm
腰/cm
底/cm
能否围成三角形
答:有 种不同的摆法。
4.(2025春 顺德区期末)如图,你能根据已知信息求出∠B的大小吗?
5.(2025春 昌邑市期末)数学课上,同学们正在进行“剪小棒摆三角形”的探索活动。
他们把长度为13cm的小棒剪成三段(三段的长度均为整厘米数,用表示剪的位置),再把这三段首尾相接摆一个三角形。请你在下面的小棒上剪一剪。
这3根小棒的长度分别是 cm、 cm、 cm。
6.(2025春 博爱县期末)下面是两块三角形的玻璃打碎后留下的部分,它们原来是什么三角形?
7.(2024秋 万州区期末)在认识平行四边形时,同学们猜想:平行四边形两组对边分别平行。
明明、天天、乐乐根据猜想展开了验证。
明明:依据在同一平面内 的两条直线互相平行,将两组对边延长,对边也不会相交的方法进行验证。
天天:依据端点分别在两条平行线上,且与平行线 的所有线段的长度都 来验证。
乐乐:依据平移三角尺的方法验证了两组对边分别平行。
最后,三人得出相同的结论:平行四边形两组对边分别平行。
8.(2024春 临潼区期末)先画出下面三角形指定底边上的高,再计算出未知角的度数。
9.(2024春 青岛期末)如图,在直角三角形ABC中,BD是AC边上的高,已知∠1=60°,你能求出∠2的度数吗?
10.(2024春 新城区期末)\在如图的三角形中,已知∠1+∠2=122°,∠1+∠3=135°,求∠1的度数。
11.(2024春 青羊区期末)如图,笑笑将一张三角形纸折叠了一个角,求∠1的度数。
12.(2024春 龙华区期末)数学课上,笑笑与同学们正在探究三角形与四边形内角和的问题。
(1)笑笑将任意一个四边形ABCD分成了两个三角形(如图),那么四边形ABCD的内角和是多少度?请写下你的想法。
(2)如图,已知∠F=58°,那么在三角形EFG中∠E+∠G是多少度?若沿图中的虚线MN剪去∠F,则∠1+∠2的度数是多少?
13.(2024春 东阳市期末)如图,直角梯形ABCD中,连接BD,分割成一个直角三角形和一个等腰三角形,请说明∠1=∠2=∠3的理由。
14.(2024春 芮城县期末)小明做了一个支架,如图,你认为这个支架稳固吗?为什么?请你在图中添加一条线段使支架变得相对稳固。
15.(2024春 大安区期末)选择符合条件的一组,并说一说选择理由。
(1)如图 组线段能围成三角形。
选择理由: 。
(2)下面 组是一个三角形的3个内角的度数。
①80°、60°、30°
②45°、60°、65°
③50°、80°、50°
选择理由: 。
16.(2024春 矿区期末)如图,延长三角形ABC的一条边BC到点D,∠ACD叫三角形ABC的一个外角。我们发现∠ACD的度数与三角形内角∠1、∠2的度数之和刚好相等,即∠ACD=∠1+∠2。
你能用所学知识解释这个结论吗?试着说一说。
17.(2024春 惠来县期末)一个三角形中,两个较小角的度数和是80°,两个较大角的度数和是155°。这个三角形三个内角分别是多少度?
18.(2024 江北区)如图1,∠1、∠2、∠3是三角形ABC的三个内角.现将三角形的三条边AB、BC、CA分别延长,形成了∠4、∠5、∠6三个角,这三个角叫三角形的外角,如图2.
不测量,你能推理得出∠4、∠5和∠6这三个外角的和是几度吗?请写出你的思考过程.
19.(2024春 郑州期末)奇奇小组在数学课上用“剪小棒摆三角形”探究三角形有关知识:
他们首先尝试把长度为14厘米的小棒剪成3段(3段的长度均为整厘米数),再把这3段首尾相接摆成一个三角形。(如图,图中每个一样长)
(1)奇奇想到了两种剪法,如图(“”表示剪的位置)。按这两种剪法剪开后的小棒能分别摆成三角形吗?如果能,请在括号里画“√”,如果不能,请在括号里画“×”。
①第一种剪法:
②第二种剪法:
(2)如果先从小棒左边剪下4厘米长的一段作为三角形的一条边,如图(“”表示剪的位置),要想摆成一个三角形,接下来应该从哪里剪开才能得到三角形的另外两条边?请你在图中画“”表示出接下来要剪的位置,并写出你的思考过程。
思考过程: 。
期末必考专题:三角形、平行四边形和梯形(真题汇编)-2024-2025学年数学四年级下册苏教版
参考答案与试题解析
一.解答题(共19小题)
1.(2025春 忠县期末)(1)在点子图中画一个钝角三角形,再把它分成两个直角三角形。
(2)在点子图中画一个等腰直角三角形,并画出斜边上的高。
【解答】解:(1)在点子图中画一个钝角三角形,再把它分成两个直角三角形。如图:
(2)在点子图中画一个等腰直角三角形,并画出斜边上的高。如图:
(画法不唯一)
2.(2025春 龙华区期末)已知∠1=120°,三角形ABC是直角三角形,三角形ABD是等腰三角形,求∠2和∠3的度数。
【解答】解:∠2=( 180°﹣120°)÷2
=60°÷2
=30°
∠3=180°﹣90°﹣30°
=90°﹣30°
=60°
答:∠2是30°,∠3是60°。
3.(2025春 奉化区期末)用18根1厘米长的小棒摆成一个等腰三角形,有几种不同的摆法?请列表说明。
腰/cm
腰/cm
底/cm
能否围成三角形
答:有 4 种不同的摆法。
【解答】解:
腰/cm 5 6 7 8
腰/cm 5 6 7 8
底/cm 8 6 4 3
能否围成三角形 能 能 能 能
因此有4种不同的摆法。
故答案为:4。
4.(2025春 顺德区期末)如图,你能根据已知信息求出∠B的大小吗?
【解答】解:180°﹣110°=70°
180°﹣70°﹣65°=45°
答:∠B的度数是45°。
5.(2025春 昌邑市期末)数学课上,同学们正在进行“剪小棒摆三角形”的探索活动。
他们把长度为13cm的小棒剪成三段(三段的长度均为整厘米数,用表示剪的位置),再把这三段首尾相接摆一个三角形。请你在下面的小棒上剪一剪。
这3根小棒的长度分别是 3 cm、 4 cm、 6 cm。
【解答】解:当三条边为3cm、4cm、6cm时:3+4=7cm,7>6,4﹣3=1cm,1<6,能组成三角形。(答案不唯一)
这3根小棒的长度分别是3cm、4cm、6cm。(答案不唯一)
故答案为:3;4;6。
6.(2025春 博爱县期末)下面是两块三角形的玻璃打碎后留下的部分,它们原来是什么三角形?
【解答】解:180°﹣30°﹣20°=130°
180°﹣50°﹣40°=90°
故答案为:
7.(2024秋 万州区期末)在认识平行四边形时,同学们猜想:平行四边形两组对边分别平行。
明明、天天、乐乐根据猜想展开了验证。
明明:依据在同一平面内 不相交 的两条直线互相平行,将两组对边延长,对边也不会相交的方法进行验证。
天天:依据端点分别在两条平行线上,且与平行线 垂直 的所有线段的长度都 相等 来验证。
乐乐:依据平移三角尺的方法验证了两组对边分别平行。
最后,三人得出相同的结论:平行四边形两组对边分别平行。
【解答】解:明明:依据在同一平面内不相交的两条直线互相平行,将两组对边延长,对边也不会相交的方法进行验证。
天天:依据端点分别在两条平行线上,且与平行线垂直的所有线段的长度都相等来验证。
乐乐:依据平移三角尺的方法验证了两组对边分别平行。
最后,三人得出相同的结论:平行四边形两组对边分别平行。
故答案为:不相交;垂直,相等。
8.(2024春 临潼区期末)先画出下面三角形指定底边上的高,再计算出未知角的度数。
【解答】解:根据分析,作图如下:
(1)180°﹣25°﹣20°
=155°﹣20°
=135°
(2)90°﹣35°=55°
9.(2024春 青岛期末)如图,在直角三角形ABC中,BD是AC边上的高,已知∠1=60°,你能求出∠2的度数吗?
【解答】解:结合图形可知:∠3=90°﹣∠1。
由三角形内角和为180° 可知:
∠2=180°﹣90°﹣∠3。
=90°﹣(90°﹣∠1)
=∠1
=60°
答:∠2的度数是60°。
10.(2024春 新城区期末)\在如图的三角形中,已知∠1+∠2=122°,∠1+∠3=135°,求∠1的度数。
【解答】解:∠3=180°﹣122°
=58°
∠2=180°﹣135°
=45°
则∠1=180°﹣∠2﹣∠3
=180°﹣58°﹣45°
=122°﹣45°
=77°
答:∠1的度数是77°。
11.(2024春 青羊区期末)如图,笑笑将一张三角形纸折叠了一个角,求∠1的度数。
【解答】解:如下图所示:
∠2=180°﹣∠3﹣35°=180°﹣70°=110°
∠1=180°﹣∠2﹣20°=180°﹣110°﹣20°=50°
答:∠1的度数是50°。
12.(2024春 龙华区期末)数学课上,笑笑与同学们正在探究三角形与四边形内角和的问题。
(1)笑笑将任意一个四边形ABCD分成了两个三角形(如图),那么四边形ABCD的内角和是多少度?请写下你的想法。
(2)如图,已知∠F=58°,那么在三角形EFG中∠E+∠G是多少度?若沿图中的虚线MN剪去∠F,则∠1+∠2的度数是多少?
【解答】解:(1)因为三角形的内角和等于180°,四边形分成两个三角形,所以四边形的内角和=180°×2=360°。
(2)因为∠F=58°
所以∠E+∠G=180°﹣58°=122°
∠1+∠2=360°﹣122°=238°
13.(2024春 东阳市期末)如图,直角梯形ABCD中,连接BD,分割成一个直角三角形和一个等腰三角形,请说明∠1=∠2=∠3的理由。
【解答】解:∠BAD=90°,∠ABC=90°
180°﹣∠BAD=90°,∠1+∠ABD=90°,∠2+∠ABD=∠ABC=90°
∠1=∠2
等腰三角形中两个底角相等,所以在三角形BDC中∠2=∠3。
所以∠1=∠2=∠3。
14.(2024春 芮城县期末)小明做了一个支架,如图,你认为这个支架稳固吗?为什么?请你在图中添加一条线段使支架变得相对稳固。
【解答】解:这个支架不稳固,因为平行四边形易变形,不具有稳定性。在图中添加一条线段使支架变得相对稳固。如图:
(画法不唯一,合理即可)
15.(2024春 大安区期末)选择符合条件的一组,并说一说选择理由。
(1)如图 ② 组线段能围成三角形。
选择理由: 符合三角形三边的关系,任意两边之和大于第三边 。
(2)下面 ③ 组是一个三角形的3个内角的度数。
①80°、60°、30°
②45°、60°、65°
③50°、80°、50°
选择理由: 三个角的和是180° 。
【解答】解:(1)①2+4=6(厘米),6厘米<7厘米,所以不能围成三角形;
②4+5=9(厘米);9厘米>8厘米,5+8=13(厘米),13厘米>4厘米,4+8=12(厘米),12厘米>5厘米,能围成三角形;
③5+5=10(厘米),10厘米<12厘米,所以不能围成三角形。
所以②组线段能围成三角形,选择理由:符合三角形三边的关系,任意两边之和大于第三边。
(2)①80°+60°+30°=170°,不满足三角形内角和是180°,所以不是三角形的3个内角;
②45°+60°+65°=170°,不满足三角形内角和是180°,所以不是三角形的3个内角;
③50°+80°+50°=180°,满足三角形内角和定理,所以是三角形的3个内角;
所以③组是一个三角形的3个内角的度数,选择理由:三个角的和是180°。
故答案为:(1)②,符合三角形三边的关系,任意两边之和大于第三边;(2)③,三个角的和是180°。
16.(2024春 矿区期末)如图,延长三角形ABC的一条边BC到点D,∠ACD叫三角形ABC的一个外角。我们发现∠ACD的度数与三角形内角∠1、∠2的度数之和刚好相等,即∠ACD=∠1+∠2。
你能用所学知识解释这个结论吗?试着说一说。
【解答】解:根据图示,结合三角形的内角和是180度,可知∠1+∠2+∠ACB=180°,结合∠ACB和∠ACD是一个平角可知,∠ACB+∠ACD=180°,比较可知∠ACD=∠1+∠2。(合理即可。)
17.(2024春 惠来县期末)一个三角形中,两个较小角的度数和是80°,两个较大角的度数和是155°。这个三角形三个内角分别是多少度?
【解答】解:中间角的度数:80°+155°﹣180°=55°
最小角:80°﹣55°=25°
最大角:155°﹣55°=100°
答:这个三角形三个内角分别是25°,55°,100°。
18.(2024 江北区)如图1,∠1、∠2、∠3是三角形ABC的三个内角.现将三角形的三条边AB、BC、CA分别延长,形成了∠4、∠5、∠6三个角,这三个角叫三角形的外角,如图2.
不测量,你能推理得出∠4、∠5和∠6这三个外角的和是几度吗?请写出你的思考过程.
【解答】解:能推理得出∠4、∠5和∠6这三个外角的和是360°,理由如下:
因为∠1+∠6=180°,∠2+∠4=180°,∠3+∠5=180°
所以∠1+∠2+∠3+∠4+∠5+∠6
=180°×3
=540°
又因为,∠1+∠2+∠3=180°
所以∠4+∠5+∠6
=540°﹣180°
=360°.
19.(2024春 郑州期末)奇奇小组在数学课上用“剪小棒摆三角形”探究三角形有关知识:
他们首先尝试把长度为14厘米的小棒剪成3段(3段的长度均为整厘米数),再把这3段首尾相接摆成一个三角形。(如图,图中每个一样长)
(1)奇奇想到了两种剪法,如图(“”表示剪的位置)。按这两种剪法剪开后的小棒能分别摆成三角形吗?如果能,请在括号里画“√”,如果不能,请在括号里画“×”。
①第一种剪法:
②第二种剪法:
(2)如果先从小棒左边剪下4厘米长的一段作为三角形的一条边,如图(“”表示剪的位置),要想摆成一个三角形,接下来应该从哪里剪开才能得到三角形的另外两条边?请你在图中画“”表示出接下来要剪的位置,并写出你的思考过程。
思考过程: 三角形任意两边之和大于第三边 。
【解答】解:(1)①剪成的三段为7厘米,6厘米,1厘米,6+1=7,所以此种剪法错误,如下图所示:
②剪成的三段为3厘米,5厘米,6厘米,3+5>6,所以此种剪法正确,如下图所示:
(2)14﹣4=10(厘米)
10÷2=5(厘米)
因为4+5>5,所以在9厘米处剪开即可。如下图所示(答案不唯一):
思考过程:三角形任意两边之和大于第三边。
故答案为:三角形任意两边之和大于第三边。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
