期末真题重组检测卷(含解析)-2024-2025学年数学七年级下册苏科版(2024)
文档属性
| 名称 | 期末真题重组检测卷(含解析)-2024-2025学年数学七年级下册苏科版(2024) |  | |
| 格式 | docx | ||
| 文件大小 | 1022.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-09 12:59:08 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
期末真题重组检测卷-2024-2025学年数学七年级下册苏科版(2024)
一.选择题(共10小题)
1.(2024秋 斗门区期末)中国“二十四节气”已被正式列入联合国教科文组织人类非物质文化遗产代表作品录.下面四幅作品分别代表“立春”、“芒种”、“白露”、“大雪”,其中是轴对称图形的是( )
A. B. C. D.
2.(2024秋 湛江校级期末)(﹣2a2)3的计算结果是( )
A.8a6 B.﹣8a6 C.6a6 D.﹣6a6
3.(2024春 宝丰县期末)已知x=1是不等式2x﹣a<0的一个解,则a的值可以是( )
A.0 B.1 C.2 D.3
4.(2024秋 新邵县期末)如果某个二元一次方程组的解中两个未知数的值是互为相反数,我们称这个方程组为“关联方程组”.若关于x,y的方程组是“关联方程组”,则a的值为( )
A.0 B.1 C.2 D.﹣2
5.(2024秋 杭州期末)已知关于x的不等式组,下列四个结论:
①若它的解集是1<x≤3,则a=7;
②当a=3,不等式组有解;
③若它的整数解仅有3个,则a的取值范围是9≤x<11;
④若不等式组有解,则a>3.
其中正确的结论个数( )
A.1个 B.2个 C.3个 D.4个
6.(2025春 河西区校级期末)下列命题是真命题的是( )
A.同位角相等
B.相等的角是对顶角
C.互为相反数的两个数的绝对值相等
D.过一点有且仅有一条直线与已知直线平行
7.(2024秋 玉溪期末)若(x+3)(x﹣4)=x2+mx﹣12,则m的值为( )
A.1 B.﹣1 C.7 D.﹣7
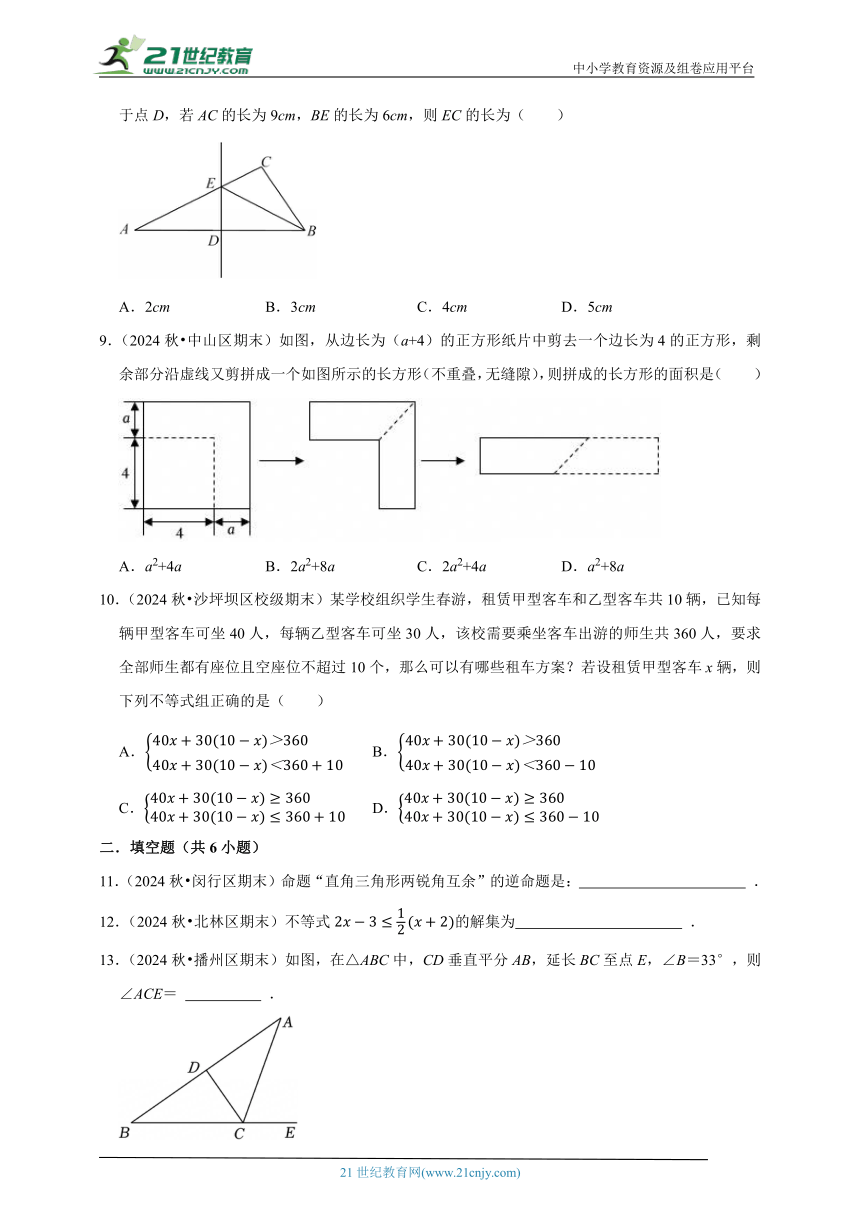
8.(2024秋 福田区期末)如图,在△ABC中,AB边上的垂直平分线分别交边AC于点E,交边AB于点D,若AC的长为9cm,BE的长为6cm,则EC的长为( )
A.2cm B.3cm C.4cm D.5cm
9.(2024秋 中山区期末)如图,从边长为(a+4)的正方形纸片中剪去一个边长为4的正方形,剩余部分沿虚线又剪拼成一个如图所示的长方形(不重叠,无缝隙),则拼成的长方形的面积是( )
A.a2+4a B.2a2+8a C.2a2+4a D.a2+8a
10.(2024秋 沙坪坝区校级期末)某学校组织学生春游,租赁甲型客车和乙型客车共10辆,已知每辆甲型客车可坐40人,每辆乙型客车可坐30人,该校需要乘坐客车出游的师生共360人,要求全部师生都有座位且空座位不超过10个,那么可以有哪些租车方案?若设租赁甲型客车x辆,则下列不等式组正确的是( )
A. B.
C. D.
二.填空题(共6小题)
11.(2024秋 闵行区期末)命题“直角三角形两锐角互余”的逆命题是: .
12.(2024秋 北林区期末)不等式的解集为 .
13.(2024秋 播州区期末)如图,在△ABC中,CD垂直平分AB,延长BC至点E,∠B=33°,则∠ACE= .
14.(2023秋 双辽市期末)一个正方形的边长增加了3cm,面积相应增加了39cm2,则原来这个正方形的边长为 cm.
15.(2022春 台山市期末)已知关于x,y的方程组的解满足x+y>1,则k的取值范围是 .
16.(2024秋 绥化期末)若关于x,y的方程组的解满足y=x+3,则m= .
三.解答题(共8小题)
17.(2024秋 寿县期末)解方程(组):
(1);
(2).
18.(2024秋 鄞州区期末)解不等式组:.
19.(2023秋 夏邑县期末)现有甲种正方形、乙种长方形卡片各若干张,卡片的边长如图所示(a>1).某同学分别拼出了两个长方形(不重叠无缝隙),如图1和图2,其面积分别为S1,S2.
(1)请用含a的式子分别表示S1,S2;
(2)当a=3时,求S1+S2的值.
20.(2024秋 任丘市期末)如图:在△ABC中,AB的垂直平分线EF交BC于点E,交AB于点F,D为线段CE的中点,BE=AC.
(1)求证:AD⊥BC;
(2)若∠B=35°,求∠C的度数.
21.(2024秋 红花岗区期末)2024年12月4日,联合国教科文组织决定将“春节——中国人庆祝传统新年的社会实践”列入人类非物质文化遗产代表作名录.而春节期间带一份包装精美的礼品走亲访友更是一种传统,因此市场上对礼品盒的需求量也随之激增.为了满足市场的需求,遵义市某工厂计划制作一批圆柱形礼品盒,已知该工厂共有90名工人,其中女工人数比男工人数的3倍少10名,并且每名工人平均每天可以制作这种礼品盒的盒身400个或盒底1000个.
(1)该工厂有男工、女工各多少名?
(2)该工厂计划安排一部分工人负责制作盒身,另一部分工人负责制作盒底,要求一个盒身配两个盒底,那么应安排制作盒身和盒底的工人各多少名,才能使每天生产的产品刚好配套?
22.(2024秋 龙泉市期末)在平面直角坐标系中,已知△ABC的三个顶点坐标分别是A(3,2),B(﹣1,4),C(4,4).
(1)在如图中作出△ABC.
(2)把△ABC向下平移5个单位,再向左平移2个单位,作出△ABC平移后的△A′B′C′,并写出点A′的坐标.
23.(2024秋 禅城区期末)为打造一河两岸景观带,需对一段长350米的河边道路进行整治,任务由A,B两个工程队先后接力完成,A工程队每天整治15米,B工程队每天整治10米,共用时30天,求两工程队用时的天数.
(1)根据题意,甲、乙两位同学分别列出了如下不完整的方程组:
甲:
乙:
根据甲、乙两同学所列的方程组,指出未知数x的含义:
甲:x表示 ;乙:x表示 .
(2)从上述方程组中任选一组,将其补全,解答问题.
24.(2024秋 茌平区期末)阅读下面材料:利用折纸可以作出角平分线.
(1)如图1,若∠AOB=58°,则∠BOC= °;
(2)折叠长方形纸片,BC,BD均为折痕,折叠后,点A落在点A′,点E落在点E′.
①如图2,当点E′在BA′上时,求∠CBD的度数;
②如图3,若∠A′BE′=44°,求∠CBD的度数;
③如图4,若∠A′CB=32°,∠A′BE′=n°,则∠DBE′的度数为 °(用含n的式子表示).
期末真题重组检测卷-2024-2025学年数学七年级下册苏科版(2024)
参考答案与试题解析
一.选择题(共10小题)
题号 1 2 3 4 5 6 7 8 9 10
答案 D B D D C C B B D C
一.选择题(共10小题)
1.(2024秋 斗门区期末)中国“二十四节气”已被正式列入联合国教科文组织人类非物质文化遗产代表作品录.下面四幅作品分别代表“立春”、“芒种”、“白露”、“大雪”,其中是轴对称图形的是( )
A. B. C. D.
【解答】解:A、不是轴对称图形,故本选项不符合题意;
B、不是轴对称图形,故本选项不符合题意;
C、不是轴对称图形,故本选项不符合题意;
D、是轴对称图形,故本选项符合题意.
故选:D.
2.(2024秋 湛江校级期末)(﹣2a2)3的计算结果是( )
A.8a6 B.﹣8a6 C.6a6 D.﹣6a6
【解答】解:(﹣2a2)3=(﹣2)3a6=﹣8a6.
故选:B.
3.(2024春 宝丰县期末)已知x=1是不等式2x﹣a<0的一个解,则a的值可以是( )
A.0 B.1 C.2 D.3
【解答】解:∵x=1是不等式2x﹣a<0的一个解,
∴2﹣a<0,
∴a>2,
∴a的值可以是3.
故选:D.
4.(2024秋 新邵县期末)如果某个二元一次方程组的解中两个未知数的值是互为相反数,我们称这个方程组为“关联方程组”.若关于x,y的方程组是“关联方程组”,则a的值为( )
A.0 B.1 C.2 D.﹣2
【解答】解:由题意得,x+y=0,
,
①+②得,2x+2y=4+2a,
即x+y=2+a,
由于x+y=0,
所以2+a=0,
解得a=﹣2,
故选:D.
5.(2024秋 杭州期末)已知关于x的不等式组,下列四个结论:
①若它的解集是1<x≤3,则a=7;
②当a=3,不等式组有解;
③若它的整数解仅有3个,则a的取值范围是9≤x<11;
④若不等式组有解,则a>3.
其中正确的结论个数( )
A.1个 B.2个 C.3个 D.4个
【解答】解:解不等式x2得:x>1,
解不等式2x﹣a≤﹣1得:,
∵若它的解集是1<x≤3,即,解得:a=7,
∴①正确,
∵当a=3,x≤1,即不等式组无解,
∴②错误,
∵若它的整数解仅有3个,即,
∴a的取值范围是9≤a<11,
∴③正确,
∵若不等式组有解,即1,则a>3,
∴④正确,
故选:C.
6.(2025春 河西区校级期末)下列命题是真命题的是( )
A.同位角相等
B.相等的角是对顶角
C.互为相反数的两个数的绝对值相等
D.过一点有且仅有一条直线与已知直线平行
【解答】解:A、两直线平行,同位角相等,故本选项命题是假命题,不符合题意;
B、相等的角不一定是对顶角,故本选项命题是假命题,不符合题意;
C、互为相反数的两个数的绝对值相等,是真命题,符合题意;
D、过直线外一点有且仅有一条直线与已知直线平行,故本选项命题是假命题,不符合题意;
故选:C.
7.(2024秋 玉溪期末)若(x+3)(x﹣4)=x2+mx﹣12,则m的值为( )
A.1 B.﹣1 C.7 D.﹣7
【解答】解:根据多项式乘多项式法则可得:
(x+3)(x﹣4)=x2﹣x﹣12=x2+mx﹣12,
∴m=﹣1;
故选:B.
8.(2024秋 福田区期末)如图,在△ABC中,AB边上的垂直平分线分别交边AC于点E,交边AB于点D,若AC的长为9cm,BE的长为6cm,则EC的长为( )
A.2cm B.3cm C.4cm D.5cm
【解答】解:∵DE是AB边上的垂直平分线,BE=6cm,
∴AE=BE=6cm,
∴EC=AC﹣EA=9﹣6=3(cm),
故选:B.
9.(2024秋 中山区期末)如图,从边长为(a+4)的正方形纸片中剪去一个边长为4的正方形,剩余部分沿虚线又剪拼成一个如图所示的长方形(不重叠,无缝隙),则拼成的长方形的面积是( )
A.a2+4a B.2a2+8a C.2a2+4a D.a2+8a
【解答】解:拼成的长方形的长为a+4+4=a+8,宽为a,因此面积为a(a+8)=a2+8a,
故选:D.
10.(2024秋 沙坪坝区校级期末)某学校组织学生春游,租赁甲型客车和乙型客车共10辆,已知每辆甲型客车可坐40人,每辆乙型客车可坐30人,该校需要乘坐客车出游的师生共360人,要求全部师生都有座位且空座位不超过10个,那么可以有哪些租车方案?若设租赁甲型客车x辆,则下列不等式组正确的是( )
A.
B.
C.
D.
【解答】解:设租赁甲型客车x辆,则租赁乙型客车(10﹣x)辆,
根据题意得,
故选:C.
二.填空题(共6小题)
11.(2024秋 闵行区期末)命题“直角三角形两锐角互余”的逆命题是: 如果三角形有两个锐角互余,那么这个三角形是直角三角形 .
【解答】解:因为“直角三角形两锐角互余”的题设是“三角形是直角三角形”,结论是“两个锐角互余”,
所以逆命题是:“如果三角形有两个锐角互余,那么这个三角形是直角三角形”.
故答案为:如果三角形有两个锐角互余,那么这个三角形是直角三角形.
12.(2024秋 北林区期末)不等式的解集为 x .
【解答】解:2x﹣3,
4x﹣6≤x+2,
4x﹣x≤2+6,
3x≤8,
x.
故答案为:x.
13.(2024秋 播州区期末)如图,在△ABC中,CD垂直平分AB,延长BC至点E,∠B=33°,则∠ACE= 66° .
【解答】解:∵CD垂直平分AB,
∴BC=AC,
∴∠A=∠B=33°,
∴∠ACE=∠A+∠B=66°.
故答案为:66°.
14.(2023秋 双辽市期末)一个正方形的边长增加了3cm,面积相应增加了39cm2,则原来这个正方形的边长为 5 cm.
【解答】解:设原来正方形的边长是xcm.根据题意得:
(x+3)2﹣x2=39,
∴(x+3+x)(x+3﹣x)=3(2x+3)=39,
解得x=5.
15.(2022春 台山市期末)已知关于x,y的方程组的解满足x+y>1,则k的取值范围是 k>4 .
【解答】解:,
①+②得:3x+3y=2k﹣1﹣4,
即:;
∵x+y>1,
∴,解得:k>4;
故答案为:k>4.
16.(2024秋 绥化期末)若关于x,y的方程组的解满足y=x+3,则m= ﹣2 .
【解答】解:,
①+②得:5x+5y=9③,
把y=x+3代入③得:5x+5(x+3)=9,
5x+5x+15=9,
10x=﹣6,
x=﹣0.6,
把x=﹣0.6代入y=x+3得:y=2.4,
把x=﹣0.6和y=2.4代入②得:m=﹣2,
故答案为:﹣2.
三.解答题(共8小题)
17.(2024秋 寿县期末)解方程(组):
(1);
(2).
【解答】解:(1),
去分母,得6x﹣2(x﹣1)=3(2x+1),
去括号,得6x﹣2x+2=6x+3,
移项,得6x﹣2x﹣6x=﹣2+3,
合并同类项,得﹣2x=1,
系数化1,得;
(2),
则②×2﹣①,得x=14﹣9=5,
把x=5代入②,得10+y=7,
解得y=﹣3,
∴方程组的解为.
18.(2024秋 鄞州区期末)解不等式组:.
【解答】解:,
解不等式①得:x>﹣2,
解不等式②得:x≤﹣1.
∴原不等式组的解集是:﹣2<x≤﹣1.
19.(2023秋 夏邑县期末)现有甲种正方形、乙种长方形卡片各若干张,卡片的边长如图所示(a>1).某同学分别拼出了两个长方形(不重叠无缝隙),如图1和图2,其面积分别为S1,S2.
(1)请用含a的式子分别表示S1,S2;
(2)当a=3时,求S1+S2的值.
【解答】解:(1)由题意得,
S1=(a+a)(a+1)
=2a(a+1)
=2a2+2a,
S2=a(a+4)=a2+4a,
即S1=2a2+2a,S2=a2+4a;
(2)由(1)题可得,
S1+S2=2a2+2a+a2+4a
=3a2+6a,
当a=3时,
S1+S2=3×32+6×3
=3×9+18
=27+18
=45.
20.(2024秋 任丘市期末)如图:在△ABC中,AB的垂直平分线EF交BC于点E,交AB于点F,D为线段CE的中点,BE=AC.
(1)求证:AD⊥BC;
(2)若∠B=35°,求∠C的度数.
【解答】(1)证明:连接AE,
∵AB的垂直平分线EF交BC于点E,
∴BE=AE,
∵AC=BE,
∴AC=AE,
∵D为线段CE的中点,
∴AD⊥BC.
(2)解:∵BE=AE,
∴∠B=∠BAE=35°,
∴∠AEC=2∠B=70°,
∵AE=AC,
∴∠C=∠AEC=2∠B=70°.
21.(2024秋 红花岗区期末)2024年12月4日,联合国教科文组织决定将“春节——中国人庆祝传统新年的社会实践”列入人类非物质文化遗产代表作名录.而春节期间带一份包装精美的礼品走亲访友更是一种传统,因此市场上对礼品盒的需求量也随之激增.为了满足市场的需求,遵义市某工厂计划制作一批圆柱形礼品盒,已知该工厂共有90名工人,其中女工人数比男工人数的3倍少10名,并且每名工人平均每天可以制作这种礼品盒的盒身400个或盒底1000个.
(1)该工厂有男工、女工各多少名?
(2)该工厂计划安排一部分工人负责制作盒身,另一部分工人负责制作盒底,要求一个盒身配两个盒底,那么应安排制作盒身和盒底的工人各多少名,才能使每天生产的产品刚好配套?
【解答】解:(1)设该工厂有男工x人,则有女工(90﹣x)人,
根据题意得:90﹣x=3x﹣10,
解得:x=25,
∴90﹣x=90﹣25=65(人).
答:该工厂有男工25人,女工65人;
(2)设y名工人制作盒身,才能使每天制作的盒身与盒底恰好配套,
根据题意得:2×400y=1000(90﹣y),
解得:y=50.
90﹣y=40(名),
答:50名工人制作盒身,40名工人制作盒底,才能使每小时制作的盒身与盒底恰好配套.
22.(2024秋 龙泉市期末)在平面直角坐标系中,已知△ABC的三个顶点坐标分别是A(3,2),B(﹣1,4),C(4,4).
(1)在如图中作出△ABC.
(2)把△ABC向下平移5个单位,再向左平移2个单位,作出△ABC平移后的△A′B′C′,并写出点A′的坐标.
【解答】解:(1)如图,△ABC即为所求;
(2)△A′B′C′为所求作,A′(1,﹣3).
23.(2024秋 禅城区期末)为打造一河两岸景观带,需对一段长350米的河边道路进行整治,任务由A,B两个工程队先后接力完成,A工程队每天整治15米,B工程队每天整治10米,共用时30天,求两工程队用时的天数.
(1)根据题意,甲、乙两位同学分别列出了如下不完整的方程组:
甲:
乙:
根据甲、乙两同学所列的方程组,指出未知数x的含义:
甲:x表示 A工程队用时的天数 ;乙:x表示 A工程队整治道路的总长度 .
(2)从上述方程组中任选一组,将其补全,解答问题.
【解答】解:(1)甲:,
乙:,
甲:x表示A工程队用时的天数;
乙:x表示A工程队整治道路的总长度.
故答案为:A工程队用时的天数;A工程队整治道路的总长度;
(2)选第一种:
,
解得.
答:A工程队用时10天,B工程队用时20天;
选第二种;
,
解得:,
A工程队用时:150÷15=10.
B工程队用时:200÷10=20.
答:A工程队用时10天,B工程队用时20天.
24.(2024秋 茌平区期末)阅读下面材料:利用折纸可以作出角平分线.
(1)如图1,若∠AOB=58°,则∠BOC= 29 °;
(2)折叠长方形纸片,BC,BD均为折痕,折叠后,点A落在点A′,点E落在点E′.
①如图2,当点E′在BA′上时,求∠CBD的度数;
②如图3,若∠A′BE′=44°,求∠CBD的度数;
③如图4,若∠A′CB=32°,∠A′BE′=n°,则∠DBE′的度数为 °(用含n的式子表示).
【解答】解:(1)∵∠AOB=58°,
由折叠知,;
(2)①由折叠知,,,
∴当点E′在BA′上时,
;
②由条件可知∠ABA′+∠EBE′=180°﹣∠A′BE′=136°,
由折叠知,,,
∴,
∴∠CBD=∠CBA′+DBE′+∠A′BE′=58°+44°=112°;
③∵∠A′CB=32°,
∴由折叠得,∠ACB=∠A′CB=32°,
∴∠ABC=90°﹣∠ACB=58°,
∴由折叠得,∠ABA′=2∠ABC=116°,
∴EBE′=180°+∠A′BE′﹣∠ABA′=180°+n°﹣116°=n°+64°,
∴由折叠得,.
故答案为:.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末真题重组检测卷-2024-2025学年数学七年级下册苏科版(2024)
一.选择题(共10小题)
1.(2024秋 斗门区期末)中国“二十四节气”已被正式列入联合国教科文组织人类非物质文化遗产代表作品录.下面四幅作品分别代表“立春”、“芒种”、“白露”、“大雪”,其中是轴对称图形的是( )
A. B. C. D.
2.(2024秋 湛江校级期末)(﹣2a2)3的计算结果是( )
A.8a6 B.﹣8a6 C.6a6 D.﹣6a6
3.(2024春 宝丰县期末)已知x=1是不等式2x﹣a<0的一个解,则a的值可以是( )
A.0 B.1 C.2 D.3
4.(2024秋 新邵县期末)如果某个二元一次方程组的解中两个未知数的值是互为相反数,我们称这个方程组为“关联方程组”.若关于x,y的方程组是“关联方程组”,则a的值为( )
A.0 B.1 C.2 D.﹣2
5.(2024秋 杭州期末)已知关于x的不等式组,下列四个结论:
①若它的解集是1<x≤3,则a=7;
②当a=3,不等式组有解;
③若它的整数解仅有3个,则a的取值范围是9≤x<11;
④若不等式组有解,则a>3.
其中正确的结论个数( )
A.1个 B.2个 C.3个 D.4个
6.(2025春 河西区校级期末)下列命题是真命题的是( )
A.同位角相等
B.相等的角是对顶角
C.互为相反数的两个数的绝对值相等
D.过一点有且仅有一条直线与已知直线平行
7.(2024秋 玉溪期末)若(x+3)(x﹣4)=x2+mx﹣12,则m的值为( )
A.1 B.﹣1 C.7 D.﹣7
8.(2024秋 福田区期末)如图,在△ABC中,AB边上的垂直平分线分别交边AC于点E,交边AB于点D,若AC的长为9cm,BE的长为6cm,则EC的长为( )
A.2cm B.3cm C.4cm D.5cm
9.(2024秋 中山区期末)如图,从边长为(a+4)的正方形纸片中剪去一个边长为4的正方形,剩余部分沿虚线又剪拼成一个如图所示的长方形(不重叠,无缝隙),则拼成的长方形的面积是( )
A.a2+4a B.2a2+8a C.2a2+4a D.a2+8a
10.(2024秋 沙坪坝区校级期末)某学校组织学生春游,租赁甲型客车和乙型客车共10辆,已知每辆甲型客车可坐40人,每辆乙型客车可坐30人,该校需要乘坐客车出游的师生共360人,要求全部师生都有座位且空座位不超过10个,那么可以有哪些租车方案?若设租赁甲型客车x辆,则下列不等式组正确的是( )
A. B.
C. D.
二.填空题(共6小题)
11.(2024秋 闵行区期末)命题“直角三角形两锐角互余”的逆命题是: .
12.(2024秋 北林区期末)不等式的解集为 .
13.(2024秋 播州区期末)如图,在△ABC中,CD垂直平分AB,延长BC至点E,∠B=33°,则∠ACE= .
14.(2023秋 双辽市期末)一个正方形的边长增加了3cm,面积相应增加了39cm2,则原来这个正方形的边长为 cm.
15.(2022春 台山市期末)已知关于x,y的方程组的解满足x+y>1,则k的取值范围是 .
16.(2024秋 绥化期末)若关于x,y的方程组的解满足y=x+3,则m= .
三.解答题(共8小题)
17.(2024秋 寿县期末)解方程(组):
(1);
(2).
18.(2024秋 鄞州区期末)解不等式组:.
19.(2023秋 夏邑县期末)现有甲种正方形、乙种长方形卡片各若干张,卡片的边长如图所示(a>1).某同学分别拼出了两个长方形(不重叠无缝隙),如图1和图2,其面积分别为S1,S2.
(1)请用含a的式子分别表示S1,S2;
(2)当a=3时,求S1+S2的值.
20.(2024秋 任丘市期末)如图:在△ABC中,AB的垂直平分线EF交BC于点E,交AB于点F,D为线段CE的中点,BE=AC.
(1)求证:AD⊥BC;
(2)若∠B=35°,求∠C的度数.
21.(2024秋 红花岗区期末)2024年12月4日,联合国教科文组织决定将“春节——中国人庆祝传统新年的社会实践”列入人类非物质文化遗产代表作名录.而春节期间带一份包装精美的礼品走亲访友更是一种传统,因此市场上对礼品盒的需求量也随之激增.为了满足市场的需求,遵义市某工厂计划制作一批圆柱形礼品盒,已知该工厂共有90名工人,其中女工人数比男工人数的3倍少10名,并且每名工人平均每天可以制作这种礼品盒的盒身400个或盒底1000个.
(1)该工厂有男工、女工各多少名?
(2)该工厂计划安排一部分工人负责制作盒身,另一部分工人负责制作盒底,要求一个盒身配两个盒底,那么应安排制作盒身和盒底的工人各多少名,才能使每天生产的产品刚好配套?
22.(2024秋 龙泉市期末)在平面直角坐标系中,已知△ABC的三个顶点坐标分别是A(3,2),B(﹣1,4),C(4,4).
(1)在如图中作出△ABC.
(2)把△ABC向下平移5个单位,再向左平移2个单位,作出△ABC平移后的△A′B′C′,并写出点A′的坐标.
23.(2024秋 禅城区期末)为打造一河两岸景观带,需对一段长350米的河边道路进行整治,任务由A,B两个工程队先后接力完成,A工程队每天整治15米,B工程队每天整治10米,共用时30天,求两工程队用时的天数.
(1)根据题意,甲、乙两位同学分别列出了如下不完整的方程组:
甲:
乙:
根据甲、乙两同学所列的方程组,指出未知数x的含义:
甲:x表示 ;乙:x表示 .
(2)从上述方程组中任选一组,将其补全,解答问题.
24.(2024秋 茌平区期末)阅读下面材料:利用折纸可以作出角平分线.
(1)如图1,若∠AOB=58°,则∠BOC= °;
(2)折叠长方形纸片,BC,BD均为折痕,折叠后,点A落在点A′,点E落在点E′.
①如图2,当点E′在BA′上时,求∠CBD的度数;
②如图3,若∠A′BE′=44°,求∠CBD的度数;
③如图4,若∠A′CB=32°,∠A′BE′=n°,则∠DBE′的度数为 °(用含n的式子表示).
期末真题重组检测卷-2024-2025学年数学七年级下册苏科版(2024)
参考答案与试题解析
一.选择题(共10小题)
题号 1 2 3 4 5 6 7 8 9 10
答案 D B D D C C B B D C
一.选择题(共10小题)
1.(2024秋 斗门区期末)中国“二十四节气”已被正式列入联合国教科文组织人类非物质文化遗产代表作品录.下面四幅作品分别代表“立春”、“芒种”、“白露”、“大雪”,其中是轴对称图形的是( )
A. B. C. D.
【解答】解:A、不是轴对称图形,故本选项不符合题意;
B、不是轴对称图形,故本选项不符合题意;
C、不是轴对称图形,故本选项不符合题意;
D、是轴对称图形,故本选项符合题意.
故选:D.
2.(2024秋 湛江校级期末)(﹣2a2)3的计算结果是( )
A.8a6 B.﹣8a6 C.6a6 D.﹣6a6
【解答】解:(﹣2a2)3=(﹣2)3a6=﹣8a6.
故选:B.
3.(2024春 宝丰县期末)已知x=1是不等式2x﹣a<0的一个解,则a的值可以是( )
A.0 B.1 C.2 D.3
【解答】解:∵x=1是不等式2x﹣a<0的一个解,
∴2﹣a<0,
∴a>2,
∴a的值可以是3.
故选:D.
4.(2024秋 新邵县期末)如果某个二元一次方程组的解中两个未知数的值是互为相反数,我们称这个方程组为“关联方程组”.若关于x,y的方程组是“关联方程组”,则a的值为( )
A.0 B.1 C.2 D.﹣2
【解答】解:由题意得,x+y=0,
,
①+②得,2x+2y=4+2a,
即x+y=2+a,
由于x+y=0,
所以2+a=0,
解得a=﹣2,
故选:D.
5.(2024秋 杭州期末)已知关于x的不等式组,下列四个结论:
①若它的解集是1<x≤3,则a=7;
②当a=3,不等式组有解;
③若它的整数解仅有3个,则a的取值范围是9≤x<11;
④若不等式组有解,则a>3.
其中正确的结论个数( )
A.1个 B.2个 C.3个 D.4个
【解答】解:解不等式x2得:x>1,
解不等式2x﹣a≤﹣1得:,
∵若它的解集是1<x≤3,即,解得:a=7,
∴①正确,
∵当a=3,x≤1,即不等式组无解,
∴②错误,
∵若它的整数解仅有3个,即,
∴a的取值范围是9≤a<11,
∴③正确,
∵若不等式组有解,即1,则a>3,
∴④正确,
故选:C.
6.(2025春 河西区校级期末)下列命题是真命题的是( )
A.同位角相等
B.相等的角是对顶角
C.互为相反数的两个数的绝对值相等
D.过一点有且仅有一条直线与已知直线平行
【解答】解:A、两直线平行,同位角相等,故本选项命题是假命题,不符合题意;
B、相等的角不一定是对顶角,故本选项命题是假命题,不符合题意;
C、互为相反数的两个数的绝对值相等,是真命题,符合题意;
D、过直线外一点有且仅有一条直线与已知直线平行,故本选项命题是假命题,不符合题意;
故选:C.
7.(2024秋 玉溪期末)若(x+3)(x﹣4)=x2+mx﹣12,则m的值为( )
A.1 B.﹣1 C.7 D.﹣7
【解答】解:根据多项式乘多项式法则可得:
(x+3)(x﹣4)=x2﹣x﹣12=x2+mx﹣12,
∴m=﹣1;
故选:B.
8.(2024秋 福田区期末)如图,在△ABC中,AB边上的垂直平分线分别交边AC于点E,交边AB于点D,若AC的长为9cm,BE的长为6cm,则EC的长为( )
A.2cm B.3cm C.4cm D.5cm
【解答】解:∵DE是AB边上的垂直平分线,BE=6cm,
∴AE=BE=6cm,
∴EC=AC﹣EA=9﹣6=3(cm),
故选:B.
9.(2024秋 中山区期末)如图,从边长为(a+4)的正方形纸片中剪去一个边长为4的正方形,剩余部分沿虚线又剪拼成一个如图所示的长方形(不重叠,无缝隙),则拼成的长方形的面积是( )
A.a2+4a B.2a2+8a C.2a2+4a D.a2+8a
【解答】解:拼成的长方形的长为a+4+4=a+8,宽为a,因此面积为a(a+8)=a2+8a,
故选:D.
10.(2024秋 沙坪坝区校级期末)某学校组织学生春游,租赁甲型客车和乙型客车共10辆,已知每辆甲型客车可坐40人,每辆乙型客车可坐30人,该校需要乘坐客车出游的师生共360人,要求全部师生都有座位且空座位不超过10个,那么可以有哪些租车方案?若设租赁甲型客车x辆,则下列不等式组正确的是( )
A.
B.
C.
D.
【解答】解:设租赁甲型客车x辆,则租赁乙型客车(10﹣x)辆,
根据题意得,
故选:C.
二.填空题(共6小题)
11.(2024秋 闵行区期末)命题“直角三角形两锐角互余”的逆命题是: 如果三角形有两个锐角互余,那么这个三角形是直角三角形 .
【解答】解:因为“直角三角形两锐角互余”的题设是“三角形是直角三角形”,结论是“两个锐角互余”,
所以逆命题是:“如果三角形有两个锐角互余,那么这个三角形是直角三角形”.
故答案为:如果三角形有两个锐角互余,那么这个三角形是直角三角形.
12.(2024秋 北林区期末)不等式的解集为 x .
【解答】解:2x﹣3,
4x﹣6≤x+2,
4x﹣x≤2+6,
3x≤8,
x.
故答案为:x.
13.(2024秋 播州区期末)如图,在△ABC中,CD垂直平分AB,延长BC至点E,∠B=33°,则∠ACE= 66° .
【解答】解:∵CD垂直平分AB,
∴BC=AC,
∴∠A=∠B=33°,
∴∠ACE=∠A+∠B=66°.
故答案为:66°.
14.(2023秋 双辽市期末)一个正方形的边长增加了3cm,面积相应增加了39cm2,则原来这个正方形的边长为 5 cm.
【解答】解:设原来正方形的边长是xcm.根据题意得:
(x+3)2﹣x2=39,
∴(x+3+x)(x+3﹣x)=3(2x+3)=39,
解得x=5.
15.(2022春 台山市期末)已知关于x,y的方程组的解满足x+y>1,则k的取值范围是 k>4 .
【解答】解:,
①+②得:3x+3y=2k﹣1﹣4,
即:;
∵x+y>1,
∴,解得:k>4;
故答案为:k>4.
16.(2024秋 绥化期末)若关于x,y的方程组的解满足y=x+3,则m= ﹣2 .
【解答】解:,
①+②得:5x+5y=9③,
把y=x+3代入③得:5x+5(x+3)=9,
5x+5x+15=9,
10x=﹣6,
x=﹣0.6,
把x=﹣0.6代入y=x+3得:y=2.4,
把x=﹣0.6和y=2.4代入②得:m=﹣2,
故答案为:﹣2.
三.解答题(共8小题)
17.(2024秋 寿县期末)解方程(组):
(1);
(2).
【解答】解:(1),
去分母,得6x﹣2(x﹣1)=3(2x+1),
去括号,得6x﹣2x+2=6x+3,
移项,得6x﹣2x﹣6x=﹣2+3,
合并同类项,得﹣2x=1,
系数化1,得;
(2),
则②×2﹣①,得x=14﹣9=5,
把x=5代入②,得10+y=7,
解得y=﹣3,
∴方程组的解为.
18.(2024秋 鄞州区期末)解不等式组:.
【解答】解:,
解不等式①得:x>﹣2,
解不等式②得:x≤﹣1.
∴原不等式组的解集是:﹣2<x≤﹣1.
19.(2023秋 夏邑县期末)现有甲种正方形、乙种长方形卡片各若干张,卡片的边长如图所示(a>1).某同学分别拼出了两个长方形(不重叠无缝隙),如图1和图2,其面积分别为S1,S2.
(1)请用含a的式子分别表示S1,S2;
(2)当a=3时,求S1+S2的值.
【解答】解:(1)由题意得,
S1=(a+a)(a+1)
=2a(a+1)
=2a2+2a,
S2=a(a+4)=a2+4a,
即S1=2a2+2a,S2=a2+4a;
(2)由(1)题可得,
S1+S2=2a2+2a+a2+4a
=3a2+6a,
当a=3时,
S1+S2=3×32+6×3
=3×9+18
=27+18
=45.
20.(2024秋 任丘市期末)如图:在△ABC中,AB的垂直平分线EF交BC于点E,交AB于点F,D为线段CE的中点,BE=AC.
(1)求证:AD⊥BC;
(2)若∠B=35°,求∠C的度数.
【解答】(1)证明:连接AE,
∵AB的垂直平分线EF交BC于点E,
∴BE=AE,
∵AC=BE,
∴AC=AE,
∵D为线段CE的中点,
∴AD⊥BC.
(2)解:∵BE=AE,
∴∠B=∠BAE=35°,
∴∠AEC=2∠B=70°,
∵AE=AC,
∴∠C=∠AEC=2∠B=70°.
21.(2024秋 红花岗区期末)2024年12月4日,联合国教科文组织决定将“春节——中国人庆祝传统新年的社会实践”列入人类非物质文化遗产代表作名录.而春节期间带一份包装精美的礼品走亲访友更是一种传统,因此市场上对礼品盒的需求量也随之激增.为了满足市场的需求,遵义市某工厂计划制作一批圆柱形礼品盒,已知该工厂共有90名工人,其中女工人数比男工人数的3倍少10名,并且每名工人平均每天可以制作这种礼品盒的盒身400个或盒底1000个.
(1)该工厂有男工、女工各多少名?
(2)该工厂计划安排一部分工人负责制作盒身,另一部分工人负责制作盒底,要求一个盒身配两个盒底,那么应安排制作盒身和盒底的工人各多少名,才能使每天生产的产品刚好配套?
【解答】解:(1)设该工厂有男工x人,则有女工(90﹣x)人,
根据题意得:90﹣x=3x﹣10,
解得:x=25,
∴90﹣x=90﹣25=65(人).
答:该工厂有男工25人,女工65人;
(2)设y名工人制作盒身,才能使每天制作的盒身与盒底恰好配套,
根据题意得:2×400y=1000(90﹣y),
解得:y=50.
90﹣y=40(名),
答:50名工人制作盒身,40名工人制作盒底,才能使每小时制作的盒身与盒底恰好配套.
22.(2024秋 龙泉市期末)在平面直角坐标系中,已知△ABC的三个顶点坐标分别是A(3,2),B(﹣1,4),C(4,4).
(1)在如图中作出△ABC.
(2)把△ABC向下平移5个单位,再向左平移2个单位,作出△ABC平移后的△A′B′C′,并写出点A′的坐标.
【解答】解:(1)如图,△ABC即为所求;
(2)△A′B′C′为所求作,A′(1,﹣3).
23.(2024秋 禅城区期末)为打造一河两岸景观带,需对一段长350米的河边道路进行整治,任务由A,B两个工程队先后接力完成,A工程队每天整治15米,B工程队每天整治10米,共用时30天,求两工程队用时的天数.
(1)根据题意,甲、乙两位同学分别列出了如下不完整的方程组:
甲:
乙:
根据甲、乙两同学所列的方程组,指出未知数x的含义:
甲:x表示 A工程队用时的天数 ;乙:x表示 A工程队整治道路的总长度 .
(2)从上述方程组中任选一组,将其补全,解答问题.
【解答】解:(1)甲:,
乙:,
甲:x表示A工程队用时的天数;
乙:x表示A工程队整治道路的总长度.
故答案为:A工程队用时的天数;A工程队整治道路的总长度;
(2)选第一种:
,
解得.
答:A工程队用时10天,B工程队用时20天;
选第二种;
,
解得:,
A工程队用时:150÷15=10.
B工程队用时:200÷10=20.
答:A工程队用时10天,B工程队用时20天.
24.(2024秋 茌平区期末)阅读下面材料:利用折纸可以作出角平分线.
(1)如图1,若∠AOB=58°,则∠BOC= 29 °;
(2)折叠长方形纸片,BC,BD均为折痕,折叠后,点A落在点A′,点E落在点E′.
①如图2,当点E′在BA′上时,求∠CBD的度数;
②如图3,若∠A′BE′=44°,求∠CBD的度数;
③如图4,若∠A′CB=32°,∠A′BE′=n°,则∠DBE′的度数为 °(用含n的式子表示).
【解答】解:(1)∵∠AOB=58°,
由折叠知,;
(2)①由折叠知,,,
∴当点E′在BA′上时,
;
②由条件可知∠ABA′+∠EBE′=180°﹣∠A′BE′=136°,
由折叠知,,,
∴,
∴∠CBD=∠CBA′+DBE′+∠A′BE′=58°+44°=112°;
③∵∠A′CB=32°,
∴由折叠得,∠ACB=∠A′CB=32°,
∴∠ABC=90°﹣∠ACB=58°,
∴由折叠得,∠ABA′=2∠ABC=116°,
∴EBE′=180°+∠A′BE′﹣∠ABA′=180°+n°﹣116°=n°+64°,
∴由折叠得,.
故答案为:.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
