期末真题重组检测卷(含解析)-2024-2025学年数学七年级下册北师大版(2024)
文档属性
| 名称 | 期末真题重组检测卷(含解析)-2024-2025学年数学七年级下册北师大版(2024) |  | |
| 格式 | docx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-09 13:04:28 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
期末真题重组检测卷-2024-2025学年数学七年级下册北师大版(2024)
一.选择题(共10小题)
1.(2024秋 大余县期末)石墨烯具有优异的光学、电学、力学特性,在材料学、微纳加工、能源、生物医学和药物传递等方面具有重要的应用前景,被认为是一种未来革命性的材料,石墨烯中每两个相邻碳原子间的键长为0.000000000142米,数字“0.000000000142”用科学记数法表示为( )
A.1.42×10﹣9 B.1.42×10﹣10
C.0.142×10﹣9 D.1.42×10﹣11
2.(2024秋 西山区期末)斐波那契螺旋线也称为“黄金螺旋线”,是根据斐波那契数列画出来的螺旋曲线,自然界中存在许多斐波那契螺旋线图案.下列斐波那契螺旋线图案中属于轴对称图形的是( )
A. B.
C. D.
3.(2024秋 文昌期末)下列计算正确的是( )
A.a2+a2=a4 B.a3 a2=a6 C.a6÷a2=a3 D.(a3)3=a9
4.(2024秋 徐水区期末)如图,点E,C,F,B在一条直线上,AB∥ED,∠A=∠D,添加下列条件不能判定△ABC≌△DEF的是( )
A.AC∥DF B.AB=DE C.EC=BF D.AC=DF
5.(2024秋 阳江期末)汉语是中华民族智慧的结晶,成语又是汉语中的精华,是中华文化的一大瑰宝,具有极强的表现力.下列成语描述的事件属于随机事件的是( )
A.旭日东升 B.画饼充饥 C.守株待兔 D.竹篮打水
6.(2024秋 重庆期末)下面四个图形中,∠1与∠2是对顶角的图形为( )
A. B.
C. D.
7.(2023春 同安区期末)某个函数的图象由线段AB和线段BC组成,如图,其中A(0,2),B(2,1),C(5,3),点M(x1,y1),N(x2,y2)是这两条线段上的点,则正确的结论是( )
A.当x1>x2>0时,y1>y2
B.当0<x1<x2<2时,y1<y2
C.当1<x1<x2<3时,y1<y2
D.当2<x1<x2<5时,y1<y2
8.(2024秋 河口区期末)某电路图如图1所示.结合数据描点,连线,画成图2所示的函数图象.若该电路的最小电阻为1Ω,则该电路能通过的( )
A.最大电流是36A B.最大电流是27A
C.最小电流是36A D.最小电流是27A
9.(2024秋 安次区期末)如图,AC与BD交于点O,若OA=OD,要用“SAS”证明△AOB≌△DOC,还需要的条件是( )
A.OB=OC B.AB=DC C.∠A=∠D D.∠B=∠C
10.(2024秋 溧阳市期末)光在不同介质中的传播速度是不同的,因此光从水中射向空气时,会发生折射.已知在水中平行的光线射向空气中时也是平行的.如图,∠1=40°,∠2=110°,则∠3+∠4的值为( )
A.100° B.110° C.120° D.150°
二.填空题(共6小题)
11.(2024秋 饶平县期末)若3m=4,3n=2,则3m+2n= .
12.(2024秋 阜平县期末)某路口红绿灯的时间设置为:红灯40秒,绿灯60秒,黄灯4秒,当车辆随意经过该路口时,遇到可能性最小的是 灯.(填“红、绿、黄”)
13.(2024秋 天津期末)计算:(a+3)(a﹣3)的结果是 .
14.(2025春 天山区校级期末)小明研究两条平行线间的拐点问题在生活中的应用,书桌上有一款长臂折叠LED护眼灯,其示意图如图所示,EF与桌面MN垂直.当发光的灯管AB恰好与桌面MN平行时,若∠DEF=126°,∠BCD=104°,则∠CDE的度数为 .
15.(2024秋 临颍县期末)如图,在△ABC中,ED垂直平分BC,CD=5,△BCE的周长为22,则BE= .
16.(2024秋 丰城市期末)如图,直线PQ经过Rt△ABC的直角顶点C,△ABC的边上有两个动点D、E,点D以1cm/s的速度从点A出发,沿AC→CB移动到点B,点E以3cm/s的速度从点B出发,沿BC→CA移动到点A,两动点中有一个点到达终点后另一个点继续移动到终点.过点D、E分别作DM⊥PQ,EN⊥PQ,垂足分别为点M、N,若AC=6cm,BC=8cm,设运动时间为t,则当t= s时,以点D、M、C为顶点的三角形与以点E、N、C为顶点的三角形全等.
三.解答题(共8小题)
17.(2024秋 房山区期末)如图,C是AB的中点,CD∥BE,CD=BE,连接AD,CE.求证:AD=CE.
18.(2024秋 东湖区期末)将幂的运算逆向思维可以得到am+n=am an,amn=(am)n,anbn=(ab)n,在解题过程中,根据算式的结构特征,逆向运用幂的运算法则,常可化繁为简,化难为易,使问题巧妙获解.
(1)若am=2,an=3,求a3m+2n的值;
(2)若2×4x×8x=216,求x的值.
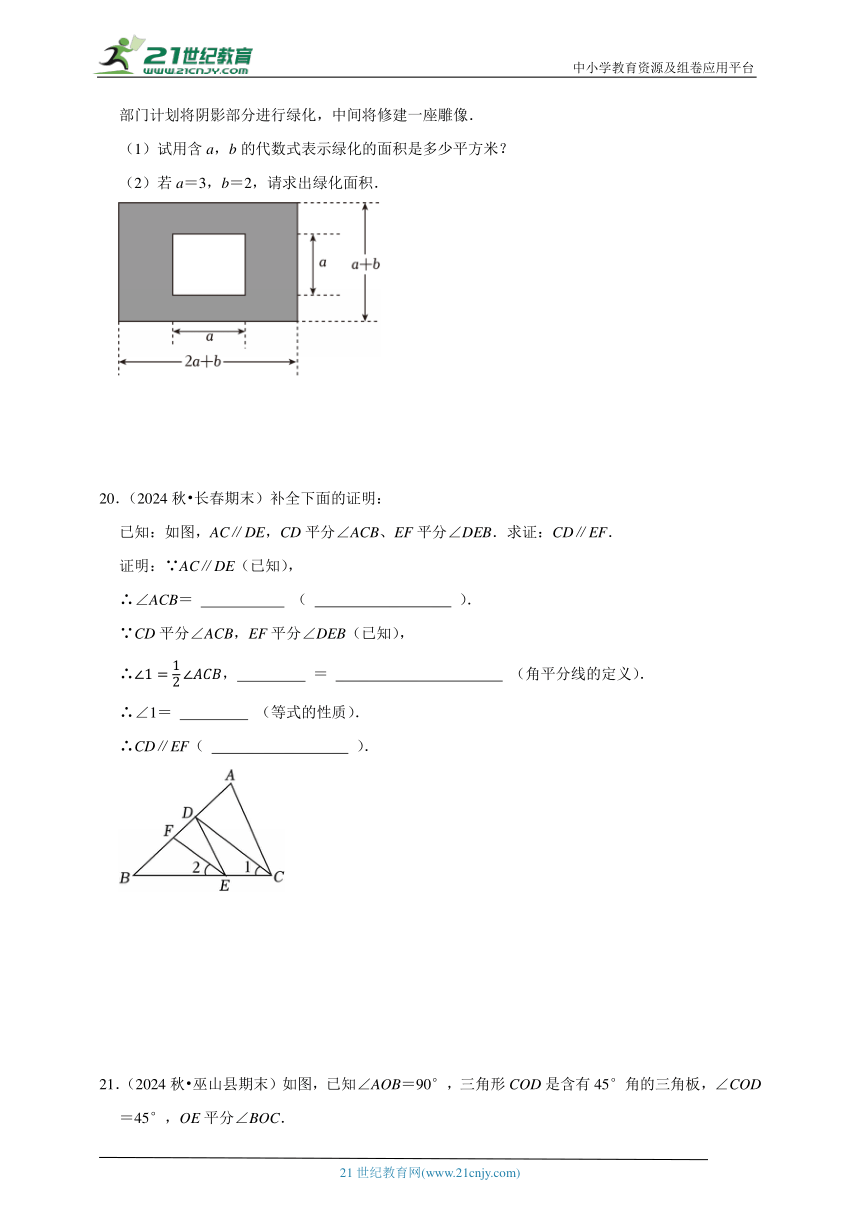
19.(2024秋 项城市期末)如图,某市有一块长为(2a+b)米,宽为(a+b)米的长方形地块,规划部门计划将阴影部分进行绿化,中间将修建一座雕像.
(1)试用含a,b的代数式表示绿化的面积是多少平方米?
(2)若a=3,b=2,请求出绿化面积.
20.(2024秋 长春期末)补全下面的证明:
已知:如图,AC∥DE,CD平分∠ACB、EF平分∠DEB.求证:CD∥EF.
证明:∵AC∥DE(已知),
∴∠ACB= ( ).
∵CD平分∠ACB,EF平分∠DEB(已知),
∴, = (角平分线的定义).
∴∠1= (等式的性质).
∴CD∥EF( ).
21.(2024秋 巫山县期末)如图,已知∠AOB=90°,三角形COD是含有45°角的三角板,∠COD=45°,OE平分∠BOC.
(1)如图1,当∠AOC=30°时,∠DOE= °;
(2)如图2,当∠AOC=60°时,∠DOE= °;
(3)如图3,当∠AOC=α(90°<α<180°)时,求∠DOE的度数(用α表示);
(4)由前三步的计算,当0°<∠AOC<180°时,请直接写出∠AOC与∠DOE的数量关系为 .
22.(2024秋 埇桥区期末)如图,△ABC三个顶点的坐标分别为A(2,4),B(1,1),C(3,2).
(1)请作出△ABC关于x轴对称的△A1B1C1;
(2)写出A1的坐标;
(3)计算△A1B1C1的面积.
23.(2024秋 吴桥县期末)如图,嘉嘉想知道一堵墙上的点A距地面的高度AO(墙与地面垂直,即AO⊥OD),但又不便直接测量,于是嘉嘉同学设计了下面的方案:
第一步:找一根长度大于OA的直杆,使直杆斜靠在墙上,且顶端与点A重合,记下直杆与地面的夹∠ABO;第二步:使直杆顶端竖直缓慢下滑,直到 =∠ABO.标记此时直杆的底端点D;
第三步:测量 的长度,即为点A距地面的高度.
(1)请你先补全方案,再说明这样设计的理由;
(2)若测得BO=1.2m,DO=2.5m,求AC的长度.
24.(2024秋 醴陵市期末)问题背景:如图1,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,E,F分别是BC,CD上的点,且∠EAF=60°,探究图中线段BE,EF,FD之间的数量关系,小王同学探究此问题的方法是,延长FD到点G.使DG=BE.连接AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是 ;
探索延伸:如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°,E,F分别是BC,CD上的点,且∠EAF∠BAD,上述结论是否仍然成立,并说明理由;
实际应用:如图3,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西30°的A处,舰艇乙在指挥中心南偏东70°的B处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以70海里/小时的速度前进,舰艇乙沿北偏东50°的方向以90海里/小时的速度,前进2小时后,指挥中心观测到甲、乙两舰艇分别到达E,F处,且两舰艇之间的夹角为70°,试求此时两舰艇之间的距离.
期末真题重组检测卷-2024-2025学年数学七年级下册北师大版(2024)
参考答案与试题解析
一.选择题(共10小题)
题号 1 2 3 4 5 6 7 8 9 10
答案 B A D A C C D A A B
一.选择题(共10小题)
1.(2024秋 大余县期末)石墨烯具有优异的光学、电学、力学特性,在材料学、微纳加工、能源、生物医学和药物传递等方面具有重要的应用前景,被认为是一种未来革命性的材料,石墨烯中每两个相邻碳原子间的键长为0.000000000142米,数字“0.000000000142”用科学记数法表示为( )
A.1.42×10﹣9 B.1.42×10﹣10
C.0.142×10﹣9 D.1.42×10﹣11
【解答】解:0.000000000142=1.42×10﹣10.
故选:B.
2.(2024秋 西山区期末)斐波那契螺旋线也称为“黄金螺旋线”,是根据斐波那契数列画出来的螺旋曲线,自然界中存在许多斐波那契螺旋线图案.下列斐波那契螺旋线图案中属于轴对称图形的是( )
A. B.
C. D.
【解答】解:A、是轴对称图形,故本选项正确;
B、不是轴对称图形,故本选项错误;
C、不是轴对称图形,故本选项错误;
D、不是轴对称图形,故本选项错误.
故选:A.
3.(2024秋 文昌期末)下列计算正确的是( )
A.a2+a2=a4 B.a3 a2=a6 C.a6÷a2=a3 D.(a3)3=a9
【解答】解:A、a2+a2=2a2,故此选项不符合题意;
B、a3 a2=a4,故此选项不符合题意;
C、a6÷a2=a4,故此选项不符合题意;
D、(a3)3=a9,故此选项符合题意;
故选:D.
4.(2024秋 徐水区期末)如图,点E,C,F,B在一条直线上,AB∥ED,∠A=∠D,添加下列条件不能判定△ABC≌△DEF的是( )
A.AC∥DF B.AB=DE C.EC=BF D.AC=DF
【解答】解:∵AB∥ED,
∴∠E=∠B,
A、∵AC∥DF,
∴∠ACB=∠DFE,
∵∠A=∠D,∠E=∠B,
∴△ABC和△DEF不一定全等,
故A符合题意;
B、∵∠A=∠D,AB=DE,∠E=∠B,
∴△ABC≌△DEF(ASA),
故B不符合题意;
C、∵EC=BF,
∴EC+CF=BF+CF,
∴EF=BC,
∵∠A=∠D,∠E=∠B,
∴△ABC≌△DEF(AAS),
故C不符合题意;
D、∵∠A=∠D,∠E=∠B,AC=DF,
∴△ABC≌△DEF(AAS),
故D不符合题意;
故选:A.
5.(2024秋 阳江期末)汉语是中华民族智慧的结晶,成语又是汉语中的精华,是中华文化的一大瑰宝,具有极强的表现力.下列成语描述的事件属于随机事件的是( )
A.旭日东升 B.画饼充饥 C.守株待兔 D.竹篮打水
【解答】解:A、旭日东升,是必然事件,不符合题意;
B、画饼充饥,是不可能事件,不符合题意;
C、守株待兔,是随机事件,符合题意;
D、竹篮打水,是不可能事件,不符合题意;
故选:C.
6.(2024秋 重庆期末)下面四个图形中,∠1与∠2是对顶角的图形为( )
A. B.
C. D.
【解答】解:利用对顶角的定义可知,只有图C中∠1与∠2是对顶角,
故选:C.
7.(2023春 同安区期末)某个函数的图象由线段AB和线段BC组成,如图,其中A(0,2),B(2,1),C(5,3),点M(x1,y1),N(x2,y2)是这两条线段上的点,则正确的结论是( )
A.当x1>x2>0时,y1>y2
B.当0<x1<x2<2时,y1<y2
C.当1<x1<x2<3时,y1<y2
D.当2<x1<x2<5时,y1<y2
【解答】解:A、当x1>x2>0时,y随x的增大先减小后增大,不能比较y1与y2的大小,故A选项不符合题意;
B、当0<x1<x2<2时,y随x的增大而减小,y1>y2,故B选项不符合题意;
C、当1<x1<x2<3时,y随x的增大先减小后增大,不能比较y1与y2的大小,故C选项不符合题意;
D、当2<x1<x2<5时,y随x的增大而增大,y1<y2,故D选项符合题意.
故选:D.
8.(2024秋 河口区期末)某电路图如图1所示.结合数据描点,连线,画成图2所示的函数图象.若该电路的最小电阻为1Ω,则该电路能通过的( )
A.最大电流是36A B.最大电流是27A
C.最小电流是36A D.最小电流是27A
【解答】解:设,将点(4,9)代入得,解得U=36,
∴;
若该电路的最小电阻值为1Ω,该电路能通过的最大电流是,
故选:A.
9.(2024秋 安次区期末)如图,AC与BD交于点O,若OA=OD,要用“SAS”证明△AOB≌△DOC,还需要的条件是( )
A.OB=OC B.AB=DC C.∠A=∠D D.∠B=∠C
【解答】解:要用“SAS”证明△AOB≌△DOC,还需要的条件是OB=OC,
在△AOB和△DOC中,
,
∴△AOB≌△DOC(SAS),
故选:A.
10.(2024秋 溧阳市期末)光在不同介质中的传播速度是不同的,因此光从水中射向空气时,会发生折射.已知在水中平行的光线射向空气中时也是平行的.如图,∠1=40°,∠2=110°,则∠3+∠4的值为( )
A.100° B.110° C.120° D.150°
【解答】解:如图:
∵AE∥BF,
∴∠1=∠3=40°,
∵AB∥CD,
∴∠2+∠4=180°,
∵∠2=110°,
∴∠4=180°﹣∠2=70°,
∴∠3+∠4=40°+70°=110°,
故选:B.
二.填空题(共6小题)
11.(2024秋 饶平县期末)若3m=4,3n=2,则3m+2n= 16 .
【解答】解:∵3m=4,3n=2,
∴3m+2n=3m 32n=3m (3n)2=4×22=16.
故答案为:16.
12.(2024秋 阜平县期末)某路口红绿灯的时间设置为:红灯40秒,绿灯60秒,黄灯4秒,当车辆随意经过该路口时,遇到可能性最小的是 黄 灯.(填“红、绿、黄”)
【解答】解:∵遇到红灯的概率;
遇到绿灯的概率;
遇到黄灯的概率,
∴遇到黄灯的可能性最小.
故答案为:黄.
13.(2024秋 天津期末)计算:(a+3)(a﹣3)的结果是 a2﹣9 .
【解答】解:(a+3)(a﹣3)=a2﹣32=a2﹣9.
故答案为:a2﹣9.
14.(2025春 天山区校级期末)小明研究两条平行线间的拐点问题在生活中的应用,书桌上有一款长臂折叠LED护眼灯,其示意图如图所示,EF与桌面MN垂直.当发光的灯管AB恰好与桌面MN平行时,若∠DEF=126°,∠BCD=104°,则∠CDE的度数为 112° .
【解答】解:∵EF⊥MN,
∴∠MFE=90°,
如图,过点D作DG∥AB,过点E作EH∥AB,
∵AB∥MN,
∴AB∥DG∥EH∥MN,
∴∠ACD+∠CDG=180°,∠GDE=∠DEF,∠HEF=∠MFE=90°,∠DEH=GDE,
∵∠DEF=126°,∠BCD=104°,
∴∠GDE=∠DEH=∠DEF﹣90°=36°,∠CDG=180°﹣104°=76°,
∴∠CDE=∠CDG+∠GDE=112°,
故答案为:112°.
15.(2024秋 临颍县期末)如图,在△ABC中,ED垂直平分BC,CD=5,△BCE的周长为22,则BE= 6 .
【解答】解:由条件可知BC=2CD=10,CE=BE,
∵△BCE的周长为22,
∴BC+BE+CE=BC+2BE=22,即10+2BE=22,
∴BE=6,
故答案为:6.
16.(2024秋 丰城市期末)如图,直线PQ经过Rt△ABC的直角顶点C,△ABC的边上有两个动点D、E,点D以1cm/s的速度从点A出发,沿AC→CB移动到点B,点E以3cm/s的速度从点B出发,沿BC→CA移动到点A,两动点中有一个点到达终点后另一个点继续移动到终点.过点D、E分别作DM⊥PQ,EN⊥PQ,垂足分别为点M、N,若AC=6cm,BC=8cm,设运动时间为t,则当t= 1或或12 s时,以点D、M、C为顶点的三角形与以点E、N、C为顶点的三角形全等.
【解答】解:①当E在BC上,D在AC上时,即0<t,
CE=(8﹣3t)cm,CD=(6﹣t)cm,
∵以点D、M、C为顶点的三角形与以点E、N、C为顶点的三角形全等.
∴CD=CE,
∴8﹣3t=6﹣t,
∴t=1;
②当E在AC上,D在AC上时,即t<6,
CE=(3t﹣8)cm,CD=(6﹣t)cm,
∴3t﹣8=6﹣t,
∴t;
③当E到达A,D在BC上时,即6≤t≤14,
CE=6cm,CD=(t﹣6)cm,
∴6=t﹣6,
∴t=12.
综上所述,当t=1或或12s时,以点D、M、C为顶点的三角形与以点E、N、C为顶点的三角形全等.
故答案为:1或或12.
三.解答题(共8小题)
17.(2024秋 房山区期末)如图,C是AB的中点,CD∥BE,CD=BE,连接AD,CE.求证:AD=CE.
【解答】证明:∵C是AB的中点,
∴AC=CB,
∵CD∥BE,
∴∠ACD=∠B.
在△ACD和△CBE中,
,
∴△ACD≌△CBE(SAS),
∴AD=CE.
18.(2024秋 东湖区期末)将幂的运算逆向思维可以得到am+n=am an,amn=(am)n,anbn=(ab)n,在解题过程中,根据算式的结构特征,逆向运用幂的运算法则,常可化繁为简,化难为易,使问题巧妙获解.
(1)若am=2,an=3,求a3m+2n的值;
(2)若2×4x×8x=216,求x的值.
【解答】解:(1)根据题意可知,am=2,an=3,
∴a3m+2n
=a3m a2n
=(am)3 (an)2
=23×32
=8×9
=72;
(2)∵2×4x×8x
=2×(22)x×(23)x
=21+2x+3x
=216,
∴1+2x+3x=16,
5x=15,
解得:x=3.
19.(2024秋 项城市期末)如图,某市有一块长为(2a+b)米,宽为(a+b)米的长方形地块,规划部门计划将阴影部分进行绿化,中间将修建一座雕像.
(1)试用含a,b的代数式表示绿化的面积是多少平方米?
(2)若a=3,b=2,请求出绿化面积.
【解答】解:(1)绿化的面积是(2a+b) (a+b)﹣a2=2a2+3ab+b2﹣a2=a2+3ab+b2;
(2)当a=3,b=2时,原式=9+3×2×3+4=31平方米.
20.(2024秋 长春期末)补全下面的证明:
已知:如图,AC∥DE,CD平分∠ACB、EF平分∠DEB.求证:CD∥EF.
证明:∵AC∥DE(已知),
∴∠ACB= ∠DEB ( 两直线平行,同位角相等 ).
∵CD平分∠ACB,EF平分∠DEB(已知),
∴, ∠2 = ∠DEB (角平分线的定义).
∴∠1= ∠2 (等式的性质).
∴CD∥EF( 同位角相等,两直线平行 ).
【解答】证明:∵AC∥DE(已知),
∴∠ACB=∠DEB(两直线平行,同位角相等).
∵CD平分∠ACB,EF平分∠DEB(已知),
∴,(角平分线的定义).
∴∠1=∠2(等式的性质).
∴CD∥EF(同位角相等,两直线平行).
21.(2024秋 巫山县期末)如图,已知∠AOB=90°,三角形COD是含有45°角的三角板,∠COD=45°,OE平分∠BOC.
(1)如图1,当∠AOC=30°时,∠DOE= 15 °;
(2)如图2,当∠AOC=60°时,∠DOE= 30 °;
(3)如图3,当∠AOC=α(90°<α<180°)时,求∠DOE的度数(用α表示);
(4)由前三步的计算,当0°<∠AOC<180°时,请直接写出∠AOC与∠DOE的数量关系为 ∠AOC=2∠DOE .
【解答】解:∵∠AOB=90°,∠AOC=30°,
∴∠BOC=∠AOB﹣∠AOC=60°,
∵OE平分∠BOC,
∴,
∵∠COD=45°,
∴∠DOE=∠COD﹣∠EOC=15°.
故答案为:15;
(2)∵∠AOB=90°,∠AOC=60°,
∴∠BOC=∠AOB﹣∠AOC=30°,
∵OE平分∠BOC,
∴,
∵∠COD=45°,
∴∠DOE=∠COD﹣∠EOC=30°.
故答案为:30;
(3)∵∠AOB=90°,∠AOC=α(90°<α<180°),
∴∠BOC=∠AOC﹣∠AOB=α﹣90°,
∵OE平分∠BOC,
∴,
∵∠COD=45°,
∴;
(4)设∠AOC=x(0°<x<180°),
①如图1,图2,当0°<x≤90°时,
∵∠AOB=90°,∠AOC=x,
∴∠BOC=∠AOB﹣∠AOC=90°﹣x,
∵OE平分∠BOC,
∴,
∵∠COD=45°,
∴,
即∠AOC=2∠DOE;
②如图3,当90°<x<180°时,
同(3)可得:,
则∠AOC=2∠DOE;
综上,∠AOC与∠DOE的数量关系为∠AOC=2∠DOE,
故答案为:∠AOC=2∠DOE.
22.(2024秋 埇桥区期末)如图,△ABC三个顶点的坐标分别为A(2,4),B(1,1),C(3,2).
(1)请作出△ABC关于x轴对称的△A1B1C1;
(2)写出A1的坐标;
(3)计算△A1B1C1的面积.
【解答】解:(1)如图,△A1B1C1即为所求.
(2)由图可得,点A1的坐标为(2,﹣4).
(3)△A1B1C1的面积为.
23.(2024秋 吴桥县期末)如图,嘉嘉想知道一堵墙上的点A距地面的高度AO(墙与地面垂直,即AO⊥OD),但又不便直接测量,于是嘉嘉同学设计了下面的方案:
第一步:找一根长度大于OA的直杆,使直杆斜靠在墙上,且顶端与点A重合,记下直杆与地面的夹∠ABO;第二步:使直杆顶端竖直缓慢下滑,直到 ∠DCO =∠ABO.标记此时直杆的底端点D;
第三步:测量 OD 的长度,即为点A距地面的高度.
(1)请你先补全方案,再说明这样设计的理由;
(2)若测得BO=1.2m,DO=2.5m,求AC的长度.
【解答】(1)解:第一步:找一根长度大于OA的直杆,使直杆斜靠在墙上,且顶端与点A重合,记下直杆与地面的夹∠ABO;第二步:使直杆顶端竖直缓慢下滑,直到∠DCO=∠ABO.标记此时直杆的底端点D;
第三步:测量OD的长度,即为点A距地面的高度.
理由如下:
∵AO⊥OD,
∴∠AOB=∠DOC=90°,
在△AOB与△DOC中,
,
∴△AOB≌△DOC(AAS),
∴OA=OD,
故答案为:∠DCO,OD;
(2)解:∵△AOB≌△DOC,
∴OB=OC=1.2m,OA=OD=2.5m,
∴OA﹣OC=OD﹣OB=2.5﹣1.2=1.3m,
即AC=1.3m.
24.(2024秋 醴陵市期末)问题背景:如图1,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,E,F分别是BC,CD上的点,且∠EAF=60°,探究图中线段BE,EF,FD之间的数量关系,小王同学探究此问题的方法是,延长FD到点G.使DG=BE.连接AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是 EF=BE+DF ;
探索延伸:如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°,E,F分别是BC,CD上的点,且∠EAF∠BAD,上述结论是否仍然成立,并说明理由;
实际应用:如图3,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西30°的A处,舰艇乙在指挥中心南偏东70°的B处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以70海里/小时的速度前进,舰艇乙沿北偏东50°的方向以90海里/小时的速度,前进2小时后,指挥中心观测到甲、乙两舰艇分别到达E,F处,且两舰艇之间的夹角为70°,试求此时两舰艇之间的距离.
【解答】解:问题背景:由题意:△ABE≌△ADG,△AEF≌△AGF,
∴BE=DG,EF=GF,
∴EF=FG=DF+DG=BE+FD.
故答案为:EF=BE+FD.
探索延伸:EF=BE+FD仍然成立.
理由:如图2,延长FD到点G,使DG=BE,连接AG
∵∠B+∠ADC=180°,∠ADG+∠ADC=180°,
∴∠B=∠ADG,
又∵AB=AD,
在△ABE和△ADG中,
,
∴△ABE≌△ADG(SAS),
∴AE=AG,∠BAE=∠DAG,
又∵∠EAF∠BAD,
∴∠FAG=∠FAD+∠DAG=∠FAD+∠BAE=∠BAD﹣∠EAF,
=∠BAD∠BAD∠BAD,
∴∠EAF=∠GAF.
在△AEF和△AGF中,
,
∴△AEF≌△AGF(SAS),
∴EF=FG,
又∵FG=DG+DF=BE+DF,
∴EF=BE+FD.
实际应用:如图3,连接EF,延长AE,BF相交于点C,
在四边形AOBC中,
∵∠AOB=30°+90°+20°=140°,∠FOE=70°∠AOB,
又∵OA=OB,∠OAC+∠OBC=60°+120°=180°,符合探索延伸中的条件,
∴结论EF=AE+FB成立.
即,EF=AE+FB=2×(70+90)=320(海里)
答:此时两舰艇之间的距离为320海里.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末真题重组检测卷-2024-2025学年数学七年级下册北师大版(2024)
一.选择题(共10小题)
1.(2024秋 大余县期末)石墨烯具有优异的光学、电学、力学特性,在材料学、微纳加工、能源、生物医学和药物传递等方面具有重要的应用前景,被认为是一种未来革命性的材料,石墨烯中每两个相邻碳原子间的键长为0.000000000142米,数字“0.000000000142”用科学记数法表示为( )
A.1.42×10﹣9 B.1.42×10﹣10
C.0.142×10﹣9 D.1.42×10﹣11
2.(2024秋 西山区期末)斐波那契螺旋线也称为“黄金螺旋线”,是根据斐波那契数列画出来的螺旋曲线,自然界中存在许多斐波那契螺旋线图案.下列斐波那契螺旋线图案中属于轴对称图形的是( )
A. B.
C. D.
3.(2024秋 文昌期末)下列计算正确的是( )
A.a2+a2=a4 B.a3 a2=a6 C.a6÷a2=a3 D.(a3)3=a9
4.(2024秋 徐水区期末)如图,点E,C,F,B在一条直线上,AB∥ED,∠A=∠D,添加下列条件不能判定△ABC≌△DEF的是( )
A.AC∥DF B.AB=DE C.EC=BF D.AC=DF
5.(2024秋 阳江期末)汉语是中华民族智慧的结晶,成语又是汉语中的精华,是中华文化的一大瑰宝,具有极强的表现力.下列成语描述的事件属于随机事件的是( )
A.旭日东升 B.画饼充饥 C.守株待兔 D.竹篮打水
6.(2024秋 重庆期末)下面四个图形中,∠1与∠2是对顶角的图形为( )
A. B.
C. D.
7.(2023春 同安区期末)某个函数的图象由线段AB和线段BC组成,如图,其中A(0,2),B(2,1),C(5,3),点M(x1,y1),N(x2,y2)是这两条线段上的点,则正确的结论是( )
A.当x1>x2>0时,y1>y2
B.当0<x1<x2<2时,y1<y2
C.当1<x1<x2<3时,y1<y2
D.当2<x1<x2<5时,y1<y2
8.(2024秋 河口区期末)某电路图如图1所示.结合数据描点,连线,画成图2所示的函数图象.若该电路的最小电阻为1Ω,则该电路能通过的( )
A.最大电流是36A B.最大电流是27A
C.最小电流是36A D.最小电流是27A
9.(2024秋 安次区期末)如图,AC与BD交于点O,若OA=OD,要用“SAS”证明△AOB≌△DOC,还需要的条件是( )
A.OB=OC B.AB=DC C.∠A=∠D D.∠B=∠C
10.(2024秋 溧阳市期末)光在不同介质中的传播速度是不同的,因此光从水中射向空气时,会发生折射.已知在水中平行的光线射向空气中时也是平行的.如图,∠1=40°,∠2=110°,则∠3+∠4的值为( )
A.100° B.110° C.120° D.150°
二.填空题(共6小题)
11.(2024秋 饶平县期末)若3m=4,3n=2,则3m+2n= .
12.(2024秋 阜平县期末)某路口红绿灯的时间设置为:红灯40秒,绿灯60秒,黄灯4秒,当车辆随意经过该路口时,遇到可能性最小的是 灯.(填“红、绿、黄”)
13.(2024秋 天津期末)计算:(a+3)(a﹣3)的结果是 .
14.(2025春 天山区校级期末)小明研究两条平行线间的拐点问题在生活中的应用,书桌上有一款长臂折叠LED护眼灯,其示意图如图所示,EF与桌面MN垂直.当发光的灯管AB恰好与桌面MN平行时,若∠DEF=126°,∠BCD=104°,则∠CDE的度数为 .
15.(2024秋 临颍县期末)如图,在△ABC中,ED垂直平分BC,CD=5,△BCE的周长为22,则BE= .
16.(2024秋 丰城市期末)如图,直线PQ经过Rt△ABC的直角顶点C,△ABC的边上有两个动点D、E,点D以1cm/s的速度从点A出发,沿AC→CB移动到点B,点E以3cm/s的速度从点B出发,沿BC→CA移动到点A,两动点中有一个点到达终点后另一个点继续移动到终点.过点D、E分别作DM⊥PQ,EN⊥PQ,垂足分别为点M、N,若AC=6cm,BC=8cm,设运动时间为t,则当t= s时,以点D、M、C为顶点的三角形与以点E、N、C为顶点的三角形全等.
三.解答题(共8小题)
17.(2024秋 房山区期末)如图,C是AB的中点,CD∥BE,CD=BE,连接AD,CE.求证:AD=CE.
18.(2024秋 东湖区期末)将幂的运算逆向思维可以得到am+n=am an,amn=(am)n,anbn=(ab)n,在解题过程中,根据算式的结构特征,逆向运用幂的运算法则,常可化繁为简,化难为易,使问题巧妙获解.
(1)若am=2,an=3,求a3m+2n的值;
(2)若2×4x×8x=216,求x的值.
19.(2024秋 项城市期末)如图,某市有一块长为(2a+b)米,宽为(a+b)米的长方形地块,规划部门计划将阴影部分进行绿化,中间将修建一座雕像.
(1)试用含a,b的代数式表示绿化的面积是多少平方米?
(2)若a=3,b=2,请求出绿化面积.
20.(2024秋 长春期末)补全下面的证明:
已知:如图,AC∥DE,CD平分∠ACB、EF平分∠DEB.求证:CD∥EF.
证明:∵AC∥DE(已知),
∴∠ACB= ( ).
∵CD平分∠ACB,EF平分∠DEB(已知),
∴, = (角平分线的定义).
∴∠1= (等式的性质).
∴CD∥EF( ).
21.(2024秋 巫山县期末)如图,已知∠AOB=90°,三角形COD是含有45°角的三角板,∠COD=45°,OE平分∠BOC.
(1)如图1,当∠AOC=30°时,∠DOE= °;
(2)如图2,当∠AOC=60°时,∠DOE= °;
(3)如图3,当∠AOC=α(90°<α<180°)时,求∠DOE的度数(用α表示);
(4)由前三步的计算,当0°<∠AOC<180°时,请直接写出∠AOC与∠DOE的数量关系为 .
22.(2024秋 埇桥区期末)如图,△ABC三个顶点的坐标分别为A(2,4),B(1,1),C(3,2).
(1)请作出△ABC关于x轴对称的△A1B1C1;
(2)写出A1的坐标;
(3)计算△A1B1C1的面积.
23.(2024秋 吴桥县期末)如图,嘉嘉想知道一堵墙上的点A距地面的高度AO(墙与地面垂直,即AO⊥OD),但又不便直接测量,于是嘉嘉同学设计了下面的方案:
第一步:找一根长度大于OA的直杆,使直杆斜靠在墙上,且顶端与点A重合,记下直杆与地面的夹∠ABO;第二步:使直杆顶端竖直缓慢下滑,直到 =∠ABO.标记此时直杆的底端点D;
第三步:测量 的长度,即为点A距地面的高度.
(1)请你先补全方案,再说明这样设计的理由;
(2)若测得BO=1.2m,DO=2.5m,求AC的长度.
24.(2024秋 醴陵市期末)问题背景:如图1,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,E,F分别是BC,CD上的点,且∠EAF=60°,探究图中线段BE,EF,FD之间的数量关系,小王同学探究此问题的方法是,延长FD到点G.使DG=BE.连接AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是 ;
探索延伸:如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°,E,F分别是BC,CD上的点,且∠EAF∠BAD,上述结论是否仍然成立,并说明理由;
实际应用:如图3,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西30°的A处,舰艇乙在指挥中心南偏东70°的B处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以70海里/小时的速度前进,舰艇乙沿北偏东50°的方向以90海里/小时的速度,前进2小时后,指挥中心观测到甲、乙两舰艇分别到达E,F处,且两舰艇之间的夹角为70°,试求此时两舰艇之间的距离.
期末真题重组检测卷-2024-2025学年数学七年级下册北师大版(2024)
参考答案与试题解析
一.选择题(共10小题)
题号 1 2 3 4 5 6 7 8 9 10
答案 B A D A C C D A A B
一.选择题(共10小题)
1.(2024秋 大余县期末)石墨烯具有优异的光学、电学、力学特性,在材料学、微纳加工、能源、生物医学和药物传递等方面具有重要的应用前景,被认为是一种未来革命性的材料,石墨烯中每两个相邻碳原子间的键长为0.000000000142米,数字“0.000000000142”用科学记数法表示为( )
A.1.42×10﹣9 B.1.42×10﹣10
C.0.142×10﹣9 D.1.42×10﹣11
【解答】解:0.000000000142=1.42×10﹣10.
故选:B.
2.(2024秋 西山区期末)斐波那契螺旋线也称为“黄金螺旋线”,是根据斐波那契数列画出来的螺旋曲线,自然界中存在许多斐波那契螺旋线图案.下列斐波那契螺旋线图案中属于轴对称图形的是( )
A. B.
C. D.
【解答】解:A、是轴对称图形,故本选项正确;
B、不是轴对称图形,故本选项错误;
C、不是轴对称图形,故本选项错误;
D、不是轴对称图形,故本选项错误.
故选:A.
3.(2024秋 文昌期末)下列计算正确的是( )
A.a2+a2=a4 B.a3 a2=a6 C.a6÷a2=a3 D.(a3)3=a9
【解答】解:A、a2+a2=2a2,故此选项不符合题意;
B、a3 a2=a4,故此选项不符合题意;
C、a6÷a2=a4,故此选项不符合题意;
D、(a3)3=a9,故此选项符合题意;
故选:D.
4.(2024秋 徐水区期末)如图,点E,C,F,B在一条直线上,AB∥ED,∠A=∠D,添加下列条件不能判定△ABC≌△DEF的是( )
A.AC∥DF B.AB=DE C.EC=BF D.AC=DF
【解答】解:∵AB∥ED,
∴∠E=∠B,
A、∵AC∥DF,
∴∠ACB=∠DFE,
∵∠A=∠D,∠E=∠B,
∴△ABC和△DEF不一定全等,
故A符合题意;
B、∵∠A=∠D,AB=DE,∠E=∠B,
∴△ABC≌△DEF(ASA),
故B不符合题意;
C、∵EC=BF,
∴EC+CF=BF+CF,
∴EF=BC,
∵∠A=∠D,∠E=∠B,
∴△ABC≌△DEF(AAS),
故C不符合题意;
D、∵∠A=∠D,∠E=∠B,AC=DF,
∴△ABC≌△DEF(AAS),
故D不符合题意;
故选:A.
5.(2024秋 阳江期末)汉语是中华民族智慧的结晶,成语又是汉语中的精华,是中华文化的一大瑰宝,具有极强的表现力.下列成语描述的事件属于随机事件的是( )
A.旭日东升 B.画饼充饥 C.守株待兔 D.竹篮打水
【解答】解:A、旭日东升,是必然事件,不符合题意;
B、画饼充饥,是不可能事件,不符合题意;
C、守株待兔,是随机事件,符合题意;
D、竹篮打水,是不可能事件,不符合题意;
故选:C.
6.(2024秋 重庆期末)下面四个图形中,∠1与∠2是对顶角的图形为( )
A. B.
C. D.
【解答】解:利用对顶角的定义可知,只有图C中∠1与∠2是对顶角,
故选:C.
7.(2023春 同安区期末)某个函数的图象由线段AB和线段BC组成,如图,其中A(0,2),B(2,1),C(5,3),点M(x1,y1),N(x2,y2)是这两条线段上的点,则正确的结论是( )
A.当x1>x2>0时,y1>y2
B.当0<x1<x2<2时,y1<y2
C.当1<x1<x2<3时,y1<y2
D.当2<x1<x2<5时,y1<y2
【解答】解:A、当x1>x2>0时,y随x的增大先减小后增大,不能比较y1与y2的大小,故A选项不符合题意;
B、当0<x1<x2<2时,y随x的增大而减小,y1>y2,故B选项不符合题意;
C、当1<x1<x2<3时,y随x的增大先减小后增大,不能比较y1与y2的大小,故C选项不符合题意;
D、当2<x1<x2<5时,y随x的增大而增大,y1<y2,故D选项符合题意.
故选:D.
8.(2024秋 河口区期末)某电路图如图1所示.结合数据描点,连线,画成图2所示的函数图象.若该电路的最小电阻为1Ω,则该电路能通过的( )
A.最大电流是36A B.最大电流是27A
C.最小电流是36A D.最小电流是27A
【解答】解:设,将点(4,9)代入得,解得U=36,
∴;
若该电路的最小电阻值为1Ω,该电路能通过的最大电流是,
故选:A.
9.(2024秋 安次区期末)如图,AC与BD交于点O,若OA=OD,要用“SAS”证明△AOB≌△DOC,还需要的条件是( )
A.OB=OC B.AB=DC C.∠A=∠D D.∠B=∠C
【解答】解:要用“SAS”证明△AOB≌△DOC,还需要的条件是OB=OC,
在△AOB和△DOC中,
,
∴△AOB≌△DOC(SAS),
故选:A.
10.(2024秋 溧阳市期末)光在不同介质中的传播速度是不同的,因此光从水中射向空气时,会发生折射.已知在水中平行的光线射向空气中时也是平行的.如图,∠1=40°,∠2=110°,则∠3+∠4的值为( )
A.100° B.110° C.120° D.150°
【解答】解:如图:
∵AE∥BF,
∴∠1=∠3=40°,
∵AB∥CD,
∴∠2+∠4=180°,
∵∠2=110°,
∴∠4=180°﹣∠2=70°,
∴∠3+∠4=40°+70°=110°,
故选:B.
二.填空题(共6小题)
11.(2024秋 饶平县期末)若3m=4,3n=2,则3m+2n= 16 .
【解答】解:∵3m=4,3n=2,
∴3m+2n=3m 32n=3m (3n)2=4×22=16.
故答案为:16.
12.(2024秋 阜平县期末)某路口红绿灯的时间设置为:红灯40秒,绿灯60秒,黄灯4秒,当车辆随意经过该路口时,遇到可能性最小的是 黄 灯.(填“红、绿、黄”)
【解答】解:∵遇到红灯的概率;
遇到绿灯的概率;
遇到黄灯的概率,
∴遇到黄灯的可能性最小.
故答案为:黄.
13.(2024秋 天津期末)计算:(a+3)(a﹣3)的结果是 a2﹣9 .
【解答】解:(a+3)(a﹣3)=a2﹣32=a2﹣9.
故答案为:a2﹣9.
14.(2025春 天山区校级期末)小明研究两条平行线间的拐点问题在生活中的应用,书桌上有一款长臂折叠LED护眼灯,其示意图如图所示,EF与桌面MN垂直.当发光的灯管AB恰好与桌面MN平行时,若∠DEF=126°,∠BCD=104°,则∠CDE的度数为 112° .
【解答】解:∵EF⊥MN,
∴∠MFE=90°,
如图,过点D作DG∥AB,过点E作EH∥AB,
∵AB∥MN,
∴AB∥DG∥EH∥MN,
∴∠ACD+∠CDG=180°,∠GDE=∠DEF,∠HEF=∠MFE=90°,∠DEH=GDE,
∵∠DEF=126°,∠BCD=104°,
∴∠GDE=∠DEH=∠DEF﹣90°=36°,∠CDG=180°﹣104°=76°,
∴∠CDE=∠CDG+∠GDE=112°,
故答案为:112°.
15.(2024秋 临颍县期末)如图,在△ABC中,ED垂直平分BC,CD=5,△BCE的周长为22,则BE= 6 .
【解答】解:由条件可知BC=2CD=10,CE=BE,
∵△BCE的周长为22,
∴BC+BE+CE=BC+2BE=22,即10+2BE=22,
∴BE=6,
故答案为:6.
16.(2024秋 丰城市期末)如图,直线PQ经过Rt△ABC的直角顶点C,△ABC的边上有两个动点D、E,点D以1cm/s的速度从点A出发,沿AC→CB移动到点B,点E以3cm/s的速度从点B出发,沿BC→CA移动到点A,两动点中有一个点到达终点后另一个点继续移动到终点.过点D、E分别作DM⊥PQ,EN⊥PQ,垂足分别为点M、N,若AC=6cm,BC=8cm,设运动时间为t,则当t= 1或或12 s时,以点D、M、C为顶点的三角形与以点E、N、C为顶点的三角形全等.
【解答】解:①当E在BC上,D在AC上时,即0<t,
CE=(8﹣3t)cm,CD=(6﹣t)cm,
∵以点D、M、C为顶点的三角形与以点E、N、C为顶点的三角形全等.
∴CD=CE,
∴8﹣3t=6﹣t,
∴t=1;
②当E在AC上,D在AC上时,即t<6,
CE=(3t﹣8)cm,CD=(6﹣t)cm,
∴3t﹣8=6﹣t,
∴t;
③当E到达A,D在BC上时,即6≤t≤14,
CE=6cm,CD=(t﹣6)cm,
∴6=t﹣6,
∴t=12.
综上所述,当t=1或或12s时,以点D、M、C为顶点的三角形与以点E、N、C为顶点的三角形全等.
故答案为:1或或12.
三.解答题(共8小题)
17.(2024秋 房山区期末)如图,C是AB的中点,CD∥BE,CD=BE,连接AD,CE.求证:AD=CE.
【解答】证明:∵C是AB的中点,
∴AC=CB,
∵CD∥BE,
∴∠ACD=∠B.
在△ACD和△CBE中,
,
∴△ACD≌△CBE(SAS),
∴AD=CE.
18.(2024秋 东湖区期末)将幂的运算逆向思维可以得到am+n=am an,amn=(am)n,anbn=(ab)n,在解题过程中,根据算式的结构特征,逆向运用幂的运算法则,常可化繁为简,化难为易,使问题巧妙获解.
(1)若am=2,an=3,求a3m+2n的值;
(2)若2×4x×8x=216,求x的值.
【解答】解:(1)根据题意可知,am=2,an=3,
∴a3m+2n
=a3m a2n
=(am)3 (an)2
=23×32
=8×9
=72;
(2)∵2×4x×8x
=2×(22)x×(23)x
=21+2x+3x
=216,
∴1+2x+3x=16,
5x=15,
解得:x=3.
19.(2024秋 项城市期末)如图,某市有一块长为(2a+b)米,宽为(a+b)米的长方形地块,规划部门计划将阴影部分进行绿化,中间将修建一座雕像.
(1)试用含a,b的代数式表示绿化的面积是多少平方米?
(2)若a=3,b=2,请求出绿化面积.
【解答】解:(1)绿化的面积是(2a+b) (a+b)﹣a2=2a2+3ab+b2﹣a2=a2+3ab+b2;
(2)当a=3,b=2时,原式=9+3×2×3+4=31平方米.
20.(2024秋 长春期末)补全下面的证明:
已知:如图,AC∥DE,CD平分∠ACB、EF平分∠DEB.求证:CD∥EF.
证明:∵AC∥DE(已知),
∴∠ACB= ∠DEB ( 两直线平行,同位角相等 ).
∵CD平分∠ACB,EF平分∠DEB(已知),
∴, ∠2 = ∠DEB (角平分线的定义).
∴∠1= ∠2 (等式的性质).
∴CD∥EF( 同位角相等,两直线平行 ).
【解答】证明:∵AC∥DE(已知),
∴∠ACB=∠DEB(两直线平行,同位角相等).
∵CD平分∠ACB,EF平分∠DEB(已知),
∴,(角平分线的定义).
∴∠1=∠2(等式的性质).
∴CD∥EF(同位角相等,两直线平行).
21.(2024秋 巫山县期末)如图,已知∠AOB=90°,三角形COD是含有45°角的三角板,∠COD=45°,OE平分∠BOC.
(1)如图1,当∠AOC=30°时,∠DOE= 15 °;
(2)如图2,当∠AOC=60°时,∠DOE= 30 °;
(3)如图3,当∠AOC=α(90°<α<180°)时,求∠DOE的度数(用α表示);
(4)由前三步的计算,当0°<∠AOC<180°时,请直接写出∠AOC与∠DOE的数量关系为 ∠AOC=2∠DOE .
【解答】解:∵∠AOB=90°,∠AOC=30°,
∴∠BOC=∠AOB﹣∠AOC=60°,
∵OE平分∠BOC,
∴,
∵∠COD=45°,
∴∠DOE=∠COD﹣∠EOC=15°.
故答案为:15;
(2)∵∠AOB=90°,∠AOC=60°,
∴∠BOC=∠AOB﹣∠AOC=30°,
∵OE平分∠BOC,
∴,
∵∠COD=45°,
∴∠DOE=∠COD﹣∠EOC=30°.
故答案为:30;
(3)∵∠AOB=90°,∠AOC=α(90°<α<180°),
∴∠BOC=∠AOC﹣∠AOB=α﹣90°,
∵OE平分∠BOC,
∴,
∵∠COD=45°,
∴;
(4)设∠AOC=x(0°<x<180°),
①如图1,图2,当0°<x≤90°时,
∵∠AOB=90°,∠AOC=x,
∴∠BOC=∠AOB﹣∠AOC=90°﹣x,
∵OE平分∠BOC,
∴,
∵∠COD=45°,
∴,
即∠AOC=2∠DOE;
②如图3,当90°<x<180°时,
同(3)可得:,
则∠AOC=2∠DOE;
综上,∠AOC与∠DOE的数量关系为∠AOC=2∠DOE,
故答案为:∠AOC=2∠DOE.
22.(2024秋 埇桥区期末)如图,△ABC三个顶点的坐标分别为A(2,4),B(1,1),C(3,2).
(1)请作出△ABC关于x轴对称的△A1B1C1;
(2)写出A1的坐标;
(3)计算△A1B1C1的面积.
【解答】解:(1)如图,△A1B1C1即为所求.
(2)由图可得,点A1的坐标为(2,﹣4).
(3)△A1B1C1的面积为.
23.(2024秋 吴桥县期末)如图,嘉嘉想知道一堵墙上的点A距地面的高度AO(墙与地面垂直,即AO⊥OD),但又不便直接测量,于是嘉嘉同学设计了下面的方案:
第一步:找一根长度大于OA的直杆,使直杆斜靠在墙上,且顶端与点A重合,记下直杆与地面的夹∠ABO;第二步:使直杆顶端竖直缓慢下滑,直到 ∠DCO =∠ABO.标记此时直杆的底端点D;
第三步:测量 OD 的长度,即为点A距地面的高度.
(1)请你先补全方案,再说明这样设计的理由;
(2)若测得BO=1.2m,DO=2.5m,求AC的长度.
【解答】(1)解:第一步:找一根长度大于OA的直杆,使直杆斜靠在墙上,且顶端与点A重合,记下直杆与地面的夹∠ABO;第二步:使直杆顶端竖直缓慢下滑,直到∠DCO=∠ABO.标记此时直杆的底端点D;
第三步:测量OD的长度,即为点A距地面的高度.
理由如下:
∵AO⊥OD,
∴∠AOB=∠DOC=90°,
在△AOB与△DOC中,
,
∴△AOB≌△DOC(AAS),
∴OA=OD,
故答案为:∠DCO,OD;
(2)解:∵△AOB≌△DOC,
∴OB=OC=1.2m,OA=OD=2.5m,
∴OA﹣OC=OD﹣OB=2.5﹣1.2=1.3m,
即AC=1.3m.
24.(2024秋 醴陵市期末)问题背景:如图1,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,E,F分别是BC,CD上的点,且∠EAF=60°,探究图中线段BE,EF,FD之间的数量关系,小王同学探究此问题的方法是,延长FD到点G.使DG=BE.连接AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是 EF=BE+DF ;
探索延伸:如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°,E,F分别是BC,CD上的点,且∠EAF∠BAD,上述结论是否仍然成立,并说明理由;
实际应用:如图3,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西30°的A处,舰艇乙在指挥中心南偏东70°的B处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以70海里/小时的速度前进,舰艇乙沿北偏东50°的方向以90海里/小时的速度,前进2小时后,指挥中心观测到甲、乙两舰艇分别到达E,F处,且两舰艇之间的夹角为70°,试求此时两舰艇之间的距离.
【解答】解:问题背景:由题意:△ABE≌△ADG,△AEF≌△AGF,
∴BE=DG,EF=GF,
∴EF=FG=DF+DG=BE+FD.
故答案为:EF=BE+FD.
探索延伸:EF=BE+FD仍然成立.
理由:如图2,延长FD到点G,使DG=BE,连接AG
∵∠B+∠ADC=180°,∠ADG+∠ADC=180°,
∴∠B=∠ADG,
又∵AB=AD,
在△ABE和△ADG中,
,
∴△ABE≌△ADG(SAS),
∴AE=AG,∠BAE=∠DAG,
又∵∠EAF∠BAD,
∴∠FAG=∠FAD+∠DAG=∠FAD+∠BAE=∠BAD﹣∠EAF,
=∠BAD∠BAD∠BAD,
∴∠EAF=∠GAF.
在△AEF和△AGF中,
,
∴△AEF≌△AGF(SAS),
∴EF=FG,
又∵FG=DG+DF=BE+DF,
∴EF=BE+FD.
实际应用:如图3,连接EF,延长AE,BF相交于点C,
在四边形AOBC中,
∵∠AOB=30°+90°+20°=140°,∠FOE=70°∠AOB,
又∵OA=OB,∠OAC+∠OBC=60°+120°=180°,符合探索延伸中的条件,
∴结论EF=AE+FB成立.
即,EF=AE+FB=2×(70+90)=320(海里)
答:此时两舰艇之间的距离为320海里.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
