华师大版数学八年级上册第13章第五节13.5.3角平分线同步练习
文档属性
| 名称 | 华师大版数学八年级上册第13章第五节13.5.3角平分线同步练习 |  | |
| 格式 | doc | ||
| 文件大小 | 240.5KB | ||
| 资源类型 | 素材 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-06-23 09:06:02 | ||
图片预览


文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
华师大版数学八年级上册第13章第五节13.5.3角平分线同步练习
一、选择题
1.如图,在CD上求一点P,使它到OA,OB的距离相等,则P点是( )
A.线段CD的中点
B.OA与OB的中垂线的交点
C.OA与CD的中垂线的交点
D.CD与∠AOB的平分线的交点
答案:D
解答:利用角的平分线上的点到角的两边的距离相等可知CD与∠AOB的平分线的交P.
故选D.
分析:利用角的平分线上的点到角的两边的距离相等可知CD与∠AOB的平分线的交点.
2.如图,OC是∠AOB的平分线,P是OC上一点,PD⊥OA于点D,PD=6,则点P到边OB的距离为( )
A.6 B.5 C.4 D.3
答案:A
解答:如图,
过点P作PE⊥OB于点E,
∵OC是∠AOB的平分线,PD⊥OA于D,
∴PE=PD,
∵PD=6,
∴PE=6,
即点P到OB的距离是6.
故选:A.
分析:过点P作PE⊥OB于点E,根据角平分线上的点到角的两边的距离相等可得PE=PD,从而得解.
3.如图,在△ABC中,∠C=90°,∠B=30°,AD是△ABC的角平分线,DE⊥AB,垂足为E,DE=1,则BC=( )
A. B.2 C.3 D.+2
答案:C
解答:∵AD是△ABC的角平分线,DE⊥AB,∠C=90°,
∴CD=DE=1,
又∵直角△BDE中,∠B=30°,
∴BD=2DE=2,
∴BC=CD+BD=1+2=3.
故选C.
分析:根据角平分线的性质即可求得CD的长,然后在直角△BDE中,根据30°的锐角所对的直角边等于斜边的一半,即可求得BD长,则BC即可求得.
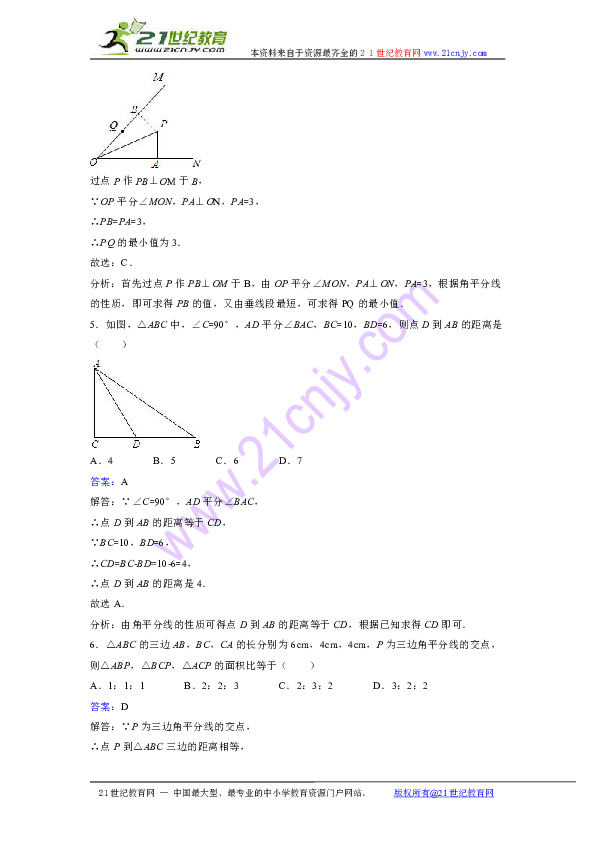
4.如图,OP平分∠MON,PA⊥ON于点A,点Q是射线OM上一个动点,若PA=3,则PQ的最小值为( )
A. B.2 C.3 D.2
答案:C
解答:
过点P作PB⊥OM于B,
∵OP平分∠MON,PA⊥ON,PA=3,
∴PB=PA=3,
∴PQ的最小值为3.
故选:C.
分析:首先过点P作PB⊥OM于B,由OP平分∠MON,PA⊥ON,PA=3,根据角平分线的性质,即可求得PB的值,又由垂线段最短,可求得PQ的最小值.
5.如图,△ABC中,∠C=90°,AD平分∠BAC,BC=10,BD=6,则点D到AB的距离是( )
A.4 B.5 C.6 D.7
答案:A
解答:∵∠C=90°,AD平分∠BAC,
∴点D到AB的距离等于CD,
∵BC=10,BD=6,
∴CD=BC-BD=10-6=4,
∴点D到AB的距离是4.
故选A.
分析:由角平分线的性质可得点D到AB的距离等于CD,根据已知求得CD即可.
6.△ABC的三边AB,BC,CA的长分别为6cm,4cm,4cm,P为三边角平分线的交点,则△ABP,△BCP,△ACP的面积比等于( )
A.1:1:1 B.2:2:3 C.2:3:2 D.3:2:2
答案:D
解答:∵P为三边角平分线的交点,
∴点P到△ABC三边的距离相等,
∵AB,BC,CA的长分别为6cm,4cm,4cm,
∴△ABP,△BCP,△ACP的面积比=6:4:4=3:2:2.
故选D.
分析:根据角平分线上的点到角的两边距离相等可得点P到△ABC三边的距离相等,然后根据等高的三角形的面积的比等于底边的比解答.
7.如图,在△ABC中,AD平分∠BAC,DE⊥AB于E,=15,DE=3,AB=6,则AC长是( )
A.7 B.6 C.5 D.4
答案:D
解答:∵DE=3,AB=6,
∴△ABD的面积为×3×6=9,
∵=15,
∴△ADC的面积=15-9=6,
∵AD平分∠BAC,DE⊥AB于E,
∴AC边上的高=DE=3,
∴AC=6×2÷3=4,
故选D.
分析:先求出△ABD的面积,再得出△ADC的面积,最后根据角平分线上的点到角的两边的距离相等可得AC边上的高,从而得解.
8.△ABC是一个任意三角形,用直尺和圆规作出∠A、∠B的平分线,如果两条平分线交于点O,那么下列选项中不正确的是( )
A.点O一定在△ABC的内部
B.∠C的平分线一定经过点O
C.点O到△ABC的三边距离一定相等
D.点O到△ABC三顶点的距离一定相等
答案:D
解答:∵三角形角平分线的性质为:三角形的三条角平分线在三角形内部且相交于一点,到三角形三条边的距离相等,
∴A、B、C三个选项均正确,D选项错误.
故选D.
分析:根据角平分线的定义与性质即可判断.
9.如图,在Rt△ABC中,∠A=90°,∠ABC的平分线BD交AC于点D,AD=3,BC=10,则△BDC的面积是( )
A.10 B.15 C.20 D.30
答案:B
解答:过D作DE⊥BC于E,
∵∠A=90°,
∴DA⊥AB,
∵BD平分∠ABC,
∴AD=DE=3,
∴△BDC的面积是×DE×BC=×10×3=15,
故选B
分析:过D作DE⊥BC于E,根据角平分线性质求出DE=3,根据三角形的面积求出即可.
10.如图是一块三角形的草坪,现要在草坪上建一凉亭供大家休息,要使凉亭到草坪三条边的距离相等,凉亭的位置应选在( )
A.△ABC的三条中线的交点
B.△ABC三边的中垂线的交点
C.△ABC三条高所在直线的交点
D.△ABC三条角平分线的交点
答案:D
解答:∵凉亭到草坪三条边的距离相等,
∴凉亭选择△ABC三条角平分线的交点.
故选D.
分析:由于凉亭到草坪三条边的距离相等,所以根据角平分线上的点到边的距离相等,可知是△ABC三条角平分线的交点.由此即可确定凉亭位置.
11.如图,直线l、l′、l″表示三条相互交叉的公路,现计划建一个加油站,要求它到三条公路的距离相等,则可供选择的地址有( )
A.一处 B.二处 C.三处 D.四处
答案:D
解答:如图所示,加油站站的地址有四处.
故选D.
分析:根据角平分线上的点到角的两边的距离相等作出图形即可得解.
12.在正方形网格中,∠AOB的位置如图所示,到∠AOB两边距离相等的点应是( )
A.M点 B.N点 C.P点 D.Q点
答案:A
解答:从图上可以看出点M在∠AOB的平分线上,其它三点不在∠AOB的平分线上.
所以点M到∠AOB两边的距离相等.故选A.
分析:根据角平分线的性质“角的平分线上的点到角的两边的距离相等”,注意观察点M、N、P、Q中的哪一点在∠AOB的平分线上.
13.如图,∠POA=∠POB,PD⊥OA于点D,PE⊥OB于点E,若OP=26,PE=10,则OD的长为( )
A.12 B.18 C.20 D.24
答案:D
解答:∵∠POA=∠POB,PD⊥OA,PE⊥OB,
∴PE=PD,∠PDO=90°,
∵PE=10,
∴PD=10,
∵OP=26,
∴OD=24,
故选D.
分析:根据角平分线性质求出PE=PD=10,再进一步求解即可.
14.如图,∠1=∠2,PD⊥OA,PE⊥OB,垂足分别为D,E,下列结论错误的是( )
A.PD=PE B.OD=OE C.∠DPO=∠EPO D.PD=OD
答案:D
解答:A.∵∠POB=∠POA,PD⊥OA,PE⊥OB,
∴PE=PD,正确,故本选项错误;
B.∵PD⊥OA,PE⊥OB,
∴∠PEO=∠PDO=90°,
∵OP=OP,PE=PD,
∴OE=OD,正确,故本选项错误;
C.∵∠PEO=∠PDO=90°,∠POB=∠POA,
∴由三角形的内角和定理得:∠DPO=∠EPO,正确,故本选项错误;
D.根据已知不能推出PD=OD,错误,故本选项正确;
故选D.
分析:由已知条件认真思考,首先可得△POE≌△POD,进而可得PD=PE,∠1=∠2,∠DPO=∠EPO;而OD,OP是无法证明是相等的,于是答案可得.
15. 如图,AD∥BC,∠ABC的平分线BP与∠BAD的平分线AP相交于点P,作PE⊥AB于点E,若PE=2,则两平行线AD与BC间的距离为( )
A.2 B.3 C.4 D.5
答案:C
解答:如图,
过点P作PF⊥AD于F,作PG⊥BC于G,
∵AP是∠BAD的平分线,PE⊥AB,
∴PF=PE,
同理可得PG=PE,
∵AD∥BC,
∴点F、P、G三点共线,
∴EG的长即为AD、BC间的距离,
∴平行线AD与BC间的距离为2+2=4.
故选C.
分析:过点P作PF⊥AD于F,作PG⊥BC于G,根据角平分线上的点到角的两边距离相等可得PF=PE,PG=PE,再根据平行线之间的距离的定义判断出EG的长即为AD、BC间的距离.
二、填空题
16.在Rt△ABC中,∠C=90°,AD平分∠BAC交BC于D,若BC=15,且BD:DC=3:2,则D到边AB的距离是 .
答案:6
解答:∵BC=15,BD:DC=3:2
∴CD=6
∵∠C=90°
AD平分∠BAC
∴D到边AB的距离=CD=6.
故答案为:6.
分析:首先由线段的比求得CD=6,然后利用角平分线的性质可得D到边AB的距离.
17.已知OC是∠AOB的平分线,点P在OC上,PD⊥OA于点D,PE⊥OB于点E,PD=10,则PE的长度为 .
答案:10
解答:∵点P在∠AOB的平分线OC上,PD⊥OA于点D,PE⊥OB于点E,
∴PD=PE,
∵PD=10,
∴PE=10,
故答案为:10.
分析:根据角平分线性质得出PE=PD,代入求出即可.
18.如图所示,△ABC中,∠A=90°,BD是角平分线,DE⊥BC,垂足是E,AC=10cm,CD=6cm,则DE的长为 cm.
答案:4
解答:∵∠A=90°,BD是角平分线,DE⊥BC,
∴DE=AD(角的平分线上的点到角的两边的距离相等)
∵AD=AC-CD=10-6=4cm,
∴DE=4cm.
故填4.
分析:由已知进行思考,结合角的平分线的性质可得DE=AD,而AD=AC-CD=10-6=4cm,即可求解.
19.如图,PD⊥OA,PE⊥OB,点D、E为垂足,PD=7cm,当PE= cm时,点P在∠AOB的平分线上.
答案:7
解答:∵PD⊥OA,PE⊥OB,PD=7cm,
∴当PE=PD,即PE=7cm时,P在∠AOB的平分线,
故答案为:7.
分析:根据角平分线性质得出PD=PE,代入求出即可.
20.如图,在Rt△ABC中,∠A=90°,BD平分∠ABC,交AC于点D,若AB=4,且点D到BC的距离为3,则BD= .
答案:5
解答:∵∠A=90°,
∴DA⊥AB,
∵BD平分∠ABC,点D到BC的距离为3,
∴AD=3,
∵AB=4,
∴BD=5.
分析:根据角平分线的性质得到AD=3,进一步求得BD.
三、解答题
21. 在学完全等三角形后,李老师给出了下列题目:
求证:角的内部到角的两边距离相等的点在角的平分线上.
答案:
解答:
已知:点P在∠AOB的平分线上,PE⊥OA于E,PF⊥OB于F,
求证:PE=PF.
证明:在△POE和△POF中,
∠POE=∠POF,∠PEO=∠PFO=90°,OP=OP,
∴△POE≌△POF,
∴PE=PF.
分析:根据题意画出图形,写出已知和求证,根据确定三角形的判定和性质证明结论.
22.现要在三角地ABC内建一中心医院,使医院到A、B两个居民小区的距离相等,并且到公路AB和AC的距离也相等,请确定这个中心医院的位置.
答案:
解答:作AB的垂直平分线EF,作∠BAC的角平分线AM,两线交于P,
则P为这个中心医院的位置.
分析:根据线段垂直平分线性质作出AB的垂直平分线,根据角平分线性质作出∠BAC的角平分线,即可得出答案.
23.如图,已知BD为∠ABC的平分线,AB=BC,点P在BD上,PM⊥AD于M,PN⊥CD于N,求证:PM=PN.
答案:
解答:∵BD为∠ABC的平分线,
∴∠ABD=∠CBD,
在△ABD和△CBD中,
AB=BC,∠ABD=∠CBD,BD=BD,
∴△ABD≌△CBD(SAS),
∴∠ADB=∠CDB,
∵点P在BD上,PM⊥AD,PN⊥CD,
∴PM=PN.
分析:根据角平分线的定义可得∠ABD=∠CBD,然后利用“边角边”证明△ABD和△CBD全等,根据全等三角形对应角相等可得∠ADB=∠CDB,然后根据角平分线上的点到角的两边的距离相等证明即可.
24.如图,在△ABC中,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E,F,BE=CF.
求证:AD是△ABC的角平分线.
答案:
解答:∵DE⊥AB,DF⊥AC,
∴Rt△BDE和Rt△DCF是直角三角形.
在Rt△BDE和Rt△DCF中
BD=DC,BE=CF,
∴Rt△BDE≌Rt△DCF(HL),
∴DE=DF,
又∵DE⊥AB,DF⊥AC,
∴AD是角平分线.
分析:首先可证明Rt△BDE≌Rt△DCF(HL)再根据三角形角平分线的逆定理求得AD是角平分线即可.
25.如图,已知P点是∠AOB平分线上一点,PC⊥OA,PD⊥OB,垂足为C、D.
(1)求证:∠PCD=∠PDC;
答案:
解答:∠PCD=∠PDC.
理由:∵OP是∠AOB的平分线,
且PC⊥OA,PD⊥OB,
∴PC=PD,
∴∠PCD=∠PDC;
(2)求证:OP是线段CD的垂直平分线.
答案:
解答:OP是CD的垂直平分线.
理由:∵∠OCP=∠ODP=90°,
在Rt△POC和Rt△POD中,
PC=PD,OP=OP,
∴Rt△POC≌Rt△POD(HL),
∴OC=OD,
由PC=PD,OC=OD,可知点O、P都是线段CD的垂直平分线上的点,
从而OP是线段CD的垂直平分线.
分析:∠PCD=∠PDC.由于P点是∠AOB平分线上一点,根据角平分线的性质可以推出PC=PD,然后利用等腰三角形的性质即可得到结论;
根据已知条件首先容易证明Rt△POC≌Rt△POD,从而得到OC=OD,由(1)有PC=PD,利用线段的垂直平分线的判定即可证明结论.
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
华师大版数学八年级上册第13章第五节13.5.3角平分线同步练习
一、选择题
1.如图,在CD上求一点P,使它到OA,OB的距离相等,则P点是( )
A.线段CD的中点
B.OA与OB的中垂线的交点
C.OA与CD的中垂线的交点
D.CD与∠AOB的平分线的交点
答案:D
解答:利用角的平分线上的点到角的两边的距离相等可知CD与∠AOB的平分线的交P.
故选D.
分析:利用角的平分线上的点到角的两边的距离相等可知CD与∠AOB的平分线的交点.
2.如图,OC是∠AOB的平分线,P是OC上一点,PD⊥OA于点D,PD=6,则点P到边OB的距离为( )
A.6 B.5 C.4 D.3
答案:A
解答:如图,
过点P作PE⊥OB于点E,
∵OC是∠AOB的平分线,PD⊥OA于D,
∴PE=PD,
∵PD=6,
∴PE=6,
即点P到OB的距离是6.
故选:A.
分析:过点P作PE⊥OB于点E,根据角平分线上的点到角的两边的距离相等可得PE=PD,从而得解.
3.如图,在△ABC中,∠C=90°,∠B=30°,AD是△ABC的角平分线,DE⊥AB,垂足为E,DE=1,则BC=( )
A. B.2 C.3 D.+2
答案:C
解答:∵AD是△ABC的角平分线,DE⊥AB,∠C=90°,
∴CD=DE=1,
又∵直角△BDE中,∠B=30°,
∴BD=2DE=2,
∴BC=CD+BD=1+2=3.
故选C.
分析:根据角平分线的性质即可求得CD的长,然后在直角△BDE中,根据30°的锐角所对的直角边等于斜边的一半,即可求得BD长,则BC即可求得.
4.如图,OP平分∠MON,PA⊥ON于点A,点Q是射线OM上一个动点,若PA=3,则PQ的最小值为( )
A. B.2 C.3 D.2
答案:C
解答:
过点P作PB⊥OM于B,
∵OP平分∠MON,PA⊥ON,PA=3,
∴PB=PA=3,
∴PQ的最小值为3.
故选:C.
分析:首先过点P作PB⊥OM于B,由OP平分∠MON,PA⊥ON,PA=3,根据角平分线的性质,即可求得PB的值,又由垂线段最短,可求得PQ的最小值.
5.如图,△ABC中,∠C=90°,AD平分∠BAC,BC=10,BD=6,则点D到AB的距离是( )
A.4 B.5 C.6 D.7
答案:A
解答:∵∠C=90°,AD平分∠BAC,
∴点D到AB的距离等于CD,
∵BC=10,BD=6,
∴CD=BC-BD=10-6=4,
∴点D到AB的距离是4.
故选A.
分析:由角平分线的性质可得点D到AB的距离等于CD,根据已知求得CD即可.
6.△ABC的三边AB,BC,CA的长分别为6cm,4cm,4cm,P为三边角平分线的交点,则△ABP,△BCP,△ACP的面积比等于( )
A.1:1:1 B.2:2:3 C.2:3:2 D.3:2:2
答案:D
解答:∵P为三边角平分线的交点,
∴点P到△ABC三边的距离相等,
∵AB,BC,CA的长分别为6cm,4cm,4cm,
∴△ABP,△BCP,△ACP的面积比=6:4:4=3:2:2.
故选D.
分析:根据角平分线上的点到角的两边距离相等可得点P到△ABC三边的距离相等,然后根据等高的三角形的面积的比等于底边的比解答.
7.如图,在△ABC中,AD平分∠BAC,DE⊥AB于E,=15,DE=3,AB=6,则AC长是( )
A.7 B.6 C.5 D.4
答案:D
解答:∵DE=3,AB=6,
∴△ABD的面积为×3×6=9,
∵=15,
∴△ADC的面积=15-9=6,
∵AD平分∠BAC,DE⊥AB于E,
∴AC边上的高=DE=3,
∴AC=6×2÷3=4,
故选D.
分析:先求出△ABD的面积,再得出△ADC的面积,最后根据角平分线上的点到角的两边的距离相等可得AC边上的高,从而得解.
8.△ABC是一个任意三角形,用直尺和圆规作出∠A、∠B的平分线,如果两条平分线交于点O,那么下列选项中不正确的是( )
A.点O一定在△ABC的内部
B.∠C的平分线一定经过点O
C.点O到△ABC的三边距离一定相等
D.点O到△ABC三顶点的距离一定相等
答案:D
解答:∵三角形角平分线的性质为:三角形的三条角平分线在三角形内部且相交于一点,到三角形三条边的距离相等,
∴A、B、C三个选项均正确,D选项错误.
故选D.
分析:根据角平分线的定义与性质即可判断.
9.如图,在Rt△ABC中,∠A=90°,∠ABC的平分线BD交AC于点D,AD=3,BC=10,则△BDC的面积是( )
A.10 B.15 C.20 D.30
答案:B
解答:过D作DE⊥BC于E,
∵∠A=90°,
∴DA⊥AB,
∵BD平分∠ABC,
∴AD=DE=3,
∴△BDC的面积是×DE×BC=×10×3=15,
故选B
分析:过D作DE⊥BC于E,根据角平分线性质求出DE=3,根据三角形的面积求出即可.
10.如图是一块三角形的草坪,现要在草坪上建一凉亭供大家休息,要使凉亭到草坪三条边的距离相等,凉亭的位置应选在( )
A.△ABC的三条中线的交点
B.△ABC三边的中垂线的交点
C.△ABC三条高所在直线的交点
D.△ABC三条角平分线的交点
答案:D
解答:∵凉亭到草坪三条边的距离相等,
∴凉亭选择△ABC三条角平分线的交点.
故选D.
分析:由于凉亭到草坪三条边的距离相等,所以根据角平分线上的点到边的距离相等,可知是△ABC三条角平分线的交点.由此即可确定凉亭位置.
11.如图,直线l、l′、l″表示三条相互交叉的公路,现计划建一个加油站,要求它到三条公路的距离相等,则可供选择的地址有( )
A.一处 B.二处 C.三处 D.四处
答案:D
解答:如图所示,加油站站的地址有四处.
故选D.
分析:根据角平分线上的点到角的两边的距离相等作出图形即可得解.
12.在正方形网格中,∠AOB的位置如图所示,到∠AOB两边距离相等的点应是( )
A.M点 B.N点 C.P点 D.Q点
答案:A
解答:从图上可以看出点M在∠AOB的平分线上,其它三点不在∠AOB的平分线上.
所以点M到∠AOB两边的距离相等.故选A.
分析:根据角平分线的性质“角的平分线上的点到角的两边的距离相等”,注意观察点M、N、P、Q中的哪一点在∠AOB的平分线上.
13.如图,∠POA=∠POB,PD⊥OA于点D,PE⊥OB于点E,若OP=26,PE=10,则OD的长为( )
A.12 B.18 C.20 D.24
答案:D
解答:∵∠POA=∠POB,PD⊥OA,PE⊥OB,
∴PE=PD,∠PDO=90°,
∵PE=10,
∴PD=10,
∵OP=26,
∴OD=24,
故选D.
分析:根据角平分线性质求出PE=PD=10,再进一步求解即可.
14.如图,∠1=∠2,PD⊥OA,PE⊥OB,垂足分别为D,E,下列结论错误的是( )
A.PD=PE B.OD=OE C.∠DPO=∠EPO D.PD=OD
答案:D
解答:A.∵∠POB=∠POA,PD⊥OA,PE⊥OB,
∴PE=PD,正确,故本选项错误;
B.∵PD⊥OA,PE⊥OB,
∴∠PEO=∠PDO=90°,
∵OP=OP,PE=PD,
∴OE=OD,正确,故本选项错误;
C.∵∠PEO=∠PDO=90°,∠POB=∠POA,
∴由三角形的内角和定理得:∠DPO=∠EPO,正确,故本选项错误;
D.根据已知不能推出PD=OD,错误,故本选项正确;
故选D.
分析:由已知条件认真思考,首先可得△POE≌△POD,进而可得PD=PE,∠1=∠2,∠DPO=∠EPO;而OD,OP是无法证明是相等的,于是答案可得.
15. 如图,AD∥BC,∠ABC的平分线BP与∠BAD的平分线AP相交于点P,作PE⊥AB于点E,若PE=2,则两平行线AD与BC间的距离为( )
A.2 B.3 C.4 D.5
答案:C
解答:如图,
过点P作PF⊥AD于F,作PG⊥BC于G,
∵AP是∠BAD的平分线,PE⊥AB,
∴PF=PE,
同理可得PG=PE,
∵AD∥BC,
∴点F、P、G三点共线,
∴EG的长即为AD、BC间的距离,
∴平行线AD与BC间的距离为2+2=4.
故选C.
分析:过点P作PF⊥AD于F,作PG⊥BC于G,根据角平分线上的点到角的两边距离相等可得PF=PE,PG=PE,再根据平行线之间的距离的定义判断出EG的长即为AD、BC间的距离.
二、填空题
16.在Rt△ABC中,∠C=90°,AD平分∠BAC交BC于D,若BC=15,且BD:DC=3:2,则D到边AB的距离是 .
答案:6
解答:∵BC=15,BD:DC=3:2
∴CD=6
∵∠C=90°
AD平分∠BAC
∴D到边AB的距离=CD=6.
故答案为:6.
分析:首先由线段的比求得CD=6,然后利用角平分线的性质可得D到边AB的距离.
17.已知OC是∠AOB的平分线,点P在OC上,PD⊥OA于点D,PE⊥OB于点E,PD=10,则PE的长度为 .
答案:10
解答:∵点P在∠AOB的平分线OC上,PD⊥OA于点D,PE⊥OB于点E,
∴PD=PE,
∵PD=10,
∴PE=10,
故答案为:10.
分析:根据角平分线性质得出PE=PD,代入求出即可.
18.如图所示,△ABC中,∠A=90°,BD是角平分线,DE⊥BC,垂足是E,AC=10cm,CD=6cm,则DE的长为 cm.
答案:4
解答:∵∠A=90°,BD是角平分线,DE⊥BC,
∴DE=AD(角的平分线上的点到角的两边的距离相等)
∵AD=AC-CD=10-6=4cm,
∴DE=4cm.
故填4.
分析:由已知进行思考,结合角的平分线的性质可得DE=AD,而AD=AC-CD=10-6=4cm,即可求解.
19.如图,PD⊥OA,PE⊥OB,点D、E为垂足,PD=7cm,当PE= cm时,点P在∠AOB的平分线上.
答案:7
解答:∵PD⊥OA,PE⊥OB,PD=7cm,
∴当PE=PD,即PE=7cm时,P在∠AOB的平分线,
故答案为:7.
分析:根据角平分线性质得出PD=PE,代入求出即可.
20.如图,在Rt△ABC中,∠A=90°,BD平分∠ABC,交AC于点D,若AB=4,且点D到BC的距离为3,则BD= .
答案:5
解答:∵∠A=90°,
∴DA⊥AB,
∵BD平分∠ABC,点D到BC的距离为3,
∴AD=3,
∵AB=4,
∴BD=5.
分析:根据角平分线的性质得到AD=3,进一步求得BD.
三、解答题
21. 在学完全等三角形后,李老师给出了下列题目:
求证:角的内部到角的两边距离相等的点在角的平分线上.
答案:
解答:
已知:点P在∠AOB的平分线上,PE⊥OA于E,PF⊥OB于F,
求证:PE=PF.
证明:在△POE和△POF中,
∠POE=∠POF,∠PEO=∠PFO=90°,OP=OP,
∴△POE≌△POF,
∴PE=PF.
分析:根据题意画出图形,写出已知和求证,根据确定三角形的判定和性质证明结论.
22.现要在三角地ABC内建一中心医院,使医院到A、B两个居民小区的距离相等,并且到公路AB和AC的距离也相等,请确定这个中心医院的位置.
答案:
解答:作AB的垂直平分线EF,作∠BAC的角平分线AM,两线交于P,
则P为这个中心医院的位置.
分析:根据线段垂直平分线性质作出AB的垂直平分线,根据角平分线性质作出∠BAC的角平分线,即可得出答案.
23.如图,已知BD为∠ABC的平分线,AB=BC,点P在BD上,PM⊥AD于M,PN⊥CD于N,求证:PM=PN.
答案:
解答:∵BD为∠ABC的平分线,
∴∠ABD=∠CBD,
在△ABD和△CBD中,
AB=BC,∠ABD=∠CBD,BD=BD,
∴△ABD≌△CBD(SAS),
∴∠ADB=∠CDB,
∵点P在BD上,PM⊥AD,PN⊥CD,
∴PM=PN.
分析:根据角平分线的定义可得∠ABD=∠CBD,然后利用“边角边”证明△ABD和△CBD全等,根据全等三角形对应角相等可得∠ADB=∠CDB,然后根据角平分线上的点到角的两边的距离相等证明即可.
24.如图,在△ABC中,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E,F,BE=CF.
求证:AD是△ABC的角平分线.
答案:
解答:∵DE⊥AB,DF⊥AC,
∴Rt△BDE和Rt△DCF是直角三角形.
在Rt△BDE和Rt△DCF中
BD=DC,BE=CF,
∴Rt△BDE≌Rt△DCF(HL),
∴DE=DF,
又∵DE⊥AB,DF⊥AC,
∴AD是角平分线.
分析:首先可证明Rt△BDE≌Rt△DCF(HL)再根据三角形角平分线的逆定理求得AD是角平分线即可.
25.如图,已知P点是∠AOB平分线上一点,PC⊥OA,PD⊥OB,垂足为C、D.
(1)求证:∠PCD=∠PDC;
答案:
解答:∠PCD=∠PDC.
理由:∵OP是∠AOB的平分线,
且PC⊥OA,PD⊥OB,
∴PC=PD,
∴∠PCD=∠PDC;
(2)求证:OP是线段CD的垂直平分线.
答案:
解答:OP是CD的垂直平分线.
理由:∵∠OCP=∠ODP=90°,
在Rt△POC和Rt△POD中,
PC=PD,OP=OP,
∴Rt△POC≌Rt△POD(HL),
∴OC=OD,
由PC=PD,OC=OD,可知点O、P都是线段CD的垂直平分线上的点,
从而OP是线段CD的垂直平分线.
分析:∠PCD=∠PDC.由于P点是∠AOB平分线上一点,根据角平分线的性质可以推出PC=PD,然后利用等腰三角形的性质即可得到结论;
根据已知条件首先容易证明Rt△POC≌Rt△POD,从而得到OC=OD,由(1)有PC=PD,利用线段的垂直平分线的判定即可证明结论.
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
