华东师大版七年级数学下册试题 第5章 一元一次方程 复习题 一元一次方程的应用 (含解析)
文档属性
| 名称 | 华东师大版七年级数学下册试题 第5章 一元一次方程 复习题 一元一次方程的应用 (含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-10 00:00:00 | ||
图片预览




文档简介
第5章《一元一次方程》复习题-- 一元一次方程的应用
专题训练01岁数问题
1.父子二人今年年龄之和为40岁,已知两年前父亲年龄是儿子的8倍,那么两年前父亲( )岁.
A.28 B.30 C.32 D.35
2.强强今年15岁,王飞今年9岁,当强强在 岁时,强强的年龄是王飞的2倍.
3.古希腊数学家丢番图(公元3~4世纪),是代数学的创始人之一.在他的墓碑上记载着:“他生命的是幸福的童年;再活了他生命的,两 长起了细细的胡须;又度过了一生的,他结婚了;再过5年,他有了儿子,感到很幸福;可是儿子只活了他全部年龄的一半;儿子死后,他在极度痛苦中度过了4年,与世长辞了.”
(1)设丢番图的寿命为x岁,根据题意得儿子出生时丢番图的年龄为_________岁,儿子的寿命为_________岁;
(2)用你喜欢的方式,求出丢番图和儿子的寿命分别为多少岁?
专题训练02数字问题
1.我国的“洛书”中记载着世界上最古老的一个幻方将这九个数字填入的方格内,使三行、三列、两对角线上的三个数之和都相等.如图所示的幻方中,字母m所表示的数是( )
A.8 B.6 C.9 D.4
2.有一列数,按一规律排列成2,,18,,162,,….其中某三个相邻数的和是,则这三个数中,中间的数是 .
3.一个五位数,个位上的数为4,这个五位数加上6120后所得的新五位数的万位、千位、百位、十位、个位上的数恰巧分别为原五位数的个位、万位、千位、百位、十位上的数,试求原五位数.
专题训练03比赛积分问题
1.兴华中学组织七年级学生数学知识竞赛答题,此活动共设有20道选择题,各题分值相同,每题必答.右表记录了小徐、小张、小高三名学生的得分情况,则另一名学生小李的得分可能是( )
学生 答对题数 答错题数 得分:
小徐 20 0 120
小张 18 2 106
小高 15 5 85
A.40 B.50 C.60 D.70
2.某市举办足球比赛,每队均需赛34场,其中胜一场得3分,平一场得1分,负一场得0分.某队在这次比赛中一场未负,共得70分,这个队在这次比赛中,胜了 场,平了 场.
3.2024年7月到8月,某市举办足球联赛,共有20支足球队参赛,经过前三轮(每个足球队比赛三场)比赛之后,A、B、C三支足球队积分如下表:
足球队 比赛场数 胜场 平场 负场 积分
A 3 3 0 0 9
B 3 2 1 0 7
C 3 1 1 1 4
思考:根据上表,我们可以得到本次足球联赛积分规则:胜利一场积 分;平一场积 分,负一场积 分;
探究:
(1)若一支足球队共进行了场比赛,胜利场,负的场数比胜利场数少5场,用含,的代数式表示这支足球队的总积分;
(2)列方程解决问题:东方足球队是20支足球队中的一员,经过18轮激战,保持连续不败,共积分48分,那么东方足球队共胜利了多少场
拓展:雄鹰足球队共进行了16场比赛,其中负了1场,那么雄鹰足球队的胜场总积分能等于它的平场总积分吗 为什么
专题训练04日历问题
1.如图,在2023年6月的日历表中用“T型”框数字,框出数字的和可能是( )
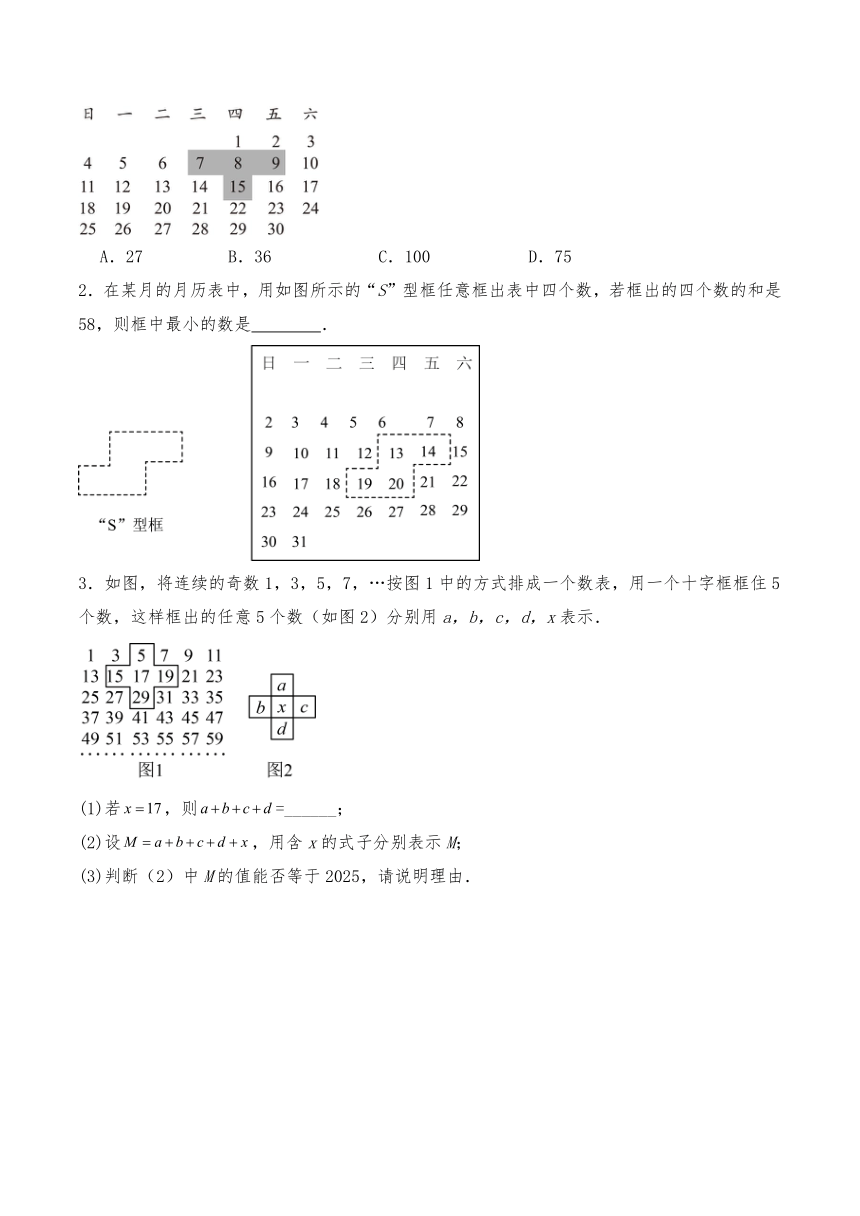
A.27 B.36 C.100 D.75
2.在某月的月历表中,用如图所示的“S”型框任意框出表中四个数,若框出的四个数的和是58,则框中最小的数是 .
3.如图,将连续的奇数1,3,5,7,…按图1中的方式排成一个数表,用一个十字框框住5个数,这样框出的任意5个数(如图2)分别用a,b,c,d,x表示.
(1)若,则=______;
(2)设,用含x的式子分别表示M;
(3)判断(2)中M的值能否等于2025,请说明理由.
专题训练05古代问题
1.《九章算术》是中国传统数学最重要的著作之一.书中记载:“今有人共买鸡,人出九,盈十一;人出六,不足十六.问人数几何?”意思是:“有若干人共同出钱买鸡,如果每人出九钱,那么多了十一钱;如果每人出六钱,那么少了十六钱.问:共有几个人?设共有个人共同出钱买鸡,根据题意,可列一元一次方程为( )
A. B.
C. D.
2.明代数学家吴敬的《九章算法比类大全》中的数学名题“宝塔装灯”原文:远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问顶层几盏灯.题目大意是:远处有一座雄伟的七层宝塔,塔上挂了许多红灯,相邻两层下一层灯的盏数是上一层灯的盏数的2倍,共有381盏灯,则塔顶灯有 盏.
3.中国的《九章算术》是世界现代数学的两大源泉之一.书中有一盈不足问题:“今有共买金,人出四百,盈三千四百;人出三百,盈一百.问人数、金价各几何?”译文:今有数人共同买金子,每人出400,多出来3400;每人出300,多出来100,问:共有多少人?金价是多少?请解决这个问题.
专题训练06销售问题
1.某商品的成本是2000元,标价为m元,现打八折出售,仍可获利,则该商品的标价m等于( )
A.1000 B.2400 C.3000 D.3600
2.某商店在某一时间以每件60元的价格卖出两件衣服,其中一件盈利,另一件亏损,卖这两件衣服总进价 .
3.某超市第一次用7000元购进甲、乙两种商品,其中甲商品的件数是乙商品件数的2倍,甲、乙两种商品的进价和售价如表:
甲 乙
进价(元/件) 40 60
售价(元/件) 50 80
(1)该超市第一次购进的甲、乙两种商品各多少件?第一次获得的总利润为多少元?
(2)该超市第一次购进的甲、乙两种商品售完后,第二次又以第一次的进价购进甲、乙两种商品,其中甲商品的件数不变,乙商品的件数是第一次的3倍;甲商品按原价销售,乙商品打折销售,第二次两种商品都售完以后获得的总利润比第一次获得的总利润少,求第二次乙商品是按原价打几折销售?
专题训练07比例分配问题
1.一个三角形的三边之比为2∶3∶3,最短边为6,则这个三角形的周长为( )
A.32 B.24 C.25 D.36
2.将一个圆分割成四个小扇形,它们的圆心角的度数之比为1:2:3:4,则这四个小扇形中圆心角的度数最大是 .
3.一种农药,用药液和水按配制而成.要配制这种农药505千克,需要药液多少千克?
专题训练08行程问题
1.小明、小亮两人相距,小明先出发,小亮再出发,小明在后小亮在前,两人同向而行,小明的速度是,小亮的速度是,小明出发多长时间后追上小亮?
2.一艘船从甲码头到乙码头顺水而行,用了小时;从乙码头返回甲码头逆水而行,用了小时.已知水流的速度是每小时千米.求船在静水中的平均速度.
3.列方程解应用题:重庆一中某校区七年级学生在教育广场乘坐旅游汽车到户外参加拓展训练,七(1)班的学生乘坐红色车,组成红队,车速为60千米小时,七(2)班的学生乘坐蓝色车,组成蓝队,车速为80千米小时.红队出发1小时后,蓝队才出发,同时蓝队派联络员小梦自驾车在两队之间不断地来回进行联络,小梦自驾车的速度为100千米小时.
(1)小梦出发多久后,第一次追上红队;
(2)小梦从出发到他折返后第一次与蓝队相遇,经过了多少时间?
(3)当蓝队追上红队时,小梦行驶的路程是多少千米?
专题训练09配套问题
1.某茶具生产车间有25名工人生产茶壶和茶杯,1个茶壶和6个茶杯配成一套.已知一名工人一天可以生产3个茶壶或7个茶杯,要使一天生产的茶壶和茶杯正好配套,应分别安排多少名工人生产茶壶和茶杯?
2.自上海迪斯尼开园后一直吸引众多游客,某玩具生产商打算生产米老鼠玩具作为旅游纪念品,并为每个米老鼠玩具配一副手套.如果某车间有28名工人,每人一天平均能生产手套24个或米老鼠玩具16个.那么应分配多少名工人生产手套,多少名工人生产玩具,才能使当天生产的手套和玩具刚好配套?
3.某车间有22名工人,每人每天可以生产1200个螺柱或2000个螺母,1个螺柱需要配2个螺母.
(1)为使每天生产的螺柱和螺母刚好配套,应安排生产螺柱和螺母的工人各多少名?
(2)若车间现有24名工人,每人每天工作8个小时,工人根据需要可以转换生产螺柱或螺母的工作岗位.如何安排工人生产,使得螺柱和螺母尽可能多的配套,最多能生产多少套?
专题训练10工程问题
装修一间房屋,如果由一名装修工人单独完成需要40小时.现在,业主先安排了一部分工人工作2小时,随后又增加了4名工人与他们一起工作了3小时,最终恰好完成了装修工作.假设每名工人的工作效率都是相同的,那么最初被安排进行装修的工人有多少名?
2.甲、乙两个工程队安装排污管道,甲队单独安装需要4天完成,乙队单独安装需要8天完成.如果甲队先安装1天,剩下的管道由甲、乙两队合作完成,那么还需要几天才能安装完这些管道?
3.某项工程,甲单独做需10天完成,乙单独做需15天完成,
(1)两人合作2天,完成的工作量占这项工程总量的几分之几?
(2)如果两人合作2天后,甲有事先离开,剩下的工程由乙单独做,还需要几天才能完成?
专题训练11图形问题
1.【提出问题】
小涵把长方体纸盒展开,得到图1,可以看成由长方形纸片和长方形纸片按照一定要求.拼接成的“”型图.小涵尝试了反向思考,对“两长方形纸片需满足什么条件,拼接成的“”型图可以是长方体的展开图.”进行了思考.
【探索问题】
探索一:两张相同长方形纸片拼接成的“”型图.
经过尝试,发现两张相同长方形纸片拼接成的“”型图都是长方体的展开图.
(1)如图2,当长方形纸片和长方形纸片的长都是,宽都是时,求的长.
(2)现有一张长为,宽为的长方形纸片,如果将它先剪成两个相同长方形,再拼接成“”型图,则该展开图折叠成的长方体的体积是_____.
探索二:两张不同长方形纸片拼接成的“”型图
再次尝试,发现两张不同长方形纸片拼接成的“”型图不一定是长方体的展开图,两长方形的长和宽需满足某种条件.
(3)如图1,若长方形纸片和长方形纸片拼接成的“”型图是某长方体的展开图,设,,,,,则、、、之间满足的关系是_____.
【结论应用】
对于(3)中的结论,反之亦成立,请解决下面的问题.
(4)甲、乙两张长方形纸片的宽分别是和,拼接成的“”型图是表面积是的长方体展开图,求甲长方形纸片的长.
2.某长方形人行道由相同的灰色正方形地砖与相同的白色等腰直角三角形地砖排列而成,图1表示此人行道的地砖排列方式,其中正方形地砖为连续排列.
[观察思考]
当正方形地砖只有1块时,等腰直角三角形地砖有6块(如图2);当正方形地砖有2块时,等腰直角三角形地砖有8块(如图3);以此类推.
[规律总结]
(1)若人行道上每增加1块正方形地砖,则等腰直角三角形地砖增加 块;
(2)若一条这样的人行道一共有n(n为正整数)块正方形地砖,则等腰直角三角形地砖的块数为 (用含n的代数式表示).
[问题解决]
(3)现有2025块等腰直角三角形地砖,若按此规律再建一条人行道,要求等腰直角三角形地砖剩余最少,则需要正方形地砖多少块?
3.根据以下素材,探索完成任务.
如何设计宣传牌?
素材1 如图1是长方形宣传牌,长,宽,拟在上面书写24个字. ()中间 可以用来设计的部分也是长方形,且长是宽的倍. ()四周空白部分的宽度相等.
素材2 如图,为了美观,将设计部分分割成大小相等的左中右三个长方形栏目,栏目与栏目之间的中缝间距相等.
素材 如图,每个栏目划出正方形方格,中间有十字间隔,竖向两列中间间隔和横向中间间隔宽度比为.
问题解决
任务 分析数量关系 设四周宽度为,用含x的代数式分别表示设计部分的长和宽.
任务 确定四周宽度 求四周宽度的值.
任务 确定栏目大小 ()求每个栏目的水平宽度; ()求长方形栏目与栏目之间中缝的间距.
专题训练12和差倍分问题
1.在某届科技大赛中,甲团队在机器人竞赛与编程竞赛项目中共获得个奖项,且编程竞赛获得的奖项比机器人竞赛获得奖项的2倍少4个.分别求编程竞赛与机器人竞赛获得奖项的个数.
2.把若干宣纸分给七年级优秀绘画爱好者,若每人分3张,则剩余12本,若每人分5张,则缺10张,绘画爱好者有几人?这批宣纸有多少张.
3.某车间为提高生产总量,在原有16名工人的基础上,新调人若干名工人,使得调整后车间的总人数是调入工人人数的3倍多4人.求调人多少名工人.
专题训练13方案问题
1.某商场销售一款运动鞋和运动袜,运动鞋每双定价200元,运动袜每双定价40元.商场决定开展促销活动,活动期间向客户提供两种优惠方案,方案一:买一双运动鞋送一双运动袜;方案二:运动鞋和运动袜都按定价的付款,现某客户要到该商场购买运动鞋10双和运动袜x双.
(1)若该客户按方案一购买,需付款________________元(需化简);若该客户按方案二购买,需付款_____________元(需化简).
(2)买多少双袜子时按方案一和方案二购买费用一样?
2.某文体中心提供阅读、观影、球类、游泳、器械等多种文体活动,现有三种收费方式.详情见下表:
收费方式 详细介绍
日卡 日卡一张元
会员卡 办卡需元,每活动小时收费元
普通卡 进入文体中心要收取元/日,可免费文体活动小时,后续收费元/小时
(注:不足一个小时的按一小时计算)
(1)小明打算这周六去文体中心活动小时,最少需要花费________元;
(2)小明打算一个月(天)都去文体中心活动,每天活动的时间为小时(为正整数,且).
①如果小明选择办会员卡一个月需要花费________元;选择办普通卡一个月需要花费________元:(用含的代数式表示)
②对于会员卡和普通卡两种不同的收费方式,哪种更划算?
3.某工厂生产一种产品,每件产品的出厂价为 40元,其成本价为 20元,在生产过程中平均每生产一件产品有0.1m的污水排出,为净化环境,工厂设计了两种处理污水的方案.
方案一∶工厂污水先净化处理后再排出,每处理1m污水所用费用为2元,并且每月排污设备损耗为15000元.
方案二∶工厂将污水排到污水处理厂统一处理,每处理1m污水需付8元的排污费.
(1)设该工厂每月生产x件产品,则方案一的利润是 元,方案二的利润是 元.(用含x的式子表示)
(2)当该工厂每月生产多少件产品时,依方案一处理污水每月所获利润比依方案二处理污水每月所获利润少6000元?
(3)当该工厂每月生产10000件产品时,若你作为厂长,在获得更多利润的前提下,会选用哪种处理污水的方案?请通过计算加以说明.(利润=出厂价-成本价-污水处理费)
专题训练14电费与水费问题
1.今年,号称“千湖之省”的湖北正遭受大旱,为提高学生环保意识,节约用水,某校数学教师编制了一道应用题:为保护水资源,某市制定一套节水的管理措施,其中对居民生活用水收费作如下规定:
月用水量(吨) 单价(元/吨)
不大于10吨部分 1.5
大于10吨不大于50吨部分 2
大于50吨部分 3
(1)若某用户六月份用水量为18吨,求其应缴纳的水费;
(2)记该用户六月份用水量为x吨,试用含x的代数式表示其所需缴纳水费y(单位:元).
(3)某用户某月交水费125元,该用户用水多少吨?
2.为了加强公民的节水意识,合理利用水资源,某市采用价格调控的手段达到节水的目的,该市自来水收费的收费标准如下表:
收费标准(注:水费按月份结算)
每月用水量 单价(元/立方米)
不超出6立方米的部分 2
超出6立方米不超出10立方米的部分 4
超出10立方米的部分 8
例如:某户居民1月份用水8立方米,应收水费为(元)
请根据上表的内容解答下列问题:
(1)该户居民2月份交水费48元,2月份用水量为______________立方米?
(2)若该户居民3月份用水a立方米(其中),请用含a的代数式表示应收水费 元.
(3)该户居民4、5两个月共用水15立方米(5月份的用水量超过了4月份的用水量),两个月共交水费44元,求该户居民4、5月份各用多少立方米?
3.长春市居民生活用电阶梯收费标准如表:
档级 月用电量 电价
第1档 170度以下(含170度) 元/度
第2档 170度度(含260度) 超过170度部分按元/度
第3档 260度以上 超过260度部分按元/度
根据收费标准,解答下列问题:
(1)小军家6月用电量为150度,求这个月应缴的电费;
(2)小军家7月用电量在第2档的范围内,若设用电量为x度,则这个月应缴电费 元(用含x的代数式表示);
(3)8月出现了高温天气,小军家缴电费元,求这个月的用电量.
专题训练15数轴动点问题
1.在数学综合实践活动课上,小张同学借助两根木棒研究数轴上的动点问题:
如图,数轴上有A,B,C三个点,分别对应有理数和6.小张把两根木棒放在数轴上,使点 P与点A重合,点M与点B重合,点Q 在点 P的左边,点N在点M 的左边,且,木棒从点B开始一直向右以每秒1个单位长度的速度匀速运动;木棒同时从点A 开始向右以每秒3个单位长度的速度匀速运动,设运动时间为t秒.
(1)当时,点Q对应的有理数为 ,点M 对应的有理数为 ;
(2)在点 P 运动到点C之前,当线段和线段的长度之和为8时,求t的值;
(3)当点P运动到C时,木棒立即以每秒2个单位的速度返回(返回过程中,仍然保持点Q在点P的左边),当点P再次运动到点A时,两根木棒立即同时停止运动,点D为木棒的中点,在整个运动过程中,是否存在某些时间段,使得点D到点P、Q、M、N的距离之和为一个定值 若存在,求出这个定值和持续的总时长;若不存在,请说明理由.
2.如图所示,已知数轴上两点对应的数分别为、,点为数轴上任意一点,其对应的数为.
(1)的长为__________;
(2)当点到点、点的距离相等时,求的值;
(3)如果点以每秒个单位长度的速度从点出发沿数轴向右运动,同时点从点出发以每秒个单位长度的速度沿数轴向左运动,当点到达点时,点与同时停止运动.设点的运动时间为秒().当点、点与点三个点中,其中一个点到另外两个点的距离相等时,请直接写出的值.
3.阅读材料:
数轴是一个非常重要的数学工具,它使数和数轴上的点建立起对应关系,揭示了数与点之间的内在联系,若、为有理数,则表示数与数的差的绝对值,也可以理解为与两数在数轴上所对应的两点之间的距离.
例如:如图①,在数轴上,有理数3与1对应两点之间的距离为;有理数5与对应两点间的距离为;有理数与3对应两点之间的距离为…
(1)问题提出:
如图②,数轴上点表示的数为,点表示的数为13,、两点之间的距离为______,若点是点和点之间的一个动点,点表示的数为,则的值为______.
(2)拓展探究:如图②,数轴上点表示的数为,点表示的数为13,若点从点出发,以每秒3个单位长度的速度沿数轴向右运动,同时点从点出发.以每秒2个单位长度的速度向左运动.设运动时间为秒
①用含的式子表示:秒后,点表示的数为______;点表示的数为______;
②求当为何值时,、两点相遇,并写出相遇点所表示的数.
(3)类比延伸:在(2)的条件下,如果、两点相遇后按照原来的速度继续运动,当各自到达线段的端点后立即改变运动方向,并以原来的速度在线段上做往复运动,那么从开始运动经过多长时间、两点第二次相遇.请直接写出所需要的时间和此时相遇点所表示的数.
专题训练16几何动点问题
1.如图,在 ABC中,,,,,为 ABC的高.
(1)求 ABC的面积和的长;
(2)若点从点出发,以的速度沿边、运动,到达点后即刻停止运动.设运动时间为,则当为何值时,的面积为?
2.如图,在 ABC中,,,,点是的中点,动点从点出发,以每秒的速度沿运动,最终到达点.若设点运动的时间是秒,那么当取何值时, APE的面积等于?
3.已知长方形中,,,连结,点从点出发,以的速度沿的方向运动,设点运动的时间为(秒)().
(1)当时, ;当时, ;
(2)若点在上,用含的代数式表示的面积;
(3)在整个运动过程中,当的面积为长方形面积的时,求的值;
(4)若动点与点同时从点出发,以的速度沿的方向运动,当、相遇时,他们同时停止运动,当为直角三角形时,直接写出的值或取值范围.
参考答案
专题训练01岁数问题
1.C
【分析】本题考查了一元一次方程的应用——年龄问题.熟练掌握年龄差不变,是解题的关键.
设两年前儿子x岁,则两年前父亲岁,根据父子二人今年年龄之和为40岁,列出一元一次方程,解方程,即可解决问题.
【详解】解:设两年前儿子x岁,则两年前父亲岁,
由题意得:,
解得:,
∴,
即两年前父亲32岁,
故选:C.
2.12
【分析】本题考查一元一次方程的应用.根据设年前强强的年龄是王飞年龄的2倍,表示出两人的年龄即可得出方程,解方程即可求解.
【详解】解:年前强强的年龄是王飞年龄的2倍,
则,
解得:,
则(岁).
故答案为:12.
3.(1)解:设丢番图的寿命为x岁,
根据题意得儿子出生时丢番图的年龄为岁,儿子的寿命为岁,
故答案为:,;
(2)设丢番图的寿命为岁,
根据题意得:,
解得:,
当时,可得儿子的寿命为,
答:丢番图的寿命为84岁,儿子的寿命为42岁.
专题训练02数字问题
1.D
【分析】本题考查了数字类规律探索,正确求出每行、每列、每条对角线上的三个数之和是解题关键.先求出每行、每列、每条对角线上的三个数之和,再求出第三行第一列的数,由此即可得.
【详解】解:∵三行、三列、两对角线上的三个数之和都相等,
∴每行、每列、每条对角线上的三个数之和为,
∴第三行第一列的数为,
∴,
解得,
故选:D.
2.1458
【分析】本题考查有理数的数字规律和一元一次方程的实际应用.正确表示出三个相邻的数,并列出方程是解题关键.根据数列规律为后一个数是前一个数的倍,则设中间的数是x,则前一个数是,后一个数是,再结合题意列出方程求解即可.
【详解】解:根据题意设中间的数是x,则前一个数是,后一个数是,
因为这三个相邻数的和是,
所以,
解得:.
所以这三个数中,中间的数是1458.
故答案为:1458.
3.解:设原五位数去掉个位数后的四位数为,则原五位数可表示为,
根据题意得,
解得,
,
答:原五位数是37644.
专题训练03比赛积分问题
1.B
【分析】本题考查了一元一次方程的应用,由记录表格可知,答对一道题得6分,答错一道题扣1分,设答对x道题,则得分分,逐一对选项求解,根据x为正整数,即可得到答案.
【详解】解:由甲同学得分情况可知,答对一道题得分,
由乙同学得分情况可知,答错一道题扣分,
丙同学得分也符合;
设答对x道题,则答错道题,
∴得分,且x为正整数,
A、,解得:,不符合题意;
B、,解得:,符合题意;
C、,解得:,不符合题意;
D、,解得:,不符合题意;
故选:B.
2. 18 16
【分析】本题考查了一元一次方程的实际应用,根据题意找准数量关系,并正确列出一元一次方程是解题的关键.设这个队在这次比赛中,胜了x场,则平了场,根据题意,共得70分,列出方程,求解方程即可解答.
【详解】解:设这个队在这次比赛中,胜了x场,则平了场,
根据题意,得:,
解得:,
所以,
所以这个队在这次比赛中,胜了18场,平了16场.
故答案为:18;16.
3.解:思考:设胜一场积x分,从A队积分得出
,
解得,
即胜一场积3分;
设平一场积y分,从B队积分得出
,解得,
即平一场积1分;
设负一场积z分,从C队积分得出
,
解得,,
即负一场积0分;
故答案为3,1,0;
探究:(1)∵胜利场,负的场数比胜利场数少5场,
∴负的场数为,
∴平的场数为,
∴积分为:
;
(2)设东方足球队共胜利了a场,则平场,根据题意得,
,
解得,,
答:东方足球队共胜利了15场;
拓展:设雄鹰足球队胜b场,则平了场,由题意,得
,
解得,,
由于场数是整数,故不合题意,
所以雄鹰足球队的胜场总积分不能等于它的平场总积分.
专题训练04日历问题
1.A
【分析】本题考查一元一次方程的实际应用,找出等了关系列出相应的方程、正确验证是解题的关键.
设第一行的中间的数为x,则其它的三个数分别为:,, ,于是这四个数的和可以表示为,然后代入各选项的数进行求解验证即可.
【详解】解:设第一行的中间的数为x,且x为正整数,
则其它的三个数分别为:,, 则这四个数的和为:;
A.若,解得,故该选项符合题意;
B.若,解得,不是整数,故该选项不符合题意;
C.若,解得,不是整数,故该选项不符合题意;
D.若,解得,由于17在日历表中位于最右边的位置,故该选项不符合题意;
故选:A.
2.11
【分析】本题主要考查一元一次方程的应用,设四个数中最小的数为x,则另外三个数分别为,,,进而可得出四个数之和,求出x的值即可得出结论.
【详解】解:设四个数中最小的数为x,则另外三个数分别为,,,
∴四个数的和.
当时,,
解得,,
故答案为:11.
3.(1)解:∵,
∴,,,,
∴;
故答案为:68;
(2)解:由题意得,,,;
∴,
∴;
(3)解:能等于2025,理由如下:
∵,
当时,,
∵405为奇数,,所以2025在第34行第5列,
∴的值能等于2025.
专题训练05古代问题
1.C
【分析】本题考查了一元一次方程的应用,弄清题意,找准等量关系列出方程是解题的关键;
根据“鸡的价钱人数;鸡的价钱人数”即可列出方程;
【详解】解:共有个人共同出钱买鸡,
根据题意,则有;
故选:C
2.3
【分析】此题考查了一元一次方程的实际应用,正确理解题意确定等量关系是解题的关键.
设顶层有x盏灯,根据“有一座七层高塔,从底层开始,每层安装的灯的数目都是上一层的2倍”列出一元一次方程求解即可.
【详解】解:设顶层有x盏灯,
由题意得,
解得,
故答案为:3.
3.解:设共有x人,
根据题意,得,
解得,
则.
答:共有33人,金价是9800.
专题训练06销售问题
1.C
【分析】本题主要考查了一元一次方程的应用——折扣问题,熟练掌握售卖价、成本、利润的关系列出方程是解题关键.
根据售卖价、成本、利润的关系依列出方程并求解即可.
【详解】解:根据题意,
得,
解得,
即该商品的标价是3000元.
故选:C.
2.元
【分析】本题考查了一元一次方程的应用,理解题意并正确列方程是解题关键.分别设盈利的衣服进价为元,亏损的衣服进价为元,根据题意列一元一次方程求解即可.
【详解】解:设盈利的衣服进价为元,
则,
解得:,
设亏损的衣服进价为元,
则,
解得:,
元,
卖这两件衣服总进价为元,
故答案为:元.
3.(1)解:设第一次购进乙种商品x件,则购进甲种商品件,
根据题意得:,
解得:,
∴,
第一次获得的总利润为:(元)
答:该超市第一次购进甲种商品100件,乙种商品50件,第一次获得的总利润为2000元;
(2)设第二次乙种商品是按原价打y折销售,
根据题意得:,
解得:,
答:第二次乙商品是按原价打8折销售.
专题训练07比例分配问题
1.B
【分析】此题等量关系明确,不过要掌握有比例出现的题目中未知数的设法,设一份为x,此题可设三角形三边分别为2x、3x、3x,由最短边长6,列方程即可求解.
【详解】所求三角形的三边的比是2:3:3,可设三角形三边分别为2x、3x、3x,
2x=6,解得x=3,
因而另外两边的长是3x=9,3x=9.
则三角形的周长是6+9+9=24.
故选:B.
2.144°
【解析】略
3.解:设需要药液千克,则需要水千克,由题意得:
,
解得:,
答:需要药液5千克.
专题训练08行程问题
1.解:设小明出发x小时后追上小亮,
由题意得:,
解得,
答:小明出发2小时后追上小亮.
2.解:设船在静水中的平均速度为每小时千米.
根据题意得:
解得
答:船在静水中的平均速度为每小时千米.
3.(1)解:设小梦出发小时后,第一次追上红队,
依据题意可得:,
解得:,
答:小梦出发小时后,第一次追上红队;
(2)解:设小梦从出发到他折返后第一次与蓝队相遇,经过了小时,
依据题意可得:,
解得:,
答:小梦从出发到他折返后第一次与蓝队相遇,经过了小时;
(3)解:设蓝队出发后经过小时追上红队,
依据题意可得:,
解得:,
蓝队出发后经过小时追上红队,
此时小梦行驶的路程是:(千米),
答:当蓝队追上红队时,小梦行驶的路程是千米.
专题训练09配套问题
1.解:设安排名工人生产茶壶,则安排名工人生产茶杯,
每天生产的茶壶数为:个,每天生产的茶杯为:个,
根据题意得:,
解得,
,
答:应安排7名工人生产茶壶,安排18名工人生产茶杯使一天生产的茶壶和茶杯正好配套.
2.解:设应分配x名工人生产手套,则名工人生产玩具,
根据题意得,,
解得,
∴(名),
∴应分配16名工人生产手套,则12名工人生产玩具.
3.(1)解:设应安排x名工人生产螺柱,名工人生产螺母.
解得
答:应安排10名工人生产螺柱,12名工人生产螺母.
(2)设安排y小时生产螺柱.
解得.
.
根据实际意义取13090.
根据实际意义螺柱取,
则首先安排10名工人生产12000个螺柱,13名工人生产26000个螺母,
另外1名工人用个小时生产1090个螺柱,剩余个小时生产个螺母.但最多生产螺柱和螺母13090套.
专题训练10工程问题
1.解:设先安排整理的人员有x人,依题意得,
,
解得: ,
答:先安排整理的人员有5人.
2.解:设还需x天才能完成任务,根据题意得:
,
解得:,
答:甲、乙两队合作还需2天才能完成任务.
3.(1)解:根据题意:,
答:两人合作2天,完成的工作量占这项工程总量的;
(2)解:设乙还需要x天才能完成,根据题意:
解得:,
答:乙还需要10天才能完成.
专题训练11图形问题
1.解:(1)如图2,
∵两张相同长方形纸片拼接成的“”型图是长方体的展开图,且长方形纸片和长方形纸片的长都是,宽都是,
∴,,,
设,则,
依题意,得:,
解得:,
∴,
即的长为;
(2)①剪成长为,宽为的两个长方形,拼成“”型图如下图,
此时长方体的体积为:;
②剪成长为,宽为的两个长方形,拼成“”型图如下图,
此时长方体的体积为:;
综上所述,该展开图折叠成的长方体的体积是或,
故答案为:或;
(3)∵长方形纸片和长方形纸片拼接成的“”型图是某长方体的展开图,且,,,
∴,,
∴,
∴,
∴,
∴;
故答案为:;
(4)设甲长方形纸片的长为,则乙长方形纸片的长为,
依题意,得:,
解得:,
∴甲长方形纸片的长为.
2.解:(1)观察图1可知:中间的每个正方形都对应了两个等腰直角三角形,所以每增加一块正方形地砖,等腰直角三角形地砖就增加2块;
故答案为:2;
(2)观察图形2可知:中间一个正方形的左上、左边、左下共有3个等腰直角三角形,它右上和右下各对应了一个等腰直角三角形,右边还有1个等腰直角三角形,即;图3和图1中间正方形右上和右下都对应了两个等腰直角三角形,均有图2一样的规律,图3:;归纳得:(即);
∴若一条这样的人行道一共有n(n为正整数)块正方形地砖,则等腰直角三角形地砖的块数为 块;
故答案为:;
(3)由规律知:等腰直角三角形地砖块数是偶数,
∴用块,
再由题意得:,
解得:,
∴等腰直角三角形地砖剩余最少为1块,则需要正方形地砖1010块.
3.解:任务:由题意可得设计部分的长为,宽为,
任务:∵设计的部分也是长方形,且长是宽的倍,
∴,
解得:
∴四周宽度的值为;
任务:()设每个栏目的水平宽度为,每个栏目竖向两列中间间隔为,则横向中间间隔为,
根据正方形边长相等可得:,
解得,
答:每个栏目的水平宽度为;
(),
∴长方形栏目与栏目之间的中缝的间距为.
专题训练12和差倍分问题
1.解:设编程竞赛获得个奖项,则机器人竞赛获得个奖项.
可得.
解得,
所以.
答:编程竞赛获得个奖项,机器人竞赛获得个奖项.
2.解:设绘画爱好者有x人,
,
解得,
即绘画爱好者有人,
则,
即这批宣纸有张,
答:绘画爱好者有人,这批宣纸有张.
3.解:设调入名工人,
根据题意得:,
解得:,
∴调入6名工人.
专题训练13方案问题
1.(1)解:由题意得:若该客户按方案一购买,需付款为(元),
若该客户按方案二购买,需付款为(元),
故答案为:;.
(2)解:由题意得:,
解得,
答:买50双袜子时按方案一和方案二购买费用一样.
2.(1)解:(1)办日卡,需要花费元,
办会员卡,办卡就需元,显然不合题意,
办普通卡,需要花费元,
最少需要花费元;
(2)①办会员卡需要花费,
办普通卡需要花费,
故答案为:,;
②解方程,
解得,
时,办普通卡划算,
时,办哪种卡一样,
时,办会员卡划算;
3.(1)方案一的利润为:(元);
方案二的利润为:(元).
故答案为:;
(2)根据题意,得
,
解得.
所以当该工厂每月生产15000件产品时,方案一处理污水每月所获利润比方案二每月所获利润少6000元;
(3)当时,
,
因为,
所以选择方案二.
专题训练14电费与水费问题
1.(1)解:∵,
∴应缴纳水费为:
元;
(2)吨时,,
时,,
时,
;
∴
(3)因为当时, ,
,
所以 ,
解得:,
则该用户用水60吨.
2.(1)解:当用水量为6立方米时,应交水费(元),
当用水量为10立方米时,应交水费(元),
∵该户居民2月份交水费48元,
∴该户居民2月份用水量超过10立方米
∴设该户居民2月份用水量 x立方米
根据题意得,
解得
∴2月份用水量为立方米;
(2)解:∵该户居民3月份用水a立方米(其中)
∴;
∴应收水费元;
(3)解:设该户居民4月份用水m立方米,则5月份用水立方米,
∵5月份的用水量超过了4月份的用水量
∴当4月份用水不超过6立方米,5月份用水不超过10立方米时,
根据题意得,
解得
∴,不符合题意,应舍去
当4月份用水不超过6立方米,5月份用水超过10立方米时,
解得
∴(立方米)
∴该户居民4月份用水4立方米,则5月份用水11立方米;
当4月份用水超过6立方米,5月份用水不超过10立方米时,
根据题意得,
方程无解,应舍去
综上所述,该户居民4月份用水4立方米,则5月份用水11立方米.
3.(1)解:因为,
所以这个月应缴的电费为(元),
答:小军家这个月应缴的电费为元.
(2)解:因为小军家7月用电量在第2档的范围内,
所以小军家这个月应缴电费为元,
故答案为:.
(3)解:设这个月的用电量为度,
因为,
所以,
则可列方程为,
解得,
答:这个月的用电量为280度.
专题训练15数轴动点问题
1.(1)解:∵数轴上有A,B,C三个点,分别对应有理数和6.小张把两根木棒放在数轴上,使点 P与点A重合,点M与点B重合,点Q 在点 P的左边,点N在点M 的左边,且,
∴时,点Q对应的有理数是,点M,点N分别对应的有理数为,,
∵木棒从点B开始一直向右以每秒1个单位长度的速度匀速运动;木棒同时从点A 开始向右以每秒3个单位长度的速度匀速运动,设运动时间为t秒.
∴当时,则点Q对应的有理数是,点M对应的有理数为,
故答案为:;
(2)解:依题意,点P运动到点C所需要的时间是(秒),
在点P运动到点C之前,点P,点Q所对应的有理数是,,点M,点N所对应的有理数是,,
当未追上时,则,
,
∵线段和线段的长度之和为8,
∴
解得;
当追上后,则,
,
∵线段和线段的长度之和为8,
∴
解得(舍去);
(3)解:存在,过程如下:
∵点D为木棒的中点,且在点P运动到点C之前,点P,点Q所对应的有理数是,,
∴点D所对应的有理数是,点D到点P、Q的距离之和为一个定值,即为的长度,即为2,
∵使得点D到点P、Q、M、N的距离之和为一个定值,
∴点D所对应的有理数在木棒内部(包括木棒的端点上)会满足条件,
∵点M,点N所对应的有理数是,,
∴当点D与点N所对应的有理数是相等时,则,
解得,
∴当点D与点M所对应的有理数是相等时,则,
解得,
在时,,
∴(秒),
此时点D到点P、Q、M、N的距离之和为一个定值,且为,
当点P运动到点C后返回时,
则,,,
∴点D所对应的有理数是,
∴当点D与点N所对应的有理数是相等时,则,
解得,
∴当点D与点M所对应的有理数是相等时,则,
解得,
在时,,
∴(秒),
此时点D到点P、Q、M、N的距离之和为一个定值,且为,
综上所述,点D到点P、Q、M、N的距离之和为一个定值,且为,持续的总时长为(秒).
2.(1)解:的长为,
故答案为:;
(2)解:根据题意,只有点在点、之间时才有点到点、点的距离相等,
∴,
解得:;
(3)解:由题意可得,,
∴秒后,点表示的数是,点表示的数是,
当时,,
解得:或(舍去);
当时,,
解得:或;
当时,,
解得:或(舍去);
综上,或或或.
3.(1)解:∵A表示的数为,点B表示的数为13,
∴,
∵点是点和点之间的一个动点,点表示的数为,
∴,,
∴;
故答案为:15;15;
(2)解:①t秒后,点P表示的数为,点Q表示的数为;
故答案为:;;
②根据题意得:,
解得,
相遇点所表示的数为;
答:当t为3时,P,Q两点相遇,相遇点所表示的数是7;
(3)解:由已知得:P运动5秒到B,Q运动秒到A,
返回途中,P表示的数是,Q表示的数是,
根据题意得:,
解得,
第二次相遇点所表示的数为:,
答:所需要的时间为9秒,相遇点所表示的数是1.
专题训练16几何动点问题
1.(1)解:∵在 ABC中,,,,
∴,
又∵,为 ABC的高,
∴,
∴;
(2)解:①当点在上时,
由得,
∴;
②当在上时,,
由得,
解得,
∴的值为2.5或14.5时,的面积为.
2.解:①如图1,当点P在上,
∵在 ABC中,,,,点是的中点,
∴,,
∵,
∴;
②如图2,当点P在上时,
∵E是的中点,
∴,
又,
∴,
∵,
∴,
解得:;
综上所述,当或时, APE的面积等于10.
3.(1)当时,点在上,
∴,
当时,点在上,
∴的运动路程为,
∴,
∴,
故答案为:;;
(2)∵点在上,
∴,
∴;
(3)四边形的面积为,
∴的面积为长方形面积的时,,
当点在上时,,
解得;
当在上时,,
∴,
解得;
当在上时,,
∴,
解得;
当在上时,,
∴,
解得;
综上,当的面积为长方形面积的时,的值为或或或;
(4)有两种情况:
当点在上时,是直角三角形,
此时,
当点在上,点在上时,是直角三角形,
即,
∴,
解得,
则后,都在上,不是直角三角形,
综上,当为直角三角形时,或
专题训练01岁数问题
1.父子二人今年年龄之和为40岁,已知两年前父亲年龄是儿子的8倍,那么两年前父亲( )岁.
A.28 B.30 C.32 D.35
2.强强今年15岁,王飞今年9岁,当强强在 岁时,强强的年龄是王飞的2倍.
3.古希腊数学家丢番图(公元3~4世纪),是代数学的创始人之一.在他的墓碑上记载着:“他生命的是幸福的童年;再活了他生命的,两 长起了细细的胡须;又度过了一生的,他结婚了;再过5年,他有了儿子,感到很幸福;可是儿子只活了他全部年龄的一半;儿子死后,他在极度痛苦中度过了4年,与世长辞了.”
(1)设丢番图的寿命为x岁,根据题意得儿子出生时丢番图的年龄为_________岁,儿子的寿命为_________岁;
(2)用你喜欢的方式,求出丢番图和儿子的寿命分别为多少岁?
专题训练02数字问题
1.我国的“洛书”中记载着世界上最古老的一个幻方将这九个数字填入的方格内,使三行、三列、两对角线上的三个数之和都相等.如图所示的幻方中,字母m所表示的数是( )
A.8 B.6 C.9 D.4
2.有一列数,按一规律排列成2,,18,,162,,….其中某三个相邻数的和是,则这三个数中,中间的数是 .
3.一个五位数,个位上的数为4,这个五位数加上6120后所得的新五位数的万位、千位、百位、十位、个位上的数恰巧分别为原五位数的个位、万位、千位、百位、十位上的数,试求原五位数.
专题训练03比赛积分问题
1.兴华中学组织七年级学生数学知识竞赛答题,此活动共设有20道选择题,各题分值相同,每题必答.右表记录了小徐、小张、小高三名学生的得分情况,则另一名学生小李的得分可能是( )
学生 答对题数 答错题数 得分:
小徐 20 0 120
小张 18 2 106
小高 15 5 85
A.40 B.50 C.60 D.70
2.某市举办足球比赛,每队均需赛34场,其中胜一场得3分,平一场得1分,负一场得0分.某队在这次比赛中一场未负,共得70分,这个队在这次比赛中,胜了 场,平了 场.
3.2024年7月到8月,某市举办足球联赛,共有20支足球队参赛,经过前三轮(每个足球队比赛三场)比赛之后,A、B、C三支足球队积分如下表:
足球队 比赛场数 胜场 平场 负场 积分
A 3 3 0 0 9
B 3 2 1 0 7
C 3 1 1 1 4
思考:根据上表,我们可以得到本次足球联赛积分规则:胜利一场积 分;平一场积 分,负一场积 分;
探究:
(1)若一支足球队共进行了场比赛,胜利场,负的场数比胜利场数少5场,用含,的代数式表示这支足球队的总积分;
(2)列方程解决问题:东方足球队是20支足球队中的一员,经过18轮激战,保持连续不败,共积分48分,那么东方足球队共胜利了多少场
拓展:雄鹰足球队共进行了16场比赛,其中负了1场,那么雄鹰足球队的胜场总积分能等于它的平场总积分吗 为什么
专题训练04日历问题
1.如图,在2023年6月的日历表中用“T型”框数字,框出数字的和可能是( )
A.27 B.36 C.100 D.75
2.在某月的月历表中,用如图所示的“S”型框任意框出表中四个数,若框出的四个数的和是58,则框中最小的数是 .
3.如图,将连续的奇数1,3,5,7,…按图1中的方式排成一个数表,用一个十字框框住5个数,这样框出的任意5个数(如图2)分别用a,b,c,d,x表示.
(1)若,则=______;
(2)设,用含x的式子分别表示M;
(3)判断(2)中M的值能否等于2025,请说明理由.
专题训练05古代问题
1.《九章算术》是中国传统数学最重要的著作之一.书中记载:“今有人共买鸡,人出九,盈十一;人出六,不足十六.问人数几何?”意思是:“有若干人共同出钱买鸡,如果每人出九钱,那么多了十一钱;如果每人出六钱,那么少了十六钱.问:共有几个人?设共有个人共同出钱买鸡,根据题意,可列一元一次方程为( )
A. B.
C. D.
2.明代数学家吴敬的《九章算法比类大全》中的数学名题“宝塔装灯”原文:远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问顶层几盏灯.题目大意是:远处有一座雄伟的七层宝塔,塔上挂了许多红灯,相邻两层下一层灯的盏数是上一层灯的盏数的2倍,共有381盏灯,则塔顶灯有 盏.
3.中国的《九章算术》是世界现代数学的两大源泉之一.书中有一盈不足问题:“今有共买金,人出四百,盈三千四百;人出三百,盈一百.问人数、金价各几何?”译文:今有数人共同买金子,每人出400,多出来3400;每人出300,多出来100,问:共有多少人?金价是多少?请解决这个问题.
专题训练06销售问题
1.某商品的成本是2000元,标价为m元,现打八折出售,仍可获利,则该商品的标价m等于( )
A.1000 B.2400 C.3000 D.3600
2.某商店在某一时间以每件60元的价格卖出两件衣服,其中一件盈利,另一件亏损,卖这两件衣服总进价 .
3.某超市第一次用7000元购进甲、乙两种商品,其中甲商品的件数是乙商品件数的2倍,甲、乙两种商品的进价和售价如表:
甲 乙
进价(元/件) 40 60
售价(元/件) 50 80
(1)该超市第一次购进的甲、乙两种商品各多少件?第一次获得的总利润为多少元?
(2)该超市第一次购进的甲、乙两种商品售完后,第二次又以第一次的进价购进甲、乙两种商品,其中甲商品的件数不变,乙商品的件数是第一次的3倍;甲商品按原价销售,乙商品打折销售,第二次两种商品都售完以后获得的总利润比第一次获得的总利润少,求第二次乙商品是按原价打几折销售?
专题训练07比例分配问题
1.一个三角形的三边之比为2∶3∶3,最短边为6,则这个三角形的周长为( )
A.32 B.24 C.25 D.36
2.将一个圆分割成四个小扇形,它们的圆心角的度数之比为1:2:3:4,则这四个小扇形中圆心角的度数最大是 .
3.一种农药,用药液和水按配制而成.要配制这种农药505千克,需要药液多少千克?
专题训练08行程问题
1.小明、小亮两人相距,小明先出发,小亮再出发,小明在后小亮在前,两人同向而行,小明的速度是,小亮的速度是,小明出发多长时间后追上小亮?
2.一艘船从甲码头到乙码头顺水而行,用了小时;从乙码头返回甲码头逆水而行,用了小时.已知水流的速度是每小时千米.求船在静水中的平均速度.
3.列方程解应用题:重庆一中某校区七年级学生在教育广场乘坐旅游汽车到户外参加拓展训练,七(1)班的学生乘坐红色车,组成红队,车速为60千米小时,七(2)班的学生乘坐蓝色车,组成蓝队,车速为80千米小时.红队出发1小时后,蓝队才出发,同时蓝队派联络员小梦自驾车在两队之间不断地来回进行联络,小梦自驾车的速度为100千米小时.
(1)小梦出发多久后,第一次追上红队;
(2)小梦从出发到他折返后第一次与蓝队相遇,经过了多少时间?
(3)当蓝队追上红队时,小梦行驶的路程是多少千米?
专题训练09配套问题
1.某茶具生产车间有25名工人生产茶壶和茶杯,1个茶壶和6个茶杯配成一套.已知一名工人一天可以生产3个茶壶或7个茶杯,要使一天生产的茶壶和茶杯正好配套,应分别安排多少名工人生产茶壶和茶杯?
2.自上海迪斯尼开园后一直吸引众多游客,某玩具生产商打算生产米老鼠玩具作为旅游纪念品,并为每个米老鼠玩具配一副手套.如果某车间有28名工人,每人一天平均能生产手套24个或米老鼠玩具16个.那么应分配多少名工人生产手套,多少名工人生产玩具,才能使当天生产的手套和玩具刚好配套?
3.某车间有22名工人,每人每天可以生产1200个螺柱或2000个螺母,1个螺柱需要配2个螺母.
(1)为使每天生产的螺柱和螺母刚好配套,应安排生产螺柱和螺母的工人各多少名?
(2)若车间现有24名工人,每人每天工作8个小时,工人根据需要可以转换生产螺柱或螺母的工作岗位.如何安排工人生产,使得螺柱和螺母尽可能多的配套,最多能生产多少套?
专题训练10工程问题
装修一间房屋,如果由一名装修工人单独完成需要40小时.现在,业主先安排了一部分工人工作2小时,随后又增加了4名工人与他们一起工作了3小时,最终恰好完成了装修工作.假设每名工人的工作效率都是相同的,那么最初被安排进行装修的工人有多少名?
2.甲、乙两个工程队安装排污管道,甲队单独安装需要4天完成,乙队单独安装需要8天完成.如果甲队先安装1天,剩下的管道由甲、乙两队合作完成,那么还需要几天才能安装完这些管道?
3.某项工程,甲单独做需10天完成,乙单独做需15天完成,
(1)两人合作2天,完成的工作量占这项工程总量的几分之几?
(2)如果两人合作2天后,甲有事先离开,剩下的工程由乙单独做,还需要几天才能完成?
专题训练11图形问题
1.【提出问题】
小涵把长方体纸盒展开,得到图1,可以看成由长方形纸片和长方形纸片按照一定要求.拼接成的“”型图.小涵尝试了反向思考,对“两长方形纸片需满足什么条件,拼接成的“”型图可以是长方体的展开图.”进行了思考.
【探索问题】
探索一:两张相同长方形纸片拼接成的“”型图.
经过尝试,发现两张相同长方形纸片拼接成的“”型图都是长方体的展开图.
(1)如图2,当长方形纸片和长方形纸片的长都是,宽都是时,求的长.
(2)现有一张长为,宽为的长方形纸片,如果将它先剪成两个相同长方形,再拼接成“”型图,则该展开图折叠成的长方体的体积是_____.
探索二:两张不同长方形纸片拼接成的“”型图
再次尝试,发现两张不同长方形纸片拼接成的“”型图不一定是长方体的展开图,两长方形的长和宽需满足某种条件.
(3)如图1,若长方形纸片和长方形纸片拼接成的“”型图是某长方体的展开图,设,,,,,则、、、之间满足的关系是_____.
【结论应用】
对于(3)中的结论,反之亦成立,请解决下面的问题.
(4)甲、乙两张长方形纸片的宽分别是和,拼接成的“”型图是表面积是的长方体展开图,求甲长方形纸片的长.
2.某长方形人行道由相同的灰色正方形地砖与相同的白色等腰直角三角形地砖排列而成,图1表示此人行道的地砖排列方式,其中正方形地砖为连续排列.
[观察思考]
当正方形地砖只有1块时,等腰直角三角形地砖有6块(如图2);当正方形地砖有2块时,等腰直角三角形地砖有8块(如图3);以此类推.
[规律总结]
(1)若人行道上每增加1块正方形地砖,则等腰直角三角形地砖增加 块;
(2)若一条这样的人行道一共有n(n为正整数)块正方形地砖,则等腰直角三角形地砖的块数为 (用含n的代数式表示).
[问题解决]
(3)现有2025块等腰直角三角形地砖,若按此规律再建一条人行道,要求等腰直角三角形地砖剩余最少,则需要正方形地砖多少块?
3.根据以下素材,探索完成任务.
如何设计宣传牌?
素材1 如图1是长方形宣传牌,长,宽,拟在上面书写24个字. ()中间 可以用来设计的部分也是长方形,且长是宽的倍. ()四周空白部分的宽度相等.
素材2 如图,为了美观,将设计部分分割成大小相等的左中右三个长方形栏目,栏目与栏目之间的中缝间距相等.
素材 如图,每个栏目划出正方形方格,中间有十字间隔,竖向两列中间间隔和横向中间间隔宽度比为.
问题解决
任务 分析数量关系 设四周宽度为,用含x的代数式分别表示设计部分的长和宽.
任务 确定四周宽度 求四周宽度的值.
任务 确定栏目大小 ()求每个栏目的水平宽度; ()求长方形栏目与栏目之间中缝的间距.
专题训练12和差倍分问题
1.在某届科技大赛中,甲团队在机器人竞赛与编程竞赛项目中共获得个奖项,且编程竞赛获得的奖项比机器人竞赛获得奖项的2倍少4个.分别求编程竞赛与机器人竞赛获得奖项的个数.
2.把若干宣纸分给七年级优秀绘画爱好者,若每人分3张,则剩余12本,若每人分5张,则缺10张,绘画爱好者有几人?这批宣纸有多少张.
3.某车间为提高生产总量,在原有16名工人的基础上,新调人若干名工人,使得调整后车间的总人数是调入工人人数的3倍多4人.求调人多少名工人.
专题训练13方案问题
1.某商场销售一款运动鞋和运动袜,运动鞋每双定价200元,运动袜每双定价40元.商场决定开展促销活动,活动期间向客户提供两种优惠方案,方案一:买一双运动鞋送一双运动袜;方案二:运动鞋和运动袜都按定价的付款,现某客户要到该商场购买运动鞋10双和运动袜x双.
(1)若该客户按方案一购买,需付款________________元(需化简);若该客户按方案二购买,需付款_____________元(需化简).
(2)买多少双袜子时按方案一和方案二购买费用一样?
2.某文体中心提供阅读、观影、球类、游泳、器械等多种文体活动,现有三种收费方式.详情见下表:
收费方式 详细介绍
日卡 日卡一张元
会员卡 办卡需元,每活动小时收费元
普通卡 进入文体中心要收取元/日,可免费文体活动小时,后续收费元/小时
(注:不足一个小时的按一小时计算)
(1)小明打算这周六去文体中心活动小时,最少需要花费________元;
(2)小明打算一个月(天)都去文体中心活动,每天活动的时间为小时(为正整数,且).
①如果小明选择办会员卡一个月需要花费________元;选择办普通卡一个月需要花费________元:(用含的代数式表示)
②对于会员卡和普通卡两种不同的收费方式,哪种更划算?
3.某工厂生产一种产品,每件产品的出厂价为 40元,其成本价为 20元,在生产过程中平均每生产一件产品有0.1m的污水排出,为净化环境,工厂设计了两种处理污水的方案.
方案一∶工厂污水先净化处理后再排出,每处理1m污水所用费用为2元,并且每月排污设备损耗为15000元.
方案二∶工厂将污水排到污水处理厂统一处理,每处理1m污水需付8元的排污费.
(1)设该工厂每月生产x件产品,则方案一的利润是 元,方案二的利润是 元.(用含x的式子表示)
(2)当该工厂每月生产多少件产品时,依方案一处理污水每月所获利润比依方案二处理污水每月所获利润少6000元?
(3)当该工厂每月生产10000件产品时,若你作为厂长,在获得更多利润的前提下,会选用哪种处理污水的方案?请通过计算加以说明.(利润=出厂价-成本价-污水处理费)
专题训练14电费与水费问题
1.今年,号称“千湖之省”的湖北正遭受大旱,为提高学生环保意识,节约用水,某校数学教师编制了一道应用题:为保护水资源,某市制定一套节水的管理措施,其中对居民生活用水收费作如下规定:
月用水量(吨) 单价(元/吨)
不大于10吨部分 1.5
大于10吨不大于50吨部分 2
大于50吨部分 3
(1)若某用户六月份用水量为18吨,求其应缴纳的水费;
(2)记该用户六月份用水量为x吨,试用含x的代数式表示其所需缴纳水费y(单位:元).
(3)某用户某月交水费125元,该用户用水多少吨?
2.为了加强公民的节水意识,合理利用水资源,某市采用价格调控的手段达到节水的目的,该市自来水收费的收费标准如下表:
收费标准(注:水费按月份结算)
每月用水量 单价(元/立方米)
不超出6立方米的部分 2
超出6立方米不超出10立方米的部分 4
超出10立方米的部分 8
例如:某户居民1月份用水8立方米,应收水费为(元)
请根据上表的内容解答下列问题:
(1)该户居民2月份交水费48元,2月份用水量为______________立方米?
(2)若该户居民3月份用水a立方米(其中),请用含a的代数式表示应收水费 元.
(3)该户居民4、5两个月共用水15立方米(5月份的用水量超过了4月份的用水量),两个月共交水费44元,求该户居民4、5月份各用多少立方米?
3.长春市居民生活用电阶梯收费标准如表:
档级 月用电量 电价
第1档 170度以下(含170度) 元/度
第2档 170度度(含260度) 超过170度部分按元/度
第3档 260度以上 超过260度部分按元/度
根据收费标准,解答下列问题:
(1)小军家6月用电量为150度,求这个月应缴的电费;
(2)小军家7月用电量在第2档的范围内,若设用电量为x度,则这个月应缴电费 元(用含x的代数式表示);
(3)8月出现了高温天气,小军家缴电费元,求这个月的用电量.
专题训练15数轴动点问题
1.在数学综合实践活动课上,小张同学借助两根木棒研究数轴上的动点问题:
如图,数轴上有A,B,C三个点,分别对应有理数和6.小张把两根木棒放在数轴上,使点 P与点A重合,点M与点B重合,点Q 在点 P的左边,点N在点M 的左边,且,木棒从点B开始一直向右以每秒1个单位长度的速度匀速运动;木棒同时从点A 开始向右以每秒3个单位长度的速度匀速运动,设运动时间为t秒.
(1)当时,点Q对应的有理数为 ,点M 对应的有理数为 ;
(2)在点 P 运动到点C之前,当线段和线段的长度之和为8时,求t的值;
(3)当点P运动到C时,木棒立即以每秒2个单位的速度返回(返回过程中,仍然保持点Q在点P的左边),当点P再次运动到点A时,两根木棒立即同时停止运动,点D为木棒的中点,在整个运动过程中,是否存在某些时间段,使得点D到点P、Q、M、N的距离之和为一个定值 若存在,求出这个定值和持续的总时长;若不存在,请说明理由.
2.如图所示,已知数轴上两点对应的数分别为、,点为数轴上任意一点,其对应的数为.
(1)的长为__________;
(2)当点到点、点的距离相等时,求的值;
(3)如果点以每秒个单位长度的速度从点出发沿数轴向右运动,同时点从点出发以每秒个单位长度的速度沿数轴向左运动,当点到达点时,点与同时停止运动.设点的运动时间为秒().当点、点与点三个点中,其中一个点到另外两个点的距离相等时,请直接写出的值.
3.阅读材料:
数轴是一个非常重要的数学工具,它使数和数轴上的点建立起对应关系,揭示了数与点之间的内在联系,若、为有理数,则表示数与数的差的绝对值,也可以理解为与两数在数轴上所对应的两点之间的距离.
例如:如图①,在数轴上,有理数3与1对应两点之间的距离为;有理数5与对应两点间的距离为;有理数与3对应两点之间的距离为…
(1)问题提出:
如图②,数轴上点表示的数为,点表示的数为13,、两点之间的距离为______,若点是点和点之间的一个动点,点表示的数为,则的值为______.
(2)拓展探究:如图②,数轴上点表示的数为,点表示的数为13,若点从点出发,以每秒3个单位长度的速度沿数轴向右运动,同时点从点出发.以每秒2个单位长度的速度向左运动.设运动时间为秒
①用含的式子表示:秒后,点表示的数为______;点表示的数为______;
②求当为何值时,、两点相遇,并写出相遇点所表示的数.
(3)类比延伸:在(2)的条件下,如果、两点相遇后按照原来的速度继续运动,当各自到达线段的端点后立即改变运动方向,并以原来的速度在线段上做往复运动,那么从开始运动经过多长时间、两点第二次相遇.请直接写出所需要的时间和此时相遇点所表示的数.
专题训练16几何动点问题
1.如图,在 ABC中,,,,,为 ABC的高.
(1)求 ABC的面积和的长;
(2)若点从点出发,以的速度沿边、运动,到达点后即刻停止运动.设运动时间为,则当为何值时,的面积为?
2.如图,在 ABC中,,,,点是的中点,动点从点出发,以每秒的速度沿运动,最终到达点.若设点运动的时间是秒,那么当取何值时, APE的面积等于?
3.已知长方形中,,,连结,点从点出发,以的速度沿的方向运动,设点运动的时间为(秒)().
(1)当时, ;当时, ;
(2)若点在上,用含的代数式表示的面积;
(3)在整个运动过程中,当的面积为长方形面积的时,求的值;
(4)若动点与点同时从点出发,以的速度沿的方向运动,当、相遇时,他们同时停止运动,当为直角三角形时,直接写出的值或取值范围.
参考答案
专题训练01岁数问题
1.C
【分析】本题考查了一元一次方程的应用——年龄问题.熟练掌握年龄差不变,是解题的关键.
设两年前儿子x岁,则两年前父亲岁,根据父子二人今年年龄之和为40岁,列出一元一次方程,解方程,即可解决问题.
【详解】解:设两年前儿子x岁,则两年前父亲岁,
由题意得:,
解得:,
∴,
即两年前父亲32岁,
故选:C.
2.12
【分析】本题考查一元一次方程的应用.根据设年前强强的年龄是王飞年龄的2倍,表示出两人的年龄即可得出方程,解方程即可求解.
【详解】解:年前强强的年龄是王飞年龄的2倍,
则,
解得:,
则(岁).
故答案为:12.
3.(1)解:设丢番图的寿命为x岁,
根据题意得儿子出生时丢番图的年龄为岁,儿子的寿命为岁,
故答案为:,;
(2)设丢番图的寿命为岁,
根据题意得:,
解得:,
当时,可得儿子的寿命为,
答:丢番图的寿命为84岁,儿子的寿命为42岁.
专题训练02数字问题
1.D
【分析】本题考查了数字类规律探索,正确求出每行、每列、每条对角线上的三个数之和是解题关键.先求出每行、每列、每条对角线上的三个数之和,再求出第三行第一列的数,由此即可得.
【详解】解:∵三行、三列、两对角线上的三个数之和都相等,
∴每行、每列、每条对角线上的三个数之和为,
∴第三行第一列的数为,
∴,
解得,
故选:D.
2.1458
【分析】本题考查有理数的数字规律和一元一次方程的实际应用.正确表示出三个相邻的数,并列出方程是解题关键.根据数列规律为后一个数是前一个数的倍,则设中间的数是x,则前一个数是,后一个数是,再结合题意列出方程求解即可.
【详解】解:根据题意设中间的数是x,则前一个数是,后一个数是,
因为这三个相邻数的和是,
所以,
解得:.
所以这三个数中,中间的数是1458.
故答案为:1458.
3.解:设原五位数去掉个位数后的四位数为,则原五位数可表示为,
根据题意得,
解得,
,
答:原五位数是37644.
专题训练03比赛积分问题
1.B
【分析】本题考查了一元一次方程的应用,由记录表格可知,答对一道题得6分,答错一道题扣1分,设答对x道题,则得分分,逐一对选项求解,根据x为正整数,即可得到答案.
【详解】解:由甲同学得分情况可知,答对一道题得分,
由乙同学得分情况可知,答错一道题扣分,
丙同学得分也符合;
设答对x道题,则答错道题,
∴得分,且x为正整数,
A、,解得:,不符合题意;
B、,解得:,符合题意;
C、,解得:,不符合题意;
D、,解得:,不符合题意;
故选:B.
2. 18 16
【分析】本题考查了一元一次方程的实际应用,根据题意找准数量关系,并正确列出一元一次方程是解题的关键.设这个队在这次比赛中,胜了x场,则平了场,根据题意,共得70分,列出方程,求解方程即可解答.
【详解】解:设这个队在这次比赛中,胜了x场,则平了场,
根据题意,得:,
解得:,
所以,
所以这个队在这次比赛中,胜了18场,平了16场.
故答案为:18;16.
3.解:思考:设胜一场积x分,从A队积分得出
,
解得,
即胜一场积3分;
设平一场积y分,从B队积分得出
,解得,
即平一场积1分;
设负一场积z分,从C队积分得出
,
解得,,
即负一场积0分;
故答案为3,1,0;
探究:(1)∵胜利场,负的场数比胜利场数少5场,
∴负的场数为,
∴平的场数为,
∴积分为:
;
(2)设东方足球队共胜利了a场,则平场,根据题意得,
,
解得,,
答:东方足球队共胜利了15场;
拓展:设雄鹰足球队胜b场,则平了场,由题意,得
,
解得,,
由于场数是整数,故不合题意,
所以雄鹰足球队的胜场总积分不能等于它的平场总积分.
专题训练04日历问题
1.A
【分析】本题考查一元一次方程的实际应用,找出等了关系列出相应的方程、正确验证是解题的关键.
设第一行的中间的数为x,则其它的三个数分别为:,, ,于是这四个数的和可以表示为,然后代入各选项的数进行求解验证即可.
【详解】解:设第一行的中间的数为x,且x为正整数,
则其它的三个数分别为:,, 则这四个数的和为:;
A.若,解得,故该选项符合题意;
B.若,解得,不是整数,故该选项不符合题意;
C.若,解得,不是整数,故该选项不符合题意;
D.若,解得,由于17在日历表中位于最右边的位置,故该选项不符合题意;
故选:A.
2.11
【分析】本题主要考查一元一次方程的应用,设四个数中最小的数为x,则另外三个数分别为,,,进而可得出四个数之和,求出x的值即可得出结论.
【详解】解:设四个数中最小的数为x,则另外三个数分别为,,,
∴四个数的和.
当时,,
解得,,
故答案为:11.
3.(1)解:∵,
∴,,,,
∴;
故答案为:68;
(2)解:由题意得,,,;
∴,
∴;
(3)解:能等于2025,理由如下:
∵,
当时,,
∵405为奇数,,所以2025在第34行第5列,
∴的值能等于2025.
专题训练05古代问题
1.C
【分析】本题考查了一元一次方程的应用,弄清题意,找准等量关系列出方程是解题的关键;
根据“鸡的价钱人数;鸡的价钱人数”即可列出方程;
【详解】解:共有个人共同出钱买鸡,
根据题意,则有;
故选:C
2.3
【分析】此题考查了一元一次方程的实际应用,正确理解题意确定等量关系是解题的关键.
设顶层有x盏灯,根据“有一座七层高塔,从底层开始,每层安装的灯的数目都是上一层的2倍”列出一元一次方程求解即可.
【详解】解:设顶层有x盏灯,
由题意得,
解得,
故答案为:3.
3.解:设共有x人,
根据题意,得,
解得,
则.
答:共有33人,金价是9800.
专题训练06销售问题
1.C
【分析】本题主要考查了一元一次方程的应用——折扣问题,熟练掌握售卖价、成本、利润的关系列出方程是解题关键.
根据售卖价、成本、利润的关系依列出方程并求解即可.
【详解】解:根据题意,
得,
解得,
即该商品的标价是3000元.
故选:C.
2.元
【分析】本题考查了一元一次方程的应用,理解题意并正确列方程是解题关键.分别设盈利的衣服进价为元,亏损的衣服进价为元,根据题意列一元一次方程求解即可.
【详解】解:设盈利的衣服进价为元,
则,
解得:,
设亏损的衣服进价为元,
则,
解得:,
元,
卖这两件衣服总进价为元,
故答案为:元.
3.(1)解:设第一次购进乙种商品x件,则购进甲种商品件,
根据题意得:,
解得:,
∴,
第一次获得的总利润为:(元)
答:该超市第一次购进甲种商品100件,乙种商品50件,第一次获得的总利润为2000元;
(2)设第二次乙种商品是按原价打y折销售,
根据题意得:,
解得:,
答:第二次乙商品是按原价打8折销售.
专题训练07比例分配问题
1.B
【分析】此题等量关系明确,不过要掌握有比例出现的题目中未知数的设法,设一份为x,此题可设三角形三边分别为2x、3x、3x,由最短边长6,列方程即可求解.
【详解】所求三角形的三边的比是2:3:3,可设三角形三边分别为2x、3x、3x,
2x=6,解得x=3,
因而另外两边的长是3x=9,3x=9.
则三角形的周长是6+9+9=24.
故选:B.
2.144°
【解析】略
3.解:设需要药液千克,则需要水千克,由题意得:
,
解得:,
答:需要药液5千克.
专题训练08行程问题
1.解:设小明出发x小时后追上小亮,
由题意得:,
解得,
答:小明出发2小时后追上小亮.
2.解:设船在静水中的平均速度为每小时千米.
根据题意得:
解得
答:船在静水中的平均速度为每小时千米.
3.(1)解:设小梦出发小时后,第一次追上红队,
依据题意可得:,
解得:,
答:小梦出发小时后,第一次追上红队;
(2)解:设小梦从出发到他折返后第一次与蓝队相遇,经过了小时,
依据题意可得:,
解得:,
答:小梦从出发到他折返后第一次与蓝队相遇,经过了小时;
(3)解:设蓝队出发后经过小时追上红队,
依据题意可得:,
解得:,
蓝队出发后经过小时追上红队,
此时小梦行驶的路程是:(千米),
答:当蓝队追上红队时,小梦行驶的路程是千米.
专题训练09配套问题
1.解:设安排名工人生产茶壶,则安排名工人生产茶杯,
每天生产的茶壶数为:个,每天生产的茶杯为:个,
根据题意得:,
解得,
,
答:应安排7名工人生产茶壶,安排18名工人生产茶杯使一天生产的茶壶和茶杯正好配套.
2.解:设应分配x名工人生产手套,则名工人生产玩具,
根据题意得,,
解得,
∴(名),
∴应分配16名工人生产手套,则12名工人生产玩具.
3.(1)解:设应安排x名工人生产螺柱,名工人生产螺母.
解得
答:应安排10名工人生产螺柱,12名工人生产螺母.
(2)设安排y小时生产螺柱.
解得.
.
根据实际意义取13090.
根据实际意义螺柱取,
则首先安排10名工人生产12000个螺柱,13名工人生产26000个螺母,
另外1名工人用个小时生产1090个螺柱,剩余个小时生产个螺母.但最多生产螺柱和螺母13090套.
专题训练10工程问题
1.解:设先安排整理的人员有x人,依题意得,
,
解得: ,
答:先安排整理的人员有5人.
2.解:设还需x天才能完成任务,根据题意得:
,
解得:,
答:甲、乙两队合作还需2天才能完成任务.
3.(1)解:根据题意:,
答:两人合作2天,完成的工作量占这项工程总量的;
(2)解:设乙还需要x天才能完成,根据题意:
解得:,
答:乙还需要10天才能完成.
专题训练11图形问题
1.解:(1)如图2,
∵两张相同长方形纸片拼接成的“”型图是长方体的展开图,且长方形纸片和长方形纸片的长都是,宽都是,
∴,,,
设,则,
依题意,得:,
解得:,
∴,
即的长为;
(2)①剪成长为,宽为的两个长方形,拼成“”型图如下图,
此时长方体的体积为:;
②剪成长为,宽为的两个长方形,拼成“”型图如下图,
此时长方体的体积为:;
综上所述,该展开图折叠成的长方体的体积是或,
故答案为:或;
(3)∵长方形纸片和长方形纸片拼接成的“”型图是某长方体的展开图,且,,,
∴,,
∴,
∴,
∴,
∴;
故答案为:;
(4)设甲长方形纸片的长为,则乙长方形纸片的长为,
依题意,得:,
解得:,
∴甲长方形纸片的长为.
2.解:(1)观察图1可知:中间的每个正方形都对应了两个等腰直角三角形,所以每增加一块正方形地砖,等腰直角三角形地砖就增加2块;
故答案为:2;
(2)观察图形2可知:中间一个正方形的左上、左边、左下共有3个等腰直角三角形,它右上和右下各对应了一个等腰直角三角形,右边还有1个等腰直角三角形,即;图3和图1中间正方形右上和右下都对应了两个等腰直角三角形,均有图2一样的规律,图3:;归纳得:(即);
∴若一条这样的人行道一共有n(n为正整数)块正方形地砖,则等腰直角三角形地砖的块数为 块;
故答案为:;
(3)由规律知:等腰直角三角形地砖块数是偶数,
∴用块,
再由题意得:,
解得:,
∴等腰直角三角形地砖剩余最少为1块,则需要正方形地砖1010块.
3.解:任务:由题意可得设计部分的长为,宽为,
任务:∵设计的部分也是长方形,且长是宽的倍,
∴,
解得:
∴四周宽度的值为;
任务:()设每个栏目的水平宽度为,每个栏目竖向两列中间间隔为,则横向中间间隔为,
根据正方形边长相等可得:,
解得,
答:每个栏目的水平宽度为;
(),
∴长方形栏目与栏目之间的中缝的间距为.
专题训练12和差倍分问题
1.解:设编程竞赛获得个奖项,则机器人竞赛获得个奖项.
可得.
解得,
所以.
答:编程竞赛获得个奖项,机器人竞赛获得个奖项.
2.解:设绘画爱好者有x人,
,
解得,
即绘画爱好者有人,
则,
即这批宣纸有张,
答:绘画爱好者有人,这批宣纸有张.
3.解:设调入名工人,
根据题意得:,
解得:,
∴调入6名工人.
专题训练13方案问题
1.(1)解:由题意得:若该客户按方案一购买,需付款为(元),
若该客户按方案二购买,需付款为(元),
故答案为:;.
(2)解:由题意得:,
解得,
答:买50双袜子时按方案一和方案二购买费用一样.
2.(1)解:(1)办日卡,需要花费元,
办会员卡,办卡就需元,显然不合题意,
办普通卡,需要花费元,
最少需要花费元;
(2)①办会员卡需要花费,
办普通卡需要花费,
故答案为:,;
②解方程,
解得,
时,办普通卡划算,
时,办哪种卡一样,
时,办会员卡划算;
3.(1)方案一的利润为:(元);
方案二的利润为:(元).
故答案为:;
(2)根据题意,得
,
解得.
所以当该工厂每月生产15000件产品时,方案一处理污水每月所获利润比方案二每月所获利润少6000元;
(3)当时,
,
因为,
所以选择方案二.
专题训练14电费与水费问题
1.(1)解:∵,
∴应缴纳水费为:
元;
(2)吨时,,
时,,
时,
;
∴
(3)因为当时, ,
,
所以 ,
解得:,
则该用户用水60吨.
2.(1)解:当用水量为6立方米时,应交水费(元),
当用水量为10立方米时,应交水费(元),
∵该户居民2月份交水费48元,
∴该户居民2月份用水量超过10立方米
∴设该户居民2月份用水量 x立方米
根据题意得,
解得
∴2月份用水量为立方米;
(2)解:∵该户居民3月份用水a立方米(其中)
∴;
∴应收水费元;
(3)解:设该户居民4月份用水m立方米,则5月份用水立方米,
∵5月份的用水量超过了4月份的用水量
∴当4月份用水不超过6立方米,5月份用水不超过10立方米时,
根据题意得,
解得
∴,不符合题意,应舍去
当4月份用水不超过6立方米,5月份用水超过10立方米时,
解得
∴(立方米)
∴该户居民4月份用水4立方米,则5月份用水11立方米;
当4月份用水超过6立方米,5月份用水不超过10立方米时,
根据题意得,
方程无解,应舍去
综上所述,该户居民4月份用水4立方米,则5月份用水11立方米.
3.(1)解:因为,
所以这个月应缴的电费为(元),
答:小军家这个月应缴的电费为元.
(2)解:因为小军家7月用电量在第2档的范围内,
所以小军家这个月应缴电费为元,
故答案为:.
(3)解:设这个月的用电量为度,
因为,
所以,
则可列方程为,
解得,
答:这个月的用电量为280度.
专题训练15数轴动点问题
1.(1)解:∵数轴上有A,B,C三个点,分别对应有理数和6.小张把两根木棒放在数轴上,使点 P与点A重合,点M与点B重合,点Q 在点 P的左边,点N在点M 的左边,且,
∴时,点Q对应的有理数是,点M,点N分别对应的有理数为,,
∵木棒从点B开始一直向右以每秒1个单位长度的速度匀速运动;木棒同时从点A 开始向右以每秒3个单位长度的速度匀速运动,设运动时间为t秒.
∴当时,则点Q对应的有理数是,点M对应的有理数为,
故答案为:;
(2)解:依题意,点P运动到点C所需要的时间是(秒),
在点P运动到点C之前,点P,点Q所对应的有理数是,,点M,点N所对应的有理数是,,
当未追上时,则,
,
∵线段和线段的长度之和为8,
∴
解得;
当追上后,则,
,
∵线段和线段的长度之和为8,
∴
解得(舍去);
(3)解:存在,过程如下:
∵点D为木棒的中点,且在点P运动到点C之前,点P,点Q所对应的有理数是,,
∴点D所对应的有理数是,点D到点P、Q的距离之和为一个定值,即为的长度,即为2,
∵使得点D到点P、Q、M、N的距离之和为一个定值,
∴点D所对应的有理数在木棒内部(包括木棒的端点上)会满足条件,
∵点M,点N所对应的有理数是,,
∴当点D与点N所对应的有理数是相等时,则,
解得,
∴当点D与点M所对应的有理数是相等时,则,
解得,
在时,,
∴(秒),
此时点D到点P、Q、M、N的距离之和为一个定值,且为,
当点P运动到点C后返回时,
则,,,
∴点D所对应的有理数是,
∴当点D与点N所对应的有理数是相等时,则,
解得,
∴当点D与点M所对应的有理数是相等时,则,
解得,
在时,,
∴(秒),
此时点D到点P、Q、M、N的距离之和为一个定值,且为,
综上所述,点D到点P、Q、M、N的距离之和为一个定值,且为,持续的总时长为(秒).
2.(1)解:的长为,
故答案为:;
(2)解:根据题意,只有点在点、之间时才有点到点、点的距离相等,
∴,
解得:;
(3)解:由题意可得,,
∴秒后,点表示的数是,点表示的数是,
当时,,
解得:或(舍去);
当时,,
解得:或;
当时,,
解得:或(舍去);
综上,或或或.
3.(1)解:∵A表示的数为,点B表示的数为13,
∴,
∵点是点和点之间的一个动点,点表示的数为,
∴,,
∴;
故答案为:15;15;
(2)解:①t秒后,点P表示的数为,点Q表示的数为;
故答案为:;;
②根据题意得:,
解得,
相遇点所表示的数为;
答:当t为3时,P,Q两点相遇,相遇点所表示的数是7;
(3)解:由已知得:P运动5秒到B,Q运动秒到A,
返回途中,P表示的数是,Q表示的数是,
根据题意得:,
解得,
第二次相遇点所表示的数为:,
答:所需要的时间为9秒,相遇点所表示的数是1.
专题训练16几何动点问题
1.(1)解:∵在 ABC中,,,,
∴,
又∵,为 ABC的高,
∴,
∴;
(2)解:①当点在上时,
由得,
∴;
②当在上时,,
由得,
解得,
∴的值为2.5或14.5时,的面积为.
2.解:①如图1,当点P在上,
∵在 ABC中,,,,点是的中点,
∴,,
∵,
∴;
②如图2,当点P在上时,
∵E是的中点,
∴,
又,
∴,
∵,
∴,
解得:;
综上所述,当或时, APE的面积等于10.
3.(1)当时,点在上,
∴,
当时,点在上,
∴的运动路程为,
∴,
∴,
故答案为:;;
(2)∵点在上,
∴,
∴;
(3)四边形的面积为,
∴的面积为长方形面积的时,,
当点在上时,,
解得;
当在上时,,
∴,
解得;
当在上时,,
∴,
解得;
当在上时,,
∴,
解得;
综上,当的面积为长方形面积的时,的值为或或或;
(4)有两种情况:
当点在上时,是直角三角形,
此时,
当点在上,点在上时,是直角三角形,
即,
∴,
解得,
则后,都在上,不是直角三角形,
综上,当为直角三角形时,或
