专题02勾股定理-2025年春八年级数学下学期期末复习PPT课件(人教版)(共69张PPT)
文档属性
| 名称 | 专题02勾股定理-2025年春八年级数学下学期期末复习PPT课件(人教版)(共69张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-10 00:00:00 | ||
图片预览




文档简介
(共69张PPT)
专题02 勾股定理
(3考点+2专项突破+4易错)
八年级数学下学期期末复习
人教版
01
02
04
03
目
录
易错易混
题型剖析
考点透视
押题预测
三大常考点:知识梳理+针对训练
二大专项突破(利用勾股定理解决折叠+最短路径问题)
四大易错易混经典例题+针对训练
精选3道期末真题对应考点练
直角
正整
知识结构
如果直角三角形的两条直角边长分别为a,b,斜边长为c,那么a2+b2=c2.
A
C
B
b
a
c
即直角三角形两直角边的平方和等于斜边的平方.
几何语言:
在Rt△ABC中,∠C=90°,
∴a2+b2=c2.
知识梳理
知识点一:勾股定理
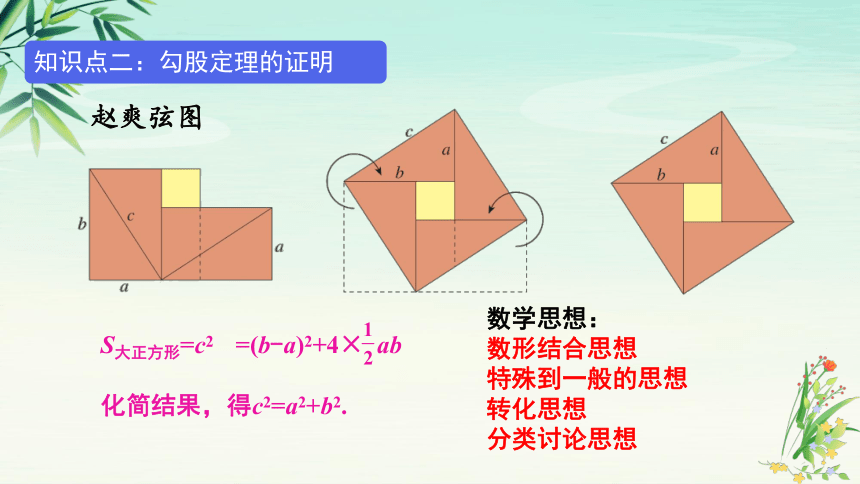
赵爽弦图
S大正方形=c2
=(b-a)2+4× ab
化简结果,得c2=a2+b2.
数学思想:
数形结合思想
特殊到一般的思想
转化思想
分类讨论思想
知识点二:勾股定理的证明
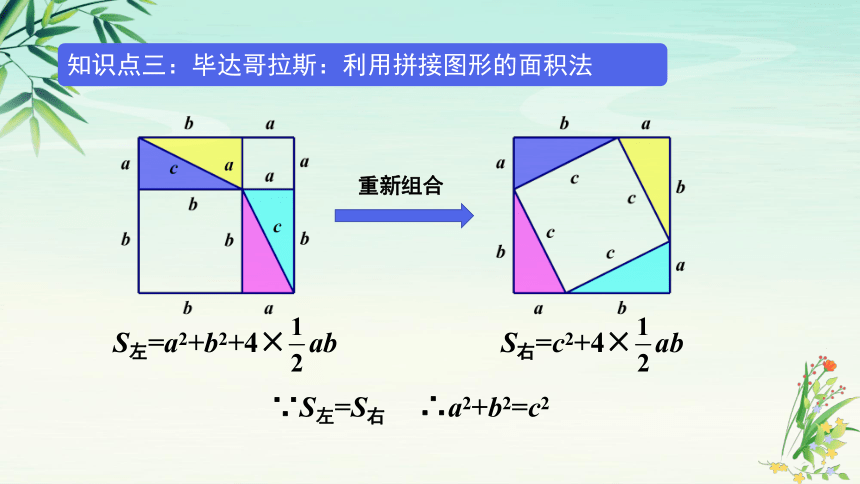
重新组合
S左=a2+b2+4× ab
S右=c2+4× ab
∵S左=S右
∴a2+b2=c2
知识点三:毕达哥拉斯:利用拼接图形的面积法
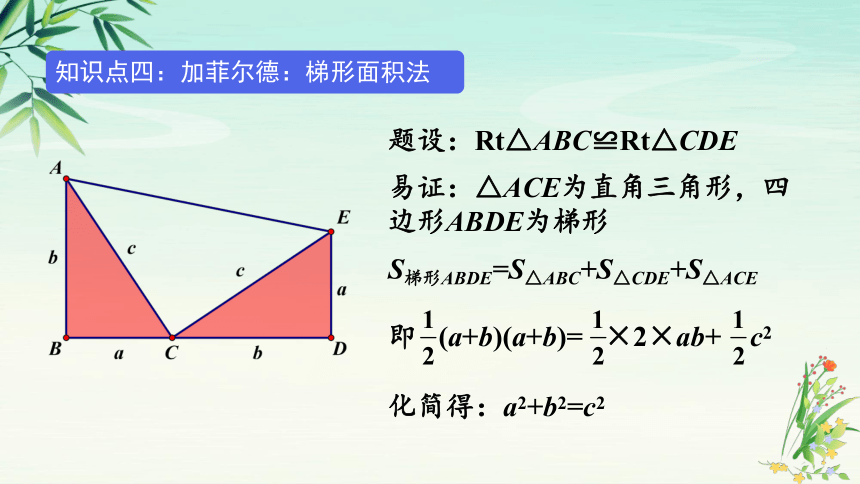
题设:Rt△ABC≌Rt△CDE
易证:△ACE为直角三角形,四边形ABDE为梯形
S梯形ABDE=S△ABC+S△CDE+S△ACE
即 (a+b)(a+b)= ×2×ab+ c2
化简得:a2+b2=c2
知识点四:加菲尔德:梯形面积法
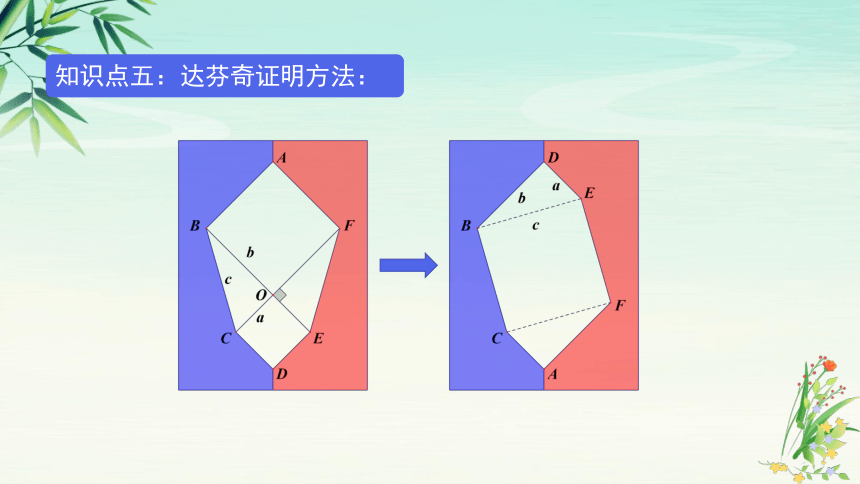
知识点五:达芬奇证明方法:
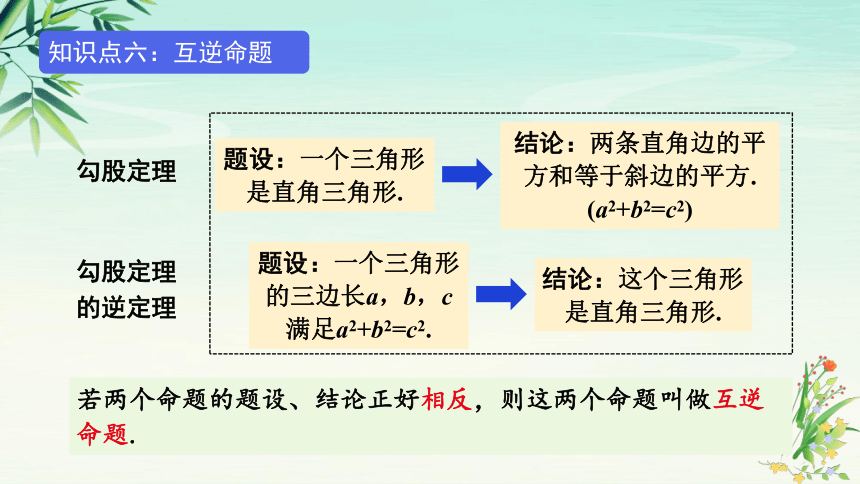
勾股定理
题设:一个三角形是直角三角形.
结论:两条直角边的平方和等于斜边的平方.
(a2+b2=c2)
勾股定理
的逆定理
题设:一个三角形的三边长a,b,c满足a2+b2=c2.
结论:这个三角形是直角三角形.
若两个命题的题设、结论正好相反,则这两个命题叫做互逆命题.
知识点六:互逆命题
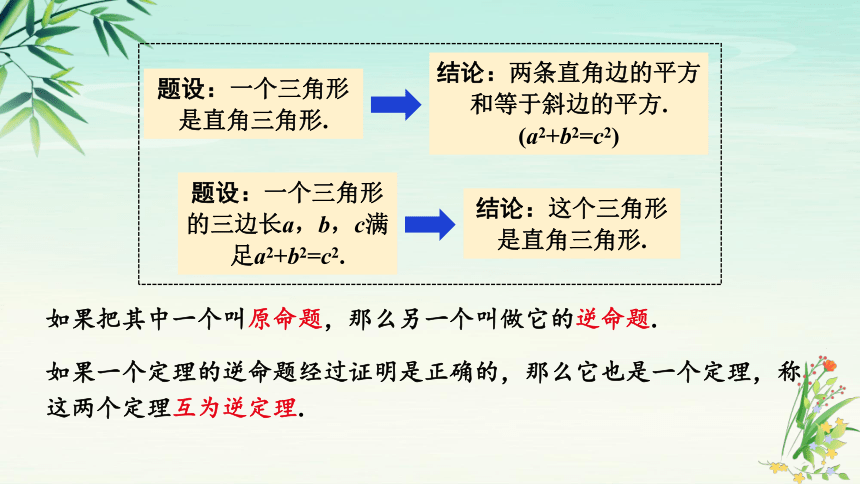
题设:一个三角形是直角三角形.
结论:两条直角边的平方和等于斜边的平方.
(a2+b2=c2)
题设:一个三角形的三边长a,b,c满足a2+b2=c2.
结论:这个三角形是直角三角形.
如果把其中一个叫原命题,那么另一个叫做它的逆命题.
如果一个定理的逆命题经过证明是正确的,那么它也是一个定理,称这两个定理互为逆定理.
考点1 勾股定理
1.在中, ,,,则 的长为( )
B
A.5 B. C.3 D.
针对训练
2.[2024· 天津模拟] 如图,的顶点 的坐标为
,顶点,分别在第一、四象限,且 轴,
若,,则点 的坐标是( )
D
A. B. C. D.
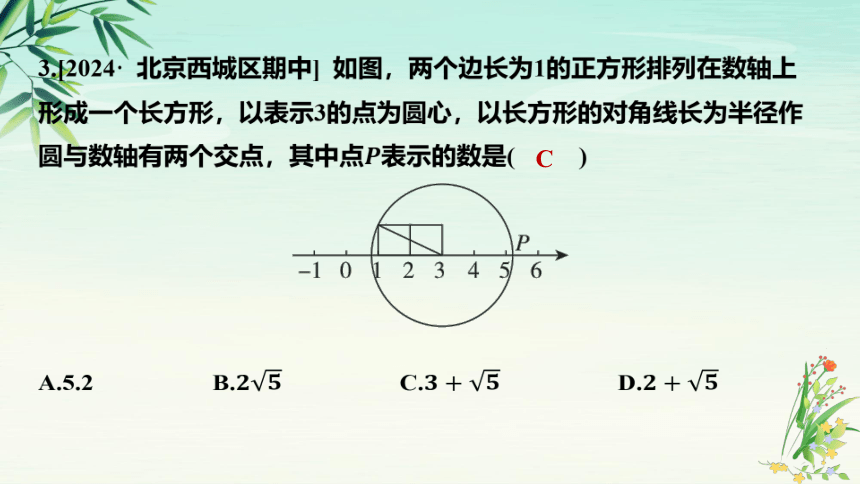
3.[2024· 北京西城区期中] 如图,两个边长为1的正方形排列在数轴上
形成一个长方形,以表示3的点为圆心,以长方形的对角线长为半径作
圆与数轴有两个交点,其中点 表示的数是( )
C
A.5.2 B. C. D.
4.[2024· 浙江] 如图,正方形 由四个全等的直角
三角形 和中间一个小
正方形组成,连接.若, ,则
的长为( )
C
A.5 B. C. D.4
5. 如图,图中所有的三角形都是
直角三角形,所有的四边形都是正方形,已知
,,,,则 的值是
( )
B
A.18 B.10 C.36 D.40
6.[2024· 北京朝阳区期中] 如图,在中, , ,
,,则 的长为 ( )
B
A.1.5 B.2 C.3 D.4
[解析] 点拨: , ,
, .
, ,
解得(负值已舍去), .
, , ,
, .
考点2 勾股定理的逆定理
7.[2024· 重庆铜梁区期中] 下列各组数中是勾股数的是( )
D
A.,, B.1,2, C.4,5,7 D.5,12,13
8.在单位长度为1的正方形网格中,下面的三角形是直角三角形的是
( )
C
A. B. C. D.
9.下面三个定理中,存在逆定理的有( )
①角平分线上的点到角的两边的距离相等;
②全等三角形的对应角相等;③内错角相等,两直线平行.
C
A.0个 B.1个 C.2个 D.3个
10.如图,在中,,,,以 为直径的
半圆过点,再分别以, 为直径向外作半圆,则阴影部分的面积
为____.
30
11.如图,已知等腰三角形 的底边长
,是 上的一点,且
, .
(1)求证: ;
证明:,,, ,
.
是直角三角形,且 .
(2)求 的面积.
解:设,则 .
, .
在中, , ,
即,解得 .
.
的面积为 .
考点3 勾股定理及其逆定理的实际应用
12. “今有方池一丈,葭生其中央,出水
一尺,引葭赴岸,适与岸齐.问:水深几何?”这是我国
数学史上的“葭生池中”问题.如图,即 ,
,,则 ( )
C
A.8 B.10 C.12 D.13
13. 《勾股》中记载了这样一个问题:“今有开门去阃
一尺不合2寸,问门广几何?”意思是:如图,推开两扇门
和,门边沿,两点到门槛的距离是1尺(1尺寸),两扇门的间隙为2寸,则门槛 长为_____寸.
101
14. 如图为某品牌婴儿车简化结构示意图.根据安全标
准需满足,现测得,, ,
,其中与之间由一个固定为 的零件连接
(即 ),通过计算说明该婴儿车是否符合安全标准.
解:在中, ,, ,
由勾股定理得 ,
在中,,, ,
, ,
,
是直角三角形, ,即 ,
该婴儿车符合安全标准.
利用勾股定理解决折叠问题
专项突破一
题型一 一次折叠问题
(第1题)
1.如图,在中,, ,
,将折叠,使点落在边上的点
处,是折痕,则 的周长为( )
C
A.6 B.8 C.12 D.14
(第2题)
2.[2024·莆田期中] 如图,, ,
将沿着直线折叠,点落在点 处,
与轴交于点,与交于点,则点 的坐
标是( )
B
A. B. C. D.
3.如图,把一张长方形纸片沿折叠,点 与点
重合,点落在点处,连接.若长方形的长 为8,
宽 为4,求:
(1)和 的长;
解: 四边形 为长方形,
,, .
由折叠得,, ,
设,则 ,
在中, ,
,解得,, .
(2)阴影部分的面积.
解:过点作于点 ,
,, ,
,
, ,
即阴影部分的面积为 .
题型二 两次折叠问题
4.如图,在三角形纸片中, ,, .沿过
点的直线将纸片折叠,使点落在边上的点 处;再折叠纸片,使
点与点重合,第二条折痕与的交点为,求 的长.
解:由折叠得, ,
, ,
, ,
,
, ,
设,则 ,
,解得,即 .
5.如图,正方形纸片的边长为3,点,分别在边,上,将,
分别沿,折叠,点,恰好都落在点处.已知,求 的长.
解:设,由折叠的性质,得, 正方
形 的边长为3,
,, .
由题意得,点,,三点共线. .
在中, ,
,解得 .
.
利用勾股定理解决最短路径问题
专项突破二
图例 基本策略
模型一 ________________ 确定动点 所在的直线;利用对称性,将同侧的, 两点转化为异侧的两点,,则最短路径即为线段 ;常构造直角三角形 ,利用勾股定理求解
图例 基本策略
模型二 利用“垂线段最短”确定最短路径;
构造直角三角形,利用勾股定理求解
类型一 平面图形中的最短路径问题
1.如图,在中, ,,
的平分线交于点,且,是边 上一动
点,则 的最小值为( )
C
A.2 B. C.1 D.
2.[2024·天津和平区月考] 如图,在 中,
,,,为 边上一动
点,连接,与关于直线 对称,连
接,则 的最小值为( )
B
A. B.1 C. D.
3.[2024·佛山禅城区期中] 如图,在等边三角形
中,是高,点,分别在,上,点是边 上的
动点,连接,,若,,则 的
最小值为( )
B
A.4 B.5 C.6 D.7
[解析] 点拨:如图,作点关于直线的对称点 ,
连接交于点,连接 ,
易知此时 的值最小,最小值为
,
是等边三角形, 是高,
,
由对称可知,, ,
,
,
的最小值为5.
4.如图,在中,,,且,若点 在
边上(不含端点)运动,则线段 的最小值为___.
[解析] 点拨:根据垂线段最短知,
当时, 的值最小,
,,, ,
当时, ,
即, ,
此时 ,
点在边上, 线段的最小值为 .
5.[2024·成都] 如图,在平面直角坐标系中,已知, ,
过点作轴的垂线,为直线上一动点,连接,,则
的最小值为___.
5
[解析] 点拨:如图,作点关于直线的对称点 ,
连接交直线于点,连接, ,
则,, ,
,
当,,三点共线,即点与点 重合时,
的值最小,为线段 的长,
直线轴, 轴.
,,,, ,
在 中,
.
的最小值为5.
类型二 几何体中的最短路径问题
图例 基本策略
圆柱 __________________________________________ 将立体图形展开成平面图形,
利用“两点之间,线段最短”确
定最短路径;构造直角三角
形,利用勾股定理求解
注意:长方体不同的展开方法
构造的直角三角形的各边长不
同,因此要先分类讨论再计算
比较
图例 基本策略
长方体 ___________________________________________________ 将立体图形展开成平面图形,
利用“两点之间,线段最短”确
定最短路径;构造直角三角
形,利用勾股定理求解
注意:长方体不同的展开方法
构造的直角三角形的各边长不
同,因此要先分类讨论再计算
比较
阶梯 ____________________________________________________________________________
续表
6.小南同学报名参加了攀岩选修课,攀岩墙近似一个
长方体的两个侧面,如图所示.他根据学过的数学知
识准确地判断出,从点攀爬到点 的最短路径长为
( )
D
A. B. C. D.
7.如图,圆柱的轴截面 是边长为4的正方形,动点
从点出发,沿着圆柱的侧面移动到的中点 的最短
距离的平方为( )
A
A. B. C. D.
8.[2024·武汉经开区期末] 如图,长方体的长、宽、高分别为 ,
,,一只蚂蚁沿着长方体的表面从点爬到点 ,则蚂蚁爬行
的最短路径的长是______ .
[解析] 点拨:如图①,展开前面和上面,连接
, ;如图
②,展开前面和右面,连接 ,
;如图③,展
开左面和上面,连接 ,
.
, 最短路径的长为 .
9.如图是一个三级台阶,它的每一级的长、
宽、高分别为,和,和
是这个台阶的两个相对的端点, 点处有一
只蚂蚁,想到 点去吃可口的食物,则这只
蚂蚁从点出发沿着台阶爬到 点的最短距离
是____ .
73
[解析] 点拨:将台阶展开成平面图形,连接 ,
如图所示.
因为每级台阶长、宽、高分别为,
和 ,
所以 ,
,
在中, ,
所以最短距离是 .
10.如图,长方体的长和宽分别为和,高为 .
如果用一根细线从点开始经过四个侧面缠绕一圈达到点 ,那么所用
细线最短需要______ .
类型三 利用数形结合解决最短路径问题
11.[2024·莆田涵江区期中] 【问题背景】
在中,,,三边的长分别为,, ,求这个三
角形的面积.小蔡同学在解答这道题时,先建立一个正方形网格
(每个小正方形的边长均为1),然后在网格中画出格点
(即三个顶点都在小正方形的顶点处, ,
, ),如图①.这样不需求
的高,借用网格就能计算出它的面积.这种求 面积的方法
叫做构图法.
【问题解决】
(1)借用网格计算出图①中 的面积为_ _.
【思维拓展】
(2)请运用构图法比较与 的大小,在图②的正方形网格
(每个小正方形的边长均为1)中画出相应的图形.
解:如图①,由图可得, ,
,
由三角形的三边关系可知 ,
.
【探索创新】
(3)已知是正数,请运用构图法求出 的最小
值.(画出相应的图形)
解:如图②, 的最小值可转
化为平面直角坐标系中轴正半轴上一点 到
, 两点的距离的和的最小值,
作关于轴的对称点,连接, ,
则, ,
当,,三点共线时,的值最小,最小值为 的长度.
, ,
,
的最小值为 .
易错点1.审题不到位,受思维定式的干扰
【例1】在△ABC中,∠A,∠B,∠C的对边分别为a,b,c,且(a+b)
(a-b)=c2,则 ( )
A. ∠A为直角
B. ∠B为直角
C. ∠C为直角
D. △ABC不是直角三角形
易混易错
错解:C.
错解分析:常见的直角三角形表示中,一般将直角标注为∠C,因此容易思维定式选择∠C为直角,加之对本题所给条件的分析不缜密,导致错误.该题中的条件应转化为a2-b2=c2,即a2=b2+c2,再根据勾股定理进行判断,较长边对应的角是直角.
正解:A.
【针对训练】填空:
(1)在Rt△ABC中,AB=6,AC=8,则斜边BC长为 ;
(2)在Rt△ABC中,AB=6,AC=8,则第三边长为 .
10或2
10
易错点2.概念不明确,混淆勾股定理及其逆定理
【例2】下列各组数据中的三个数,可作为三边长构成直角三角形的是
( )
A.1,2,3 B.62,82,102
C. D.
错解:B.
错解分析:未能彻底区分勾股定理及其逆定理,对概念的理解流于表面形式.判断直角三角形时,应将所给数据进行平方,看是否满足a2+b2=c2的形式.
正解:因为,故选C.
【针对训练】(1)以下列各组数为边长,能构成直角三角形的是( )
A. ,2 B. 1,2,
C. D. 4,5,6
(2)已知∠A,∠B,∠C的对边分别为a,b,c,则由下列条件不能判定△ABC为直角三角形的是( )
A. ∠A+∠C=∠B B. =3,=4,=5
C.(a+b)2-c2=2ab D. ∠A∶∠B∶∠C=5∶3∶2
B
C
易错点3.方向角问题中方向不明确时,结果没有进行分类
【例3】如图D17-1-1,某港口O位于东西海岸线上,甲、乙两艘渔船同时离开港口O,各自沿一固定方向航行,甲船沿北偏东30°方向以每小时16 n mile的速度航行,乙船沿某方向以每小时12 n mile的速度航行,2 h后,甲船到达点A处,两艘船相距40 n mile,问乙船沿哪个方向航行?
图D17-1-1
错解:如图D17-1-2,假设2 h后乙船到达点B处.
由题意,得OA=16×2=32(n mile),OB=12×2=24(n mile).
∵OA2+OB2=322+242=1 600,AB2=402=1 600,
∴OA2+OB2=AB2.
∴△OAB是直角三角形,且∠AOB=90°.
∵甲船沿北偏东30°方向航行,
∴90°-30°=60°.
∴乙船沿北偏西60°方向航行.
图D17-1-2
错解分析:该解题过程错在只讨论了其中一种情况,导致漏解,这题没有给出航行方向,乙船可能沿北偏西的某个方向航行,也可能沿南偏东的某个方向航行,需要自己画图分类讨论.
由题意,得OA=16×2=32(n mile),
OB=12×2=24(n mile).
∵OA2+OB2=322+242=1 600,AB2=402=1 600,
∴OA2+OB2=AB2.
∴△OAB是直角三角形,且∠AOB=90°.
∵甲船沿北偏东30°方向航行,
∴90°-30°=60°.
∴乙船沿北偏西60°或南偏东60°方向航行.
正解:如图D17-1-3,假设2 h后乙船到达点B处.
图D17-1-3
【针对训练】某港口A位于东西海岸线上,甲、乙两船同时离开港口,各自沿一固定方向航行,甲船每小时航行45 n mile,乙船每小时航行60 n mile,它们离开港口1.2 h后分别位于点B,C处,且相距90 n mile.若甲船沿南偏西25°方向航行,问乙船沿哪个方向航行?
解:如答图D17-1-1.
由题意,得AB=45×1.2=54(n mile),AC=60×1.2=72(n mile).
∵AB2+AC2=542+722=8 100,BC2=902=8 100.
∴AB2+AC2=BC2.
∴△ABC是直角三角形,且∠BAC=90°.
∵甲船沿南偏西25°方向航行,∴90°-25°=65°.
∴乙船沿南偏东65°或北偏西65°方向航行.
答图D17-1-1
易错点4.分析不深入,以偏概全而造成漏解
【例4】在△ABC中,若AC=15,BC=13,AB边上的高CD=12,求△ABC的周长.
错解:∵AC=15,BC=13,AB边上的高CD=12,
∴AD==9,BD==5.
∴AB=AD+BD=9+5=14.
∴△ABC的周长为14+13+15=42.
错解分析:本题求解时,容易分析不深入,以偏概全而造成漏解,只考虑了三角形的高在形内的情况,遗漏了三角形的高可能在形外这一情况,因而导致出现漏解,造成解题答案不完整.
正解:∵AC=15,BC=13,AB边上的高CD=12,
∴AD==9,
BD==5.
如图D17-1-4①,CD在△ABC内部时,
AB=AD+BD=9+5=14.
此时△ABC的周长为14+13+15=42;
如图D17-1-4②,CD在△ABC外部时,
AB=AD-BD=9-5=4.
此时△ABC的周长为4+13+15=32.
综上所述,△ABC的周长为42或32.
图D17-1-4
【针对训练】在△ABC中,AD为BC边上的高,AC=5,BC=6,△ABC的面积为12,求AB的长.
解:∵AC=5,BC=6,AD为BC边上的高,
∴S△ABC=BC·AD=×6×AD=12.
解得AD=4.
由勾股定理,得CD==3.
如答图D17-1-2①,当AD在△ABC内部时,BD=BC-CD=6-3=3.
此时AB==5;
答图D17-1-2
如答图D17-1-2②,当AD在△ABC外部时,BD=BC+CD=6+3=9.
此时AB=.
综上所述,AB的长为5或.
1.[2024·聊城期末] 如图,数轴上的点, 分别对
应的数是1,2,过点作,以点 为圆
心,长为半径画弧,交于点 ;以数轴原点
(点)为圆心, 长为半径画弧,交数轴于点
,则点 对应的数是( )
D
A. B. C. D.
押题预测
2. 如图,这是一个供滑板
爱好者使用的型池示意图,该 型池可以看成是
长方体去掉一个“半圆柱”而成,中间可供滑行部
分的截面是直径为 的半圆,其边缘
,点在上, ,一
C
A. B. C. D.
名滑板爱好者从点滑到 点,则他滑行的最短距离约为(边缘部分的
厚度忽略不计, 取3,结果精确到 )( )
3. 如图, 是等腰直角
三角形,,点在 的斜边上.求证:
.
证明:如图,作,垂足为, .
在中, .
, 易得 .
,
,
, .
专题02 勾股定理
(3考点+2专项突破+4易错)
八年级数学下学期期末复习
人教版
01
02
04
03
目
录
易错易混
题型剖析
考点透视
押题预测
三大常考点:知识梳理+针对训练
二大专项突破(利用勾股定理解决折叠+最短路径问题)
四大易错易混经典例题+针对训练
精选3道期末真题对应考点练
直角
正整
知识结构
如果直角三角形的两条直角边长分别为a,b,斜边长为c,那么a2+b2=c2.
A
C
B
b
a
c
即直角三角形两直角边的平方和等于斜边的平方.
几何语言:
在Rt△ABC中,∠C=90°,
∴a2+b2=c2.
知识梳理
知识点一:勾股定理
赵爽弦图
S大正方形=c2
=(b-a)2+4× ab
化简结果,得c2=a2+b2.
数学思想:
数形结合思想
特殊到一般的思想
转化思想
分类讨论思想
知识点二:勾股定理的证明
重新组合
S左=a2+b2+4× ab
S右=c2+4× ab
∵S左=S右
∴a2+b2=c2
知识点三:毕达哥拉斯:利用拼接图形的面积法
题设:Rt△ABC≌Rt△CDE
易证:△ACE为直角三角形,四边形ABDE为梯形
S梯形ABDE=S△ABC+S△CDE+S△ACE
即 (a+b)(a+b)= ×2×ab+ c2
化简得:a2+b2=c2
知识点四:加菲尔德:梯形面积法
知识点五:达芬奇证明方法:
勾股定理
题设:一个三角形是直角三角形.
结论:两条直角边的平方和等于斜边的平方.
(a2+b2=c2)
勾股定理
的逆定理
题设:一个三角形的三边长a,b,c满足a2+b2=c2.
结论:这个三角形是直角三角形.
若两个命题的题设、结论正好相反,则这两个命题叫做互逆命题.
知识点六:互逆命题
题设:一个三角形是直角三角形.
结论:两条直角边的平方和等于斜边的平方.
(a2+b2=c2)
题设:一个三角形的三边长a,b,c满足a2+b2=c2.
结论:这个三角形是直角三角形.
如果把其中一个叫原命题,那么另一个叫做它的逆命题.
如果一个定理的逆命题经过证明是正确的,那么它也是一个定理,称这两个定理互为逆定理.
考点1 勾股定理
1.在中, ,,,则 的长为( )
B
A.5 B. C.3 D.
针对训练
2.[2024· 天津模拟] 如图,的顶点 的坐标为
,顶点,分别在第一、四象限,且 轴,
若,,则点 的坐标是( )
D
A. B. C. D.
3.[2024· 北京西城区期中] 如图,两个边长为1的正方形排列在数轴上
形成一个长方形,以表示3的点为圆心,以长方形的对角线长为半径作
圆与数轴有两个交点,其中点 表示的数是( )
C
A.5.2 B. C. D.
4.[2024· 浙江] 如图,正方形 由四个全等的直角
三角形 和中间一个小
正方形组成,连接.若, ,则
的长为( )
C
A.5 B. C. D.4
5. 如图,图中所有的三角形都是
直角三角形,所有的四边形都是正方形,已知
,,,,则 的值是
( )
B
A.18 B.10 C.36 D.40
6.[2024· 北京朝阳区期中] 如图,在中, , ,
,,则 的长为 ( )
B
A.1.5 B.2 C.3 D.4
[解析] 点拨: , ,
, .
, ,
解得(负值已舍去), .
, , ,
, .
考点2 勾股定理的逆定理
7.[2024· 重庆铜梁区期中] 下列各组数中是勾股数的是( )
D
A.,, B.1,2, C.4,5,7 D.5,12,13
8.在单位长度为1的正方形网格中,下面的三角形是直角三角形的是
( )
C
A. B. C. D.
9.下面三个定理中,存在逆定理的有( )
①角平分线上的点到角的两边的距离相等;
②全等三角形的对应角相等;③内错角相等,两直线平行.
C
A.0个 B.1个 C.2个 D.3个
10.如图,在中,,,,以 为直径的
半圆过点,再分别以, 为直径向外作半圆,则阴影部分的面积
为____.
30
11.如图,已知等腰三角形 的底边长
,是 上的一点,且
, .
(1)求证: ;
证明:,,, ,
.
是直角三角形,且 .
(2)求 的面积.
解:设,则 .
, .
在中, , ,
即,解得 .
.
的面积为 .
考点3 勾股定理及其逆定理的实际应用
12. “今有方池一丈,葭生其中央,出水
一尺,引葭赴岸,适与岸齐.问:水深几何?”这是我国
数学史上的“葭生池中”问题.如图,即 ,
,,则 ( )
C
A.8 B.10 C.12 D.13
13. 《勾股》中记载了这样一个问题:“今有开门去阃
一尺不合2寸,问门广几何?”意思是:如图,推开两扇门
和,门边沿,两点到门槛的距离是1尺(1尺寸),两扇门的间隙为2寸,则门槛 长为_____寸.
101
14. 如图为某品牌婴儿车简化结构示意图.根据安全标
准需满足,现测得,, ,
,其中与之间由一个固定为 的零件连接
(即 ),通过计算说明该婴儿车是否符合安全标准.
解:在中, ,, ,
由勾股定理得 ,
在中,,, ,
, ,
,
是直角三角形, ,即 ,
该婴儿车符合安全标准.
利用勾股定理解决折叠问题
专项突破一
题型一 一次折叠问题
(第1题)
1.如图,在中,, ,
,将折叠,使点落在边上的点
处,是折痕,则 的周长为( )
C
A.6 B.8 C.12 D.14
(第2题)
2.[2024·莆田期中] 如图,, ,
将沿着直线折叠,点落在点 处,
与轴交于点,与交于点,则点 的坐
标是( )
B
A. B. C. D.
3.如图,把一张长方形纸片沿折叠,点 与点
重合,点落在点处,连接.若长方形的长 为8,
宽 为4,求:
(1)和 的长;
解: 四边形 为长方形,
,, .
由折叠得,, ,
设,则 ,
在中, ,
,解得,, .
(2)阴影部分的面积.
解:过点作于点 ,
,, ,
,
, ,
即阴影部分的面积为 .
题型二 两次折叠问题
4.如图,在三角形纸片中, ,, .沿过
点的直线将纸片折叠,使点落在边上的点 处;再折叠纸片,使
点与点重合,第二条折痕与的交点为,求 的长.
解:由折叠得, ,
, ,
, ,
,
, ,
设,则 ,
,解得,即 .
5.如图,正方形纸片的边长为3,点,分别在边,上,将,
分别沿,折叠,点,恰好都落在点处.已知,求 的长.
解:设,由折叠的性质,得, 正方
形 的边长为3,
,, .
由题意得,点,,三点共线. .
在中, ,
,解得 .
.
利用勾股定理解决最短路径问题
专项突破二
图例 基本策略
模型一 ________________ 确定动点 所在的直线;利用对称性,将同侧的, 两点转化为异侧的两点,,则最短路径即为线段 ;常构造直角三角形 ,利用勾股定理求解
图例 基本策略
模型二 利用“垂线段最短”确定最短路径;
构造直角三角形,利用勾股定理求解
类型一 平面图形中的最短路径问题
1.如图,在中, ,,
的平分线交于点,且,是边 上一动
点,则 的最小值为( )
C
A.2 B. C.1 D.
2.[2024·天津和平区月考] 如图,在 中,
,,,为 边上一动
点,连接,与关于直线 对称,连
接,则 的最小值为( )
B
A. B.1 C. D.
3.[2024·佛山禅城区期中] 如图,在等边三角形
中,是高,点,分别在,上,点是边 上的
动点,连接,,若,,则 的
最小值为( )
B
A.4 B.5 C.6 D.7
[解析] 点拨:如图,作点关于直线的对称点 ,
连接交于点,连接 ,
易知此时 的值最小,最小值为
,
是等边三角形, 是高,
,
由对称可知,, ,
,
,
的最小值为5.
4.如图,在中,,,且,若点 在
边上(不含端点)运动,则线段 的最小值为___.
[解析] 点拨:根据垂线段最短知,
当时, 的值最小,
,,, ,
当时, ,
即, ,
此时 ,
点在边上, 线段的最小值为 .
5.[2024·成都] 如图,在平面直角坐标系中,已知, ,
过点作轴的垂线,为直线上一动点,连接,,则
的最小值为___.
5
[解析] 点拨:如图,作点关于直线的对称点 ,
连接交直线于点,连接, ,
则,, ,
,
当,,三点共线,即点与点 重合时,
的值最小,为线段 的长,
直线轴, 轴.
,,,, ,
在 中,
.
的最小值为5.
类型二 几何体中的最短路径问题
图例 基本策略
圆柱 __________________________________________ 将立体图形展开成平面图形,
利用“两点之间,线段最短”确
定最短路径;构造直角三角
形,利用勾股定理求解
注意:长方体不同的展开方法
构造的直角三角形的各边长不
同,因此要先分类讨论再计算
比较
图例 基本策略
长方体 ___________________________________________________ 将立体图形展开成平面图形,
利用“两点之间,线段最短”确
定最短路径;构造直角三角
形,利用勾股定理求解
注意:长方体不同的展开方法
构造的直角三角形的各边长不
同,因此要先分类讨论再计算
比较
阶梯 ____________________________________________________________________________
续表
6.小南同学报名参加了攀岩选修课,攀岩墙近似一个
长方体的两个侧面,如图所示.他根据学过的数学知
识准确地判断出,从点攀爬到点 的最短路径长为
( )
D
A. B. C. D.
7.如图,圆柱的轴截面 是边长为4的正方形,动点
从点出发,沿着圆柱的侧面移动到的中点 的最短
距离的平方为( )
A
A. B. C. D.
8.[2024·武汉经开区期末] 如图,长方体的长、宽、高分别为 ,
,,一只蚂蚁沿着长方体的表面从点爬到点 ,则蚂蚁爬行
的最短路径的长是______ .
[解析] 点拨:如图①,展开前面和上面,连接
, ;如图
②,展开前面和右面,连接 ,
;如图③,展
开左面和上面,连接 ,
.
, 最短路径的长为 .
9.如图是一个三级台阶,它的每一级的长、
宽、高分别为,和,和
是这个台阶的两个相对的端点, 点处有一
只蚂蚁,想到 点去吃可口的食物,则这只
蚂蚁从点出发沿着台阶爬到 点的最短距离
是____ .
73
[解析] 点拨:将台阶展开成平面图形,连接 ,
如图所示.
因为每级台阶长、宽、高分别为,
和 ,
所以 ,
,
在中, ,
所以最短距离是 .
10.如图,长方体的长和宽分别为和,高为 .
如果用一根细线从点开始经过四个侧面缠绕一圈达到点 ,那么所用
细线最短需要______ .
类型三 利用数形结合解决最短路径问题
11.[2024·莆田涵江区期中] 【问题背景】
在中,,,三边的长分别为,, ,求这个三
角形的面积.小蔡同学在解答这道题时,先建立一个正方形网格
(每个小正方形的边长均为1),然后在网格中画出格点
(即三个顶点都在小正方形的顶点处, ,
, ),如图①.这样不需求
的高,借用网格就能计算出它的面积.这种求 面积的方法
叫做构图法.
【问题解决】
(1)借用网格计算出图①中 的面积为_ _.
【思维拓展】
(2)请运用构图法比较与 的大小,在图②的正方形网格
(每个小正方形的边长均为1)中画出相应的图形.
解:如图①,由图可得, ,
,
由三角形的三边关系可知 ,
.
【探索创新】
(3)已知是正数,请运用构图法求出 的最小
值.(画出相应的图形)
解:如图②, 的最小值可转
化为平面直角坐标系中轴正半轴上一点 到
, 两点的距离的和的最小值,
作关于轴的对称点,连接, ,
则, ,
当,,三点共线时,的值最小,最小值为 的长度.
, ,
,
的最小值为 .
易错点1.审题不到位,受思维定式的干扰
【例1】在△ABC中,∠A,∠B,∠C的对边分别为a,b,c,且(a+b)
(a-b)=c2,则 ( )
A. ∠A为直角
B. ∠B为直角
C. ∠C为直角
D. △ABC不是直角三角形
易混易错
错解:C.
错解分析:常见的直角三角形表示中,一般将直角标注为∠C,因此容易思维定式选择∠C为直角,加之对本题所给条件的分析不缜密,导致错误.该题中的条件应转化为a2-b2=c2,即a2=b2+c2,再根据勾股定理进行判断,较长边对应的角是直角.
正解:A.
【针对训练】填空:
(1)在Rt△ABC中,AB=6,AC=8,则斜边BC长为 ;
(2)在Rt△ABC中,AB=6,AC=8,则第三边长为 .
10或2
10
易错点2.概念不明确,混淆勾股定理及其逆定理
【例2】下列各组数据中的三个数,可作为三边长构成直角三角形的是
( )
A.1,2,3 B.62,82,102
C. D.
错解:B.
错解分析:未能彻底区分勾股定理及其逆定理,对概念的理解流于表面形式.判断直角三角形时,应将所给数据进行平方,看是否满足a2+b2=c2的形式.
正解:因为,故选C.
【针对训练】(1)以下列各组数为边长,能构成直角三角形的是( )
A. ,2 B. 1,2,
C. D. 4,5,6
(2)已知∠A,∠B,∠C的对边分别为a,b,c,则由下列条件不能判定△ABC为直角三角形的是( )
A. ∠A+∠C=∠B B. =3,=4,=5
C.(a+b)2-c2=2ab D. ∠A∶∠B∶∠C=5∶3∶2
B
C
易错点3.方向角问题中方向不明确时,结果没有进行分类
【例3】如图D17-1-1,某港口O位于东西海岸线上,甲、乙两艘渔船同时离开港口O,各自沿一固定方向航行,甲船沿北偏东30°方向以每小时16 n mile的速度航行,乙船沿某方向以每小时12 n mile的速度航行,2 h后,甲船到达点A处,两艘船相距40 n mile,问乙船沿哪个方向航行?
图D17-1-1
错解:如图D17-1-2,假设2 h后乙船到达点B处.
由题意,得OA=16×2=32(n mile),OB=12×2=24(n mile).
∵OA2+OB2=322+242=1 600,AB2=402=1 600,
∴OA2+OB2=AB2.
∴△OAB是直角三角形,且∠AOB=90°.
∵甲船沿北偏东30°方向航行,
∴90°-30°=60°.
∴乙船沿北偏西60°方向航行.
图D17-1-2
错解分析:该解题过程错在只讨论了其中一种情况,导致漏解,这题没有给出航行方向,乙船可能沿北偏西的某个方向航行,也可能沿南偏东的某个方向航行,需要自己画图分类讨论.
由题意,得OA=16×2=32(n mile),
OB=12×2=24(n mile).
∵OA2+OB2=322+242=1 600,AB2=402=1 600,
∴OA2+OB2=AB2.
∴△OAB是直角三角形,且∠AOB=90°.
∵甲船沿北偏东30°方向航行,
∴90°-30°=60°.
∴乙船沿北偏西60°或南偏东60°方向航行.
正解:如图D17-1-3,假设2 h后乙船到达点B处.
图D17-1-3
【针对训练】某港口A位于东西海岸线上,甲、乙两船同时离开港口,各自沿一固定方向航行,甲船每小时航行45 n mile,乙船每小时航行60 n mile,它们离开港口1.2 h后分别位于点B,C处,且相距90 n mile.若甲船沿南偏西25°方向航行,问乙船沿哪个方向航行?
解:如答图D17-1-1.
由题意,得AB=45×1.2=54(n mile),AC=60×1.2=72(n mile).
∵AB2+AC2=542+722=8 100,BC2=902=8 100.
∴AB2+AC2=BC2.
∴△ABC是直角三角形,且∠BAC=90°.
∵甲船沿南偏西25°方向航行,∴90°-25°=65°.
∴乙船沿南偏东65°或北偏西65°方向航行.
答图D17-1-1
易错点4.分析不深入,以偏概全而造成漏解
【例4】在△ABC中,若AC=15,BC=13,AB边上的高CD=12,求△ABC的周长.
错解:∵AC=15,BC=13,AB边上的高CD=12,
∴AD==9,BD==5.
∴AB=AD+BD=9+5=14.
∴△ABC的周长为14+13+15=42.
错解分析:本题求解时,容易分析不深入,以偏概全而造成漏解,只考虑了三角形的高在形内的情况,遗漏了三角形的高可能在形外这一情况,因而导致出现漏解,造成解题答案不完整.
正解:∵AC=15,BC=13,AB边上的高CD=12,
∴AD==9,
BD==5.
如图D17-1-4①,CD在△ABC内部时,
AB=AD+BD=9+5=14.
此时△ABC的周长为14+13+15=42;
如图D17-1-4②,CD在△ABC外部时,
AB=AD-BD=9-5=4.
此时△ABC的周长为4+13+15=32.
综上所述,△ABC的周长为42或32.
图D17-1-4
【针对训练】在△ABC中,AD为BC边上的高,AC=5,BC=6,△ABC的面积为12,求AB的长.
解:∵AC=5,BC=6,AD为BC边上的高,
∴S△ABC=BC·AD=×6×AD=12.
解得AD=4.
由勾股定理,得CD==3.
如答图D17-1-2①,当AD在△ABC内部时,BD=BC-CD=6-3=3.
此时AB==5;
答图D17-1-2
如答图D17-1-2②,当AD在△ABC外部时,BD=BC+CD=6+3=9.
此时AB=.
综上所述,AB的长为5或.
1.[2024·聊城期末] 如图,数轴上的点, 分别对
应的数是1,2,过点作,以点 为圆
心,长为半径画弧,交于点 ;以数轴原点
(点)为圆心, 长为半径画弧,交数轴于点
,则点 对应的数是( )
D
A. B. C. D.
押题预测
2. 如图,这是一个供滑板
爱好者使用的型池示意图,该 型池可以看成是
长方体去掉一个“半圆柱”而成,中间可供滑行部
分的截面是直径为 的半圆,其边缘
,点在上, ,一
C
A. B. C. D.
名滑板爱好者从点滑到 点,则他滑行的最短距离约为(边缘部分的
厚度忽略不计, 取3,结果精确到 )( )
3. 如图, 是等腰直角
三角形,,点在 的斜边上.求证:
.
证明:如图,作,垂足为, .
在中, .
, 易得 .
,
,
, .
同课章节目录
