专题04数据的分析-2025年春八年级数学下学期期末复习PPT课件(人教版)(共75张PPT)
文档属性
| 名称 | 专题04数据的分析-2025年春八年级数学下学期期末复习PPT课件(人教版)(共75张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-10 00:00:00 | ||
图片预览









文档简介
(共75张PPT)
专题04 数据的分析
(3考点+2思想+专题突破+4易错)
八年级数学下学期期末复习
人教版
01
02
04
03
目
录
易错易混
题型剖析
考点透视
押题预测
三大常考点:知识梳理+针对训练
二大思想方法+专题突破(数据分析中的决策问题)
四大易错易混经典例题+针对训练
精选3道期末真题对应考点练
最多
越大
越小
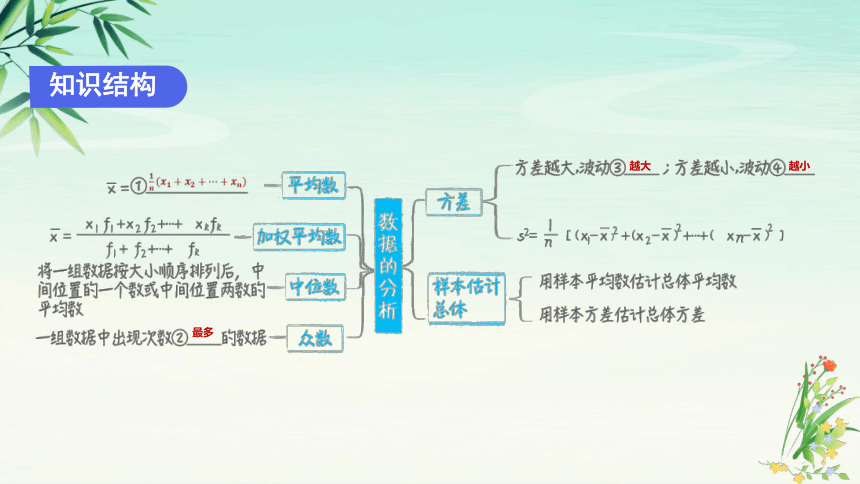
知识结构
平均数 定义 一组数据的平均值称为这组数据的平均数
算术平 均数 一般地,如果有n个数x1,x2,…,xn,那么_____________________叫做这n个数的平均数.
加权平 均数 一般地,若n个数x1,x2,…,xn的权分别
是w1,w2,…,wn,则
___________________
叫做这n个数的加权平均数.
知识梳理
知识点一:数据的集中趋势
最多
中间位置的数
两个数据的平均数
中位数 定义 将一组数据按照由小到大(或由大到小)的顺序排列,如果数据的个数是奇数,则处于________________就是这组数据的中位数,如果数据的个数是偶数,则中间_________________________就是这组数据的中位数
防错 提醒 确定中位数时,一定要注意先把整组数据按照大小顺序排列,再确定
众 数 定义 一组数据中出现次数________的数据叫做这组数据的众数
防错 提醒 (1)一组数据中众数不一定只有一个;(2)当一组数据中出现异常值时,其平均数往往不能正确反映这组数据的集中趋势,就应考虑用中位数或众数来分析
平均数
大
表示波 动的量 定义 意义
方差 设有n个数据x1,x2,x3,…,xn,各数据与它们的________的差的平方分别是(x1-x)2,(x2-x)2,…,(xn-x)2,我们用它们的平均数,即用________________________来衡量这组数据的波动大小,并把它叫做这组数据的方差,记作s2 方差越大,数据的波动越___,反之也成立
知识点二:数据的波动程度
1.统计的基本思想:用样本的特征(平均数和方差)估计总体的特征.
2.统计的决策依据:利用数据做决策时,要全面、多角度地去分析已有数据,从数据的变化中发现它们的规律和变化趋势,减少人为因素的影响.
知识点三:用样本估计总体
考点1 平均数、中位数、众数
1.[2024 湖南] 某班的5名同学1分钟跳绳的成绩(单位:次)分别为:
179,130,192,158,141.这组数据的中位数是( )
B
A.130 B.158 C.160 D.192
针对训练
2.[2024 无锡] 一组数据:31,32,35,37,35,这组数据的平均数和
中位数分别是( )
C
A.34,34 B.35,35 C.34,35 D.35,34
3.[2024 扬州] 第8个全国近视防控宣传教育月的主题是“有效减少近视
发生,共同守护光明未来”.某校积极响应,开展视力检查.某班45名同学
视力检查数据如下表:
视力 4.3 4.4 4.5 4.6 4.7 4.8 4.9 5.0
人数 1 4 4 7 11 10 5 3
这45名同学视力检查数据的众数是( )
B
A.4.6 B.4.7 C.4.8 D.4.9
4.[2024 南京鼓楼区一模] 如图为某班35名学
生投篮成绩的条形统计图,其中上面部分数据
破损导致数据不完全.已知此班学生投篮成绩
的中位数是5,则根据下图,无法确定下列哪
一选项中的数值( )
C
A.4球以下的人数 B.5球以下的人数
C.6球以下的人数 D.7球以下的人数
(第5题)
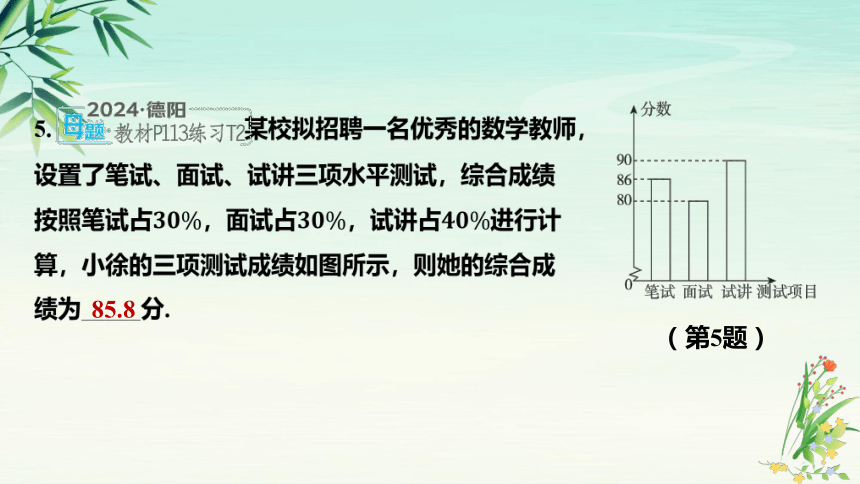
5. 某校拟招聘一名优秀的数学教师,
设置了笔试、面试、试讲三项水平测试,综合成绩
按照笔试占,面试占,试讲占 进行计
算,小徐的三项测试成绩如图所示,则她的综合成
绩为_____分.
85.8
(第6题)
6.[2024 镇江] 小丽6次射击的成绩如图所示,则她的
射击成绩的中位数为____环.
7.5
7.样本数据3,,4, ,8的平均数是5,众数是3,则这组数据的中位
数是___.
4
8.某企业加强了管理,准备采取每天的任务定额和超产有奖的措施,以
提高工作效率.下面是该企业10名员工过去一天中各自装配机器的数量
(单位:台):6,8,16,14,11,10,6,13,10,6.
(1)求这组数据的平均数、众数和中位数.
解:平均数是
;
将这组数据从小到大排列为6,6,6,8,10,10,11,13,14,16,
则中位数是 ;
数据6出现次数最多, 众数是6.
(2)管理者为了提高员工的工作效率,又不能挫伤其积极性,应确定
每名员工的标准日产量为多少台比较恰当?
解:管理者应确定每名员工的标准日产量为10台比较恰当.
考点2 方差
9.[2024 雅安] 某校开展了红色经典故事演讲比赛,其中8名同学的成绩
(单位:分)分别为85,81,82,86,82,83,92,89.关于这组数据,
下列说法中正确的是( )
D
A.众数是92 B.中位数是84.5 C.平均数是84 D.方差是13
10.[2024 云南] 甲、乙、丙、丁四名运动员参加射击项目选拔赛,每人
10次射击成绩的平均数(单位:环)和方差 如下表所示:
甲 乙 丙 丁
9.9 9.5 8.2 8.5
0.09 0.65 0.16 2.85
根据表中数据,从中选择一名成绩好且发挥稳定的运动员参加比赛,应
该选择( )
A
A.甲 B.乙 C.丙 D.丁
11.如图是甲、乙两名同学五次数学测试成绩的折线图.比较甲、乙两名
同学的成绩,下列说法正确的是( )
D
A.甲同学成绩的平均分高,波动较小
B.甲同学成绩的平均分高,波动较大
C.乙同学成绩的平均分高,波动较小
D.乙同学成绩的平均分高,波动较大
.评委打分的平均数、中位数、众数如下:
平均数 中位数 众数
教师评委 91 91
学生评委 90.8 93
根据以上信息,回答下列问题:
①的值为____, 的值位于学生评委打分数据分组的第___组;
②若去掉教师评委打分中的最高分和最低分,记其余8名教师评委打分
的平均数为,则___91(填“ ”“”或“ ”);
4
(2)决赛由5名专业评委给每位选手打分(百分制).对每位选手,计
算5名专业评委给其打分的平均数和方差.平均数较大的选手排序靠前,
若平均数相同,则方差较小的选手排序靠前,5名专业评委给进入决赛
的甲、乙、丙三位选手的打分如下:
评委1 评委2 评委3 评委4 评委5
甲 93 90 92 93 92
乙 91 92 92 92 92
丙 90 94 90 94
若丙在甲、乙、丙三位选手中的排序居中,则这三位选手中排序最靠前
的是____,表中( 为整数)的值为____.
甲
92
[解析] 点拨: ,
,
, .
丙在甲、乙、丙三位选手中的排序居中, ,
,
解得 .
为整数,或92.当时, ,
此时 ,
,
乙在甲、乙、丙三位选手中的排序居中,不合题意;当 时,
,此时
,
, 丙在甲、乙、丙三位选手中的排序居中,符合题意,故
这三位选手中排序最靠前的是甲, 的值为92.
考点3 用样本估计总体
13.某学校在开展“节约每一滴水”的活动中,从七年级的180名同学中任选
出10名同学汇报了各自家庭一个月的节水情况,将有关数据整理如下表:
节水量/吨 0.5 1 1.5 2
人数 2 3 4 1
请你估计这180名同学的家庭一个月节约用水的总量是( )
C
A.180吨 B.200吨 C.216吨 D.360吨
14. 2024年10月30日,神舟十九号载人飞船在酒泉卫星
发射中心成功发射,进一步激发了青少年热爱科学的热情.某校为了普
及“航空航天”知识,从该校1 200名学生中随机抽取了200名学生参加
“航空航天”知识测试,将成绩整理绘制成如下不完整的统计图表:
成绩统计表
组别 成绩 分 百分比
A
B
C
D
根据所给信息,解答下列问题:
(1)本次调查的成绩统计表中 ____%,并补全条形统计图;
20
解:补全条形统计图如图:
(2)这200名学生成绩的中位数会落在___组(填A,B,C,D或 );
D
(3)试估计该校1 200名学生中成绩在90分以上(包括90分)的人数.
解: (名).
所以估计该校1 200名学生中成绩在90分以上(包括90分)的人数为300.
思想2 统计思想
17.[2024 湖北] 某校为增强学生身体素质,以“阳光运动,健康成长”为
主题开展体育训练,并对学生进行专项体能测试,以下是某次八年级男
生引体向上测试成绩的抽样与数据分析过程.
【收集数据】随机抽取若干名男生的测试成绩.
【整理数据】将抽取的成绩进行整理,用 (引体向上个数)表示成绩,
分成四组:
A组,B组 ,
C组,D组 .
【描述数据】根据抽取的男生成绩,绘制出如下不完整的统计图.
【分析数据】抽取的八年级男生测试成绩的平均数为8,中位数为8,众
数为11.
根据以上信息,解答下列问题:
(1)求A组人数,并补全条形统计图;
解:样本容量为 ,
故A组人数为 .
补全条形统计图如图:
(2)估计该校八年级参加测试的400名男生中成绩不低于10个的人数;
解: (名).
答:估计该校八年级参加测试的400名男生中成绩不低于10个的人数为
180.
(3)从平均数、中位数和众数这三个统计量中任选一个,解释其在本
题中的意义.
解:平均数8表示抽取的40名男生的平均成绩为8.(答案不唯一)
数据分析中的决策问题
专项突破
1.某风景区对5个旅游景点的门票价格进行了调整,据统计,调价前后各景点的游客人数基本不变.有关数据如下表所示:
景点 A B C D E
原价/元 10 10 15 20 25
现价/元 5 5 15 25 30
日平均人数/千人 1 1 2 3 2
(1)该风景区称调整前后这5个景点门票的平均价格不变,日平均总收入持平.风景区是怎样计算的?
(2)另一方面,游客认为调整价格后风景区的日平均总收入相对于调价前,实际上增加了约9.4%.游客是怎样计算的?
(3)你认为风景区和游客哪一个的说法较能反映整体实际情况?
【解】根据加权平均数的定义可知,游客的说法较能反映整体实际情况.(合理即可)
2. 某班为了从甲、乙两人中选出一人担任班长,进行了一次测评活动,邀请了五位老师作为评委,对学生进行个人测评,全班同学进行民主测评,结果如下:
规则:①个人测评得分(x1)算法:去掉一个最高分和一个最低分后,再算出平均分;
②民主测评得分(x2)算法:“优”票数×3+“良”票数×2+“中”票数×1;
③综合得分(X)算法:X=0.4x1+0.6x2.
根据以上信息,解决下列问题:
(1)如果只采用个人测评规则,获胜者是______(填“甲”或“乙”).
甲
(2)甲的民主测评得分为________,乙的民主测评得分为________.
139
148
【点拨】甲的民主测评得分为40×3+7×2+5×1=139(分),乙的民主测评得分为45×3+6×2+1×1=148(分).
(3)综合得分高的学生当选为班长,通过计算,判断最终当选的是甲还是乙?
3.[2024重庆]为了解学生的安全知识掌握情况,某校举办了安全知识竞赛.现从七、八年级的学生中各随机抽取20名学生的竞赛成绩(百分制)进行收集、整理、描述、分析.所有学生的成绩均高于60分(成绩得分用x表示,共分成四组:A.60<x≤70;B.70<x≤80;C.80<x≤90;D.90<x≤100),下面给出了部分信息:
七年级20名学生的竞赛成绩为:
66,67,68,68,75,83,84,86,86,86,
86,87,87,89,95,95,96,98,98,100.
八年级20名学生的竞赛成绩在C组的数据是:81,82,84,87,88,89.
七、八年级所抽取学生的竞赛成绩统计表
年级 七年级 八年级
平均数 85 85
中位数 86 b
众数 a 79
根据以上信息,解答下列问题:
(1)上述图表中,a=________,b=________,m=________.
86
87.5
40
(2)根据以上数据分析,你认为该校七、八年级中哪个年级学生的安全知识竞赛成绩较好?请说明理由(写出一条理由即可).
【解】八年级学生的安全知识竞赛成绩较好.理由如下:
因为两个年级成绩的平均数相同,但八年级的中位数高于七年级,所以八年级学生的安全知识竞赛成绩较好.(答案不唯一)
(3)该校七年级有400名学生、八年级有500名学生参加了此次安全知识竞赛,估计该校七、八年级参加此次安全知识竞赛成绩优秀(x>90)的学生人数是多少?
返回
4. 某校初三年级开展了系列交通安全知识竞赛,从中随机抽取30名学生两次知识竞赛的成绩(百分制),并对数据(成绩)进行收集、整理、描述和分析.下面给出了部分信息.
a.这30名学生第一次竞赛成绩
和第二次竞赛成绩得分情况统计
图如下:
b.这30名学生两次知识竞赛的获奖情况统计如下表:(规定:分数≥90,获卓越奖;85≤分数<90,获优秀奖;分 数<85,获参与奖)
参与奖 优秀奖 卓越奖
第一次竞赛 人数 10 10 10
平均分 82 87 95
第二次竞赛 人数 2 12 16
平均分 84 87 93
c. 第二次竞赛获卓越奖的学生成绩如下:90,90,91,91,91,91,92,93,93,94,94,94,95,95,96,98.
d. 两次竞赛成绩样本数据的平均数、中位数、众数如表:
平均数 中位数 众数
第一次竞赛 m 87.5 88
第二次竞赛 90 n 91
根据以上信息,回答下列问题:
(1)小松同学第一次竞赛成绩是89分,第二次竞赛成绩是91分,在图中用“〇”圈出代表小松同学的点;
【解】如图所示.
(2)直接写出m,n的值;
(3)请判断第几次竞赛中初三年级全体学生的成绩水平较高,并说明理由.
【解】m=88,n=90.
第二次竞赛中初三年级全体学生的成绩水平较高.理由:第二次竞赛学生成绩的平均数、中位数、众数都高于第一次竞赛.
5. 据了解,“i深圳”体育场地一键预约平台是市委、市政府打造“民生幸福标杆”城市过程中,推动的惠民利民重要举措,在满足市民健身需求、激发全民健身热情、促进体育消费等方面具有重大意义.按照符合条件的学校体育场馆和社会体育场馆“应接尽接”原则,“i深圳”体育场馆一键预约平台实现了“让想运动的人找到场地,已有的体育场地得到有效利用”.
小明爸爸决定在周六上午预约一所学校的操场锻炼身体,现有A,B两所学校适合,小明收集了这两所学校过去10周周六上午的预约人数:
学校A:28,30,40,45,48,48,48,48,48,50
学校B:
(1)
学校 平均数 众数 中位数 方差
A ______ 48 83.299
B 48.4 ______ ______ 354.04
43.3
25
47.5
(2)根据上述材料分析,小明爸爸应该预约哪所学校?请说明你的理由.
【解】小明爸爸应该预约A学校.理由如下:
因为两所学校的平均数接近,但A学校的方差小于B学校,即A学校预约人数比较稳定,所以小明爸爸应该预约A学校.
6. “惜餐为荣,殄物为耻”,为了解落实“光盘行动”的情况,某校调查了七、八年级部分班级某一天的餐后垃圾质量.从七、八年级各随机抽取10个班餐后垃圾质量的数据(单位:kg),进行整理和分析(餐后垃圾质量用x表示,共分为四个等级:A.x<1;B.1≤x<1.5;C.1.5≤x<2;D.x≥2),下面给出了部分信息.
七年级10个班餐后垃圾质量:0.8,0.8,0.8,0.9,1.1,1.1,1.6,1.7,1.9,2.3.
八年级10个班餐后垃圾质量中B等级包含的所有数据为:1.0,1.0,1.0,1.1,1.1.
七、八年级抽取的班级餐后垃圾质量统计表
年级 平均数 中位数 众数 方差 A等级所
占百分比
七年级 1.3 1.1 a 0.26 40%
八年级 1.3 b 1.0 0.23 m%
根据以上信息,解答下列问题:
(1)直接写出上述表中a,b,m的值;
【解】a=0.8,b=1.05,m=20.
(2)该校八年级共有30个班,估计八年级这一天餐后垃圾质量符合A等级的班级数;
【解】30×20%=6(个).
答:估计八年级这一天餐后垃圾质量符合A等级的班级数为6个.
(3)根据以上信息,你认为该校七、八年级的“光盘行动”,哪个年级落实得更好?请说明理由(写出一条理由即可).
【解】七年级.理由:七年级各班餐后垃圾质量A等级所占百分比高于八年级(答案不唯一).
易错点1.平均数的概念理解不清晰
【例1】10名学生的平均成绩是x分,如果另外5名学生每人得84分,那么整个组15人的平均成绩是 ( )
A.分 B.分
C.分 D.分
错解:选A.
错解分析:由于对平均数的概念理解不清晰,误认为10名学生的平均成绩与另外5名学生的平均成绩的平均数即是15人的平均成绩.
易混易错
正解:因为10名学生的平均成绩是x分,所以10名学生的总成绩是10x分,故整个组的平均成绩是(分),故选B.
【针对训练】为了调查某一路口某时段的汽车流量,记录了30天中每天同一时段通过该路口的汽车辆数,其中有4天是284辆,4天是290辆,12天是312辆,10天是314辆,则这30天该路口同一时段通过的汽车平均数为 辆.
306
易错点2.众数的概念理解不清晰
【例2】求下列数据的众数:3,6,1,3,4,3,6,6.
错解:众数是3或众数是6.
错解分析:认为众数是3或众数是6,是没有正确理解众数的概念,众数是一组数据中,出现次数最多的数据,如果一组数据中有几个数据重复的次数相同,并且次数都是最高的,那么这几个数据都是这组数据的众数,即一组数据的众数不一定唯一,因此众数可能有一个、多个、也可能没有.
正解:众数是3和6.
【针对训练】(2023·鞍山)九(1)班30名同学在一次测试中,某道题目(满分4分)的得分情况如表:
则这道题目得分的众数和中位数分别是( )
A.8,3 B.8,2
C.3,3 D.3,2
C
得分 0 1 2 3 4
人数 1 3 4 14 8
易错点3.中位数的概念理解不清晰
【例3】某民营企业员工的个人月工资统计如下:
月工资 人数
9 000元 1
7 500元 2
5 500元 5
5 000元 20
4 800元 35
该企业员工的月工资的中位数是 元.
错解:5 500.
错解分析:本题表面上看员工的个人月工资数据已经排序,可以求数据的中位数,但注意观察可以发现:题目中的数据实际是小组数据,小组的人数才是数据的真正个数.因此,不能直接求数据的中位数,而应先求出63名员工数据的中间数据.
正解:(63+1)÷2=32,所以第32名员工的月工资为中位数,从表中人数栏数出第32名员工的月工资为4 800元,即该企业员工的月工资的中位数是4 800元.
A.8 B.7 C.6 D.5
图D20-1-1
【针对训练】 (2023·株洲)申报某个项目时,某7个区域提交的申报表数量的前5名的数据统计如图D20-1-1所示,则这7个区域提交该项目的申报表数量的中位数是( )
C
易错点4.方差的概念及计算易出错
【例4】某中学为了选拔1名运动员参加市级运动会100 m短跑比赛,现有甲、乙、丙3名运动员备选,他们100 m短跑的平均成绩一样,方差分别为=2.5,=2.3,=1.1.如果要推选一名成绩优秀且稳定的人去参赛,推选人应为 .
错解:甲.
错解分析:对描述数据离散程度的特征数——方差理解出错,从而本题出现错解.一组数据的方差越大,这组数据的波动越大,方差越小,数据的波动越小.
正解:丙.
【针对训练】某校组织数学学科竞赛为参加区级比赛做选手选拔工作,经过多次测试后,有四位同学成为晋级的候选人,具体情况如下表,如果从这四位同学中选出一名晋级(总体水平高且状态稳定),你会推荐 .
丙
候选人 甲 乙 丙 丁
平均分/分 92 94 94 92
方差 35 35 23 23
1.[2024·眉山] 为落实阳光体育活动,学校鼓励学生积极参加体育锻炼.
已知某天五名同学体育锻炼的时间分别为(单位:小时), ,
,2, ,这组数据的中位数和众数分别是( )
A
A., B., C., D.1,2
押题预测
2.已知某外卖平台设置送餐距离超过 无法配送,由于给送餐员的费
用与送餐距离有关,为更合理设置送餐费用,该平台随机抽取80名点外
卖的用户进行统计,按送餐距离分类,统计结果如下表:
送餐距离
用户数量/名 12 20 24 16 8
估计利用该平台点外卖的用户的平均送餐距离为_________.
3. 近年来,由于智能聊
天机器人的横空出世,大型语言模型成
为人工智能领域的热门话题. 有关人员开
展了,两款 聊天机器人的使用满意
度评分测验,并从中各随机抽取20份,
抽取的对款 聊天机器人的评分数据中“满意”的数据为84,86,86,
87,88,89.
对数据进行整理、描述和分析(评分分数用 表示,分为四个等级:
不满意,比较满意,满意 ,非常满意
),下面给出了部分信息:
抽取的对款 聊天机器人的评分数据如下:
67,68,69,83,85,86,87,87,87,88,88,89,95,96,96,96,
96,98,99,100.
抽取的对,两款 聊天机器人的评分统计表:
设备 平均数 中位数 众数 “非常满意”所占百分比
88 96
88 88
根据以上信息,解答下列问题:
(1)上述图表中____,_____, ____;
15
88.5
96
(2)根据以上数据,你认为哪款 聊天机器人更受用户喜爱?请说明
理由(写出一条理由即可);
解:款 聊天机器人更受用户喜爱,理由如下:
因为两款的评分数据的平均数都是88,但款评分数据的中位数比 款
高,所以款 聊天机器人更受用户喜爱.(答案不唯一,合理即可)
(3)在此次测验中,有240人对款 聊天机器人进行了评分,300人对
款聊天机器人进行了评分,请通过计算,估计此次测验中对 聊天
机器人不满意的共有多少人.
解:对款 聊天机器人不满意的有3人,所占百分比为
, 估计此次测验中对 聊天机器人不满意的共有
(人).
专题04 数据的分析
(3考点+2思想+专题突破+4易错)
八年级数学下学期期末复习
人教版
01
02
04
03
目
录
易错易混
题型剖析
考点透视
押题预测
三大常考点:知识梳理+针对训练
二大思想方法+专题突破(数据分析中的决策问题)
四大易错易混经典例题+针对训练
精选3道期末真题对应考点练
最多
越大
越小
知识结构
平均数 定义 一组数据的平均值称为这组数据的平均数
算术平 均数 一般地,如果有n个数x1,x2,…,xn,那么_____________________叫做这n个数的平均数.
加权平 均数 一般地,若n个数x1,x2,…,xn的权分别
是w1,w2,…,wn,则
___________________
叫做这n个数的加权平均数.
知识梳理
知识点一:数据的集中趋势
最多
中间位置的数
两个数据的平均数
中位数 定义 将一组数据按照由小到大(或由大到小)的顺序排列,如果数据的个数是奇数,则处于________________就是这组数据的中位数,如果数据的个数是偶数,则中间_________________________就是这组数据的中位数
防错 提醒 确定中位数时,一定要注意先把整组数据按照大小顺序排列,再确定
众 数 定义 一组数据中出现次数________的数据叫做这组数据的众数
防错 提醒 (1)一组数据中众数不一定只有一个;(2)当一组数据中出现异常值时,其平均数往往不能正确反映这组数据的集中趋势,就应考虑用中位数或众数来分析
平均数
大
表示波 动的量 定义 意义
方差 设有n个数据x1,x2,x3,…,xn,各数据与它们的________的差的平方分别是(x1-x)2,(x2-x)2,…,(xn-x)2,我们用它们的平均数,即用________________________来衡量这组数据的波动大小,并把它叫做这组数据的方差,记作s2 方差越大,数据的波动越___,反之也成立
知识点二:数据的波动程度
1.统计的基本思想:用样本的特征(平均数和方差)估计总体的特征.
2.统计的决策依据:利用数据做决策时,要全面、多角度地去分析已有数据,从数据的变化中发现它们的规律和变化趋势,减少人为因素的影响.
知识点三:用样本估计总体
考点1 平均数、中位数、众数
1.[2024 湖南] 某班的5名同学1分钟跳绳的成绩(单位:次)分别为:
179,130,192,158,141.这组数据的中位数是( )
B
A.130 B.158 C.160 D.192
针对训练
2.[2024 无锡] 一组数据:31,32,35,37,35,这组数据的平均数和
中位数分别是( )
C
A.34,34 B.35,35 C.34,35 D.35,34
3.[2024 扬州] 第8个全国近视防控宣传教育月的主题是“有效减少近视
发生,共同守护光明未来”.某校积极响应,开展视力检查.某班45名同学
视力检查数据如下表:
视力 4.3 4.4 4.5 4.6 4.7 4.8 4.9 5.0
人数 1 4 4 7 11 10 5 3
这45名同学视力检查数据的众数是( )
B
A.4.6 B.4.7 C.4.8 D.4.9
4.[2024 南京鼓楼区一模] 如图为某班35名学
生投篮成绩的条形统计图,其中上面部分数据
破损导致数据不完全.已知此班学生投篮成绩
的中位数是5,则根据下图,无法确定下列哪
一选项中的数值( )
C
A.4球以下的人数 B.5球以下的人数
C.6球以下的人数 D.7球以下的人数
(第5题)
5. 某校拟招聘一名优秀的数学教师,
设置了笔试、面试、试讲三项水平测试,综合成绩
按照笔试占,面试占,试讲占 进行计
算,小徐的三项测试成绩如图所示,则她的综合成
绩为_____分.
85.8
(第6题)
6.[2024 镇江] 小丽6次射击的成绩如图所示,则她的
射击成绩的中位数为____环.
7.5
7.样本数据3,,4, ,8的平均数是5,众数是3,则这组数据的中位
数是___.
4
8.某企业加强了管理,准备采取每天的任务定额和超产有奖的措施,以
提高工作效率.下面是该企业10名员工过去一天中各自装配机器的数量
(单位:台):6,8,16,14,11,10,6,13,10,6.
(1)求这组数据的平均数、众数和中位数.
解:平均数是
;
将这组数据从小到大排列为6,6,6,8,10,10,11,13,14,16,
则中位数是 ;
数据6出现次数最多, 众数是6.
(2)管理者为了提高员工的工作效率,又不能挫伤其积极性,应确定
每名员工的标准日产量为多少台比较恰当?
解:管理者应确定每名员工的标准日产量为10台比较恰当.
考点2 方差
9.[2024 雅安] 某校开展了红色经典故事演讲比赛,其中8名同学的成绩
(单位:分)分别为85,81,82,86,82,83,92,89.关于这组数据,
下列说法中正确的是( )
D
A.众数是92 B.中位数是84.5 C.平均数是84 D.方差是13
10.[2024 云南] 甲、乙、丙、丁四名运动员参加射击项目选拔赛,每人
10次射击成绩的平均数(单位:环)和方差 如下表所示:
甲 乙 丙 丁
9.9 9.5 8.2 8.5
0.09 0.65 0.16 2.85
根据表中数据,从中选择一名成绩好且发挥稳定的运动员参加比赛,应
该选择( )
A
A.甲 B.乙 C.丙 D.丁
11.如图是甲、乙两名同学五次数学测试成绩的折线图.比较甲、乙两名
同学的成绩,下列说法正确的是( )
D
A.甲同学成绩的平均分高,波动较小
B.甲同学成绩的平均分高,波动较大
C.乙同学成绩的平均分高,波动较小
D.乙同学成绩的平均分高,波动较大
.评委打分的平均数、中位数、众数如下:
平均数 中位数 众数
教师评委 91 91
学生评委 90.8 93
根据以上信息,回答下列问题:
①的值为____, 的值位于学生评委打分数据分组的第___组;
②若去掉教师评委打分中的最高分和最低分,记其余8名教师评委打分
的平均数为,则___91(填“ ”“”或“ ”);
4
(2)决赛由5名专业评委给每位选手打分(百分制).对每位选手,计
算5名专业评委给其打分的平均数和方差.平均数较大的选手排序靠前,
若平均数相同,则方差较小的选手排序靠前,5名专业评委给进入决赛
的甲、乙、丙三位选手的打分如下:
评委1 评委2 评委3 评委4 评委5
甲 93 90 92 93 92
乙 91 92 92 92 92
丙 90 94 90 94
若丙在甲、乙、丙三位选手中的排序居中,则这三位选手中排序最靠前
的是____,表中( 为整数)的值为____.
甲
92
[解析] 点拨: ,
,
, .
丙在甲、乙、丙三位选手中的排序居中, ,
,
解得 .
为整数,或92.当时, ,
此时 ,
,
乙在甲、乙、丙三位选手中的排序居中,不合题意;当 时,
,此时
,
, 丙在甲、乙、丙三位选手中的排序居中,符合题意,故
这三位选手中排序最靠前的是甲, 的值为92.
考点3 用样本估计总体
13.某学校在开展“节约每一滴水”的活动中,从七年级的180名同学中任选
出10名同学汇报了各自家庭一个月的节水情况,将有关数据整理如下表:
节水量/吨 0.5 1 1.5 2
人数 2 3 4 1
请你估计这180名同学的家庭一个月节约用水的总量是( )
C
A.180吨 B.200吨 C.216吨 D.360吨
14. 2024年10月30日,神舟十九号载人飞船在酒泉卫星
发射中心成功发射,进一步激发了青少年热爱科学的热情.某校为了普
及“航空航天”知识,从该校1 200名学生中随机抽取了200名学生参加
“航空航天”知识测试,将成绩整理绘制成如下不完整的统计图表:
成绩统计表
组别 成绩 分 百分比
A
B
C
D
根据所给信息,解答下列问题:
(1)本次调查的成绩统计表中 ____%,并补全条形统计图;
20
解:补全条形统计图如图:
(2)这200名学生成绩的中位数会落在___组(填A,B,C,D或 );
D
(3)试估计该校1 200名学生中成绩在90分以上(包括90分)的人数.
解: (名).
所以估计该校1 200名学生中成绩在90分以上(包括90分)的人数为300.
思想2 统计思想
17.[2024 湖北] 某校为增强学生身体素质,以“阳光运动,健康成长”为
主题开展体育训练,并对学生进行专项体能测试,以下是某次八年级男
生引体向上测试成绩的抽样与数据分析过程.
【收集数据】随机抽取若干名男生的测试成绩.
【整理数据】将抽取的成绩进行整理,用 (引体向上个数)表示成绩,
分成四组:
A组,B组 ,
C组,D组 .
【描述数据】根据抽取的男生成绩,绘制出如下不完整的统计图.
【分析数据】抽取的八年级男生测试成绩的平均数为8,中位数为8,众
数为11.
根据以上信息,解答下列问题:
(1)求A组人数,并补全条形统计图;
解:样本容量为 ,
故A组人数为 .
补全条形统计图如图:
(2)估计该校八年级参加测试的400名男生中成绩不低于10个的人数;
解: (名).
答:估计该校八年级参加测试的400名男生中成绩不低于10个的人数为
180.
(3)从平均数、中位数和众数这三个统计量中任选一个,解释其在本
题中的意义.
解:平均数8表示抽取的40名男生的平均成绩为8.(答案不唯一)
数据分析中的决策问题
专项突破
1.某风景区对5个旅游景点的门票价格进行了调整,据统计,调价前后各景点的游客人数基本不变.有关数据如下表所示:
景点 A B C D E
原价/元 10 10 15 20 25
现价/元 5 5 15 25 30
日平均人数/千人 1 1 2 3 2
(1)该风景区称调整前后这5个景点门票的平均价格不变,日平均总收入持平.风景区是怎样计算的?
(2)另一方面,游客认为调整价格后风景区的日平均总收入相对于调价前,实际上增加了约9.4%.游客是怎样计算的?
(3)你认为风景区和游客哪一个的说法较能反映整体实际情况?
【解】根据加权平均数的定义可知,游客的说法较能反映整体实际情况.(合理即可)
2. 某班为了从甲、乙两人中选出一人担任班长,进行了一次测评活动,邀请了五位老师作为评委,对学生进行个人测评,全班同学进行民主测评,结果如下:
规则:①个人测评得分(x1)算法:去掉一个最高分和一个最低分后,再算出平均分;
②民主测评得分(x2)算法:“优”票数×3+“良”票数×2+“中”票数×1;
③综合得分(X)算法:X=0.4x1+0.6x2.
根据以上信息,解决下列问题:
(1)如果只采用个人测评规则,获胜者是______(填“甲”或“乙”).
甲
(2)甲的民主测评得分为________,乙的民主测评得分为________.
139
148
【点拨】甲的民主测评得分为40×3+7×2+5×1=139(分),乙的民主测评得分为45×3+6×2+1×1=148(分).
(3)综合得分高的学生当选为班长,通过计算,判断最终当选的是甲还是乙?
3.[2024重庆]为了解学生的安全知识掌握情况,某校举办了安全知识竞赛.现从七、八年级的学生中各随机抽取20名学生的竞赛成绩(百分制)进行收集、整理、描述、分析.所有学生的成绩均高于60分(成绩得分用x表示,共分成四组:A.60<x≤70;B.70<x≤80;C.80<x≤90;D.90<x≤100),下面给出了部分信息:
七年级20名学生的竞赛成绩为:
66,67,68,68,75,83,84,86,86,86,
86,87,87,89,95,95,96,98,98,100.
八年级20名学生的竞赛成绩在C组的数据是:81,82,84,87,88,89.
七、八年级所抽取学生的竞赛成绩统计表
年级 七年级 八年级
平均数 85 85
中位数 86 b
众数 a 79
根据以上信息,解答下列问题:
(1)上述图表中,a=________,b=________,m=________.
86
87.5
40
(2)根据以上数据分析,你认为该校七、八年级中哪个年级学生的安全知识竞赛成绩较好?请说明理由(写出一条理由即可).
【解】八年级学生的安全知识竞赛成绩较好.理由如下:
因为两个年级成绩的平均数相同,但八年级的中位数高于七年级,所以八年级学生的安全知识竞赛成绩较好.(答案不唯一)
(3)该校七年级有400名学生、八年级有500名学生参加了此次安全知识竞赛,估计该校七、八年级参加此次安全知识竞赛成绩优秀(x>90)的学生人数是多少?
返回
4. 某校初三年级开展了系列交通安全知识竞赛,从中随机抽取30名学生两次知识竞赛的成绩(百分制),并对数据(成绩)进行收集、整理、描述和分析.下面给出了部分信息.
a.这30名学生第一次竞赛成绩
和第二次竞赛成绩得分情况统计
图如下:
b.这30名学生两次知识竞赛的获奖情况统计如下表:(规定:分数≥90,获卓越奖;85≤分数<90,获优秀奖;分 数<85,获参与奖)
参与奖 优秀奖 卓越奖
第一次竞赛 人数 10 10 10
平均分 82 87 95
第二次竞赛 人数 2 12 16
平均分 84 87 93
c. 第二次竞赛获卓越奖的学生成绩如下:90,90,91,91,91,91,92,93,93,94,94,94,95,95,96,98.
d. 两次竞赛成绩样本数据的平均数、中位数、众数如表:
平均数 中位数 众数
第一次竞赛 m 87.5 88
第二次竞赛 90 n 91
根据以上信息,回答下列问题:
(1)小松同学第一次竞赛成绩是89分,第二次竞赛成绩是91分,在图中用“〇”圈出代表小松同学的点;
【解】如图所示.
(2)直接写出m,n的值;
(3)请判断第几次竞赛中初三年级全体学生的成绩水平较高,并说明理由.
【解】m=88,n=90.
第二次竞赛中初三年级全体学生的成绩水平较高.理由:第二次竞赛学生成绩的平均数、中位数、众数都高于第一次竞赛.
5. 据了解,“i深圳”体育场地一键预约平台是市委、市政府打造“民生幸福标杆”城市过程中,推动的惠民利民重要举措,在满足市民健身需求、激发全民健身热情、促进体育消费等方面具有重大意义.按照符合条件的学校体育场馆和社会体育场馆“应接尽接”原则,“i深圳”体育场馆一键预约平台实现了“让想运动的人找到场地,已有的体育场地得到有效利用”.
小明爸爸决定在周六上午预约一所学校的操场锻炼身体,现有A,B两所学校适合,小明收集了这两所学校过去10周周六上午的预约人数:
学校A:28,30,40,45,48,48,48,48,48,50
学校B:
(1)
学校 平均数 众数 中位数 方差
A ______ 48 83.299
B 48.4 ______ ______ 354.04
43.3
25
47.5
(2)根据上述材料分析,小明爸爸应该预约哪所学校?请说明你的理由.
【解】小明爸爸应该预约A学校.理由如下:
因为两所学校的平均数接近,但A学校的方差小于B学校,即A学校预约人数比较稳定,所以小明爸爸应该预约A学校.
6. “惜餐为荣,殄物为耻”,为了解落实“光盘行动”的情况,某校调查了七、八年级部分班级某一天的餐后垃圾质量.从七、八年级各随机抽取10个班餐后垃圾质量的数据(单位:kg),进行整理和分析(餐后垃圾质量用x表示,共分为四个等级:A.x<1;B.1≤x<1.5;C.1.5≤x<2;D.x≥2),下面给出了部分信息.
七年级10个班餐后垃圾质量:0.8,0.8,0.8,0.9,1.1,1.1,1.6,1.7,1.9,2.3.
八年级10个班餐后垃圾质量中B等级包含的所有数据为:1.0,1.0,1.0,1.1,1.1.
七、八年级抽取的班级餐后垃圾质量统计表
年级 平均数 中位数 众数 方差 A等级所
占百分比
七年级 1.3 1.1 a 0.26 40%
八年级 1.3 b 1.0 0.23 m%
根据以上信息,解答下列问题:
(1)直接写出上述表中a,b,m的值;
【解】a=0.8,b=1.05,m=20.
(2)该校八年级共有30个班,估计八年级这一天餐后垃圾质量符合A等级的班级数;
【解】30×20%=6(个).
答:估计八年级这一天餐后垃圾质量符合A等级的班级数为6个.
(3)根据以上信息,你认为该校七、八年级的“光盘行动”,哪个年级落实得更好?请说明理由(写出一条理由即可).
【解】七年级.理由:七年级各班餐后垃圾质量A等级所占百分比高于八年级(答案不唯一).
易错点1.平均数的概念理解不清晰
【例1】10名学生的平均成绩是x分,如果另外5名学生每人得84分,那么整个组15人的平均成绩是 ( )
A.分 B.分
C.分 D.分
错解:选A.
错解分析:由于对平均数的概念理解不清晰,误认为10名学生的平均成绩与另外5名学生的平均成绩的平均数即是15人的平均成绩.
易混易错
正解:因为10名学生的平均成绩是x分,所以10名学生的总成绩是10x分,故整个组的平均成绩是(分),故选B.
【针对训练】为了调查某一路口某时段的汽车流量,记录了30天中每天同一时段通过该路口的汽车辆数,其中有4天是284辆,4天是290辆,12天是312辆,10天是314辆,则这30天该路口同一时段通过的汽车平均数为 辆.
306
易错点2.众数的概念理解不清晰
【例2】求下列数据的众数:3,6,1,3,4,3,6,6.
错解:众数是3或众数是6.
错解分析:认为众数是3或众数是6,是没有正确理解众数的概念,众数是一组数据中,出现次数最多的数据,如果一组数据中有几个数据重复的次数相同,并且次数都是最高的,那么这几个数据都是这组数据的众数,即一组数据的众数不一定唯一,因此众数可能有一个、多个、也可能没有.
正解:众数是3和6.
【针对训练】(2023·鞍山)九(1)班30名同学在一次测试中,某道题目(满分4分)的得分情况如表:
则这道题目得分的众数和中位数分别是( )
A.8,3 B.8,2
C.3,3 D.3,2
C
得分 0 1 2 3 4
人数 1 3 4 14 8
易错点3.中位数的概念理解不清晰
【例3】某民营企业员工的个人月工资统计如下:
月工资 人数
9 000元 1
7 500元 2
5 500元 5
5 000元 20
4 800元 35
该企业员工的月工资的中位数是 元.
错解:5 500.
错解分析:本题表面上看员工的个人月工资数据已经排序,可以求数据的中位数,但注意观察可以发现:题目中的数据实际是小组数据,小组的人数才是数据的真正个数.因此,不能直接求数据的中位数,而应先求出63名员工数据的中间数据.
正解:(63+1)÷2=32,所以第32名员工的月工资为中位数,从表中人数栏数出第32名员工的月工资为4 800元,即该企业员工的月工资的中位数是4 800元.
A.8 B.7 C.6 D.5
图D20-1-1
【针对训练】 (2023·株洲)申报某个项目时,某7个区域提交的申报表数量的前5名的数据统计如图D20-1-1所示,则这7个区域提交该项目的申报表数量的中位数是( )
C
易错点4.方差的概念及计算易出错
【例4】某中学为了选拔1名运动员参加市级运动会100 m短跑比赛,现有甲、乙、丙3名运动员备选,他们100 m短跑的平均成绩一样,方差分别为=2.5,=2.3,=1.1.如果要推选一名成绩优秀且稳定的人去参赛,推选人应为 .
错解:甲.
错解分析:对描述数据离散程度的特征数——方差理解出错,从而本题出现错解.一组数据的方差越大,这组数据的波动越大,方差越小,数据的波动越小.
正解:丙.
【针对训练】某校组织数学学科竞赛为参加区级比赛做选手选拔工作,经过多次测试后,有四位同学成为晋级的候选人,具体情况如下表,如果从这四位同学中选出一名晋级(总体水平高且状态稳定),你会推荐 .
丙
候选人 甲 乙 丙 丁
平均分/分 92 94 94 92
方差 35 35 23 23
1.[2024·眉山] 为落实阳光体育活动,学校鼓励学生积极参加体育锻炼.
已知某天五名同学体育锻炼的时间分别为(单位:小时), ,
,2, ,这组数据的中位数和众数分别是( )
A
A., B., C., D.1,2
押题预测
2.已知某外卖平台设置送餐距离超过 无法配送,由于给送餐员的费
用与送餐距离有关,为更合理设置送餐费用,该平台随机抽取80名点外
卖的用户进行统计,按送餐距离分类,统计结果如下表:
送餐距离
用户数量/名 12 20 24 16 8
估计利用该平台点外卖的用户的平均送餐距离为_________.
3. 近年来,由于智能聊
天机器人的横空出世,大型语言模型成
为人工智能领域的热门话题. 有关人员开
展了,两款 聊天机器人的使用满意
度评分测验,并从中各随机抽取20份,
抽取的对款 聊天机器人的评分数据中“满意”的数据为84,86,86,
87,88,89.
对数据进行整理、描述和分析(评分分数用 表示,分为四个等级:
不满意,比较满意,满意 ,非常满意
),下面给出了部分信息:
抽取的对款 聊天机器人的评分数据如下:
67,68,69,83,85,86,87,87,87,88,88,89,95,96,96,96,
96,98,99,100.
抽取的对,两款 聊天机器人的评分统计表:
设备 平均数 中位数 众数 “非常满意”所占百分比
88 96
88 88
根据以上信息,解答下列问题:
(1)上述图表中____,_____, ____;
15
88.5
96
(2)根据以上数据,你认为哪款 聊天机器人更受用户喜爱?请说明
理由(写出一条理由即可);
解:款 聊天机器人更受用户喜爱,理由如下:
因为两款的评分数据的平均数都是88,但款评分数据的中位数比 款
高,所以款 聊天机器人更受用户喜爱.(答案不唯一,合理即可)
(3)在此次测验中,有240人对款 聊天机器人进行了评分,300人对
款聊天机器人进行了评分,请通过计算,估计此次测验中对 聊天
机器人不满意的共有多少人.
解:对款 聊天机器人不满意的有3人,所占百分比为
, 估计此次测验中对 聊天机器人不满意的共有
(人).
同课章节目录
