(期末考点培优)专题01 选择题-2024-2025学年五年级数学下册期末复习专项人教版(含解析)
文档属性
| 名称 | (期末考点培优)专题01 选择题-2024-2025学年五年级数学下册期末复习专项人教版(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 791.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-09 19:16:35 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
2024-2025学年五年级数学下册期末复习专项人教版
(期末考点培优)专题01 选择题
学校:___________姓名:___________班级:___________考号:___________
1.( )里填( )时,式子能进行简便计算。
A. B. C. D.
2.的分子加上12,要使分数的大小不变,分母应该( )。
A.加上12 B.乘3 C.乘4 D.乘12
3.有一个立方体,从前面看到,从左面看到,从上面看到,下面的立方体中符合要求的是( )。
A. B. C.
4.把一张长72cm,宽60cm的长方形纸,裁成同样大小、面积尽可能大的正方形纸,且纸无剩余,至少能裁( )张。
A.2 B.4 C.30 D.6
5.12个羽毛球特征相同,其中只有一个质量异常。现在要用一架没有砝码的天平去称,至少要称( )次才能找出那个质量异常的羽毛球。
A.4 B.3 C.2 D.1
6.从3时15分到3时45分这段时间里,分针旋转了( )。
A.180° B.90° C.60° D.30°
7.在下面的分数中,( )不是最简真分数。
A. B. C. D.
8.甲数和乙数互质,丙数是甲、乙两数的倍数。甲、乙、丙三个数的最大公因数是( )。
A.甲数 B.乙数 C.丙数 D.1
9.把一个长8厘米,宽和高都是5厘米的长方体截成一个最大的正方体后,表面积( )。
A.减少110平方厘米 B.减少85平方厘米 C.减少60平方厘米
10.小亮把一根绳子剪成了两段,第一段长m,第二段占全长的,那么这两段绳子相比,( )。
A.第一段长 B.第二段长 C.一样长 D.无法比较
11.一袋糖,4颗4颗地分、5颗5颗地分、6颗6颗地分,都正好分完而没有剩余,这袋糖最少有( )颗。
A.30 B.60 C.120 D.240
12.5个连续偶数,中间一个数是N,则最大的数是( )。
A.N+1 B.N+2 C.N+3 D.N+4
13.把的分子加上14,要使分数的大小不变,分母应该( )。
A.加上14 B.乘3 C.加上24 D.乘4
14.把一条绳子对折三次后,这时每段绳子的长度是全长的( )。
A. B. C.
15.拼一个从上面和左面看形状都是的物体,至少需要( )个小正方体。
A.4 B.5 C.3
16.下面几堆玻璃球中各有一个是次品(重一些),若用天平称,至少称3次就一定能找出这个较重的玻璃球。这堆玻璃球可能有( )个。
A.8 B.15 C.28
17.红十字会组织图书捐赠活动,张明和李丽捐了同样数量的课外书,张明捐了自己课外书的,李丽捐了自己课外书的,两人原有的课外书谁多?下面是三名同学的比较方法,正确的( )。
A.只有甲和乙 B.只有乙和丙 C.只有甲和丙 D.有甲、乙、丙
18.奇思在卡片上写出了下面的五个数,这些数共同的特点是( )。
A.都是51的因数 B.都是2的倍数 C.都是奇数 D.都是合数
19.下面各图形的阴影部分占整个图形的是( )。
A. B. C. D.
20.一条线段的是2厘米,这条线段长是( )。
A.3厘米 B.2厘米 C.4厘米 D.6厘米
21.如果A=3m,B=6m(A,B都是非零自然数),那么A,B的最大公因数是( )。
A.24m B.3m C.12m D.12
22.数学上把相差2的两个质数叫“孪生质数”,如3和5就是一对孪生质数,那么下列娜一对是孪生质数?( )
A.9和1 B.13和15 C.11和13
23.一个长方体的长,宽,高分别是a厘米,b厘米,h厘米,如果高增加2厘米,则其体积增加( )立方厘米。
A.abh B.2ab C.2ah D.ab(h+2)
24.由若干个小正方体搭成的几何体,从左面看和从正面看,看到的形状如下图所示,要搭成这样的几何体最多需要( )个小正方体。
A.7 B.8 C.10 D.12
25.著名的关于偶数的哥德巴赫猜想说的是“任意一个大于2的偶数都可以写成两个质数的和”。下面( )算式符合这个猜想。
A.38=21+17 B.32=31+1 C.36=13+23 D.34=24+10
26.把一个棱长是5dm的正方体木块截成两个大小、形状完全相等的长方体,这两个长方体的表面积一共是( )dm2。
A.125 B.150 C.200 D.300
27.一个长方体的底面是一个正方形,它的侧面展开图正好是一个面积为64平方分米的正方形。这个长方体一个底面的面积是( )平方分米。
A.64 B.16 C.8 D.4
28.要比较凉山州2024年4月、5月的气温变化情况,绘制( )统计图更合理。
A.单式条形 B.复式条形 C.单式折线 D.复式折线
29.自然数中,17的倍数( )。
A.都是偶数 B.都是奇数 C.都是质数 D.有偶数也有奇数
30.如果一个数a,只有两个因数,那么a一定是( )。
A.奇数 B.偶数 C.质数 D.合数
31.母亲节那天,文文买了一个礼品要送给妈妈作为节日礼物,得精心包装一番(如图所示),在选用丝带捆扎这个礼品盒时,遇到了一个问题,“要捆扎这种礼品盒至少需要准备( )厘米长的丝带”。(接头处长15厘米)
A.40 B.110 C.114 D.129
32.某市8路公交车每10分钟发一次车,10路公交车每12分钟发一次车。这两路公交车的起点站相同,上午6:30同时出发,则第二次同时发车的时间是( )。
A.6:52 B.7:00 C.7:30
33.有一张长方形纸,长48cm,宽36cm。如果要剪成若干张同样大小的正方形而没有剩余,剪出的正方形的边长最大是( )cm。
A.12 B.6 C.36
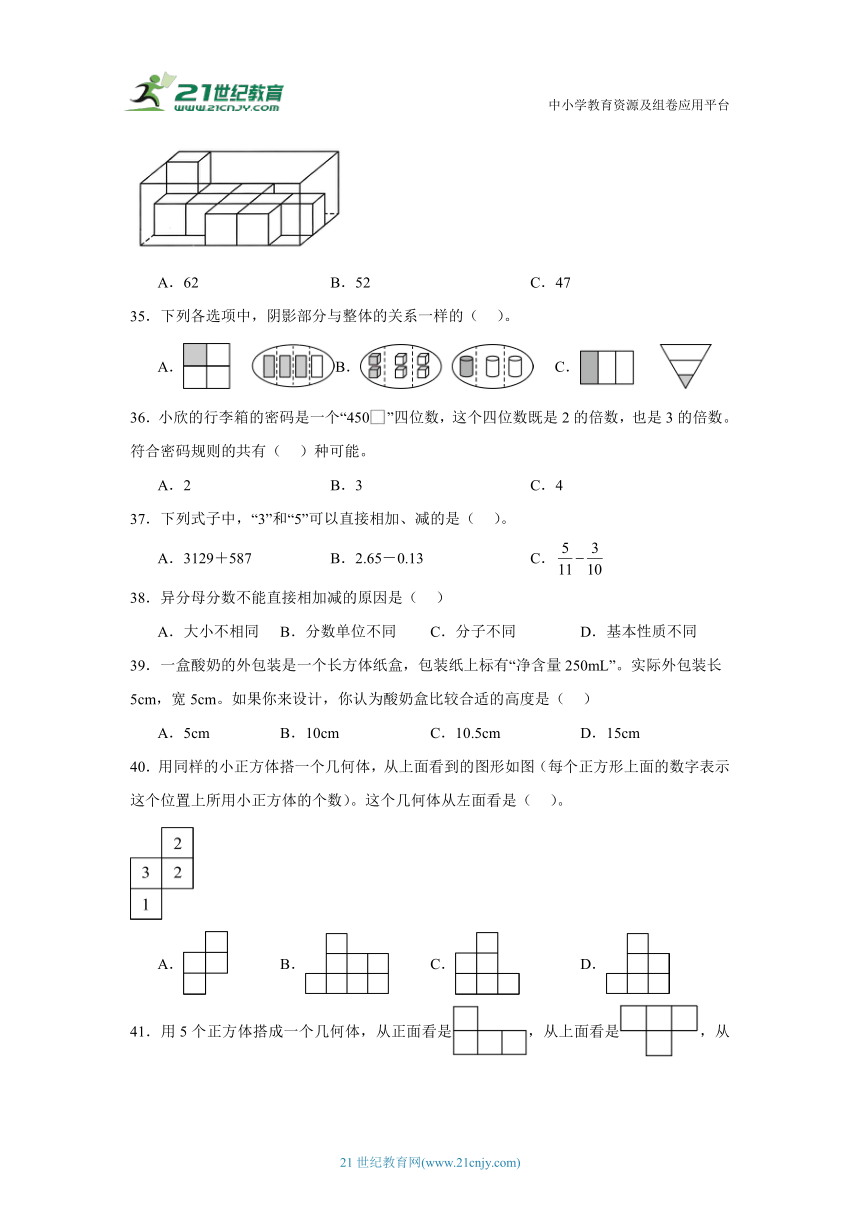
34.如图,在一个透明的无盖的长方体盒子内,放置棱长为1厘米的小正方体。这个透明的长方体盒子的表面积是( )平方厘米。
A.62 B.52 C.47
35.下列各选项中,阴影部分与整体的关系一样的( )。
A.B. C.
36.小欣的行李箱的密码是一个“450”四位数,这个四位数既是2的倍数,也是3的倍数。符合密码规则的共有( )种可能。
A.2 B.3 C.4
37.下列式子中,“3”和“5”可以直接相加、减的是( )。
A.3129+587 B.2.65-0.13 C.
38.异分母分数不能直接相加减的原因是( )
A.大小不相同 B.分数单位不同 C.分子不同 D.基本性质不同
39.一盒酸奶的外包装是一个长方体纸盒,包装纸上标有“净含量250mL”。实际外包装长5cm,宽5cm。如果你来设计,你认为酸奶盒比较合适的高度是( )
A.5cm B.10cm C.10.5cm D.15cm
40.用同样的小正方体搭一个几何体,从上面看到的图形如图(每个正方形上面的数字表示这个位置上所用小正方体的个数)。这个几何体从左面看是( )。
A. B. C. D.
41.用5个正方体搭成一个几何体,从正面看是,从上面看是,从右面看是,这个几何体是( )。
A. B. C. D.
42.一个三位数,同时是2、3、5的倍数,这个数最大是( )。
A.999 B.995 C.998 D.990
43.“龟兔赛跑”是我们熟悉的故事,大意是乌龟和兔子赛跑,兔子一开始就超过了乌龟好远,兔子看乌龟慢吞吞的,就得意地在路边睡了一觉,而乌龟一直往目的地拼命奔跑,等兔子醒来追赶了一段,但还是乌龟赢得了胜利。大致能反映这个故事情节的图像是( )。
A.B.C. D.
44.下图都是用5个相同的小正方体搭成的立体图形,从( )看,所看到的形状都是一样的。
A.上面 B.左面 C.右面 D.前面
45.如图是测量一颗铁球体积的过程:①将300毫升的水倒进一个容积为500毫升的杯子中;②将四颗相同的铁球放入水中,结果水没有满;③再将一颗同样的铁球放入水中,结果水满溢出。根据以上过程,推测这样一颗铁球的体积大约是( )cm3。
A.30~40 B.40~50 C.50~60 D.60~70
46.下面的分数中,能化成有限小数的是( )。
A. B. C. D.
47.如果(m和n是大于0的自然数)是真分数,那么( )。
A.n>m B.m>n C. D.无法确定
48.三个连续偶数中,最小的一个数为2n,则这三个偶数的和是( )。
A.6n B.6n+2 C.6n+4 D.6n+6
49.李冬设计了一个测量玻璃球体积的实验:先将200毫升的水倒进容积为500毫升的量杯中,再将1颗大玻璃球和1颗小玻璃球浸没水中,水面刚好在300毫升处,最后放入5颗小玻璃球,全都浸没水中,此时水面与量杯口齐平,刚好无水溢出。那么一颗大玻璃球的体积是( )立方厘米。
A.40 B.60 C.80 D.100
50.有8个外观相同的台球,其中一个是次品,略轻。欢欢用天平来找次品,第一次称的结果如右下图,可以推断( )一定是正品。
A.①、②、③、⑦和⑧ B.④、⑦和⑧ C.④、⑤和⑥
51.张阿姨买了3箱同样的车厘子,每箱车厘子的价格都是整数,且没有任何优惠,张阿姨可能花了( )。
A.260元 B.264元 C.268元
52.曹阿姨做了48个青团和36个艾饺,打算平均分给一些朋友。如果青团和艾饺都没有剩余,且保证分到青团和艾饺的朋友人数相同,最多能分给( )个朋友。
A.6 B.12 C.24
53.一个真分数的分子和分母同时加上一个非零自然数,得到的分数值一定( )。
A.与原分数相等 B.比原分数大 C.比原分数小 D.无法确定
54.要配制一种盐水,每100克水中要加入7克盐,这种盐水中盐的质量占盐水的( )。
A. B. C. D.
55.有12瓶矿泉水,其中11瓶质量相同,另有一瓶次品,次品质量重一些。用天平称,至少称( )次才能保证找出次品。
A.3次 B.2次 C.4次 D.5次
56.如图所示,一个长方体前面的面积是32cm2,高是4cm,宽是3cm,要计算这个长方体的体积,正确的算式是( )。
A.3×4 B.32×3 C.32×4 D.32×3×4
57.a是不等于零的自然数,2a+1一定是( )。
A.质数 B.合数 C.奇数 D.偶数
58.在一个透明的长方体盒子内放置棱长为1cm的小正方体(如图)。这个长方体盒子的表面积是( )cm2。
A.66 B.60 C.33 D.30
59.妈妈把买回来的一大瓶2.5L的可乐分别倒在只能装180mL的小子杯子里招待客人,( )个客人能喝到180mL的可乐。
A.13 B.13.888… C.14
60.一箱牛奶有12盒,其中有11盒质量相同,另有1盒质量略轻,如果能用天平称,至少称( )次可以保证找出这盒牛奶。
A.2 B.3 C.4 D.5
61.丽丽喝一杯纯牛奶她喝了杯后,用水加满,又喝了杯,再用水加满,最后一次喝完,丽丽喝的水和纯牛奶比较是( )。
A.水多 B.牛奶多 C.一样多 D.无法确定
62.将一个正方体钢坯锻造成一个长方体钢坯,长方体和正方体相比,( )。
A.体积和表面积都相等 B.体积相等,表面积不相等 C.体积不相等,表面积相等
63.要比较北京和南宁两地一年中气温的变化趋势,选择( )更合适。
A.复式条形统计图 B.单式折线统计图 C.复式折线统计图
64.下面现象属于平移的是( )。
A.索道上运行的缆车 B.钟面上转动的分针 C.飞行中直升飞机的螺旋桨
65.三张卡片上分别写着2、3、5,淘气和笑笑分别从中抽取一张,若两人抽取的卡片的数字之积是奇数,则淘气胜;若是偶数,则笑笑胜,这个游戏( )。
A.淘气胜的可能性大 B.笑笑胜的可能性大
C.两人胜的可能性一样大 D.无法判断
66.把一个棱长是8厘米的正方体钢锭,熔铸成一个长方体钢锭,已知长方体的长是5厘米,宽是8厘米,它的高是( )厘米。
A.12.6 B.12 C.9.6 D.12.8
67.一个正方体的棱长扩大到原来的2倍,棱长总和扩大到原来的( )倍,表面积扩大到原来的( )倍,体积扩大到原来的( )倍。
A.8;2;6 B.6;8;4 C.4;6;8 D.2;4;8
68.花花用5个同样的小正方体摆一个几何体,从上面看是,从左面看是。一共有( )种不同的摆法。
A.4 B.3 C.2 D.1
69.如果a÷b=15(a、b都是大于0的自然数),那么a和b的最大公因数是( )。
A.b B.15 C.a D.不确定
70.小明、小林和小军三人读同一篇文章,小明用了小时,小林用了小时,小军用了0.3小时,( )。
A.小明速度快 B.小林速度快 C.小军速度快 D.他们速度一样快
71.根据下图所给的数据,想象一下这个长方体可能是( )。
A.数学书 B.新华字典 C.纸巾盒 D.橡皮
72.把1m3的正方体木块切成1dm3的小正方体木块。如果把这些小木块排成一行组成一个长方体,那么这个长方体的长是( )。
A.1km B.100m C.1000cm
73.左图是一个长方体的3条棱(单位:cm)。从以下图形中选择6个面图出这个长方体,正确的选择是( )。
A.2个①、2个②、2个③ B.2个②、2个③、2个⑤
C.4个⑤、2个⑧ D.6个⑥
74.一个长方体的高增加5米后就变成了一个正方体,表面积增加了160平方米。原来长方体的长是( )。
A.3米 B.8米 C.32 平方米
75.在一个长8m、宽5m、高2m的水池中注满水,然后把一条长3m、宽2m、高4m的石柱立着放入水池中,水池溢出的水的体积是( )m3。
A.24 B.16 C.12
76.一次数学测试,红红做试卷用了小时,检查试卷用了小时,这时离测试结束还有小时,这次测试规定的时间是( )小时。
A. B. C.1
77.幼儿园老师给幼儿园小朋友分糖果,不管是每人5颗还是每人3颗,最后都会剩余1颗,糖果总数可能是( )颗。
A.60 B.61 C.62 D.63
78.和是两个不等于0的自然数,而且。那么,与相比较,( )。
A. B. C. D.无法比较大小
79.钟面上,时针从“8”起逆时针旋转后,时针应该指向( )。
A.3 B.5 C.12 D.11
80.把一个图形绕某点顺时针旋转60°后,所得到的图形与原来的图形相比较( )。
A.变小了 B.变大了
C.大小不变 D.无法确定大小是否变化
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案与试题解析
1.D
【分析】这是个连减运算。根据减法的性质:a-b-c=a-(b+c),那么括号里面的数如果和相加正好等于1,这个式子就能简便运算。所以,用1减即可得解。
【解析】
()里填时,式子能进行简便计算。
故答案为:D
2.C
【分析】分数的基本性质:分子和分母同时乘或除以一个相同的数(0除外),分数的大小不变,据此先算出分子加上12相当于给分子乘几,则分母也要乘相同的数,据此解答。
【解析】4+12=16
16÷4=4
7×4=28
=
的分子加上12,要使分数的大小不变,分母应该乘4。
故答案为:C
3.C
【分析】明确观察物体的方法,先确定有几列或几行,每列或每行有几个,形状是怎样的。据此分析各选项图形即可。
【解析】A.该图形从前面看有3列,2行,第一行3个并排,第二行只有中间列有1个,不符合题意。
B.该图形从左面看有2列,2行,第一行2个并排,第二行左列有1个,不符合题意。
C.该图形从前面看有3列,2行,第一行3个并排,第二行最左列有1个;从左面看有2列,2行,第一行2个并排,第二行右列有1个;从上面看有3列,2行,第二行3个并排,第一行最左列有1个。符合题意。
故答案为:C
4.C
【分析】把一块长方形纸裁成同样大小、面积尽可能大的正方形,且没有剩余,说明正方形的边长是长、宽的最大公因数,把72、60分解质因数后,把公有的相同质因数乘起来就是最大公因数,即是正方形的最大边长。再看长、宽里面分别有几个这样的最大公因数,最后相乘,即可求出至少能裁的张数。
【解析】72=2×2×2×3×3
60=2×2×3×5
72和60的最大公因数是:2×2×3=12
即正方形的边长最大是12cm。
72÷12=6(张)
60÷12=5(张)
一共:6×5=30(张)
至少能裁30张。
故答案为:C
5.A
【分析】根据题意,12个羽毛球特征相同,其中只有一个质量异常,但不知轻重,分组称重时,考虑天平平衡或不平衡时的各种情况,逐一讨论,得出至少称的次数。
【解析】第1次称量,将12个羽毛球平均分为三份①②③(每份4个),先把①和②放在天平的两边,如果天平平衡,则③里面有异常球;如果天平不平衡,则①和②中有异常羽毛球,③都是正常羽毛球;第2次称量,把①和②中的任意一份取下来,把③放上去,即可判断异常羽毛球在哪一份里,并且知道异常羽毛球的轻重;第3次称量,把有异常羽毛球的4个球平均分成两份(每份2个),把它们放在天平的两边,天平不平衡,根据轻重,判断出异常羽毛球在哪一份里;第4次称量,再把有异常羽毛球的2个球分成两份(每份1个),把它们放在天平的两边,天平不平衡,根据轻重,判断出异常羽毛球是哪一个。
所以至少要称4次才能找出那个质量异常的羽毛球。
故答案为:A
6.A
【分析】一个钟面平均分成60小格,分针走1小格表示1分钟,分针走一圈是60分钟,一圈是360°,分针走1小格是(360÷60)°;从3时15分到3时45分,分针共走了(45-15)分钟,再乘每小格的度数即可。
【解析】3时45分-3时15分=30(分钟)
360°÷60=6°
6°×30=180°
分针旋转了180°。
故答案为:A
7.C
【分析】分子比分母小的分数叫做真分数;真分数<1。分子比分母大或分子和分母相等的分数叫做假分数;假分数≥1。
最简分数是指分子和分母只有公因数1的分数。
【解析】A.<1,且24和25是互质数,所以是最简真分数;
B.<1,且7和8是互质数,所以是最简真分数;
C.>1,==,所以不是最简真分数;
D.<1,且4和21是互质数,所以是最简真分数。
故答案为:C
8.D
【分析】公因数只有1的两个非零自然数,叫做互质数。两个数公有因数叫做这两个数的公因数;其中最大的叫最大公因数。甲数和乙数互质,它们的最大公因数是1;丙数是甲、乙两数的倍数,则甲、乙、丙三个数互质,它们的最大公因数是1;可以通过举例得到答案。
【解析】如:甲数是2,乙数是3,2和3互质;丙数是6,6是2、3的倍数;2、3、6互质,2、3、6的最大公因数是1。
故答案为:D
9.C
【分析】根据正方体的特征可知,把这个长方体截成一个最大的正方体,这个正方体的棱长为5厘米,减少的面积相当于长为5厘米、宽为(8-5)厘米的4个小长方形的面积,根据长方形面积公式解答。
【解析】5×(8-5)×4
=5×3×4
=60(平方厘米)
把一个长8厘米,宽和高都是5厘米的长方体截成一个最大的正方体后,表面积减少60平方厘米。
故答案为:C
10.A
【分析】将绳子全长看作单位“1”,用单位“1”-第二段占全长的分率=第一段占全长的分率,比较两个分率即可。
【解析】第一段占全长的:
>
所以这两段绳子相比,第一段长。
故答案为:A
11.B
【分析】根据题意,一袋糖,4颗4颗地分、5颗5颗地分、6颗6颗地分,都正好分完而没有剩余,说明这袋糖最少的颗数是4、5、6的最小公倍数,据此解答。
【解析】
4、5、6的最小公倍数是2×2×3×5=60
即这袋糖最少有60颗。
故答案为:B
12.D
【分析】整数中,是2的倍数的数叫做偶数,不是2的倍数的数叫做奇数。连续偶数的特点,两个相邻的偶数相差2。
已知5个连续偶数,中间一个数是N,那么N+2+2是最大的数。
【解析】N+2+2=N+4
5个连续偶数,中间一个数是N,则最大的数是N+4。
故答案为:D
13.B
【分析】根据分数的基本性质可知,分数的分子和分母同时乘或除以一个相同的数((0除外),分数的大小不变。的分子加上14,变成了21,相当于乘(21÷7=3),所以分母也要乘3,据此解答。
【解析】由分析可得,分母应该乘3,即变成8×3=24。
A.分母加上14,变成8+14=22,不符合题意;
B.分母乘3,变成8×3=24,符合题意;
C.分母加上24,变成8+24=32,不符合题意;
D.分母乘4,变成8×4=32,不符合题意。
故答案为:B
14.B
【分析】把一根绳子对折一次,平均分成2段;对折两次,平均分成2×2=4段;对折三次,平均分成2×2×2=8段;求每段绳子的长度是全长的几分之几,用1÷平均分的段数,即1÷8解答。
【解析】2×2×2
=4×2
=8(段)
1÷8=
把一条绳子对折三次后,这时每段绳子的长度是全长的。
故答案为:B
15.A
【分析】
分析题目,从上面看到的图形是,则这个几何体的最下面一层有3个小正方体;从左面看形状还是,可知在前排的最底层上面至少还有1个小正方体,据此解答。
【解析】3+1=4(个)
拼一个从上面和左面看形状都是的物体,至少需要4个小正方体。
故答案为:A
16.B
【分析】找次品的方法:把待称的物品分成三份,能够平均分的就平均分成3份,不能平均分的,也应该使多的一份与少的一分只相差1,据此逐项解答。
【解析】A.把8个球分成3、3、2三组,把两个3个一组的放在天平上称,如平衡,则次品在2个的一组中,把这2个球分成1、1,放在天平上称,下沉的是次品,需称2次。如不平衡,刚把下沉的一组3个球分成1、1、1,任意两个放在天平上称,如平衡,没称的是次品,如不平衡,下沉的是资料品,需称2次。不符合题意。
B.把15平均分成5、5、5三组,任意称两个5,如果平衡,就从剩下的5个中找,如果不平衡,次品就在下沉的那组5中,就再把5分成2、2、1,称两个2,如果平衡,次品就在1中,如果不平衡,再就在下沉的2中,分1、1,可找出次品。即至少称3次。符合题意。
C.将28个球分成(9、9、10),称(9、9),只考虑最不利的情况,平衡,次品在10个中;将10个分成(3、3、4),称(3、3),平衡,次品在4个中;将4个分成(1、1、2),称(1、1),平衡,次品在2个中;再称一次即可确定次品,共4次。不符合题意。
故答案为:B
17.A
【分析】从题意可知:张明和李丽捐了同样数量的课外书,即张明课外书的等于李丽课外书的。
甲:根据分数的意义,将张明自己的课外书看作单位“1”, 平均分成5份,再取其中的3份(6本),即张明有6÷3×5=10本;将李丽自己的课外书看作单位“1”, 平均分成3份,再取其中的2份(6本),即李丽有6÷2×3=9本;10>9,即张明多,李丽少。比较方法正确。
乙:根据分数的意义,将张明自己的课外书看作单位“1”, 平均分成5份,再取其中的3份;将李丽自己的课外书看作单位“1”, 平均分成3份,再取其中的2份;张明的3份和李丽2份同样多,张明的5份大于李丽的3份,即张明多,李丽少。符合题意,比较方法正确。
丙:图中表示的两人捐了的课外书数量不同,即张明课外书的不等于李丽课外书的。不符合题意,比较方法错误。
【解析】根据分析可知:甲和乙的比较方法都能表示:张明和李丽捐了同样数量的课外书,张明捐了自己课外书的,李丽捐了自己课外书的,张明的课外书多,李丽的课外书少。
故答案为:A
18.D
【分析】应用列乘法算式法找出各个数的因数。除了1和它本身,还有其他因数的数,叫做合数。一个数如果能被2整除,那么这个数就是2的倍数。个位数字为0、2、4、6、8的数是偶数,个位数字为1、3、5、7、9的数是奇数。据此解答。
【解析】A.只有51是51的因数,所以该选项错误;
B.51÷2=25……1,36÷2=18,4÷2=2,9÷2=4……1,24÷2=12所以只有36,4,24是2的倍数,所以该选项错误;
C.51和9是奇数,36,4,24是偶数,所以该选项错误;
D.51,36,4,9,24都是合数,所以该选项正确。
故答案为:D
19.D
【分析】根据分数的意义,分母表示平均分的份数,分子表示取走的份数,分别用分数表示出各选项阴影部分即可。
【解析】A.不是平均分,不能用分数表示,排除;
B.阴影部分占整个图形,排除;
C.阴影部分占整个图形,排除;
D.阴影部分占整个图形,符合。
阴影部分占整个图形的是。
故答案为:D
20.D
【分析】把这条线段的全长看作单位“1”,把它平均分成3份,1份是2厘米,用1份的长乘3就是这条线段的全长。
【解析】2×3=6(厘米)
所以这条线段长是6厘米。
故答案为:D
21.B
【分析】两个数为倍数关系,则这两个数的最大公因数是较小的数,最小公倍数是较大的数。据此判断。
【解析】因为6m÷(3m)=2
所以A,B的最大公因数是3m。
故答案为:B
22.C
【分析】一个数,如果只有1和它本身两个因数,这样的数叫作质数;一个数,除了1和它本身还有别的因数,这样的数叫作合数;由题意可知,孪生质数是指两个数都是质数且它们的差为2,据此逐一分析各项即可。
【解析】A.在9和1中,9是合数,不是质数,所以9和1不是孪生质数;
B.在13和15中,13是质数,15是合数,所以13和15不是孪生质数;
C.在11和13中,11和13都是质数,且13-11=2,所以11和13是孪生质数。
所以11和13是孪生质数。
故答案为:C
23.B
【分析】如果高增加2厘米,则其增加的体积等于长a厘米、宽b厘米、高2厘米的长方体的体积,根据长方体的体积=长×宽×高,代入数据计算即可解答。
【解析】a×b×2=2ab(立方厘米)
所以一个长方体的长,宽,高分别是a厘米,b厘米,h厘米,如果高增加2厘米,则其体积增加2ab立方厘米。
故答案为:B
24.C
【分析】根据从左面看的图形,可知立体图形有三行两层;根据从正面看的图形,可知立体图形有三列两层;综合以上,则第二行第二列处必须上下重叠摆放2个小正方体,据此试着拼摆这个立体图形,并数出最多需要几个小正方体即可。
【解析】符合从左面、正面看到的图形,最少需要的小正方体块数如图1所示,最多需要的小正方体块数如图2所示,所以要搭成这样的几何体最多需要10个小正方体。
故答案为:C
25.C
【分析】根据哥德巴赫猜想,结合质数的意义,从四个加法算式中找出偶数写成两个质数的和的算式即可。
一个数,如果只有1和它本身两个因数,那么这样的数叫做质数。
整数中,是2的倍数的数叫做偶数,不是2的倍数的数叫做奇数。
【解析】A.38=21+17,38是大于2的偶数,21是合数,17是质数,不符合哥德巴赫猜想;
B.32=31+1,32是大于2的偶数,31是质数,1不是质数,不符合哥德巴赫猜想;
C.36=13+23,36是大于2的偶数,13是质数,23是质数,符合哥德巴赫猜想;
D.34=24+10,34是大于2的偶数,24是合数,10是合数,不符合哥德巴赫猜想。
故答案为:C
26.C
【分析】已知正方体木块的棱长是5dm,根据正方体的表面积公式S=6a2,求出这个正方体木块的表面积;
把这个正方体木块截成两个完全一样的长方体,表面积会增加两个截面的面积;由正方体的特征可知,每个截面是边长为5dm的正方形,根据正方形的面积公式S=a2,求出一个面的面积,再乘2,即是增加的表面积;
然后用原来正方体木块的表面积加上增加的表面积,即是截成的两个长方体的表面积之和。
【解析】5×5×6+5×5×2
=25×6+25×2
=150+50
=200(dm2)
这两个长方体的表面积一共是200dm2。
故答案为:C
27.D
【分析】根据题意,长方体的的侧面展开图正好是一个面积为64平方分米的正方形,根据正方形的面积=边长×边长,可推导出侧面展开图的边长是8分米,也就是长方体的底面周长和高都是8分米;
已知长方体的底面是一个正方形,根据正方形的周长=边长×4,那么正方形的边长=周长÷4;再根据正方形的面积=边长×边长,求出这个长方体的底面积。
【解析】因为64=8×8,所以长方体的底面周长是8分米,高是8分米;
底面边长:8÷4=2(分米)
底面积:2×2=4(平方分米)
这个长方体一个底面的面积是4平方分米。
故答案为:D
28.D
【分析】单式条形统计图可以清楚地看出数量的多少。
复式条形统计图可以用不同的条形表示两种以上的量的多少。
单式折线统计图不但可以表示出数量的多少,而且能够清楚地表示出数量增减变化的情况。
复式折线统计图通过两组以上数据的水平进行比较,可以容易地比较出两组以上数据的变化趋势,更清楚看出各类之间的比较。
【解析】要比较凉山州2024年4月、5月的气温变化情况,绘制复式折线统计图更合理。
故答案为:D
29.D
【分析】根据找一个数的倍数的方法可知,17的倍数分别是17×1的积,17×2的积,17×3的积,17×4的积……;17是奇数,根据奇数和偶数的运算性质:奇数×奇数=奇数,奇数×偶数=偶数;由此可知17的倍数既有偶数也有奇数。
整数中,是2的倍数的数叫做偶数,不是2的倍数的数叫做奇数。
【解析】17的倍数:17,34,51,68……;
其中奇数有17,51……,偶数有34,68……;
所以,自然数中,17的倍数有偶数也有奇数。
故答案为:D
30.C
【分析】整数中,是2的倍数的数叫做偶数,不是2的倍数的数叫做奇数。
一个数,如果只有1和它本身两个因数,那么这样的数叫做质数。
一个数,如果除了1和它本身还有别的因数,那么这样的数叫做合数。
【解析】A.如果a是奇数15,15的因数有:1,3,5,15;共有4个因数,不符合题意;
B.如果a是偶数6,6的因数有:1,2,3,6;共有4个因数,不符合题意;
C.如果a是质数7,7的因数有:1,7;共有2个因数,符合题意;
D.如果a是合数9,9的因数有:1,3,9;共有3个因数,不符合题意。
故答案为:C
31.D
【分析】根据题图可知,丝带捆扎的长度为4条高,2条长、2条宽,再加上接头处的长度,据此解答即可。
【解析】10×4+25×2+12×2+15
=40+50+24+15
=90+24+15
=114+15
=129(厘米)
要捆扎这种礼品盒至少需要准备129厘米长的丝带。
故答案为:D
32.C
【分析】8路公交车每10分钟发一次车,10路公交车每12分钟发一次车,求出10和12的最小公倍数,就是从第一次发车到第二次发车经过的时间,据此推算即可。
【解析】10=2×5
12=2×2×3
所以10和12的最小公倍数是:2×5×2×3=60
6时30分+60分=7时30分
故答案为:C
33.A
【分析】要求剪出的正方形的边长最大是多少,就是求48和36的最大公因数是多少。先把每个数分别分解质因数,再把两个数中的全部公有质因数提取出来连乘,所得的积就是这两个数的最大公因数,据此解答。
【解析】48=2×3×2×4
36=2×2×3×3
48和36的最大公因数是2×2×3=12
所以剪出的正方形的边长最大是12cm。
故答案为:A
34.CC
【分析】由图可知,长方体盒子的长为5厘米,宽为3厘米,高为2厘米,根据“长方体的表面积=(长×宽+宽×高+长×高)×2”求出这个盒子的表面积,因为题干明确了“无盖”,故只需要计算五个面的面积即可。据此解答。
【解析】(5×3+5×2+3×2)×2
=(15+10+6)×2
=31×2
=62(平方厘米)
62-5×3
=62-15
=47(平方厘米)
所以,这个透明的无盖的长方体盒子的表面积是47平方厘米。
故答案为:C
35.B
【分析】分数的意义:把单位“1”平均分成若干份,表示这样的一份或几份的数叫做分数;分母是平均分的总份数,分子是取的其中的几份。
【解析】
A.阴影部分表示为,阴影部分表示为,不符合题意;
B.阴影部分表示为,阴影部分表示为,符合题意;
C.阴影部分表示为,不是平均分成3份,阴影部分不能用分数表示,不符合题意。
故答案为:B
36.A
【分析】既是2的倍数又是3的倍数的特征:个位上的数字是0、2、4、6、8,各个数位上的数字的和是3的倍数的数。
【解析】
小欣的行李箱的密码是一个“450”四位数,如果是2的倍数,个位上的数字是0、2、4、6、8,4+5=9、4+5+2=11、4+5+4=13、4+5+6=15、4+5+8=17,如果既是2的倍数,也是3的倍数有4500、4506,共有2种可能。
故答案为:A
37.B
【分析】如果想“3”和“5”可以直接相加、减,那么“3”和“5”必须在相同的数位上,也就是相同单位的数才能相加、减,据此分析选项即可。
【解析】A.3129中的3在千位上,表示3个一千,587中的5在百位上,表示5个一百,不能直接相加、减。不符合题意;
B.2.65中的5在百分位上,表示5个百分之一,0.13中的3在百分位上,表示3个百分之一,可以直接相加、减。符合题意;
C.的分数单位是,其中的5表示5个,的分数单位是,其中的3表示3个,不能直接相加、减。不符合题意。
故答案为:B
38.B
【分析】把单位“1”平均分成若干份,表示其中一份的数叫分数单位;
根据分数单位的意义可知,一个分数的分母是几,其分数单位就是几分之一,分母不同,其分数单位不同;
异分母分数的加减法,先通分,变成分母相同而大小不变的分数,即分数单位相同的分数,然后按照同分母分数的加减法进行计算。
【解析】由分析可知,异分母分数不能直接相加减的原因是分数单位的不同。
故答案为:B
39.C
【分析】包装的高度一定大于酸奶的高度,“净含量250mL”说明酸奶一共有250mL,先根据公式高=长方体体积÷长÷宽,求出酸奶的高度,然后再跟选项进行比较,选择略微高出酸奶高度的酸奶盒即可。
【解析】250mL=250cm
250÷5÷5=10(cm)
10.5cm>10cm
故答案为:C
40.C
【分析】
根据从上面看到的形状和数字,可以确定这个几何体如图,从左面看有3行,下边1行3个小正方形;中间1行2个小正方形,左对齐;上边1行1个小正方形,居中;据此分析。
【解析】
根据分析,这个几何体从左面看是。
故答案为:C
41.C
【分析】A.从正面看有2行,下边1行2个小正方形,上边1行靠左1个小正方形;从上面看有2列,右边1列3个小正方形,左边1列靠上1个小正方形;从右面看有2行,下边1行3个小正方形,上边1行靠右1个小正方形;
B.从正面看有2行,下边1行3个小正方形,上边1行靠左1个小正方形;从上面看有2行,下边1行3个小正方形,上边1行中间1个小正方形;从右面看有2行,下边1行2个小正方形,上边1行靠左1个小正方形;
C.从正面看有2行,下边1行3个小正方形,上边1行靠左1个小正方形;从上面看有2行,上边1行3个小正方形,下边1行中间1个小正方形;从右面看有2行,下边1行2个小正方形,上边1行靠右1个小正方形;
D.从正面看有2行,下边1行3个小正方形,上边1行靠左1个小正方形;从上面看有2行,上边1行3个小正方形,下边1行靠左1个小正方形;从右面看有2行,下边1行2个小正方形,上边1行靠右1个小正方形。
【解析】
A.从正面看是,从上面看是,从右面看是;
B.从正面看是,从上面看是,从右面看是;
C.从正面看是,从上面看是,从右面看是;
D.从正面看是,从上面看是,从右面看是。
用5个正方体搭成一个几何体,从正面看是,从上面看是,从右面看是,这个几何体是。
故答案为:C
42.D
【分析】先根据2、5的倍数特征,由个数是否是0,判断这个三位数是否是2、5的倍数;
如果是2、5的倍数,再根据3的倍数特征判断这个三位数是否是3的倍数;
最后确定这个三位数同时是2、3、5的倍数,且最大,即可得解。
2的倍数特征:个位上是0、2、4、6、8的数。
5的倍数特征:个位上是0或5的数。
2、5的倍数特征:个位上是0的数。
3的倍数特征:一个数各位上的数的和是3的倍数,这个数就是3的倍数。
【解析】A.999的个位不是0,不是2、5的倍数,不符合题意;
B.995的个位不是0,不是2、5的倍数,不符合题意;
C.998的个位不是0,不是2、5的倍数,不符合题意;
D.990的个位是0,990是2、5的倍数;
9+9+0=18,18是3的倍数;
所以,990同时是2、3、5的倍数,且最大,符合题意。
故答案为:D
43.D
【分析】由于折线统计图的竖轴表示路程,由于最开始兔子的速度很快,那么相同时间,兔子的路程比较高,由此即可知道实线是兔子,虚线是乌龟,由于兔子在路边睡了一觉,此时的路程不变,是一条直线,兔子醒来后,追赶了一端时间,乌龟胜利,那么说明同样高度,虚线是先到的,兔子后到的,据此即可选择。
【解析】由分析可知:
大致能反映这个故事情节的图像是。
故答案为:D
44.D
【分析】分别将3个立体图形的上面、左面、右面、前面画出,再判断即可。
【解析】
用5个相同的小正方体搭成的立体图形,从前面看,所看到的形状都是。
故答案为:D
45.B
【分析】先根据进率1mL=1cm,将300mL换算成300 cm3,500mL换算成500 cm3;
根据题意,将四颗相同的铁球放入水中,结果水没有满,可知四颗铁球的体积要小于500-300=200(cm3),那么一颗铁球的体积就小于(200÷4)cm3;再将一颗同样的铁球放入水中,结果水满溢出,可知五颗铁球的体积要大于500-300=200(cm3),那么一颗铁球的体积就大于(200÷5)cm3。据此推测出一颗铁球体积的范围。
【解析】300mL=300 cm3
500mL=500 cm3
500-300=200(cm3)
200÷4=50(cm3)
200÷5=40(cm3)
40 cm3<一颗铁球的体积<50 cm3
所以,一颗铁球的体积大约在40 cm3~50 cm3。
故答案为:B
46.B
【分析】判断一个分数能否化成有限小数,首先要看这个分数是不是最简分数,如果不是最简分数,要先约分,再根据一个最简分数,如果分母中只含有质因数2或5,这个分数就能化成有限小数;如果分母中含有2或5以外的质因数,这个分数就不能化成有限小数。
【解析】A.分母是3,不能化成有限小数;
B.=,4=2×2,可以化成有限小数;
C.分母是13,不能化成有限小数;
D.12=2×2×3,质因数有3,不能化成有限小数。
故答案为:B
47.A
【分析】真分数:分子小于分母的分数是真分数,m是分子,n是分母,即m<n的时候,才是真分数,据此即可选择。
【解析】由分析可知:
如果(m和n是大于0的自然数)是真分数,那么m<n。
故答案为:A
48.D
【分析】在连续偶数中,相邻的两个偶数相差2,最小的一个偶数为2n,第2个偶数即2n+2,第三个偶数即2n+2+2。将三个偶数相加,结果化简即可判断。
【解析】2n+2n+2+2n+2+2
=(2n+2n+2n)+(2+2+2)
=6n+6
三个连续偶数中,最小的一个数为2n,则这三个偶数的和是6n+6。
故答案为:D
49.B
【分析】用500-300,求出5颗小玻璃球的体积,再除以5,求出1个小玻璃球的体积;再用300-200,求出放入1颗大玻璃球和1颗小玻璃球的体积,再减去1个小玻璃球的体积,即可解答,注意单位名数的换算。
【解析】500-300=200(毫升)
200毫升=200立方厘米
200÷5=40(立方厘米)
300-200=100(毫升)
100毫升=100立方厘米
100-40=60(立方厘米)
一颗大玻璃球的体积是60立方厘米。
故答案为:B
50.A
【分析】从图中可知,天平左右两边各放了3个台球,天平不平衡,左边重、右边轻。因为次品略轻,所以这个次品一定在右边的④⑤⑥中,由此推断哪些台球是正品。
【解析】根据第一次称的结果可知,天平左边的台球重,右边的台球轻。因为次品略轻,所以左边较重的①②③是正品,另外还没有称的台球⑦和⑧也是正品。
所以,可以推断①、②、③、⑦和⑧一定是正品。
故答案为:A
51.B
【分析】根据题意,张阿姨买了3箱同样的车厘子,每箱车厘子的价格都是整数,根据“单价×数量=总价”可知,张阿姨花的钱数是3的倍数;从三个选项中找出哪个数是3的倍数,即可得解。
3的倍数特征:一个数各位上的数的和是3的倍数,这个数就是3的倍数。
【解析】A.2+6+0=8,8不是3的倍数,则260不是3的倍数;
B.2+6+4=12,12是3的倍数,则264是3的倍数;
C.2+6+8=16,16不是3的倍数,则268不是3的倍数;
所以,张阿姨可能花了264元。
故答案为:B
52.B
【分析】根据题意,48个青团和36个艾饺正好平均分完,且没有剩余,那么分给最多的人数就是48和36的最大公因数。
48、36分解质因数后,把公有的相同质因数乘起来就是它们的最大公因数,也就是最多的人数。
【解析】48=2×2×2×2×3
36=2×2×3×3
48和36的最大公因数是:2×2×3=12
即最多能分给12个朋友。
故答案为:B
53.B
【分析】真分数的分子小于分母。本题可以举例说明,如的分子和分母同时加上1,得到,=,=,>,则>;再如的分子和分母同时加上3,得到,=,=,>,则>。据此解答。
【解析】通过分析可得:一个真分数的分子和分母同时加上一个非零自然数,得到的分数值一定比原分数大。
故答案为:B
54.B
【分析】在100克水中加入7克盐,则盐水中盐的质量是7克,盐水的质量是100+7=107(克),要求盐水中盐的质量占盐水的几分之几,用盐的质量除以盐水的质量即可。
【解析】7÷(100+7)
=7÷107
=
因此这种盐水中盐的质量占盐水的。
故答案为:B
55.A
【分析】找次品的最优策略:(1)把待分物品分成3份;(2)每份数量尽量平均,如果不能平均分的,也应该使多的一份与少的一份只相差1。
【解析】将12瓶矿泉水分成(4、4、4),称(4、4),无论平衡不平衡,都可确定次品在其中4瓶;将4瓶分成(1、1、2),称(1、1),只考虑最不利的情况,即次品在多的里面,平衡,次品在2瓶中;将2瓶分成(1、1),再称1次即可确定次品,共3次。
至少称3次才能保证找出次品。
故答案为:A
56.B
【分析】根据长方体的体积=长×宽×高,因为长方体前面的面积=长×高,所以用前面的面积乘宽等于长方体的体积。
【解析】长方体的体积:32×3=96(cm3)
要计算这个长方体的体积,正确的算式是32×3。
故答案为:B
57.C
【分析】一个数,如果只有1和它本身两个因数,那么这样的数叫做质数。
一个数,如果除了1和它本身还有别的因数,那么这样的数叫做合数。
整数中,是2的倍数的数叫做偶数,不是2的倍数的数叫做奇数。
奇数和偶数的运算性质:偶数+偶数=偶数,奇数+奇数=偶数,奇数+偶数=奇数。
【解析】A.当a=4时,2a+1=2×4+1=8+1=9,9是合数;原选项说法错误;
B.当a=2时,2a+1=2×2+1=4+1=5,5是质数;原选项说法错误;
C.无论a是奇数,还是偶数,2a一定是偶数,因为偶数+奇数=奇数,所以2a+1一定是奇数;原选项说法正确;
D.当a=3时,2a+1=2×3+1=6+1=7,7是奇数;原选项说法错误。
故答案为:C
58.A
【分析】根据图可知,这个长方体盒子的长等于4个小正方体的棱长和,宽等于3个小正方体的棱长和,高等于3个小正方体的棱长和,根据长方体表面积公式:表面积=(长×宽+长×高+宽×高)×2,代入数据,即可解答。
【解析】长:1×4=4(cm),宽:1×3=3(cm);高:1×3=3(cm)。
表面积:
(4×3+4×3+3×3)×2
=(12+12+9)×2
=(24+9)×2
=33×2
=66(cm2)
在一个透明的长方体盒子内放置棱长为1cm的小正方体(如图)。这个长方体盒子的表面积是66cm2。
故答案为:A
59.A
【分析】由于把2.5L的可乐倒在装180mL的小杯子里,即看2.5L里面有多少个180mL,根据1L=1000mL,先转换单位,庵后用2500÷180,求出结果即可,由于问多少个客人能喝到180mL的可乐,说明如果还有剩余,并且不够180mL的,则舍去,结果用去尾法保留整数即可。
【解析】2.5L=2500mL
2500÷180=13(个)……160mL
所以妈妈把买回来的一大瓶2.5L的可乐分别倒在只能装180mL的小子杯子里招待客人,13个客人能喝到180mL的可乐。
故答案为:A
60.B
【分析】找次品的最优策略:
(1)把待分物品分成3份;
(2)每份数量尽量平均,如果不能平均分的,也应该使多的一份与少的一份只相差1。
【解析】先把12分成(4、4、4);第一次称量:在天平两边各放4盒,可能出现两种情况:(把轻一些的那盒看做次品)①如果天平平衡,则次品在剩余的那4盒,分成(2、2);
第二次称量:在左、右盘中分别放2盒,上升者有次品;
第三次称量:在左、右盘中分别放1盒,上升者是次品。
②如果天平不平衡,次品在托盘上升那边的4盒里;
第二次称量:取托盘上升的4盒,在左、右盘中分别放2盒,上升者有次品;
第三次称量:取托盘上升的2盒,每一盒分别放在天平的左、右盘中,则上升者是次品。
如果用天平称,至少称3次可以保证找出这盒牛奶。
故答案为:B
61.C
【分析】最后一次喝完,也就是加了多少水就喝了多少水,第一次加了杯水,第二次加了杯水,而牛奶就是一杯;将加的两次水加起来,就是一共喝了多少水,与1杯纯牛奶比较,即可得出结论。
【解析】喝的水:(杯)
喝的牛奶:1杯
因此丽丽喝的水和纯牛奶一样多。
故答案为:C
62.B
【分析】物体所占空间的大小叫做物体的体积,物体各个面的面积之和叫做物体的表面积。
根据题意,将一个正方体钢坯锻造成一个长方体钢坯,钢坯的形状变了,则表面积发生了变化;但钢坯的大小不变,即体积没变,据此解答。
【解析】将一个正方体钢坯锻造成一个长方体钢坯,长方体和正方体相比,体积相等,表面积不相等。
故答案为:B
63.C
【分析】条形统计图可以直观地看出数量的多少;折线统计图不仅能看清数量的多少,还能反映数量的增减变化情况。复式条形统计图可以表示多种量的多少;复式折线统计图表示2个及以上的量的增减变化情况。据此解答。
【解析】通过分析可得:要比较北京和南宁两地一年中气温的变化趋势,选择复式折线统计图更合适。
故答案为:C
64.A
【分析】把一个图形整体沿某一直线方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同,图形的这种移动叫做平移,观察选项,依此解答问题。
【解析】A. 索道上运行的缆车是沿直线方向移动的,并且移动后的形状和大小不变,故正确;
B.钟面上转动的分针是绕中间一点做旋转运动,不符合平移定义,故错误;
C.飞行中直升飞机的螺旋桨是绕中间一点做旋转运动,不符合平移定义,故错误。
故答案为:A
65.B
【分析】两人从三张卡片中抽取两张,卡片的数字之积可能是:2×3=6,2×5=10,3×5=15。其中6和10是偶数,15是奇数。偶数的数量多,则两人抽取的卡片的数字之积是偶数的可能性大。据此解答。
【解析】通过分析可得:两人抽取的卡片的数字之积是偶数的可能性大,则这个游戏笑笑胜的可能性大。
故答案为:B
66.D
【分析】根据题意,正方体的钢锭的体积等于长方体钢锭的体积,根据得出正方体的体积是512立方厘米,即长方体的体积也是512立方厘米,根据,得出长方体的高=体积÷长÷宽。
【解析】8×8×8=512(平方厘米)
512÷5÷8=12.8(厘米)
它的高是12.8厘米。
故答案为:D
67.D
【分析】设原来正方体棱长为1,扩大后正方体的棱长为1×2=2;根据正方体棱长公式:棱长总和=棱长×12;表面积公式:表面积=棱长×棱长×6,体积公式:体积=棱长×棱长×棱长,代入数据,分别求出原来正方体的棱长总和,表面积,体积以及扩大后正方体棱长总和,表面积,体积,再用扩大后正方体的棱长总和÷原来正方体棱长总和;扩大后正方体表面积÷原来正方体表面积;扩大后正方体的体积÷原来正方体体积,即可解答。
【解析】设原来正方体棱长为1;扩大后正方体的棱长为1×2=2。
(2×12)÷(1×12)
=24÷12
=2
(2×2×6)÷(1×1×6)
=(4×6)÷(1×6)
=24÷6
=4
(2×2×2)÷(1×1×1)
=(4×2)÷(1×1)
=8÷1
=8
一个正方体的棱长扩大到原来的2 倍,棱长总和扩大到原来的2倍,表面积扩大到原来的4倍,体积扩大到原来的8倍。
故答案为:D
68.B
【分析】根据从上面看到的形状,可以确定底层有4个小正方体,以及这4个小正方体的摆放位置;根据从左面看到的形状,可以确定第二层的1个小正方体只能摆到并排的3个小正方体的上面,据此分析。
【解析】
如图,一共有3种不同的摆法。
故答案为:B
69.A
【分析】两个数的公有质因数的连乘积就是这两个数的最大公因数;如果两个数为倍数关系,较小的数为最大公因数;如果两个数为互质数,最大公因数是1,据此解答。
【解析】因为a÷b=15,所以a和b成倍数关系,最大公因数是b。
如果a÷b=15(a、b都是大于0的自然数),那么a和b的最大公因数是b。
故答案为:A
70.B
【分析】三人读同一篇文章,用时越少的,读的速度就越快。即比较、、0.3的大小,可以把分数化成小数,用分子除以分母即可,再根据小数大小的比较方法进行比较,得出结论。
【解析】=1÷5=0.2
=1÷6≈0.167
0.167<0.2<0.3
<<0.3
小林用时最少,所以小林速度快。
故答案为:B
71.B
【分析】通过图可知,这个物体的长、宽、高分别是13cm,9.5cm,3.5cm,之后根据生活经验,对长度单位和数据大小的认识来判断即可。
【解析】A.图中的长对数学书来说太短;不符合题意;
B.根据生活可知新华字典的长、宽、高符合图中的数据,符合题意;
C.图中的长、宽对纸巾盒来说不合适;不符合题意;
D.图中的宽对橡皮来说太长,不符合题意。
故答案为:B
72.B
【分析】1m3=1000dm3,由此可知,1 m3的正方体木块切成1dm3的小正方体木块,能分成1000个1dm3的小正方体;1dm3的小正方体的棱长是1dm3;把这些小正方体排成一排,总长度是1×1000=1000dm;再转成单位,即可解答。
【解析】1m3=1000dm3
所以1000÷1=1000(个)
1dm3的正方体的棱长是1dm。
总长:1×1000=1000(dm)
1000dm=100m=0.1km=10000cm
把1m3的正方体木块切成1dm3的小正方体木块。如果把这些小木块排成一行组成一个长方体,那么这个长方体的长是100m(或0.1km,10000cm)。
故答案为:B
73.B
【分析】根据长方体的特征:长方体有12条棱,其中4条长,4条宽,4条高;长、宽、高相交于一点,4条长互相平行且相等;4条宽互相平行且相等;4条高互相平行且相等;根据图可知,这个长方体的长是9cm,宽是7cm,高是4cm,由此可知,长方体有两个长是9cm,宽是7cm的面,即2个②;有两个长是9cm,宽是4cm的面,即2个③;有两个长是7cm,宽是4cm的面,即2个⑤,据此解答。
【解析】
根据分析可知,左图是一个长方体的3条棱(单位:cm)。选择6个面图出这个长方体,正确的选择是2个②、2个③、2个⑤。
故答案为:B
74.B
【分析】根据题意可知,将一个长方体的高增加5米就成为一个正方体可知:原长方体的长=宽=正方体的棱长,这时表面积比原来增加160平方米,表面积增加的是高5米的长方体的4个侧面的面积,因此可以求出一个侧面的面积,进而求出原来长方体的长。据此解答。
【解析】160÷4÷5=8(米)
原来长方体的长是8米。
故答案为:B
75.C
【分析】将一个石柱放入放满水的池子中,则溢出水的体积就是没入水中石柱的体积。根据长方体体积=长×宽×高,据此计算可得出答案。
【解析】根据题意得:水池水溢出的体积即为没入水中石柱的体积,没入水中石柱长3m、宽2m、高2m。
即3×2×2=12(m )。
故答案为:C
76.B
【分析】把红红做试卷用的时间加上检查试卷用的时间,再加上离测试结束的时间即可解答。
【解析】++
=++
=+
=(小时)
所以这次测试规定的时间是小时。
故答案为:B
77.B
【分析】不管是每人5颗还是每人3颗,最后都会剩余1颗,则糖果总数比5和3的公倍数多1。据此解答。
【解析】5和3的公倍数有:15、30、45、60、75……
其中60+1=61(颗),则糖果总数可能是61颗。
故答案为:B
78.B
【分析】分子相同的分数,分母越大,分数越小。据此解答。
【解析】通过分析可得:因为a>b,所以与相比较,。
故答案为:B
79.B
【分析】钟面上共有12个大格,则每个大格为360÷12=30度,钟表行走的方向就是顺时针方向,反之就是逆时针方向;逆时针旋转,即逆时针旋转90°÷30°=3个大格,据此解答即可。
【解析】90°÷30°=3(个)
8-3=5
则时针从“8”起逆时针旋转后,时针应该指向5。
故答案为:B
80.C
【分析】物体或图形旋转后,它们的形状、大小都不改变,只是位置发生了变化。据此解答。
【解析】通过分析可得:把一个图形绕某点顺时针旋转60°后,所得到的图形与原来的图形相比较,大小不变。
故答案为:C
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
中小学教育资源及组卷应用平台
2024-2025学年五年级数学下册期末复习专项人教版
(期末考点培优)专题01 选择题
学校:___________姓名:___________班级:___________考号:___________
1.( )里填( )时,式子能进行简便计算。
A. B. C. D.
2.的分子加上12,要使分数的大小不变,分母应该( )。
A.加上12 B.乘3 C.乘4 D.乘12
3.有一个立方体,从前面看到,从左面看到,从上面看到,下面的立方体中符合要求的是( )。
A. B. C.
4.把一张长72cm,宽60cm的长方形纸,裁成同样大小、面积尽可能大的正方形纸,且纸无剩余,至少能裁( )张。
A.2 B.4 C.30 D.6
5.12个羽毛球特征相同,其中只有一个质量异常。现在要用一架没有砝码的天平去称,至少要称( )次才能找出那个质量异常的羽毛球。
A.4 B.3 C.2 D.1
6.从3时15分到3时45分这段时间里,分针旋转了( )。
A.180° B.90° C.60° D.30°
7.在下面的分数中,( )不是最简真分数。
A. B. C. D.
8.甲数和乙数互质,丙数是甲、乙两数的倍数。甲、乙、丙三个数的最大公因数是( )。
A.甲数 B.乙数 C.丙数 D.1
9.把一个长8厘米,宽和高都是5厘米的长方体截成一个最大的正方体后,表面积( )。
A.减少110平方厘米 B.减少85平方厘米 C.减少60平方厘米
10.小亮把一根绳子剪成了两段,第一段长m,第二段占全长的,那么这两段绳子相比,( )。
A.第一段长 B.第二段长 C.一样长 D.无法比较
11.一袋糖,4颗4颗地分、5颗5颗地分、6颗6颗地分,都正好分完而没有剩余,这袋糖最少有( )颗。
A.30 B.60 C.120 D.240
12.5个连续偶数,中间一个数是N,则最大的数是( )。
A.N+1 B.N+2 C.N+3 D.N+4
13.把的分子加上14,要使分数的大小不变,分母应该( )。
A.加上14 B.乘3 C.加上24 D.乘4
14.把一条绳子对折三次后,这时每段绳子的长度是全长的( )。
A. B. C.
15.拼一个从上面和左面看形状都是的物体,至少需要( )个小正方体。
A.4 B.5 C.3
16.下面几堆玻璃球中各有一个是次品(重一些),若用天平称,至少称3次就一定能找出这个较重的玻璃球。这堆玻璃球可能有( )个。
A.8 B.15 C.28
17.红十字会组织图书捐赠活动,张明和李丽捐了同样数量的课外书,张明捐了自己课外书的,李丽捐了自己课外书的,两人原有的课外书谁多?下面是三名同学的比较方法,正确的( )。
A.只有甲和乙 B.只有乙和丙 C.只有甲和丙 D.有甲、乙、丙
18.奇思在卡片上写出了下面的五个数,这些数共同的特点是( )。
A.都是51的因数 B.都是2的倍数 C.都是奇数 D.都是合数
19.下面各图形的阴影部分占整个图形的是( )。
A. B. C. D.
20.一条线段的是2厘米,这条线段长是( )。
A.3厘米 B.2厘米 C.4厘米 D.6厘米
21.如果A=3m,B=6m(A,B都是非零自然数),那么A,B的最大公因数是( )。
A.24m B.3m C.12m D.12
22.数学上把相差2的两个质数叫“孪生质数”,如3和5就是一对孪生质数,那么下列娜一对是孪生质数?( )
A.9和1 B.13和15 C.11和13
23.一个长方体的长,宽,高分别是a厘米,b厘米,h厘米,如果高增加2厘米,则其体积增加( )立方厘米。
A.abh B.2ab C.2ah D.ab(h+2)
24.由若干个小正方体搭成的几何体,从左面看和从正面看,看到的形状如下图所示,要搭成这样的几何体最多需要( )个小正方体。
A.7 B.8 C.10 D.12
25.著名的关于偶数的哥德巴赫猜想说的是“任意一个大于2的偶数都可以写成两个质数的和”。下面( )算式符合这个猜想。
A.38=21+17 B.32=31+1 C.36=13+23 D.34=24+10
26.把一个棱长是5dm的正方体木块截成两个大小、形状完全相等的长方体,这两个长方体的表面积一共是( )dm2。
A.125 B.150 C.200 D.300
27.一个长方体的底面是一个正方形,它的侧面展开图正好是一个面积为64平方分米的正方形。这个长方体一个底面的面积是( )平方分米。
A.64 B.16 C.8 D.4
28.要比较凉山州2024年4月、5月的气温变化情况,绘制( )统计图更合理。
A.单式条形 B.复式条形 C.单式折线 D.复式折线
29.自然数中,17的倍数( )。
A.都是偶数 B.都是奇数 C.都是质数 D.有偶数也有奇数
30.如果一个数a,只有两个因数,那么a一定是( )。
A.奇数 B.偶数 C.质数 D.合数
31.母亲节那天,文文买了一个礼品要送给妈妈作为节日礼物,得精心包装一番(如图所示),在选用丝带捆扎这个礼品盒时,遇到了一个问题,“要捆扎这种礼品盒至少需要准备( )厘米长的丝带”。(接头处长15厘米)
A.40 B.110 C.114 D.129
32.某市8路公交车每10分钟发一次车,10路公交车每12分钟发一次车。这两路公交车的起点站相同,上午6:30同时出发,则第二次同时发车的时间是( )。
A.6:52 B.7:00 C.7:30
33.有一张长方形纸,长48cm,宽36cm。如果要剪成若干张同样大小的正方形而没有剩余,剪出的正方形的边长最大是( )cm。
A.12 B.6 C.36
34.如图,在一个透明的无盖的长方体盒子内,放置棱长为1厘米的小正方体。这个透明的长方体盒子的表面积是( )平方厘米。
A.62 B.52 C.47
35.下列各选项中,阴影部分与整体的关系一样的( )。
A.B. C.
36.小欣的行李箱的密码是一个“450”四位数,这个四位数既是2的倍数,也是3的倍数。符合密码规则的共有( )种可能。
A.2 B.3 C.4
37.下列式子中,“3”和“5”可以直接相加、减的是( )。
A.3129+587 B.2.65-0.13 C.
38.异分母分数不能直接相加减的原因是( )
A.大小不相同 B.分数单位不同 C.分子不同 D.基本性质不同
39.一盒酸奶的外包装是一个长方体纸盒,包装纸上标有“净含量250mL”。实际外包装长5cm,宽5cm。如果你来设计,你认为酸奶盒比较合适的高度是( )
A.5cm B.10cm C.10.5cm D.15cm
40.用同样的小正方体搭一个几何体,从上面看到的图形如图(每个正方形上面的数字表示这个位置上所用小正方体的个数)。这个几何体从左面看是( )。
A. B. C. D.
41.用5个正方体搭成一个几何体,从正面看是,从上面看是,从右面看是,这个几何体是( )。
A. B. C. D.
42.一个三位数,同时是2、3、5的倍数,这个数最大是( )。
A.999 B.995 C.998 D.990
43.“龟兔赛跑”是我们熟悉的故事,大意是乌龟和兔子赛跑,兔子一开始就超过了乌龟好远,兔子看乌龟慢吞吞的,就得意地在路边睡了一觉,而乌龟一直往目的地拼命奔跑,等兔子醒来追赶了一段,但还是乌龟赢得了胜利。大致能反映这个故事情节的图像是( )。
A.B.C. D.
44.下图都是用5个相同的小正方体搭成的立体图形,从( )看,所看到的形状都是一样的。
A.上面 B.左面 C.右面 D.前面
45.如图是测量一颗铁球体积的过程:①将300毫升的水倒进一个容积为500毫升的杯子中;②将四颗相同的铁球放入水中,结果水没有满;③再将一颗同样的铁球放入水中,结果水满溢出。根据以上过程,推测这样一颗铁球的体积大约是( )cm3。
A.30~40 B.40~50 C.50~60 D.60~70
46.下面的分数中,能化成有限小数的是( )。
A. B. C. D.
47.如果(m和n是大于0的自然数)是真分数,那么( )。
A.n>m B.m>n C. D.无法确定
48.三个连续偶数中,最小的一个数为2n,则这三个偶数的和是( )。
A.6n B.6n+2 C.6n+4 D.6n+6
49.李冬设计了一个测量玻璃球体积的实验:先将200毫升的水倒进容积为500毫升的量杯中,再将1颗大玻璃球和1颗小玻璃球浸没水中,水面刚好在300毫升处,最后放入5颗小玻璃球,全都浸没水中,此时水面与量杯口齐平,刚好无水溢出。那么一颗大玻璃球的体积是( )立方厘米。
A.40 B.60 C.80 D.100
50.有8个外观相同的台球,其中一个是次品,略轻。欢欢用天平来找次品,第一次称的结果如右下图,可以推断( )一定是正品。
A.①、②、③、⑦和⑧ B.④、⑦和⑧ C.④、⑤和⑥
51.张阿姨买了3箱同样的车厘子,每箱车厘子的价格都是整数,且没有任何优惠,张阿姨可能花了( )。
A.260元 B.264元 C.268元
52.曹阿姨做了48个青团和36个艾饺,打算平均分给一些朋友。如果青团和艾饺都没有剩余,且保证分到青团和艾饺的朋友人数相同,最多能分给( )个朋友。
A.6 B.12 C.24
53.一个真分数的分子和分母同时加上一个非零自然数,得到的分数值一定( )。
A.与原分数相等 B.比原分数大 C.比原分数小 D.无法确定
54.要配制一种盐水,每100克水中要加入7克盐,这种盐水中盐的质量占盐水的( )。
A. B. C. D.
55.有12瓶矿泉水,其中11瓶质量相同,另有一瓶次品,次品质量重一些。用天平称,至少称( )次才能保证找出次品。
A.3次 B.2次 C.4次 D.5次
56.如图所示,一个长方体前面的面积是32cm2,高是4cm,宽是3cm,要计算这个长方体的体积,正确的算式是( )。
A.3×4 B.32×3 C.32×4 D.32×3×4
57.a是不等于零的自然数,2a+1一定是( )。
A.质数 B.合数 C.奇数 D.偶数
58.在一个透明的长方体盒子内放置棱长为1cm的小正方体(如图)。这个长方体盒子的表面积是( )cm2。
A.66 B.60 C.33 D.30
59.妈妈把买回来的一大瓶2.5L的可乐分别倒在只能装180mL的小子杯子里招待客人,( )个客人能喝到180mL的可乐。
A.13 B.13.888… C.14
60.一箱牛奶有12盒,其中有11盒质量相同,另有1盒质量略轻,如果能用天平称,至少称( )次可以保证找出这盒牛奶。
A.2 B.3 C.4 D.5
61.丽丽喝一杯纯牛奶她喝了杯后,用水加满,又喝了杯,再用水加满,最后一次喝完,丽丽喝的水和纯牛奶比较是( )。
A.水多 B.牛奶多 C.一样多 D.无法确定
62.将一个正方体钢坯锻造成一个长方体钢坯,长方体和正方体相比,( )。
A.体积和表面积都相等 B.体积相等,表面积不相等 C.体积不相等,表面积相等
63.要比较北京和南宁两地一年中气温的变化趋势,选择( )更合适。
A.复式条形统计图 B.单式折线统计图 C.复式折线统计图
64.下面现象属于平移的是( )。
A.索道上运行的缆车 B.钟面上转动的分针 C.飞行中直升飞机的螺旋桨
65.三张卡片上分别写着2、3、5,淘气和笑笑分别从中抽取一张,若两人抽取的卡片的数字之积是奇数,则淘气胜;若是偶数,则笑笑胜,这个游戏( )。
A.淘气胜的可能性大 B.笑笑胜的可能性大
C.两人胜的可能性一样大 D.无法判断
66.把一个棱长是8厘米的正方体钢锭,熔铸成一个长方体钢锭,已知长方体的长是5厘米,宽是8厘米,它的高是( )厘米。
A.12.6 B.12 C.9.6 D.12.8
67.一个正方体的棱长扩大到原来的2倍,棱长总和扩大到原来的( )倍,表面积扩大到原来的( )倍,体积扩大到原来的( )倍。
A.8;2;6 B.6;8;4 C.4;6;8 D.2;4;8
68.花花用5个同样的小正方体摆一个几何体,从上面看是,从左面看是。一共有( )种不同的摆法。
A.4 B.3 C.2 D.1
69.如果a÷b=15(a、b都是大于0的自然数),那么a和b的最大公因数是( )。
A.b B.15 C.a D.不确定
70.小明、小林和小军三人读同一篇文章,小明用了小时,小林用了小时,小军用了0.3小时,( )。
A.小明速度快 B.小林速度快 C.小军速度快 D.他们速度一样快
71.根据下图所给的数据,想象一下这个长方体可能是( )。
A.数学书 B.新华字典 C.纸巾盒 D.橡皮
72.把1m3的正方体木块切成1dm3的小正方体木块。如果把这些小木块排成一行组成一个长方体,那么这个长方体的长是( )。
A.1km B.100m C.1000cm
73.左图是一个长方体的3条棱(单位:cm)。从以下图形中选择6个面图出这个长方体,正确的选择是( )。
A.2个①、2个②、2个③ B.2个②、2个③、2个⑤
C.4个⑤、2个⑧ D.6个⑥
74.一个长方体的高增加5米后就变成了一个正方体,表面积增加了160平方米。原来长方体的长是( )。
A.3米 B.8米 C.32 平方米
75.在一个长8m、宽5m、高2m的水池中注满水,然后把一条长3m、宽2m、高4m的石柱立着放入水池中,水池溢出的水的体积是( )m3。
A.24 B.16 C.12
76.一次数学测试,红红做试卷用了小时,检查试卷用了小时,这时离测试结束还有小时,这次测试规定的时间是( )小时。
A. B. C.1
77.幼儿园老师给幼儿园小朋友分糖果,不管是每人5颗还是每人3颗,最后都会剩余1颗,糖果总数可能是( )颗。
A.60 B.61 C.62 D.63
78.和是两个不等于0的自然数,而且。那么,与相比较,( )。
A. B. C. D.无法比较大小
79.钟面上,时针从“8”起逆时针旋转后,时针应该指向( )。
A.3 B.5 C.12 D.11
80.把一个图形绕某点顺时针旋转60°后,所得到的图形与原来的图形相比较( )。
A.变小了 B.变大了
C.大小不变 D.无法确定大小是否变化
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案与试题解析
1.D
【分析】这是个连减运算。根据减法的性质:a-b-c=a-(b+c),那么括号里面的数如果和相加正好等于1,这个式子就能简便运算。所以,用1减即可得解。
【解析】
()里填时,式子能进行简便计算。
故答案为:D
2.C
【分析】分数的基本性质:分子和分母同时乘或除以一个相同的数(0除外),分数的大小不变,据此先算出分子加上12相当于给分子乘几,则分母也要乘相同的数,据此解答。
【解析】4+12=16
16÷4=4
7×4=28
=
的分子加上12,要使分数的大小不变,分母应该乘4。
故答案为:C
3.C
【分析】明确观察物体的方法,先确定有几列或几行,每列或每行有几个,形状是怎样的。据此分析各选项图形即可。
【解析】A.该图形从前面看有3列,2行,第一行3个并排,第二行只有中间列有1个,不符合题意。
B.该图形从左面看有2列,2行,第一行2个并排,第二行左列有1个,不符合题意。
C.该图形从前面看有3列,2行,第一行3个并排,第二行最左列有1个;从左面看有2列,2行,第一行2个并排,第二行右列有1个;从上面看有3列,2行,第二行3个并排,第一行最左列有1个。符合题意。
故答案为:C
4.C
【分析】把一块长方形纸裁成同样大小、面积尽可能大的正方形,且没有剩余,说明正方形的边长是长、宽的最大公因数,把72、60分解质因数后,把公有的相同质因数乘起来就是最大公因数,即是正方形的最大边长。再看长、宽里面分别有几个这样的最大公因数,最后相乘,即可求出至少能裁的张数。
【解析】72=2×2×2×3×3
60=2×2×3×5
72和60的最大公因数是:2×2×3=12
即正方形的边长最大是12cm。
72÷12=6(张)
60÷12=5(张)
一共:6×5=30(张)
至少能裁30张。
故答案为:C
5.A
【分析】根据题意,12个羽毛球特征相同,其中只有一个质量异常,但不知轻重,分组称重时,考虑天平平衡或不平衡时的各种情况,逐一讨论,得出至少称的次数。
【解析】第1次称量,将12个羽毛球平均分为三份①②③(每份4个),先把①和②放在天平的两边,如果天平平衡,则③里面有异常球;如果天平不平衡,则①和②中有异常羽毛球,③都是正常羽毛球;第2次称量,把①和②中的任意一份取下来,把③放上去,即可判断异常羽毛球在哪一份里,并且知道异常羽毛球的轻重;第3次称量,把有异常羽毛球的4个球平均分成两份(每份2个),把它们放在天平的两边,天平不平衡,根据轻重,判断出异常羽毛球在哪一份里;第4次称量,再把有异常羽毛球的2个球分成两份(每份1个),把它们放在天平的两边,天平不平衡,根据轻重,判断出异常羽毛球是哪一个。
所以至少要称4次才能找出那个质量异常的羽毛球。
故答案为:A
6.A
【分析】一个钟面平均分成60小格,分针走1小格表示1分钟,分针走一圈是60分钟,一圈是360°,分针走1小格是(360÷60)°;从3时15分到3时45分,分针共走了(45-15)分钟,再乘每小格的度数即可。
【解析】3时45分-3时15分=30(分钟)
360°÷60=6°
6°×30=180°
分针旋转了180°。
故答案为:A
7.C
【分析】分子比分母小的分数叫做真分数;真分数<1。分子比分母大或分子和分母相等的分数叫做假分数;假分数≥1。
最简分数是指分子和分母只有公因数1的分数。
【解析】A.<1,且24和25是互质数,所以是最简真分数;
B.<1,且7和8是互质数,所以是最简真分数;
C.>1,==,所以不是最简真分数;
D.<1,且4和21是互质数,所以是最简真分数。
故答案为:C
8.D
【分析】公因数只有1的两个非零自然数,叫做互质数。两个数公有因数叫做这两个数的公因数;其中最大的叫最大公因数。甲数和乙数互质,它们的最大公因数是1;丙数是甲、乙两数的倍数,则甲、乙、丙三个数互质,它们的最大公因数是1;可以通过举例得到答案。
【解析】如:甲数是2,乙数是3,2和3互质;丙数是6,6是2、3的倍数;2、3、6互质,2、3、6的最大公因数是1。
故答案为:D
9.C
【分析】根据正方体的特征可知,把这个长方体截成一个最大的正方体,这个正方体的棱长为5厘米,减少的面积相当于长为5厘米、宽为(8-5)厘米的4个小长方形的面积,根据长方形面积公式解答。
【解析】5×(8-5)×4
=5×3×4
=60(平方厘米)
把一个长8厘米,宽和高都是5厘米的长方体截成一个最大的正方体后,表面积减少60平方厘米。
故答案为:C
10.A
【分析】将绳子全长看作单位“1”,用单位“1”-第二段占全长的分率=第一段占全长的分率,比较两个分率即可。
【解析】第一段占全长的:
>
所以这两段绳子相比,第一段长。
故答案为:A
11.B
【分析】根据题意,一袋糖,4颗4颗地分、5颗5颗地分、6颗6颗地分,都正好分完而没有剩余,说明这袋糖最少的颗数是4、5、6的最小公倍数,据此解答。
【解析】
4、5、6的最小公倍数是2×2×3×5=60
即这袋糖最少有60颗。
故答案为:B
12.D
【分析】整数中,是2的倍数的数叫做偶数,不是2的倍数的数叫做奇数。连续偶数的特点,两个相邻的偶数相差2。
已知5个连续偶数,中间一个数是N,那么N+2+2是最大的数。
【解析】N+2+2=N+4
5个连续偶数,中间一个数是N,则最大的数是N+4。
故答案为:D
13.B
【分析】根据分数的基本性质可知,分数的分子和分母同时乘或除以一个相同的数((0除外),分数的大小不变。的分子加上14,变成了21,相当于乘(21÷7=3),所以分母也要乘3,据此解答。
【解析】由分析可得,分母应该乘3,即变成8×3=24。
A.分母加上14,变成8+14=22,不符合题意;
B.分母乘3,变成8×3=24,符合题意;
C.分母加上24,变成8+24=32,不符合题意;
D.分母乘4,变成8×4=32,不符合题意。
故答案为:B
14.B
【分析】把一根绳子对折一次,平均分成2段;对折两次,平均分成2×2=4段;对折三次,平均分成2×2×2=8段;求每段绳子的长度是全长的几分之几,用1÷平均分的段数,即1÷8解答。
【解析】2×2×2
=4×2
=8(段)
1÷8=
把一条绳子对折三次后,这时每段绳子的长度是全长的。
故答案为:B
15.A
【分析】
分析题目,从上面看到的图形是,则这个几何体的最下面一层有3个小正方体;从左面看形状还是,可知在前排的最底层上面至少还有1个小正方体,据此解答。
【解析】3+1=4(个)
拼一个从上面和左面看形状都是的物体,至少需要4个小正方体。
故答案为:A
16.B
【分析】找次品的方法:把待称的物品分成三份,能够平均分的就平均分成3份,不能平均分的,也应该使多的一份与少的一分只相差1,据此逐项解答。
【解析】A.把8个球分成3、3、2三组,把两个3个一组的放在天平上称,如平衡,则次品在2个的一组中,把这2个球分成1、1,放在天平上称,下沉的是次品,需称2次。如不平衡,刚把下沉的一组3个球分成1、1、1,任意两个放在天平上称,如平衡,没称的是次品,如不平衡,下沉的是资料品,需称2次。不符合题意。
B.把15平均分成5、5、5三组,任意称两个5,如果平衡,就从剩下的5个中找,如果不平衡,次品就在下沉的那组5中,就再把5分成2、2、1,称两个2,如果平衡,次品就在1中,如果不平衡,再就在下沉的2中,分1、1,可找出次品。即至少称3次。符合题意。
C.将28个球分成(9、9、10),称(9、9),只考虑最不利的情况,平衡,次品在10个中;将10个分成(3、3、4),称(3、3),平衡,次品在4个中;将4个分成(1、1、2),称(1、1),平衡,次品在2个中;再称一次即可确定次品,共4次。不符合题意。
故答案为:B
17.A
【分析】从题意可知:张明和李丽捐了同样数量的课外书,即张明课外书的等于李丽课外书的。
甲:根据分数的意义,将张明自己的课外书看作单位“1”, 平均分成5份,再取其中的3份(6本),即张明有6÷3×5=10本;将李丽自己的课外书看作单位“1”, 平均分成3份,再取其中的2份(6本),即李丽有6÷2×3=9本;10>9,即张明多,李丽少。比较方法正确。
乙:根据分数的意义,将张明自己的课外书看作单位“1”, 平均分成5份,再取其中的3份;将李丽自己的课外书看作单位“1”, 平均分成3份,再取其中的2份;张明的3份和李丽2份同样多,张明的5份大于李丽的3份,即张明多,李丽少。符合题意,比较方法正确。
丙:图中表示的两人捐了的课外书数量不同,即张明课外书的不等于李丽课外书的。不符合题意,比较方法错误。
【解析】根据分析可知:甲和乙的比较方法都能表示:张明和李丽捐了同样数量的课外书,张明捐了自己课外书的,李丽捐了自己课外书的,张明的课外书多,李丽的课外书少。
故答案为:A
18.D
【分析】应用列乘法算式法找出各个数的因数。除了1和它本身,还有其他因数的数,叫做合数。一个数如果能被2整除,那么这个数就是2的倍数。个位数字为0、2、4、6、8的数是偶数,个位数字为1、3、5、7、9的数是奇数。据此解答。
【解析】A.只有51是51的因数,所以该选项错误;
B.51÷2=25……1,36÷2=18,4÷2=2,9÷2=4……1,24÷2=12所以只有36,4,24是2的倍数,所以该选项错误;
C.51和9是奇数,36,4,24是偶数,所以该选项错误;
D.51,36,4,9,24都是合数,所以该选项正确。
故答案为:D
19.D
【分析】根据分数的意义,分母表示平均分的份数,分子表示取走的份数,分别用分数表示出各选项阴影部分即可。
【解析】A.不是平均分,不能用分数表示,排除;
B.阴影部分占整个图形,排除;
C.阴影部分占整个图形,排除;
D.阴影部分占整个图形,符合。
阴影部分占整个图形的是。
故答案为:D
20.D
【分析】把这条线段的全长看作单位“1”,把它平均分成3份,1份是2厘米,用1份的长乘3就是这条线段的全长。
【解析】2×3=6(厘米)
所以这条线段长是6厘米。
故答案为:D
21.B
【分析】两个数为倍数关系,则这两个数的最大公因数是较小的数,最小公倍数是较大的数。据此判断。
【解析】因为6m÷(3m)=2
所以A,B的最大公因数是3m。
故答案为:B
22.C
【分析】一个数,如果只有1和它本身两个因数,这样的数叫作质数;一个数,除了1和它本身还有别的因数,这样的数叫作合数;由题意可知,孪生质数是指两个数都是质数且它们的差为2,据此逐一分析各项即可。
【解析】A.在9和1中,9是合数,不是质数,所以9和1不是孪生质数;
B.在13和15中,13是质数,15是合数,所以13和15不是孪生质数;
C.在11和13中,11和13都是质数,且13-11=2,所以11和13是孪生质数。
所以11和13是孪生质数。
故答案为:C
23.B
【分析】如果高增加2厘米,则其增加的体积等于长a厘米、宽b厘米、高2厘米的长方体的体积,根据长方体的体积=长×宽×高,代入数据计算即可解答。
【解析】a×b×2=2ab(立方厘米)
所以一个长方体的长,宽,高分别是a厘米,b厘米,h厘米,如果高增加2厘米,则其体积增加2ab立方厘米。
故答案为:B
24.C
【分析】根据从左面看的图形,可知立体图形有三行两层;根据从正面看的图形,可知立体图形有三列两层;综合以上,则第二行第二列处必须上下重叠摆放2个小正方体,据此试着拼摆这个立体图形,并数出最多需要几个小正方体即可。
【解析】符合从左面、正面看到的图形,最少需要的小正方体块数如图1所示,最多需要的小正方体块数如图2所示,所以要搭成这样的几何体最多需要10个小正方体。
故答案为:C
25.C
【分析】根据哥德巴赫猜想,结合质数的意义,从四个加法算式中找出偶数写成两个质数的和的算式即可。
一个数,如果只有1和它本身两个因数,那么这样的数叫做质数。
整数中,是2的倍数的数叫做偶数,不是2的倍数的数叫做奇数。
【解析】A.38=21+17,38是大于2的偶数,21是合数,17是质数,不符合哥德巴赫猜想;
B.32=31+1,32是大于2的偶数,31是质数,1不是质数,不符合哥德巴赫猜想;
C.36=13+23,36是大于2的偶数,13是质数,23是质数,符合哥德巴赫猜想;
D.34=24+10,34是大于2的偶数,24是合数,10是合数,不符合哥德巴赫猜想。
故答案为:C
26.C
【分析】已知正方体木块的棱长是5dm,根据正方体的表面积公式S=6a2,求出这个正方体木块的表面积;
把这个正方体木块截成两个完全一样的长方体,表面积会增加两个截面的面积;由正方体的特征可知,每个截面是边长为5dm的正方形,根据正方形的面积公式S=a2,求出一个面的面积,再乘2,即是增加的表面积;
然后用原来正方体木块的表面积加上增加的表面积,即是截成的两个长方体的表面积之和。
【解析】5×5×6+5×5×2
=25×6+25×2
=150+50
=200(dm2)
这两个长方体的表面积一共是200dm2。
故答案为:C
27.D
【分析】根据题意,长方体的的侧面展开图正好是一个面积为64平方分米的正方形,根据正方形的面积=边长×边长,可推导出侧面展开图的边长是8分米,也就是长方体的底面周长和高都是8分米;
已知长方体的底面是一个正方形,根据正方形的周长=边长×4,那么正方形的边长=周长÷4;再根据正方形的面积=边长×边长,求出这个长方体的底面积。
【解析】因为64=8×8,所以长方体的底面周长是8分米,高是8分米;
底面边长:8÷4=2(分米)
底面积:2×2=4(平方分米)
这个长方体一个底面的面积是4平方分米。
故答案为:D
28.D
【分析】单式条形统计图可以清楚地看出数量的多少。
复式条形统计图可以用不同的条形表示两种以上的量的多少。
单式折线统计图不但可以表示出数量的多少,而且能够清楚地表示出数量增减变化的情况。
复式折线统计图通过两组以上数据的水平进行比较,可以容易地比较出两组以上数据的变化趋势,更清楚看出各类之间的比较。
【解析】要比较凉山州2024年4月、5月的气温变化情况,绘制复式折线统计图更合理。
故答案为:D
29.D
【分析】根据找一个数的倍数的方法可知,17的倍数分别是17×1的积,17×2的积,17×3的积,17×4的积……;17是奇数,根据奇数和偶数的运算性质:奇数×奇数=奇数,奇数×偶数=偶数;由此可知17的倍数既有偶数也有奇数。
整数中,是2的倍数的数叫做偶数,不是2的倍数的数叫做奇数。
【解析】17的倍数:17,34,51,68……;
其中奇数有17,51……,偶数有34,68……;
所以,自然数中,17的倍数有偶数也有奇数。
故答案为:D
30.C
【分析】整数中,是2的倍数的数叫做偶数,不是2的倍数的数叫做奇数。
一个数,如果只有1和它本身两个因数,那么这样的数叫做质数。
一个数,如果除了1和它本身还有别的因数,那么这样的数叫做合数。
【解析】A.如果a是奇数15,15的因数有:1,3,5,15;共有4个因数,不符合题意;
B.如果a是偶数6,6的因数有:1,2,3,6;共有4个因数,不符合题意;
C.如果a是质数7,7的因数有:1,7;共有2个因数,符合题意;
D.如果a是合数9,9的因数有:1,3,9;共有3个因数,不符合题意。
故答案为:C
31.D
【分析】根据题图可知,丝带捆扎的长度为4条高,2条长、2条宽,再加上接头处的长度,据此解答即可。
【解析】10×4+25×2+12×2+15
=40+50+24+15
=90+24+15
=114+15
=129(厘米)
要捆扎这种礼品盒至少需要准备129厘米长的丝带。
故答案为:D
32.C
【分析】8路公交车每10分钟发一次车,10路公交车每12分钟发一次车,求出10和12的最小公倍数,就是从第一次发车到第二次发车经过的时间,据此推算即可。
【解析】10=2×5
12=2×2×3
所以10和12的最小公倍数是:2×5×2×3=60
6时30分+60分=7时30分
故答案为:C
33.A
【分析】要求剪出的正方形的边长最大是多少,就是求48和36的最大公因数是多少。先把每个数分别分解质因数,再把两个数中的全部公有质因数提取出来连乘,所得的积就是这两个数的最大公因数,据此解答。
【解析】48=2×3×2×4
36=2×2×3×3
48和36的最大公因数是2×2×3=12
所以剪出的正方形的边长最大是12cm。
故答案为:A
34.CC
【分析】由图可知,长方体盒子的长为5厘米,宽为3厘米,高为2厘米,根据“长方体的表面积=(长×宽+宽×高+长×高)×2”求出这个盒子的表面积,因为题干明确了“无盖”,故只需要计算五个面的面积即可。据此解答。
【解析】(5×3+5×2+3×2)×2
=(15+10+6)×2
=31×2
=62(平方厘米)
62-5×3
=62-15
=47(平方厘米)
所以,这个透明的无盖的长方体盒子的表面积是47平方厘米。
故答案为:C
35.B
【分析】分数的意义:把单位“1”平均分成若干份,表示这样的一份或几份的数叫做分数;分母是平均分的总份数,分子是取的其中的几份。
【解析】
A.阴影部分表示为,阴影部分表示为,不符合题意;
B.阴影部分表示为,阴影部分表示为,符合题意;
C.阴影部分表示为,不是平均分成3份,阴影部分不能用分数表示,不符合题意。
故答案为:B
36.A
【分析】既是2的倍数又是3的倍数的特征:个位上的数字是0、2、4、6、8,各个数位上的数字的和是3的倍数的数。
【解析】
小欣的行李箱的密码是一个“450”四位数,如果是2的倍数,个位上的数字是0、2、4、6、8,4+5=9、4+5+2=11、4+5+4=13、4+5+6=15、4+5+8=17,如果既是2的倍数,也是3的倍数有4500、4506,共有2种可能。
故答案为:A
37.B
【分析】如果想“3”和“5”可以直接相加、减,那么“3”和“5”必须在相同的数位上,也就是相同单位的数才能相加、减,据此分析选项即可。
【解析】A.3129中的3在千位上,表示3个一千,587中的5在百位上,表示5个一百,不能直接相加、减。不符合题意;
B.2.65中的5在百分位上,表示5个百分之一,0.13中的3在百分位上,表示3个百分之一,可以直接相加、减。符合题意;
C.的分数单位是,其中的5表示5个,的分数单位是,其中的3表示3个,不能直接相加、减。不符合题意。
故答案为:B
38.B
【分析】把单位“1”平均分成若干份,表示其中一份的数叫分数单位;
根据分数单位的意义可知,一个分数的分母是几,其分数单位就是几分之一,分母不同,其分数单位不同;
异分母分数的加减法,先通分,变成分母相同而大小不变的分数,即分数单位相同的分数,然后按照同分母分数的加减法进行计算。
【解析】由分析可知,异分母分数不能直接相加减的原因是分数单位的不同。
故答案为:B
39.C
【分析】包装的高度一定大于酸奶的高度,“净含量250mL”说明酸奶一共有250mL,先根据公式高=长方体体积÷长÷宽,求出酸奶的高度,然后再跟选项进行比较,选择略微高出酸奶高度的酸奶盒即可。
【解析】250mL=250cm
250÷5÷5=10(cm)
10.5cm>10cm
故答案为:C
40.C
【分析】
根据从上面看到的形状和数字,可以确定这个几何体如图,从左面看有3行,下边1行3个小正方形;中间1行2个小正方形,左对齐;上边1行1个小正方形,居中;据此分析。
【解析】
根据分析,这个几何体从左面看是。
故答案为:C
41.C
【分析】A.从正面看有2行,下边1行2个小正方形,上边1行靠左1个小正方形;从上面看有2列,右边1列3个小正方形,左边1列靠上1个小正方形;从右面看有2行,下边1行3个小正方形,上边1行靠右1个小正方形;
B.从正面看有2行,下边1行3个小正方形,上边1行靠左1个小正方形;从上面看有2行,下边1行3个小正方形,上边1行中间1个小正方形;从右面看有2行,下边1行2个小正方形,上边1行靠左1个小正方形;
C.从正面看有2行,下边1行3个小正方形,上边1行靠左1个小正方形;从上面看有2行,上边1行3个小正方形,下边1行中间1个小正方形;从右面看有2行,下边1行2个小正方形,上边1行靠右1个小正方形;
D.从正面看有2行,下边1行3个小正方形,上边1行靠左1个小正方形;从上面看有2行,上边1行3个小正方形,下边1行靠左1个小正方形;从右面看有2行,下边1行2个小正方形,上边1行靠右1个小正方形。
【解析】
A.从正面看是,从上面看是,从右面看是;
B.从正面看是,从上面看是,从右面看是;
C.从正面看是,从上面看是,从右面看是;
D.从正面看是,从上面看是,从右面看是。
用5个正方体搭成一个几何体,从正面看是,从上面看是,从右面看是,这个几何体是。
故答案为:C
42.D
【分析】先根据2、5的倍数特征,由个数是否是0,判断这个三位数是否是2、5的倍数;
如果是2、5的倍数,再根据3的倍数特征判断这个三位数是否是3的倍数;
最后确定这个三位数同时是2、3、5的倍数,且最大,即可得解。
2的倍数特征:个位上是0、2、4、6、8的数。
5的倍数特征:个位上是0或5的数。
2、5的倍数特征:个位上是0的数。
3的倍数特征:一个数各位上的数的和是3的倍数,这个数就是3的倍数。
【解析】A.999的个位不是0,不是2、5的倍数,不符合题意;
B.995的个位不是0,不是2、5的倍数,不符合题意;
C.998的个位不是0,不是2、5的倍数,不符合题意;
D.990的个位是0,990是2、5的倍数;
9+9+0=18,18是3的倍数;
所以,990同时是2、3、5的倍数,且最大,符合题意。
故答案为:D
43.D
【分析】由于折线统计图的竖轴表示路程,由于最开始兔子的速度很快,那么相同时间,兔子的路程比较高,由此即可知道实线是兔子,虚线是乌龟,由于兔子在路边睡了一觉,此时的路程不变,是一条直线,兔子醒来后,追赶了一端时间,乌龟胜利,那么说明同样高度,虚线是先到的,兔子后到的,据此即可选择。
【解析】由分析可知:
大致能反映这个故事情节的图像是。
故答案为:D
44.D
【分析】分别将3个立体图形的上面、左面、右面、前面画出,再判断即可。
【解析】
用5个相同的小正方体搭成的立体图形,从前面看,所看到的形状都是。
故答案为:D
45.B
【分析】先根据进率1mL=1cm,将300mL换算成300 cm3,500mL换算成500 cm3;
根据题意,将四颗相同的铁球放入水中,结果水没有满,可知四颗铁球的体积要小于500-300=200(cm3),那么一颗铁球的体积就小于(200÷4)cm3;再将一颗同样的铁球放入水中,结果水满溢出,可知五颗铁球的体积要大于500-300=200(cm3),那么一颗铁球的体积就大于(200÷5)cm3。据此推测出一颗铁球体积的范围。
【解析】300mL=300 cm3
500mL=500 cm3
500-300=200(cm3)
200÷4=50(cm3)
200÷5=40(cm3)
40 cm3<一颗铁球的体积<50 cm3
所以,一颗铁球的体积大约在40 cm3~50 cm3。
故答案为:B
46.B
【分析】判断一个分数能否化成有限小数,首先要看这个分数是不是最简分数,如果不是最简分数,要先约分,再根据一个最简分数,如果分母中只含有质因数2或5,这个分数就能化成有限小数;如果分母中含有2或5以外的质因数,这个分数就不能化成有限小数。
【解析】A.分母是3,不能化成有限小数;
B.=,4=2×2,可以化成有限小数;
C.分母是13,不能化成有限小数;
D.12=2×2×3,质因数有3,不能化成有限小数。
故答案为:B
47.A
【分析】真分数:分子小于分母的分数是真分数,m是分子,n是分母,即m<n的时候,才是真分数,据此即可选择。
【解析】由分析可知:
如果(m和n是大于0的自然数)是真分数,那么m<n。
故答案为:A
48.D
【分析】在连续偶数中,相邻的两个偶数相差2,最小的一个偶数为2n,第2个偶数即2n+2,第三个偶数即2n+2+2。将三个偶数相加,结果化简即可判断。
【解析】2n+2n+2+2n+2+2
=(2n+2n+2n)+(2+2+2)
=6n+6
三个连续偶数中,最小的一个数为2n,则这三个偶数的和是6n+6。
故答案为:D
49.B
【分析】用500-300,求出5颗小玻璃球的体积,再除以5,求出1个小玻璃球的体积;再用300-200,求出放入1颗大玻璃球和1颗小玻璃球的体积,再减去1个小玻璃球的体积,即可解答,注意单位名数的换算。
【解析】500-300=200(毫升)
200毫升=200立方厘米
200÷5=40(立方厘米)
300-200=100(毫升)
100毫升=100立方厘米
100-40=60(立方厘米)
一颗大玻璃球的体积是60立方厘米。
故答案为:B
50.A
【分析】从图中可知,天平左右两边各放了3个台球,天平不平衡,左边重、右边轻。因为次品略轻,所以这个次品一定在右边的④⑤⑥中,由此推断哪些台球是正品。
【解析】根据第一次称的结果可知,天平左边的台球重,右边的台球轻。因为次品略轻,所以左边较重的①②③是正品,另外还没有称的台球⑦和⑧也是正品。
所以,可以推断①、②、③、⑦和⑧一定是正品。
故答案为:A
51.B
【分析】根据题意,张阿姨买了3箱同样的车厘子,每箱车厘子的价格都是整数,根据“单价×数量=总价”可知,张阿姨花的钱数是3的倍数;从三个选项中找出哪个数是3的倍数,即可得解。
3的倍数特征:一个数各位上的数的和是3的倍数,这个数就是3的倍数。
【解析】A.2+6+0=8,8不是3的倍数,则260不是3的倍数;
B.2+6+4=12,12是3的倍数,则264是3的倍数;
C.2+6+8=16,16不是3的倍数,则268不是3的倍数;
所以,张阿姨可能花了264元。
故答案为:B
52.B
【分析】根据题意,48个青团和36个艾饺正好平均分完,且没有剩余,那么分给最多的人数就是48和36的最大公因数。
48、36分解质因数后,把公有的相同质因数乘起来就是它们的最大公因数,也就是最多的人数。
【解析】48=2×2×2×2×3
36=2×2×3×3
48和36的最大公因数是:2×2×3=12
即最多能分给12个朋友。
故答案为:B
53.B
【分析】真分数的分子小于分母。本题可以举例说明,如的分子和分母同时加上1,得到,=,=,>,则>;再如的分子和分母同时加上3,得到,=,=,>,则>。据此解答。
【解析】通过分析可得:一个真分数的分子和分母同时加上一个非零自然数,得到的分数值一定比原分数大。
故答案为:B
54.B
【分析】在100克水中加入7克盐,则盐水中盐的质量是7克,盐水的质量是100+7=107(克),要求盐水中盐的质量占盐水的几分之几,用盐的质量除以盐水的质量即可。
【解析】7÷(100+7)
=7÷107
=
因此这种盐水中盐的质量占盐水的。
故答案为:B
55.A
【分析】找次品的最优策略:(1)把待分物品分成3份;(2)每份数量尽量平均,如果不能平均分的,也应该使多的一份与少的一份只相差1。
【解析】将12瓶矿泉水分成(4、4、4),称(4、4),无论平衡不平衡,都可确定次品在其中4瓶;将4瓶分成(1、1、2),称(1、1),只考虑最不利的情况,即次品在多的里面,平衡,次品在2瓶中;将2瓶分成(1、1),再称1次即可确定次品,共3次。
至少称3次才能保证找出次品。
故答案为:A
56.B
【分析】根据长方体的体积=长×宽×高,因为长方体前面的面积=长×高,所以用前面的面积乘宽等于长方体的体积。
【解析】长方体的体积:32×3=96(cm3)
要计算这个长方体的体积,正确的算式是32×3。
故答案为:B
57.C
【分析】一个数,如果只有1和它本身两个因数,那么这样的数叫做质数。
一个数,如果除了1和它本身还有别的因数,那么这样的数叫做合数。
整数中,是2的倍数的数叫做偶数,不是2的倍数的数叫做奇数。
奇数和偶数的运算性质:偶数+偶数=偶数,奇数+奇数=偶数,奇数+偶数=奇数。
【解析】A.当a=4时,2a+1=2×4+1=8+1=9,9是合数;原选项说法错误;
B.当a=2时,2a+1=2×2+1=4+1=5,5是质数;原选项说法错误;
C.无论a是奇数,还是偶数,2a一定是偶数,因为偶数+奇数=奇数,所以2a+1一定是奇数;原选项说法正确;
D.当a=3时,2a+1=2×3+1=6+1=7,7是奇数;原选项说法错误。
故答案为:C
58.A
【分析】根据图可知,这个长方体盒子的长等于4个小正方体的棱长和,宽等于3个小正方体的棱长和,高等于3个小正方体的棱长和,根据长方体表面积公式:表面积=(长×宽+长×高+宽×高)×2,代入数据,即可解答。
【解析】长:1×4=4(cm),宽:1×3=3(cm);高:1×3=3(cm)。
表面积:
(4×3+4×3+3×3)×2
=(12+12+9)×2
=(24+9)×2
=33×2
=66(cm2)
在一个透明的长方体盒子内放置棱长为1cm的小正方体(如图)。这个长方体盒子的表面积是66cm2。
故答案为:A
59.A
【分析】由于把2.5L的可乐倒在装180mL的小杯子里,即看2.5L里面有多少个180mL,根据1L=1000mL,先转换单位,庵后用2500÷180,求出结果即可,由于问多少个客人能喝到180mL的可乐,说明如果还有剩余,并且不够180mL的,则舍去,结果用去尾法保留整数即可。
【解析】2.5L=2500mL
2500÷180=13(个)……160mL
所以妈妈把买回来的一大瓶2.5L的可乐分别倒在只能装180mL的小子杯子里招待客人,13个客人能喝到180mL的可乐。
故答案为:A
60.B
【分析】找次品的最优策略:
(1)把待分物品分成3份;
(2)每份数量尽量平均,如果不能平均分的,也应该使多的一份与少的一份只相差1。
【解析】先把12分成(4、4、4);第一次称量:在天平两边各放4盒,可能出现两种情况:(把轻一些的那盒看做次品)①如果天平平衡,则次品在剩余的那4盒,分成(2、2);
第二次称量:在左、右盘中分别放2盒,上升者有次品;
第三次称量:在左、右盘中分别放1盒,上升者是次品。
②如果天平不平衡,次品在托盘上升那边的4盒里;
第二次称量:取托盘上升的4盒,在左、右盘中分别放2盒,上升者有次品;
第三次称量:取托盘上升的2盒,每一盒分别放在天平的左、右盘中,则上升者是次品。
如果用天平称,至少称3次可以保证找出这盒牛奶。
故答案为:B
61.C
【分析】最后一次喝完,也就是加了多少水就喝了多少水,第一次加了杯水,第二次加了杯水,而牛奶就是一杯;将加的两次水加起来,就是一共喝了多少水,与1杯纯牛奶比较,即可得出结论。
【解析】喝的水:(杯)
喝的牛奶:1杯
因此丽丽喝的水和纯牛奶一样多。
故答案为:C
62.B
【分析】物体所占空间的大小叫做物体的体积,物体各个面的面积之和叫做物体的表面积。
根据题意,将一个正方体钢坯锻造成一个长方体钢坯,钢坯的形状变了,则表面积发生了变化;但钢坯的大小不变,即体积没变,据此解答。
【解析】将一个正方体钢坯锻造成一个长方体钢坯,长方体和正方体相比,体积相等,表面积不相等。
故答案为:B
63.C
【分析】条形统计图可以直观地看出数量的多少;折线统计图不仅能看清数量的多少,还能反映数量的增减变化情况。复式条形统计图可以表示多种量的多少;复式折线统计图表示2个及以上的量的增减变化情况。据此解答。
【解析】通过分析可得:要比较北京和南宁两地一年中气温的变化趋势,选择复式折线统计图更合适。
故答案为:C
64.A
【分析】把一个图形整体沿某一直线方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同,图形的这种移动叫做平移,观察选项,依此解答问题。
【解析】A. 索道上运行的缆车是沿直线方向移动的,并且移动后的形状和大小不变,故正确;
B.钟面上转动的分针是绕中间一点做旋转运动,不符合平移定义,故错误;
C.飞行中直升飞机的螺旋桨是绕中间一点做旋转运动,不符合平移定义,故错误。
故答案为:A
65.B
【分析】两人从三张卡片中抽取两张,卡片的数字之积可能是:2×3=6,2×5=10,3×5=15。其中6和10是偶数,15是奇数。偶数的数量多,则两人抽取的卡片的数字之积是偶数的可能性大。据此解答。
【解析】通过分析可得:两人抽取的卡片的数字之积是偶数的可能性大,则这个游戏笑笑胜的可能性大。
故答案为:B
66.D
【分析】根据题意,正方体的钢锭的体积等于长方体钢锭的体积,根据得出正方体的体积是512立方厘米,即长方体的体积也是512立方厘米,根据,得出长方体的高=体积÷长÷宽。
【解析】8×8×8=512(平方厘米)
512÷5÷8=12.8(厘米)
它的高是12.8厘米。
故答案为:D
67.D
【分析】设原来正方体棱长为1,扩大后正方体的棱长为1×2=2;根据正方体棱长公式:棱长总和=棱长×12;表面积公式:表面积=棱长×棱长×6,体积公式:体积=棱长×棱长×棱长,代入数据,分别求出原来正方体的棱长总和,表面积,体积以及扩大后正方体棱长总和,表面积,体积,再用扩大后正方体的棱长总和÷原来正方体棱长总和;扩大后正方体表面积÷原来正方体表面积;扩大后正方体的体积÷原来正方体体积,即可解答。
【解析】设原来正方体棱长为1;扩大后正方体的棱长为1×2=2。
(2×12)÷(1×12)
=24÷12
=2
(2×2×6)÷(1×1×6)
=(4×6)÷(1×6)
=24÷6
=4
(2×2×2)÷(1×1×1)
=(4×2)÷(1×1)
=8÷1
=8
一个正方体的棱长扩大到原来的2 倍,棱长总和扩大到原来的2倍,表面积扩大到原来的4倍,体积扩大到原来的8倍。
故答案为:D
68.B
【分析】根据从上面看到的形状,可以确定底层有4个小正方体,以及这4个小正方体的摆放位置;根据从左面看到的形状,可以确定第二层的1个小正方体只能摆到并排的3个小正方体的上面,据此分析。
【解析】
如图,一共有3种不同的摆法。
故答案为:B
69.A
【分析】两个数的公有质因数的连乘积就是这两个数的最大公因数;如果两个数为倍数关系,较小的数为最大公因数;如果两个数为互质数,最大公因数是1,据此解答。
【解析】因为a÷b=15,所以a和b成倍数关系,最大公因数是b。
如果a÷b=15(a、b都是大于0的自然数),那么a和b的最大公因数是b。
故答案为:A
70.B
【分析】三人读同一篇文章,用时越少的,读的速度就越快。即比较、、0.3的大小,可以把分数化成小数,用分子除以分母即可,再根据小数大小的比较方法进行比较,得出结论。
【解析】=1÷5=0.2
=1÷6≈0.167
0.167<0.2<0.3
<<0.3
小林用时最少,所以小林速度快。
故答案为:B
71.B
【分析】通过图可知,这个物体的长、宽、高分别是13cm,9.5cm,3.5cm,之后根据生活经验,对长度单位和数据大小的认识来判断即可。
【解析】A.图中的长对数学书来说太短;不符合题意;
B.根据生活可知新华字典的长、宽、高符合图中的数据,符合题意;
C.图中的长、宽对纸巾盒来说不合适;不符合题意;
D.图中的宽对橡皮来说太长,不符合题意。
故答案为:B
72.B
【分析】1m3=1000dm3,由此可知,1 m3的正方体木块切成1dm3的小正方体木块,能分成1000个1dm3的小正方体;1dm3的小正方体的棱长是1dm3;把这些小正方体排成一排,总长度是1×1000=1000dm;再转成单位,即可解答。
【解析】1m3=1000dm3
所以1000÷1=1000(个)
1dm3的正方体的棱长是1dm。
总长:1×1000=1000(dm)
1000dm=100m=0.1km=10000cm
把1m3的正方体木块切成1dm3的小正方体木块。如果把这些小木块排成一行组成一个长方体,那么这个长方体的长是100m(或0.1km,10000cm)。
故答案为:B
73.B
【分析】根据长方体的特征:长方体有12条棱,其中4条长,4条宽,4条高;长、宽、高相交于一点,4条长互相平行且相等;4条宽互相平行且相等;4条高互相平行且相等;根据图可知,这个长方体的长是9cm,宽是7cm,高是4cm,由此可知,长方体有两个长是9cm,宽是7cm的面,即2个②;有两个长是9cm,宽是4cm的面,即2个③;有两个长是7cm,宽是4cm的面,即2个⑤,据此解答。
【解析】
根据分析可知,左图是一个长方体的3条棱(单位:cm)。选择6个面图出这个长方体,正确的选择是2个②、2个③、2个⑤。
故答案为:B
74.B
【分析】根据题意可知,将一个长方体的高增加5米就成为一个正方体可知:原长方体的长=宽=正方体的棱长,这时表面积比原来增加160平方米,表面积增加的是高5米的长方体的4个侧面的面积,因此可以求出一个侧面的面积,进而求出原来长方体的长。据此解答。
【解析】160÷4÷5=8(米)
原来长方体的长是8米。
故答案为:B
75.C
【分析】将一个石柱放入放满水的池子中,则溢出水的体积就是没入水中石柱的体积。根据长方体体积=长×宽×高,据此计算可得出答案。
【解析】根据题意得:水池水溢出的体积即为没入水中石柱的体积,没入水中石柱长3m、宽2m、高2m。
即3×2×2=12(m )。
故答案为:C
76.B
【分析】把红红做试卷用的时间加上检查试卷用的时间,再加上离测试结束的时间即可解答。
【解析】++
=++
=+
=(小时)
所以这次测试规定的时间是小时。
故答案为:B
77.B
【分析】不管是每人5颗还是每人3颗,最后都会剩余1颗,则糖果总数比5和3的公倍数多1。据此解答。
【解析】5和3的公倍数有:15、30、45、60、75……
其中60+1=61(颗),则糖果总数可能是61颗。
故答案为:B
78.B
【分析】分子相同的分数,分母越大,分数越小。据此解答。
【解析】通过分析可得:因为a>b,所以与相比较,。
故答案为:B
79.B
【分析】钟面上共有12个大格,则每个大格为360÷12=30度,钟表行走的方向就是顺时针方向,反之就是逆时针方向;逆时针旋转,即逆时针旋转90°÷30°=3个大格,据此解答即可。
【解析】90°÷30°=3(个)
8-3=5
则时针从“8”起逆时针旋转后,时针应该指向5。
故答案为:B
80.C
【分析】物体或图形旋转后,它们的形状、大小都不改变,只是位置发生了变化。据此解答。
【解析】通过分析可得:把一个图形绕某点顺时针旋转60°后,所得到的图形与原来的图形相比较,大小不变。
故答案为:C
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
同课章节目录
