2024-2025年人教版五年级下册数学期末情境化提升训练(含解析)
文档属性
| 名称 | 2024-2025年人教版五年级下册数学期末情境化提升训练(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-09 19:23:46 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
2024-2025年人教版五年级下册数学期末情境化提升训练
一、选择题
1.红光小学鼓号队有31人,暑假期间有一个紧急演出,李老师需要尽快通知到每个队员。如果用打电话的方式,每分钟通知1人,每个同学接到电话后又打给其它同学,同时李老师也在不停的打,要通知全体队员至少需要_____分钟才能通知到所有人。( )
A.7 B.6 C.5 D.4
2.二十四节气是中国古代劳动人民长期经验积累的结晶,它与白昼时长密切相关。春分,秋分时,昼夜时长大致相等。夏至时,白昼时长最长。如图是一年中部分节气所对应的白昼时长示意图。在下列四个节气中,( )的白昼时长超过了13小时。
A.立春 B.小暑 C.秋分 D.冬至
3.为了规范共享单车、助力车的摆放,整体提升城市形象,城市管理部门在公共区域画了一个长方形地作为专用停车场,规划好后发现长和宽都是质数,并且周长是36m,这个指定的长方形停车场的面积最大是( )。
A. B. C. D.
4.《西游记》是我国四大名著之一,书中的孙悟空去西天取经的路上遇到妖精,每次拔一根猴毛就能变成一个孙悟空,变出的孙悟空也能每次拔一根猴毛变成一个孙悟空,每次变化需要的时间是2秒钟,10秒钟最多能变出( )个孙悟空。
A.15 B.32 C.31 D.60
5.学校设立“红领巾交换书屋”鼓励学生课外阅读。4月23日“世界读书日”前夕,大队辅导员想了解全校学生年阅读量情况,以下四位同学介绍的关于书屋的信息对他最有帮助的是( )。
A.小东:602班去年一共借阅1000本 B.小红:去年全校人均借阅14.5本
C.小力:周一借出1256本 D.小君:我上周借阅了3本
二、填空题
6.在括号里填上合适的体积或容积单位。
壮壮家的冰箱容积是190( ),星期六上午他从冰箱中拿出1个体积约为300( )的苹果和3个体积约为120( )的枇杷,将苹果和枇杷放入容积为1.5( )的保鲜盒中,再带上1瓶550( )的矿泉水就和朋友一起去公园玩了。
7.中国结是中国特有的民间手工编结艺术,它以其独特的东方神韵、丰富多彩的变化,充分体现了中国人民的智慧和深厚的文化底蕴。用一根5m长的红绳正好可以编织8个同样的中国结。每个中国结用了这根红绳的( ),每个中国结用了( )m红绳。
8.火树银花元夕夜,彩灯万盏增霞流。为弘扬传统文化,元宵节前夕军军和同学们用一根铁丝扎成一个长7cm,宽5cm,高3cm的长方体花灯框架。如果用同样长的铁丝扎成一个正方体花灯框架,这个正方体的棱长是( )cm。军军想给这个正方体花灯框架表面贴上纸片(上面不贴),至少需要( )cm2的纸片。
9.中国结是一种具有中国特色的手工编织工艺品,它代表着团结、吉祥和平安,深受人们的喜爱。用一根5米长的红绳正好可以编织8个中国结,每个中国结用了这根红绳的( ),每个中国结用了( )米的红绳。
10.街道人员制作一批灯笼庆祝“建军节”,先用一根长铁丝制作了一个棱长为6分米的正方体灯笼框架(铁丝刚好用完无剩余)。如果用同样长度的铁丝另外制作一个长方体灯笼框架,长、宽都为8分米,那么这个长方体的高是( )。
11.同学们,你们知道吗?中国第一次参加奥运会的年份是一个四位数。这个四位数千位上的数既不是质数也不是合数,百位上的数是一位数中最大的奇数,十位上的数的最小倍数是3,个位上的数是最小的质数。中国第一次参加奥运会是( )年。
12.哥德巴赫猜想被称为“数学皇冠上的明珠”,中国20世纪三十年代就开始着手这一研究。新中国成立后,我国数学家陈景润在这一领域取得了举世瞩目的成果。这一猜想是:所有大于2的偶数,可以表示为两个质数的和,如:,。照这样想:18=( )。
13.编程兴趣小组制作了一款“青蛙跳跳跳”的游戏。游戏设定,甲、乙两只青蛙同时从起点开始跳跃,每秒跳1次。甲青蛙每次跳10厘米,乙青蛙每次跳15厘米,两只青蛙都能跳到的点位称为相同距离点。每只青蛙跳到相同距离点时,这个点位都会出现一片荷叶,跳离这个点位时,荷叶就会消失。当乙青蛙跳到90厘米这个点位时,电脑一共出现了( )次荷叶。
14.做“花灯”是一种富有文化意义的传统手工艺,苹苹准备做一个长方体花灯,如图所示。先做框架,制作框架至少需要准备( )分米长的木条;再把四个侧面贴上彩纸,至少需要( )平方分米的彩纸;最后把上、下两面用盖子封上,这个花灯的体积是( )立方分米。
15.《庄子·天下首》中有述:“一尺之棰,日取其半,万此不竭”!意思是·尺长的棍棒,今日截取它的一半,即一,明日取它一半的一半……永远也截不完。按照这样的方法,如果木棒长24分米,第三日截取的长度是( )分米,这三日截取的长度占总长度的( ),它的分数单位是( )。
16.中医是我国的瑰宝,中药学是我国古代优秀文化遗产的重要组成部分。奶奶因病案到中药馆买中药9服,每服药共计重200g。但由于药师的疏忽,其中一服中药少放了一味药,用天平至少称( )次,才能保证找到这服中药。
17.一个四位数的手机屏幕解锁密码提示:它的最高位上的数既不是质数也不是合数,第二个数字既是偶数又是质数,第三个数字既是奇数也是合数,个位上的数是最小的自然数,这个四位数的手机解锁密码是( )。
三、判断题
18.钟表上分针转动的速度是秒针的。( )
19.为清楚地比较上海和北京两城市去年各月平均气温的变化情况,最合适的是用扇形统计图来表示。( )
20.一个正方体,先在它每个面上涂上红色,再把它切成棱长是1厘米的小正方体,如果两面涂色的小正方体有24个,那么这个正方体的体积是64立方厘米。( )
21.一个立体图形,从上面看到的形状是,从正面看到的形状是,搭成这样的立体图形,至少需要6个小正方体。( )
22.家庭用燃油小轿车油箱的容积大约是50mL。( )
四、计算题
23.直接写出得数。
3.6+0.7= 4-0.4= 2.4×0.3= 0.48÷0.6=
24.怎样简便怎样算。
25.解方程。
x+= 3x-4.5=10.2 2(x+1.8)=9.6
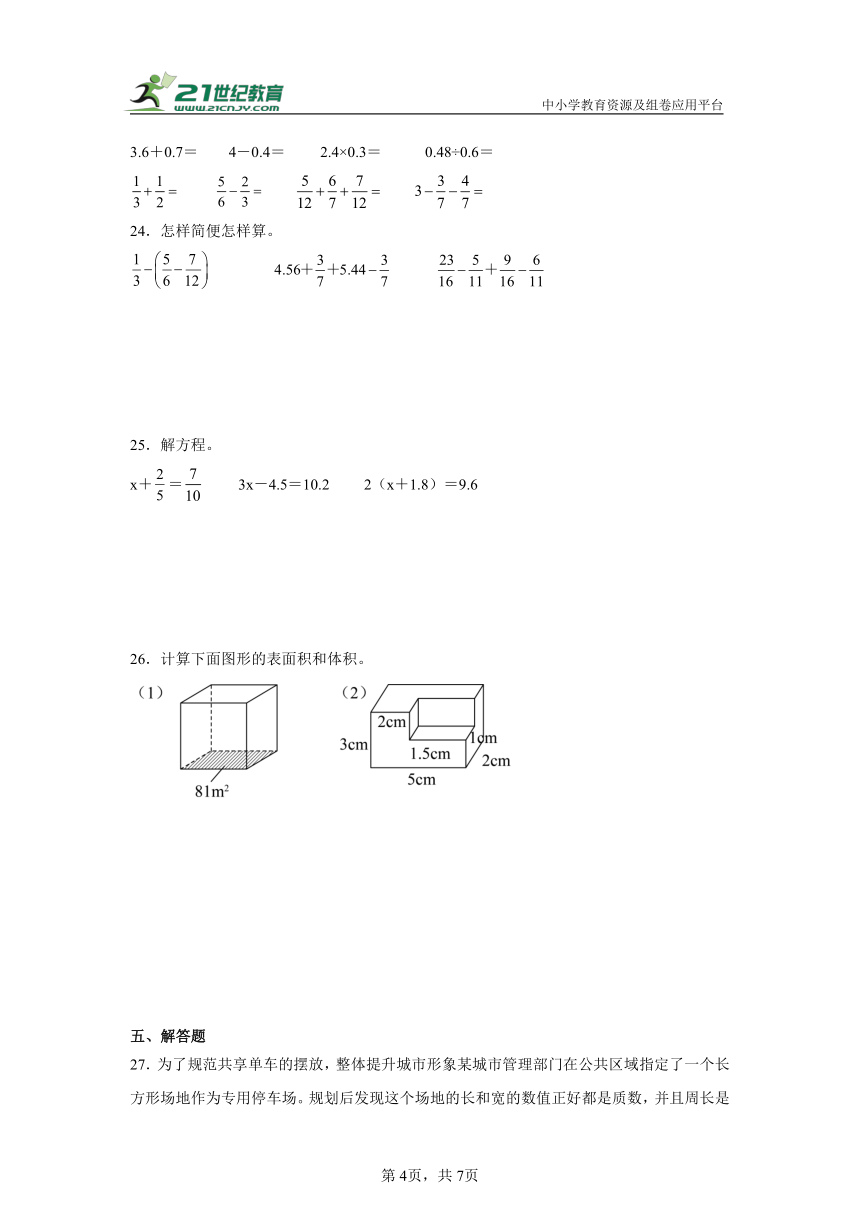
26.计算下面图形的表面积和体积。
五、解答题
27.为了规范共享单车的摆放,整体提升城市形象某城市管理部门在公共区域指定了一个长方形场地作为专用停车场。规划后发现这个场地的长和宽的数值正好都是质数,并且周长是32米,这个长方形停车场的面积是多少平方米?
28.日晷是我国古代的计时仪器,主要是根据日影的位置,以指定当时的时辰或刻数。
(1)日晷的指针随着太阳移动指向不同时辰可以看作( )现象。(填“平移”或“旋转”)
(2)日晷表面被平均分成了12格,某刻指针指向酉时,若指针再转6格,指针就指向( )时,此时指针在原来的( )方向。
(3)两个相邻的时辰相隔2小时,若指针从辰时转到申时,代表时间经过了多少小时?
29.在2024年巴黎奥运会上,中国代表团以40枚金牌、27枚银牌、24枚铜牌的优异成绩,位列金牌榜并列第一、奖牌榜第二位,创造了中国境外参加奥运会的历史最佳战绩。
(1)此次奥运会上我国奥运健儿获得的铜牌枚数是银牌总数的几分之几?
(2)此次奥运会上我国奥运健儿获得的金牌枚数是奖牌总数的几分之几?
30.下图是第25~30届奥运会上中国和美国获金牌数量的统计图。
(1)两个国家的奥运会金牌数量是逐年提高的吗?哪一届奥运会上两国金牌数量相差最少?
(2)中国和美国哪个国家金牌数量变化得较平稳?
31.2024年7月30日,我国选手王楚钦和孙颖莎一路“过关斩将”获得中国奥运会乒乓球混双首金。实验小学六(1)班热爱兵乓球的学生们在家观看了比赛,观看比赛的人数是8的倍数,且在60~70人之间。六(1)班观看比赛的学生有多少人?
32.“绿绿粽叶裹吉祥,喜庆佳节又端阳”,端午节是我国传统节日,粽子是端午节必不可少的传统美食。今年端午节来临之际,劳动社团开展了包粽子献爱心活动,一共包了81个白米粽和72个火腿粽,把它们分别装到礼盒中送到福利院,粽子不得混装且要每盒装的数量都相等,每盒最多装几个?
33.2024年的环广西公路自行车世界巡回赛(以下简称“环广西”),路线涉及防城港、崇左、百色、河池、来宾、南宁等6个设区市的19个县(市、区)。王叔叔为参加比赛做了一些训练,如下图,训练场地分三段:从起点到全程的处是平地,从全程的处到全程的处是上坡,其余是下坡。
(1)上坡路程占全程的几分之几?
(2)王叔叔从起点出发,骑了全程的后原地休息,然后又骑了全程的,此时王叔叔在训练场地的哪一路段?(请列式计算说明)
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
第6页,共7页
第7页,共7页
《2024-2025年人教版五年级下册数学期末情境化提升训练》参考答案
1.C
【分析】打电话通知队员时,每分钟通知1人,并且在下一分钟知道演出消息的人再分别通知1人,以此类推就是最快的通知方式。下一分钟知道消息的人数(包含老师)是这分钟的2倍。据此通过例举的方式,解题即可。
【详解】第一分钟通知到1个队员;
第二分钟最多可通知到1+2=3(个)队员;
第三分钟最多可通知到3+4=7(个)队员;
第四分钟最多可通知到7+8=15(个)队员;
第五分钟最多可通知到15+16=31(个)队员。
所以,要通知全体队员至少需要5分钟才能通知到所有人。
故答案为:C
2.B
【分析】观察折线统计图,横轴表示节气,纵轴表示白昼时长,每小格表示1小时;找出各选项中节气对应的白昼时长范围,得出哪个节气的白昼时长超过了13小时,据此解答。
【详解】A.10小时<立春白昼时长<11小时,没有超过13小时,不符合题意;
B.14小时<小暑<15小时,超过13小时,符合题意;
C.12小时<秋分<13小时,没有超过13小时,不符合题意;
D.冬至<10小时,没有超过13小时,不符合题意。
故答案为:B
3.A
【分析】长方形周长=(长+宽)×2,将周长除以2,求出长和宽的和。又因为长和宽都是质数,找出符合题意的长和宽,再根据长方形面积=长×宽,求出停车场的面积。
【详解】36÷2=18(m)
18=5+13
18=11+7
5×13=65(m2)
7×11=77(m2)
65<77
这个指定的长方形停车场的面积最大是77m2。
故答案为:A
4.C
【分析】每次变化需要的时间是2秒钟,10秒可以变化5次,每次拔1根猴毛就能变成1个孙悟空,第1次变出1个,现有孙悟空2个;第2次2个孙悟空一起变出2个,现有孙悟空4个;第3次4个孙悟空一起变出4个,现有孙悟空8个;第4次8个孙悟空一起变出8个,现有孙悟空16个;第5次16个孙悟空一起变出16个,现有孙悟空32个;减去开始的第一个孙悟空,即可求出最多能变出几个孙悟空。
【详解】10÷2=5(次)
2×2×2×2×2-1
=4×2×2×2-1
=8×2×2-1
=16×2-1
=32-1
=31(个)
故答案为:C
【点睛】解决本题的关键找出每次变化的数量规律,注意不能多算或少算。
5.B
【分析】根据题意,大队辅导员想了解全校学生年阅读量情况,要从整个学校的阅读情况出发寻找信息,据此选择。
【详解】学校设立“红领巾交换书屋”鼓励学生课外阅读。4月23日“世界读书日”前夕,大队辅导员想了解全校学生年阅读量情况需要的信息是去年全校人均借阅14.5本。
故答案为:B
【点睛】本题考查了根据需要选择合适的信息的能力。
6. 升/L 立方厘米/cm3 立方厘米/cm3 升/L 毫升/mL
【分析】棱长1厘米的正方体,体积是1立方厘米,大约是1个手指头的大小,1立方厘米=1毫升;棱长1分米的正方体,体积是1立方分米,大约是2个拳头的大小,1立方分米=1升,据此根据容积和体积单位的认识,以及生活经验进行填空。
【详解】壮壮家的冰箱容积是190升,星期六上午他从冰箱中拿出1个体积约为300立方厘米的苹果和3个体积约为120立方厘米的枇杷,将苹果和枇杷放入容积为1.5升的保鲜盒中,再带上1瓶550毫升的矿泉水就和朋友一起去公园玩了。
7.
【分析】求每个中国结用了这根红绳的几分之几,平均分的是单位“1”,求的是分率;求每个中国结用多少米红绳,平均分的是具体的数量5米,求的是具体的数量;都用除法计算。
【详解】1÷8=
5÷8=(米)
每个中国结用了这根红绳的,每个中国结用了m红绳。
8. 5 125
【分析】根据题意,用一根铁丝扎成一个长方体花灯框架,那么这根铁丝的长度就是长方体的棱长总和;根据长方体的棱长总和=(长+宽+高)×4,求出这根铁丝的长度;
再用同样长的铁丝扎成一个正方体花灯框架,那么这根铁丝的长度就是正方体的棱长总和;根据正方体的棱长总和=棱长×12,可得正方体的棱长=棱长总和÷12,据此求出这个正方体的棱长;
给这个正方体花灯框架表面贴上纸片(上面不贴),求至少需要纸片的面积,就是求正方体5个面的面积之和,根据“棱长×棱长×5”,代入数据计算求解。
【详解】铁丝的长度(长方体的棱长总和):
(7+5+3)×4
=15×4
=60(cm)
正方体的棱长:
60÷12=5(cm)
纸片的面积:
5×5×5
=25×5
=125(cm2)
如果用同样长的铁丝扎成一个正方体花灯框架,这个正方体的棱长是(5)cm。军军想给这个正方体花灯框架表面贴上纸片(上面不贴),至少需要(125)cm2的纸片。
9. /0.625
【分析】用一根5米长的红绳正好可以编织8个中国结,把一根红绳的全长看作单位“1”,平均分成8份,用1除以8,即是每个中国结用了这根红绳的几分之几;
用这根红绳的全长除以8,求出每个中国结用了红绳的长度。
【详解】1÷8=
5÷8=(米)
每个中国结用了这根红绳的,每个中国结用了米的红绳。
10.2分米/2dm
【分析】铁丝长度相当于棱长总和,根据正方体棱长总和=棱长×12,长方体的高=棱长总和÷4-长-宽,列式计算即可。
【详解】6×12=72(分米)
72÷4-8-8
=18-8-8
=2(分米)
这个长方体的高是2分米。
11.1932
【分析】一个数,只有1和它本身两个因数,这样的数叫做质数;一个数,除了1和它本身外,还有其它因数,这样的数叫做合数;1既不是质数,也不是合数;最小的质数是2;能被2整除的数叫做偶数,不能被2整除的数叫做奇数;一个数,最小的倍数是它本身,据此分析解答。
【详解】1既不是质数,不是合数,千位上的数是1;
一位数中,最大的奇数是9,百位上的数是9;
3的最小倍数是3,十位上的数是3;
最小的质数是2,个位上的数是2;
中国第一次参加奥运会是1932年。
12.或
【分析】一个数,如果只有1和它本身两个因数,这样的数叫做质数。根据质数的意义,先写出18以内的质数,再从中找出哪两个质数的和是18。
【详解】18以内的质数有2,3,5,7,11,13,17。其中5+13=18,7+11=18。所以18=5+13或18=7+11。
【点睛】明确质数的意义是解决此题的关键。
13.5
【分析】由题意可知,相同距离点的位置同时是10和15的公倍数,先用短除法求出这两个数的最小公倍数,再找出90以内这两个数的公倍数,每只青蛙跳到相同距离点时,都会出现一片荷叶,分别求出甲青蛙和乙青蛙各出现了几次荷叶,最后数出出现荷叶的总次数,据此解答。
【详解】
10和15的最小公倍数:5×2×3=30
30×1=30(厘米)
30×2=60(厘米)
30×3=90(厘米)
乙青蛙:30÷15=2(秒)
60÷15=4(秒)
90÷15=6(秒)
即乙青蛙跳到90厘米这个点位时,共用6秒。乙青蛙第2秒、第4秒、第6秒各出现一次荷叶,共3次;
6秒(含)之内,甲青蛙:30÷10=3(秒)
60÷10=6(秒)
所以,甲青蛙第3秒、第6秒各出现一次荷叶,有2次;
一共出现3+2=5次荷叶。
【点睛】本题主要考查公倍数的应用,根据符合条件的公倍数分别求出两只青蛙出现荷叶的次数是解答题目的关键。
14. 68 144 135
【分析】长方体的棱长之和=(长+宽+高)×4,把图中数据代入公式求出需要木条的长度;长方体的表面积=(长×宽+宽×高+长×高)×2,计算需要彩纸的面积就是求长方体的表面积,但是只需计算四个侧面的面积即可;长方体的体积=长×宽×高,把图中数据代入公式求出这个花灯的体积,据此解答。
【详解】(3+5+9)×4
=17×4
=68(分米)
(3×9+5×9)×2
=(27+45)×2
=72×2
=144(平方分米)
3×5×9
=15×9
=135(立方分米)
所以,制作框架至少需要准备68分米长的木条,再把四个侧面贴上彩纸,至少需要144平方分米的彩纸,这个花灯的体积是135立方分米。
15. 3 /0.875
【分析】由题意可知,将这根木棍的长度看成单位“1”,第一天截取全长的,剩下全长的1-=;第二天截取全长的÷2=。剩下全长的-=;第三天截取全长的÷2=;即把总长度看作单位“1”,平均分成8份,第三天截取的长度占其中的一份,据此求出第三日截取的长度是多少分米;再把这三日截取的长度分率相加,求出这三日截取的长度占总长度的分率,把单位“1”平均分成若干份,表示其中一份的数叫分数单位,据此解答。
【详解】1-=
第二天截取全长的:÷2
=×
=
剩下全长的-=
第三天截取全长的÷2
=×
=
24÷8=3(分米)
++
=+
=
所以第三日截取的长度是3分米,这三日截取的长度占总长度的,它的分数单位是。
16.2
【分析】找次品的最优策略:一是把待测物品分成3份;二是要尽量平均分,不能平均分的,应该使多的一份与少的一份只相差1。这样不但能保证找出次品,而且称的次数一定最少。据此解答。
【详解】买中药9服,其中一服中药少放了一味药,比其它略轻。先分成(3,3,3)三份。
第一次称重:天平两边各放3服药,若天平平衡,则少一味药的那服中药在剩下的3服药中;若天平不平衡,则少一味药的那服中药在较轻的3服药中;
第二次称重:将含有少一味药的那服中药的那3服药,天平两边各放1服,若天平不平衡,则少一味药的那服中药就是较轻的那个;则若天平平衡,则剩下的那1服就是少一味药的那服中药。
买中药9服,每服药共计重200g。但由于药师的疏忽,其中一服中药少放了一味药,用天平至少称2次,才能保证找到这服中药。
17.1290
【分析】质数是因数只有1和它本身的数;合数是因数除了1和它本身之外还有其他因数的数;不是2的倍数的数是奇数,据此分析。
【详解】既不是质数也不是合数的数是1,2是最小的质数也是唯一的偶质数,10以内的是奇数又是合数的数是9,最小的自然数是0。
所以这个四位数的手机密码是:1290。
【点睛】此题考查质数合数以及奇数偶数的应用,掌握这些数的特点是解题的关键。
18.×
【分析】钟表上分针转1小格,秒针转60小格,据此判断。
【详解】1÷60=
钟表上分针转动的速度是秒针的。
原题干说法错误。
故答案为:×
19.×
【分析】条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图能反映部分与整体的关系;据此判断。
【详解】为清楚地比较上海和北京两城市去年各月平均气温的变化情况,最合适的是用折线统计图表示。
原题说法错误。
故答案为:×
20.√
【分析】如果一个大的正方体每条棱上有n个(n≥3)小正方体,则两面涂色的小正方体位于棱上,每条棱上有(n-2)个,共有(n-2)×12个。已知两面涂色的小正方体有24个,据此列出方程,求出大正方体每条棱上小正方体的个数,再根据正方体的体积公式V=a3,求出大正方体的体积。
【详解】解:设大正方体每条棱上有n个小正方体。
(n-2)×12=24
(n-2)×12÷12=24÷12
n-2=2
n-2+2=2+2
n=4
正方体的体积:4×4×4=64(立方厘米)
这个正方体的体积是64立方厘米。
原题说法正确。
故答案为:√
21.×
【分析】根据从正面看到的形状可知,这个立体图形有2层,从上面看到的形状可知,底层有4个,前后排分别有2个;上层有至少有1个。据此解答。
【详解】4+1=5(个)
根据分析可知,一个立体图形,从上面看到的形状是,从正面看到的形状是,搭成这样的立体图形,至少需要5个小正方体。所以原题说法错误。
故答案为:×
22.×
【分析】结合生活实际可知,1盒牛奶大约是250毫升,1桶食用油是5升,1升=1000毫升,据此结合容积单位和数据大小解答即可。
【详解】根据分析可知,家庭用燃油小轿车油箱的容积大约是50L,原题说法错误。
故答案为:×
23.4.3;3.6;0.72;0.8
;;;2
【详解】略
24.;10;1
【分析】-(-),先计算括号里的减法,再计算括号外的减法;
4.56++5.44-,根据加法交换律,原式化为:4.56+5.44+-,再根据加法结合律,原式化为:(4.56+5.44)+(-),再进行计算;
-+-,根据带符号搬家,原式化为:+--,再根据加法结合律和减法性质,原式化为:(+)-(+),再进行计算。
【详解】-(-)
=-(-)
=-
=-
=
4.56++5.44-
=4.56+5.44+-
=(4.56+5.44)+(-)
=10+0
=10
-+-
=+--
=(+)-(+)
=2-1
=1
25.x=;x=4.9;x=3
【分析】(1)利用等式的性质1,方程两边同时减去;
(2)先利用等式的性质1,方程两边同时加上4.5,再利用等式的性质2,方程两边同时除以3;
(3)先利用等式的性质2,方程两边同时除以2,再利用等式的性质1,方程两边同时减去1.8。
【详解】(1)x+=
解:x+-=-
x=
(2)3x-4.5=10.2
解:3x-4.5+4.5=10.2+4.5
3x=14.7
3x÷3=14.7÷3
x=4.9
(3)2(x+1.8)=9.6
解:2(x+1.8)÷2=9.6÷2
x+1.8=4.8
x+1.8-1.8=4.8-1.8
x=3
26.(1)表面积486cm2;体积729cm3;
(2)表面积62cm2;体积27cm3
【分析】(1)从图中可知,正方体的底面积是81cm2,因为正方体的6个面都是相同的正方形,根据正方形的面积=边长×边长,由此得出正方体的棱长;
根据正方体的表面积公式S=6a2,正方体的体积公式V=Sh,代入数据计算,求出它的表面积和体积。
(2)从图中可知,大长方体的右上角挖掉了一个小长方体,露出了3个面,这3个面向外平移,正好把长方体的表面补全,根据长方体的表面积公式S=2(ab+ah+bh),求出组合体的表面积;
组合体的体积=大长方体的体积-小长方体的体积,根据长方体的体积公式V=abh,求出组合体的体积。
【详解】(1)81=9×9,所以正方体的棱长是9cm;
正方体的表面积:81×6=486(cm2)
正方体的体积:81×9=729(cm3)
正方体的表面积是486cm2,体积是729cm3。
(2)组合体的表面积:
(5×2+5×3+2×3)×2
=(10+15+6)×2
=31×2
=62(cm2)
组合体的体积:
5×2×3-1.5×1×2
=30-3
=27(cm3)
组合体的表面积是62cm2,体积是27cm3。
27.39平方米或55平方米
【分析】根据长方形的周长=(长+宽)×2,可知长方形的长、宽之和=周长÷2,据此求出这个长方形停车场长、宽之和;
再根据质数的意义找出哪两个质数之和等于长、宽之和,那么这两个质数分别是长方形的长、宽;最后根据长方形的面积=长×宽,求出这个停车场的面积。
【详解】长、宽之和:32÷2=16(米)
16=3+13=5+11
13×3=39(平方米)
11×5=55(平方米)
答:这个长方形停车场的面积是39平方米或55平方米。
28.(1)旋转(2)卯;正东(3)8小时
【详解】(1)旋转:将图形绕某个点或某条线作圆周运动。这个点叫做旋转中心,图形转动的角度叫做旋转角,其中对应点到旋转中心的距离相等,对应线段的长度、对应角的大小相等,旋转前后图形的形状、大小不变;
(2)指针指向西时是指向酉时,看图可知指针是顺时针旋转,所以再转6格,指针就指向卯时;根据图上方向上北下南,左西右东可知,此时指针在原来的正东方向;
(3)由题意可得:经过的格数×每相邻两个时辰相隔的时间=经过的时间,据此可以解答。
【解答】(1)日晷的指针随着太阳移动指向不同时辰可以看作旋转现象;
(2)日晷表面被平均分成了12格,某刻指针指向酉时,若指针再转6格,指针就指向卯时,此时指针在原来的正东方向。
(3)指针从辰时转到申时经过了4格
4×2=8(小时)
答:代表时间经过了8小时。
29.(1)
(2)
【分析】(1)用奥运会上我国奥运健儿获得的铜牌枚数除以银牌总数,求出此次奥运会上我国奥运健儿获得的铜牌枚数是银牌总数的几分之几。
(2)先用加法求出奖牌总数,再用奥运会上我国奥运健儿获得的金牌枚数除以奖牌总数,求出此次奥运会上我国奥运健儿获得的金牌枚数是奖牌总数的几分之几。
【详解】(1)24÷27=
答:此次奥运会上我国奥运健儿获得的铜牌枚数是银牌总数的。
(2)40÷(40+24+27)
=40÷91
=
答:此次奥运会上我国奥运健儿获得的金牌枚数是奖牌总数的。
30.(1)不是;第28届
(2)美国
【分析】(1)观察复式折线统计图,两条折线有升有降,所以不是逐年提高。
两条折线的叉口最小时,说明这一届奥运会上两国金牌数量相差最少。
(2)观察统计图中两条折线的变化趋势,虚线起伏比较大,实线比较平稳,据此解答。
【详解】(1)两个国家的奥运会金牌数量都不是逐年提高的,第28届奥运会上两国金牌数量相差最少。
(2)美国金牌数量变化得较平稳。
31.64人
【分析】列乘法算式找倍数,按照从小到大的顺序,一组一组地写出这个数与非0自然数的乘法算式,乘法算式中的积就是这个数的倍数。据此找到60~70之间8的倍数即可。
【详解】8×1=8
8×2=16
8×3=24
8×4=32
8×5=40
8×6=48
8×7=56
8×8=64
60~70之间8的倍数是64。
答:六(1)班观看比赛的学生有64人。
32.9个
【分析】求出81和72的最大公因数,,就是每盒装的最多个数。全部共有的质因数(公有质因数))相乘的积就是这几个数的最大公因数。
【详解】81=3×3×3×3
72=2×2×2×3×3
81和72的最大公因数是3×3=9。
答:每盒最多装9个。
33.(1)
(2)下坡训练地段
【分析】(1)用全程的减去平地占全程的,即可求出上坡路程占全程的分率;
(2)先用+,求出王叔叔骑了全程的分率,再和各路段占的分率进行比较,即可求出王叔叔在训练地的哪一路段。
【详解】(1)-
=-
=
答:上坡路占全程的。
(2)+
=+
=
>,王叔叔在训练地的下坡路段。
答:王叔叔在训练地的下坡路段。
答案第2页,共15页
答案第15页,共15页
中小学教育资源及组卷应用平台
2024-2025年人教版五年级下册数学期末情境化提升训练
一、选择题
1.红光小学鼓号队有31人,暑假期间有一个紧急演出,李老师需要尽快通知到每个队员。如果用打电话的方式,每分钟通知1人,每个同学接到电话后又打给其它同学,同时李老师也在不停的打,要通知全体队员至少需要_____分钟才能通知到所有人。( )
A.7 B.6 C.5 D.4
2.二十四节气是中国古代劳动人民长期经验积累的结晶,它与白昼时长密切相关。春分,秋分时,昼夜时长大致相等。夏至时,白昼时长最长。如图是一年中部分节气所对应的白昼时长示意图。在下列四个节气中,( )的白昼时长超过了13小时。
A.立春 B.小暑 C.秋分 D.冬至
3.为了规范共享单车、助力车的摆放,整体提升城市形象,城市管理部门在公共区域画了一个长方形地作为专用停车场,规划好后发现长和宽都是质数,并且周长是36m,这个指定的长方形停车场的面积最大是( )。
A. B. C. D.
4.《西游记》是我国四大名著之一,书中的孙悟空去西天取经的路上遇到妖精,每次拔一根猴毛就能变成一个孙悟空,变出的孙悟空也能每次拔一根猴毛变成一个孙悟空,每次变化需要的时间是2秒钟,10秒钟最多能变出( )个孙悟空。
A.15 B.32 C.31 D.60
5.学校设立“红领巾交换书屋”鼓励学生课外阅读。4月23日“世界读书日”前夕,大队辅导员想了解全校学生年阅读量情况,以下四位同学介绍的关于书屋的信息对他最有帮助的是( )。
A.小东:602班去年一共借阅1000本 B.小红:去年全校人均借阅14.5本
C.小力:周一借出1256本 D.小君:我上周借阅了3本
二、填空题
6.在括号里填上合适的体积或容积单位。
壮壮家的冰箱容积是190( ),星期六上午他从冰箱中拿出1个体积约为300( )的苹果和3个体积约为120( )的枇杷,将苹果和枇杷放入容积为1.5( )的保鲜盒中,再带上1瓶550( )的矿泉水就和朋友一起去公园玩了。
7.中国结是中国特有的民间手工编结艺术,它以其独特的东方神韵、丰富多彩的变化,充分体现了中国人民的智慧和深厚的文化底蕴。用一根5m长的红绳正好可以编织8个同样的中国结。每个中国结用了这根红绳的( ),每个中国结用了( )m红绳。
8.火树银花元夕夜,彩灯万盏增霞流。为弘扬传统文化,元宵节前夕军军和同学们用一根铁丝扎成一个长7cm,宽5cm,高3cm的长方体花灯框架。如果用同样长的铁丝扎成一个正方体花灯框架,这个正方体的棱长是( )cm。军军想给这个正方体花灯框架表面贴上纸片(上面不贴),至少需要( )cm2的纸片。
9.中国结是一种具有中国特色的手工编织工艺品,它代表着团结、吉祥和平安,深受人们的喜爱。用一根5米长的红绳正好可以编织8个中国结,每个中国结用了这根红绳的( ),每个中国结用了( )米的红绳。
10.街道人员制作一批灯笼庆祝“建军节”,先用一根长铁丝制作了一个棱长为6分米的正方体灯笼框架(铁丝刚好用完无剩余)。如果用同样长度的铁丝另外制作一个长方体灯笼框架,长、宽都为8分米,那么这个长方体的高是( )。
11.同学们,你们知道吗?中国第一次参加奥运会的年份是一个四位数。这个四位数千位上的数既不是质数也不是合数,百位上的数是一位数中最大的奇数,十位上的数的最小倍数是3,个位上的数是最小的质数。中国第一次参加奥运会是( )年。
12.哥德巴赫猜想被称为“数学皇冠上的明珠”,中国20世纪三十年代就开始着手这一研究。新中国成立后,我国数学家陈景润在这一领域取得了举世瞩目的成果。这一猜想是:所有大于2的偶数,可以表示为两个质数的和,如:,。照这样想:18=( )。
13.编程兴趣小组制作了一款“青蛙跳跳跳”的游戏。游戏设定,甲、乙两只青蛙同时从起点开始跳跃,每秒跳1次。甲青蛙每次跳10厘米,乙青蛙每次跳15厘米,两只青蛙都能跳到的点位称为相同距离点。每只青蛙跳到相同距离点时,这个点位都会出现一片荷叶,跳离这个点位时,荷叶就会消失。当乙青蛙跳到90厘米这个点位时,电脑一共出现了( )次荷叶。
14.做“花灯”是一种富有文化意义的传统手工艺,苹苹准备做一个长方体花灯,如图所示。先做框架,制作框架至少需要准备( )分米长的木条;再把四个侧面贴上彩纸,至少需要( )平方分米的彩纸;最后把上、下两面用盖子封上,这个花灯的体积是( )立方分米。
15.《庄子·天下首》中有述:“一尺之棰,日取其半,万此不竭”!意思是·尺长的棍棒,今日截取它的一半,即一,明日取它一半的一半……永远也截不完。按照这样的方法,如果木棒长24分米,第三日截取的长度是( )分米,这三日截取的长度占总长度的( ),它的分数单位是( )。
16.中医是我国的瑰宝,中药学是我国古代优秀文化遗产的重要组成部分。奶奶因病案到中药馆买中药9服,每服药共计重200g。但由于药师的疏忽,其中一服中药少放了一味药,用天平至少称( )次,才能保证找到这服中药。
17.一个四位数的手机屏幕解锁密码提示:它的最高位上的数既不是质数也不是合数,第二个数字既是偶数又是质数,第三个数字既是奇数也是合数,个位上的数是最小的自然数,这个四位数的手机解锁密码是( )。
三、判断题
18.钟表上分针转动的速度是秒针的。( )
19.为清楚地比较上海和北京两城市去年各月平均气温的变化情况,最合适的是用扇形统计图来表示。( )
20.一个正方体,先在它每个面上涂上红色,再把它切成棱长是1厘米的小正方体,如果两面涂色的小正方体有24个,那么这个正方体的体积是64立方厘米。( )
21.一个立体图形,从上面看到的形状是,从正面看到的形状是,搭成这样的立体图形,至少需要6个小正方体。( )
22.家庭用燃油小轿车油箱的容积大约是50mL。( )
四、计算题
23.直接写出得数。
3.6+0.7= 4-0.4= 2.4×0.3= 0.48÷0.6=
24.怎样简便怎样算。
25.解方程。
x+= 3x-4.5=10.2 2(x+1.8)=9.6
26.计算下面图形的表面积和体积。
五、解答题
27.为了规范共享单车的摆放,整体提升城市形象某城市管理部门在公共区域指定了一个长方形场地作为专用停车场。规划后发现这个场地的长和宽的数值正好都是质数,并且周长是32米,这个长方形停车场的面积是多少平方米?
28.日晷是我国古代的计时仪器,主要是根据日影的位置,以指定当时的时辰或刻数。
(1)日晷的指针随着太阳移动指向不同时辰可以看作( )现象。(填“平移”或“旋转”)
(2)日晷表面被平均分成了12格,某刻指针指向酉时,若指针再转6格,指针就指向( )时,此时指针在原来的( )方向。
(3)两个相邻的时辰相隔2小时,若指针从辰时转到申时,代表时间经过了多少小时?
29.在2024年巴黎奥运会上,中国代表团以40枚金牌、27枚银牌、24枚铜牌的优异成绩,位列金牌榜并列第一、奖牌榜第二位,创造了中国境外参加奥运会的历史最佳战绩。
(1)此次奥运会上我国奥运健儿获得的铜牌枚数是银牌总数的几分之几?
(2)此次奥运会上我国奥运健儿获得的金牌枚数是奖牌总数的几分之几?
30.下图是第25~30届奥运会上中国和美国获金牌数量的统计图。
(1)两个国家的奥运会金牌数量是逐年提高的吗?哪一届奥运会上两国金牌数量相差最少?
(2)中国和美国哪个国家金牌数量变化得较平稳?
31.2024年7月30日,我国选手王楚钦和孙颖莎一路“过关斩将”获得中国奥运会乒乓球混双首金。实验小学六(1)班热爱兵乓球的学生们在家观看了比赛,观看比赛的人数是8的倍数,且在60~70人之间。六(1)班观看比赛的学生有多少人?
32.“绿绿粽叶裹吉祥,喜庆佳节又端阳”,端午节是我国传统节日,粽子是端午节必不可少的传统美食。今年端午节来临之际,劳动社团开展了包粽子献爱心活动,一共包了81个白米粽和72个火腿粽,把它们分别装到礼盒中送到福利院,粽子不得混装且要每盒装的数量都相等,每盒最多装几个?
33.2024年的环广西公路自行车世界巡回赛(以下简称“环广西”),路线涉及防城港、崇左、百色、河池、来宾、南宁等6个设区市的19个县(市、区)。王叔叔为参加比赛做了一些训练,如下图,训练场地分三段:从起点到全程的处是平地,从全程的处到全程的处是上坡,其余是下坡。
(1)上坡路程占全程的几分之几?
(2)王叔叔从起点出发,骑了全程的后原地休息,然后又骑了全程的,此时王叔叔在训练场地的哪一路段?(请列式计算说明)
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
第6页,共7页
第7页,共7页
《2024-2025年人教版五年级下册数学期末情境化提升训练》参考答案
1.C
【分析】打电话通知队员时,每分钟通知1人,并且在下一分钟知道演出消息的人再分别通知1人,以此类推就是最快的通知方式。下一分钟知道消息的人数(包含老师)是这分钟的2倍。据此通过例举的方式,解题即可。
【详解】第一分钟通知到1个队员;
第二分钟最多可通知到1+2=3(个)队员;
第三分钟最多可通知到3+4=7(个)队员;
第四分钟最多可通知到7+8=15(个)队员;
第五分钟最多可通知到15+16=31(个)队员。
所以,要通知全体队员至少需要5分钟才能通知到所有人。
故答案为:C
2.B
【分析】观察折线统计图,横轴表示节气,纵轴表示白昼时长,每小格表示1小时;找出各选项中节气对应的白昼时长范围,得出哪个节气的白昼时长超过了13小时,据此解答。
【详解】A.10小时<立春白昼时长<11小时,没有超过13小时,不符合题意;
B.14小时<小暑<15小时,超过13小时,符合题意;
C.12小时<秋分<13小时,没有超过13小时,不符合题意;
D.冬至<10小时,没有超过13小时,不符合题意。
故答案为:B
3.A
【分析】长方形周长=(长+宽)×2,将周长除以2,求出长和宽的和。又因为长和宽都是质数,找出符合题意的长和宽,再根据长方形面积=长×宽,求出停车场的面积。
【详解】36÷2=18(m)
18=5+13
18=11+7
5×13=65(m2)
7×11=77(m2)
65<77
这个指定的长方形停车场的面积最大是77m2。
故答案为:A
4.C
【分析】每次变化需要的时间是2秒钟,10秒可以变化5次,每次拔1根猴毛就能变成1个孙悟空,第1次变出1个,现有孙悟空2个;第2次2个孙悟空一起变出2个,现有孙悟空4个;第3次4个孙悟空一起变出4个,现有孙悟空8个;第4次8个孙悟空一起变出8个,现有孙悟空16个;第5次16个孙悟空一起变出16个,现有孙悟空32个;减去开始的第一个孙悟空,即可求出最多能变出几个孙悟空。
【详解】10÷2=5(次)
2×2×2×2×2-1
=4×2×2×2-1
=8×2×2-1
=16×2-1
=32-1
=31(个)
故答案为:C
【点睛】解决本题的关键找出每次变化的数量规律,注意不能多算或少算。
5.B
【分析】根据题意,大队辅导员想了解全校学生年阅读量情况,要从整个学校的阅读情况出发寻找信息,据此选择。
【详解】学校设立“红领巾交换书屋”鼓励学生课外阅读。4月23日“世界读书日”前夕,大队辅导员想了解全校学生年阅读量情况需要的信息是去年全校人均借阅14.5本。
故答案为:B
【点睛】本题考查了根据需要选择合适的信息的能力。
6. 升/L 立方厘米/cm3 立方厘米/cm3 升/L 毫升/mL
【分析】棱长1厘米的正方体,体积是1立方厘米,大约是1个手指头的大小,1立方厘米=1毫升;棱长1分米的正方体,体积是1立方分米,大约是2个拳头的大小,1立方分米=1升,据此根据容积和体积单位的认识,以及生活经验进行填空。
【详解】壮壮家的冰箱容积是190升,星期六上午他从冰箱中拿出1个体积约为300立方厘米的苹果和3个体积约为120立方厘米的枇杷,将苹果和枇杷放入容积为1.5升的保鲜盒中,再带上1瓶550毫升的矿泉水就和朋友一起去公园玩了。
7.
【分析】求每个中国结用了这根红绳的几分之几,平均分的是单位“1”,求的是分率;求每个中国结用多少米红绳,平均分的是具体的数量5米,求的是具体的数量;都用除法计算。
【详解】1÷8=
5÷8=(米)
每个中国结用了这根红绳的,每个中国结用了m红绳。
8. 5 125
【分析】根据题意,用一根铁丝扎成一个长方体花灯框架,那么这根铁丝的长度就是长方体的棱长总和;根据长方体的棱长总和=(长+宽+高)×4,求出这根铁丝的长度;
再用同样长的铁丝扎成一个正方体花灯框架,那么这根铁丝的长度就是正方体的棱长总和;根据正方体的棱长总和=棱长×12,可得正方体的棱长=棱长总和÷12,据此求出这个正方体的棱长;
给这个正方体花灯框架表面贴上纸片(上面不贴),求至少需要纸片的面积,就是求正方体5个面的面积之和,根据“棱长×棱长×5”,代入数据计算求解。
【详解】铁丝的长度(长方体的棱长总和):
(7+5+3)×4
=15×4
=60(cm)
正方体的棱长:
60÷12=5(cm)
纸片的面积:
5×5×5
=25×5
=125(cm2)
如果用同样长的铁丝扎成一个正方体花灯框架,这个正方体的棱长是(5)cm。军军想给这个正方体花灯框架表面贴上纸片(上面不贴),至少需要(125)cm2的纸片。
9. /0.625
【分析】用一根5米长的红绳正好可以编织8个中国结,把一根红绳的全长看作单位“1”,平均分成8份,用1除以8,即是每个中国结用了这根红绳的几分之几;
用这根红绳的全长除以8,求出每个中国结用了红绳的长度。
【详解】1÷8=
5÷8=(米)
每个中国结用了这根红绳的,每个中国结用了米的红绳。
10.2分米/2dm
【分析】铁丝长度相当于棱长总和,根据正方体棱长总和=棱长×12,长方体的高=棱长总和÷4-长-宽,列式计算即可。
【详解】6×12=72(分米)
72÷4-8-8
=18-8-8
=2(分米)
这个长方体的高是2分米。
11.1932
【分析】一个数,只有1和它本身两个因数,这样的数叫做质数;一个数,除了1和它本身外,还有其它因数,这样的数叫做合数;1既不是质数,也不是合数;最小的质数是2;能被2整除的数叫做偶数,不能被2整除的数叫做奇数;一个数,最小的倍数是它本身,据此分析解答。
【详解】1既不是质数,不是合数,千位上的数是1;
一位数中,最大的奇数是9,百位上的数是9;
3的最小倍数是3,十位上的数是3;
最小的质数是2,个位上的数是2;
中国第一次参加奥运会是1932年。
12.或
【分析】一个数,如果只有1和它本身两个因数,这样的数叫做质数。根据质数的意义,先写出18以内的质数,再从中找出哪两个质数的和是18。
【详解】18以内的质数有2,3,5,7,11,13,17。其中5+13=18,7+11=18。所以18=5+13或18=7+11。
【点睛】明确质数的意义是解决此题的关键。
13.5
【分析】由题意可知,相同距离点的位置同时是10和15的公倍数,先用短除法求出这两个数的最小公倍数,再找出90以内这两个数的公倍数,每只青蛙跳到相同距离点时,都会出现一片荷叶,分别求出甲青蛙和乙青蛙各出现了几次荷叶,最后数出出现荷叶的总次数,据此解答。
【详解】
10和15的最小公倍数:5×2×3=30
30×1=30(厘米)
30×2=60(厘米)
30×3=90(厘米)
乙青蛙:30÷15=2(秒)
60÷15=4(秒)
90÷15=6(秒)
即乙青蛙跳到90厘米这个点位时,共用6秒。乙青蛙第2秒、第4秒、第6秒各出现一次荷叶,共3次;
6秒(含)之内,甲青蛙:30÷10=3(秒)
60÷10=6(秒)
所以,甲青蛙第3秒、第6秒各出现一次荷叶,有2次;
一共出现3+2=5次荷叶。
【点睛】本题主要考查公倍数的应用,根据符合条件的公倍数分别求出两只青蛙出现荷叶的次数是解答题目的关键。
14. 68 144 135
【分析】长方体的棱长之和=(长+宽+高)×4,把图中数据代入公式求出需要木条的长度;长方体的表面积=(长×宽+宽×高+长×高)×2,计算需要彩纸的面积就是求长方体的表面积,但是只需计算四个侧面的面积即可;长方体的体积=长×宽×高,把图中数据代入公式求出这个花灯的体积,据此解答。
【详解】(3+5+9)×4
=17×4
=68(分米)
(3×9+5×9)×2
=(27+45)×2
=72×2
=144(平方分米)
3×5×9
=15×9
=135(立方分米)
所以,制作框架至少需要准备68分米长的木条,再把四个侧面贴上彩纸,至少需要144平方分米的彩纸,这个花灯的体积是135立方分米。
15. 3 /0.875
【分析】由题意可知,将这根木棍的长度看成单位“1”,第一天截取全长的,剩下全长的1-=;第二天截取全长的÷2=。剩下全长的-=;第三天截取全长的÷2=;即把总长度看作单位“1”,平均分成8份,第三天截取的长度占其中的一份,据此求出第三日截取的长度是多少分米;再把这三日截取的长度分率相加,求出这三日截取的长度占总长度的分率,把单位“1”平均分成若干份,表示其中一份的数叫分数单位,据此解答。
【详解】1-=
第二天截取全长的:÷2
=×
=
剩下全长的-=
第三天截取全长的÷2
=×
=
24÷8=3(分米)
++
=+
=
所以第三日截取的长度是3分米,这三日截取的长度占总长度的,它的分数单位是。
16.2
【分析】找次品的最优策略:一是把待测物品分成3份;二是要尽量平均分,不能平均分的,应该使多的一份与少的一份只相差1。这样不但能保证找出次品,而且称的次数一定最少。据此解答。
【详解】买中药9服,其中一服中药少放了一味药,比其它略轻。先分成(3,3,3)三份。
第一次称重:天平两边各放3服药,若天平平衡,则少一味药的那服中药在剩下的3服药中;若天平不平衡,则少一味药的那服中药在较轻的3服药中;
第二次称重:将含有少一味药的那服中药的那3服药,天平两边各放1服,若天平不平衡,则少一味药的那服中药就是较轻的那个;则若天平平衡,则剩下的那1服就是少一味药的那服中药。
买中药9服,每服药共计重200g。但由于药师的疏忽,其中一服中药少放了一味药,用天平至少称2次,才能保证找到这服中药。
17.1290
【分析】质数是因数只有1和它本身的数;合数是因数除了1和它本身之外还有其他因数的数;不是2的倍数的数是奇数,据此分析。
【详解】既不是质数也不是合数的数是1,2是最小的质数也是唯一的偶质数,10以内的是奇数又是合数的数是9,最小的自然数是0。
所以这个四位数的手机密码是:1290。
【点睛】此题考查质数合数以及奇数偶数的应用,掌握这些数的特点是解题的关键。
18.×
【分析】钟表上分针转1小格,秒针转60小格,据此判断。
【详解】1÷60=
钟表上分针转动的速度是秒针的。
原题干说法错误。
故答案为:×
19.×
【分析】条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图能反映部分与整体的关系;据此判断。
【详解】为清楚地比较上海和北京两城市去年各月平均气温的变化情况,最合适的是用折线统计图表示。
原题说法错误。
故答案为:×
20.√
【分析】如果一个大的正方体每条棱上有n个(n≥3)小正方体,则两面涂色的小正方体位于棱上,每条棱上有(n-2)个,共有(n-2)×12个。已知两面涂色的小正方体有24个,据此列出方程,求出大正方体每条棱上小正方体的个数,再根据正方体的体积公式V=a3,求出大正方体的体积。
【详解】解:设大正方体每条棱上有n个小正方体。
(n-2)×12=24
(n-2)×12÷12=24÷12
n-2=2
n-2+2=2+2
n=4
正方体的体积:4×4×4=64(立方厘米)
这个正方体的体积是64立方厘米。
原题说法正确。
故答案为:√
21.×
【分析】根据从正面看到的形状可知,这个立体图形有2层,从上面看到的形状可知,底层有4个,前后排分别有2个;上层有至少有1个。据此解答。
【详解】4+1=5(个)
根据分析可知,一个立体图形,从上面看到的形状是,从正面看到的形状是,搭成这样的立体图形,至少需要5个小正方体。所以原题说法错误。
故答案为:×
22.×
【分析】结合生活实际可知,1盒牛奶大约是250毫升,1桶食用油是5升,1升=1000毫升,据此结合容积单位和数据大小解答即可。
【详解】根据分析可知,家庭用燃油小轿车油箱的容积大约是50L,原题说法错误。
故答案为:×
23.4.3;3.6;0.72;0.8
;;;2
【详解】略
24.;10;1
【分析】-(-),先计算括号里的减法,再计算括号外的减法;
4.56++5.44-,根据加法交换律,原式化为:4.56+5.44+-,再根据加法结合律,原式化为:(4.56+5.44)+(-),再进行计算;
-+-,根据带符号搬家,原式化为:+--,再根据加法结合律和减法性质,原式化为:(+)-(+),再进行计算。
【详解】-(-)
=-(-)
=-
=-
=
4.56++5.44-
=4.56+5.44+-
=(4.56+5.44)+(-)
=10+0
=10
-+-
=+--
=(+)-(+)
=2-1
=1
25.x=;x=4.9;x=3
【分析】(1)利用等式的性质1,方程两边同时减去;
(2)先利用等式的性质1,方程两边同时加上4.5,再利用等式的性质2,方程两边同时除以3;
(3)先利用等式的性质2,方程两边同时除以2,再利用等式的性质1,方程两边同时减去1.8。
【详解】(1)x+=
解:x+-=-
x=
(2)3x-4.5=10.2
解:3x-4.5+4.5=10.2+4.5
3x=14.7
3x÷3=14.7÷3
x=4.9
(3)2(x+1.8)=9.6
解:2(x+1.8)÷2=9.6÷2
x+1.8=4.8
x+1.8-1.8=4.8-1.8
x=3
26.(1)表面积486cm2;体积729cm3;
(2)表面积62cm2;体积27cm3
【分析】(1)从图中可知,正方体的底面积是81cm2,因为正方体的6个面都是相同的正方形,根据正方形的面积=边长×边长,由此得出正方体的棱长;
根据正方体的表面积公式S=6a2,正方体的体积公式V=Sh,代入数据计算,求出它的表面积和体积。
(2)从图中可知,大长方体的右上角挖掉了一个小长方体,露出了3个面,这3个面向外平移,正好把长方体的表面补全,根据长方体的表面积公式S=2(ab+ah+bh),求出组合体的表面积;
组合体的体积=大长方体的体积-小长方体的体积,根据长方体的体积公式V=abh,求出组合体的体积。
【详解】(1)81=9×9,所以正方体的棱长是9cm;
正方体的表面积:81×6=486(cm2)
正方体的体积:81×9=729(cm3)
正方体的表面积是486cm2,体积是729cm3。
(2)组合体的表面积:
(5×2+5×3+2×3)×2
=(10+15+6)×2
=31×2
=62(cm2)
组合体的体积:
5×2×3-1.5×1×2
=30-3
=27(cm3)
组合体的表面积是62cm2,体积是27cm3。
27.39平方米或55平方米
【分析】根据长方形的周长=(长+宽)×2,可知长方形的长、宽之和=周长÷2,据此求出这个长方形停车场长、宽之和;
再根据质数的意义找出哪两个质数之和等于长、宽之和,那么这两个质数分别是长方形的长、宽;最后根据长方形的面积=长×宽,求出这个停车场的面积。
【详解】长、宽之和:32÷2=16(米)
16=3+13=5+11
13×3=39(平方米)
11×5=55(平方米)
答:这个长方形停车场的面积是39平方米或55平方米。
28.(1)旋转(2)卯;正东(3)8小时
【详解】(1)旋转:将图形绕某个点或某条线作圆周运动。这个点叫做旋转中心,图形转动的角度叫做旋转角,其中对应点到旋转中心的距离相等,对应线段的长度、对应角的大小相等,旋转前后图形的形状、大小不变;
(2)指针指向西时是指向酉时,看图可知指针是顺时针旋转,所以再转6格,指针就指向卯时;根据图上方向上北下南,左西右东可知,此时指针在原来的正东方向;
(3)由题意可得:经过的格数×每相邻两个时辰相隔的时间=经过的时间,据此可以解答。
【解答】(1)日晷的指针随着太阳移动指向不同时辰可以看作旋转现象;
(2)日晷表面被平均分成了12格,某刻指针指向酉时,若指针再转6格,指针就指向卯时,此时指针在原来的正东方向。
(3)指针从辰时转到申时经过了4格
4×2=8(小时)
答:代表时间经过了8小时。
29.(1)
(2)
【分析】(1)用奥运会上我国奥运健儿获得的铜牌枚数除以银牌总数,求出此次奥运会上我国奥运健儿获得的铜牌枚数是银牌总数的几分之几。
(2)先用加法求出奖牌总数,再用奥运会上我国奥运健儿获得的金牌枚数除以奖牌总数,求出此次奥运会上我国奥运健儿获得的金牌枚数是奖牌总数的几分之几。
【详解】(1)24÷27=
答:此次奥运会上我国奥运健儿获得的铜牌枚数是银牌总数的。
(2)40÷(40+24+27)
=40÷91
=
答:此次奥运会上我国奥运健儿获得的金牌枚数是奖牌总数的。
30.(1)不是;第28届
(2)美国
【分析】(1)观察复式折线统计图,两条折线有升有降,所以不是逐年提高。
两条折线的叉口最小时,说明这一届奥运会上两国金牌数量相差最少。
(2)观察统计图中两条折线的变化趋势,虚线起伏比较大,实线比较平稳,据此解答。
【详解】(1)两个国家的奥运会金牌数量都不是逐年提高的,第28届奥运会上两国金牌数量相差最少。
(2)美国金牌数量变化得较平稳。
31.64人
【分析】列乘法算式找倍数,按照从小到大的顺序,一组一组地写出这个数与非0自然数的乘法算式,乘法算式中的积就是这个数的倍数。据此找到60~70之间8的倍数即可。
【详解】8×1=8
8×2=16
8×3=24
8×4=32
8×5=40
8×6=48
8×7=56
8×8=64
60~70之间8的倍数是64。
答:六(1)班观看比赛的学生有64人。
32.9个
【分析】求出81和72的最大公因数,,就是每盒装的最多个数。全部共有的质因数(公有质因数))相乘的积就是这几个数的最大公因数。
【详解】81=3×3×3×3
72=2×2×2×3×3
81和72的最大公因数是3×3=9。
答:每盒最多装9个。
33.(1)
(2)下坡训练地段
【分析】(1)用全程的减去平地占全程的,即可求出上坡路程占全程的分率;
(2)先用+,求出王叔叔骑了全程的分率,再和各路段占的分率进行比较,即可求出王叔叔在训练地的哪一路段。
【详解】(1)-
=-
=
答:上坡路占全程的。
(2)+
=+
=
>,王叔叔在训练地的下坡路段。
答:王叔叔在训练地的下坡路段。
答案第2页,共15页
答案第15页,共15页
同课章节目录
