人教版数学九年级上册 23.2.3 关于原点对称的点的坐标--教学课件(29张PPT)
文档属性
| 名称 | 人教版数学九年级上册 23.2.3 关于原点对称的点的坐标--教学课件(29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 8.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-10 09:20:59 | ||
图片预览




文档简介
第二十三章
旋 转
23.2.3 关于原点对称的点的坐标
教学目标/Teaching aims
1
会识别中心对称图形.
3
会运用中心对称图形的性质解决实际问题.
2
知道中心对称和中心对称图形的区别和联系.
复习回顾
问题1:
(1)点P(-1,2)关于x轴对称的点的坐标为 ,点P到x轴的距离为______,点P到y轴的距离为____
(2)点P(-3,-4)关于y轴对称的点的坐标为______,点P到x轴的距离为______,点P到y轴的距离为______.
(-1,-2)
2
1
(3,-4)
4
3
新知探究
在直角坐标系中,作出下列已知点关于原点O的对称点,并写出它们的坐标.这些坐标和已知点的坐标有什么关系?
A(4,0)、B(0,-3)、C(2,1)、D(-1,2)、E(-3,-4).
探究:
关于原点对称的点的坐标
新知探究
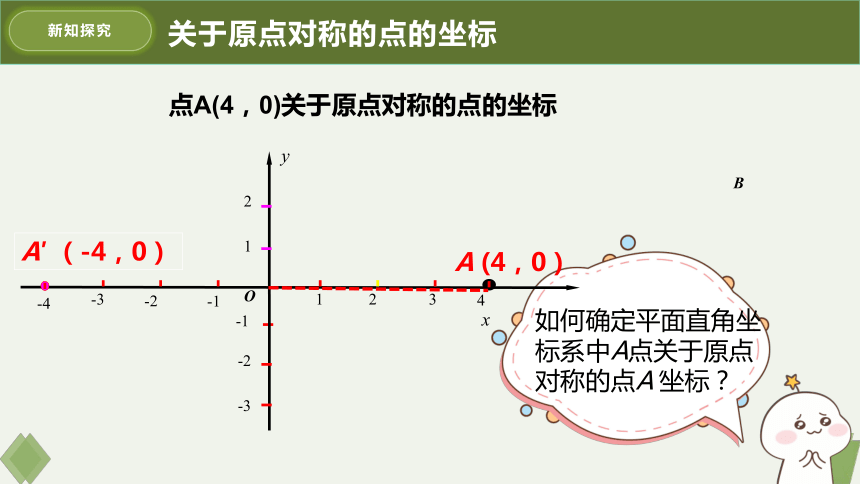
关于原点对称的点的坐标
如何确定平面直角坐标系中A点关于原点对称的点A′坐标?
A (4,0 )
A′ (-4,0)
x
O
1
2
3
-1
-2
-3
1
2
-1
-2
-3
y
B
-4
4
点A(4,0)关于原点对称的点的坐标
新知探究
关于原点对称的点的坐标
点B(0,-3)关于原点对称的点的坐标
B (0,-3 )
B′ (0,3)
x
O
1
2
3
-1
-2
-3
1
2
-1
-2
-3
y
-4
4
3
新知探究
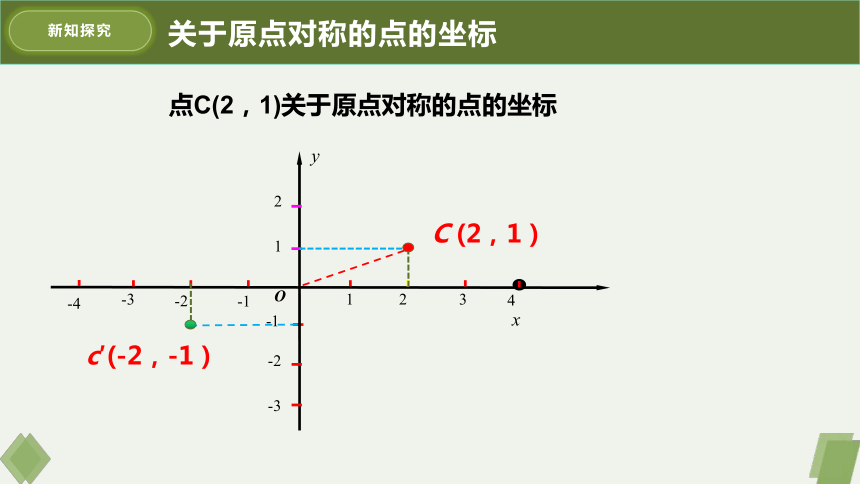
关于原点对称的点的坐标
点C(2,1)关于原点对称的点的坐标
C (2,1 )
x
O
1
2
3
-1
-2
-3
1
2
-1
-2
-3
y
-4
4
c′(-2,-1 )
新知探究
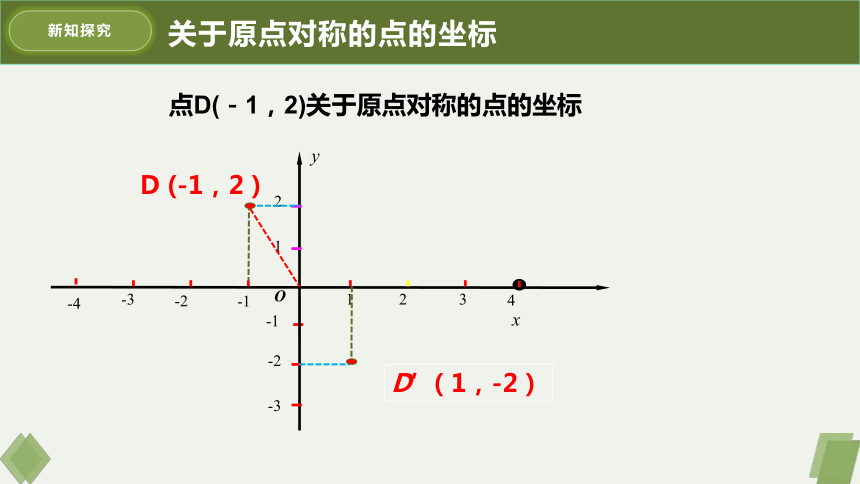
关于原点对称的点的坐标
点D(-1,2)关于原点对称的点的坐标
D (-1,2 )
D′ (1,-2)
x
O
1
2
3
-1
-2
-3
1
2
-1
-2
-3
y
-4
4
新知探究
关于原点对称的点的坐标
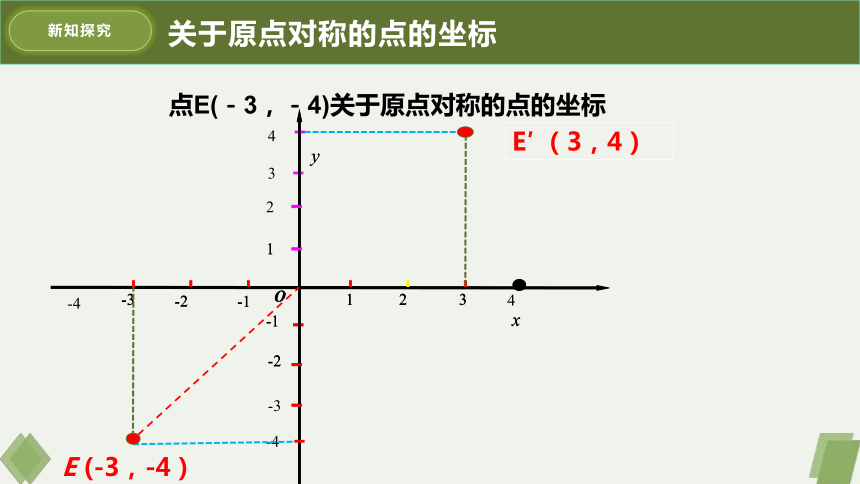
点E(-3,-4)关于原点对称的点的坐标
E (-3,-4 )
E′ (3,4)
x
O
1
2
3
-1
-2
-3
1
2
-1
-2
-3
y
-4
4
x
O
1
2
3
-1
-2
-3
1
-1
-2
y
3
4
-4
归纳小结
关于原点对称的点的坐标
发现规律
A(4,0) B(0,-3) C(2,1) D(-1,2) E(-3,-4)
A′(4,0) B′(0,-3) C′(2,1) D′(-1,2) E′(-3,-4)
两个点关于原点对称时,它们的坐标符号相反,即点P(x,y)关于原点的对称点为P′(-x,-y)
归纳小结
关于原点对称的点的坐标
类比归纳
点P(a,b)关于原点对称的点的坐标为P′(-a,-b);
点P(a,b)关于x轴对称的点的坐标为P′(a,-b);
点P(a,b)关于y轴对称的点的坐标为P′(-a, b).
简记为:“关于谁,谁不变,关于原点都改变”.
巩固练习
1.完成下表.
已知点
(2,-3)
(-1,2)
(-6,-5)
(0,-1.6)
(4,0)
关于x轴的对称点
关于y轴的对称点
关于原点的对称点
(-2, 3)
(2,3)
(-1,-2)
(1, -2)
(6, 5)
(-6, 5)
(0, 1.6)
(0,1.6)
(-4,0)
(4,0)
(-2, -3)
(1, 2)
(6, -5)
(0, -1.6)
(-4,0)
巩固练习
2.下列个点中哪两个点关于原点O对称?
A(-5,0),B(0,2),C(2,-1),D(2,0),
E(0,5),F(-2,1),G(-2,-1).
解:C、F关于原点O对称.
巩固练习
3.已知点A(a,1)与A’(5,b)关于原点对称,求a,b的值。
解:∵点A与点A’关于原点对称
∴a=-5,b=-1
新知探究
利用关于原点对称的点的坐标的关系作图
如图,利用关于原点对称的点的坐标的特点,作出△ABC关于原点对称的图形.
3
1
4
2
5
-2
-4
-1
-3
O
1
2
3
4
5
-4
-3
-2
-1
x
y
·
A
C
B
A′
C′
B′
解:①△ABC的三个顶点
A(-4,1),B(-1, -1),C(-3,2)
A′(4,-1),B′(1,1),C′(3,-2)
②关于原点的对称点分别为
③依次连接A ′B ′ ,B ′ C ′ ,C ′ A ′ ,就可得到与△ABC关于原点对称的
△ A′B′ C ′ .
归纳小结
步骤
(1)写出各点关于原点对称的点的坐标;
(2)在坐标平面内描出这些对称点;
(3)参照原图形顺次连接各点,作出新图形.
利用关于原点对称的点的坐标的关系作图
巩固练习
课堂练习
1.在平面直角坐标系中,已知点A(-4,3)与点B关于原点对称,则点B的坐标为( )
A.(-4,-3) B.(4,3)
C.(4,-3) D.(-4,3)
C
课堂练习
2.已知点P1(-4,3)和P2(-4,-3),则点P1和P2( )
A.关于原点对称 B.关于y轴对称
C.关于x轴对称 D.不存在对称关系
C
3.直角坐标系中,点 P 的坐标为(a+5,a﹣5),则 P 点关于原点的对称点 P′不可能在的象限是( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
D
课堂练习
4. 已知点P(a-3,2-a)关于原点对称的点在第四象限,则a的取值范围在数轴上表示正确的是( )
C
课堂练习
5.已知点P(-b,2)与点Q(3,2a)关于原点对称,则ab的值是__ __
-3
6.将点P(-2,3)向右平移3个单位得到点P1,点P2与点P1关于原点对称,则P2的坐标是______
(-1,-3)
课堂练习
7.已知点M(2m+1,m-1)与点N关于原点对称,若点N在第二象限,则的取值范围是________.
8.在平面直角坐标系内有两点A(x,y),B(c,d),且x+c=0,y+d=0,试判断点A与点B是不是关于原点对称?
解:因为x+c=0,y+d=0,所以x=-c,y=-d,即点A的坐标为(-c,-d),所以点A与点B关于原点对称.
巩固练习
9. 如图所示,每个小正方形的边长为1个单位长度,作出△ABC关于原点对称的△A1B1C1,并写出A1,B1,C1的坐标.
复习回顾
解:根据图形,可知A(-2,2),B(-3,0),C(-1,-1),
如图所示,△A1B1C1即为所求.
各点的坐标分别是:
A1(2,-2),B1(3,0),C1(1,1).
9. 如图所示,每个小正方形的边长为1个单位长度,作出△ABC关于原点对称的△A1B1C1,并写出A1,B1,C1的坐标.
单击此处添加大标题
新课导入
10.如图所示,点P的坐标为(1,3),把点P绕坐标原点O逆时针旋转90°得到点Q.(1)写出点Q的坐标是 . (2)若把点Q向右平移a个单位长度,向下平移a个单位长度后,
得到的点M(m,n)落在第四象限,求a的取值范围.(3)在(2)的条件下,当a取何值时,代数式m2+2n+5取得最小值?
(-3,1)
单击此处添加大标题
新课导入
(2)若把点Q向右平移a个单位长度,向下平移a个单位长度后,得到的点M(m,n)落在第四象限,求a的取值范围.
解:(2)由题意得点M的坐标为(-3+a,1-a).
又∵点M在第四象限,则有解得a>3,
∴a的取值范围为a>3.
单击此处添加大标题
新课导入
解:(3)由(2)得m=-3+a,n=1-a,
∴m2+2n+5=(a-3)2+2(1-a)+5=a2-8a+16=(a-4)2,
∵(a-4)2≥0,a>3,∴当a=4时,代数式m2+2n+5取得最小值,最小值为0.
(3)在(2)的条件下,当a取何值时,代数式m2+2n+5取得最小值?
课堂总结
关于原点对称的点的坐标
特征
P(x,y)关于原点的对称点为P'(-x,-y).
作图
作出关于原点对称的图形,先求出对称点的坐标再描点画图.
23.2.3 关于原点对称的点的坐标
谢谢观看
旋转
旋 转
23.2.3 关于原点对称的点的坐标
教学目标/Teaching aims
1
会识别中心对称图形.
3
会运用中心对称图形的性质解决实际问题.
2
知道中心对称和中心对称图形的区别和联系.
复习回顾
问题1:
(1)点P(-1,2)关于x轴对称的点的坐标为 ,点P到x轴的距离为______,点P到y轴的距离为____
(2)点P(-3,-4)关于y轴对称的点的坐标为______,点P到x轴的距离为______,点P到y轴的距离为______.
(-1,-2)
2
1
(3,-4)
4
3
新知探究
在直角坐标系中,作出下列已知点关于原点O的对称点,并写出它们的坐标.这些坐标和已知点的坐标有什么关系?
A(4,0)、B(0,-3)、C(2,1)、D(-1,2)、E(-3,-4).
探究:
关于原点对称的点的坐标
新知探究
关于原点对称的点的坐标
如何确定平面直角坐标系中A点关于原点对称的点A′坐标?
A (4,0 )
A′ (-4,0)
x
O
1
2
3
-1
-2
-3
1
2
-1
-2
-3
y
B
-4
4
点A(4,0)关于原点对称的点的坐标
新知探究
关于原点对称的点的坐标
点B(0,-3)关于原点对称的点的坐标
B (0,-3 )
B′ (0,3)
x
O
1
2
3
-1
-2
-3
1
2
-1
-2
-3
y
-4
4
3
新知探究
关于原点对称的点的坐标
点C(2,1)关于原点对称的点的坐标
C (2,1 )
x
O
1
2
3
-1
-2
-3
1
2
-1
-2
-3
y
-4
4
c′(-2,-1 )
新知探究
关于原点对称的点的坐标
点D(-1,2)关于原点对称的点的坐标
D (-1,2 )
D′ (1,-2)
x
O
1
2
3
-1
-2
-3
1
2
-1
-2
-3
y
-4
4
新知探究
关于原点对称的点的坐标
点E(-3,-4)关于原点对称的点的坐标
E (-3,-4 )
E′ (3,4)
x
O
1
2
3
-1
-2
-3
1
2
-1
-2
-3
y
-4
4
x
O
1
2
3
-1
-2
-3
1
-1
-2
y
3
4
-4
归纳小结
关于原点对称的点的坐标
发现规律
A(4,0) B(0,-3) C(2,1) D(-1,2) E(-3,-4)
A′(4,0) B′(0,-3) C′(2,1) D′(-1,2) E′(-3,-4)
两个点关于原点对称时,它们的坐标符号相反,即点P(x,y)关于原点的对称点为P′(-x,-y)
归纳小结
关于原点对称的点的坐标
类比归纳
点P(a,b)关于原点对称的点的坐标为P′(-a,-b);
点P(a,b)关于x轴对称的点的坐标为P′(a,-b);
点P(a,b)关于y轴对称的点的坐标为P′(-a, b).
简记为:“关于谁,谁不变,关于原点都改变”.
巩固练习
1.完成下表.
已知点
(2,-3)
(-1,2)
(-6,-5)
(0,-1.6)
(4,0)
关于x轴的对称点
关于y轴的对称点
关于原点的对称点
(-2, 3)
(2,3)
(-1,-2)
(1, -2)
(6, 5)
(-6, 5)
(0, 1.6)
(0,1.6)
(-4,0)
(4,0)
(-2, -3)
(1, 2)
(6, -5)
(0, -1.6)
(-4,0)
巩固练习
2.下列个点中哪两个点关于原点O对称?
A(-5,0),B(0,2),C(2,-1),D(2,0),
E(0,5),F(-2,1),G(-2,-1).
解:C、F关于原点O对称.
巩固练习
3.已知点A(a,1)与A’(5,b)关于原点对称,求a,b的值。
解:∵点A与点A’关于原点对称
∴a=-5,b=-1
新知探究
利用关于原点对称的点的坐标的关系作图
如图,利用关于原点对称的点的坐标的特点,作出△ABC关于原点对称的图形.
3
1
4
2
5
-2
-4
-1
-3
O
1
2
3
4
5
-4
-3
-2
-1
x
y
·
A
C
B
A′
C′
B′
解:①△ABC的三个顶点
A(-4,1),B(-1, -1),C(-3,2)
A′(4,-1),B′(1,1),C′(3,-2)
②关于原点的对称点分别为
③依次连接A ′B ′ ,B ′ C ′ ,C ′ A ′ ,就可得到与△ABC关于原点对称的
△ A′B′ C ′ .
归纳小结
步骤
(1)写出各点关于原点对称的点的坐标;
(2)在坐标平面内描出这些对称点;
(3)参照原图形顺次连接各点,作出新图形.
利用关于原点对称的点的坐标的关系作图
巩固练习
课堂练习
1.在平面直角坐标系中,已知点A(-4,3)与点B关于原点对称,则点B的坐标为( )
A.(-4,-3) B.(4,3)
C.(4,-3) D.(-4,3)
C
课堂练习
2.已知点P1(-4,3)和P2(-4,-3),则点P1和P2( )
A.关于原点对称 B.关于y轴对称
C.关于x轴对称 D.不存在对称关系
C
3.直角坐标系中,点 P 的坐标为(a+5,a﹣5),则 P 点关于原点的对称点 P′不可能在的象限是( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
D
课堂练习
4. 已知点P(a-3,2-a)关于原点对称的点在第四象限,则a的取值范围在数轴上表示正确的是( )
C
课堂练习
5.已知点P(-b,2)与点Q(3,2a)关于原点对称,则ab的值是__ __
-3
6.将点P(-2,3)向右平移3个单位得到点P1,点P2与点P1关于原点对称,则P2的坐标是______
(-1,-3)
课堂练习
7.已知点M(2m+1,m-1)与点N关于原点对称,若点N在第二象限,则的取值范围是________.
8.在平面直角坐标系内有两点A(x,y),B(c,d),且x+c=0,y+d=0,试判断点A与点B是不是关于原点对称?
解:因为x+c=0,y+d=0,所以x=-c,y=-d,即点A的坐标为(-c,-d),所以点A与点B关于原点对称.
巩固练习
9. 如图所示,每个小正方形的边长为1个单位长度,作出△ABC关于原点对称的△A1B1C1,并写出A1,B1,C1的坐标.
复习回顾
解:根据图形,可知A(-2,2),B(-3,0),C(-1,-1),
如图所示,△A1B1C1即为所求.
各点的坐标分别是:
A1(2,-2),B1(3,0),C1(1,1).
9. 如图所示,每个小正方形的边长为1个单位长度,作出△ABC关于原点对称的△A1B1C1,并写出A1,B1,C1的坐标.
单击此处添加大标题
新课导入
10.如图所示,点P的坐标为(1,3),把点P绕坐标原点O逆时针旋转90°得到点Q.(1)写出点Q的坐标是 . (2)若把点Q向右平移a个单位长度,向下平移a个单位长度后,
得到的点M(m,n)落在第四象限,求a的取值范围.(3)在(2)的条件下,当a取何值时,代数式m2+2n+5取得最小值?
(-3,1)
单击此处添加大标题
新课导入
(2)若把点Q向右平移a个单位长度,向下平移a个单位长度后,得到的点M(m,n)落在第四象限,求a的取值范围.
解:(2)由题意得点M的坐标为(-3+a,1-a).
又∵点M在第四象限,则有解得a>3,
∴a的取值范围为a>3.
单击此处添加大标题
新课导入
解:(3)由(2)得m=-3+a,n=1-a,
∴m2+2n+5=(a-3)2+2(1-a)+5=a2-8a+16=(a-4)2,
∵(a-4)2≥0,a>3,∴当a=4时,代数式m2+2n+5取得最小值,最小值为0.
(3)在(2)的条件下,当a取何值时,代数式m2+2n+5取得最小值?
课堂总结
关于原点对称的点的坐标
特征
P(x,y)关于原点的对称点为P'(-x,-y).
作图
作出关于原点对称的图形,先求出对称点的坐标再描点画图.
23.2.3 关于原点对称的点的坐标
谢谢观看
旋转
同课章节目录
