人教版数学九年级上册 23.3 课题学习 图案设计 课件(共50张PPT)
文档属性
| 名称 | 人教版数学九年级上册 23.3 课题学习 图案设计 课件(共50张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 30.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-10 08:51:20 | ||
图片预览







文档简介
(共50张PPT)
新课标 人教版 九年级上册
第二十三章旋转
23.3课题学习 图案设计
学习目标
1.利用旋转、轴对称或平移进行简单的图案设计.
2.灵活运用平移与旋转组合的方式进行一些图案设计.
3.会分析一种图案的设计方式.
情境引入
生活中我们会看到很多由一些几何图形组成的优美图案,你知道它们是怎样形成的吗?
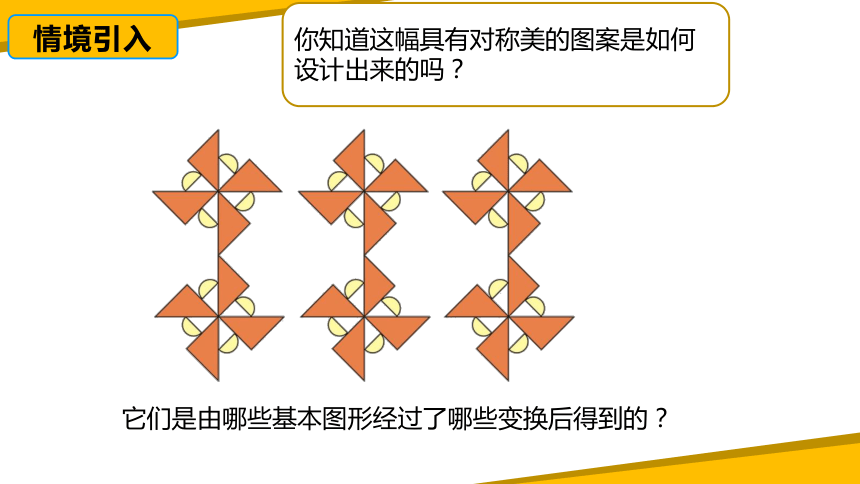
你知道这幅具有对称美的图案是如何设计出来的吗?
情境引入
它们是由哪些基本图形经过了哪些变换后得到的?
探究新知
分析图案的形成过程时,要认真观察整个图案,从中找出基本图形,从基本图形的大小、形状、位置、距离等方面加以分析,确定由基本图形得到整个图案的变换方式.
基本图形可能是一种图形,也可能是两种或更多种图形的组合图形,一个图案中的基本图形可以有多个.
探究新知
将 按如图所示的方式逆时针旋转90°,经过三次旋转,得到图形如下:
以l为对称轴继续作图,得到图形为:
l
例题讲解
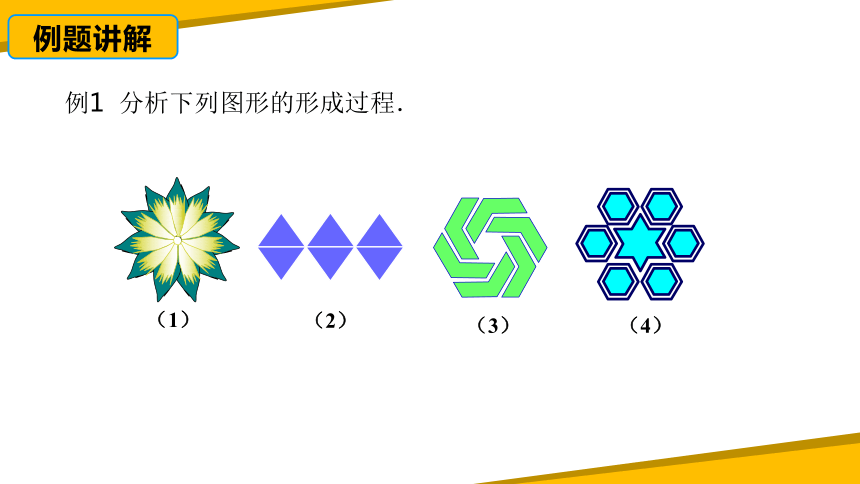
例1 分析下列图形的形成过程.
(1)
(2)
(3)
(4)
例题讲解
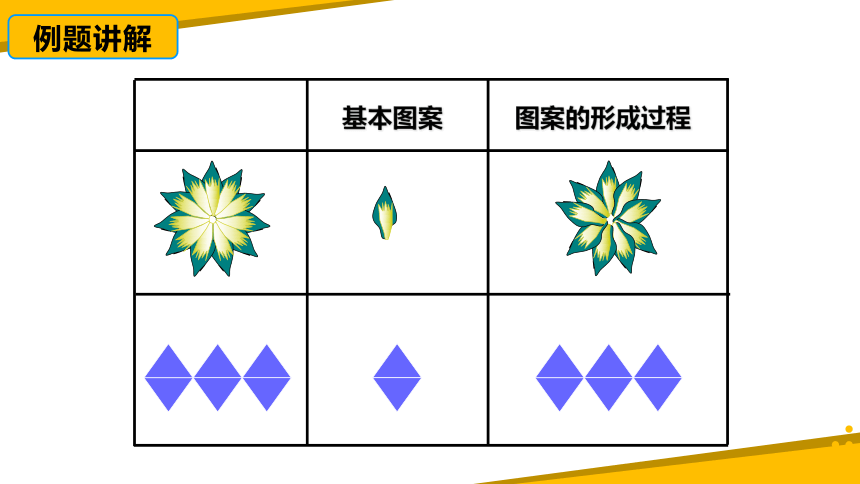
基本图案
图案的形成过程
例题讲解
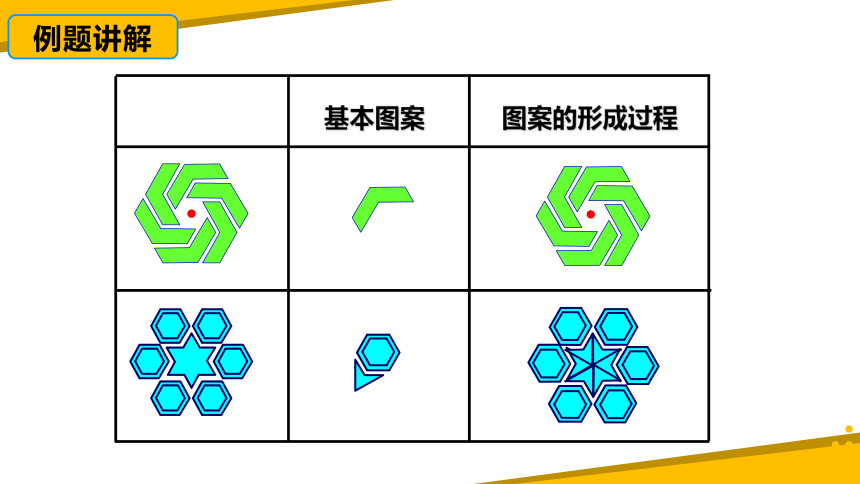
基本图案
图案的形成过程
归纳总结
分析图案的形成过程应按如下步骤进行:
1.划分出组成原图案的基本图形;
2.说明将该基本图形运用平移、旋转、轴对称中的哪些图形变换,通过怎样的变换方式得到原图案.
合作交流一
下面花边中的图案以正方形为基础,由圆弧、圆或线段构成.仿照例图,请你为班级的板报设计一条花边.要求:
(1)只要画出组成花边的一个图案;
(2)以所给的正方形为基础,用圆弧、圆或线段画出;
(3)图案应有美感。
图案的设计
合作交流二
A
B
C
O
D
E
F
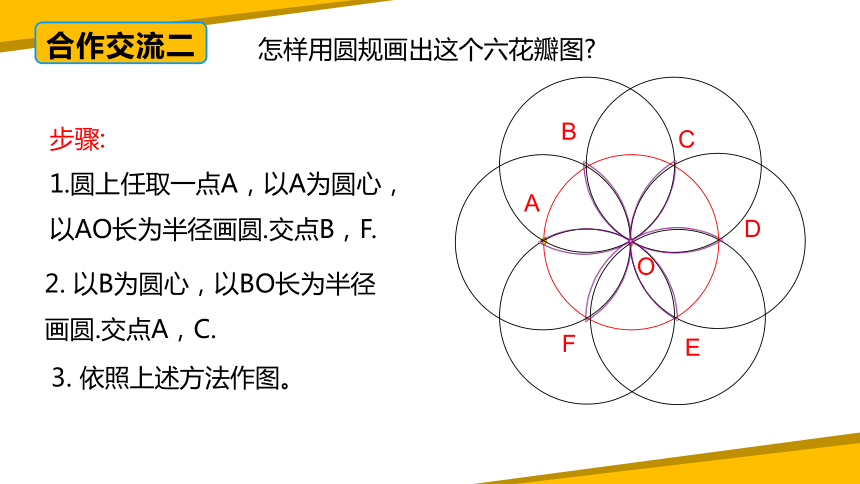
怎样用圆规画出这个六花瓣图
步骤:
1.圆上任取一点A,以A为圆心,以AO长为半径画圆.交点B,F.
2. 以B为圆心,以BO长为半径画圆.交点A,C.
3. 依照上述方法作图。
随堂练习
1.在方格纸中,选择标有序号①②③④中的一个小正方形涂黑,使其与图中阴影部分构成中心对称图形.该小正方形的序号是( )
A.① B.②
C.③ D.④
B
随堂练习
2.如图, ①中的图案是由六个全等的菱形拼成的,它也可以看作是以一个图案为基本图形,通过旋转得到的,图 ②的图案中,不能作为基本图形的是( )
B
3.下列图形均可由“基本图形”通过变换得到.
① ② ③
(1)由平移变换得到的是__________;
(2)由旋转变换得到的是__________;
(3)由轴对称变换得到的是__________ .
③
①②③
②
随堂练习
4.如图,在方格纸中,△ABC经过变换得到△DEF,
正确的变换是( )
A.把△ABC绕点C逆时针方向旋转90°,
再向下平移2格
B.把△ABC绕点C顺时针方向旋转90°,
再向下平移5格
C.把△ABC向下平移4格,再绕点C逆时
针方向旋转180°
D.把△ABC向下平移5格,再绕点C顺时
针方向旋转180°
B
随堂练习
随堂练习
5.下面四个图案中,不能由基本图案旋转得到的是( )
A
随堂练习
6.如图,如果将其中的右图变成左图,那么经过的变换正确的是( )
A.旋转、平移 B.轴对称、平移
C.旋转、轴对称 D.旋转、旋转
C
随堂练习
7.如图,在直角坐标系中,△AOB可以看作是由△0CD经过两次图形的
变化(平移、轴对称、旋转)得到的,这个变化过程不可能是( )
A.先平移,再轴对称 B.先旋转,再平移
C.先轴对称,再旋转 D.先轴对称,再平移
B
B
8.某地板厂要制作一批正六边形形状的地板砖,为适应市场多样化需求,要求在地板砖上设计的图案能够把正六边形6等分,请你帮他们设计等分图案.
解:如图所示:
随堂练习
中考链接
1.(2023·四川绵阳·统考中考真题)下列图案中,属于轴对称图形的是( )
A
中考链接
2.(2023 四川内江 统考中考真题)下列图形中,既是轴对称图形,又是中心对称图形的是( )
A
中考链接
3.(2023 四川自贡 统考中考真题)下列交通标志图案中,既是中心对称图形又是轴对称图形的是( )
B
中考链接
4.(2023 四川广安 统考中考真题)将边长为2的正方形剪成四个全等的直角三角形,用这四个直角三角形拼成符合要求的四边形,请在下列网格中画出你拼成的四边形(注:①网格中每个小正方形的边长为1;②所拼的图形不得与原图形相同;③四边形的各顶点都在格点上).
中考链接
解:
课堂小结
图案
设计
分析图案设计
分清基本图形
知道形成过程
设计方法
利用图形变换
轴对称
平 移
旋 转
动手设计
赏心悦目的图案
图案设计的步骤
(1)整体构思:
①图案的设计要突出主题,即设计图案的意图,要求简洁、自然、别致,具有一定的意义;
②确定整幅图案的形状和基本图案;
③构思图案的形成过程,首先要构思该图案是由哪几部分组成,再构思如何运用平移、对称、旋转等方式进行图形变换。
(2)具体作图:
根据草图,运用尺规作图的方法准确作出图案,也可以运用电脑技术进行设计和绘图,同时对图案进行具体的修饰等.
课堂小结
当堂测试
下列各组图形中,△A'B'C'与△ABC成中心对称的是( )
A. B.
C. D.
D
当堂测试
2. 下列图形是中心对称图形的是( )
A.
B.
C.
D.
C
当堂测试
3.下列图形中,绕某个点旋转72度后能与自身重合的是( )
B
当堂测试
4.永州的文化底蕴深厚,永州人民的生活健康向上,如瑶族长鼓舞,东安武术,宁远举重等,下面的四幅简笔画是从永州的文化活动中抽象出来的,其中是轴对称图形的是( )
C
当堂测试
5.如图,在平面直角坐标系中,点B、C、E在y轴上,Rt△ABC经过变换得到Rt△ODE,若点C的坐标为(0,1),AC=3,则这种变换可以是( )
A.将△ABC绕点C顺时针旋转90°,再向下平移4个单位长度
B.将△ABC绕点C顺时针旋转90°,再向下平移1个单位长度
C.将△ABC绕点C逆时针旋转90°,再向下平移1个单位长度
D.将△ABC绕点C逆时针旋转90°,再向下平移4个单位长度
A
当堂测试
6.如图,正方形网格中,已有两个小正方形被涂黑,再将图中其余小正方形涂黑一个,使整个图案构成一个轴对称图形,那么涂法共有( )
A.3种 B.4种 C.5种 D.6种
C
当堂测试
7.如图,下列4×4网格图都是由16个相同的小正方形组成,每个网格图中有4个小正方形已涂上阴影,请你在空白小正方形中,按下列要求涂上阴影:
(1)在图1中选取1个空白小正方形涂上阴影,使5个阴影小正方形组成一个轴对称图形;
(2)在图2中选取2个空白小正方形涂上阴影,使6个阴影小正方形组成一个中心对称图形.(请将两个小题依次作答在图1,图2中,均只需画出符合条件的一种情形)
当堂测试
解:(1)选取1个空白小正方形涂上阴影,使5个阴影小正方形组成一个轴对称图形,如下图1:
(2)选取2个空白小正方形涂上阴影,使6个阴影小正方形组成一个中心对称图形,如下图2:
分层作业
【基础达标作业】
1.下列图案可以通过一个“基本图形”平移得到的是( )
B
分层作业
【基础达标作业】
2.如图,将正方形图案绕中心O旋转180° 后,得到的图案是( )
C
分层作业
【基础达标作业】
3.如图,两个五角星关于某一点成中心对称,则对称中心和点A的对称点是( )
A.A和H B.I和E C.E和F D.E和I
D
分层作业
【基础达标作业】
4.如图,△ABC与△A′B′C′关于点O成中心对称,则下列结论不成立
的是( )
A.点A与点A′是对称点 B.BO=B′O
C.∠AOB=∠A′OB′ D.∠ACB=∠C′A′B′
D
分层作业
【基础达标作业】
5.如图是用围棋棋子在6×6的正方形网格中摆出的图案,棋子的位置用有序数对表示,如A点为(5,1),若再摆一黑一白两枚棋子,使这9枚棋子组成的图案既是轴对称图形又是中心对称图形,则下列摆放正确的是( )
A.黑(1,5),白(5,5) B.黑(3,2),白(3,3)
C.黑(3,3),白(3,1) D.黑(3,1),白(3,3)
D
分层作业
6.七巧板是我们祖先的一项卓越创造,被西方人誉为“东方魔板”.已知如图所示的“正方形”是由七块七巧板拼成的正方形(相同的板规定序号相同).现从七巧板取出四块(序号可以相同)拼成一个小正方形(无空隙不重叠),则无法拼成的序号为( )
A.②③④ B.①③⑤ C.①②③ D.①③④
A
【能力提升作业】
分层作业
【能力提升作业】
7.在数学活动课上,王老师要求学生将图1所示的3×3正方形方格纸,剪掉其中两个方格,使之成为轴对称图形.规定:凡通过旋转能重合的图形视为同一种图形,如图2的四幅图就视为同一种设计方案(阴影部分为要剪掉部分)
分层作业
【能力提升作业】
请在图中画出4种不同的设计方案,将每种方案中要剪掉的两个方格涂黑(每个3×3的正方形方格画一种,例图除外)
分层作业
【能力提升作业】
解:根据剪掉其中两个方格,使之成为轴对称图形;即如图所示:
分层作业
【拓展延伸作业】
8.动手操作,解决问题:如图所示,有两种形状不同的直角三角形纸片
各两块,其中一种纸片的两条直角边长都为3,另一种纸片的两条直角边长
分别为1和3.图1、图2、图3是三张形状、大小完全相同的方格纸,方格纸
中的每个小正方形的边长均为1.
分层作业
【拓展延伸作业】
(1)请用三种方法(拼出的两个图形只要不全等就认为是不同的拼法)将图中所给的四块直角三角形纸片拼成平行四边形(非矩形),每种方法要把图中所给的四块直角三角形纸片全部用上,互不重叠且不留空隙,并把你所拼得的图形按实际大小画在图1、图2、图3的方格纸上(要求:所画图形各顶点必须与方格纸中的小正方形顶点重合;画图时,要保留四块直角三角形纸片的拼接痕迹);
(2)三种方法所拼得的平行四边形的面积分别是: , , ;
(3)三种方法所拼得的平行四边形的周长分别是: , , .
分层作业
【拓展延伸作业】
解:(1)图形如图所示:
分层作业
【拓展延伸作业】
(2)根据题意拼接后的面积等于4个三角形的面积,则面积都为12,故答案为: 12,12,12;
(3)根据勾股定理可得
图1中,周长= +8,
图2中,周长= 2+,
图3中,周长=8+2.
故答案为: +8 ,2+ ,8+2.
分层作业
【拓展延伸作业】
9.如图,△ABO与△CDO关于O点成中心对称,点E、F在线段AC上,且AF=CE.求证:FD=BE,FD∥BE.
分层作业
【拓展延伸作业】
证明:连接BF、DE,
∵△ABO与△CDO关于O点成中心对称,
∴OB=OD,OA=OC.
∵AF=CE,
∴OF=OE.
∴四边形BEDF是平行四边形,
∴FD=BE,FD∥BE.
新课标 人教版 九年级上册
第二十三章旋转
23.3课题学习 图案设计
学习目标
1.利用旋转、轴对称或平移进行简单的图案设计.
2.灵活运用平移与旋转组合的方式进行一些图案设计.
3.会分析一种图案的设计方式.
情境引入
生活中我们会看到很多由一些几何图形组成的优美图案,你知道它们是怎样形成的吗?
你知道这幅具有对称美的图案是如何设计出来的吗?
情境引入
它们是由哪些基本图形经过了哪些变换后得到的?
探究新知
分析图案的形成过程时,要认真观察整个图案,从中找出基本图形,从基本图形的大小、形状、位置、距离等方面加以分析,确定由基本图形得到整个图案的变换方式.
基本图形可能是一种图形,也可能是两种或更多种图形的组合图形,一个图案中的基本图形可以有多个.
探究新知
将 按如图所示的方式逆时针旋转90°,经过三次旋转,得到图形如下:
以l为对称轴继续作图,得到图形为:
l
例题讲解
例1 分析下列图形的形成过程.
(1)
(2)
(3)
(4)
例题讲解
基本图案
图案的形成过程
例题讲解
基本图案
图案的形成过程
归纳总结
分析图案的形成过程应按如下步骤进行:
1.划分出组成原图案的基本图形;
2.说明将该基本图形运用平移、旋转、轴对称中的哪些图形变换,通过怎样的变换方式得到原图案.
合作交流一
下面花边中的图案以正方形为基础,由圆弧、圆或线段构成.仿照例图,请你为班级的板报设计一条花边.要求:
(1)只要画出组成花边的一个图案;
(2)以所给的正方形为基础,用圆弧、圆或线段画出;
(3)图案应有美感。
图案的设计
合作交流二
A
B
C
O
D
E
F
怎样用圆规画出这个六花瓣图
步骤:
1.圆上任取一点A,以A为圆心,以AO长为半径画圆.交点B,F.
2. 以B为圆心,以BO长为半径画圆.交点A,C.
3. 依照上述方法作图。
随堂练习
1.在方格纸中,选择标有序号①②③④中的一个小正方形涂黑,使其与图中阴影部分构成中心对称图形.该小正方形的序号是( )
A.① B.②
C.③ D.④
B
随堂练习
2.如图, ①中的图案是由六个全等的菱形拼成的,它也可以看作是以一个图案为基本图形,通过旋转得到的,图 ②的图案中,不能作为基本图形的是( )
B
3.下列图形均可由“基本图形”通过变换得到.
① ② ③
(1)由平移变换得到的是__________;
(2)由旋转变换得到的是__________;
(3)由轴对称变换得到的是__________ .
③
①②③
②
随堂练习
4.如图,在方格纸中,△ABC经过变换得到△DEF,
正确的变换是( )
A.把△ABC绕点C逆时针方向旋转90°,
再向下平移2格
B.把△ABC绕点C顺时针方向旋转90°,
再向下平移5格
C.把△ABC向下平移4格,再绕点C逆时
针方向旋转180°
D.把△ABC向下平移5格,再绕点C顺时
针方向旋转180°
B
随堂练习
随堂练习
5.下面四个图案中,不能由基本图案旋转得到的是( )
A
随堂练习
6.如图,如果将其中的右图变成左图,那么经过的变换正确的是( )
A.旋转、平移 B.轴对称、平移
C.旋转、轴对称 D.旋转、旋转
C
随堂练习
7.如图,在直角坐标系中,△AOB可以看作是由△0CD经过两次图形的
变化(平移、轴对称、旋转)得到的,这个变化过程不可能是( )
A.先平移,再轴对称 B.先旋转,再平移
C.先轴对称,再旋转 D.先轴对称,再平移
B
B
8.某地板厂要制作一批正六边形形状的地板砖,为适应市场多样化需求,要求在地板砖上设计的图案能够把正六边形6等分,请你帮他们设计等分图案.
解:如图所示:
随堂练习
中考链接
1.(2023·四川绵阳·统考中考真题)下列图案中,属于轴对称图形的是( )
A
中考链接
2.(2023 四川内江 统考中考真题)下列图形中,既是轴对称图形,又是中心对称图形的是( )
A
中考链接
3.(2023 四川自贡 统考中考真题)下列交通标志图案中,既是中心对称图形又是轴对称图形的是( )
B
中考链接
4.(2023 四川广安 统考中考真题)将边长为2的正方形剪成四个全等的直角三角形,用这四个直角三角形拼成符合要求的四边形,请在下列网格中画出你拼成的四边形(注:①网格中每个小正方形的边长为1;②所拼的图形不得与原图形相同;③四边形的各顶点都在格点上).
中考链接
解:
课堂小结
图案
设计
分析图案设计
分清基本图形
知道形成过程
设计方法
利用图形变换
轴对称
平 移
旋 转
动手设计
赏心悦目的图案
图案设计的步骤
(1)整体构思:
①图案的设计要突出主题,即设计图案的意图,要求简洁、自然、别致,具有一定的意义;
②确定整幅图案的形状和基本图案;
③构思图案的形成过程,首先要构思该图案是由哪几部分组成,再构思如何运用平移、对称、旋转等方式进行图形变换。
(2)具体作图:
根据草图,运用尺规作图的方法准确作出图案,也可以运用电脑技术进行设计和绘图,同时对图案进行具体的修饰等.
课堂小结
当堂测试
下列各组图形中,△A'B'C'与△ABC成中心对称的是( )
A. B.
C. D.
D
当堂测试
2. 下列图形是中心对称图形的是( )
A.
B.
C.
D.
C
当堂测试
3.下列图形中,绕某个点旋转72度后能与自身重合的是( )
B
当堂测试
4.永州的文化底蕴深厚,永州人民的生活健康向上,如瑶族长鼓舞,东安武术,宁远举重等,下面的四幅简笔画是从永州的文化活动中抽象出来的,其中是轴对称图形的是( )
C
当堂测试
5.如图,在平面直角坐标系中,点B、C、E在y轴上,Rt△ABC经过变换得到Rt△ODE,若点C的坐标为(0,1),AC=3,则这种变换可以是( )
A.将△ABC绕点C顺时针旋转90°,再向下平移4个单位长度
B.将△ABC绕点C顺时针旋转90°,再向下平移1个单位长度
C.将△ABC绕点C逆时针旋转90°,再向下平移1个单位长度
D.将△ABC绕点C逆时针旋转90°,再向下平移4个单位长度
A
当堂测试
6.如图,正方形网格中,已有两个小正方形被涂黑,再将图中其余小正方形涂黑一个,使整个图案构成一个轴对称图形,那么涂法共有( )
A.3种 B.4种 C.5种 D.6种
C
当堂测试
7.如图,下列4×4网格图都是由16个相同的小正方形组成,每个网格图中有4个小正方形已涂上阴影,请你在空白小正方形中,按下列要求涂上阴影:
(1)在图1中选取1个空白小正方形涂上阴影,使5个阴影小正方形组成一个轴对称图形;
(2)在图2中选取2个空白小正方形涂上阴影,使6个阴影小正方形组成一个中心对称图形.(请将两个小题依次作答在图1,图2中,均只需画出符合条件的一种情形)
当堂测试
解:(1)选取1个空白小正方形涂上阴影,使5个阴影小正方形组成一个轴对称图形,如下图1:
(2)选取2个空白小正方形涂上阴影,使6个阴影小正方形组成一个中心对称图形,如下图2:
分层作业
【基础达标作业】
1.下列图案可以通过一个“基本图形”平移得到的是( )
B
分层作业
【基础达标作业】
2.如图,将正方形图案绕中心O旋转180° 后,得到的图案是( )
C
分层作业
【基础达标作业】
3.如图,两个五角星关于某一点成中心对称,则对称中心和点A的对称点是( )
A.A和H B.I和E C.E和F D.E和I
D
分层作业
【基础达标作业】
4.如图,△ABC与△A′B′C′关于点O成中心对称,则下列结论不成立
的是( )
A.点A与点A′是对称点 B.BO=B′O
C.∠AOB=∠A′OB′ D.∠ACB=∠C′A′B′
D
分层作业
【基础达标作业】
5.如图是用围棋棋子在6×6的正方形网格中摆出的图案,棋子的位置用有序数对表示,如A点为(5,1),若再摆一黑一白两枚棋子,使这9枚棋子组成的图案既是轴对称图形又是中心对称图形,则下列摆放正确的是( )
A.黑(1,5),白(5,5) B.黑(3,2),白(3,3)
C.黑(3,3),白(3,1) D.黑(3,1),白(3,3)
D
分层作业
6.七巧板是我们祖先的一项卓越创造,被西方人誉为“东方魔板”.已知如图所示的“正方形”是由七块七巧板拼成的正方形(相同的板规定序号相同).现从七巧板取出四块(序号可以相同)拼成一个小正方形(无空隙不重叠),则无法拼成的序号为( )
A.②③④ B.①③⑤ C.①②③ D.①③④
A
【能力提升作业】
分层作业
【能力提升作业】
7.在数学活动课上,王老师要求学生将图1所示的3×3正方形方格纸,剪掉其中两个方格,使之成为轴对称图形.规定:凡通过旋转能重合的图形视为同一种图形,如图2的四幅图就视为同一种设计方案(阴影部分为要剪掉部分)
分层作业
【能力提升作业】
请在图中画出4种不同的设计方案,将每种方案中要剪掉的两个方格涂黑(每个3×3的正方形方格画一种,例图除外)
分层作业
【能力提升作业】
解:根据剪掉其中两个方格,使之成为轴对称图形;即如图所示:
分层作业
【拓展延伸作业】
8.动手操作,解决问题:如图所示,有两种形状不同的直角三角形纸片
各两块,其中一种纸片的两条直角边长都为3,另一种纸片的两条直角边长
分别为1和3.图1、图2、图3是三张形状、大小完全相同的方格纸,方格纸
中的每个小正方形的边长均为1.
分层作业
【拓展延伸作业】
(1)请用三种方法(拼出的两个图形只要不全等就认为是不同的拼法)将图中所给的四块直角三角形纸片拼成平行四边形(非矩形),每种方法要把图中所给的四块直角三角形纸片全部用上,互不重叠且不留空隙,并把你所拼得的图形按实际大小画在图1、图2、图3的方格纸上(要求:所画图形各顶点必须与方格纸中的小正方形顶点重合;画图时,要保留四块直角三角形纸片的拼接痕迹);
(2)三种方法所拼得的平行四边形的面积分别是: , , ;
(3)三种方法所拼得的平行四边形的周长分别是: , , .
分层作业
【拓展延伸作业】
解:(1)图形如图所示:
分层作业
【拓展延伸作业】
(2)根据题意拼接后的面积等于4个三角形的面积,则面积都为12,故答案为: 12,12,12;
(3)根据勾股定理可得
图1中,周长= +8,
图2中,周长= 2+,
图3中,周长=8+2.
故答案为: +8 ,2+ ,8+2.
分层作业
【拓展延伸作业】
9.如图,△ABO与△CDO关于O点成中心对称,点E、F在线段AC上,且AF=CE.求证:FD=BE,FD∥BE.
分层作业
【拓展延伸作业】
证明:连接BF、DE,
∵△ABO与△CDO关于O点成中心对称,
∴OB=OD,OA=OC.
∵AF=CE,
∴OF=OE.
∴四边形BEDF是平行四边形,
∴FD=BE,FD∥BE.
同课章节目录
