浙江省2025年八年级下册期末考试数学模拟卷 含答案
文档属性
| 名称 | 浙江省2025年八年级下册期末考试数学模拟卷 含答案 |

|
|
| 格式 | docx | ||
| 文件大小 | 738.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-09 20:35:05 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
浙江省2025年八年级下册期末考试数学模拟卷
满分120分 时间120分钟
一.选择题(共10小题,满分30分,每小题3分)
1.下列二次根式中,最简二次根式是( )
A. B. C. D.
2.下列与杭州亚运会有关的图案中,中心对称图形是( )
A. B. C. D.
3.一元二次方程x2﹣8x﹣2=0,配方的结果是( )
A.(x+4)2=18 B.(x+4)2=14 C.(x﹣4)2=18 D.(x﹣4)2=14
4.一次空气污染指数抽查中,收集到9天的数据如下:60,70,70,56,81,91,92,91,75.该组数据的中位数是( )
A.70 B.81 C.91 D.75
5.下列说法错误的是( )
A.平行四边形的对角线互相平分
B.矩形的对角线互相垂直且相等
C.菱形的对角线互相垂直平分
D.正方形的对角线互相垂直平分且相等
6.如图,要测量池塘两岸相对的A,B两点间的距离,可以在池塘外选一点C,连接AC、BC,分别取AC,BC的中点D,E,测得DE=8m,则AB的长是( )
A.14m B.16m C.18m D.20m
7.已知三点P1(x1,y1),P2(x2,y2),P3(1,﹣2)都在反比例函数的图象上,若x1<0<x2,则下列式子正确的是( )
A.y1<y2<0 B.y1<0<y2 C.y1>y2>0 D.y1>0>y2
8.在用求根公式求一元二次方程的根时,小珺正确地代入了a,b,c得到,则她求解的一元二次方程是( )
A.2x2﹣3x﹣1=0 B.2x2+4x﹣1=0
C.﹣x2﹣3x+2=0 D.3x2﹣2x+1=0
9.利用如图①的四个全等直角三角形,可以拼成如图②或图③所示的两个正方形,则图②与图③两个正方形的边长比值是( )
A. B. C. D.
10.如图,将含30°的三角尺放在平面直角坐标系xOy中,点B在x轴上,AC∥x轴,点M为斜边AB的中点.若反比例函数的图象经过A,M两点,反比例函数的图象经过点C,则m与n满足的等量关系是( )
A.n=3m B.n=2m C. D.
二.填空题(共6小题,满分18分,每小题3分)
11.比较大小: 5(填“>”“<”或“=”).
12.为了倡导节约用水,某家庭记录了去年12个月的月用水量如表(1≤a≤3,且为整数).根据下列关于用水量的统计,推算平均数、中位数、众数、方差中,不会发生变化的是 .
用水量x/吨 3 4 5 6 7
频数 1 2 5 4﹣a a
13.如图,四边形ABCD为平行四边形,延长AD到E,使DE=AD,连结EB,EC,DB,要使四边形DBCE成为矩形,可添加一个条件是 .(只要写出一个条件即可)
14.已知点A(x1,y1),B(x2,y2)都在反比例函数的图象上.若x1 x2=﹣2,则y1 y2的值为 .
15.甲、乙二人同时从同一地点出发,甲的速度为每秒1.5米,乙的速度为每秒1米,乙一直向东走,甲先向南走10米,后又朝北偏东某个方向走了一段后与乙相遇,则乙走了 米.
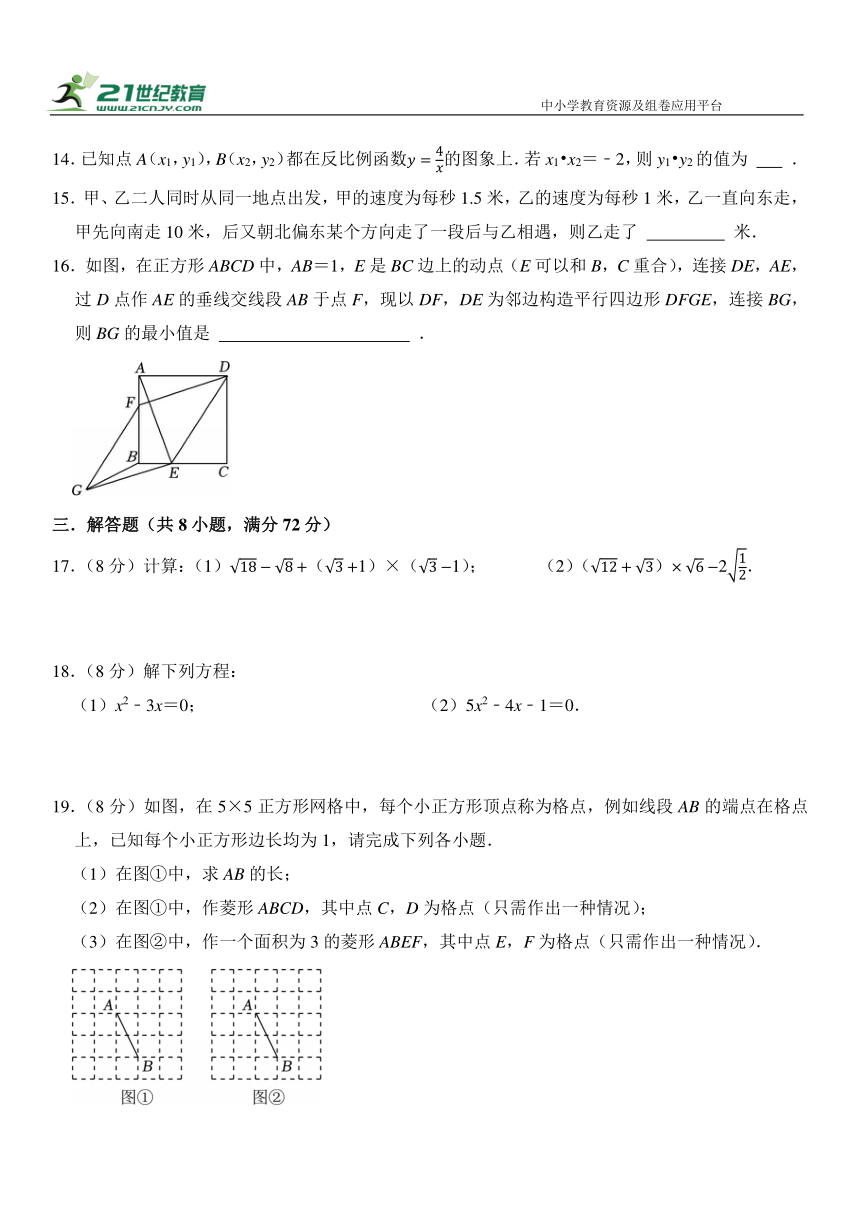
16.如图,在正方形ABCD中,AB=1,E是BC边上的动点(E可以和B,C重合),连接DE,AE,过D点作AE的垂线交线段AB于点F,现以DF,DE为邻边构造平行四边形DFGE,连接BG,则BG的最小值是 .
三.解答题(共8小题,满分72分)
17.(8分)计算:(1)(1)×(1); (2)()2.
18.(8分)解下列方程:
(1)x2﹣3x=0; (2)5x2﹣4x﹣1=0.
19.(8分)如图,在5×5正方形网格中,每个小正方形顶点称为格点,例如线段AB的端点在格点上,已知每个小正方形边长均为1,请完成下列各小题.
(1)在图①中,求AB的长;
(2)在图①中,作菱形ABCD,其中点C,D为格点(只需作出一种情况);
(3)在图②中,作一个面积为3的菱形ABEF,其中点E,F为格点(只需作出一种情况).
20.(8分)某校文化节举行班级反诈小品比赛,分为初赛和决赛,有关信息如下.
表一:初赛阶段某班评委打分情况统计表(单位:分)
评委1 评委2 评委3 评委4 评委5 评委6 评委7
9.1 9.7 9.3 9.5 9.5 9.2 9.5
表二:决宴阶段评委打分情况统计表(单位:分)
班级 台词表达 情感演绎 教育意义
甲 9.3 9.4 9.3
乙 9.5 9.1 9.8
(1)请根据表一中的信息,写出初赛阶段评委打分数据的中位数和众数.
(2)决赛阶段甲乙两班角逐冠亚军,评委分别从台词表达、情感演绎、教育意义三个方面打分,如表二(单位:分),最终得分按台词表达、情感演绎、教育意义以3:3:4的比例确定,请你通过计算说明,哪个班级最终获得了冠军.
21.(8分)如图,在菱形ABCD中,点P是BC边上的点,连结AP交对角线BD于点E,连结EC.
(1)求证:AE=CE.
(2)若∠ABC=45°,AE=PC,求∠BAP的度数.
22.(10分)如图,一次函数y1=﹣x+2的图象与反比例函数的图象交于点A(﹣1,m)和点B(n,﹣1).
(1)求反比例函数的解析式;
(2)当y1>y2时,直接写出x的取值范围.
23.(10分)定义,若四边形的一条对角线平分这个四边形的面积,则称这个四边形为倍分四边形,这条对角线称为这个四边形的倍分线.如图1,在四边形ABCD中,若S△ABC=S△ADC,则四边形ABCD为倍分四边形,AC为四边形ABCD的倍分线.
探究问题:
(1)判断:平行四边形 倍分四边形(填“是”或者“不是”);
(2)如图1,在倍分四边形ABCD中,AC是倍分线,若AC⊥AB,AB=3,AD=DC=5,求BC的长;
(3)如图2,在△ABC中,AB=BC,过点B、C分别BM⊥AC,CN⊥AB,垂足为点M、N,连接MN,若四边形BCMN为倍分四边形时,求的值.
24.(12分)如图,反比例函数与一次函数y2=k2x+b(k2≠0)的图象都经过点A(1,m)和点B(﹣2,﹣2),以AB为边作正方形ABCD(点A、B、C、D逆时针排列).
(1)求m的值和一次函数y2的解析式.
(2)求点C的坐标.
(3)将正方形ABCD平移得到正方形MNPQ,在平移过程中,使点A的对应顶点M始终在第一象限内且在反比例函数y1的图象上(点M与点A不重合),当正方形MNPQ与正方形ABCD的重叠部分为正方形时,求重叠正方形的边长.
参考答案
一.选择题(共10小题,满分30分,每小题3分)
题号 1 2 3 4 5 6 7 8 9 10
答案 C A C D B B D A C A
二.填空题(共6小题,满分18分,每小题3分)
11.>.
12.中位数和众数.
13.CD=BE或∠ADB=90°或CE⊥DE.
14.﹣8.
15.24.
16..
三.解答题(共8小题,满分72分)
17.解:(1)原式=323﹣1
2;
(2)原式=(2)
=3
=9
=8.
18.解:(1)x2﹣3x=0,
x(x﹣3)=0,
x=0或x﹣3=0,
x1=0,x2=3;
(2)5x2﹣4x﹣1=0,
(5x+1)(x﹣1)=0,
5x+1=0或x﹣1=0,
x1,x2=1.
19.解:(1)AB;
(2)如图①中,菱形ABCD即为所求;
(3)如图②中,菱形ABEF即为所求.
20.解:(1)这组数据从小到大排列为9.1,9.2,9.3,9.5,9.5,9.5,9.7,
中位数为9.5,众数为9.5;
(2)甲班得分为9.33(分),
乙班得分为9.5(分),
∵9.5>9.33,
∴乙班获得冠军.
21.(1)证明:∵四边形ABCD为菱形,
∴BA=BC,∠ABD=∠CBD,
在△ABE和△CBE中,
,
∴△ABE≌△CBE(SAS),
∴AE=CE;
(2)解:设∠BAP=α,
∵△ABE≌△CBE,
∴∠BAP=∠BCE=α,
∵AE=PC,AE=CE,
∴PC=CE,
∴∠CPE=∠CEP(180°﹣∠BCE)=90°α,
∵∠CPE是△ABP的一个外角,∠ABC=45°,
∴∠CPE=∠ABC+∠BAP,
∴90°α=45°+α,
∴α=30°,
∴∠BAP=α=30°.
22.解:(1)A(﹣1,m)代入y1=﹣x+2得m=1+2=3,
∴A(﹣1,3),
将A点坐标(﹣1,3)代入,
得,
解得,k=﹣3,
∴反比例函数的解析式为;
(2)把B(n,﹣1)代入y1=﹣x+2得﹣n+2=﹣1,
解得n=3,
∴B(3,﹣1)
∴当y1>y2时,x<﹣1或0<x<3.
23.解:(1)∵平行四边形是中心对称图形,
∴将平行四边形绕它的对称中心旋转180°可与自身重合,
∴平行四边形的一条对角线将该平行四边形分为两个全等的三角形,
∴平行四边形的一条对角线平分该平行四边形的面积,
∴平行四边形是倍分四边形,
故答案为:是.
(2)如图1,作DL⊥AC于点D,则∠CLD=90°,S△ADCAC DL,
∵AC⊥AB,
∴∠BAC=90°,S△ABCAC AB,
∵四边形ABCD是倍分四边形,AC是倍分线,
∴S△ADC=S△ABC,
∴AC DLAC AB,
∴DL=AB=3,
∵AD=DC=5,
∴AL=CL4,
∴AC=2AL=8,
∴BC,
∴BC的长是.
(3)∵AB=BC,BM⊥AC于点M,
∴AM=CM,∠BMC=90°,
∴S△ABM=S△CBM,
∵S△NBM≠S△ABM,
∴S△NBM≠S△CBM,
∵四边形BCMN为倍分四边形,
∴S△MCN=S△BCN,
如图2,取BC的中点G,连接MG交CN于点H,则BG=CG,
∴MG∥AB,
∵CN⊥AB于点N,
∴∠MHC=∠ANC=∠BNC=90°,
∴NM=CM=AMAC,
∵MH⊥CN,
∴NH=CH,
∴GHBN,
∵CN MHCN BN,
∴MH=BN,
设GH=x,则MH=BN=2GH=2x,
∴MG=BG=CG=GH+MH=x+2x=3x,
∴BC=2BG=6x,
∴CN4x,
∴CHCN=2x,
∴CM2x,
∴BM2x,
∴,
∴的值为.
24.解:(1)将点A、B的坐标代入反比例函数表达式得:k1=﹣2×(﹣2)=1×m,
解得:m=4,
将点A(1,4)、B的坐标代入函数表达式得:
,解得:,
则一次函数的表达式为:y=2x+2;
(2)过点B作y轴的平行线交过点A和x轴的平行线于点G,交故点C和x轴的平行线于点H,
∵∠GBA+∠CBH=90°,∠CBH+∠HBC=90°,
∴∠GAB=∠HBC,
∵∠BGA=∠CHB=90°,AB=CB,
∴△BGA≌△CHB(AAS),
则CH=GB=4﹣(﹣2)=6,BH=GA=1﹣(﹣2)=3,
则点C(4,﹣5);
(3)当正方形MNPQ与正方形ABCD的重叠部分为正方形时,则点M在AC上,
由点A、C的坐标得,直线AC的表达式为:y=﹣3x+7,
由(1)知,反比例函数表达式为:y,
联立上述两个函数表达式得:﹣3x+7,
解得:x=1(舍去)或,
即点M(,3),
由点C、M的坐标得,CM,
则重叠正方形的边长为CM.
浙江省2025年八年级下册期末考试数学模拟卷
满分120分 时间120分钟
一.选择题(共10小题,满分30分,每小题3分)
1.下列二次根式中,最简二次根式是( )
A. B. C. D.
2.下列与杭州亚运会有关的图案中,中心对称图形是( )
A. B. C. D.
3.一元二次方程x2﹣8x﹣2=0,配方的结果是( )
A.(x+4)2=18 B.(x+4)2=14 C.(x﹣4)2=18 D.(x﹣4)2=14
4.一次空气污染指数抽查中,收集到9天的数据如下:60,70,70,56,81,91,92,91,75.该组数据的中位数是( )
A.70 B.81 C.91 D.75
5.下列说法错误的是( )
A.平行四边形的对角线互相平分
B.矩形的对角线互相垂直且相等
C.菱形的对角线互相垂直平分
D.正方形的对角线互相垂直平分且相等
6.如图,要测量池塘两岸相对的A,B两点间的距离,可以在池塘外选一点C,连接AC、BC,分别取AC,BC的中点D,E,测得DE=8m,则AB的长是( )
A.14m B.16m C.18m D.20m
7.已知三点P1(x1,y1),P2(x2,y2),P3(1,﹣2)都在反比例函数的图象上,若x1<0<x2,则下列式子正确的是( )
A.y1<y2<0 B.y1<0<y2 C.y1>y2>0 D.y1>0>y2
8.在用求根公式求一元二次方程的根时,小珺正确地代入了a,b,c得到,则她求解的一元二次方程是( )
A.2x2﹣3x﹣1=0 B.2x2+4x﹣1=0
C.﹣x2﹣3x+2=0 D.3x2﹣2x+1=0
9.利用如图①的四个全等直角三角形,可以拼成如图②或图③所示的两个正方形,则图②与图③两个正方形的边长比值是( )
A. B. C. D.
10.如图,将含30°的三角尺放在平面直角坐标系xOy中,点B在x轴上,AC∥x轴,点M为斜边AB的中点.若反比例函数的图象经过A,M两点,反比例函数的图象经过点C,则m与n满足的等量关系是( )
A.n=3m B.n=2m C. D.
二.填空题(共6小题,满分18分,每小题3分)
11.比较大小: 5(填“>”“<”或“=”).
12.为了倡导节约用水,某家庭记录了去年12个月的月用水量如表(1≤a≤3,且为整数).根据下列关于用水量的统计,推算平均数、中位数、众数、方差中,不会发生变化的是 .
用水量x/吨 3 4 5 6 7
频数 1 2 5 4﹣a a
13.如图,四边形ABCD为平行四边形,延长AD到E,使DE=AD,连结EB,EC,DB,要使四边形DBCE成为矩形,可添加一个条件是 .(只要写出一个条件即可)
14.已知点A(x1,y1),B(x2,y2)都在反比例函数的图象上.若x1 x2=﹣2,则y1 y2的值为 .
15.甲、乙二人同时从同一地点出发,甲的速度为每秒1.5米,乙的速度为每秒1米,乙一直向东走,甲先向南走10米,后又朝北偏东某个方向走了一段后与乙相遇,则乙走了 米.
16.如图,在正方形ABCD中,AB=1,E是BC边上的动点(E可以和B,C重合),连接DE,AE,过D点作AE的垂线交线段AB于点F,现以DF,DE为邻边构造平行四边形DFGE,连接BG,则BG的最小值是 .
三.解答题(共8小题,满分72分)
17.(8分)计算:(1)(1)×(1); (2)()2.
18.(8分)解下列方程:
(1)x2﹣3x=0; (2)5x2﹣4x﹣1=0.
19.(8分)如图,在5×5正方形网格中,每个小正方形顶点称为格点,例如线段AB的端点在格点上,已知每个小正方形边长均为1,请完成下列各小题.
(1)在图①中,求AB的长;
(2)在图①中,作菱形ABCD,其中点C,D为格点(只需作出一种情况);
(3)在图②中,作一个面积为3的菱形ABEF,其中点E,F为格点(只需作出一种情况).
20.(8分)某校文化节举行班级反诈小品比赛,分为初赛和决赛,有关信息如下.
表一:初赛阶段某班评委打分情况统计表(单位:分)
评委1 评委2 评委3 评委4 评委5 评委6 评委7
9.1 9.7 9.3 9.5 9.5 9.2 9.5
表二:决宴阶段评委打分情况统计表(单位:分)
班级 台词表达 情感演绎 教育意义
甲 9.3 9.4 9.3
乙 9.5 9.1 9.8
(1)请根据表一中的信息,写出初赛阶段评委打分数据的中位数和众数.
(2)决赛阶段甲乙两班角逐冠亚军,评委分别从台词表达、情感演绎、教育意义三个方面打分,如表二(单位:分),最终得分按台词表达、情感演绎、教育意义以3:3:4的比例确定,请你通过计算说明,哪个班级最终获得了冠军.
21.(8分)如图,在菱形ABCD中,点P是BC边上的点,连结AP交对角线BD于点E,连结EC.
(1)求证:AE=CE.
(2)若∠ABC=45°,AE=PC,求∠BAP的度数.
22.(10分)如图,一次函数y1=﹣x+2的图象与反比例函数的图象交于点A(﹣1,m)和点B(n,﹣1).
(1)求反比例函数的解析式;
(2)当y1>y2时,直接写出x的取值范围.
23.(10分)定义,若四边形的一条对角线平分这个四边形的面积,则称这个四边形为倍分四边形,这条对角线称为这个四边形的倍分线.如图1,在四边形ABCD中,若S△ABC=S△ADC,则四边形ABCD为倍分四边形,AC为四边形ABCD的倍分线.
探究问题:
(1)判断:平行四边形 倍分四边形(填“是”或者“不是”);
(2)如图1,在倍分四边形ABCD中,AC是倍分线,若AC⊥AB,AB=3,AD=DC=5,求BC的长;
(3)如图2,在△ABC中,AB=BC,过点B、C分别BM⊥AC,CN⊥AB,垂足为点M、N,连接MN,若四边形BCMN为倍分四边形时,求的值.
24.(12分)如图,反比例函数与一次函数y2=k2x+b(k2≠0)的图象都经过点A(1,m)和点B(﹣2,﹣2),以AB为边作正方形ABCD(点A、B、C、D逆时针排列).
(1)求m的值和一次函数y2的解析式.
(2)求点C的坐标.
(3)将正方形ABCD平移得到正方形MNPQ,在平移过程中,使点A的对应顶点M始终在第一象限内且在反比例函数y1的图象上(点M与点A不重合),当正方形MNPQ与正方形ABCD的重叠部分为正方形时,求重叠正方形的边长.
参考答案
一.选择题(共10小题,满分30分,每小题3分)
题号 1 2 3 4 5 6 7 8 9 10
答案 C A C D B B D A C A
二.填空题(共6小题,满分18分,每小题3分)
11.>.
12.中位数和众数.
13.CD=BE或∠ADB=90°或CE⊥DE.
14.﹣8.
15.24.
16..
三.解答题(共8小题,满分72分)
17.解:(1)原式=323﹣1
2;
(2)原式=(2)
=3
=9
=8.
18.解:(1)x2﹣3x=0,
x(x﹣3)=0,
x=0或x﹣3=0,
x1=0,x2=3;
(2)5x2﹣4x﹣1=0,
(5x+1)(x﹣1)=0,
5x+1=0或x﹣1=0,
x1,x2=1.
19.解:(1)AB;
(2)如图①中,菱形ABCD即为所求;
(3)如图②中,菱形ABEF即为所求.
20.解:(1)这组数据从小到大排列为9.1,9.2,9.3,9.5,9.5,9.5,9.7,
中位数为9.5,众数为9.5;
(2)甲班得分为9.33(分),
乙班得分为9.5(分),
∵9.5>9.33,
∴乙班获得冠军.
21.(1)证明:∵四边形ABCD为菱形,
∴BA=BC,∠ABD=∠CBD,
在△ABE和△CBE中,
,
∴△ABE≌△CBE(SAS),
∴AE=CE;
(2)解:设∠BAP=α,
∵△ABE≌△CBE,
∴∠BAP=∠BCE=α,
∵AE=PC,AE=CE,
∴PC=CE,
∴∠CPE=∠CEP(180°﹣∠BCE)=90°α,
∵∠CPE是△ABP的一个外角,∠ABC=45°,
∴∠CPE=∠ABC+∠BAP,
∴90°α=45°+α,
∴α=30°,
∴∠BAP=α=30°.
22.解:(1)A(﹣1,m)代入y1=﹣x+2得m=1+2=3,
∴A(﹣1,3),
将A点坐标(﹣1,3)代入,
得,
解得,k=﹣3,
∴反比例函数的解析式为;
(2)把B(n,﹣1)代入y1=﹣x+2得﹣n+2=﹣1,
解得n=3,
∴B(3,﹣1)
∴当y1>y2时,x<﹣1或0<x<3.
23.解:(1)∵平行四边形是中心对称图形,
∴将平行四边形绕它的对称中心旋转180°可与自身重合,
∴平行四边形的一条对角线将该平行四边形分为两个全等的三角形,
∴平行四边形的一条对角线平分该平行四边形的面积,
∴平行四边形是倍分四边形,
故答案为:是.
(2)如图1,作DL⊥AC于点D,则∠CLD=90°,S△ADCAC DL,
∵AC⊥AB,
∴∠BAC=90°,S△ABCAC AB,
∵四边形ABCD是倍分四边形,AC是倍分线,
∴S△ADC=S△ABC,
∴AC DLAC AB,
∴DL=AB=3,
∵AD=DC=5,
∴AL=CL4,
∴AC=2AL=8,
∴BC,
∴BC的长是.
(3)∵AB=BC,BM⊥AC于点M,
∴AM=CM,∠BMC=90°,
∴S△ABM=S△CBM,
∵S△NBM≠S△ABM,
∴S△NBM≠S△CBM,
∵四边形BCMN为倍分四边形,
∴S△MCN=S△BCN,
如图2,取BC的中点G,连接MG交CN于点H,则BG=CG,
∴MG∥AB,
∵CN⊥AB于点N,
∴∠MHC=∠ANC=∠BNC=90°,
∴NM=CM=AMAC,
∵MH⊥CN,
∴NH=CH,
∴GHBN,
∵CN MHCN BN,
∴MH=BN,
设GH=x,则MH=BN=2GH=2x,
∴MG=BG=CG=GH+MH=x+2x=3x,
∴BC=2BG=6x,
∴CN4x,
∴CHCN=2x,
∴CM2x,
∴BM2x,
∴,
∴的值为.
24.解:(1)将点A、B的坐标代入反比例函数表达式得:k1=﹣2×(﹣2)=1×m,
解得:m=4,
将点A(1,4)、B的坐标代入函数表达式得:
,解得:,
则一次函数的表达式为:y=2x+2;
(2)过点B作y轴的平行线交过点A和x轴的平行线于点G,交故点C和x轴的平行线于点H,
∵∠GBA+∠CBH=90°,∠CBH+∠HBC=90°,
∴∠GAB=∠HBC,
∵∠BGA=∠CHB=90°,AB=CB,
∴△BGA≌△CHB(AAS),
则CH=GB=4﹣(﹣2)=6,BH=GA=1﹣(﹣2)=3,
则点C(4,﹣5);
(3)当正方形MNPQ与正方形ABCD的重叠部分为正方形时,则点M在AC上,
由点A、C的坐标得,直线AC的表达式为:y=﹣3x+7,
由(1)知,反比例函数表达式为:y,
联立上述两个函数表达式得:﹣3x+7,
解得:x=1(舍去)或,
即点M(,3),
由点C、M的坐标得,CM,
则重叠正方形的边长为CM.
同课章节目录
