【期末押题预测】期末核心考点 变化的量(含解析)2024-2025学年六年级下册数学北师大版
文档属性
| 名称 | 【期末押题预测】期末核心考点 变化的量(含解析)2024-2025学年六年级下册数学北师大版 |  | |
| 格式 | docx | ||
| 文件大小 | 158.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-10 05:05:49 | ||
图片预览


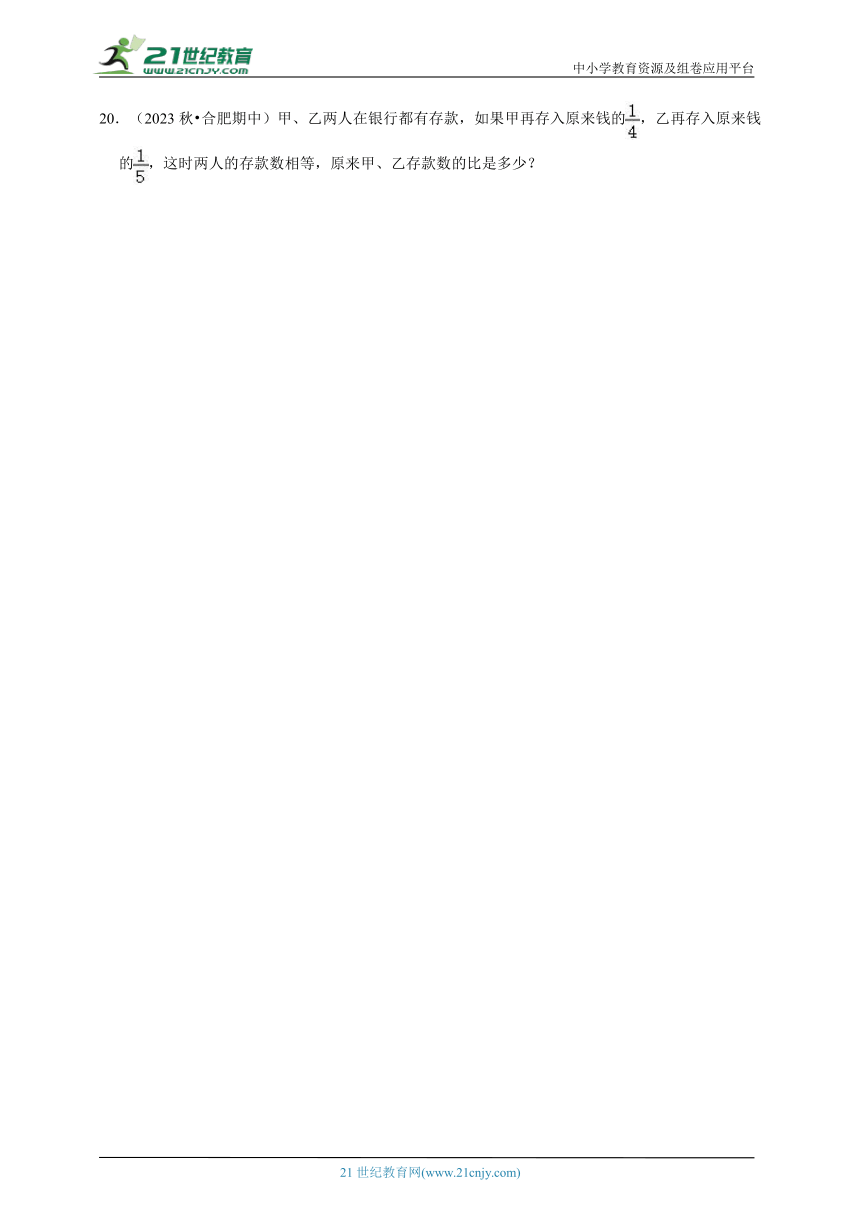


文档简介
中小学教育资源及组卷应用平台
期末核心考点 变化的量
一.选择题(共5小题)
1.(2025春 潍城区期中)一个圆柱的侧面沿高展开后是一个正方形,那么它的高和底面半径的比是( )
A.π:1 B.π:2 C.2π:1 D.1:1
2.(2025春 罗湖区期中)甲数的等于乙数的(甲、乙都不为0),那么甲数和乙数的比是( )
A.2:1 B.1:4 C.4:1 D.1:2
3.(2025春 南京期中)中国古代数学名著《算法统宗》中记载了一些诗歌形式的数学问题,其中一个问题是:“三百七十八里关,初行健步不为难,次日脚痛减一半,六朝才得到其关,要见每朝行里数,请公仔细算相还。”意思是:一个人到关口要走378里路,第一天健步行走,从第二天起因脚痛,每天走的路程为前一天的一半,走了6天到达关口,算算每天行走的里数。根据题中的信息,这个人第一天走的路程与总路程的最简整数比是( )
A.1:2 B.32:63 C.1:3 D.32:64
4.(2025春 溧阳市期中)一个平行四边形底和高的比是2:3,把这个平行四边形按4:1的比放大后,底与高的比是( )
A.2:3 B.4:1 C.8:3 D.3:8
5.(2025春 江宁区期中)星华小学六(1)班一共有40名同学,该班男、女同学人数的比不可能是( )
A.5:3 B.3:2 C.3:5 D.3:4
二.填空题(共5小题)
6.(2025春 丰县期中)某班男生人数是全班人数的,男、女生人数的比是 : 。
7.(2025春 牡丹区校级期中)A牌纯净水比B牌纯净水的容量多20%,A牌纯净水与B牌纯净水容量的是最简整数比是 .
8.(2024秋 黔江区期末)如图,阴影部分的面积与三角形的比是4:9;阴影部分与大正方形的面积比是8:27,那么,三角形和大正方形的面积比是 : ;三角形的空白部分与正方形的空白部分的面积比是 : 。
9.(2024秋 鹰手营子矿区期末)两个圆半径的比是2:3,它们直径的比是 ,周长的比是 ,面积的比是 。
A.4:9
B.2:3
10.(2024秋 崂山区期末)六(1)班男生人数占全班总人数的,那么女生人数和全班总人数的比是 ,男生人数是女生人数的 %。
三.判断题(共5小题)
11.(2024秋 灞桥区期末)1千克盐溶解在100千克水中,盐与盐水的比是1:100。
12.(2024秋 兰州期末)白兔比灰兔多40%,则白兔与灰兔只数的比是7:5。
13.(2024秋 崂山区期末)一个三角形,三条边的比可能是1:3:5。
14.(2024秋 河东区期末)六年一班共有38人,该班男生和女生人数的比可能是3:2。
15.(2024秋 蓝田县期末)如果甲数比乙数多,那么甲数与乙数的比是2:3。
四.计算题(共1小题)
16.(2022春 临泉县期中)化简比.
2.5:0.45
五.应用题(共4小题)
17.(2024 深圳模拟)有甲、乙、丙三个相互咬合的齿轮,当甲轮转5圈时,乙轮转7圈,丙轮转2圈,求这三个齿轮的齿数比.
18.(2023秋 宣恩县月考)要从一个长5分米,宽4分米的长方形木板上锯下一个最大的圆,剩下的木板与圆面积的比是多少?
19.(2022秋 盱眙县期末)动物的小腿骨(胫骨)与大腿骨(股骨)的长度比值越大的动物跑得越快,
动物 盐都龙 马 羚羊
胫骨与股骨的比 59:50 23:25 5:4
根据这个结论,计算并比较三种动物中,谁跑得最快?
20.(2023秋 合肥期中)甲、乙两人在银行都有存款,如果甲再存入原来钱的,乙再存入原来钱的,这时两人的存款数相等,原来甲、乙存款数的比是多少?
期末核心考点押题预测 变化的量
参考答案与试题解析
一.选择题(共5小题)
1.(2025春 潍城区期中)一个圆柱的侧面沿高展开后是一个正方形,那么它的高和底面半径的比是( )
A.π:1 B.π:2 C.2π:1 D.1:1
【考点】比的意义.
【专题】应用意识.
【答案】C
【分析】圆柱的侧面沿高展开后是一个正方形,即圆柱的底面周长和高相同,据此解答。
【解答】解:设圆柱底面半径为r,则底面周长=圆柱高=2πr,
所以2πr:r=2π:1。
即圆柱的高和底面半径的比是2π:1。
故选:C。
【点评】本题考查了比的意义以及圆柱侧面展开图的应用。
2.(2025春 罗湖区期中)甲数的等于乙数的(甲、乙都不为0),那么甲数和乙数的比是( )
A.2:1 B.1:4 C.4:1 D.1:2
【考点】比的意义.
【专题】数感.
【答案】C
【分析】把甲数(或乙数)看作“1”,根据分数乘、除法的意义,求出乙数(或甲数),再根据比的意义即可写出甲数和乙数的比,再化成最简整数比。
【解答】解:把甲数看作1
则乙数是:1×÷
=×
=
1:=4:1
答:甲数和乙数的比是4:1。
故选:C。
【点评】关键是两数中一个看作“1”,根据分数乘、除法的意义,求出另一个数。
3.(2025春 南京期中)中国古代数学名著《算法统宗》中记载了一些诗歌形式的数学问题,其中一个问题是:“三百七十八里关,初行健步不为难,次日脚痛减一半,六朝才得到其关,要见每朝行里数,请公仔细算相还。”意思是:一个人到关口要走378里路,第一天健步行走,从第二天起因脚痛,每天走的路程为前一天的一半,走了6天到达关口,算算每天行走的里数。根据题中的信息,这个人第一天走的路程与总路程的最简整数比是( )
A.1:2 B.32:63 C.1:3 D.32:64
【考点】比的意义.
【专题】运算能力.
【答案】B
【分析】根据题意,设第一天走的路程为x里,第二天走的路程为x里,第三天走的路程为x里,第四天走的路程为x里,第五天走的路程为x里,第六天走的路程为x里,这六天一共走了378里,据此列出方程,求出第一天走的路程,再求出这个人第一天走的路程与总路程的最简整数比即可。
【解答】解:设第一天走的路程为x里,第二天走的路程为x里,第三天走的路程为x里,第四天走的路程为x里,第五天走的路程为x里,第六天走的路程为x里。
x+x+x+x+x+x=378
x=378
x=192
192:378=32:63
答:这个人第一天走的路程与总路程的最简单的整数比是32:63。
故选:B。
【点评】本题考查了比的意义和应用知识,结合题意分析解答即可。
4.(2025春 溧阳市期中)一个平行四边形底和高的比是2:3,把这个平行四边形按4:1的比放大后,底与高的比是( )
A.2:3 B.4:1 C.8:3 D.3:8
【考点】比的意义.
【专题】数据分析观念.
【答案】A
【分析】将平行四边形按4:1的比放大就是把原图的底和高分别扩大4倍,据此解答。
【解答】解:由分析可知:把这个平行四边形按4:1的比放大后,底和高分别扩大4倍,它们的比仍然是2:3。
故选:A。
【点评】本题主要考查图形的放大与缩小的灵活应用。
5.(2025春 江宁区期中)星华小学六(1)班一共有40名同学,该班男、女同学人数的比不可能是( )
A.5:3 B.3:2 C.3:5 D.3:4
【考点】比的意义.
【专题】应用意识.
【答案】D
【分析】男女生人数的份数之和是40的因数,据此判断。
【解答】解:A.5+3=8,8是40的因数,符合题意;
B.3+2=5,5是40的因数,符合题意;
C.3+5=8,8是40的因数,符合题意;
D.3+4=7,7不是40的因数,不符合题意。
故选:D。
【点评】本题考查了比的意义的应用。
二.填空题(共5小题)
6.(2025春 丰县期中)某班男生人数是全班人数的,男、女生人数的比是 7 : 5 。
【考点】比的意义.
【专题】运算能力.
【答案】7:5。
【分析】欲求男、女生人数的比,先把全班学生看作单位“1”再求出女生人数占全班人数的几分之几,然后把男女生各占全班人数的分率相比即可求得。
【解答】解::(1﹣)
=:
=(×12):(×12)
=7:5
答:男、女生人数的比是7:5。
故答案为:7:5。
【点评】这道题重点考查了比的意义,同时也考查分数的意义,由它可求出女生的人数占全班人数的几分之几,本题也可用按比例分配去解答。
7.(2025春 牡丹区校级期中)A牌纯净水比B牌纯净水的容量多20%,A牌纯净水与B牌纯净水容量的是最简整数比是 6:5 .
【考点】比的意义;百分数的意义、读写及应用.
【专题】比和比例.
【答案】见试题解答内容
【分析】设B牌纯净水的容量为1,则A牌纯净水的容量为1+20%,写出比,然后根据比的基本性质化成最简整数比即可解答.
【解答】解:(1+20%):1=120%:1=6:5.
故答案为:6:5.
【点评】本题主要考查百分数的意义和比的基本性质,根据题意写出比是解答本题的关键.
8.(2024秋 黔江区期末)如图,阴影部分的面积与三角形的比是4:9;阴影部分与大正方形的面积比是8:27,那么,三角形和大正方形的面积比是 2 : 3 ;三角形的空白部分与正方形的空白部分的面积比是 10 : 19 。
【考点】比的意义.
【专题】推理能力;应用意识.
【答案】2,3;10,19。
【分析】设阴影部分面积是8;根据题意,阴影部分面积与三角形面积比是4:9,即阴影部分面积是三角形面积的;把三角形面积看作单位“1”,阴影部分占三角形面积的,对应的是阴影部分面积8,求单位“1”,用8÷,求出三角形面积。
阴影部分与大正方形面积比是8:27,即阴影部分面积是大正方形面积的,把大正方形面积看作单位“1”,阴影部分面积占大正方形面积的,对应的是阴影部分面积8,求大正方形面积,用8÷,求出大正方形面积;再根据比的意义,用三角形面积:大正方形面积,即可解答。
再用三角形面积﹣阴影部分面积,求出三角形的空白面积;再用大正方形面积﹣阴影部分面积,求出大正方形空白面积,根据比的意义,用三角形的空白面积:大正方形空白面积,即可解答。
【解答】解:设阴影部分面积是8。
三角形面积:
8÷
=8×
=18
大正方形面积:
8÷
=8×
=27
18:27
=(18÷9):(27÷9)
=2:3
(18﹣8):(27﹣8)=10:19
答:三角形和大正方形的面积比是2:3;三角形的空白部分与正方形的空白部分的面积比是10:19。
故答案为:2,3;10,19。
【点评】本题主要考查了比的意义,解答此题的关键:把比转化为分数,即转化为同一单位“1”下进行比较,进而得出结论。
9.(2024秋 鹰手营子矿区期末)两个圆半径的比是2:3,它们直径的比是 B ,周长的比是 B ,面积的比是 A 。
A.4:9
B.2:3
【考点】比的意义;圆、圆环的周长;圆、圆环的面积.
【专题】应用意识.
【答案】B,B,A。
【分析】把两个圆的半径分别看作“2”、“3”,根据半径与直径的关系“d=2r”分别求出两个圆直径,根据比的意义即可写出它们的直径比,再化成最简整数比;根据圆周长计算公式“C=2πr”分别求出两个圆的周长,据比的意义即可写出它们的周长比,再化成最简整数比;根据圆面积计算公式“S=πr2”分别求出两个圆的面积,据比的意义即可写出它们的面积比,再化成最简整数比。
【解答】解:(2×2):(3×2)
=4:6
=2:3
(2π×2):(2π×3)
=4π:6π
=2:3
(π×22):(π×32)
=4π:9π
=4:9
答:它们直径的比是2:3,周长的比是2:3,面积的比是4:9。
故答案为:B,B,A。
【点评】此题考查了比的意义及化简。关键是掌握圆半径与直径的关系、圆周长计算公式、圆面积计算公式。
10.(2024秋 崂山区期末)六(1)班男生人数占全班总人数的,那么女生人数和全班总人数的比是 4:9 ,男生人数是女生人数的 125 %。
【考点】比的意义;百分数的实际应用.
【专题】应用意识.
【答案】4:9;125。
【分析】根据题意,把六(1)班男生人数看作5份,全班人数看作9份,则女生人数为(9﹣5)份,用女生人数的份数除以全班人数的份数即可求出女生人数和全班总人数的比,用男生人数的份数除以女生人数的份数即可求出男生人数是女生人数的百分数。据此解答。
【解答】解:(9﹣5):9=4:9
5÷4×100%=125%
答:女生人数和全班总人数的比是4:9,男生人数是女生人数的125%。
故答案为:4:9;125。
【点评】本题考查了比的意义的应用以及百分数的应用。
三.判断题(共5小题)
11.(2024秋 灞桥区期末)1千克盐溶解在100千克水中,盐与盐水的比是1:100。 ×
【考点】比的意义.
【专题】应用意识.
【答案】×
【分析】盐与盐水的比是盐比(盐的质量+水的质量),据此解答即可。
【解答】解:盐与盐水的比是:
1:(1+100)=1:101
所以盐与盐水的比是1:101。
所以原题说法错误。
故答案为:×。
【点评】明确盐与盐水的比是用盐的质量比盐与水的质量和是解题的关键。
12.(2024秋 兰州期末)白兔比灰兔多40%,则白兔与灰兔只数的比是7:5。 √
【考点】比的意义.
【专题】分数和百分数;比和比例;运算能力.
【答案】√。
【分析】灰兔的只数看作单位“1”,白兔的只数是灰兔的(1+40%),根据比的意义,两个数相除,也叫两个数的比。即可解答。
【解答】解:(1+40%):1=7:5
白兔比灰兔多40%,则白兔与灰兔只数的比是7:5。原题说法是正确的。
故答案为:√。
【点评】本题考查了百分数的意义和比的意义。
13.(2024秋 崂山区期末)一个三角形,三条边的比可能是1:3:5。 ×
【考点】比的意义.
【专题】应用意识.
【答案】×。
【分析】根据三角形三边关系:两边之和大于第三边,把三角形的三边看作1份,3份,5份,两份之和小于第三份,原说法错误。
【解答】解:1+3<5,即两边之和小于第三边,不符合三角形三边关系,即原说法错误。
故答案为:×。
【点评】本题考查了比的意义的应用以及三角形三边关系的应用。
14.(2024秋 河东区期末)六年一班共有38人,该班男生和女生人数的比可能是3:2。 ×
【考点】比的意义.
【专题】应用意识.
【答案】×。
【分析】男生和女生人数的比可能是3:2,即男生人数占全班人数的份数是3份,女生人数占全班人数的份数是2份,男女生份数之和即为(3+2)份,是全班人数38的因数,据此判断。
【解答】解:38÷(3+2)=7……3
即38不是份数和的倍数,即原说法错误。
故答案为:×。
【点评】本题考查了比的意义的应用。
15.(2024秋 蓝田县期末)如果甲数比乙数多,那么甲数与乙数的比是2:3。 ×
【考点】比的意义.
【专题】比和比例;应用意识.
【答案】×。
【分析】把乙数看作单位“1”,那么甲数是(1+),再写出它们的比,再化简,即可解答。
【解答】解:(1+):1
=
=
=5:3
答:甲数与乙数的比是5:3。
所以原题说法错误。
故答案为:×。
【点评】本题考查的是比的意义,理解和应用比的意义是解答关键。
四.计算题(共1小题)
16.(2022春 临泉县期中)化简比.
2.5:0.45
【考点】比的意义.
【专题】比和比例;运算能力.
【答案】见试题解答内容
【分析】根据比的基本性质,即比的前项和后项同时乘或除以一个相同的数(0除外)比值不变,进而把比化成最简比.
【解答】解:(1):
=():()
=4:3;
(2):0.5
=(×8):(0.5×8)
=5:4;
(3)2.5:0.45
=(2.5×20):(0.45×20)
=50:9;
(4)15:
=(15÷):(÷)
=25:1.
【点评】此题主要考查了化简比的方法,另外还要注意化简比的结果是一个比,它的前项和后项都是整数,并且是互质数.
五.应用题(共4小题)
17.(2024 深圳模拟)有甲、乙、丙三个相互咬合的齿轮,当甲轮转5圈时,乙轮转7圈,丙轮转2圈,求这三个齿轮的齿数比.
【考点】比的意义.
【专题】比和比例;数感.
【答案】见试题解答内容
【分析】甲乙丙三个齿轮转数比为5:7:2,根据齿数与转数成反比例的关系,甲齿:乙齿=7:5=14:10,乙齿:丙齿=2:7=10:35,所以甲齿:乙齿:丙齿=14:10:35.
【解答】解:甲乙丙三个齿轮转数比为5:7:2,
根据齿数与转数成反比例的关系可得:
甲齿:乙齿=7:5=14:10
乙齿:丙齿=2:7=10:35
所以甲齿:乙齿:丙齿=14:10:35
答:这三个齿轮的齿数比是14:10:35.
【点评】解答此题关键是明确齿数与转数成反比例.
18.(2023秋 宣恩县月考)要从一个长5分米,宽4分米的长方形木板上锯下一个最大的圆,剩下的木板与圆面积的比是多少?
【考点】比的意义.
【专题】应用题;应用意识.
【答案】93:157。
【分析】根据题意可知,锯下的圆以长方形的宽为直径,再求出圆的面积和长方形的面积,用求得的长方形的面积减去圆的面积求出剩下木板的面积,根据比的意义写出剩下的木板与圆面积的比即可。
【解答】解:4÷2=2(分米)
3.14×22
=3.14×4
=12.56(平方分米)
5×4=20(平方分米)
20﹣12.56=7.44(平方分米)
7.44:12.56=(7.44÷8):(12.56÷8)=0.93:1.57=(0.93×100):(1.57×100)=93:157
答:剩下的木板与圆面积的比是93:157。
【点评】此题考查比的应用。掌握长方形、圆形的面积计算公式和化简比是解答的关键。
19.(2022秋 盱眙县期末)动物的小腿骨(胫骨)与大腿骨(股骨)的长度比值越大的动物跑得越快,
动物 盐都龙 马 羚羊
胫骨与股骨的比 59:50 23:25 5:4
根据这个结论,计算并比较三种动物中,谁跑得最快?
【考点】比的意义.
【专题】比和比例.
【答案】见试题解答内容
【分析】比值是比的前项除以后项的商,据此即可求出三种动物小腿骨(胫骨)与大腿骨(股骨)的长度比值,通过比较即可确定这一种动物中哪种跑得最快.
【解答】解:盐都龙:59:50=59÷50=1.18
马:23:25=23÷25=0.92
羚羊:5÷4=5÷4=1.25
1.25>1.18>0.92
答:羚羊跑得最快.
【点评】此题主要是考查求比值,根据比值的意义即可求得比的比值.比值既可用小数表示,也可用分数表示,还可用整数表示.
20.(2023秋 合肥期中)甲、乙两人在银行都有存款,如果甲再存入原来钱的,乙再存入原来钱的,这时两人的存款数相等,原来甲、乙存款数的比是多少?
【考点】比的意义.
【专题】比和比例;数感;运算能力.
【答案】24:25。
【分析】把甲原来存款数看作单位“1”,再存入原来钱的,就相当于原来存款数的(1+)。把甲存入原来钱的后的钱数、乙再存入原来钱的后的钱数都看作a,根据分数除法的意义,用a除以(1+)就是甲原来的存款数,用a除以(1+)就是乙原来的存款数,再根据比的意义即可写出原来甲、乙存款数,并化成最简整数比。
【解答】解:[a÷(1+)]:[a÷(1+)]
=a:a
=24:25
答:原来甲、乙存款的比是24:25。
【点评】此题是考查比的意义及化简。关键是求出甲、乙原来的存款数。也可这样解答,甲存入原来钱数的,把甲原来的钱数看作是4份,现在的钱数就是5份;乙再存入原来钱数的,乙原来的钱数是5份,现在的钱数就是6份,5和6的最小公倍数是30,甲的钱每份是6,乙的钱每份是5,则原来甲、乙存款钱数的比是:(4×6):(5×5)=24:25。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末核心考点 变化的量
一.选择题(共5小题)
1.(2025春 潍城区期中)一个圆柱的侧面沿高展开后是一个正方形,那么它的高和底面半径的比是( )
A.π:1 B.π:2 C.2π:1 D.1:1
2.(2025春 罗湖区期中)甲数的等于乙数的(甲、乙都不为0),那么甲数和乙数的比是( )
A.2:1 B.1:4 C.4:1 D.1:2
3.(2025春 南京期中)中国古代数学名著《算法统宗》中记载了一些诗歌形式的数学问题,其中一个问题是:“三百七十八里关,初行健步不为难,次日脚痛减一半,六朝才得到其关,要见每朝行里数,请公仔细算相还。”意思是:一个人到关口要走378里路,第一天健步行走,从第二天起因脚痛,每天走的路程为前一天的一半,走了6天到达关口,算算每天行走的里数。根据题中的信息,这个人第一天走的路程与总路程的最简整数比是( )
A.1:2 B.32:63 C.1:3 D.32:64
4.(2025春 溧阳市期中)一个平行四边形底和高的比是2:3,把这个平行四边形按4:1的比放大后,底与高的比是( )
A.2:3 B.4:1 C.8:3 D.3:8
5.(2025春 江宁区期中)星华小学六(1)班一共有40名同学,该班男、女同学人数的比不可能是( )
A.5:3 B.3:2 C.3:5 D.3:4
二.填空题(共5小题)
6.(2025春 丰县期中)某班男生人数是全班人数的,男、女生人数的比是 : 。
7.(2025春 牡丹区校级期中)A牌纯净水比B牌纯净水的容量多20%,A牌纯净水与B牌纯净水容量的是最简整数比是 .
8.(2024秋 黔江区期末)如图,阴影部分的面积与三角形的比是4:9;阴影部分与大正方形的面积比是8:27,那么,三角形和大正方形的面积比是 : ;三角形的空白部分与正方形的空白部分的面积比是 : 。
9.(2024秋 鹰手营子矿区期末)两个圆半径的比是2:3,它们直径的比是 ,周长的比是 ,面积的比是 。
A.4:9
B.2:3
10.(2024秋 崂山区期末)六(1)班男生人数占全班总人数的,那么女生人数和全班总人数的比是 ,男生人数是女生人数的 %。
三.判断题(共5小题)
11.(2024秋 灞桥区期末)1千克盐溶解在100千克水中,盐与盐水的比是1:100。
12.(2024秋 兰州期末)白兔比灰兔多40%,则白兔与灰兔只数的比是7:5。
13.(2024秋 崂山区期末)一个三角形,三条边的比可能是1:3:5。
14.(2024秋 河东区期末)六年一班共有38人,该班男生和女生人数的比可能是3:2。
15.(2024秋 蓝田县期末)如果甲数比乙数多,那么甲数与乙数的比是2:3。
四.计算题(共1小题)
16.(2022春 临泉县期中)化简比.
2.5:0.45
五.应用题(共4小题)
17.(2024 深圳模拟)有甲、乙、丙三个相互咬合的齿轮,当甲轮转5圈时,乙轮转7圈,丙轮转2圈,求这三个齿轮的齿数比.
18.(2023秋 宣恩县月考)要从一个长5分米,宽4分米的长方形木板上锯下一个最大的圆,剩下的木板与圆面积的比是多少?
19.(2022秋 盱眙县期末)动物的小腿骨(胫骨)与大腿骨(股骨)的长度比值越大的动物跑得越快,
动物 盐都龙 马 羚羊
胫骨与股骨的比 59:50 23:25 5:4
根据这个结论,计算并比较三种动物中,谁跑得最快?
20.(2023秋 合肥期中)甲、乙两人在银行都有存款,如果甲再存入原来钱的,乙再存入原来钱的,这时两人的存款数相等,原来甲、乙存款数的比是多少?
期末核心考点押题预测 变化的量
参考答案与试题解析
一.选择题(共5小题)
1.(2025春 潍城区期中)一个圆柱的侧面沿高展开后是一个正方形,那么它的高和底面半径的比是( )
A.π:1 B.π:2 C.2π:1 D.1:1
【考点】比的意义.
【专题】应用意识.
【答案】C
【分析】圆柱的侧面沿高展开后是一个正方形,即圆柱的底面周长和高相同,据此解答。
【解答】解:设圆柱底面半径为r,则底面周长=圆柱高=2πr,
所以2πr:r=2π:1。
即圆柱的高和底面半径的比是2π:1。
故选:C。
【点评】本题考查了比的意义以及圆柱侧面展开图的应用。
2.(2025春 罗湖区期中)甲数的等于乙数的(甲、乙都不为0),那么甲数和乙数的比是( )
A.2:1 B.1:4 C.4:1 D.1:2
【考点】比的意义.
【专题】数感.
【答案】C
【分析】把甲数(或乙数)看作“1”,根据分数乘、除法的意义,求出乙数(或甲数),再根据比的意义即可写出甲数和乙数的比,再化成最简整数比。
【解答】解:把甲数看作1
则乙数是:1×÷
=×
=
1:=4:1
答:甲数和乙数的比是4:1。
故选:C。
【点评】关键是两数中一个看作“1”,根据分数乘、除法的意义,求出另一个数。
3.(2025春 南京期中)中国古代数学名著《算法统宗》中记载了一些诗歌形式的数学问题,其中一个问题是:“三百七十八里关,初行健步不为难,次日脚痛减一半,六朝才得到其关,要见每朝行里数,请公仔细算相还。”意思是:一个人到关口要走378里路,第一天健步行走,从第二天起因脚痛,每天走的路程为前一天的一半,走了6天到达关口,算算每天行走的里数。根据题中的信息,这个人第一天走的路程与总路程的最简整数比是( )
A.1:2 B.32:63 C.1:3 D.32:64
【考点】比的意义.
【专题】运算能力.
【答案】B
【分析】根据题意,设第一天走的路程为x里,第二天走的路程为x里,第三天走的路程为x里,第四天走的路程为x里,第五天走的路程为x里,第六天走的路程为x里,这六天一共走了378里,据此列出方程,求出第一天走的路程,再求出这个人第一天走的路程与总路程的最简整数比即可。
【解答】解:设第一天走的路程为x里,第二天走的路程为x里,第三天走的路程为x里,第四天走的路程为x里,第五天走的路程为x里,第六天走的路程为x里。
x+x+x+x+x+x=378
x=378
x=192
192:378=32:63
答:这个人第一天走的路程与总路程的最简单的整数比是32:63。
故选:B。
【点评】本题考查了比的意义和应用知识,结合题意分析解答即可。
4.(2025春 溧阳市期中)一个平行四边形底和高的比是2:3,把这个平行四边形按4:1的比放大后,底与高的比是( )
A.2:3 B.4:1 C.8:3 D.3:8
【考点】比的意义.
【专题】数据分析观念.
【答案】A
【分析】将平行四边形按4:1的比放大就是把原图的底和高分别扩大4倍,据此解答。
【解答】解:由分析可知:把这个平行四边形按4:1的比放大后,底和高分别扩大4倍,它们的比仍然是2:3。
故选:A。
【点评】本题主要考查图形的放大与缩小的灵活应用。
5.(2025春 江宁区期中)星华小学六(1)班一共有40名同学,该班男、女同学人数的比不可能是( )
A.5:3 B.3:2 C.3:5 D.3:4
【考点】比的意义.
【专题】应用意识.
【答案】D
【分析】男女生人数的份数之和是40的因数,据此判断。
【解答】解:A.5+3=8,8是40的因数,符合题意;
B.3+2=5,5是40的因数,符合题意;
C.3+5=8,8是40的因数,符合题意;
D.3+4=7,7不是40的因数,不符合题意。
故选:D。
【点评】本题考查了比的意义的应用。
二.填空题(共5小题)
6.(2025春 丰县期中)某班男生人数是全班人数的,男、女生人数的比是 7 : 5 。
【考点】比的意义.
【专题】运算能力.
【答案】7:5。
【分析】欲求男、女生人数的比,先把全班学生看作单位“1”再求出女生人数占全班人数的几分之几,然后把男女生各占全班人数的分率相比即可求得。
【解答】解::(1﹣)
=:
=(×12):(×12)
=7:5
答:男、女生人数的比是7:5。
故答案为:7:5。
【点评】这道题重点考查了比的意义,同时也考查分数的意义,由它可求出女生的人数占全班人数的几分之几,本题也可用按比例分配去解答。
7.(2025春 牡丹区校级期中)A牌纯净水比B牌纯净水的容量多20%,A牌纯净水与B牌纯净水容量的是最简整数比是 6:5 .
【考点】比的意义;百分数的意义、读写及应用.
【专题】比和比例.
【答案】见试题解答内容
【分析】设B牌纯净水的容量为1,则A牌纯净水的容量为1+20%,写出比,然后根据比的基本性质化成最简整数比即可解答.
【解答】解:(1+20%):1=120%:1=6:5.
故答案为:6:5.
【点评】本题主要考查百分数的意义和比的基本性质,根据题意写出比是解答本题的关键.
8.(2024秋 黔江区期末)如图,阴影部分的面积与三角形的比是4:9;阴影部分与大正方形的面积比是8:27,那么,三角形和大正方形的面积比是 2 : 3 ;三角形的空白部分与正方形的空白部分的面积比是 10 : 19 。
【考点】比的意义.
【专题】推理能力;应用意识.
【答案】2,3;10,19。
【分析】设阴影部分面积是8;根据题意,阴影部分面积与三角形面积比是4:9,即阴影部分面积是三角形面积的;把三角形面积看作单位“1”,阴影部分占三角形面积的,对应的是阴影部分面积8,求单位“1”,用8÷,求出三角形面积。
阴影部分与大正方形面积比是8:27,即阴影部分面积是大正方形面积的,把大正方形面积看作单位“1”,阴影部分面积占大正方形面积的,对应的是阴影部分面积8,求大正方形面积,用8÷,求出大正方形面积;再根据比的意义,用三角形面积:大正方形面积,即可解答。
再用三角形面积﹣阴影部分面积,求出三角形的空白面积;再用大正方形面积﹣阴影部分面积,求出大正方形空白面积,根据比的意义,用三角形的空白面积:大正方形空白面积,即可解答。
【解答】解:设阴影部分面积是8。
三角形面积:
8÷
=8×
=18
大正方形面积:
8÷
=8×
=27
18:27
=(18÷9):(27÷9)
=2:3
(18﹣8):(27﹣8)=10:19
答:三角形和大正方形的面积比是2:3;三角形的空白部分与正方形的空白部分的面积比是10:19。
故答案为:2,3;10,19。
【点评】本题主要考查了比的意义,解答此题的关键:把比转化为分数,即转化为同一单位“1”下进行比较,进而得出结论。
9.(2024秋 鹰手营子矿区期末)两个圆半径的比是2:3,它们直径的比是 B ,周长的比是 B ,面积的比是 A 。
A.4:9
B.2:3
【考点】比的意义;圆、圆环的周长;圆、圆环的面积.
【专题】应用意识.
【答案】B,B,A。
【分析】把两个圆的半径分别看作“2”、“3”,根据半径与直径的关系“d=2r”分别求出两个圆直径,根据比的意义即可写出它们的直径比,再化成最简整数比;根据圆周长计算公式“C=2πr”分别求出两个圆的周长,据比的意义即可写出它们的周长比,再化成最简整数比;根据圆面积计算公式“S=πr2”分别求出两个圆的面积,据比的意义即可写出它们的面积比,再化成最简整数比。
【解答】解:(2×2):(3×2)
=4:6
=2:3
(2π×2):(2π×3)
=4π:6π
=2:3
(π×22):(π×32)
=4π:9π
=4:9
答:它们直径的比是2:3,周长的比是2:3,面积的比是4:9。
故答案为:B,B,A。
【点评】此题考查了比的意义及化简。关键是掌握圆半径与直径的关系、圆周长计算公式、圆面积计算公式。
10.(2024秋 崂山区期末)六(1)班男生人数占全班总人数的,那么女生人数和全班总人数的比是 4:9 ,男生人数是女生人数的 125 %。
【考点】比的意义;百分数的实际应用.
【专题】应用意识.
【答案】4:9;125。
【分析】根据题意,把六(1)班男生人数看作5份,全班人数看作9份,则女生人数为(9﹣5)份,用女生人数的份数除以全班人数的份数即可求出女生人数和全班总人数的比,用男生人数的份数除以女生人数的份数即可求出男生人数是女生人数的百分数。据此解答。
【解答】解:(9﹣5):9=4:9
5÷4×100%=125%
答:女生人数和全班总人数的比是4:9,男生人数是女生人数的125%。
故答案为:4:9;125。
【点评】本题考查了比的意义的应用以及百分数的应用。
三.判断题(共5小题)
11.(2024秋 灞桥区期末)1千克盐溶解在100千克水中,盐与盐水的比是1:100。 ×
【考点】比的意义.
【专题】应用意识.
【答案】×
【分析】盐与盐水的比是盐比(盐的质量+水的质量),据此解答即可。
【解答】解:盐与盐水的比是:
1:(1+100)=1:101
所以盐与盐水的比是1:101。
所以原题说法错误。
故答案为:×。
【点评】明确盐与盐水的比是用盐的质量比盐与水的质量和是解题的关键。
12.(2024秋 兰州期末)白兔比灰兔多40%,则白兔与灰兔只数的比是7:5。 √
【考点】比的意义.
【专题】分数和百分数;比和比例;运算能力.
【答案】√。
【分析】灰兔的只数看作单位“1”,白兔的只数是灰兔的(1+40%),根据比的意义,两个数相除,也叫两个数的比。即可解答。
【解答】解:(1+40%):1=7:5
白兔比灰兔多40%,则白兔与灰兔只数的比是7:5。原题说法是正确的。
故答案为:√。
【点评】本题考查了百分数的意义和比的意义。
13.(2024秋 崂山区期末)一个三角形,三条边的比可能是1:3:5。 ×
【考点】比的意义.
【专题】应用意识.
【答案】×。
【分析】根据三角形三边关系:两边之和大于第三边,把三角形的三边看作1份,3份,5份,两份之和小于第三份,原说法错误。
【解答】解:1+3<5,即两边之和小于第三边,不符合三角形三边关系,即原说法错误。
故答案为:×。
【点评】本题考查了比的意义的应用以及三角形三边关系的应用。
14.(2024秋 河东区期末)六年一班共有38人,该班男生和女生人数的比可能是3:2。 ×
【考点】比的意义.
【专题】应用意识.
【答案】×。
【分析】男生和女生人数的比可能是3:2,即男生人数占全班人数的份数是3份,女生人数占全班人数的份数是2份,男女生份数之和即为(3+2)份,是全班人数38的因数,据此判断。
【解答】解:38÷(3+2)=7……3
即38不是份数和的倍数,即原说法错误。
故答案为:×。
【点评】本题考查了比的意义的应用。
15.(2024秋 蓝田县期末)如果甲数比乙数多,那么甲数与乙数的比是2:3。 ×
【考点】比的意义.
【专题】比和比例;应用意识.
【答案】×。
【分析】把乙数看作单位“1”,那么甲数是(1+),再写出它们的比,再化简,即可解答。
【解答】解:(1+):1
=
=
=5:3
答:甲数与乙数的比是5:3。
所以原题说法错误。
故答案为:×。
【点评】本题考查的是比的意义,理解和应用比的意义是解答关键。
四.计算题(共1小题)
16.(2022春 临泉县期中)化简比.
2.5:0.45
【考点】比的意义.
【专题】比和比例;运算能力.
【答案】见试题解答内容
【分析】根据比的基本性质,即比的前项和后项同时乘或除以一个相同的数(0除外)比值不变,进而把比化成最简比.
【解答】解:(1):
=():()
=4:3;
(2):0.5
=(×8):(0.5×8)
=5:4;
(3)2.5:0.45
=(2.5×20):(0.45×20)
=50:9;
(4)15:
=(15÷):(÷)
=25:1.
【点评】此题主要考查了化简比的方法,另外还要注意化简比的结果是一个比,它的前项和后项都是整数,并且是互质数.
五.应用题(共4小题)
17.(2024 深圳模拟)有甲、乙、丙三个相互咬合的齿轮,当甲轮转5圈时,乙轮转7圈,丙轮转2圈,求这三个齿轮的齿数比.
【考点】比的意义.
【专题】比和比例;数感.
【答案】见试题解答内容
【分析】甲乙丙三个齿轮转数比为5:7:2,根据齿数与转数成反比例的关系,甲齿:乙齿=7:5=14:10,乙齿:丙齿=2:7=10:35,所以甲齿:乙齿:丙齿=14:10:35.
【解答】解:甲乙丙三个齿轮转数比为5:7:2,
根据齿数与转数成反比例的关系可得:
甲齿:乙齿=7:5=14:10
乙齿:丙齿=2:7=10:35
所以甲齿:乙齿:丙齿=14:10:35
答:这三个齿轮的齿数比是14:10:35.
【点评】解答此题关键是明确齿数与转数成反比例.
18.(2023秋 宣恩县月考)要从一个长5分米,宽4分米的长方形木板上锯下一个最大的圆,剩下的木板与圆面积的比是多少?
【考点】比的意义.
【专题】应用题;应用意识.
【答案】93:157。
【分析】根据题意可知,锯下的圆以长方形的宽为直径,再求出圆的面积和长方形的面积,用求得的长方形的面积减去圆的面积求出剩下木板的面积,根据比的意义写出剩下的木板与圆面积的比即可。
【解答】解:4÷2=2(分米)
3.14×22
=3.14×4
=12.56(平方分米)
5×4=20(平方分米)
20﹣12.56=7.44(平方分米)
7.44:12.56=(7.44÷8):(12.56÷8)=0.93:1.57=(0.93×100):(1.57×100)=93:157
答:剩下的木板与圆面积的比是93:157。
【点评】此题考查比的应用。掌握长方形、圆形的面积计算公式和化简比是解答的关键。
19.(2022秋 盱眙县期末)动物的小腿骨(胫骨)与大腿骨(股骨)的长度比值越大的动物跑得越快,
动物 盐都龙 马 羚羊
胫骨与股骨的比 59:50 23:25 5:4
根据这个结论,计算并比较三种动物中,谁跑得最快?
【考点】比的意义.
【专题】比和比例.
【答案】见试题解答内容
【分析】比值是比的前项除以后项的商,据此即可求出三种动物小腿骨(胫骨)与大腿骨(股骨)的长度比值,通过比较即可确定这一种动物中哪种跑得最快.
【解答】解:盐都龙:59:50=59÷50=1.18
马:23:25=23÷25=0.92
羚羊:5÷4=5÷4=1.25
1.25>1.18>0.92
答:羚羊跑得最快.
【点评】此题主要是考查求比值,根据比值的意义即可求得比的比值.比值既可用小数表示,也可用分数表示,还可用整数表示.
20.(2023秋 合肥期中)甲、乙两人在银行都有存款,如果甲再存入原来钱的,乙再存入原来钱的,这时两人的存款数相等,原来甲、乙存款数的比是多少?
【考点】比的意义.
【专题】比和比例;数感;运算能力.
【答案】24:25。
【分析】把甲原来存款数看作单位“1”,再存入原来钱的,就相当于原来存款数的(1+)。把甲存入原来钱的后的钱数、乙再存入原来钱的后的钱数都看作a,根据分数除法的意义,用a除以(1+)就是甲原来的存款数,用a除以(1+)就是乙原来的存款数,再根据比的意义即可写出原来甲、乙存款数,并化成最简整数比。
【解答】解:[a÷(1+)]:[a÷(1+)]
=a:a
=24:25
答:原来甲、乙存款的比是24:25。
【点评】此题是考查比的意义及化简。关键是求出甲、乙原来的存款数。也可这样解答,甲存入原来钱数的,把甲原来的钱数看作是4份,现在的钱数就是5份;乙再存入原来钱数的,乙原来的钱数是5份,现在的钱数就是6份,5和6的最小公倍数是30,甲的钱每份是6,乙的钱每份是5,则原来甲、乙存款钱数的比是:(4×6):(5×5)=24:25。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
