【期末押题预测】期末核心考点 反比例(含解析)2024-2025学年六年级下册数学北师大版
文档属性
| 名称 | 【期末押题预测】期末核心考点 反比例(含解析)2024-2025学年六年级下册数学北师大版 |  | |
| 格式 | docx | ||
| 文件大小 | 444.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-10 05:06:11 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
期末核心考点 反比例
一.选择题(共5小题)
1.(2025春 宁乡市期中)下列各题中的两种量,成反比例的是( )
A.小东的身高和体重
B.修一条水渠,每天修的米数和天数
C.圆的半径和周长
D.订《中国少年报》的份数和总钱数
2.(2025春 福田区期中)如表中如果x和y成反比例,“?”处填____;如果x和y成正比例,“?”处填____。横线上应填( )
x 8 10
y 12 ?
A.9.6;10 B.15;9.6 C.9.6;15 D.10;15
3.(2025春 福田区期中)下列各式中,( )成正比例关系。(a、b≠0)
A. B. C. D.
4.(2025春 宁乡市期中)下面各种关系中,成反比例关系的是( )
A.长方形的周长一定,长和宽
B.铺地面积一定,每块砖的边长和铺砖的块数
C.分数值一定,分母和分子
D.圆锥的体积一定,它的底面积和高
5.(2025春 福清市期中)节约用水,人人有责。若一个没有关紧的水龙头,每时大约滴水3.6千克。照这样计算,滴水的质量与时间( )
A.不成比例 B.成正比例 C.成反比例 D.无法确定
二.填空题(共5小题)
6.(2025春 福清市期中)已知6x=4y,则x与y成 比例关系;若(a、b均不为0),则a、b成 比例关系。
7.(2025春 汶上县期中)如果,则x和y成 比例。
8.(2025春 宝安区期中)表格中,如果x与y两个量成正比例关系,那么a的值是 ;如果x与y两个量成反比例关系,那么a的值是 。
x 8 a
y 40 64
9.(2025春 陕州区期中)(X、Y均不为0),如果3X=Y,那么X和Y成 比例,如果=Y,那么X和Y成 比例。
10.(2025春 嘉祥县期中)A、B均不为0,如果A=12B,那么A和B成 比例关系;若,那么A和B成 比例关系。
三.判断题(共5小题)
11.(2025春 陕州区期中)圆的直径一定,它的周长和圆周率成正比例关系。
12.(2024 诸暨市)如果4x﹣7y=0(x、y不等于0),那么x和y成正比例。
13.(2024春 惠民县期中)车轮的半径一定,所行驶的路程与车轮的转数成正比例。
14.(2024春 丹江口市期中)当梯形的上、下底之和一定时,梯形的面积与高成正比例。
15.(2024春 霞山区校级期中)一件商品八五折出售,现价和原价成正比例。
四.应用题(共5小题)
16.一辆汽车在高速公路上行驶的路程与耗油量的关系如下表:
行驶路程/km 50 100 150 200 250 …
耗油量/L 5 10 15 20 25 …
(1)根据表中的数据,在图中描出这辆汽车行驶的路程和耗油量所对应的点,再把它们按顺序连起来.
(2)这辆汽车在高速公路上行驶的路程和耗油量成什么比例?为什么?
(3)根据图象推算,这辆汽车行驶350千米的耗油量.
(4)这辆汽车出发时油箱里有汽油40升,如果汽车要在高速公路上行驶460千米,你认为司机在途中需要加油吗?
17.组装一批电动车,每天组装的辆数和需要的天数如表.
每天组装辆数 20 15
10
需要的天数
12 15
(1)请把上表补充完整.
(2)每天组装的辆数和需要的天数成什么比例?为什么?
(3)如果每天组装30辆,需要组装多少天?如果打算4天完成组装任务,每天需要组装多少辆?
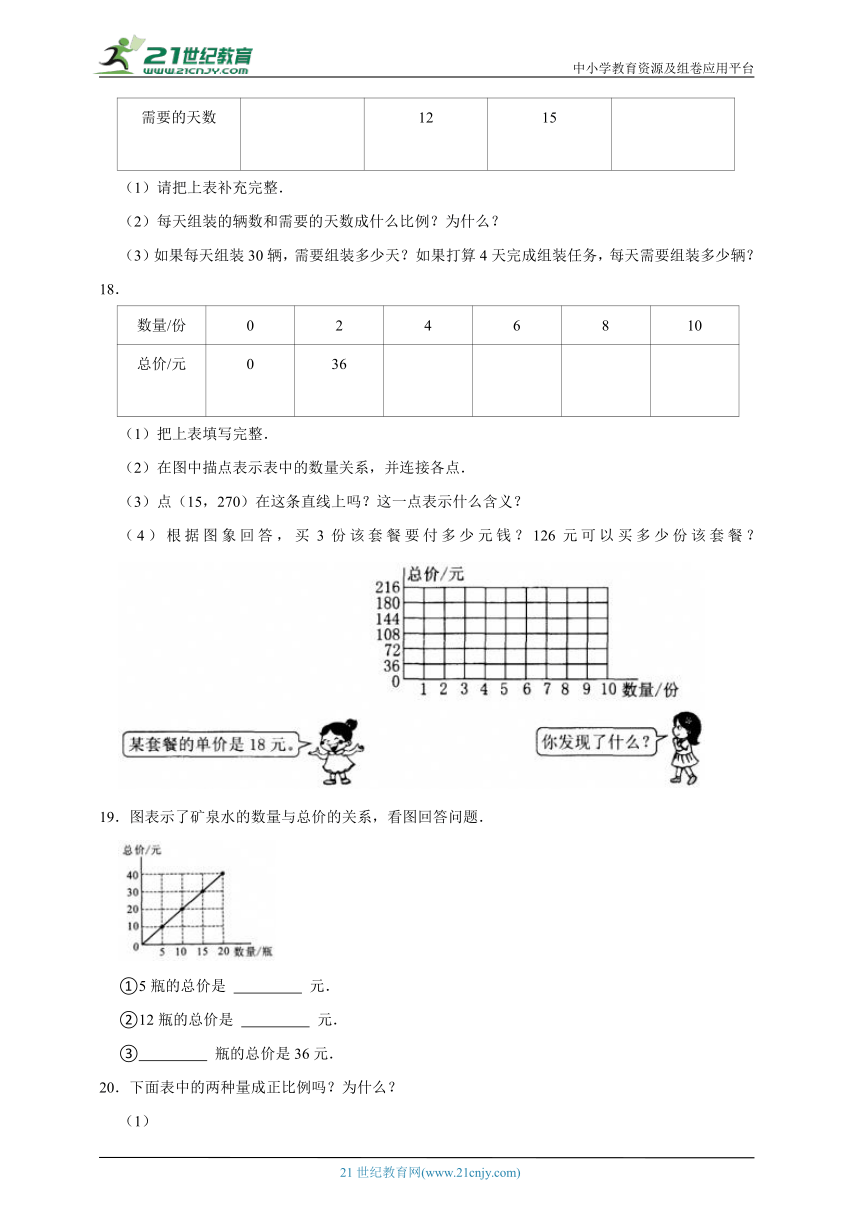
18.
数量/份 0 2 4 6 8 10
总价/元 0 36
(1)把上表填写完整.
(2)在图中描点表示表中的数量关系,并连接各点.
(3)点(15,270)在这条直线上吗?这一点表示什么含义?
(4)根据图象回答,买3份该套餐要付多少元钱?126元可以买多少份该套餐?
19.图表示了矿泉水的数量与总价的关系,看图回答问题.
①5瓶的总价是 元.
②12瓶的总价是 元.
③ 瓶的总价是36元.
20.下面表中的两种量成正比例吗?为什么?
(1)
成年人数(人) 1 50 1000 10亿
每天呼出二氧化碳(kg) 0.9 45 900 9亿
(2)
阔叶林面积(km2) 1 50 1000 90万
每天吸收二氧化碳(吨) 100 5000 100000 9000万
期末核心考点 反比例
参考答案与试题解析
一.选择题(共5小题)
1.(2025春 宁乡市期中)下列各题中的两种量,成反比例的是( )
A.小东的身高和体重
B.修一条水渠,每天修的米数和天数
C.圆的半径和周长
D.订《中国少年报》的份数和总钱数
【考点】辨识成正比例的量与成反比例的量.
【答案】B
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【解答】解:选项A.小东的身高和体重之间不成比例关系;
选项B.每天修的米数×天数=水渠的总长度(一定),乘积一定,所以平均每天修的米数和天数成反比例;
选项C.圆的周长÷半径=2π(一定),所以圆的半径和周长成正比例;
选项D.订《中国少年报》的总钱数:份数=《中国少年报》的单价(一定),是对应的比值一定,所以订《中国少年报》的份数和总钱数成正比例。
故选:B。
【点评】本题主要考查辨识成正比例的量和成反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断。
2.(2025春 福田区期中)如表中如果x和y成反比例,“?”处填____;如果x和y成正比例,“?”处填____。横线上应填( )
x 8 10
y 12 ?
A.9.6;10 B.15;9.6 C.9.6;15 D.10;15
【考点】正比例和反比例的意义.
【专题】运算能力.
【答案】C
【分析】两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫成正比例的量,它们的关系就叫正比例关系;两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的乘积一定,这两种量就叫成反比例的量,它们的关系就叫反比例关系。
【解答】解:x和y成反比例:
10y=8×12
10y=96
y=9.6
x和y成正比例:
10:y=8:12
8y=10×12
8y=120
y=15
如表中如果x和y成反比例,“?”处填9.6;如果x和y成正比例,“?”处填15。
故选:C。
【点评】本题考查了正、反比例的意义,辨识两种相关联的量成不成比例,成什么比例,就看这两种量是对应的比值一定,还是对应的乘积一定,还是对应的其它量一定,再判断即可。
3.(2025春 福田区期中)下列各式中,( )成正比例关系。(a、b≠0)
A. B. C. D.
【考点】辨识成正比例的量与成反比例的量.
【专题】应用意识.
【答案】A
【分析】两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量所对应的数的比值一定,这两种量成正比例关系;如果这两种量所对应的数的积一定,这两种量成反比例关系;四个选项中,a与b比值一定的,a和b就成正比例,a和b积一定的,a和b就成反比例。
【解答】解:A.因为=b,可知=4,a和b的商一定,所以a和b成正比例。
B.因为=b,可知ab=4,a和b的积一定,所以a和b成反比例。
C.因为ab=,a和b的积一定,所以a和b成反比例。
D.因为=,可知ab=4,a和b的积一定,所以a和b成反比例。
故选:A。
【点评】此题是考查辨析两种量成正、反比例,关键是看这两种量中所对应的数的比值(商)一定还是积一定。
4.(2025春 宁乡市期中)下面各种关系中,成反比例关系的是( )
A.长方形的周长一定,长和宽
B.铺地面积一定,每块砖的边长和铺砖的块数
C.分数值一定,分母和分子
D.圆锥的体积一定,它的底面积和高
【考点】辨识成正比例的量与成反比例的量.
【专题】推理能力.
【答案】D
【分析】两种相关联的量,若其比值(商)一定,这两种量成长比例关系;若其乘积一定,这两种量成反比例关系,据此解答。
【解答】解:选项A,长方形的长+宽=周长÷2,所以当长方形的周长一定时,长和宽不成比例;
选项B,每块砖的边长×边长×铺砖的块数=铺地面积,所以当铺地面积一定时,每块砖的边长和铺砖的块数不成比例;
选项C,分子÷分母=分数值,所以当分数值一定时,分母和分子成正比例关系;
选项D,圆锥的底面积×高=圆锥的体积×3,所以当圆锥的体积一定时,它的底面积和高成反比例关系。
故选:D。
【点评】辨识两种相关联的量成正比例关系还是成反比例关系,就看这两种量是存在比值(商)一定还是乘积一定。
5.(2025春 福清市期中)节约用水,人人有责。若一个没有关紧的水龙头,每时大约滴水3.6千克。照这样计算,滴水的质量与时间( )
A.不成比例 B.成正比例 C.成反比例 D.无法确定
【考点】辨识成正比例的量与成反比例的量.
【专题】应用意识.
【答案】B
【分析】判断两种相关联的量成不成比例,成什么比例,就看这两种量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,就成反比例,如果是其它的量一定或乘积、比值不一定,就不成比例。
【解答】解:“照这样计算”说明每小时滴水的质量是相同的,
所以,滴水的总质量÷时间=每小时滴水的质量(一定),
因此,滴水的质量与时间成正比例。
故选:B。
【点评】此题属于根据正、反比例的意义,辨识两种相关联的量成不成比例,成什么比例,就看这两种量是对应的比值一定,还是对应的乘积一定,还是对应的其它量一定,再做出判断。
二.填空题(共5小题)
6.(2025春 福清市期中)已知6x=4y,则x与y成 正 比例关系;若(a、b均不为0),则a、b成 反 比例关系。
【考点】辨识成正比例的量与成反比例的量.
【专题】数感;应用意识.
【答案】正;反。
【分析】根据x÷y=k(一定),x和y成正比例关系;xy=k(一定),x和y成反比例关系,进行分析。
【解答】解:已知6x=4y,则x÷y=,因此x与y成正比例关系;
若(a、b均不为0),则ab=,因此a、b成反比例关系。
故答案为:正;反。
【点评】掌握辨别成正比例的量和成反比例的量是解题的关键。
7.(2025春 汶上县期中)如果,则x和y成 反 比例。
【考点】辨识成正比例的量与成反比例的量.
【专题】数感;运算能力.
【答案】反。
【分析】要想判定x和y成什么比例关系,要看x和y是比值一定还是乘积一定,从而判定成什么比例关系。
【解答】解:因为,所以5xy=2
xy=0.4(一定)
可以看出,xy两种相关联的量,xy化而变化,0.4是一定的,也就是xy对应数的乘积一定,符合反比例的意义,所以xy反比例关系。
故答案为:反。
【点评】此题重点考查用正比例和反比例的意义来辨识成正比例的量和成反比例的量。
8.(2025春 宝安区期中)表格中,如果x与y两个量成正比例关系,那么a的值是 12.8 ;如果x与y两个量成反比例关系,那么a的值是 5 。
x 8 a
y 40 64
【考点】正比例和反比例的意义.
【专题】运算能力.
【答案】12.8;5。
【分析】两个相关联的量,若成正比例关系,则其比值一定;若成反比例关系,则其乘积一定;据此解答。
【解答】解:如果x与y两个量成正比例关系,则:
8:40=a:64
40a=8×64
40a=512
a=12.8
如果x与y两个量成反比例关系,则:
64a=40×8
64a=320
a=5
故答案为:12.8;5。
【点评】本题考查的是根据成哪种比例关系列比例式并解比例,解比例时要根据等式的性质解答。
9.(2025春 陕州区期中)(X、Y均不为0),如果3X=Y,那么X和Y成 正 比例,如果=Y,那么X和Y成 反 比例。
【考点】辨识成正比例的量与成反比例的量.
【专题】常见的量.
【答案】正;反。
【分析】如果两种量中相对应的两个数的比值(或商)一定,这两种量就叫作成正比例的量,它们的关系叫作正比例关系;如果两种量中相对应的两个数的积一定,这两种量就叫作成反比例的量,它们的关系叫作反比例关系。据此解答。
【解答】解:如果3X=Y,那么X÷Y=,所以X和Y成正比例,如果=Y,那么X×Y=3,所以X和Y成反比例。
故答案为:正;反。
【点评】本题考查了成正比例关系和成反比例关系的应用。
10.(2025春 嘉祥县期中)A、B均不为0,如果A=12B,那么A和B成 正 比例关系;若,那么A和B成 反 比例关系。
【考点】辨识成正比例的量与成反比例的量.
【专题】数感;运算能力.
【答案】正,反。
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【解答】解:如果A=12B(A、B均不为0),即A:B=12,是比值一定,那么A和B成正比例关系;
如果A=(A、B均不为0),即AB=12,是乘积一定,那么A和B成反比例关系。
故答案为:正,反。
【点评】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再作判断。
三.判断题(共5小题)
11.(2025春 陕州区期中)圆的直径一定,它的周长和圆周率成正比例关系。 ×
【考点】辨识成正比例的量与成反比例的量.
【专题】比和比例;运算能力.
【答案】×
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【解答】解:因为圆的周长C=πd,
在此题中圆的直径一定,圆周率也是一定的,
所以周长也是一定的,
即三个量都是一定的,不存在变量问题,
所以圆的周长和圆周率不成比例;所以原题说法错误。
故答案为:×。
【点评】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断。
12.(2024 诸暨市)如果4x﹣7y=0(x、y不等于0),那么x和y成正比例。 √
【考点】辨识成正比例的量与成反比例的量.
【专题】数感;运算能力.
【答案】√。
【分析】判断x和y是否成正比例,就看这两种量是否是对应的比值一定,如果是比值一定,就成正比例,如果不是比值一定或比值不一定,就不成正比例。
【解答】解:因为4x﹣7y=0,
则有4x=7y,x:y=7:4=(一定),是x和y对应的比值一定,所以x和y成正比例关系;原题说法正确。
故答案为:√。
【点评】此题属于根据正、反比例的意义,辨识两种相关联的量是否成正比例,就看这两种量是否是对应的比值一定,再作出判断。
13.(2024春 惠民县期中)车轮的半径一定,所行驶的路程与车轮的转数成正比例。 √
【考点】辨识成正比例的量与成反比例的量.
【专题】应用意识.
【答案】√。
【分析】判断两种相关联的量之间成什么比例,就看这两个量是对应的比值(商)一定,还是对应的乘积一定;如果是比值(商)一定,这两种相关联的量成正比例;据此解答。
【解答】解:因为行驶的路程:车轮的转数=2×车轮的半径×圆周率(一定),所以行驶的路程和车轮的转数成正比例。原题说法正确。
故答案为:√。
【点评】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再作判断。
14.(2024春 丹江口市期中)当梯形的上、下底之和一定时,梯形的面积与高成正比例。 √
【考点】辨识成正比例的量与成反比例的量.
【专题】应用意识.
【答案】√。
【分析】判断两种相关联的量之间成什么比例,就看这两个量是对应的比值(商)一定,还是对应的乘积一定;如果是比值(商)一定,这两种相关联的量成正比例;据此解答。
【解答】解:梯形的面积÷高=×(上底+下底),上底与下底的和一定,它们的和的就一定,是梯形的面积与高的比值一定,所以它的面积与高成正比例关系。原题说法正确。
故答案为:√。
【点评】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再作判断。
15.(2024春 霞山区校级期中)一件商品八五折出售,现价和原价成正比例。 √
【考点】辨识成正比例的量与成反比例的量.
【专题】应用意识.
【答案】√。
【分析】判断两种相关联的量之间成什么比例,就看这两个量是对应的比值(商)一定,还是对应的乘积一定;如果是比值(商)一定,这两种相关联的量成正比例;据此解答。
【解答】解:由分析可得:现价÷原价×100%=折扣(一定),商一定,则现价与原价成正比例,原题说法正确。
故答案为:√。
【点评】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再作判断。
四.应用题(共5小题)
16.一辆汽车在高速公路上行驶的路程与耗油量的关系如下表:
行驶路程/km 50 100 150 200 250 …
耗油量/L 5 10 15 20 25 …
(1)根据表中的数据,在图中描出这辆汽车行驶的路程和耗油量所对应的点,再把它们按顺序连起来.
(2)这辆汽车在高速公路上行驶的路程和耗油量成什么比例?为什么?
(3)根据图象推算,这辆汽车行驶350千米的耗油量.
(4)这辆汽车出发时油箱里有汽油40升,如果汽车要在高速公路上行驶460千米,你认为司机在途中需要加油吗?
【考点】正比例和反比例的意义.
【专题】比和比例应用题.
【答案】见试题解答内容
【分析】(1)根据统计表中的数据完成统计图.
(2)判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例;由此解答即可.
(3)根据耗油量=汽车行驶的路程除以每升油行驶的路程,计算即可.
(4)计算460千米需要多少升汽油,与40升进行比较,即可得出结论.
【解答】解:(1)统计图如下:
(2)50÷5=100÷10=150÷15=10(一定),即:汽车行驶的路程÷耗油量=每升油行驶的路程(一定),
所以这辆汽车行驶的路程和耗油量成正比例.
(3)350÷10=35(升)
答:这辆汽车行驶350千米的耗油量为35升.
(4)460÷10=46(升)
46>40
答:司机在途中需要加油.
【点评】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断.
17.组装一批电动车,每天组装的辆数和需要的天数如表.
每天组装辆数 20 15
12
10
需要的天数
9
12 15
18
(1)请把上表补充完整.
(2)每天组装的辆数和需要的天数成什么比例?为什么?
(3)如果每天组装30辆,需要组装多少天?如果打算4天完成组装任务,每天需要组装多少辆?
【考点】正比例和反比例的意义.
【专题】比和比例;模型思想.
【答案】见试题解答内容
【分析】两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫作成正比例的量,它们的关系叫作正比例关系.用字母表示是=k(一定)
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫作成反比例的量,它们的关系叫作反比例关系.用字母表示是x×y=k(一定).
(1)这一批电动车的数量是个定值12×15=180辆,也就是:每天组装辆数×需要的天数=180辆,据此计算填表即可.
(2)根据每天组装辆数×需要的天数=180辆(一定)可解答.
(3)根据需要的天数=180÷每天组装辆数;每天组装辆数=180÷需要的天数即可.
【解答】解:(1)15×12=180(辆)
180÷20=9(天)
180÷15=12(辆)
180÷10=18(天)
每天组装辆数 20 15 12 10
需要的天数 9 12 15 18
(2)因为每天组装辆数×需要的天数=180辆(一定),即乘积一定.所以每天组装的辆数和需要的天数成反比例.
(3)180÷30=6(天)
180÷4=45(辆)
答:每天组装30辆,需要组装6天;打算4天完成组装任务,每天需要组装45辆.
故答案为:12,9,18.
【点评】此题主要考查成反比例的量,理解成反比例的量的定义,是解决此题的关键.
18.
数量/份 0 2 4 6 8 10
总价/元 0 36
72
108
144
180
(1)把上表填写完整.
(2)在图中描点表示表中的数量关系,并连接各点.
(3)点(15,270)在这条直线上吗?这一点表示什么含义?
(4)根据图象回答,买3份该套餐要付多少元钱?126元可以买多少份该套餐?
【考点】正比例和反比例的意义.
【专题】图示法;列表法;比和比例;应用题;数据分析观念.
【答案】见试题解答内容
【分析】(1)先计算出单价36÷2=18(元),分别用单价×数量=总价,计算后填完整表格.
(2)根据表格中数据可在右图中描点连线,得出统计图.
(3)因为270÷15=18(元),单价一定,点(15,270)在这条直线上,这一点表示15份套餐需要270元钱.
(4)每份该套餐18元乘以份数即可得买3份该套餐要付多少元钱,用总钱数除以每份的价格即可得126元可以买多少份该套餐.
【解答】解:
数量/份 0 2 4 6 8 10
总价/元 0 36 72 108 144 180
(1)总价与质量成正比例.
(2)根据表格中数据可在右图中描点连线,得出统计图如图:
(3)点(15,270)在这条直线上,这一点表示15份套餐需要270元钱.
(4)3×18=54(元),
126÷18=7(份),
答:买3份该套餐要付54元钱,126元可以买7份该套餐.
【点评】此题考查正比例的意义,绘制折线统计图的方法,以及成正比例关系的量的特点,明确成正比例的两个量必须得比值一定.
19.图表示了矿泉水的数量与总价的关系,看图回答问题.
①5瓶的总价是 10 元.
②12瓶的总价是 24 元.
③ 18 瓶的总价是36元.
【考点】正比例和反比例的意义.
【专题】比和比例;应用意识.
【答案】见试题解答内容
【分析】①仔细观察图表,5瓶的售价是10元;
②先利用所给的数据求出一瓶矿泉水的价格,再根据总价=单价×数量解答即可;
③先利用所给的数据求出一瓶矿泉水的价格,用数量=总价÷单价解答即可.
【解答】解:(1)5瓶的售价是10元.
(2)10÷5×12
=2×12
=24(元);
答:12瓶的售价是 24元.
(3)36÷(10÷5)
=36÷2
=18(瓶);
答:18瓶的售价是36元.
故答案为:10,24,18.
【点评】此题主要考查正比例的意义在生活实际中的灵活应用.
20.下面表中的两种量成正比例吗?为什么?
(1)
成年人数(人) 1 50 1000 10亿
每天呼出二氧化碳(kg) 0.9 45 900 9亿
(2)
阔叶林面积(km2) 1 50 1000 90万
每天吸收二氧化碳(吨) 100 5000 100000 9000万
【考点】辨识成正比例的量与成反比例的量.
【专题】应用意识.
【答案】成正比例,因为表中的这两种量,一种量变化,另一种也随着变化,并且这两种量中相对应的两个数的比值一定,所以,这两种量就叫做成正比例的量。
【分析】两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的乘积一定,这两种量叫做成反比例的量,它们的关系叫做反比例关系;两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量叫做成正比例的量,它们的关系叫做正比例关系。
【解答】解:(1)1:0.9=
50:45=
1000:900=
10亿:9亿=
因为:=(一定),所以表中的两个量成正比例关系。
(2)1:100=
50:5000=
1000:100000=
90万:9000万=
因为=(一定),所以,表中的两种量成正比例关系。
答:(1)(2)表中的两种量成正比例关系。因为表中的这两种量,一种量变化,另一种也随着变化,并且这两种量中相对应的两个数的比值一定,所以,这两种量就叫做成正比例的量。
【点评】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再作判断。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末核心考点 反比例
一.选择题(共5小题)
1.(2025春 宁乡市期中)下列各题中的两种量,成反比例的是( )
A.小东的身高和体重
B.修一条水渠,每天修的米数和天数
C.圆的半径和周长
D.订《中国少年报》的份数和总钱数
2.(2025春 福田区期中)如表中如果x和y成反比例,“?”处填____;如果x和y成正比例,“?”处填____。横线上应填( )
x 8 10
y 12 ?
A.9.6;10 B.15;9.6 C.9.6;15 D.10;15
3.(2025春 福田区期中)下列各式中,( )成正比例关系。(a、b≠0)
A. B. C. D.
4.(2025春 宁乡市期中)下面各种关系中,成反比例关系的是( )
A.长方形的周长一定,长和宽
B.铺地面积一定,每块砖的边长和铺砖的块数
C.分数值一定,分母和分子
D.圆锥的体积一定,它的底面积和高
5.(2025春 福清市期中)节约用水,人人有责。若一个没有关紧的水龙头,每时大约滴水3.6千克。照这样计算,滴水的质量与时间( )
A.不成比例 B.成正比例 C.成反比例 D.无法确定
二.填空题(共5小题)
6.(2025春 福清市期中)已知6x=4y,则x与y成 比例关系;若(a、b均不为0),则a、b成 比例关系。
7.(2025春 汶上县期中)如果,则x和y成 比例。
8.(2025春 宝安区期中)表格中,如果x与y两个量成正比例关系,那么a的值是 ;如果x与y两个量成反比例关系,那么a的值是 。
x 8 a
y 40 64
9.(2025春 陕州区期中)(X、Y均不为0),如果3X=Y,那么X和Y成 比例,如果=Y,那么X和Y成 比例。
10.(2025春 嘉祥县期中)A、B均不为0,如果A=12B,那么A和B成 比例关系;若,那么A和B成 比例关系。
三.判断题(共5小题)
11.(2025春 陕州区期中)圆的直径一定,它的周长和圆周率成正比例关系。
12.(2024 诸暨市)如果4x﹣7y=0(x、y不等于0),那么x和y成正比例。
13.(2024春 惠民县期中)车轮的半径一定,所行驶的路程与车轮的转数成正比例。
14.(2024春 丹江口市期中)当梯形的上、下底之和一定时,梯形的面积与高成正比例。
15.(2024春 霞山区校级期中)一件商品八五折出售,现价和原价成正比例。
四.应用题(共5小题)
16.一辆汽车在高速公路上行驶的路程与耗油量的关系如下表:
行驶路程/km 50 100 150 200 250 …
耗油量/L 5 10 15 20 25 …
(1)根据表中的数据,在图中描出这辆汽车行驶的路程和耗油量所对应的点,再把它们按顺序连起来.
(2)这辆汽车在高速公路上行驶的路程和耗油量成什么比例?为什么?
(3)根据图象推算,这辆汽车行驶350千米的耗油量.
(4)这辆汽车出发时油箱里有汽油40升,如果汽车要在高速公路上行驶460千米,你认为司机在途中需要加油吗?
17.组装一批电动车,每天组装的辆数和需要的天数如表.
每天组装辆数 20 15
10
需要的天数
12 15
(1)请把上表补充完整.
(2)每天组装的辆数和需要的天数成什么比例?为什么?
(3)如果每天组装30辆,需要组装多少天?如果打算4天完成组装任务,每天需要组装多少辆?
18.
数量/份 0 2 4 6 8 10
总价/元 0 36
(1)把上表填写完整.
(2)在图中描点表示表中的数量关系,并连接各点.
(3)点(15,270)在这条直线上吗?这一点表示什么含义?
(4)根据图象回答,买3份该套餐要付多少元钱?126元可以买多少份该套餐?
19.图表示了矿泉水的数量与总价的关系,看图回答问题.
①5瓶的总价是 元.
②12瓶的总价是 元.
③ 瓶的总价是36元.
20.下面表中的两种量成正比例吗?为什么?
(1)
成年人数(人) 1 50 1000 10亿
每天呼出二氧化碳(kg) 0.9 45 900 9亿
(2)
阔叶林面积(km2) 1 50 1000 90万
每天吸收二氧化碳(吨) 100 5000 100000 9000万
期末核心考点 反比例
参考答案与试题解析
一.选择题(共5小题)
1.(2025春 宁乡市期中)下列各题中的两种量,成反比例的是( )
A.小东的身高和体重
B.修一条水渠,每天修的米数和天数
C.圆的半径和周长
D.订《中国少年报》的份数和总钱数
【考点】辨识成正比例的量与成反比例的量.
【答案】B
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【解答】解:选项A.小东的身高和体重之间不成比例关系;
选项B.每天修的米数×天数=水渠的总长度(一定),乘积一定,所以平均每天修的米数和天数成反比例;
选项C.圆的周长÷半径=2π(一定),所以圆的半径和周长成正比例;
选项D.订《中国少年报》的总钱数:份数=《中国少年报》的单价(一定),是对应的比值一定,所以订《中国少年报》的份数和总钱数成正比例。
故选:B。
【点评】本题主要考查辨识成正比例的量和成反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断。
2.(2025春 福田区期中)如表中如果x和y成反比例,“?”处填____;如果x和y成正比例,“?”处填____。横线上应填( )
x 8 10
y 12 ?
A.9.6;10 B.15;9.6 C.9.6;15 D.10;15
【考点】正比例和反比例的意义.
【专题】运算能力.
【答案】C
【分析】两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫成正比例的量,它们的关系就叫正比例关系;两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的乘积一定,这两种量就叫成反比例的量,它们的关系就叫反比例关系。
【解答】解:x和y成反比例:
10y=8×12
10y=96
y=9.6
x和y成正比例:
10:y=8:12
8y=10×12
8y=120
y=15
如表中如果x和y成反比例,“?”处填9.6;如果x和y成正比例,“?”处填15。
故选:C。
【点评】本题考查了正、反比例的意义,辨识两种相关联的量成不成比例,成什么比例,就看这两种量是对应的比值一定,还是对应的乘积一定,还是对应的其它量一定,再判断即可。
3.(2025春 福田区期中)下列各式中,( )成正比例关系。(a、b≠0)
A. B. C. D.
【考点】辨识成正比例的量与成反比例的量.
【专题】应用意识.
【答案】A
【分析】两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量所对应的数的比值一定,这两种量成正比例关系;如果这两种量所对应的数的积一定,这两种量成反比例关系;四个选项中,a与b比值一定的,a和b就成正比例,a和b积一定的,a和b就成反比例。
【解答】解:A.因为=b,可知=4,a和b的商一定,所以a和b成正比例。
B.因为=b,可知ab=4,a和b的积一定,所以a和b成反比例。
C.因为ab=,a和b的积一定,所以a和b成反比例。
D.因为=,可知ab=4,a和b的积一定,所以a和b成反比例。
故选:A。
【点评】此题是考查辨析两种量成正、反比例,关键是看这两种量中所对应的数的比值(商)一定还是积一定。
4.(2025春 宁乡市期中)下面各种关系中,成反比例关系的是( )
A.长方形的周长一定,长和宽
B.铺地面积一定,每块砖的边长和铺砖的块数
C.分数值一定,分母和分子
D.圆锥的体积一定,它的底面积和高
【考点】辨识成正比例的量与成反比例的量.
【专题】推理能力.
【答案】D
【分析】两种相关联的量,若其比值(商)一定,这两种量成长比例关系;若其乘积一定,这两种量成反比例关系,据此解答。
【解答】解:选项A,长方形的长+宽=周长÷2,所以当长方形的周长一定时,长和宽不成比例;
选项B,每块砖的边长×边长×铺砖的块数=铺地面积,所以当铺地面积一定时,每块砖的边长和铺砖的块数不成比例;
选项C,分子÷分母=分数值,所以当分数值一定时,分母和分子成正比例关系;
选项D,圆锥的底面积×高=圆锥的体积×3,所以当圆锥的体积一定时,它的底面积和高成反比例关系。
故选:D。
【点评】辨识两种相关联的量成正比例关系还是成反比例关系,就看这两种量是存在比值(商)一定还是乘积一定。
5.(2025春 福清市期中)节约用水,人人有责。若一个没有关紧的水龙头,每时大约滴水3.6千克。照这样计算,滴水的质量与时间( )
A.不成比例 B.成正比例 C.成反比例 D.无法确定
【考点】辨识成正比例的量与成反比例的量.
【专题】应用意识.
【答案】B
【分析】判断两种相关联的量成不成比例,成什么比例,就看这两种量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,就成反比例,如果是其它的量一定或乘积、比值不一定,就不成比例。
【解答】解:“照这样计算”说明每小时滴水的质量是相同的,
所以,滴水的总质量÷时间=每小时滴水的质量(一定),
因此,滴水的质量与时间成正比例。
故选:B。
【点评】此题属于根据正、反比例的意义,辨识两种相关联的量成不成比例,成什么比例,就看这两种量是对应的比值一定,还是对应的乘积一定,还是对应的其它量一定,再做出判断。
二.填空题(共5小题)
6.(2025春 福清市期中)已知6x=4y,则x与y成 正 比例关系;若(a、b均不为0),则a、b成 反 比例关系。
【考点】辨识成正比例的量与成反比例的量.
【专题】数感;应用意识.
【答案】正;反。
【分析】根据x÷y=k(一定),x和y成正比例关系;xy=k(一定),x和y成反比例关系,进行分析。
【解答】解:已知6x=4y,则x÷y=,因此x与y成正比例关系;
若(a、b均不为0),则ab=,因此a、b成反比例关系。
故答案为:正;反。
【点评】掌握辨别成正比例的量和成反比例的量是解题的关键。
7.(2025春 汶上县期中)如果,则x和y成 反 比例。
【考点】辨识成正比例的量与成反比例的量.
【专题】数感;运算能力.
【答案】反。
【分析】要想判定x和y成什么比例关系,要看x和y是比值一定还是乘积一定,从而判定成什么比例关系。
【解答】解:因为,所以5xy=2
xy=0.4(一定)
可以看出,xy两种相关联的量,xy化而变化,0.4是一定的,也就是xy对应数的乘积一定,符合反比例的意义,所以xy反比例关系。
故答案为:反。
【点评】此题重点考查用正比例和反比例的意义来辨识成正比例的量和成反比例的量。
8.(2025春 宝安区期中)表格中,如果x与y两个量成正比例关系,那么a的值是 12.8 ;如果x与y两个量成反比例关系,那么a的值是 5 。
x 8 a
y 40 64
【考点】正比例和反比例的意义.
【专题】运算能力.
【答案】12.8;5。
【分析】两个相关联的量,若成正比例关系,则其比值一定;若成反比例关系,则其乘积一定;据此解答。
【解答】解:如果x与y两个量成正比例关系,则:
8:40=a:64
40a=8×64
40a=512
a=12.8
如果x与y两个量成反比例关系,则:
64a=40×8
64a=320
a=5
故答案为:12.8;5。
【点评】本题考查的是根据成哪种比例关系列比例式并解比例,解比例时要根据等式的性质解答。
9.(2025春 陕州区期中)(X、Y均不为0),如果3X=Y,那么X和Y成 正 比例,如果=Y,那么X和Y成 反 比例。
【考点】辨识成正比例的量与成反比例的量.
【专题】常见的量.
【答案】正;反。
【分析】如果两种量中相对应的两个数的比值(或商)一定,这两种量就叫作成正比例的量,它们的关系叫作正比例关系;如果两种量中相对应的两个数的积一定,这两种量就叫作成反比例的量,它们的关系叫作反比例关系。据此解答。
【解答】解:如果3X=Y,那么X÷Y=,所以X和Y成正比例,如果=Y,那么X×Y=3,所以X和Y成反比例。
故答案为:正;反。
【点评】本题考查了成正比例关系和成反比例关系的应用。
10.(2025春 嘉祥县期中)A、B均不为0,如果A=12B,那么A和B成 正 比例关系;若,那么A和B成 反 比例关系。
【考点】辨识成正比例的量与成反比例的量.
【专题】数感;运算能力.
【答案】正,反。
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【解答】解:如果A=12B(A、B均不为0),即A:B=12,是比值一定,那么A和B成正比例关系;
如果A=(A、B均不为0),即AB=12,是乘积一定,那么A和B成反比例关系。
故答案为:正,反。
【点评】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再作判断。
三.判断题(共5小题)
11.(2025春 陕州区期中)圆的直径一定,它的周长和圆周率成正比例关系。 ×
【考点】辨识成正比例的量与成反比例的量.
【专题】比和比例;运算能力.
【答案】×
【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【解答】解:因为圆的周长C=πd,
在此题中圆的直径一定,圆周率也是一定的,
所以周长也是一定的,
即三个量都是一定的,不存在变量问题,
所以圆的周长和圆周率不成比例;所以原题说法错误。
故答案为:×。
【点评】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断。
12.(2024 诸暨市)如果4x﹣7y=0(x、y不等于0),那么x和y成正比例。 √
【考点】辨识成正比例的量与成反比例的量.
【专题】数感;运算能力.
【答案】√。
【分析】判断x和y是否成正比例,就看这两种量是否是对应的比值一定,如果是比值一定,就成正比例,如果不是比值一定或比值不一定,就不成正比例。
【解答】解:因为4x﹣7y=0,
则有4x=7y,x:y=7:4=(一定),是x和y对应的比值一定,所以x和y成正比例关系;原题说法正确。
故答案为:√。
【点评】此题属于根据正、反比例的意义,辨识两种相关联的量是否成正比例,就看这两种量是否是对应的比值一定,再作出判断。
13.(2024春 惠民县期中)车轮的半径一定,所行驶的路程与车轮的转数成正比例。 √
【考点】辨识成正比例的量与成反比例的量.
【专题】应用意识.
【答案】√。
【分析】判断两种相关联的量之间成什么比例,就看这两个量是对应的比值(商)一定,还是对应的乘积一定;如果是比值(商)一定,这两种相关联的量成正比例;据此解答。
【解答】解:因为行驶的路程:车轮的转数=2×车轮的半径×圆周率(一定),所以行驶的路程和车轮的转数成正比例。原题说法正确。
故答案为:√。
【点评】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再作判断。
14.(2024春 丹江口市期中)当梯形的上、下底之和一定时,梯形的面积与高成正比例。 √
【考点】辨识成正比例的量与成反比例的量.
【专题】应用意识.
【答案】√。
【分析】判断两种相关联的量之间成什么比例,就看这两个量是对应的比值(商)一定,还是对应的乘积一定;如果是比值(商)一定,这两种相关联的量成正比例;据此解答。
【解答】解:梯形的面积÷高=×(上底+下底),上底与下底的和一定,它们的和的就一定,是梯形的面积与高的比值一定,所以它的面积与高成正比例关系。原题说法正确。
故答案为:√。
【点评】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再作判断。
15.(2024春 霞山区校级期中)一件商品八五折出售,现价和原价成正比例。 √
【考点】辨识成正比例的量与成反比例的量.
【专题】应用意识.
【答案】√。
【分析】判断两种相关联的量之间成什么比例,就看这两个量是对应的比值(商)一定,还是对应的乘积一定;如果是比值(商)一定,这两种相关联的量成正比例;据此解答。
【解答】解:由分析可得:现价÷原价×100%=折扣(一定),商一定,则现价与原价成正比例,原题说法正确。
故答案为:√。
【点评】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再作判断。
四.应用题(共5小题)
16.一辆汽车在高速公路上行驶的路程与耗油量的关系如下表:
行驶路程/km 50 100 150 200 250 …
耗油量/L 5 10 15 20 25 …
(1)根据表中的数据,在图中描出这辆汽车行驶的路程和耗油量所对应的点,再把它们按顺序连起来.
(2)这辆汽车在高速公路上行驶的路程和耗油量成什么比例?为什么?
(3)根据图象推算,这辆汽车行驶350千米的耗油量.
(4)这辆汽车出发时油箱里有汽油40升,如果汽车要在高速公路上行驶460千米,你认为司机在途中需要加油吗?
【考点】正比例和反比例的意义.
【专题】比和比例应用题.
【答案】见试题解答内容
【分析】(1)根据统计表中的数据完成统计图.
(2)判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例;由此解答即可.
(3)根据耗油量=汽车行驶的路程除以每升油行驶的路程,计算即可.
(4)计算460千米需要多少升汽油,与40升进行比较,即可得出结论.
【解答】解:(1)统计图如下:
(2)50÷5=100÷10=150÷15=10(一定),即:汽车行驶的路程÷耗油量=每升油行驶的路程(一定),
所以这辆汽车行驶的路程和耗油量成正比例.
(3)350÷10=35(升)
答:这辆汽车行驶350千米的耗油量为35升.
(4)460÷10=46(升)
46>40
答:司机在途中需要加油.
【点评】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断.
17.组装一批电动车,每天组装的辆数和需要的天数如表.
每天组装辆数 20 15
12
10
需要的天数
9
12 15
18
(1)请把上表补充完整.
(2)每天组装的辆数和需要的天数成什么比例?为什么?
(3)如果每天组装30辆,需要组装多少天?如果打算4天完成组装任务,每天需要组装多少辆?
【考点】正比例和反比例的意义.
【专题】比和比例;模型思想.
【答案】见试题解答内容
【分析】两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫作成正比例的量,它们的关系叫作正比例关系.用字母表示是=k(一定)
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫作成反比例的量,它们的关系叫作反比例关系.用字母表示是x×y=k(一定).
(1)这一批电动车的数量是个定值12×15=180辆,也就是:每天组装辆数×需要的天数=180辆,据此计算填表即可.
(2)根据每天组装辆数×需要的天数=180辆(一定)可解答.
(3)根据需要的天数=180÷每天组装辆数;每天组装辆数=180÷需要的天数即可.
【解答】解:(1)15×12=180(辆)
180÷20=9(天)
180÷15=12(辆)
180÷10=18(天)
每天组装辆数 20 15 12 10
需要的天数 9 12 15 18
(2)因为每天组装辆数×需要的天数=180辆(一定),即乘积一定.所以每天组装的辆数和需要的天数成反比例.
(3)180÷30=6(天)
180÷4=45(辆)
答:每天组装30辆,需要组装6天;打算4天完成组装任务,每天需要组装45辆.
故答案为:12,9,18.
【点评】此题主要考查成反比例的量,理解成反比例的量的定义,是解决此题的关键.
18.
数量/份 0 2 4 6 8 10
总价/元 0 36
72
108
144
180
(1)把上表填写完整.
(2)在图中描点表示表中的数量关系,并连接各点.
(3)点(15,270)在这条直线上吗?这一点表示什么含义?
(4)根据图象回答,买3份该套餐要付多少元钱?126元可以买多少份该套餐?
【考点】正比例和反比例的意义.
【专题】图示法;列表法;比和比例;应用题;数据分析观念.
【答案】见试题解答内容
【分析】(1)先计算出单价36÷2=18(元),分别用单价×数量=总价,计算后填完整表格.
(2)根据表格中数据可在右图中描点连线,得出统计图.
(3)因为270÷15=18(元),单价一定,点(15,270)在这条直线上,这一点表示15份套餐需要270元钱.
(4)每份该套餐18元乘以份数即可得买3份该套餐要付多少元钱,用总钱数除以每份的价格即可得126元可以买多少份该套餐.
【解答】解:
数量/份 0 2 4 6 8 10
总价/元 0 36 72 108 144 180
(1)总价与质量成正比例.
(2)根据表格中数据可在右图中描点连线,得出统计图如图:
(3)点(15,270)在这条直线上,这一点表示15份套餐需要270元钱.
(4)3×18=54(元),
126÷18=7(份),
答:买3份该套餐要付54元钱,126元可以买7份该套餐.
【点评】此题考查正比例的意义,绘制折线统计图的方法,以及成正比例关系的量的特点,明确成正比例的两个量必须得比值一定.
19.图表示了矿泉水的数量与总价的关系,看图回答问题.
①5瓶的总价是 10 元.
②12瓶的总价是 24 元.
③ 18 瓶的总价是36元.
【考点】正比例和反比例的意义.
【专题】比和比例;应用意识.
【答案】见试题解答内容
【分析】①仔细观察图表,5瓶的售价是10元;
②先利用所给的数据求出一瓶矿泉水的价格,再根据总价=单价×数量解答即可;
③先利用所给的数据求出一瓶矿泉水的价格,用数量=总价÷单价解答即可.
【解答】解:(1)5瓶的售价是10元.
(2)10÷5×12
=2×12
=24(元);
答:12瓶的售价是 24元.
(3)36÷(10÷5)
=36÷2
=18(瓶);
答:18瓶的售价是36元.
故答案为:10,24,18.
【点评】此题主要考查正比例的意义在生活实际中的灵活应用.
20.下面表中的两种量成正比例吗?为什么?
(1)
成年人数(人) 1 50 1000 10亿
每天呼出二氧化碳(kg) 0.9 45 900 9亿
(2)
阔叶林面积(km2) 1 50 1000 90万
每天吸收二氧化碳(吨) 100 5000 100000 9000万
【考点】辨识成正比例的量与成反比例的量.
【专题】应用意识.
【答案】成正比例,因为表中的这两种量,一种量变化,另一种也随着变化,并且这两种量中相对应的两个数的比值一定,所以,这两种量就叫做成正比例的量。
【分析】两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的乘积一定,这两种量叫做成反比例的量,它们的关系叫做反比例关系;两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量叫做成正比例的量,它们的关系叫做正比例关系。
【解答】解:(1)1:0.9=
50:45=
1000:900=
10亿:9亿=
因为:=(一定),所以表中的两个量成正比例关系。
(2)1:100=
50:5000=
1000:100000=
90万:9000万=
因为=(一定),所以,表中的两种量成正比例关系。
答:(1)(2)表中的两种量成正比例关系。因为表中的这两种量,一种量变化,另一种也随着变化,并且这两种量中相对应的两个数的比值一定,所以,这两种量就叫做成正比例的量。
【点评】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再作判断。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
