【期末押题预测】期末核心考点 长方体与正方体的体积(含解析)2024-2025学年五年级下册数学北师大版
文档属性
| 名称 | 【期末押题预测】期末核心考点 长方体与正方体的体积(含解析)2024-2025学年五年级下册数学北师大版 |
|
|
| 格式 | docx | ||
| 文件大小 | 579.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-10 05:12:46 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
期末核心考点 长方体与正方体的体积
一.选择题(共5小题)
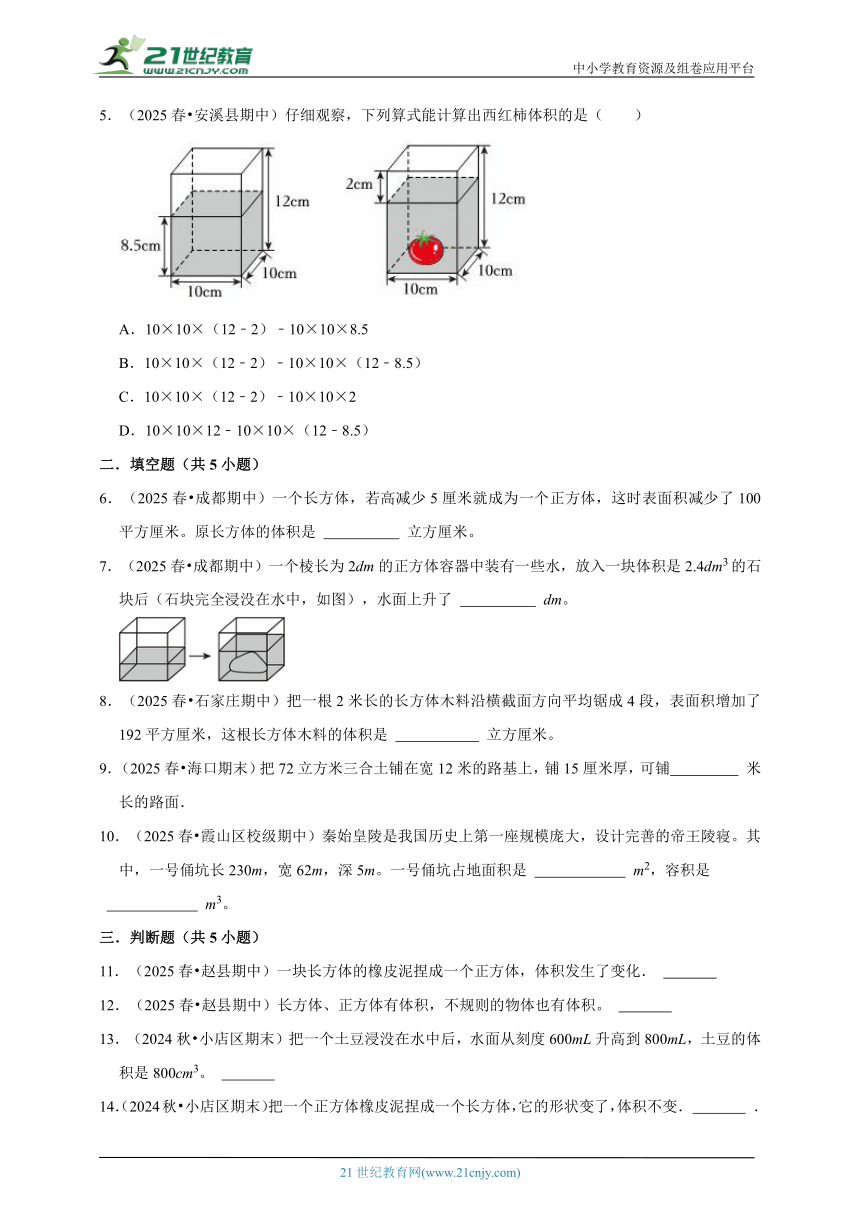
1.(2025春 霞山区校级期中)观察如图,大球的体积是( )cm3。
A.4 B.6 C.8 D.10
2.(2025春 霞山区校级期中)有一块棱长是10厘米的实心正方体铁块,要把它熔化后做成一个实心长方体,已知实心长方体的长是25厘米,宽是10厘米,则这个实心长方体的高是( )厘米。
A.4 B.6 C.7 D.8
3.(2025春 安溪县期中)安安把他的一只拳头慢慢伸进盛满水的容器中,溢出来的水的体积大约是( )
A.0.5m3 B.0.5dm3 C.0.6cm3 D.0.5mL
4.(2025春 安溪县期中)把一块铁块分别放进四个容器中(如下图),铁块都能完全浸没在水中,且水未溢出容器。水位上升最多的容器是( )
A. B.
C. D.
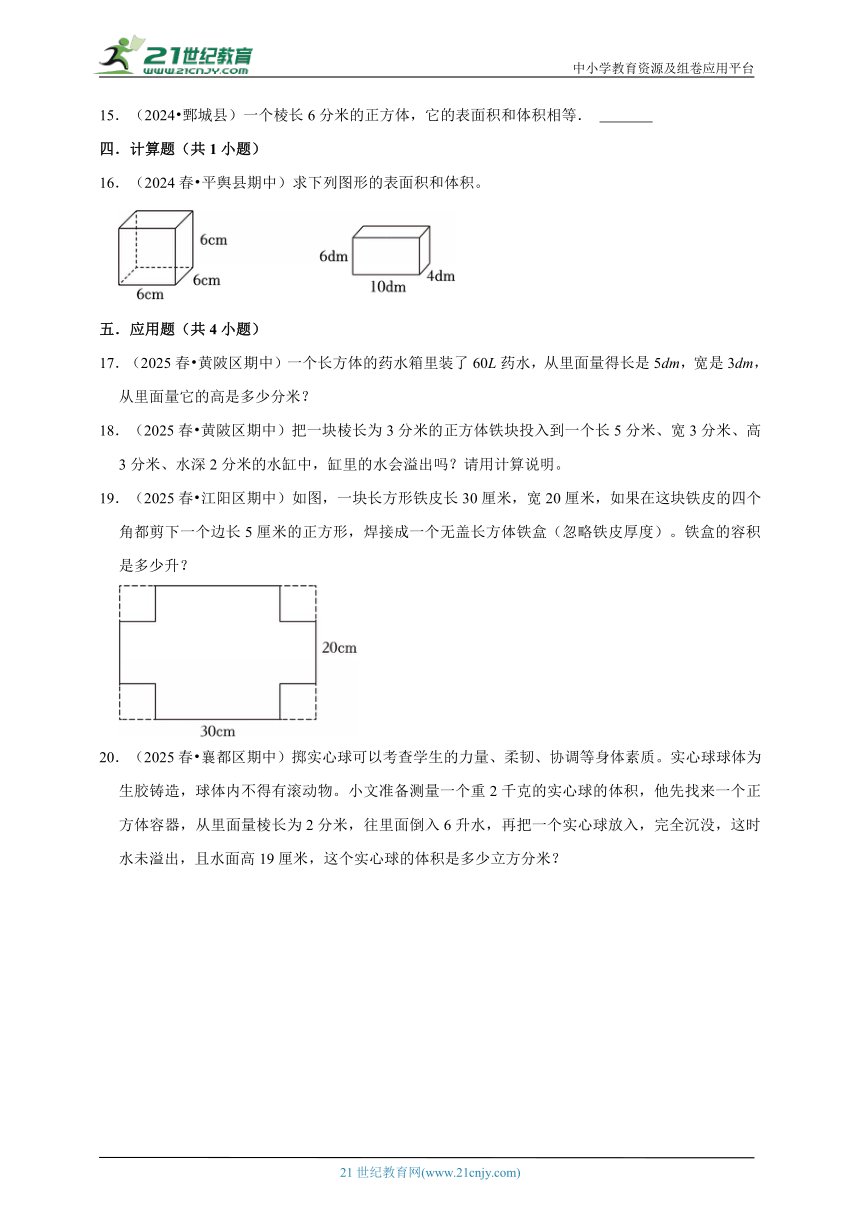
5.(2025春 安溪县期中)仔细观察,下列算式能计算出西红柿体积的是( )
A.10×10×(12﹣2)﹣10×10×8.5
B.10×10×(12﹣2)﹣10×10×(12﹣8.5)
C.10×10×(12﹣2)﹣10×10×2
D.10×10×12﹣10×10×(12﹣8.5)
二.填空题(共5小题)
6.(2025春 成都期中)一个长方体,若高减少5厘米就成为一个正方体,这时表面积减少了100平方厘米。原长方体的体积是 立方厘米。
7.(2025春 成都期中)一个棱长为2dm的正方体容器中装有一些水,放入一块体积是2.4dm3的石块后(石块完全浸没在水中,如图),水面上升了 dm。
8.(2025春 石家庄期中)把一根2米长的长方体木料沿横截面方向平均锯成4段,表面积增加了192平方厘米,这根长方体木料的体积是 立方厘米。
9.(2025春 海口期末)把72立方米三合土铺在宽12米的路基上,铺15厘米厚,可铺 米长的路面.
10.(2025春 霞山区校级期中)秦始皇陵是我国历史上第一座规模庞大,设计完善的帝王陵寝。其中,一号俑坑长230m,宽62m,深5m。一号俑坑占地面积是 m2,容积是
m3。
三.判断题(共5小题)
11.(2025春 赵县期中)一块长方体的橡皮泥捏成一个正方体,体积发生了变化.
12.(2025春 赵县期中)长方体、正方体有体积,不规则的物体也有体积。
13.(2024秋 小店区期末)把一个土豆浸没在水中后,水面从刻度600mL升高到800mL,土豆的体积是800cm3。
14.(2024秋 小店区期末)把一个正方体橡皮泥捏成一个长方体,它的形状变了,体积不变. .
15.(2024 鄄城县)一个棱长6分米的正方体,它的表面积和体积相等.
四.计算题(共1小题)
16.(2024春 平舆县期中)求下列图形的表面积和体积。
五.应用题(共4小题)
17.(2025春 黄陂区期中)一个长方体的药水箱里装了60L药水,从里面量得长是5dm,宽是3dm,从里面量它的高是多少分米?
18.(2025春 黄陂区期中)把一块棱长为3分米的正方体铁块投入到一个长5分米、宽3分米、高3分米、水深2分米的水缸中,缸里的水会溢出吗?请用计算说明。
19.(2025春 江阳区期中)如图,一块长方形铁皮长30厘米,宽20厘米,如果在这块铁皮的四个角都剪下一个边长5厘米的正方形,焊接成一个无盖长方体铁盒(忽略铁皮厚度)。铁盒的容积是多少升?
20.(2025春 襄都区期中)掷实心球可以考查学生的力量、柔韧、协调等身体素质。实心球球体为生胶铸造,球体内不得有滚动物。小文准备测量一个重2千克的实心球的体积,他先找来一个正方体容器,从里面量棱长为2分米,往里面倒入6升水,再把一个实心球放入,完全沉没,这时水未溢出,且水面高19厘米,这个实心球的体积是多少立方分米?
期末核心考点 长方体与正方体的体积
参考答案与试题解析
一.选择题(共5小题)
1.(2025春 霞山区校级期中)观察如图,大球的体积是( )cm3。
A.4 B.6 C.8 D.10
【考点】探索某些实物体积的测量方法.
【专题】应用题;数据分析观念.
【答案】C
【分析】1个大球和1个小球的体积是12立方厘米,1个大球和4个小球的体积是24立方厘米,计算出1个小球的体积,然后计算大球的体积。
【解答】解:小球体积:(24﹣12)÷(4﹣1)
=12÷3
=4(立方厘米)
大球体积:12﹣4=8(立方厘米)
答:大球体积8立方厘米。
故选:C。
【点评】本题通过图示找出大球和小球体积之间的数量关系从而计算大球的体积。
2.(2025春 霞山区校级期中)有一块棱长是10厘米的实心正方体铁块,要把它熔化后做成一个实心长方体,已知实心长方体的长是25厘米,宽是10厘米,则这个实心长方体的高是( )厘米。
A.4 B.6 C.7 D.8
【考点】长方体和正方体的体积.
【专题】应用题;数据分析观念.
【答案】A
【分析】根据题意,把一个实心正方体铁块熔化后做成一个实心长方体,那么铁块的体积不变;根据正方体的体积公式V=a3,求出铁块儿的体积;
已知实心长方体的长和宽,根据长方体的高h=V÷a÷b,代入数据计算,即可求出长方体的高。
【解答】解:铁块的体积:
10×10×10=1000(立方厘米)
长方体的高:
1000÷25÷10
=40÷10
=4(厘米)
答:这个实心长方体的高是4厘米。
故选:A。
【点评】本题考查的是长方体的体积公式的应用。
3.(2025春 安溪县期中)安安把他的一只拳头慢慢伸进盛满水的容器中,溢出来的水的体积大约是( )
A.0.5m3 B.0.5dm3 C.0.6cm3 D.0.5mL
【考点】体积、容积及其单位.
【专题】长度、面积、体积单位;数据分析观念.
【答案】B
【分析】一个拳头的体积大约是0.5立方分米,据此解答。
【解答】解:安安把他的一只拳头慢慢伸进盛满水的容器中,溢出来的水的体积大约是0.5dm3。
故选:B。
【点评】此题考查体积单位的认识。
4.(2025春 安溪县期中)把一块铁块分别放进四个容器中(如下图),铁块都能完全浸没在水中,且水未溢出容器。水位上升最多的容器是( )
A. B.
C. D.
【考点】长方体和正方体的体积.
【专题】对应法;空间观念.
【答案】B
【分析】铁块浸没后排开的水的体积=容器底面积×水面上升高度,铁块体积不变,据此比较底面积大小得解。
【解答】解:A.容器底面积:8×8=64
B.容器底面积:4×6=24
C.容器底面积:6×6=36
D.容器底面积:10×5=50
24<36<50<64
底面积越小,水面上升越多。
故选:B。
【点评】本题考查了体积公式的理解与应用问题,铁块的体积不变,排开的水的体积相同,即容器底面积与水面上升高度值的乘积不变,底面积越大,上升的高度值越小,反之,水面上升的高度值则越大。
5.(2025春 安溪县期中)仔细观察,下列算式能计算出西红柿体积的是( )
A.10×10×(12﹣2)﹣10×10×8.5
B.10×10×(12﹣2)﹣10×10×(12﹣8.5)
C.10×10×(12﹣2)﹣10×10×2
D.10×10×12﹣10×10×(12﹣8.5)
【考点】探索某些实物体积的测量方法.
【专题】应用意识.
【答案】A
【分析】利用排水法求不规则物体(西红柿)体积,西红柿体积等于放入西红柿后水和西红柿总体积减去原来水的体积。需要先根据图中数据确定相关高度,再结合长方体体积公式计算。长方体容器底面积为(10×10)平方厘米,原来水高8.5厘米,放入西红柿后水面高度为(12﹣2)厘米。根据“长方体体积公式V=Sh(S是底面积,h是高)”,计算水和西红柿的总体积以及原来水的体积;西红柿体积=放入西红柿后水和西红柿总体积﹣原来水的体积,据此解答。
【解答】解:确定相关体积计算数据;长方体容器底面积为(10×10)平方厘米,
原来水高8.5厘米,放入西红柿后水面高度为12﹣2=10(厘米),
放入西红柿后水和西红柿总体积:根据长方体体积公式V=Sh(S是底面积,h是高),
总体积为10×10×(12﹣2)立方厘米,
原来水的体积:10×10×8.5立方厘米,
计算西红柿体积:
西红柿体积=放入西红柿后水和西红柿总体积﹣原来水的体积,
即10×10×(12﹣2)﹣10×10×8.5
所以A选项正确。
故选:A。
【点评】本题考查利用排水法求不规则物体体积,涉及长方体体积公式的应用。
二.填空题(共5小题)
6.(2025春 成都期中)一个长方体,若高减少5厘米就成为一个正方体,这时表面积减少了100平方厘米。原长方体的体积是 250 立方厘米。
【考点】长方体和正方体的体积.
【专题】综合填空题;应用意识.
【答案】250。
【分析】根据题意,长方体的高减少5厘米后,表面积减少100平方厘米,变成一个正方体,说明原来长方体的长、宽相等;减少的表面积是4个完全一样的长方形的面积,长方形的宽是5厘米,长是原来长方体的长或宽,用减少的表面积除以4,求出一个长方形的面积,再除以5,即可求出原来长方体的长、宽;再用长方体的长或宽加上5厘米,即是原来长方体的高;最后根据长方体的体积=长×宽×高,求出原来长方体的体积。
【解答】解:原来长方体的长、宽:
100÷4÷5
=25÷5
=5(厘米)
原来长方体的高:
5+5=10(厘米)
原来长方体的体积:
5×5×10=250(立方厘米)
答:原来的长方体的体积是250立方厘米。
故答案为:250。
【点评】本题考查长方体表面积、体积公式的运用,关键是分析出减少的表面积是哪些面的面积,以此为突破口,求出原来长方体的长、宽、高是解题的关键。
7.(2025春 成都期中)一个棱长为2dm的正方体容器中装有一些水,放入一块体积是2.4dm3的石块后(石块完全浸没在水中,如图),水面上升了 0.6 dm。
【考点】探索某些实物体积的测量方法.
【专题】几何直观.
【答案】0.6。
【分析】根据用“排水法”测量实物体积的方法,水上升的体积等于石块的体积,结合长方体的体积公式V=abh解答即可。
【解答】解:2.4÷(2×2)
=2.4÷4
=0.6(分米)
答:水面上升了0.6分米。
故答案为:0.6。
【点评】本题考查了用“排水法”测量实物体积的方法,结合长方体的体积公式V=abh解答即可。
8.(2025春 石家庄期中)把一根2米长的长方体木料沿横截面方向平均锯成4段,表面积增加了192平方厘米,这根长方体木料的体积是 6400 立方厘米。
【考点】长方体和正方体的体积.
【专题】综合填空题;应用意识.
【答案】6400。
【分析】根据题意,沿与横截面平行的方向锯成4段,那么增加了6个底面,用增加的面积192平方厘米除以6求出一个底面积,再根据长方体的体积公式:V=Sh,把数据代入公式解答。
【解答】解:2米=200厘米
192÷6×200
=32×200
=6400(立方厘米)
答:这根长方体木料的体积是6400立方厘米。
故答案为:6400。
【点评】此题主要考查立体图形的切割问题,根据增加的面积求出长方体的底面积是解题关键;注意统一单位。
9.(2025春 海口期末)把72立方米三合土铺在宽12米的路基上,铺15厘米厚,可铺 40 米长的路面.
【考点】长方体和正方体的体积.
【专题】立体图形的认识与计算.
【答案】见试题解答内容
【分析】根据长方体的体积公式:V=sh,那么h=V÷S,把数据代入公式解答.
【解答】解:15厘米=0.15米
72÷(12×0.15)
=72÷1.8
=40(米)
答:可以铺40米长的路面.
故答案为:40.
【点评】此题主要考查长方体的体积公式的灵活运用,关键是熟记公式.
10.(2025春 霞山区校级期中)秦始皇陵是我国历史上第一座规模庞大,设计完善的帝王陵寝。其中,一号俑坑长230m,宽62m,深5m。一号俑坑占地面积是 14260 m2,容积是 71300 m3。
【考点】长方体和正方体的体积.
【专题】应用题;几何直观.
【答案】14260,71300。
【分析】求一号蛹坑的占地面积就是求长方体的底面积,利用“长方形的面积=长×宽”求出一号俑坑的占地面积;根据长方体容积公式:容积=长×宽×高,代入数据,即可解答。
【解答】解:230×62=14260(m2)
230×65×5
=14260×5
=71300(m3)
答:一号俑坑占地面积是14260m2,容积是71300m3。
故答案为:14260,71300。
【点评】本题考查的是长方体的体积公式,长方形的面积公式的应用。
三.判断题(共5小题)
11.(2025春 赵县期中)一块长方体的橡皮泥捏成一个正方体,体积发生了变化. ×
【考点】长方体和正方体的体积.
【专题】立体图形的认识与计算;应用意识.
【答案】×
【分析】根据体积的意义,物体所占空间的大小叫做物体的体积,所以把一块长方体橡皮泥捏成一个正方体后,只是形状变了,但体积不变.据此解答.
【解答】解:把一块长方体橡皮泥捏成一个正方体后,只是形状变了,但体积不变,故原题说法错误;
故答案为:×.
【点评】此题考查的目的是理解掌握物体体积的意义,物体所占空间的大小叫做物体的体积.
12.(2025春 赵县期中)长方体、正方体有体积,不规则的物体也有体积。 √
【考点】长方体和正方体的体积.
【专题】空间观念.
【答案】√
【分析】根据体积的意义,物体所占空间的大小叫做物体的体积。据此判断。
【解答】解:根据分析可知,长方体、正方体有体积,不规则的物体也有体积。此说法是正确的。
故答案为:√。
【点评】正确理解体积的意义,是解答此题的关键。
13.(2024秋 小店区期末)把一个土豆浸没在水中后,水面从刻度600mL升高到800mL,土豆的体积是800cm3。 ×
【考点】探索某些实物体积的测量方法.
【专题】几何直观.
【答案】×。
【分析】根据用“排水法”测量实物体积的方法,把一个土豆浸没在水中后,水面从刻度600mL升高到800mL,土豆的体积是水上升的体积,据此解答即可。
【解答】解:800﹣600=200(毫升)
200毫升=200立方厘米
答:土豆的体积是200立方厘米,所以原题说法错误。
故答案为:×。
【点评】本题考查了用“排水法”测量实物体积的方法,结合题意分析解答即可。
14.(2024秋 小店区期末)把一个正方体橡皮泥捏成一个长方体,它的形状变了,体积不变. √ .
【考点】长方体和正方体的体积.
【专题】综合判断题;立体图形的认识与计算.
【答案】√
【分析】物体的体积是指:物体所占空间的大小.把一块橡皮泥无论捏成一个正方体还是一个长方体,它的形状虽然变了,但是所占空间的大小没变,即体积不变,解答判断即可.
【解答】解:把一块橡皮泥无论捏成一个正方体还是一个长方体,它的形状虽然变了,但是所占空间的大小没变,即体积不变.
所以“把一个正方体橡皮泥捏成一个长方体,它的形状变了,体积不变”的说法是正确的.
故答案为:√
【点评】此题考查对物体体积的理解,虽然形状变了,但是所占空间的大小没变,即体积不变.
15.(2024 鄄城县)一个棱长6分米的正方体,它的表面积和体积相等. ×
【考点】长方体和正方体的体积.
【专题】立体图形的认识与计算.
【答案】×
【分析】正方体的表面积公式:s=6a2,正方体的体积公式:v=a3,因为表面积和体积不是同类量,无法进行比较.由此解答.
【解答】解:表面积:6×6×6=216(平方分米)
体积:6×6×6=216(立方分米)
因为表面积和体积不是同类量,无法进行比较.
故原来的说法是错误的.
故答案为:×.
【点评】此题解答关键是明确:只有同类量才能进行比较大小,不是同类量无法进行比较.
四.计算题(共1小题)
16.(2024春 平舆县期中)求下列图形的表面积和体积。
【考点】长方体和正方体的体积;长方体和正方体的表面积.
【专题】应用意识.
【答案】216平方厘米,216立方厘米;248平方分米,240立方分米。
【分析】根据正方体的表面积公式:S=6a2,正方体的体积公式:V=a3,长方体的表面积公式:S=(ab+ah+bh)×2,长方体的体积公式:V=abh,把数据代入公式解答。
【解答】解:6×6×6
=36×6
=216(平方厘米)
6×6×6
=36×6
=216(立方厘米)
(10×4+10×6+4×6)×2
=(40+60+24)×2
=124×2
=248(平方分米)
10×4×6
=40×6
=240(立方分米)
答:正方体的表面积是216平方厘米,体积是216立方厘米,长方体的表面积是248平方分米,体积是240立方分米。
【点评】此题主要考查正方体、长方体的表面积公式、体积公式的灵活运用,关键是熟记公式。
五.应用题(共4小题)
17.(2025春 黄陂区期中)一个长方体的药水箱里装了60L药水,从里面量得长是5dm,宽是3dm,从里面量它的高是多少分米?
【考点】长方体和正方体的体积.
【专题】应用意识.
【答案】4分米。
【分析】根据长方体的体积(容积)的计算方法,把容积单位换算成体积单位,用体积除以底面积即可求出高;由此解答。
【解答】解:解:60升=60立方分米
60÷(5×3)
=60÷15
=4(分米)
答:从里面量它的高是4分米。
【点评】此题主要考查长方体的体积(容积)的计算,能够根据体积(容积)的计算方法解决有关的实际问题。
18.(2025春 黄陂区期中)把一块棱长为3分米的正方体铁块投入到一个长5分米、宽3分米、高3分米、水深2分米的水缸中,缸里的水会溢出吗?请用计算说明。
【考点】长方体和正方体的体积.
【专题】对应法;空间观念.
【答案】会;铁块体积大于缸口容积,即铁块排开的水的体积大于缸口剩下容积。
【分析】先算出缸口未存水容积,再算出铁块体积,进而比大小得解。
【解答】解:水缸缸口未存水容积:
5×3×(3﹣2)
=15×1
=15(立方分米)
铁块体积:
3×3×3
=9×3
=27(立方分米)
15立方分米<27立方分米
答:缸里的水会溢出,因为铁块体积大于缸口容积,即铁块排开的水的体积大于缸口剩下容积。
【点评】本题考查了长方体、正方体体积(容积)计算的实际应用问题,解答时一定要熟练掌握相关的计算公式。
19.(2025春 江阳区期中)如图,一块长方形铁皮长30厘米,宽20厘米,如果在这块铁皮的四个角都剪下一个边长5厘米的正方形,焊接成一个无盖长方体铁盒(忽略铁皮厚度)。铁盒的容积是多少升?
【考点】长方体和正方体的体积.
【专题】计算题;几何直观.
【答案】1升。
【分析】这个长方体的高是5厘米,长是(30﹣5×2)厘米,宽是(20﹣5×2)厘米,利用“长方体的体积=长×宽×高”,结合题中数据计算即可。
【解答】解:(30﹣5×2)×(20﹣5×2)×5
=20×10×5
=1000(立方厘米)
1000立方厘米=1升
答:铁盒的容积是1升。
【点评】本题考查的是长方体的体积公式的应用。
20.(2025春 襄都区期中)掷实心球可以考查学生的力量、柔韧、协调等身体素质。实心球球体为生胶铸造,球体内不得有滚动物。小文准备测量一个重2千克的实心球的体积,他先找来一个正方体容器,从里面量棱长为2分米,往里面倒入6升水,再把一个实心球放入,完全沉没,这时水未溢出,且水面高19厘米,这个实心球的体积是多少立方分米?
【考点】探索某些实物体积的测量方法.
【专题】应用意识.
【答案】1.6立方分米。
【分析】根据特殊物体体积的测量方法,利用排水法,把实心球放入有6升水的正方体容器中,上升部分水的体积就等于这个实心球的体积,根据长方体的体积公式:V=abh,把数据代入公式解答。
【解答】解:6升=6立方分米
19厘米=1.9分米
2×2×1.9﹣6
=4×1.9﹣6
=7.6﹣6
=1.6(立方分米)
答:这个实心球的体积是1.6立方分米。
【点评】此题考查的目的是理解掌握特殊物体体积的测量方法及应用,长方体的体积公式及应用。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末核心考点 长方体与正方体的体积
一.选择题(共5小题)
1.(2025春 霞山区校级期中)观察如图,大球的体积是( )cm3。
A.4 B.6 C.8 D.10
2.(2025春 霞山区校级期中)有一块棱长是10厘米的实心正方体铁块,要把它熔化后做成一个实心长方体,已知实心长方体的长是25厘米,宽是10厘米,则这个实心长方体的高是( )厘米。
A.4 B.6 C.7 D.8
3.(2025春 安溪县期中)安安把他的一只拳头慢慢伸进盛满水的容器中,溢出来的水的体积大约是( )
A.0.5m3 B.0.5dm3 C.0.6cm3 D.0.5mL
4.(2025春 安溪县期中)把一块铁块分别放进四个容器中(如下图),铁块都能完全浸没在水中,且水未溢出容器。水位上升最多的容器是( )
A. B.
C. D.
5.(2025春 安溪县期中)仔细观察,下列算式能计算出西红柿体积的是( )
A.10×10×(12﹣2)﹣10×10×8.5
B.10×10×(12﹣2)﹣10×10×(12﹣8.5)
C.10×10×(12﹣2)﹣10×10×2
D.10×10×12﹣10×10×(12﹣8.5)
二.填空题(共5小题)
6.(2025春 成都期中)一个长方体,若高减少5厘米就成为一个正方体,这时表面积减少了100平方厘米。原长方体的体积是 立方厘米。
7.(2025春 成都期中)一个棱长为2dm的正方体容器中装有一些水,放入一块体积是2.4dm3的石块后(石块完全浸没在水中,如图),水面上升了 dm。
8.(2025春 石家庄期中)把一根2米长的长方体木料沿横截面方向平均锯成4段,表面积增加了192平方厘米,这根长方体木料的体积是 立方厘米。
9.(2025春 海口期末)把72立方米三合土铺在宽12米的路基上,铺15厘米厚,可铺 米长的路面.
10.(2025春 霞山区校级期中)秦始皇陵是我国历史上第一座规模庞大,设计完善的帝王陵寝。其中,一号俑坑长230m,宽62m,深5m。一号俑坑占地面积是 m2,容积是
m3。
三.判断题(共5小题)
11.(2025春 赵县期中)一块长方体的橡皮泥捏成一个正方体,体积发生了变化.
12.(2025春 赵县期中)长方体、正方体有体积,不规则的物体也有体积。
13.(2024秋 小店区期末)把一个土豆浸没在水中后,水面从刻度600mL升高到800mL,土豆的体积是800cm3。
14.(2024秋 小店区期末)把一个正方体橡皮泥捏成一个长方体,它的形状变了,体积不变. .
15.(2024 鄄城县)一个棱长6分米的正方体,它的表面积和体积相等.
四.计算题(共1小题)
16.(2024春 平舆县期中)求下列图形的表面积和体积。
五.应用题(共4小题)
17.(2025春 黄陂区期中)一个长方体的药水箱里装了60L药水,从里面量得长是5dm,宽是3dm,从里面量它的高是多少分米?
18.(2025春 黄陂区期中)把一块棱长为3分米的正方体铁块投入到一个长5分米、宽3分米、高3分米、水深2分米的水缸中,缸里的水会溢出吗?请用计算说明。
19.(2025春 江阳区期中)如图,一块长方形铁皮长30厘米,宽20厘米,如果在这块铁皮的四个角都剪下一个边长5厘米的正方形,焊接成一个无盖长方体铁盒(忽略铁皮厚度)。铁盒的容积是多少升?
20.(2025春 襄都区期中)掷实心球可以考查学生的力量、柔韧、协调等身体素质。实心球球体为生胶铸造,球体内不得有滚动物。小文准备测量一个重2千克的实心球的体积,他先找来一个正方体容器,从里面量棱长为2分米,往里面倒入6升水,再把一个实心球放入,完全沉没,这时水未溢出,且水面高19厘米,这个实心球的体积是多少立方分米?
期末核心考点 长方体与正方体的体积
参考答案与试题解析
一.选择题(共5小题)
1.(2025春 霞山区校级期中)观察如图,大球的体积是( )cm3。
A.4 B.6 C.8 D.10
【考点】探索某些实物体积的测量方法.
【专题】应用题;数据分析观念.
【答案】C
【分析】1个大球和1个小球的体积是12立方厘米,1个大球和4个小球的体积是24立方厘米,计算出1个小球的体积,然后计算大球的体积。
【解答】解:小球体积:(24﹣12)÷(4﹣1)
=12÷3
=4(立方厘米)
大球体积:12﹣4=8(立方厘米)
答:大球体积8立方厘米。
故选:C。
【点评】本题通过图示找出大球和小球体积之间的数量关系从而计算大球的体积。
2.(2025春 霞山区校级期中)有一块棱长是10厘米的实心正方体铁块,要把它熔化后做成一个实心长方体,已知实心长方体的长是25厘米,宽是10厘米,则这个实心长方体的高是( )厘米。
A.4 B.6 C.7 D.8
【考点】长方体和正方体的体积.
【专题】应用题;数据分析观念.
【答案】A
【分析】根据题意,把一个实心正方体铁块熔化后做成一个实心长方体,那么铁块的体积不变;根据正方体的体积公式V=a3,求出铁块儿的体积;
已知实心长方体的长和宽,根据长方体的高h=V÷a÷b,代入数据计算,即可求出长方体的高。
【解答】解:铁块的体积:
10×10×10=1000(立方厘米)
长方体的高:
1000÷25÷10
=40÷10
=4(厘米)
答:这个实心长方体的高是4厘米。
故选:A。
【点评】本题考查的是长方体的体积公式的应用。
3.(2025春 安溪县期中)安安把他的一只拳头慢慢伸进盛满水的容器中,溢出来的水的体积大约是( )
A.0.5m3 B.0.5dm3 C.0.6cm3 D.0.5mL
【考点】体积、容积及其单位.
【专题】长度、面积、体积单位;数据分析观念.
【答案】B
【分析】一个拳头的体积大约是0.5立方分米,据此解答。
【解答】解:安安把他的一只拳头慢慢伸进盛满水的容器中,溢出来的水的体积大约是0.5dm3。
故选:B。
【点评】此题考查体积单位的认识。
4.(2025春 安溪县期中)把一块铁块分别放进四个容器中(如下图),铁块都能完全浸没在水中,且水未溢出容器。水位上升最多的容器是( )
A. B.
C. D.
【考点】长方体和正方体的体积.
【专题】对应法;空间观念.
【答案】B
【分析】铁块浸没后排开的水的体积=容器底面积×水面上升高度,铁块体积不变,据此比较底面积大小得解。
【解答】解:A.容器底面积:8×8=64
B.容器底面积:4×6=24
C.容器底面积:6×6=36
D.容器底面积:10×5=50
24<36<50<64
底面积越小,水面上升越多。
故选:B。
【点评】本题考查了体积公式的理解与应用问题,铁块的体积不变,排开的水的体积相同,即容器底面积与水面上升高度值的乘积不变,底面积越大,上升的高度值越小,反之,水面上升的高度值则越大。
5.(2025春 安溪县期中)仔细观察,下列算式能计算出西红柿体积的是( )
A.10×10×(12﹣2)﹣10×10×8.5
B.10×10×(12﹣2)﹣10×10×(12﹣8.5)
C.10×10×(12﹣2)﹣10×10×2
D.10×10×12﹣10×10×(12﹣8.5)
【考点】探索某些实物体积的测量方法.
【专题】应用意识.
【答案】A
【分析】利用排水法求不规则物体(西红柿)体积,西红柿体积等于放入西红柿后水和西红柿总体积减去原来水的体积。需要先根据图中数据确定相关高度,再结合长方体体积公式计算。长方体容器底面积为(10×10)平方厘米,原来水高8.5厘米,放入西红柿后水面高度为(12﹣2)厘米。根据“长方体体积公式V=Sh(S是底面积,h是高)”,计算水和西红柿的总体积以及原来水的体积;西红柿体积=放入西红柿后水和西红柿总体积﹣原来水的体积,据此解答。
【解答】解:确定相关体积计算数据;长方体容器底面积为(10×10)平方厘米,
原来水高8.5厘米,放入西红柿后水面高度为12﹣2=10(厘米),
放入西红柿后水和西红柿总体积:根据长方体体积公式V=Sh(S是底面积,h是高),
总体积为10×10×(12﹣2)立方厘米,
原来水的体积:10×10×8.5立方厘米,
计算西红柿体积:
西红柿体积=放入西红柿后水和西红柿总体积﹣原来水的体积,
即10×10×(12﹣2)﹣10×10×8.5
所以A选项正确。
故选:A。
【点评】本题考查利用排水法求不规则物体体积,涉及长方体体积公式的应用。
二.填空题(共5小题)
6.(2025春 成都期中)一个长方体,若高减少5厘米就成为一个正方体,这时表面积减少了100平方厘米。原长方体的体积是 250 立方厘米。
【考点】长方体和正方体的体积.
【专题】综合填空题;应用意识.
【答案】250。
【分析】根据题意,长方体的高减少5厘米后,表面积减少100平方厘米,变成一个正方体,说明原来长方体的长、宽相等;减少的表面积是4个完全一样的长方形的面积,长方形的宽是5厘米,长是原来长方体的长或宽,用减少的表面积除以4,求出一个长方形的面积,再除以5,即可求出原来长方体的长、宽;再用长方体的长或宽加上5厘米,即是原来长方体的高;最后根据长方体的体积=长×宽×高,求出原来长方体的体积。
【解答】解:原来长方体的长、宽:
100÷4÷5
=25÷5
=5(厘米)
原来长方体的高:
5+5=10(厘米)
原来长方体的体积:
5×5×10=250(立方厘米)
答:原来的长方体的体积是250立方厘米。
故答案为:250。
【点评】本题考查长方体表面积、体积公式的运用,关键是分析出减少的表面积是哪些面的面积,以此为突破口,求出原来长方体的长、宽、高是解题的关键。
7.(2025春 成都期中)一个棱长为2dm的正方体容器中装有一些水,放入一块体积是2.4dm3的石块后(石块完全浸没在水中,如图),水面上升了 0.6 dm。
【考点】探索某些实物体积的测量方法.
【专题】几何直观.
【答案】0.6。
【分析】根据用“排水法”测量实物体积的方法,水上升的体积等于石块的体积,结合长方体的体积公式V=abh解答即可。
【解答】解:2.4÷(2×2)
=2.4÷4
=0.6(分米)
答:水面上升了0.6分米。
故答案为:0.6。
【点评】本题考查了用“排水法”测量实物体积的方法,结合长方体的体积公式V=abh解答即可。
8.(2025春 石家庄期中)把一根2米长的长方体木料沿横截面方向平均锯成4段,表面积增加了192平方厘米,这根长方体木料的体积是 6400 立方厘米。
【考点】长方体和正方体的体积.
【专题】综合填空题;应用意识.
【答案】6400。
【分析】根据题意,沿与横截面平行的方向锯成4段,那么增加了6个底面,用增加的面积192平方厘米除以6求出一个底面积,再根据长方体的体积公式:V=Sh,把数据代入公式解答。
【解答】解:2米=200厘米
192÷6×200
=32×200
=6400(立方厘米)
答:这根长方体木料的体积是6400立方厘米。
故答案为:6400。
【点评】此题主要考查立体图形的切割问题,根据增加的面积求出长方体的底面积是解题关键;注意统一单位。
9.(2025春 海口期末)把72立方米三合土铺在宽12米的路基上,铺15厘米厚,可铺 40 米长的路面.
【考点】长方体和正方体的体积.
【专题】立体图形的认识与计算.
【答案】见试题解答内容
【分析】根据长方体的体积公式:V=sh,那么h=V÷S,把数据代入公式解答.
【解答】解:15厘米=0.15米
72÷(12×0.15)
=72÷1.8
=40(米)
答:可以铺40米长的路面.
故答案为:40.
【点评】此题主要考查长方体的体积公式的灵活运用,关键是熟记公式.
10.(2025春 霞山区校级期中)秦始皇陵是我国历史上第一座规模庞大,设计完善的帝王陵寝。其中,一号俑坑长230m,宽62m,深5m。一号俑坑占地面积是 14260 m2,容积是 71300 m3。
【考点】长方体和正方体的体积.
【专题】应用题;几何直观.
【答案】14260,71300。
【分析】求一号蛹坑的占地面积就是求长方体的底面积,利用“长方形的面积=长×宽”求出一号俑坑的占地面积;根据长方体容积公式:容积=长×宽×高,代入数据,即可解答。
【解答】解:230×62=14260(m2)
230×65×5
=14260×5
=71300(m3)
答:一号俑坑占地面积是14260m2,容积是71300m3。
故答案为:14260,71300。
【点评】本题考查的是长方体的体积公式,长方形的面积公式的应用。
三.判断题(共5小题)
11.(2025春 赵县期中)一块长方体的橡皮泥捏成一个正方体,体积发生了变化. ×
【考点】长方体和正方体的体积.
【专题】立体图形的认识与计算;应用意识.
【答案】×
【分析】根据体积的意义,物体所占空间的大小叫做物体的体积,所以把一块长方体橡皮泥捏成一个正方体后,只是形状变了,但体积不变.据此解答.
【解答】解:把一块长方体橡皮泥捏成一个正方体后,只是形状变了,但体积不变,故原题说法错误;
故答案为:×.
【点评】此题考查的目的是理解掌握物体体积的意义,物体所占空间的大小叫做物体的体积.
12.(2025春 赵县期中)长方体、正方体有体积,不规则的物体也有体积。 √
【考点】长方体和正方体的体积.
【专题】空间观念.
【答案】√
【分析】根据体积的意义,物体所占空间的大小叫做物体的体积。据此判断。
【解答】解:根据分析可知,长方体、正方体有体积,不规则的物体也有体积。此说法是正确的。
故答案为:√。
【点评】正确理解体积的意义,是解答此题的关键。
13.(2024秋 小店区期末)把一个土豆浸没在水中后,水面从刻度600mL升高到800mL,土豆的体积是800cm3。 ×
【考点】探索某些实物体积的测量方法.
【专题】几何直观.
【答案】×。
【分析】根据用“排水法”测量实物体积的方法,把一个土豆浸没在水中后,水面从刻度600mL升高到800mL,土豆的体积是水上升的体积,据此解答即可。
【解答】解:800﹣600=200(毫升)
200毫升=200立方厘米
答:土豆的体积是200立方厘米,所以原题说法错误。
故答案为:×。
【点评】本题考查了用“排水法”测量实物体积的方法,结合题意分析解答即可。
14.(2024秋 小店区期末)把一个正方体橡皮泥捏成一个长方体,它的形状变了,体积不变. √ .
【考点】长方体和正方体的体积.
【专题】综合判断题;立体图形的认识与计算.
【答案】√
【分析】物体的体积是指:物体所占空间的大小.把一块橡皮泥无论捏成一个正方体还是一个长方体,它的形状虽然变了,但是所占空间的大小没变,即体积不变,解答判断即可.
【解答】解:把一块橡皮泥无论捏成一个正方体还是一个长方体,它的形状虽然变了,但是所占空间的大小没变,即体积不变.
所以“把一个正方体橡皮泥捏成一个长方体,它的形状变了,体积不变”的说法是正确的.
故答案为:√
【点评】此题考查对物体体积的理解,虽然形状变了,但是所占空间的大小没变,即体积不变.
15.(2024 鄄城县)一个棱长6分米的正方体,它的表面积和体积相等. ×
【考点】长方体和正方体的体积.
【专题】立体图形的认识与计算.
【答案】×
【分析】正方体的表面积公式:s=6a2,正方体的体积公式:v=a3,因为表面积和体积不是同类量,无法进行比较.由此解答.
【解答】解:表面积:6×6×6=216(平方分米)
体积:6×6×6=216(立方分米)
因为表面积和体积不是同类量,无法进行比较.
故原来的说法是错误的.
故答案为:×.
【点评】此题解答关键是明确:只有同类量才能进行比较大小,不是同类量无法进行比较.
四.计算题(共1小题)
16.(2024春 平舆县期中)求下列图形的表面积和体积。
【考点】长方体和正方体的体积;长方体和正方体的表面积.
【专题】应用意识.
【答案】216平方厘米,216立方厘米;248平方分米,240立方分米。
【分析】根据正方体的表面积公式:S=6a2,正方体的体积公式:V=a3,长方体的表面积公式:S=(ab+ah+bh)×2,长方体的体积公式:V=abh,把数据代入公式解答。
【解答】解:6×6×6
=36×6
=216(平方厘米)
6×6×6
=36×6
=216(立方厘米)
(10×4+10×6+4×6)×2
=(40+60+24)×2
=124×2
=248(平方分米)
10×4×6
=40×6
=240(立方分米)
答:正方体的表面积是216平方厘米,体积是216立方厘米,长方体的表面积是248平方分米,体积是240立方分米。
【点评】此题主要考查正方体、长方体的表面积公式、体积公式的灵活运用,关键是熟记公式。
五.应用题(共4小题)
17.(2025春 黄陂区期中)一个长方体的药水箱里装了60L药水,从里面量得长是5dm,宽是3dm,从里面量它的高是多少分米?
【考点】长方体和正方体的体积.
【专题】应用意识.
【答案】4分米。
【分析】根据长方体的体积(容积)的计算方法,把容积单位换算成体积单位,用体积除以底面积即可求出高;由此解答。
【解答】解:解:60升=60立方分米
60÷(5×3)
=60÷15
=4(分米)
答:从里面量它的高是4分米。
【点评】此题主要考查长方体的体积(容积)的计算,能够根据体积(容积)的计算方法解决有关的实际问题。
18.(2025春 黄陂区期中)把一块棱长为3分米的正方体铁块投入到一个长5分米、宽3分米、高3分米、水深2分米的水缸中,缸里的水会溢出吗?请用计算说明。
【考点】长方体和正方体的体积.
【专题】对应法;空间观念.
【答案】会;铁块体积大于缸口容积,即铁块排开的水的体积大于缸口剩下容积。
【分析】先算出缸口未存水容积,再算出铁块体积,进而比大小得解。
【解答】解:水缸缸口未存水容积:
5×3×(3﹣2)
=15×1
=15(立方分米)
铁块体积:
3×3×3
=9×3
=27(立方分米)
15立方分米<27立方分米
答:缸里的水会溢出,因为铁块体积大于缸口容积,即铁块排开的水的体积大于缸口剩下容积。
【点评】本题考查了长方体、正方体体积(容积)计算的实际应用问题,解答时一定要熟练掌握相关的计算公式。
19.(2025春 江阳区期中)如图,一块长方形铁皮长30厘米,宽20厘米,如果在这块铁皮的四个角都剪下一个边长5厘米的正方形,焊接成一个无盖长方体铁盒(忽略铁皮厚度)。铁盒的容积是多少升?
【考点】长方体和正方体的体积.
【专题】计算题;几何直观.
【答案】1升。
【分析】这个长方体的高是5厘米,长是(30﹣5×2)厘米,宽是(20﹣5×2)厘米,利用“长方体的体积=长×宽×高”,结合题中数据计算即可。
【解答】解:(30﹣5×2)×(20﹣5×2)×5
=20×10×5
=1000(立方厘米)
1000立方厘米=1升
答:铁盒的容积是1升。
【点评】本题考查的是长方体的体积公式的应用。
20.(2025春 襄都区期中)掷实心球可以考查学生的力量、柔韧、协调等身体素质。实心球球体为生胶铸造,球体内不得有滚动物。小文准备测量一个重2千克的实心球的体积,他先找来一个正方体容器,从里面量棱长为2分米,往里面倒入6升水,再把一个实心球放入,完全沉没,这时水未溢出,且水面高19厘米,这个实心球的体积是多少立方分米?
【考点】探索某些实物体积的测量方法.
【专题】应用意识.
【答案】1.6立方分米。
【分析】根据特殊物体体积的测量方法,利用排水法,把实心球放入有6升水的正方体容器中,上升部分水的体积就等于这个实心球的体积,根据长方体的体积公式:V=abh,把数据代入公式解答。
【解答】解:6升=6立方分米
19厘米=1.9分米
2×2×1.9﹣6
=4×1.9﹣6
=7.6﹣6
=1.6(立方分米)
答:这个实心球的体积是1.6立方分米。
【点评】此题考查的目的是理解掌握特殊物体体积的测量方法及应用,长方体的体积公式及应用。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
