广东省东莞市五校2024?2025学年高一下学期联考数学试卷(含详解)
文档属性
| 名称 | 广东省东莞市五校2024?2025学年高一下学期联考数学试卷(含详解) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-10 00:53:55 | ||
图片预览



文档简介
广东省东莞市五校2024 2025学年高一下学期联考数学试卷
一、单选题
1.从一个含有个个体的总体中抽取一容量为的样本,当选取抽签法、随机数法和分层随机抽样三种不同方法时,总体中每个个体被抽中的概率分别为,三者关系可能是( )
A. B. C. D.
2.在复平面内,复数(其中i为虚数单位)的共轭复数对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.在中,已知,则C=( )
A.60° B.30° C.30°或150° D.60°或120°
4.下面四个命题:
①过一点和一条直线垂直的直线有且只有一条;
②过一点和一个平面垂直的直线有且只有一条;
③过一点和一条直线垂直的平面有且只有一个;
④过一点和一个平面垂直的平面有且只有一个.
其中正确的是( )
A.①④ B.②③ C.①② D.③④
5.如图,在中,,点是的中点,设,则( )
A. B.
C. D.
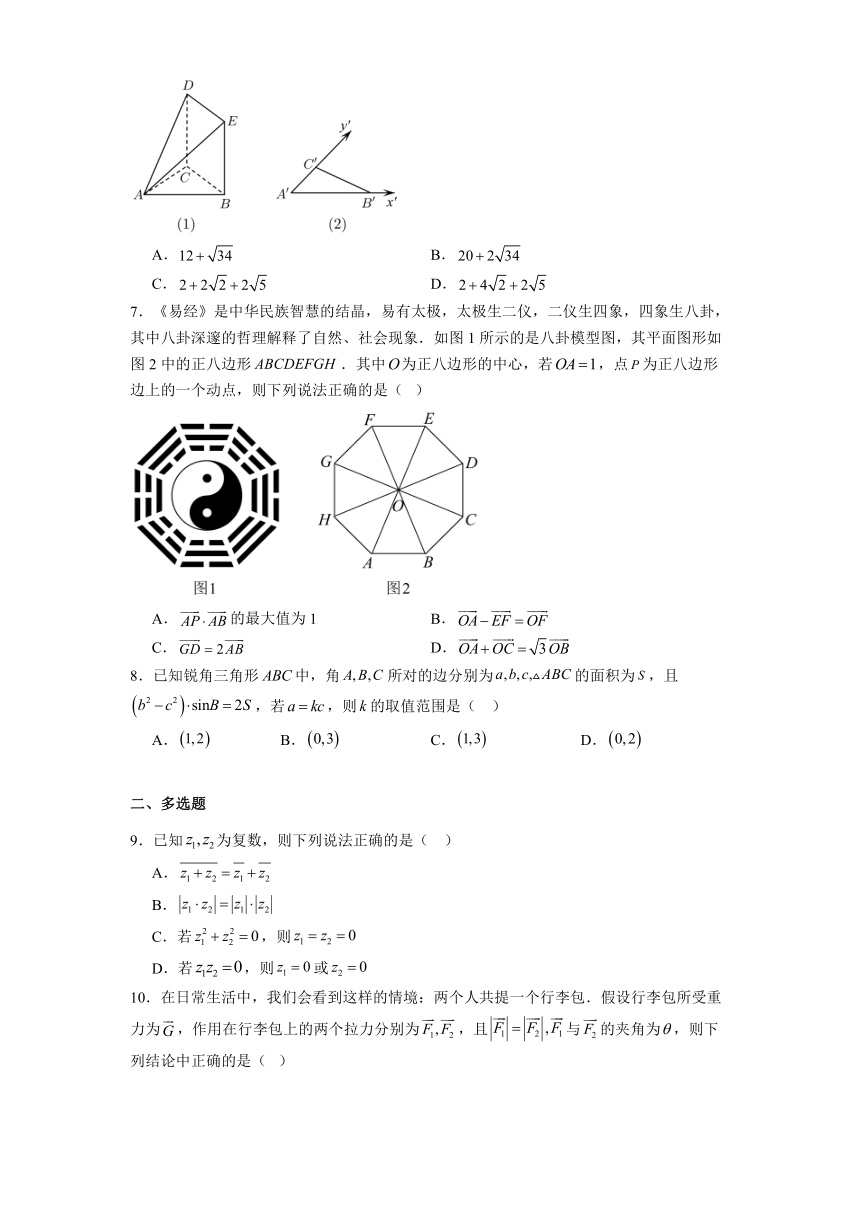
6.在如图(1)所示的四棱锥中,底面为正方形,且侧面垂直于底面,水平放置的侧面的斜二测直观图如图(2)所示,已知,,则四棱锥的侧面积是( )
A. B.
C. D.
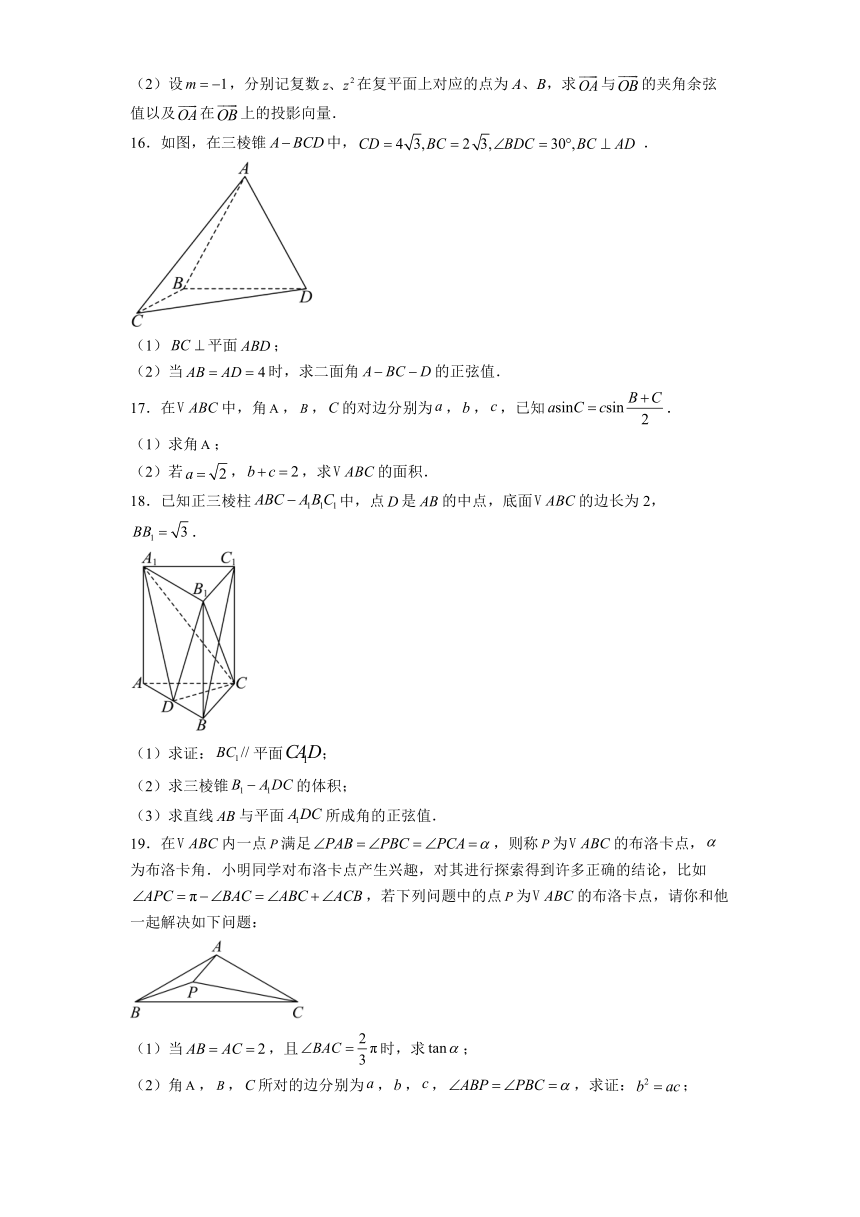
7.《易经》是中华民族智慧的结晶,易有太极,太极生二仪,二仪生四象,四象生八卦,其中八卦深邃的哲理解释了自然、社会现象.如图1所示的是八卦模型图,其平面图形如图2中的正八边形.其中为正八边形的中心,若,点为正八边形边上的一个动点,则下列说法正确的是( )
A.的最大值为1 B.
C. D.
8.已知锐角三角形中,角所对的边分别为的面积为,且,若,则的取值范围是( )
A. B. C. D.
二、多选题
9.已知为复数,则下列说法正确的是( )
A.
B.
C.若,则
D.若,则或
10.在日常生活中,我们会看到这样的情境:两个人共提一个行李包.假设行李包所受重力为,作用在行李包上的两个拉力分别为,且与的夹角为,则下列结论中正确的是( )
A. B.越小越费力,越大越省力
C.当时, D.的范围为
11.如图,在棱长为1正方体中,点P,Q分别是线段,上的动点,点E是棱的中点,下列命题正确的有( )
A.异面直线与所成的角为定值
B.的最小值为
C.三棱锥的体积随P点的变化而变化
D.过点E作平面,当//平面时,平面与正方体表面的交线构成平面多边形的周长为
三、填空题
12.已知单位向量满足,则 .
13.已知复数满足,当的虚部取最小值时,
14.农历五月初五是端午节.这一天民间有吃粽子的习俗,据说是为了纪念战国时期楚国大臣、爱国诗人屈原.粽子的形状有多种.今有某种粽子类似于由一个直角三角形绕它的一条直角边旋转(如图)而成.如果粽子的馅可以看成是这个几何体内的一个球状物,则粽子馅的最大体积为 .
四、解答题
15.已知复数,其中.
(1)设,若是纯虚数,求实数m的值;
(2)设,分别记复数在复平面上对应的点为A、B,求与的夹角余弦值以及在上的投影向量.
16.如图,在三棱锥中,.
(1)平面;
(2)当时,求二面角的正弦值.
17.在中,角,,的对边分别为,,,已知.
(1)求角;
(2)若,,求的面积.
18.已知正三棱柱中,点是的中点,底面的边长为2,.
(1)求证:平面;
(2)求三棱锥的体积;
(3)求直线与平面所成角的正弦值.
19.在内一点满足,则称为的布洛卡点,为布洛卡角.小明同学对布洛卡点产生兴趣,对其进行探索得到许多正确的结论,比如,若下列问题中的点为的布洛卡点,请你和他一起解决如下问题:
(1)当,且时,求;
(2)角,,所对的边分别为,,,,求证:;
(3)在(2)的条件下,若的周长为4,试把表示为的函数,并求的值域.
参考答案
1.【答案】B
【分析】根据抽样的概念,每个个体被抽中的概率是均等的,进而即可选择答案.
【详解】因为在抽签法抽样、随机数法抽样和分层随机抽样中,每个个体被抽中的概率均为,
所以.
故选B.
2.【答案】B
【详解】因为,
所以的共轭复数为,对应点的坐标为,位于第二象限.
故选B.
3.【答案】D
【详解】由正弦定理可得,即,解得,
则或.
故选D
4.【答案】B
【详解】对于①:过一点和一条直线垂直的直线有无数条,故①不正确;
对于②:过一点和一个平面垂直的直线有且只有一条;故②正确;
对于③:过一点和一条直线垂直的平面有且只有一个;故③正确;
对于④:过一点和一个平面垂直的平面有无数个,故④不正确;
易知②③均正确,
故选B.
5.【答案】D
【详解】因为即,点为的中点,
所以,
所以.
故选D.
6.【答案】D
【详解】四棱锥中,底面为正方形,且侧面垂直于底面,
则侧面,侧面
由水平放置的侧面的斜二测直观图可知,,
由勾股定理可得,,
所以等腰三角形的面积为,
直角三角形与直角三角形的面积均为,
等腰直角三角形的面积为,
故该几何体的侧面积是.
故选D
7.【答案】A
【详解】在正八边形中,线段被点平分,,
,在中,,
对于A,当点在线段上时,在上的投影向量的模最大,而,
因此的最大值为,A正确;
对于B,,B错误;
对于C,在中,,
,C错误;
对于D,,因此,D错误.
故选A
8.【答案】A
【分析】根据面积公式,余弦定理和题干条件得到,结合正弦定理得到,由为锐角三角形,求出,从而求出,求出的取值范围.
【详解】因为,所以,
即,
所以,
整理得:,
因为,
所以,
由正弦定理得:,
因为,
所以,
因为为锐角三角形,
所以为锐角,
所以,即,
由,解得:,
因为,
所以,
解得:.
故选A.
【思路导引】三角形相关的边的取值范围问题,通常转化为角,利用三角函数恒等变换及三角函数的值域等求出边的取值范围,或利用基本不等式进行求解.
9.【答案】ABD
【详解】设,,因为,
,所以,故A正确;
又,
,
,
所以,故B正确;
取,,可得,故C错误;
若,由B选项知,所以或,可得或,故D正确;
故选ABD.
10.【答案】AC
【详解】
因为,所以平行四边形法则为菱形,故,即,故A正确;
根据向量加法的平行四边形法则越小越省力,越大越费力,故B错误;
当时,,又,所以为等边三角形,即,故C正确;
若,则,与矛盾,所以,故D错误;
故选AC.
11.【答案】ABD
【详解】由于平面平面,
平面,所以平面,平面,所以,则异面直线与所成的角为90°,故A正确;
把平面沿直线翻折到平面,使得与共面且不重合,点翻折到点M的位置,过A作交于点R,
由于与为全等的直角三角形,且,
所以,故,
故,则的最小值为线段的长,故B正确;
因为,由于为定值,且到底面的距离为定值,故体积为定值,故C错误.
分别取的中点为,连接构成六边形,则平面平面,故平面即为六边形所在的平面,由于六边形为正六边形,且边长为,故其周长为,故D正确.
故选ABD.
12.【答案】
【详解】因为,所以,所以,
则,故.
13.【答案】
【详解】设,则,
依题意,,即,
由,得,解得,
当的虚部取最小值时,即当时,则,解得,
所以.
14.【答案】
【详解】如图所示:是的中点,连接,,,,
则,,
根据对称性,球心在平面内,设为,设球半径为,
当球体积最大时,球与平面,平面,平面和直线相切,
设切点分别为,,,,平面与直线交于点,
则四边形为正方形,边长为,
中,,,
根据等面积法:,解得,
球的体积.
15.【答案】(1)
(2),
【详解】(1),因为是纯虚数,
所以且,解得;
(2)当时,,故,
,故.
设,则;
所以在上的数量投影向量为.
16.【答案】(1)见详解
(2)
【详解】(1)在中,,
由余弦定理,
即,解得,
所以,即,所以,
又,,平面,
所以平面;
(2)因为平面,又平面,所以,
又,所以为二面角的平面角,
取的中点,连接,因为,所以,
又,所以,
所以,
所以二面角的正弦值为.
17.【答案】(1)
(2).
【详解】(1)在中,因为,可得.
因为,由正弦定理得,.
由,所以,可得,所以.
又由,所以,所以,所以,可得.
(2),
解得:,
故.
18.【答案】(1)见详解
(2)1
(3)
【详解】(1)连接交于点,连接,
因为四边形是矩形,所以为的中点,又是的中点,
又,又平面,平面,
所以平面.
(2)由于,又是的中点,所以,
在正三棱柱中,平面,平面,所以,
又平面平面,
所以平面,所以是三棱锥的高,又,所以,
(3)设点到平面的距离为,直线与平面所成角为,
由(2)有平面,又平面,所以,
因为,,所以,
又,即,解得,
所以,
所以直线与平面所成角的正弦值为.
19.【答案】(1);
(2)见详解;
(3)
【详解】(1)当,且时,得,
由余弦定理,得,所以,
又,所以,,
在中,由正弦定理得,解得,
比如,
在中,由正弦定理得,解得,
所以,解得.
(2)由,则,
在中,由正弦定理得,解得①,
在中,,
由正弦定理得,,得②,
由①②+,即.
由正弦定理,可得.
(3)由题意有,,则
,
所以,
因为,解得,
又由三角形边的关系知,则,即
,整理得,解得,即,
而时,单调递减,,,
所以的值域为.
一、单选题
1.从一个含有个个体的总体中抽取一容量为的样本,当选取抽签法、随机数法和分层随机抽样三种不同方法时,总体中每个个体被抽中的概率分别为,三者关系可能是( )
A. B. C. D.
2.在复平面内,复数(其中i为虚数单位)的共轭复数对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.在中,已知,则C=( )
A.60° B.30° C.30°或150° D.60°或120°
4.下面四个命题:
①过一点和一条直线垂直的直线有且只有一条;
②过一点和一个平面垂直的直线有且只有一条;
③过一点和一条直线垂直的平面有且只有一个;
④过一点和一个平面垂直的平面有且只有一个.
其中正确的是( )
A.①④ B.②③ C.①② D.③④
5.如图,在中,,点是的中点,设,则( )
A. B.
C. D.
6.在如图(1)所示的四棱锥中,底面为正方形,且侧面垂直于底面,水平放置的侧面的斜二测直观图如图(2)所示,已知,,则四棱锥的侧面积是( )
A. B.
C. D.
7.《易经》是中华民族智慧的结晶,易有太极,太极生二仪,二仪生四象,四象生八卦,其中八卦深邃的哲理解释了自然、社会现象.如图1所示的是八卦模型图,其平面图形如图2中的正八边形.其中为正八边形的中心,若,点为正八边形边上的一个动点,则下列说法正确的是( )
A.的最大值为1 B.
C. D.
8.已知锐角三角形中,角所对的边分别为的面积为,且,若,则的取值范围是( )
A. B. C. D.
二、多选题
9.已知为复数,则下列说法正确的是( )
A.
B.
C.若,则
D.若,则或
10.在日常生活中,我们会看到这样的情境:两个人共提一个行李包.假设行李包所受重力为,作用在行李包上的两个拉力分别为,且与的夹角为,则下列结论中正确的是( )
A. B.越小越费力,越大越省力
C.当时, D.的范围为
11.如图,在棱长为1正方体中,点P,Q分别是线段,上的动点,点E是棱的中点,下列命题正确的有( )
A.异面直线与所成的角为定值
B.的最小值为
C.三棱锥的体积随P点的变化而变化
D.过点E作平面,当//平面时,平面与正方体表面的交线构成平面多边形的周长为
三、填空题
12.已知单位向量满足,则 .
13.已知复数满足,当的虚部取最小值时,
14.农历五月初五是端午节.这一天民间有吃粽子的习俗,据说是为了纪念战国时期楚国大臣、爱国诗人屈原.粽子的形状有多种.今有某种粽子类似于由一个直角三角形绕它的一条直角边旋转(如图)而成.如果粽子的馅可以看成是这个几何体内的一个球状物,则粽子馅的最大体积为 .
四、解答题
15.已知复数,其中.
(1)设,若是纯虚数,求实数m的值;
(2)设,分别记复数在复平面上对应的点为A、B,求与的夹角余弦值以及在上的投影向量.
16.如图,在三棱锥中,.
(1)平面;
(2)当时,求二面角的正弦值.
17.在中,角,,的对边分别为,,,已知.
(1)求角;
(2)若,,求的面积.
18.已知正三棱柱中,点是的中点,底面的边长为2,.
(1)求证:平面;
(2)求三棱锥的体积;
(3)求直线与平面所成角的正弦值.
19.在内一点满足,则称为的布洛卡点,为布洛卡角.小明同学对布洛卡点产生兴趣,对其进行探索得到许多正确的结论,比如,若下列问题中的点为的布洛卡点,请你和他一起解决如下问题:
(1)当,且时,求;
(2)角,,所对的边分别为,,,,求证:;
(3)在(2)的条件下,若的周长为4,试把表示为的函数,并求的值域.
参考答案
1.【答案】B
【分析】根据抽样的概念,每个个体被抽中的概率是均等的,进而即可选择答案.
【详解】因为在抽签法抽样、随机数法抽样和分层随机抽样中,每个个体被抽中的概率均为,
所以.
故选B.
2.【答案】B
【详解】因为,
所以的共轭复数为,对应点的坐标为,位于第二象限.
故选B.
3.【答案】D
【详解】由正弦定理可得,即,解得,
则或.
故选D
4.【答案】B
【详解】对于①:过一点和一条直线垂直的直线有无数条,故①不正确;
对于②:过一点和一个平面垂直的直线有且只有一条;故②正确;
对于③:过一点和一条直线垂直的平面有且只有一个;故③正确;
对于④:过一点和一个平面垂直的平面有无数个,故④不正确;
易知②③均正确,
故选B.
5.【答案】D
【详解】因为即,点为的中点,
所以,
所以.
故选D.
6.【答案】D
【详解】四棱锥中,底面为正方形,且侧面垂直于底面,
则侧面,侧面
由水平放置的侧面的斜二测直观图可知,,
由勾股定理可得,,
所以等腰三角形的面积为,
直角三角形与直角三角形的面积均为,
等腰直角三角形的面积为,
故该几何体的侧面积是.
故选D
7.【答案】A
【详解】在正八边形中,线段被点平分,,
,在中,,
对于A,当点在线段上时,在上的投影向量的模最大,而,
因此的最大值为,A正确;
对于B,,B错误;
对于C,在中,,
,C错误;
对于D,,因此,D错误.
故选A
8.【答案】A
【分析】根据面积公式,余弦定理和题干条件得到,结合正弦定理得到,由为锐角三角形,求出,从而求出,求出的取值范围.
【详解】因为,所以,
即,
所以,
整理得:,
因为,
所以,
由正弦定理得:,
因为,
所以,
因为为锐角三角形,
所以为锐角,
所以,即,
由,解得:,
因为,
所以,
解得:.
故选A.
【思路导引】三角形相关的边的取值范围问题,通常转化为角,利用三角函数恒等变换及三角函数的值域等求出边的取值范围,或利用基本不等式进行求解.
9.【答案】ABD
【详解】设,,因为,
,所以,故A正确;
又,
,
,
所以,故B正确;
取,,可得,故C错误;
若,由B选项知,所以或,可得或,故D正确;
故选ABD.
10.【答案】AC
【详解】
因为,所以平行四边形法则为菱形,故,即,故A正确;
根据向量加法的平行四边形法则越小越省力,越大越费力,故B错误;
当时,,又,所以为等边三角形,即,故C正确;
若,则,与矛盾,所以,故D错误;
故选AC.
11.【答案】ABD
【详解】由于平面平面,
平面,所以平面,平面,所以,则异面直线与所成的角为90°,故A正确;
把平面沿直线翻折到平面,使得与共面且不重合,点翻折到点M的位置,过A作交于点R,
由于与为全等的直角三角形,且,
所以,故,
故,则的最小值为线段的长,故B正确;
因为,由于为定值,且到底面的距离为定值,故体积为定值,故C错误.
分别取的中点为,连接构成六边形,则平面平面,故平面即为六边形所在的平面,由于六边形为正六边形,且边长为,故其周长为,故D正确.
故选ABD.
12.【答案】
【详解】因为,所以,所以,
则,故.
13.【答案】
【详解】设,则,
依题意,,即,
由,得,解得,
当的虚部取最小值时,即当时,则,解得,
所以.
14.【答案】
【详解】如图所示:是的中点,连接,,,,
则,,
根据对称性,球心在平面内,设为,设球半径为,
当球体积最大时,球与平面,平面,平面和直线相切,
设切点分别为,,,,平面与直线交于点,
则四边形为正方形,边长为,
中,,,
根据等面积法:,解得,
球的体积.
15.【答案】(1)
(2),
【详解】(1),因为是纯虚数,
所以且,解得;
(2)当时,,故,
,故.
设,则;
所以在上的数量投影向量为.
16.【答案】(1)见详解
(2)
【详解】(1)在中,,
由余弦定理,
即,解得,
所以,即,所以,
又,,平面,
所以平面;
(2)因为平面,又平面,所以,
又,所以为二面角的平面角,
取的中点,连接,因为,所以,
又,所以,
所以,
所以二面角的正弦值为.
17.【答案】(1)
(2).
【详解】(1)在中,因为,可得.
因为,由正弦定理得,.
由,所以,可得,所以.
又由,所以,所以,所以,可得.
(2),
解得:,
故.
18.【答案】(1)见详解
(2)1
(3)
【详解】(1)连接交于点,连接,
因为四边形是矩形,所以为的中点,又是的中点,
又,又平面,平面,
所以平面.
(2)由于,又是的中点,所以,
在正三棱柱中,平面,平面,所以,
又平面平面,
所以平面,所以是三棱锥的高,又,所以,
(3)设点到平面的距离为,直线与平面所成角为,
由(2)有平面,又平面,所以,
因为,,所以,
又,即,解得,
所以,
所以直线与平面所成角的正弦值为.
19.【答案】(1);
(2)见详解;
(3)
【详解】(1)当,且时,得,
由余弦定理,得,所以,
又,所以,,
在中,由正弦定理得,解得,
比如,
在中,由正弦定理得,解得,
所以,解得.
(2)由,则,
在中,由正弦定理得,解得①,
在中,,
由正弦定理得,,得②,
由①②+,即.
由正弦定理,可得.
(3)由题意有,,则
,
所以,
因为,解得,
又由三角形边的关系知,则,即
,整理得,解得,即,
而时,单调递减,,,
所以的值域为.
同课章节目录
