高一上学期数学北师大版(2019)必修第一册 4.3 一元二次不等式的应用 课件(共42张PPT)
文档属性
| 名称 | 高一上学期数学北师大版(2019)必修第一册 4.3 一元二次不等式的应用 课件(共42张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-12 20:40:46 | ||
图片预览











文档简介
(共42张PPT)
4.3 一元二次不等式的应用
课标要求 素养要求
1.经历从实际情境中抽象出一元二次不等式的过程,了解一元二次不等式的现实意义.能借助一元二次函数求解一元二次不等式,并能用集合表示一元二次不等式的解集. 2.借助一元二次函数的图象,了解一元二次不等式与相应函数、方程的联系. 从函数观点认识不等式,感悟数学知识之间的关联,认识函数的重要性,重点提升数学抽象和数学运算素养.
新知探究
汽车在行驶中,由于惯性的作用,刹车后还要继续向前滑行一段距离才能停住,我们称这段距离为“刹车距离”,刹车距离是分析事故的一个重要因素.
在一个限速为40 km/h的弯道上,甲、乙两辆汽车相向而行, 发现情况不对,同时刹车,但还是相撞了.事后现场勘查测得甲车的刹车距离略超过12 m,乙车的刹车距离略超过10 m.又知甲、乙两种车型的刹车距离s(m)与车速x(km/h)之间分别有如下关系:s甲=0.1x+0.01x2,s乙=0.05x+0.005x2.
问题 如何判断甲、乙两车是否超速?
提示 由题意知,对于甲车,有0.1x+0.01x2>12,即x2+10x-1 200>0,
解得x>30或x<-40(不符合实际意义,舍去).
这表明甲车的车速超过30 km/h,但根据题意刹车距离略超过12 m,由此估计甲车车速不会超过限速40 km/h.
对于乙车,有0.05x+0.005x2>10,即x2+10x-2 000>0,
解得x>40或x<-50(不符合实际意义,舍去).
这表明乙车的车速超过40 km/h,超过规定限速.
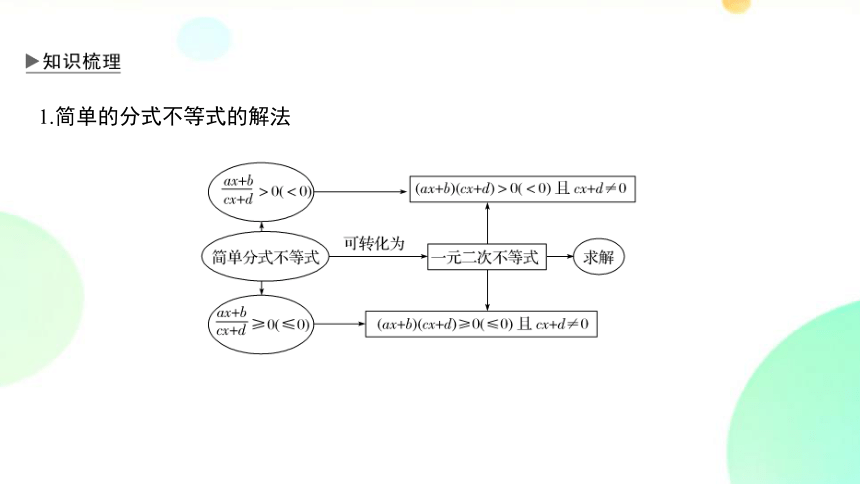
1.简单的分式不等式的解法
2.一元二次不等式恒成立问题
3.利用不等式解决实际问题的一般步骤如下:
(1)选取合适的字母表示题目中的未知数;
(2)由题目中给出的不等关系,列出关于未知数的不等式(组);
(3)求解所列出的不等式(组);
(4)结合题目的实际意义确定答案.
×
√
√
答案 -14
2.已知不等式x2+ax+1≥0的解集为R,则a的取值范围是________.
答案 [-2,2]
3.不等式x2-2x+3≤a2-2a-1在R上的解集是 ,则实数a的取值范围是________.
答案 (-1,3)
[微思考]
M≥y恒成立与M≥y有解等价吗?
提示 不等价.M≥y恒成立 M≥ymax;M≥y有解 M≥ymin.
题型一 分式不等式的解法
【例1】 解不等式:
解 (1)原不等式可化为(x+1)(2x-1)<0,
故原不等式的解集为{x|x<-2}.
【训练1】 解下列不等式.
(2)法一 原不等式可化为
法二 原不等式可化为
题型二 不等式的恒成立问题
角度1 无限制范围的恒成立
【例2-1】 (1)已知不等式kx2+2kx-(k+2)<0恒成立,求实数k的取值范围.
(2)若不等式-x2+2x+3≤a2-3a对任意实数x恒成立,求实数a的取值范围.
解 (1)当k=0时,原不等式化为-2<0,显然符合题意.
当k≠0时,令y=kx2+2kx-(k+2),由y<0恒成立,
∴其图象都在x轴的下方,即开口向下,且与x轴无交点.
(2)∵-x2+2x+3=-(x-1)2+4≤4.
又∵-x2+2x+3≤a2-3a对任意x恒成立.
∴a2-3a≥4,即a2-3a-4≥0.
解得a≤-1或a≥4.
∴a的取值范围是(-∞,-1]∪[4,+∞).
图① 图②
角度2 有限制范围的恒成立
【例2-2】 (1)当x∈[1,2]时,不等式x2+mx+4<0恒成立,求实数m的取值范围.
(2)对任意x∈[-1,1],函数y=x2+(a-4)x+4-2a的值恒大于0,求a的取值范围.
解 (1)令y=x2+mx+4.
∵y<0在[1,2]上恒成立.
∴y=0的根一个在(-∞,1)上,另一个在(2,+∞)上.
∴m的取值范围是(-∞,-5).
(2)∵x2+(a-4)x+4-2a>0恒成立,
即x2+ax-4x+4-2a>0恒成立.
∴(x-2)·a>-x2+4x-4.
∵-1≤x≤1,∴x-2<0.
y=2-x在[-1,1]上y随x的增大而减小,
∴(2-x)min=1,∴a<1.
故a的取值范围是(-∞,1).
规律方法 含参数的一元二次不等式在某一区间上恒成立问题,求解时主要有两种方法:一种是将参数分离,转化为恒成立问题;另一种是利用二次不等式根的分布及数形结合思想求解.
角度3 给定参数范围恒成立问题
【例2-3】 已知a∈[-1,1]时,不等式x2+(a-4)x+4-2a>0恒成立,则x的取值范围为________.
答案 (-∞,1)∪(3,+∞)
规律方法 解决恒成立问题一定要搞清谁是主元,谁是参数,一般地知道谁的范围,谁就是主元,求谁的范围,谁就是参数.
【训练2】 设函数y=mx2-mx-1.
(1)若对于一切实数x,y<0恒成立,求m的取值范围;
(2)对于x∈[1,3],y<-m+5恒成立,求m的取值范围.
解 (1)若m=0,显然-1<0恒成立;
∴m的取值范围为(-4,0].
当m=0时,-6<0恒成立.
当m>0时,在[1,3]上s随x的增大而增大,
∴smax=s|x=3=7m-6.
法二 y<-m+5恒成立,
即m(x2-x+1)-6<0恒成立,
当m<0时,在[1,3]上s随x的增大而减小.
∴smax=s|x=1=m-6<0,解得m<6,
∴m<0.
又m(x2-x+1)-6<0,
题型三 一元二次不等式的实际应用
【例3】 某农贸公司按每担200元的价格收购某农产品,并每100元纳税10元(又称征税率为10个百分点),计划可收购a万担.政府为了鼓励收购公司多收购这种农产品,决定将征税率降低x(x>0)个百分点,预测收购量可增加2x个百分点.
(1)写出降税后税收y(万元)与x的函数关系式;
(2)要使此项税收在税率调节后,不少于原计划税收的83.2%,试确定x的取值范围.
解 (1)降低税率后的税率为(10-x)%,农产品的收购量为a(1+2x%)万担,收购总金额为200a(1+2x%)万元.依题意得y=200a(1+2x%)(10-x)%
(2)原计划税收为200a×10%=20a(万元).
化简得x2+40x-84≤0,解得-42≤x≤2.
又因为0<x<10,所以0<x≤2.
即x的取值范围为(0,2].
规律方法 解不等式应用题的步骤
【训练3】 某汽车厂上年度生产汽车的投入成本为10万元/辆,出厂价为12万元/辆,年销售量为10 000辆.本年度为适应市场需求,计划提高产品质量,适度增加投入成本.若每辆车投入成本增加的比例为x(0<x<1),则出厂价相应地提高比例为0.75x,同时预计年销售量增加的比例为0.6x,已知年利润=(出厂价-投入成本)×年销售量.
(1)写出本年度预计的年利润y与投入成本增加的比例x的关系式;
(2)为使本年度的年利润比上年度有所增加,则投入成本增加的比例x应在什么范围内?
解 (1)由题意得
y=[12(1+0.75x)-10(1+x)]×10 000×(1+0.6x)(0<x<1),
整理得y=-6 000x2+2 000x+20 000(0<x<1).
(2)要保证本年度的年利润比上年度有所增加,
一、素养落地
1.通过本节课的学习,重点提升学生的数学抽象素养及数学运算素养.
2.在解决不等式ax2+bx+c>0(≥0)对一切x∈R恒成立问题时,当二次项系数含有字母时,需要对a进行分类讨论.
3.含参数一元二次不等式在某区间上恒成立时,处理的原则是转化为最值问题,常有两种处理方法:一是利用二次函数在区间上最值来处理,二是先分离参数,再求函数最值.
4.利用一元二次不等式来解决问题时,应注意实际意义.
二、素养训练
1.不等式x(2-x)>0的解集为( )
A.{x|x>0} B.{x|x<2}
C.{x|x>2或x<0} D.{x|0解析 原不等式化为x(x-2)<0,故0答案 D
答案 A
3.若产品的总成本y(万元)与产量x(台)之间的关系式是y=3 000+20x-0.1x2(0<x<240),若每台产品的售价为25万元,则生产者不亏本(销售收入不小于总成本)时的最低产量是________台.
解析 y-25x=-0.1x2-5x+3 000≤0,
即x2+50x-30 000≥0,解得x≥150或x≤-200(舍去).
答案 150
4.不等式-3x2+5x-4>0的解集为________.
解析 原不等式变形为3x2-5x+4<0.
因为Δ=(-5)2-4×3×4=-23<0,
所以由函数y=3x2-5x+4的图象可知,3x2-5x+4<0的解集为 .
答案
4.3 一元二次不等式的应用
课标要求 素养要求
1.经历从实际情境中抽象出一元二次不等式的过程,了解一元二次不等式的现实意义.能借助一元二次函数求解一元二次不等式,并能用集合表示一元二次不等式的解集. 2.借助一元二次函数的图象,了解一元二次不等式与相应函数、方程的联系. 从函数观点认识不等式,感悟数学知识之间的关联,认识函数的重要性,重点提升数学抽象和数学运算素养.
新知探究
汽车在行驶中,由于惯性的作用,刹车后还要继续向前滑行一段距离才能停住,我们称这段距离为“刹车距离”,刹车距离是分析事故的一个重要因素.
在一个限速为40 km/h的弯道上,甲、乙两辆汽车相向而行, 发现情况不对,同时刹车,但还是相撞了.事后现场勘查测得甲车的刹车距离略超过12 m,乙车的刹车距离略超过10 m.又知甲、乙两种车型的刹车距离s(m)与车速x(km/h)之间分别有如下关系:s甲=0.1x+0.01x2,s乙=0.05x+0.005x2.
问题 如何判断甲、乙两车是否超速?
提示 由题意知,对于甲车,有0.1x+0.01x2>12,即x2+10x-1 200>0,
解得x>30或x<-40(不符合实际意义,舍去).
这表明甲车的车速超过30 km/h,但根据题意刹车距离略超过12 m,由此估计甲车车速不会超过限速40 km/h.
对于乙车,有0.05x+0.005x2>10,即x2+10x-2 000>0,
解得x>40或x<-50(不符合实际意义,舍去).
这表明乙车的车速超过40 km/h,超过规定限速.
1.简单的分式不等式的解法
2.一元二次不等式恒成立问题
3.利用不等式解决实际问题的一般步骤如下:
(1)选取合适的字母表示题目中的未知数;
(2)由题目中给出的不等关系,列出关于未知数的不等式(组);
(3)求解所列出的不等式(组);
(4)结合题目的实际意义确定答案.
×
√
√
答案 -14
2.已知不等式x2+ax+1≥0的解集为R,则a的取值范围是________.
答案 [-2,2]
3.不等式x2-2x+3≤a2-2a-1在R上的解集是 ,则实数a的取值范围是________.
答案 (-1,3)
[微思考]
M≥y恒成立与M≥y有解等价吗?
提示 不等价.M≥y恒成立 M≥ymax;M≥y有解 M≥ymin.
题型一 分式不等式的解法
【例1】 解不等式:
解 (1)原不等式可化为(x+1)(2x-1)<0,
故原不等式的解集为{x|x<-2}.
【训练1】 解下列不等式.
(2)法一 原不等式可化为
法二 原不等式可化为
题型二 不等式的恒成立问题
角度1 无限制范围的恒成立
【例2-1】 (1)已知不等式kx2+2kx-(k+2)<0恒成立,求实数k的取值范围.
(2)若不等式-x2+2x+3≤a2-3a对任意实数x恒成立,求实数a的取值范围.
解 (1)当k=0时,原不等式化为-2<0,显然符合题意.
当k≠0时,令y=kx2+2kx-(k+2),由y<0恒成立,
∴其图象都在x轴的下方,即开口向下,且与x轴无交点.
(2)∵-x2+2x+3=-(x-1)2+4≤4.
又∵-x2+2x+3≤a2-3a对任意x恒成立.
∴a2-3a≥4,即a2-3a-4≥0.
解得a≤-1或a≥4.
∴a的取值范围是(-∞,-1]∪[4,+∞).
图① 图②
角度2 有限制范围的恒成立
【例2-2】 (1)当x∈[1,2]时,不等式x2+mx+4<0恒成立,求实数m的取值范围.
(2)对任意x∈[-1,1],函数y=x2+(a-4)x+4-2a的值恒大于0,求a的取值范围.
解 (1)令y=x2+mx+4.
∵y<0在[1,2]上恒成立.
∴y=0的根一个在(-∞,1)上,另一个在(2,+∞)上.
∴m的取值范围是(-∞,-5).
(2)∵x2+(a-4)x+4-2a>0恒成立,
即x2+ax-4x+4-2a>0恒成立.
∴(x-2)·a>-x2+4x-4.
∵-1≤x≤1,∴x-2<0.
y=2-x在[-1,1]上y随x的增大而减小,
∴(2-x)min=1,∴a<1.
故a的取值范围是(-∞,1).
规律方法 含参数的一元二次不等式在某一区间上恒成立问题,求解时主要有两种方法:一种是将参数分离,转化为恒成立问题;另一种是利用二次不等式根的分布及数形结合思想求解.
角度3 给定参数范围恒成立问题
【例2-3】 已知a∈[-1,1]时,不等式x2+(a-4)x+4-2a>0恒成立,则x的取值范围为________.
答案 (-∞,1)∪(3,+∞)
规律方法 解决恒成立问题一定要搞清谁是主元,谁是参数,一般地知道谁的范围,谁就是主元,求谁的范围,谁就是参数.
【训练2】 设函数y=mx2-mx-1.
(1)若对于一切实数x,y<0恒成立,求m的取值范围;
(2)对于x∈[1,3],y<-m+5恒成立,求m的取值范围.
解 (1)若m=0,显然-1<0恒成立;
∴m的取值范围为(-4,0].
当m=0时,-6<0恒成立.
当m>0时,在[1,3]上s随x的增大而增大,
∴smax=s|x=3=7m-6.
法二 y<-m+5恒成立,
即m(x2-x+1)-6<0恒成立,
当m<0时,在[1,3]上s随x的增大而减小.
∴smax=s|x=1=m-6<0,解得m<6,
∴m<0.
又m(x2-x+1)-6<0,
题型三 一元二次不等式的实际应用
【例3】 某农贸公司按每担200元的价格收购某农产品,并每100元纳税10元(又称征税率为10个百分点),计划可收购a万担.政府为了鼓励收购公司多收购这种农产品,决定将征税率降低x(x>0)个百分点,预测收购量可增加2x个百分点.
(1)写出降税后税收y(万元)与x的函数关系式;
(2)要使此项税收在税率调节后,不少于原计划税收的83.2%,试确定x的取值范围.
解 (1)降低税率后的税率为(10-x)%,农产品的收购量为a(1+2x%)万担,收购总金额为200a(1+2x%)万元.依题意得y=200a(1+2x%)(10-x)%
(2)原计划税收为200a×10%=20a(万元).
化简得x2+40x-84≤0,解得-42≤x≤2.
又因为0<x<10,所以0<x≤2.
即x的取值范围为(0,2].
规律方法 解不等式应用题的步骤
【训练3】 某汽车厂上年度生产汽车的投入成本为10万元/辆,出厂价为12万元/辆,年销售量为10 000辆.本年度为适应市场需求,计划提高产品质量,适度增加投入成本.若每辆车投入成本增加的比例为x(0<x<1),则出厂价相应地提高比例为0.75x,同时预计年销售量增加的比例为0.6x,已知年利润=(出厂价-投入成本)×年销售量.
(1)写出本年度预计的年利润y与投入成本增加的比例x的关系式;
(2)为使本年度的年利润比上年度有所增加,则投入成本增加的比例x应在什么范围内?
解 (1)由题意得
y=[12(1+0.75x)-10(1+x)]×10 000×(1+0.6x)(0<x<1),
整理得y=-6 000x2+2 000x+20 000(0<x<1).
(2)要保证本年度的年利润比上年度有所增加,
一、素养落地
1.通过本节课的学习,重点提升学生的数学抽象素养及数学运算素养.
2.在解决不等式ax2+bx+c>0(≥0)对一切x∈R恒成立问题时,当二次项系数含有字母时,需要对a进行分类讨论.
3.含参数一元二次不等式在某区间上恒成立时,处理的原则是转化为最值问题,常有两种处理方法:一是利用二次函数在区间上最值来处理,二是先分离参数,再求函数最值.
4.利用一元二次不等式来解决问题时,应注意实际意义.
二、素养训练
1.不等式x(2-x)>0的解集为( )
A.{x|x>0} B.{x|x<2}
C.{x|x>2或x<0} D.{x|0
答案 A
3.若产品的总成本y(万元)与产量x(台)之间的关系式是y=3 000+20x-0.1x2(0<x<240),若每台产品的售价为25万元,则生产者不亏本(销售收入不小于总成本)时的最低产量是________台.
解析 y-25x=-0.1x2-5x+3 000≤0,
即x2+50x-30 000≥0,解得x≥150或x≤-200(舍去).
答案 150
4.不等式-3x2+5x-4>0的解集为________.
解析 原不等式变形为3x2-5x+4<0.
因为Δ=(-5)2-4×3×4=-23<0,
所以由函数y=3x2-5x+4的图象可知,3x2-5x+4<0的解集为 .
答案
同课章节目录
- 第一章 预备知识
- 1 集合
- 2 常用逻辑用语
- 3 不等式
- 4 一元二次函数与一元二次不等式
- 第二章 函数
- 1 生活中的变量关系
- 2 函数
- 3 函数的单调性和最值
- 4 函数的奇偶性与简单的幂函数
- 第三章 指数运算与指数函数
- 1 指数幂的拓展
- 2 指数幂的运算性质
- 3 指数函数
- 第四章 对数运算和对数函数
- 1 对数的概念
- 2 对数的运算
- 3 对数函数
- 4 指数函数、幂函数、对数函数增长的比较
- 5 信息技术支持的函数研究
- 第五章 函数应用
- 1 方程解的存在性及方程的近似解
- 2 实际问题中的函数模型
- 第六章 统计
- 1 获取数据的途径
- 2 抽样的基本方法
- 3 用样本估计总体分布
- 4 用样本估计总体数字特征
- 第七章 概率
- 1 随机现象与随机事件
- 2 古典概型
- 3 频率与概率
- 4 事件的独立性
- 第八章 数学建模活动(一)
- 1 走进数学建模
- 2 数学建模的主要步骤
- 3 数学建模活动的主要过程
