高一上学期数学北师大版(2019)必修第一册 4.4 指数函数、幂函数、对数函数增长的比较 课件(共23张PPT)
文档属性
| 名称 | 高一上学期数学北师大版(2019)必修第一册 4.4 指数函数、幂函数、对数函数增长的比较 课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 790.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-12 21:54:09 | ||
图片预览




文档简介
(共23张PPT)
4.4指数函数、幂函数、对数函数增长的比较
复习回顾:指数函数、对数函数、幂函数的单调性
指数函数y=ax (a>1),对数函数y=logax(a>1)和幂函数(在区间(0,+∞)上的单调性如何?
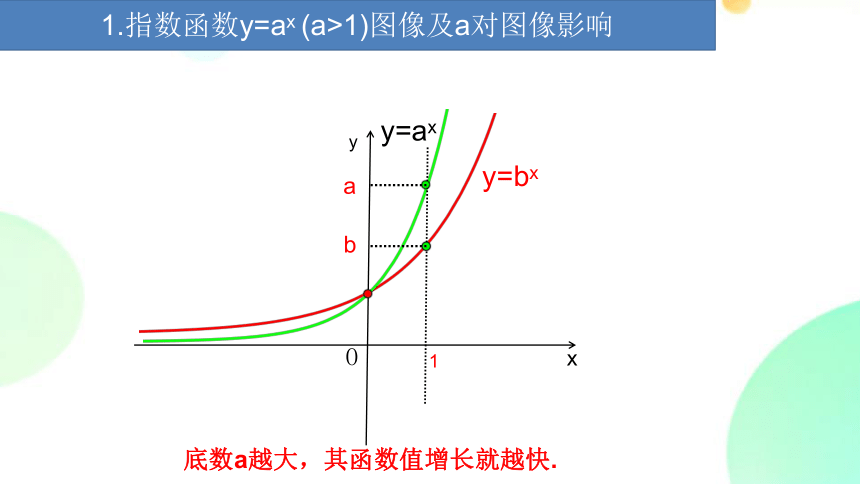
1.指数函数y=ax (a>1)图像及a对图像影响
y=bx
y=ax
y
x
O
1
b
a
底数a越大,其函数值增长就越快.
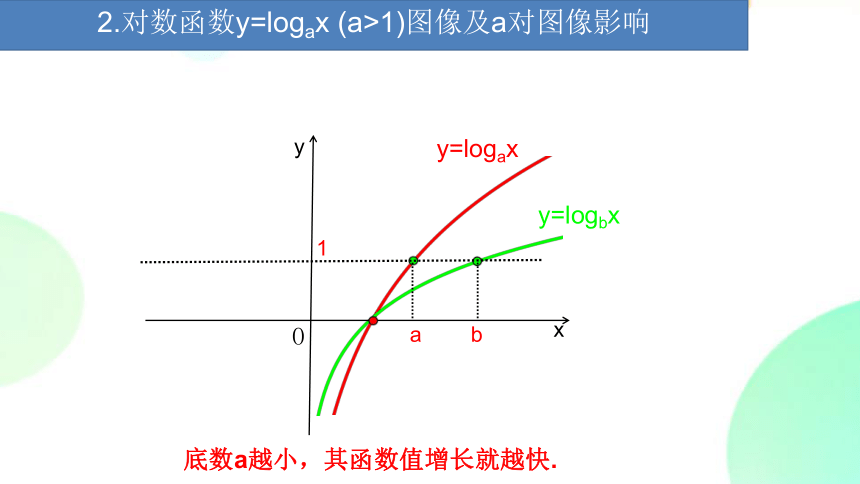
2.对数函数y=logax (a>1)图像及a对图像影响
底数a越小,其函数值增长就越快.
y=logax
y=logbx
y
x
O
1
a
b
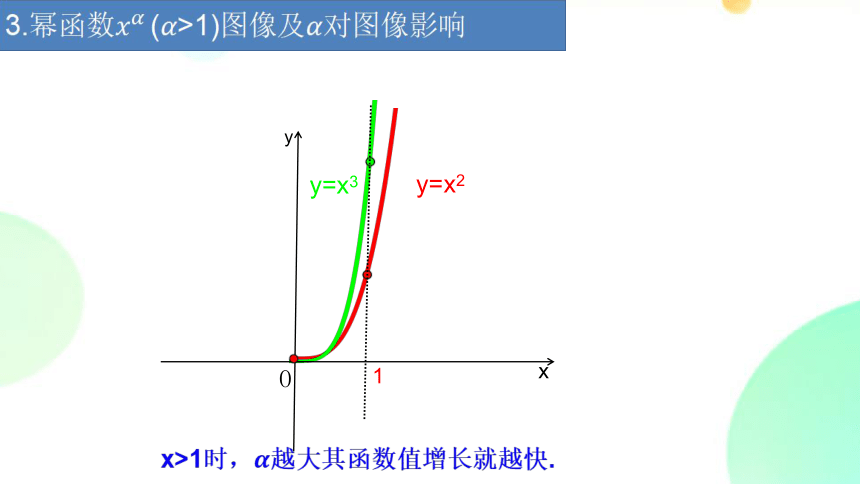
3.幂函数 (>1)图像及对图像影响
y=x2
y=x3
y
x
O
x>1时,越大其函数值增长就越快.
1
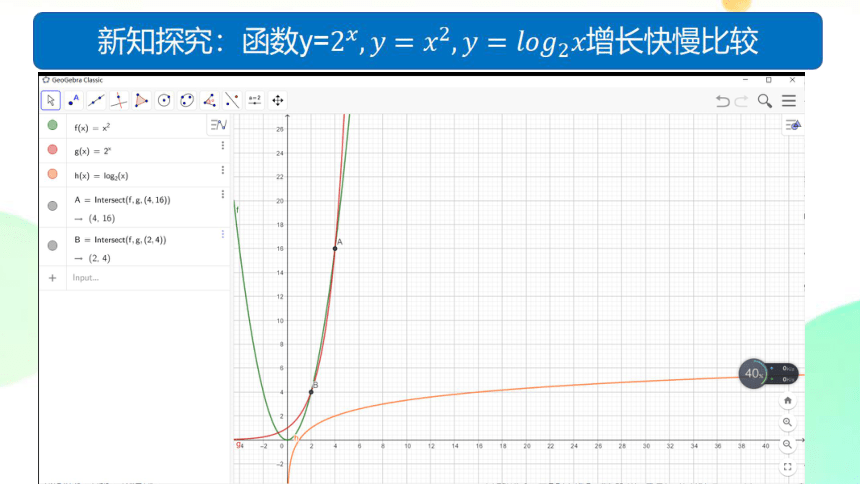
新知探究:函数y=
①对数函数 y=log2x增长最慢
②在(0,2),幂函数比指数函数增长快;在(4,+∞),指数函数比幂函数增长快
新知探究:函数y=
抽象和概括
①对数函数增长最慢
②当自变量x大于某一个特定值时,指数函数比幂函数增长快
③由于指数函数增长非常快,人们常称这种现象为“指数爆炸”
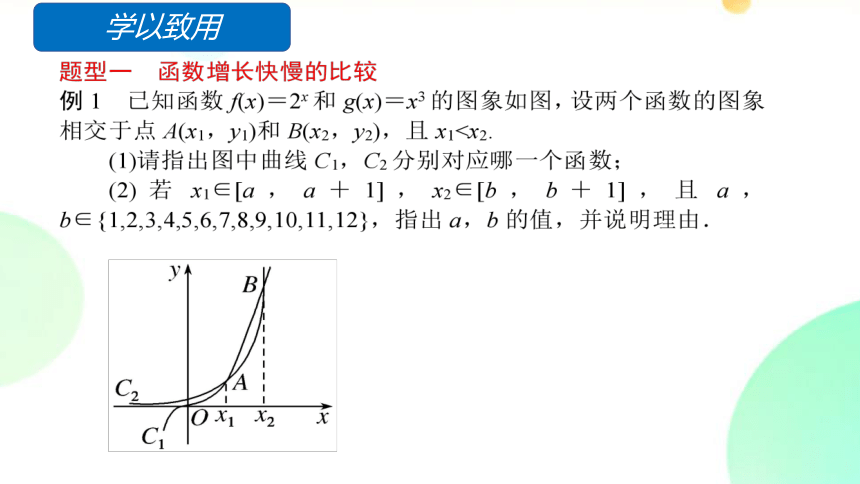
学以致用
学以致用
针对练习
抽象概括
常见的函数模型及增长特点
(1)线性函数模型
线性函数模型y=kx+b(k>0)的增长特点是直线上升,其增长速度不变.
(2)指数函数模型
指数函数模型y=ax(a>1)的增长特点是随着自变量的增大,函数值增大的速度越来越快,形象地称为“指数爆炸”.
(3)对数函数模型
对数函数模型y=logax(a>1)的增长特点是随着自变量的增大,函数值增大的速度越来越慢,即增长速度平缓.
(4)幂函数模型
幂函数y=xn(n>0)的增长速度介于指数增长和对数增长之间.
1.下列函数中,随x的增大,增长速度最快的是( ).
A.y=100x B.y=x100 C.y=100x D.y=log100x(x∈N*)
2.某工厂8年来某种产品的总产量C与时间t(单位:年)的函数关系如图所示.
有下列四种说法:
①前三年产量增长的速度越来越快;
②前三年产量增长的速度越来越慢;
③第三年后这种产品停止生产;
④第三年后产量保持不变.
其中说法正确的是 .
课后作业
3.以下是三个变量y1,y2,y3随变量x变化的函数值表:
其中,关于x呈指数函数变化的变量是 .
x 1 2 3 4 5 6 7 8 …
y1 2 4 8 16 32 64 128 256 …
y2 1 4 9 16 25 36 49 64 …
y3 0 1 1.585 2 2.322 2.585 2.807 3 …
1.下列函数中,随x的增大,增长速度最快的是( ).
A.y=100x B.y=x100 C.y=100x D.y=log100x(x∈N*)
【解析】四个函数中,增长速度由慢到快依次是y=log100x,y=100x,y=x100,y=100x.
C
2.某工厂8年来某种产品的总产量C与时间t(单位:年)的函数关系如图所示.
有下列四种说法:
①前三年产量增长的速度越来越快;
②前三年产量增长的速度越来越慢;
③第三年后这种产品停止生产;
④第三年后产量保持不变.
其中说法正确的是 .
【解析】由t∈[0,3]的图象联想到幂函数y=xα(0<α<1),反映了C随时间的变化逐渐增长但速度越来越慢.由t∈[3,8]的图象可知,总产量C没有变化,即第三年后停产,所以②③正确.
②③
3.以下是三个变量y1,y2,y3随变量x变化的函数值表:
其中,关于x呈指数函数变化的变量是 .
【解析】从表格可以看出三个变量y1,y2,y3都随x的增大而增大,但增长速度不同,其中y1的增长速度最快,画出它的散点图(图略)知变量y1关于x呈指数函数变化.
y1
x 1 2 3 4 5 6 7 8 …
y1 2 4 8 16 32 64 128 256 …
y2 1 4 9 16 25 36 49 64 …
y3 0 1 1.585 2 2.322 2.585 2.807 3 …
4.4指数函数、幂函数、对数函数增长的比较
复习回顾:指数函数、对数函数、幂函数的单调性
指数函数y=ax (a>1),对数函数y=logax(a>1)和幂函数(在区间(0,+∞)上的单调性如何?
1.指数函数y=ax (a>1)图像及a对图像影响
y=bx
y=ax
y
x
O
1
b
a
底数a越大,其函数值增长就越快.
2.对数函数y=logax (a>1)图像及a对图像影响
底数a越小,其函数值增长就越快.
y=logax
y=logbx
y
x
O
1
a
b
3.幂函数 (>1)图像及对图像影响
y=x2
y=x3
y
x
O
x>1时,越大其函数值增长就越快.
1
新知探究:函数y=
①对数函数 y=log2x增长最慢
②在(0,2),幂函数比指数函数增长快;在(4,+∞),指数函数比幂函数增长快
新知探究:函数y=
抽象和概括
①对数函数增长最慢
②当自变量x大于某一个特定值时,指数函数比幂函数增长快
③由于指数函数增长非常快,人们常称这种现象为“指数爆炸”
学以致用
学以致用
针对练习
抽象概括
常见的函数模型及增长特点
(1)线性函数模型
线性函数模型y=kx+b(k>0)的增长特点是直线上升,其增长速度不变.
(2)指数函数模型
指数函数模型y=ax(a>1)的增长特点是随着自变量的增大,函数值增大的速度越来越快,形象地称为“指数爆炸”.
(3)对数函数模型
对数函数模型y=logax(a>1)的增长特点是随着自变量的增大,函数值增大的速度越来越慢,即增长速度平缓.
(4)幂函数模型
幂函数y=xn(n>0)的增长速度介于指数增长和对数增长之间.
1.下列函数中,随x的增大,增长速度最快的是( ).
A.y=100x B.y=x100 C.y=100x D.y=log100x(x∈N*)
2.某工厂8年来某种产品的总产量C与时间t(单位:年)的函数关系如图所示.
有下列四种说法:
①前三年产量增长的速度越来越快;
②前三年产量增长的速度越来越慢;
③第三年后这种产品停止生产;
④第三年后产量保持不变.
其中说法正确的是 .
课后作业
3.以下是三个变量y1,y2,y3随变量x变化的函数值表:
其中,关于x呈指数函数变化的变量是 .
x 1 2 3 4 5 6 7 8 …
y1 2 4 8 16 32 64 128 256 …
y2 1 4 9 16 25 36 49 64 …
y3 0 1 1.585 2 2.322 2.585 2.807 3 …
1.下列函数中,随x的增大,增长速度最快的是( ).
A.y=100x B.y=x100 C.y=100x D.y=log100x(x∈N*)
【解析】四个函数中,增长速度由慢到快依次是y=log100x,y=100x,y=x100,y=100x.
C
2.某工厂8年来某种产品的总产量C与时间t(单位:年)的函数关系如图所示.
有下列四种说法:
①前三年产量增长的速度越来越快;
②前三年产量增长的速度越来越慢;
③第三年后这种产品停止生产;
④第三年后产量保持不变.
其中说法正确的是 .
【解析】由t∈[0,3]的图象联想到幂函数y=xα(0<α<1),反映了C随时间的变化逐渐增长但速度越来越慢.由t∈[3,8]的图象可知,总产量C没有变化,即第三年后停产,所以②③正确.
②③
3.以下是三个变量y1,y2,y3随变量x变化的函数值表:
其中,关于x呈指数函数变化的变量是 .
【解析】从表格可以看出三个变量y1,y2,y3都随x的增大而增大,但增长速度不同,其中y1的增长速度最快,画出它的散点图(图略)知变量y1关于x呈指数函数变化.
y1
x 1 2 3 4 5 6 7 8 …
y1 2 4 8 16 32 64 128 256 …
y2 1 4 9 16 25 36 49 64 …
y3 0 1 1.585 2 2.322 2.585 2.807 3 …
同课章节目录
- 第一章 预备知识
- 1 集合
- 2 常用逻辑用语
- 3 不等式
- 4 一元二次函数与一元二次不等式
- 第二章 函数
- 1 生活中的变量关系
- 2 函数
- 3 函数的单调性和最值
- 4 函数的奇偶性与简单的幂函数
- 第三章 指数运算与指数函数
- 1 指数幂的拓展
- 2 指数幂的运算性质
- 3 指数函数
- 第四章 对数运算和对数函数
- 1 对数的概念
- 2 对数的运算
- 3 对数函数
- 4 指数函数、幂函数、对数函数增长的比较
- 5 信息技术支持的函数研究
- 第五章 函数应用
- 1 方程解的存在性及方程的近似解
- 2 实际问题中的函数模型
- 第六章 统计
- 1 获取数据的途径
- 2 抽样的基本方法
- 3 用样本估计总体分布
- 4 用样本估计总体数字特征
- 第七章 概率
- 1 随机现象与随机事件
- 2 古典概型
- 3 频率与概率
- 4 事件的独立性
- 第八章 数学建模活动(一)
- 1 走进数学建模
- 2 数学建模的主要步骤
- 3 数学建模活动的主要过程
