高一上学期数学北师大版(2019)必修第一册 5.2.2 用函数模型解决实际问题 课件(共23张PPT)
文档属性
| 名称 | 高一上学期数学北师大版(2019)必修第一册 5.2.2 用函数模型解决实际问题 课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-12 21:59:52 | ||
图片预览








文档简介
(共23张PPT)
5.2.2 用函数模型解决实际问题
数学模型是针对或参照某种事物的主要特征、主要关系,用形式化的数学语言,抽象概括地、简化近似地表述出来的一种数学结构.其中,函数模型是应用最广泛的数学模型之一.实际问题一旦被认定是函数关系,就可以通过研究这个函数的性质,使问题得到解决
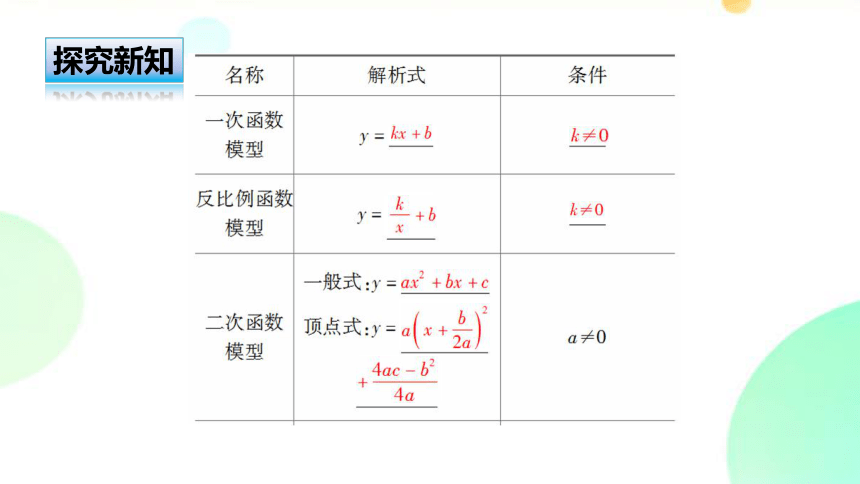
探究新知
探究新知
探究新知
典例剖析
例5 要建造一段5000m的高速公路,工队需要把600 人分成两组,一组完成一段2000m的软地带公路的建造任务,同时另一完成剩下的3000 m 的硬地带公路的建造任务.据测算,软、硬土地每米公路的工程量分别是 50 人·天和 30 人·天.问如何安排两组的人数,才能使全队筑路工期最短
典例剖析
设在软土地带工作的人数为x人,则在硬地带工作的人数为(600-x)人.根据题意,在软土地带筑路时间为
在硬土地带筑路时间为
其中x∈(0,600),x∈.
因为函数f(x)在区间(0,600)上是减函数,函数 g(x)在区间(0,600)上是增函数,所以全队筑路工期为
解析
典例剖析
因为函数 t(x)在区间(0,]上减,在区间[,600)上递增,所以是函数 t(x)的最小值点.但315.8 不是整数,于是计算t (315)和t(316),其中较小者即为所求.
经计算,t(315) 317.46,t(316) 316.90.
于是,当安排 316 人到软土地带工作,284 人到硬土地带工作时,可以使全队筑路工期最短.
解析
典例剖析
例6 某公司每年需要某种计算机元件 8 000个,每次购买元件需手续费 500元,每个元件的库存费是每年 2元.若将这些元件一次购进,则可少花手续费,但即便不考虑资金占用,8 000个元件的库存费也不少,若多次进货,则可减少库存费,但手续费要增加.现在需要确定:每年进货几次最经济(总费用最少)
典例剖析
首先要做一些假设:
(1)每天需同样多的元件;(2)其他费用可以作为常数看待.
将8 000个元件所需的总费用记为F元,一年总库存费记为 E元,购买元件总手续费记为 H元,其他费用记为 C元(C为常数),则
F=E+H+C.
若每年平均进货n次(n∈),则每次的进货量为q=个.假设用完q个元件的时间为 年,在[0, ]内,t时刻的库存量为 V(t),满足
解析
典例剖析
如图5-10,阴影部分的面积是第一个 时间段内需支付库存费的库存量的总和,相当于 年内每一时刻需支付库存费的库存量均为
解析
典例剖析
在 年内,每个元件的库存费为,则元件的库存费为
一年总库存费为
另外,H=500n元,所以
由基本不等式,得
当且仅当500n,即n=4 时,上面的不等式取等号,此时总费用最少,故每年进货4次最经济.
解析
表格信息类建模问题
巩固练习
巩固练习
巩固练习
解析
巩固练习
解析
巩固练习
解析
规律方法
图像信息解读问题
巩固练习
巩固练习
巩固练习
解析
规律方法
课堂小结
课堂小结
5.2.2 用函数模型解决实际问题
数学模型是针对或参照某种事物的主要特征、主要关系,用形式化的数学语言,抽象概括地、简化近似地表述出来的一种数学结构.其中,函数模型是应用最广泛的数学模型之一.实际问题一旦被认定是函数关系,就可以通过研究这个函数的性质,使问题得到解决
探究新知
探究新知
探究新知
典例剖析
例5 要建造一段5000m的高速公路,工队需要把600 人分成两组,一组完成一段2000m的软地带公路的建造任务,同时另一完成剩下的3000 m 的硬地带公路的建造任务.据测算,软、硬土地每米公路的工程量分别是 50 人·天和 30 人·天.问如何安排两组的人数,才能使全队筑路工期最短
典例剖析
设在软土地带工作的人数为x人,则在硬地带工作的人数为(600-x)人.根据题意,在软土地带筑路时间为
在硬土地带筑路时间为
其中x∈(0,600),x∈.
因为函数f(x)在区间(0,600)上是减函数,函数 g(x)在区间(0,600)上是增函数,所以全队筑路工期为
解析
典例剖析
因为函数 t(x)在区间(0,]上减,在区间[,600)上递增,所以是函数 t(x)的最小值点.但315.8 不是整数,于是计算t (315)和t(316),其中较小者即为所求.
经计算,t(315) 317.46,t(316) 316.90.
于是,当安排 316 人到软土地带工作,284 人到硬土地带工作时,可以使全队筑路工期最短.
解析
典例剖析
例6 某公司每年需要某种计算机元件 8 000个,每次购买元件需手续费 500元,每个元件的库存费是每年 2元.若将这些元件一次购进,则可少花手续费,但即便不考虑资金占用,8 000个元件的库存费也不少,若多次进货,则可减少库存费,但手续费要增加.现在需要确定:每年进货几次最经济(总费用最少)
典例剖析
首先要做一些假设:
(1)每天需同样多的元件;(2)其他费用可以作为常数看待.
将8 000个元件所需的总费用记为F元,一年总库存费记为 E元,购买元件总手续费记为 H元,其他费用记为 C元(C为常数),则
F=E+H+C.
若每年平均进货n次(n∈),则每次的进货量为q=个.假设用完q个元件的时间为 年,在[0, ]内,t时刻的库存量为 V(t),满足
解析
典例剖析
如图5-10,阴影部分的面积是第一个 时间段内需支付库存费的库存量的总和,相当于 年内每一时刻需支付库存费的库存量均为
解析
典例剖析
在 年内,每个元件的库存费为,则元件的库存费为
一年总库存费为
另外,H=500n元,所以
由基本不等式,得
当且仅当500n,即n=4 时,上面的不等式取等号,此时总费用最少,故每年进货4次最经济.
解析
表格信息类建模问题
巩固练习
巩固练习
巩固练习
解析
巩固练习
解析
巩固练习
解析
规律方法
图像信息解读问题
巩固练习
巩固练习
巩固练习
解析
规律方法
课堂小结
课堂小结
同课章节目录
- 第一章 预备知识
- 1 集合
- 2 常用逻辑用语
- 3 不等式
- 4 一元二次函数与一元二次不等式
- 第二章 函数
- 1 生活中的变量关系
- 2 函数
- 3 函数的单调性和最值
- 4 函数的奇偶性与简单的幂函数
- 第三章 指数运算与指数函数
- 1 指数幂的拓展
- 2 指数幂的运算性质
- 3 指数函数
- 第四章 对数运算和对数函数
- 1 对数的概念
- 2 对数的运算
- 3 对数函数
- 4 指数函数、幂函数、对数函数增长的比较
- 5 信息技术支持的函数研究
- 第五章 函数应用
- 1 方程解的存在性及方程的近似解
- 2 实际问题中的函数模型
- 第六章 统计
- 1 获取数据的途径
- 2 抽样的基本方法
- 3 用样本估计总体分布
- 4 用样本估计总体数字特征
- 第七章 概率
- 1 随机现象与随机事件
- 2 古典概型
- 3 频率与概率
- 4 事件的独立性
- 第八章 数学建模活动(一)
- 1 走进数学建模
- 2 数学建模的主要步骤
- 3 数学建模活动的主要过程
