【中考押题预测】2025年中考数学核心考点考前冲刺 尺规作图(含解析)
文档属性
| 名称 | 【中考押题预测】2025年中考数学核心考点考前冲刺 尺规作图(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 994.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-10 20:41:42 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
中考数学考前冲刺 尺规作图
一.选择题(共10小题)
1.(2020 襄阳)如图,Rt△ABC中,∠ABC=90°,根据尺规作图的痕迹判断以下结论错误的是( )
A.DB=DE B.AB=AE C.∠EDC=∠BAC D.∠DAC=∠C
2.(2019 河北)根据尺规作图的痕迹,可用直尺成功找到三角形外心的是( )
A. B.
C. D.
3.(2019 长春)如图,在△ABC中,∠ACB为钝角.用直尺和圆规在边AB上确定一点D.使∠ADC=2∠B,则符合要求的作图痕迹是( )
A. B.
C. D.
4.(2024秋 大东区期末)下列画图的语句中,正确的为( )
A.画直线AB=10cm
B.画射线OB=10cm
C.延长射线BA到C,使BA=BC
D.过直线AB外一点画一条直线和直线AB相交
5.(2019秋 缙云县期末)下列尺规作图分别表示:①作一个角的平分线;②作一个角等于已知角;③作一条线段的垂直平分线.其中作法正确的是( )
A.①② B.①③ C.②③ D.①②③
6.(2015 三明)如图,在△ABC中,∠ACB=90°,分别以点A和B为圆心,以相同的长(大于AB)为半径作弧,两弧相交于点M和N,作直线MN交AB于点D,交BC于点E,连接CD,下列结论不一定正确的是( )
A.AD=BD B.BD=CD C.∠A=∠BED D.∠ECD=∠EDC
7.(2024 烟台)某班开展“用直尺和圆规作角平分线”的探究活动,各组展示作图痕迹如下,其中射线OP为∠AOB的平分线的有( )
A.1个 B.2个 C.3个 D.4个
8.(2023 河北)综合实践课上,嘉嘉画出△ABD,利用尺规作图找一点C,使得四边形ABCD为平行四边形.(1)~(3)是其作图过程.
(1)作BD的垂直平分线交BD于点O;
(2)连接AO,在AO的延长线上截取OC=AO;
(3)连接DC,BC,则四边形ABCD即为所求.
在嘉嘉的作法中,可直接判定四边形ABCD为平行四边形的条件是( )
A.两组对边分别平行 B.两组对边分别相等
C.对角线互相平分 D.一组对边平行且相等
9.(2016 杭州模拟)如图,用尺规作出∠OBF=∠AOB,所画痕迹是( )
A.以点B为圆心,OD为半径的弧
B.以点C为圆心,DC为半径的弧
C.以点E为圆心,OD为半径的弧
D.以点E为圆心,DC为半径的弧
10.(2023秋 永吉县期末)已知∠AOB,求作射线OC,使OC平分∠AOB,那么作法的合理顺序是( )
①作射线OC;
②在射线OA和OB上分别截取OD、OE,使OD=OE;
③分别以D、E为圆心,大于DE的长为半径在∠AOB内作弧,两弧交于点C.
A.①②③ B.②①③ C.②③① D.③①②
二.填空题(共5小题)
11.(2020 潍坊)如图,在Rt△ABC中,∠C=90°,∠B=20°,PQ垂直平分AB,垂足为Q,交BC于点P.按以下步骤作图:①以点A为圆心,以适当的长为半径作弧,分别交边AC,AB于点D,E;②分别以点D,E为圆心,以大于DE的长为半径作弧,两弧相交于点F;③作射线AF,与直线PQ交于点M.若AF与PQ的夹角为α,则α= °.
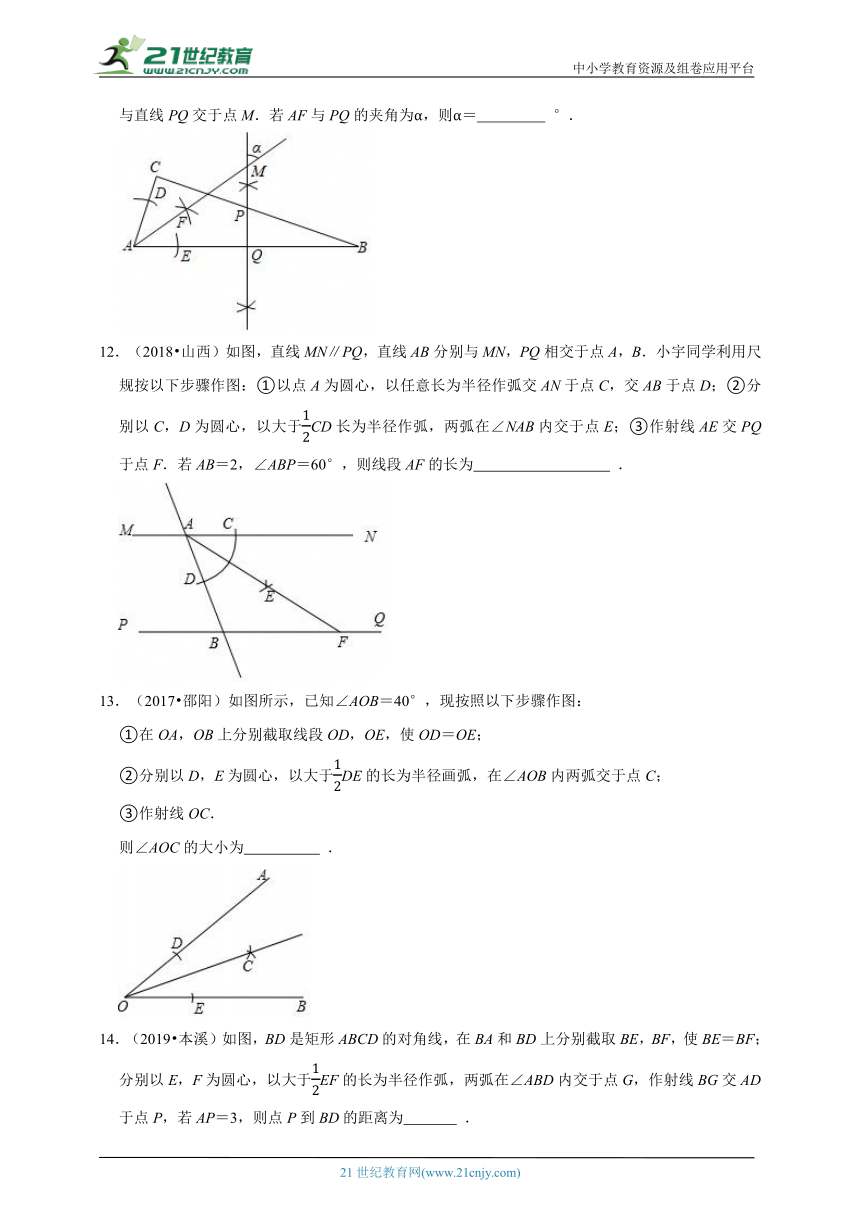
12.(2018 山西)如图,直线MN∥PQ,直线AB分别与MN,PQ相交于点A,B.小宇同学利用尺规按以下步骤作图:①以点A为圆心,以任意长为半径作弧交AN于点C,交AB于点D;②分别以C,D为圆心,以大于CD长为半径作弧,两弧在∠NAB内交于点E;③作射线AE交PQ于点F.若AB=2,∠ABP=60°,则线段AF的长为 .
13.(2017 邵阳)如图所示,已知∠AOB=40°,现按照以下步骤作图:
①在OA,OB上分别截取线段OD,OE,使OD=OE;
②分别以D,E为圆心,以大于DE的长为半径画弧,在∠AOB内两弧交于点C;
③作射线OC.
则∠AOC的大小为 .
14.(2019 本溪)如图,BD是矩形ABCD的对角线,在BA和BD上分别截取BE,BF,使BE=BF;分别以E,F为圆心,以大于EF的长为半径作弧,两弧在∠ABD内交于点G,作射线BG交AD于点P,若AP=3,则点P到BD的距离为 .
15.(2019 宁夏)如图,在Rt△ABC中,∠C=90°,以顶点B为圆心,适当长度为半径画弧,分别交AB,BC于点M,N,再分别以点M,N为圆心,大于MN的长为半径画弧,两弧交于点P,作射线BP交AC于点D.若∠A=30°,则 .
三.解答题(共5小题)
16.(2025 鼓楼区校级一模)如图,已知△ABC(AC<AB<BC),请用直尺(不带刻度)和圆规,按下列要求作图(不要求写作法,但要保留作图痕迹):
(1)在边BC上确定一点P,使得PA+PC=BC;
(2)作出一个△DEF,使得:①△DEF是直角三角形;②△DEF的周长等于边BC的长.
17.(2008 黔东南州)如图,学校有一块三角形空地(即△ABC),现准备将它分成面积相等的两块地,栽种不同的花草,请你把它分出来.(作图题要求:尺规作图,保留作图痕迹,不写作法,不要求证明).
18.(2016春 太原期末)作图题(要求:用尺规作图,保留作图痕迹,不写作法和证明)
已知:(如图)线段a和∠α,
求作:△ABC,使AB=AC=a,∠A=∠α.
19.(2018 常州)(1)如图1,已知EK垂直平分BC,垂足为D,AB与EK相交于点F,连接CF.求证:∠AFE=∠CFD.
(2)如图2,在Rt△GMN中,∠M=90°,P为MN的中点.
①用直尺和圆规在GN边上求作点Q,使得∠GQM=∠PQN(保留作图痕迹,不要求写作法);
②在①的条件下,如果∠G=60°,那么Q是GN的中点吗?为什么?
20.(2018 无锡)如图,平面直角坐标系中,已知点B的坐标为(6,4).
(1)请用直尺(不带刻度)和圆规作一条直线AC,它与x轴和y轴的正半轴分别交于点A和点C,且使∠ABC=90°,△ABC与△AOC的面积相等.(作图不必写作法,但要保留作图痕迹.)
(2)问:(1)中这样的直线AC是否唯一?若唯一,请说明理由;若不唯一,请在图中画出所有这样的直线AC,并写出与之对应的函数表达式.
中考数学考前冲刺 尺规作图
参考答案与试题解析
一.选择题(共10小题)
1.(2020 襄阳)如图,Rt△ABC中,∠ABC=90°,根据尺规作图的痕迹判断以下结论错误的是( )
A.DB=DE B.AB=AE C.∠EDC=∠BAC D.∠DAC=∠C
【考点】作图—基本作图.
【专题】作图题;应用意识.
【答案】D
【分析】证明△ADE≌△ADB即可判断A,B正确,再根据同角的补角相等,证明∠EDC=∠BAC即可.
【解答】解:由作图可知,∠DAE=∠DAB,∠DEA=∠B=90°,
∵AD=AD,
∴△ADE≌△ADB(AAS),
∴DB=DE,AB=AE,
∵∠AED+∠B=180°
∴∠BAC+∠BDE=180°,
∵∠EDC+∠BDE=180°,
∴∠EDC=∠BAC,
故A,B,C正确,
故选:D.
【点评】本题考查作图﹣基本作图,全等三角形的判定和性质等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
2.(2019 河北)根据尺规作图的痕迹,可用直尺成功找到三角形外心的是( )
A. B.
C. D.
【考点】作图—基本作图;三角形的外接圆与外心.
【专题】作图题.
【答案】C
【分析】根据三角形外心的定义,三角形外心为三边的垂直平分线的交点,然后利用基本作图和选项进行判断.
【解答】解:三角形外心为三边的垂直平分线的交点,由基本作图得到C选项作了两边的垂直平分线,从而可用直尺成功找到三角形外心.
故选:C.
【点评】本题考查了作图﹣基本作图:熟练掌握基本作图(作一条线段等于已知线段;作一个角等于已知角;作已知线段的垂直平分线;作已知角的角平分线;过一点作已知直线的垂线).也考查了三角形的外心.
3.(2019 长春)如图,在△ABC中,∠ACB为钝角.用直尺和圆规在边AB上确定一点D.使∠ADC=2∠B,则符合要求的作图痕迹是( )
A. B.
C. D.
【考点】作图—复杂作图.
【专题】作图题.
【答案】B
【分析】由∠ADC=2∠B且∠ADC=∠B+∠BCD知∠B=∠BCD,据此得DB=DC,由线段的中垂线的性质可得答案.
【解答】解:∵∠ADC=2∠B且∠ADC=∠B+∠BCD,
∴∠B=∠BCD,
∴DB=DC,
∴点D是线段BC中垂线与AB的交点,
故选:B.
【点评】本题主要考查作图﹣复杂作图,解题的关键是掌握三角形外角的性质、中垂线的性质及其尺规作图.
4.(2024秋 大东区期末)下列画图的语句中,正确的为( )
A.画直线AB=10cm
B.画射线OB=10cm
C.延长射线BA到C,使BA=BC
D.过直线AB外一点画一条直线和直线AB相交
【考点】作图—尺规作图的定义.
【专题】常规题型.
【答案】D
【分析】根据直线、射线、线段的性质即可一一判断;
【解答】解:A、错误.直线没有长度;
B、错误.射线没有长度;
C、错误.射线有无限延伸性,不需要延长;
D、正确.
故选:D.
【点评】本题考查作图﹣尺规作图,解题的关键是熟练掌握基本概念,属于中考基础题.
5.(2019秋 缙云县期末)下列尺规作图分别表示:①作一个角的平分线;②作一个角等于已知角;③作一条线段的垂直平分线.其中作法正确的是( )
A.①② B.①③ C.②③ D.①②③
【考点】作图—基本作图.
【专题】作图题.
【答案】A
【分析】利用作一个角等于已知角;作一个角的平分线;作一条线段的垂直平分线的作法进而判断即可得出答案.
【解答】解:①作一个角的平分线的作法正确;
②作一个角等于已知角的方法正确;
③作一条线段的垂直平分线,缺少另一个交点,故作法错误;
故选:A.
【点评】此题主要考查了基本作图,正确把握作图方法是解题关键.
6.(2015 三明)如图,在△ABC中,∠ACB=90°,分别以点A和B为圆心,以相同的长(大于AB)为半径作弧,两弧相交于点M和N,作直线MN交AB于点D,交BC于点E,连接CD,下列结论不一定正确的是( )
A.AD=BD B.BD=CD C.∠A=∠BED D.∠ECD=∠EDC
【考点】作图—基本作图;线段垂直平分线的性质;直角三角形斜边上的中线.
【答案】D
【分析】由题意可知:MN为AB的垂直平分线,可以得出AD=BD;CD为直角三角形ABC斜边上的中线,得出CD=BD;利用三角形的内角和得出∠A=∠BED;因为∠A≠60°,得不出AC=AD,无法得出EC=ED,则∠ECD=∠EDC不成立;由此选择答案即可.
【解答】解:∵MN为AB的垂直平分线,
∴AD=BD,∠BDE=90°;
∵∠ACB=90°,
∴CD=BD;
∵∠A+∠B=∠B+∠BED=90°,
∴∠A=∠BED;
∵当∠A≠60°时,AC≠AD,
∴EC≠ED,
∴∠ECD≠∠EDC.
故选:D.
【点评】此题考查了线段垂直平分线的性质以及直角三角形的性质.注意垂直平分线上任意一点,到线段两端点的距离相等.
7.(2024 烟台)某班开展“用直尺和圆规作角平分线”的探究活动,各组展示作图痕迹如下,其中射线OP为∠AOB的平分线的有( )
A.1个 B.2个 C.3个 D.4个
【考点】作图—基本作图;角平分线的定义.
【专题】作图题;几何直观.
【答案】D
【分析】根据角平分线的定义即可得到结论.
【解答】解:A:由作图痕迹可知,射线OP为∠AOB的平分线;
B:由作图痕迹可知,OC=OD,OA=OB,
又∵∠AOD=∠BOC,
∴△ADO≌△BCO(SAS),
同理可得△ACP≌△BDP(AAS),△APO≌△BPO(SSS),
∴∠AOP=∠BOP,
射线OP为∠AOB的平分线;
C:由作图痕迹可知,∠ACP=∠AOB,CP∥OB,
可得∠CPO=∠POB,
又由图可知CO=CP,
∴∠COP=∠CPO,
∴∠POB=∠COP,
射线OP为∠AOB的平分线;
D:由作图痕迹可知,CO=OD,△OCD是等腰三角形,
∴射线OP是CD的垂直平分线,
也是∠AOB的平分线.
故选:D.
【点评】本题考查了作图﹣基本作图,角平分线的定义,正确地识别图形是解题的关键.
8.(2023 河北)综合实践课上,嘉嘉画出△ABD,利用尺规作图找一点C,使得四边形ABCD为平行四边形.(1)~(3)是其作图过程.
(1)作BD的垂直平分线交BD于点O;
(2)连接AO,在AO的延长线上截取OC=AO;
(3)连接DC,BC,则四边形ABCD即为所求.
在嘉嘉的作法中,可直接判定四边形ABCD为平行四边形的条件是( )
A.两组对边分别平行 B.两组对边分别相等
C.对角线互相平分 D.一组对边平行且相等
【考点】作图—复杂作图;平行四边形的判定.
【专题】作图题;推理能力.
【答案】C
【分析】根据:“对角线互相平分的四边形是平行四边形”证明.
【解答】解:由作图得:DO=BO,AO=CO,
∴四边形ABCD为平行四边形,
故选:C.
【点评】本题考查了复杂作图,掌握平行四边形的判定定理是解题的关键.
9.(2016 杭州模拟)如图,用尺规作出∠OBF=∠AOB,所画痕迹是( )
A.以点B为圆心,OD为半径的弧
B.以点C为圆心,DC为半径的弧
C.以点E为圆心,OD为半径的弧
D.以点E为圆心,DC为半径的弧
【考点】作图—基本作图.
【答案】D
【分析】根据作一个角等于已知角的作法进行解答即可.
【解答】解:作∠OBF=∠AOB的作法,由图可知,
①以点O为圆心,以任意长为半径画圆,分别交射线OA、OB分别为点C,D;
②以点B为圆心,以OC为半径画圆,分别交射线BO、MB分别为点E,F;
③以点E为圆心,以CD为半径画圆,交于点N,连接BN即可得出∠OBF,则∠OBF=∠AOB.
故选:D.
【点评】本题考查的是基本作图,熟知作一个角等于已知角的基本步骤是解答此题的关键.
10.(2023秋 永吉县期末)已知∠AOB,求作射线OC,使OC平分∠AOB,那么作法的合理顺序是( )
①作射线OC;
②在射线OA和OB上分别截取OD、OE,使OD=OE;
③分别以D、E为圆心,大于DE的长为半径在∠AOB内作弧,两弧交于点C.
A.①②③ B.②①③ C.②③① D.③①②
【考点】作图—基本作图.
【专题】作图题;推理能力.
【答案】C
【分析】根据作一个角的平分线的过程即可进行判断.
【解答】解:根据作一个角的平分线的过程可知:
②在射线OA和OB上分别截取OD、OE,使OD=OE;
③分别以D、E为圆心,大于DE的长为半径在∠AOB内作弧,两弧交于点C;
①作射线OC.
则射线OC平分∠AOB.
所以作法的合理顺序是②③①.
故选:C.
【点评】本题考查了作图﹣基本作图,解决本题的关键是掌握基本作图方法.
二.填空题(共5小题)
11.(2020 潍坊)如图,在Rt△ABC中,∠C=90°,∠B=20°,PQ垂直平分AB,垂足为Q,交BC于点P.按以下步骤作图:①以点A为圆心,以适当的长为半径作弧,分别交边AC,AB于点D,E;②分别以点D,E为圆心,以大于DE的长为半径作弧,两弧相交于点F;③作射线AF,与直线PQ交于点M.若AF与PQ的夹角为α,则α= 55 °.
【考点】作图—基本作图;线段垂直平分线的性质.
【专题】作图题;几何直观;运算能力.
【答案】见试题解答内容
【分析】根据直角三角形两锐角互余得∠BAC=70°,由角平分线的定义得∠BAM=35°,由线段垂直平分线可得△AQM是直角三角形,故可得∠AMQ+∠BAM=90°,即可求出α.
【解答】解:∵△ABC是直角三角形,∠C=90°,
∴∠B+∠BAC=90°,
∵∠B=20°,
∴∠BAC=90°﹣∠B=90°﹣20°=70°,
∵AM是∠BAC的平分线,
∴∠BAMBAC=35°,
∵PQ是AB的垂直平分线,
∴△AMQ是直角三角形,
∴∠AMQ+∠BAM=90°,
∴∠AMQ=90°﹣∠BAM=90°﹣35°=55°,
∴α=∠AMQ=55°.
故答案为:55°.
【点评】此题考查了直角三角形两锐角互余,角平分线的定义,线段垂直平分线的性质,对顶角相等等知识,熟练掌握相关定义和性质是解题的关键.
12.(2018 山西)如图,直线MN∥PQ,直线AB分别与MN,PQ相交于点A,B.小宇同学利用尺规按以下步骤作图:①以点A为圆心,以任意长为半径作弧交AN于点C,交AB于点D;②分别以C,D为圆心,以大于CD长为半径作弧,两弧在∠NAB内交于点E;③作射线AE交PQ于点F.若AB=2,∠ABP=60°,则线段AF的长为 2 .
【考点】作图—基本作图;解直角三角形;平行线的性质.
【专题】作图题;线段、角、相交线与平行线.
【答案】见试题解答内容
【分析】作高线BG,根据直角三角形30度角的性质得:BG=1,AG,可得AF的长.
【解答】解:∵MN∥PQ,
∴∠NAB=∠ABP=60°,
由题意得:AF平分∠NAB,
∴∠1=∠2=30°,
∵∠ABP=∠1+∠3,
∴∠3=30°,
∴∠1=∠3=30°,
∴AB=BF,AG=GF,
∵AB=2,
∴BGAB=1,
∴AG,
∴AF=2AG=2,
故答案为:2.
【点评】本题考查了平行线的性质、角平分线的基本作图、直角三角形30度角的性质,此题难度不大,熟练掌握平行线和角平分线的基本作图是关键.
13.(2017 邵阳)如图所示,已知∠AOB=40°,现按照以下步骤作图:
①在OA,OB上分别截取线段OD,OE,使OD=OE;
②分别以D,E为圆心,以大于DE的长为半径画弧,在∠AOB内两弧交于点C;
③作射线OC.
则∠AOC的大小为 20° .
【考点】作图—基本作图.
【答案】见试题解答内容
【分析】直接根据角平分线的作法即可得出结论.
【解答】解:∵由作法可知,OC是∠AOB的平分线,
∴∠AOC∠AOB=20°.
故答案为:20°.
【点评】本题考查的是作图﹣基本作图,熟知角平分线的作法是解答此题的关键.
14.(2019 本溪)如图,BD是矩形ABCD的对角线,在BA和BD上分别截取BE,BF,使BE=BF;分别以E,F为圆心,以大于EF的长为半径作弧,两弧在∠ABD内交于点G,作射线BG交AD于点P,若AP=3,则点P到BD的距离为 3 .
【考点】作图—复杂作图;角平分线的性质;矩形的性质.
【专题】线段、角、相交线与平行线;矩形 菱形 正方形.
【答案】见试题解答内容
【分析】首先结合作图的过程确定BP是∠ABD的平分线,然后根据角平分线的性质求得点P到BD的距离即可.
【解答】解:结合作图的过程知:BP平分∠ABD,
∵∠A=90°,AP=3,
∴点P到BD的距离等于AP的长,为3,
故答案为:3.
【点评】考查了尺规作图的知识及角平分线的性质、矩形的性质等知识,解题的关键是根据图形确定BP平分∠ABD.
15.(2019 宁夏)如图,在Rt△ABC中,∠C=90°,以顶点B为圆心,适当长度为半径画弧,分别交AB,BC于点M,N,再分别以点M,N为圆心,大于MN的长为半径画弧,两弧交于点P,作射线BP交AC于点D.若∠A=30°,则 .
【考点】作图—基本作图;角平分线的性质;含30度角的直角三角形.
【专题】作图题.
【答案】见试题解答内容
【分析】利用基本作图得BD平分∠ABC,再计算出∠ABD=∠CBD=30°,所以DA=DB,利用BD=2CD得到AD=2CD,然后根据三角形面积公式可得到的值.
【解答】解:由作法得BD平分∠ABC,
∵∠C=90°,∠A=30°,
∴∠ABC=60°,
∴∠ABD=∠CBD=30°,
∴DA=DB,
在Rt△BCD中,BD=2CD,
∴AD=2CD,
∴.
故答案为.
【点评】本题考查了作图﹣基本作图:熟练掌握基本作图(作一条线段等于已知线段;作一个角等于已知角;作已知线段的垂直平分线;作已知角的角平分线;过一点作已知直线的垂线).
三.解答题(共5小题)
16.(2025 鼓楼区校级一模)如图,已知△ABC(AC<AB<BC),请用直尺(不带刻度)和圆规,按下列要求作图(不要求写作法,但要保留作图痕迹):
(1)在边BC上确定一点P,使得PA+PC=BC;
(2)作出一个△DEF,使得:①△DEF是直角三角形;②△DEF的周长等于边BC的长.
【考点】作图—复杂作图.
【专题】作图题.
【答案】见试题解答内容
【分析】(1)作AB的垂直平分线,交BC于点P,则点P即为所求;
(2)在BC上取点D,过点D作BC的垂线,在垂线上取点E使DE=DB,连接EC,作EC的垂直平分线交BC于点F;则Rt△DEF即为所求.
【解答】解:(1)如图,作AB的垂直平分线,交BC于点P,则点P即为所求;
(2)如图,①在BC上取点D,过点D作BC的垂线,②在垂线上取点E使DE=DB,连接EC,③作EC的垂直平分线交BC于点F;
∴Rt△DEF即为所求.
【点评】本题主要考查了复杂作图,解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.
17.(2008 黔东南州)如图,学校有一块三角形空地(即△ABC),现准备将它分成面积相等的两块地,栽种不同的花草,请你把它分出来.(作图题要求:尺规作图,保留作图痕迹,不写作法,不要求证明).
【考点】作图—应用与设计作图.
【专题】作图题;压轴题.
【答案】见试题解答内容
【分析】作BC边上的中线,即可把△ABC分成面积相等的两块地.
【解答】解:作图如下:
.
【点评】此题主要考查三角形中线的作法以及等底等高的知识点.
18.(2016春 太原期末)作图题(要求:用尺规作图,保留作图痕迹,不写作法和证明)
已知:(如图)线段a和∠α,
求作:△ABC,使AB=AC=a,∠A=∠α.
【考点】作图—基本作图.
【答案】见试题解答内容
【分析】可做∠A=∠α,然后在∠A的两边上分别截取AC=AB=a,连接BC即可.
【解答】解:
【点评】本题考查作图﹣基本作图,用到的知识点为:边角边可判定两三角形全等;注意先画一个角等于已知角.
19.(2018 常州)(1)如图1,已知EK垂直平分BC,垂足为D,AB与EK相交于点F,连接CF.求证:∠AFE=∠CFD.
(2)如图2,在Rt△GMN中,∠M=90°,P为MN的中点.
①用直尺和圆规在GN边上求作点Q,使得∠GQM=∠PQN(保留作图痕迹,不要求写作法);
②在①的条件下,如果∠G=60°,那么Q是GN的中点吗?为什么?
【考点】作图—复杂作图;线段垂直平分线的性质;直角三角形斜边上的中线.
【专题】作图题.
【答案】见试题解答内容
【分析】(1)只要证明FC=FB即可解决问题;
(2)①作点P关于GN的对称点P′,连接P′M交GN于Q,连接PQ,点Q即为所求.
②结论:Q是GN的中点.想办法证明∠N=∠QMN=30°,∠G=∠GMQ=60°,可得QM=QN,QM=QG;
【解答】(1)证明:如图1中,
∵EK垂直平分线段BC,
∴FC=FB,
∴∠CFD=∠BFD,
∵∠BFD=∠AFE,
∴∠AFE=∠CFD.
(2)①作点P关于GN的对称点P′,连接P′M交GN于Q,连接PQ,点Q即为所求.
理由:∵GN垂直平分PP′,
∴QP′=QP,∠KQP′=∠KQP,
∵∠GQM=∠KQP′,
∴∠GQM=∠PQK,
∴点P即为所求.
②结论:Q是GN的中点.
理由:设PP′交GN于K.
∵∠G=60°,∠GMN=90°,
∴∠N=30°,
∵PK⊥KN,
∴PK=KP′PN,
∴PP′=PN=PM,
∴∠P′=∠PMP′,
∵∠NPK=∠P′+∠PMP′=60°,
∴∠PMP′=30°,
∴∠N=∠QMN=30°,∠G=∠GMQ=60°,
∴QM=QN,QM=QG,
∴QG=QN,
∴Q是GN的中点.
【点评】本题考查作图﹣复杂作图、线段的垂直平分线的性质、直角三角形斜边中线的性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.
20.(2018 无锡)如图,平面直角坐标系中,已知点B的坐标为(6,4).
(1)请用直尺(不带刻度)和圆规作一条直线AC,它与x轴和y轴的正半轴分别交于点A和点C,且使∠ABC=90°,△ABC与△AOC的面积相等.(作图不必写作法,但要保留作图痕迹.)
(2)问:(1)中这样的直线AC是否唯一?若唯一,请说明理由;若不唯一,请在图中画出所有这样的直线AC,并写出与之对应的函数表达式.
【考点】作图—复杂作图;待定系数法求一次函数解析式.
【专题】作图题.
【答案】见试题解答内容
【分析】(1)①作线段OB的垂直平分线AC,满足条件,②作矩形OA′BC′,直线A′C′,满足条件;
(2)分两种情形分别求解即可解决问题;
【解答】(1)解:如图△ABC即为所求;
(2)解:这样的直线不唯一.
①作线段OB的垂直平分线AC,满足条件,此时直线的解析式为yx.
②作矩形OA′BC′,直线A′C′,满足条件,此时直线A′C′的解析式为yx+4.
【点评】本题考查作图﹣复杂作图,待定系数法等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
中考数学考前冲刺 尺规作图
一.选择题(共10小题)
1.(2020 襄阳)如图,Rt△ABC中,∠ABC=90°,根据尺规作图的痕迹判断以下结论错误的是( )
A.DB=DE B.AB=AE C.∠EDC=∠BAC D.∠DAC=∠C
2.(2019 河北)根据尺规作图的痕迹,可用直尺成功找到三角形外心的是( )
A. B.
C. D.
3.(2019 长春)如图,在△ABC中,∠ACB为钝角.用直尺和圆规在边AB上确定一点D.使∠ADC=2∠B,则符合要求的作图痕迹是( )
A. B.
C. D.
4.(2024秋 大东区期末)下列画图的语句中,正确的为( )
A.画直线AB=10cm
B.画射线OB=10cm
C.延长射线BA到C,使BA=BC
D.过直线AB外一点画一条直线和直线AB相交
5.(2019秋 缙云县期末)下列尺规作图分别表示:①作一个角的平分线;②作一个角等于已知角;③作一条线段的垂直平分线.其中作法正确的是( )
A.①② B.①③ C.②③ D.①②③
6.(2015 三明)如图,在△ABC中,∠ACB=90°,分别以点A和B为圆心,以相同的长(大于AB)为半径作弧,两弧相交于点M和N,作直线MN交AB于点D,交BC于点E,连接CD,下列结论不一定正确的是( )
A.AD=BD B.BD=CD C.∠A=∠BED D.∠ECD=∠EDC
7.(2024 烟台)某班开展“用直尺和圆规作角平分线”的探究活动,各组展示作图痕迹如下,其中射线OP为∠AOB的平分线的有( )
A.1个 B.2个 C.3个 D.4个
8.(2023 河北)综合实践课上,嘉嘉画出△ABD,利用尺规作图找一点C,使得四边形ABCD为平行四边形.(1)~(3)是其作图过程.
(1)作BD的垂直平分线交BD于点O;
(2)连接AO,在AO的延长线上截取OC=AO;
(3)连接DC,BC,则四边形ABCD即为所求.
在嘉嘉的作法中,可直接判定四边形ABCD为平行四边形的条件是( )
A.两组对边分别平行 B.两组对边分别相等
C.对角线互相平分 D.一组对边平行且相等
9.(2016 杭州模拟)如图,用尺规作出∠OBF=∠AOB,所画痕迹是( )
A.以点B为圆心,OD为半径的弧
B.以点C为圆心,DC为半径的弧
C.以点E为圆心,OD为半径的弧
D.以点E为圆心,DC为半径的弧
10.(2023秋 永吉县期末)已知∠AOB,求作射线OC,使OC平分∠AOB,那么作法的合理顺序是( )
①作射线OC;
②在射线OA和OB上分别截取OD、OE,使OD=OE;
③分别以D、E为圆心,大于DE的长为半径在∠AOB内作弧,两弧交于点C.
A.①②③ B.②①③ C.②③① D.③①②
二.填空题(共5小题)
11.(2020 潍坊)如图,在Rt△ABC中,∠C=90°,∠B=20°,PQ垂直平分AB,垂足为Q,交BC于点P.按以下步骤作图:①以点A为圆心,以适当的长为半径作弧,分别交边AC,AB于点D,E;②分别以点D,E为圆心,以大于DE的长为半径作弧,两弧相交于点F;③作射线AF,与直线PQ交于点M.若AF与PQ的夹角为α,则α= °.
12.(2018 山西)如图,直线MN∥PQ,直线AB分别与MN,PQ相交于点A,B.小宇同学利用尺规按以下步骤作图:①以点A为圆心,以任意长为半径作弧交AN于点C,交AB于点D;②分别以C,D为圆心,以大于CD长为半径作弧,两弧在∠NAB内交于点E;③作射线AE交PQ于点F.若AB=2,∠ABP=60°,则线段AF的长为 .
13.(2017 邵阳)如图所示,已知∠AOB=40°,现按照以下步骤作图:
①在OA,OB上分别截取线段OD,OE,使OD=OE;
②分别以D,E为圆心,以大于DE的长为半径画弧,在∠AOB内两弧交于点C;
③作射线OC.
则∠AOC的大小为 .
14.(2019 本溪)如图,BD是矩形ABCD的对角线,在BA和BD上分别截取BE,BF,使BE=BF;分别以E,F为圆心,以大于EF的长为半径作弧,两弧在∠ABD内交于点G,作射线BG交AD于点P,若AP=3,则点P到BD的距离为 .
15.(2019 宁夏)如图,在Rt△ABC中,∠C=90°,以顶点B为圆心,适当长度为半径画弧,分别交AB,BC于点M,N,再分别以点M,N为圆心,大于MN的长为半径画弧,两弧交于点P,作射线BP交AC于点D.若∠A=30°,则 .
三.解答题(共5小题)
16.(2025 鼓楼区校级一模)如图,已知△ABC(AC<AB<BC),请用直尺(不带刻度)和圆规,按下列要求作图(不要求写作法,但要保留作图痕迹):
(1)在边BC上确定一点P,使得PA+PC=BC;
(2)作出一个△DEF,使得:①△DEF是直角三角形;②△DEF的周长等于边BC的长.
17.(2008 黔东南州)如图,学校有一块三角形空地(即△ABC),现准备将它分成面积相等的两块地,栽种不同的花草,请你把它分出来.(作图题要求:尺规作图,保留作图痕迹,不写作法,不要求证明).
18.(2016春 太原期末)作图题(要求:用尺规作图,保留作图痕迹,不写作法和证明)
已知:(如图)线段a和∠α,
求作:△ABC,使AB=AC=a,∠A=∠α.
19.(2018 常州)(1)如图1,已知EK垂直平分BC,垂足为D,AB与EK相交于点F,连接CF.求证:∠AFE=∠CFD.
(2)如图2,在Rt△GMN中,∠M=90°,P为MN的中点.
①用直尺和圆规在GN边上求作点Q,使得∠GQM=∠PQN(保留作图痕迹,不要求写作法);
②在①的条件下,如果∠G=60°,那么Q是GN的中点吗?为什么?
20.(2018 无锡)如图,平面直角坐标系中,已知点B的坐标为(6,4).
(1)请用直尺(不带刻度)和圆规作一条直线AC,它与x轴和y轴的正半轴分别交于点A和点C,且使∠ABC=90°,△ABC与△AOC的面积相等.(作图不必写作法,但要保留作图痕迹.)
(2)问:(1)中这样的直线AC是否唯一?若唯一,请说明理由;若不唯一,请在图中画出所有这样的直线AC,并写出与之对应的函数表达式.
中考数学考前冲刺 尺规作图
参考答案与试题解析
一.选择题(共10小题)
1.(2020 襄阳)如图,Rt△ABC中,∠ABC=90°,根据尺规作图的痕迹判断以下结论错误的是( )
A.DB=DE B.AB=AE C.∠EDC=∠BAC D.∠DAC=∠C
【考点】作图—基本作图.
【专题】作图题;应用意识.
【答案】D
【分析】证明△ADE≌△ADB即可判断A,B正确,再根据同角的补角相等,证明∠EDC=∠BAC即可.
【解答】解:由作图可知,∠DAE=∠DAB,∠DEA=∠B=90°,
∵AD=AD,
∴△ADE≌△ADB(AAS),
∴DB=DE,AB=AE,
∵∠AED+∠B=180°
∴∠BAC+∠BDE=180°,
∵∠EDC+∠BDE=180°,
∴∠EDC=∠BAC,
故A,B,C正确,
故选:D.
【点评】本题考查作图﹣基本作图,全等三角形的判定和性质等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
2.(2019 河北)根据尺规作图的痕迹,可用直尺成功找到三角形外心的是( )
A. B.
C. D.
【考点】作图—基本作图;三角形的外接圆与外心.
【专题】作图题.
【答案】C
【分析】根据三角形外心的定义,三角形外心为三边的垂直平分线的交点,然后利用基本作图和选项进行判断.
【解答】解:三角形外心为三边的垂直平分线的交点,由基本作图得到C选项作了两边的垂直平分线,从而可用直尺成功找到三角形外心.
故选:C.
【点评】本题考查了作图﹣基本作图:熟练掌握基本作图(作一条线段等于已知线段;作一个角等于已知角;作已知线段的垂直平分线;作已知角的角平分线;过一点作已知直线的垂线).也考查了三角形的外心.
3.(2019 长春)如图,在△ABC中,∠ACB为钝角.用直尺和圆规在边AB上确定一点D.使∠ADC=2∠B,则符合要求的作图痕迹是( )
A. B.
C. D.
【考点】作图—复杂作图.
【专题】作图题.
【答案】B
【分析】由∠ADC=2∠B且∠ADC=∠B+∠BCD知∠B=∠BCD,据此得DB=DC,由线段的中垂线的性质可得答案.
【解答】解:∵∠ADC=2∠B且∠ADC=∠B+∠BCD,
∴∠B=∠BCD,
∴DB=DC,
∴点D是线段BC中垂线与AB的交点,
故选:B.
【点评】本题主要考查作图﹣复杂作图,解题的关键是掌握三角形外角的性质、中垂线的性质及其尺规作图.
4.(2024秋 大东区期末)下列画图的语句中,正确的为( )
A.画直线AB=10cm
B.画射线OB=10cm
C.延长射线BA到C,使BA=BC
D.过直线AB外一点画一条直线和直线AB相交
【考点】作图—尺规作图的定义.
【专题】常规题型.
【答案】D
【分析】根据直线、射线、线段的性质即可一一判断;
【解答】解:A、错误.直线没有长度;
B、错误.射线没有长度;
C、错误.射线有无限延伸性,不需要延长;
D、正确.
故选:D.
【点评】本题考查作图﹣尺规作图,解题的关键是熟练掌握基本概念,属于中考基础题.
5.(2019秋 缙云县期末)下列尺规作图分别表示:①作一个角的平分线;②作一个角等于已知角;③作一条线段的垂直平分线.其中作法正确的是( )
A.①② B.①③ C.②③ D.①②③
【考点】作图—基本作图.
【专题】作图题.
【答案】A
【分析】利用作一个角等于已知角;作一个角的平分线;作一条线段的垂直平分线的作法进而判断即可得出答案.
【解答】解:①作一个角的平分线的作法正确;
②作一个角等于已知角的方法正确;
③作一条线段的垂直平分线,缺少另一个交点,故作法错误;
故选:A.
【点评】此题主要考查了基本作图,正确把握作图方法是解题关键.
6.(2015 三明)如图,在△ABC中,∠ACB=90°,分别以点A和B为圆心,以相同的长(大于AB)为半径作弧,两弧相交于点M和N,作直线MN交AB于点D,交BC于点E,连接CD,下列结论不一定正确的是( )
A.AD=BD B.BD=CD C.∠A=∠BED D.∠ECD=∠EDC
【考点】作图—基本作图;线段垂直平分线的性质;直角三角形斜边上的中线.
【答案】D
【分析】由题意可知:MN为AB的垂直平分线,可以得出AD=BD;CD为直角三角形ABC斜边上的中线,得出CD=BD;利用三角形的内角和得出∠A=∠BED;因为∠A≠60°,得不出AC=AD,无法得出EC=ED,则∠ECD=∠EDC不成立;由此选择答案即可.
【解答】解:∵MN为AB的垂直平分线,
∴AD=BD,∠BDE=90°;
∵∠ACB=90°,
∴CD=BD;
∵∠A+∠B=∠B+∠BED=90°,
∴∠A=∠BED;
∵当∠A≠60°时,AC≠AD,
∴EC≠ED,
∴∠ECD≠∠EDC.
故选:D.
【点评】此题考查了线段垂直平分线的性质以及直角三角形的性质.注意垂直平分线上任意一点,到线段两端点的距离相等.
7.(2024 烟台)某班开展“用直尺和圆规作角平分线”的探究活动,各组展示作图痕迹如下,其中射线OP为∠AOB的平分线的有( )
A.1个 B.2个 C.3个 D.4个
【考点】作图—基本作图;角平分线的定义.
【专题】作图题;几何直观.
【答案】D
【分析】根据角平分线的定义即可得到结论.
【解答】解:A:由作图痕迹可知,射线OP为∠AOB的平分线;
B:由作图痕迹可知,OC=OD,OA=OB,
又∵∠AOD=∠BOC,
∴△ADO≌△BCO(SAS),
同理可得△ACP≌△BDP(AAS),△APO≌△BPO(SSS),
∴∠AOP=∠BOP,
射线OP为∠AOB的平分线;
C:由作图痕迹可知,∠ACP=∠AOB,CP∥OB,
可得∠CPO=∠POB,
又由图可知CO=CP,
∴∠COP=∠CPO,
∴∠POB=∠COP,
射线OP为∠AOB的平分线;
D:由作图痕迹可知,CO=OD,△OCD是等腰三角形,
∴射线OP是CD的垂直平分线,
也是∠AOB的平分线.
故选:D.
【点评】本题考查了作图﹣基本作图,角平分线的定义,正确地识别图形是解题的关键.
8.(2023 河北)综合实践课上,嘉嘉画出△ABD,利用尺规作图找一点C,使得四边形ABCD为平行四边形.(1)~(3)是其作图过程.
(1)作BD的垂直平分线交BD于点O;
(2)连接AO,在AO的延长线上截取OC=AO;
(3)连接DC,BC,则四边形ABCD即为所求.
在嘉嘉的作法中,可直接判定四边形ABCD为平行四边形的条件是( )
A.两组对边分别平行 B.两组对边分别相等
C.对角线互相平分 D.一组对边平行且相等
【考点】作图—复杂作图;平行四边形的判定.
【专题】作图题;推理能力.
【答案】C
【分析】根据:“对角线互相平分的四边形是平行四边形”证明.
【解答】解:由作图得:DO=BO,AO=CO,
∴四边形ABCD为平行四边形,
故选:C.
【点评】本题考查了复杂作图,掌握平行四边形的判定定理是解题的关键.
9.(2016 杭州模拟)如图,用尺规作出∠OBF=∠AOB,所画痕迹是( )
A.以点B为圆心,OD为半径的弧
B.以点C为圆心,DC为半径的弧
C.以点E为圆心,OD为半径的弧
D.以点E为圆心,DC为半径的弧
【考点】作图—基本作图.
【答案】D
【分析】根据作一个角等于已知角的作法进行解答即可.
【解答】解:作∠OBF=∠AOB的作法,由图可知,
①以点O为圆心,以任意长为半径画圆,分别交射线OA、OB分别为点C,D;
②以点B为圆心,以OC为半径画圆,分别交射线BO、MB分别为点E,F;
③以点E为圆心,以CD为半径画圆,交于点N,连接BN即可得出∠OBF,则∠OBF=∠AOB.
故选:D.
【点评】本题考查的是基本作图,熟知作一个角等于已知角的基本步骤是解答此题的关键.
10.(2023秋 永吉县期末)已知∠AOB,求作射线OC,使OC平分∠AOB,那么作法的合理顺序是( )
①作射线OC;
②在射线OA和OB上分别截取OD、OE,使OD=OE;
③分别以D、E为圆心,大于DE的长为半径在∠AOB内作弧,两弧交于点C.
A.①②③ B.②①③ C.②③① D.③①②
【考点】作图—基本作图.
【专题】作图题;推理能力.
【答案】C
【分析】根据作一个角的平分线的过程即可进行判断.
【解答】解:根据作一个角的平分线的过程可知:
②在射线OA和OB上分别截取OD、OE,使OD=OE;
③分别以D、E为圆心,大于DE的长为半径在∠AOB内作弧,两弧交于点C;
①作射线OC.
则射线OC平分∠AOB.
所以作法的合理顺序是②③①.
故选:C.
【点评】本题考查了作图﹣基本作图,解决本题的关键是掌握基本作图方法.
二.填空题(共5小题)
11.(2020 潍坊)如图,在Rt△ABC中,∠C=90°,∠B=20°,PQ垂直平分AB,垂足为Q,交BC于点P.按以下步骤作图:①以点A为圆心,以适当的长为半径作弧,分别交边AC,AB于点D,E;②分别以点D,E为圆心,以大于DE的长为半径作弧,两弧相交于点F;③作射线AF,与直线PQ交于点M.若AF与PQ的夹角为α,则α= 55 °.
【考点】作图—基本作图;线段垂直平分线的性质.
【专题】作图题;几何直观;运算能力.
【答案】见试题解答内容
【分析】根据直角三角形两锐角互余得∠BAC=70°,由角平分线的定义得∠BAM=35°,由线段垂直平分线可得△AQM是直角三角形,故可得∠AMQ+∠BAM=90°,即可求出α.
【解答】解:∵△ABC是直角三角形,∠C=90°,
∴∠B+∠BAC=90°,
∵∠B=20°,
∴∠BAC=90°﹣∠B=90°﹣20°=70°,
∵AM是∠BAC的平分线,
∴∠BAMBAC=35°,
∵PQ是AB的垂直平分线,
∴△AMQ是直角三角形,
∴∠AMQ+∠BAM=90°,
∴∠AMQ=90°﹣∠BAM=90°﹣35°=55°,
∴α=∠AMQ=55°.
故答案为:55°.
【点评】此题考查了直角三角形两锐角互余,角平分线的定义,线段垂直平分线的性质,对顶角相等等知识,熟练掌握相关定义和性质是解题的关键.
12.(2018 山西)如图,直线MN∥PQ,直线AB分别与MN,PQ相交于点A,B.小宇同学利用尺规按以下步骤作图:①以点A为圆心,以任意长为半径作弧交AN于点C,交AB于点D;②分别以C,D为圆心,以大于CD长为半径作弧,两弧在∠NAB内交于点E;③作射线AE交PQ于点F.若AB=2,∠ABP=60°,则线段AF的长为 2 .
【考点】作图—基本作图;解直角三角形;平行线的性质.
【专题】作图题;线段、角、相交线与平行线.
【答案】见试题解答内容
【分析】作高线BG,根据直角三角形30度角的性质得:BG=1,AG,可得AF的长.
【解答】解:∵MN∥PQ,
∴∠NAB=∠ABP=60°,
由题意得:AF平分∠NAB,
∴∠1=∠2=30°,
∵∠ABP=∠1+∠3,
∴∠3=30°,
∴∠1=∠3=30°,
∴AB=BF,AG=GF,
∵AB=2,
∴BGAB=1,
∴AG,
∴AF=2AG=2,
故答案为:2.
【点评】本题考查了平行线的性质、角平分线的基本作图、直角三角形30度角的性质,此题难度不大,熟练掌握平行线和角平分线的基本作图是关键.
13.(2017 邵阳)如图所示,已知∠AOB=40°,现按照以下步骤作图:
①在OA,OB上分别截取线段OD,OE,使OD=OE;
②分别以D,E为圆心,以大于DE的长为半径画弧,在∠AOB内两弧交于点C;
③作射线OC.
则∠AOC的大小为 20° .
【考点】作图—基本作图.
【答案】见试题解答内容
【分析】直接根据角平分线的作法即可得出结论.
【解答】解:∵由作法可知,OC是∠AOB的平分线,
∴∠AOC∠AOB=20°.
故答案为:20°.
【点评】本题考查的是作图﹣基本作图,熟知角平分线的作法是解答此题的关键.
14.(2019 本溪)如图,BD是矩形ABCD的对角线,在BA和BD上分别截取BE,BF,使BE=BF;分别以E,F为圆心,以大于EF的长为半径作弧,两弧在∠ABD内交于点G,作射线BG交AD于点P,若AP=3,则点P到BD的距离为 3 .
【考点】作图—复杂作图;角平分线的性质;矩形的性质.
【专题】线段、角、相交线与平行线;矩形 菱形 正方形.
【答案】见试题解答内容
【分析】首先结合作图的过程确定BP是∠ABD的平分线,然后根据角平分线的性质求得点P到BD的距离即可.
【解答】解:结合作图的过程知:BP平分∠ABD,
∵∠A=90°,AP=3,
∴点P到BD的距离等于AP的长,为3,
故答案为:3.
【点评】考查了尺规作图的知识及角平分线的性质、矩形的性质等知识,解题的关键是根据图形确定BP平分∠ABD.
15.(2019 宁夏)如图,在Rt△ABC中,∠C=90°,以顶点B为圆心,适当长度为半径画弧,分别交AB,BC于点M,N,再分别以点M,N为圆心,大于MN的长为半径画弧,两弧交于点P,作射线BP交AC于点D.若∠A=30°,则 .
【考点】作图—基本作图;角平分线的性质;含30度角的直角三角形.
【专题】作图题.
【答案】见试题解答内容
【分析】利用基本作图得BD平分∠ABC,再计算出∠ABD=∠CBD=30°,所以DA=DB,利用BD=2CD得到AD=2CD,然后根据三角形面积公式可得到的值.
【解答】解:由作法得BD平分∠ABC,
∵∠C=90°,∠A=30°,
∴∠ABC=60°,
∴∠ABD=∠CBD=30°,
∴DA=DB,
在Rt△BCD中,BD=2CD,
∴AD=2CD,
∴.
故答案为.
【点评】本题考查了作图﹣基本作图:熟练掌握基本作图(作一条线段等于已知线段;作一个角等于已知角;作已知线段的垂直平分线;作已知角的角平分线;过一点作已知直线的垂线).
三.解答题(共5小题)
16.(2025 鼓楼区校级一模)如图,已知△ABC(AC<AB<BC),请用直尺(不带刻度)和圆规,按下列要求作图(不要求写作法,但要保留作图痕迹):
(1)在边BC上确定一点P,使得PA+PC=BC;
(2)作出一个△DEF,使得:①△DEF是直角三角形;②△DEF的周长等于边BC的长.
【考点】作图—复杂作图.
【专题】作图题.
【答案】见试题解答内容
【分析】(1)作AB的垂直平分线,交BC于点P,则点P即为所求;
(2)在BC上取点D,过点D作BC的垂线,在垂线上取点E使DE=DB,连接EC,作EC的垂直平分线交BC于点F;则Rt△DEF即为所求.
【解答】解:(1)如图,作AB的垂直平分线,交BC于点P,则点P即为所求;
(2)如图,①在BC上取点D,过点D作BC的垂线,②在垂线上取点E使DE=DB,连接EC,③作EC的垂直平分线交BC于点F;
∴Rt△DEF即为所求.
【点评】本题主要考查了复杂作图,解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.
17.(2008 黔东南州)如图,学校有一块三角形空地(即△ABC),现准备将它分成面积相等的两块地,栽种不同的花草,请你把它分出来.(作图题要求:尺规作图,保留作图痕迹,不写作法,不要求证明).
【考点】作图—应用与设计作图.
【专题】作图题;压轴题.
【答案】见试题解答内容
【分析】作BC边上的中线,即可把△ABC分成面积相等的两块地.
【解答】解:作图如下:
.
【点评】此题主要考查三角形中线的作法以及等底等高的知识点.
18.(2016春 太原期末)作图题(要求:用尺规作图,保留作图痕迹,不写作法和证明)
已知:(如图)线段a和∠α,
求作:△ABC,使AB=AC=a,∠A=∠α.
【考点】作图—基本作图.
【答案】见试题解答内容
【分析】可做∠A=∠α,然后在∠A的两边上分别截取AC=AB=a,连接BC即可.
【解答】解:
【点评】本题考查作图﹣基本作图,用到的知识点为:边角边可判定两三角形全等;注意先画一个角等于已知角.
19.(2018 常州)(1)如图1,已知EK垂直平分BC,垂足为D,AB与EK相交于点F,连接CF.求证:∠AFE=∠CFD.
(2)如图2,在Rt△GMN中,∠M=90°,P为MN的中点.
①用直尺和圆规在GN边上求作点Q,使得∠GQM=∠PQN(保留作图痕迹,不要求写作法);
②在①的条件下,如果∠G=60°,那么Q是GN的中点吗?为什么?
【考点】作图—复杂作图;线段垂直平分线的性质;直角三角形斜边上的中线.
【专题】作图题.
【答案】见试题解答内容
【分析】(1)只要证明FC=FB即可解决问题;
(2)①作点P关于GN的对称点P′,连接P′M交GN于Q,连接PQ,点Q即为所求.
②结论:Q是GN的中点.想办法证明∠N=∠QMN=30°,∠G=∠GMQ=60°,可得QM=QN,QM=QG;
【解答】(1)证明:如图1中,
∵EK垂直平分线段BC,
∴FC=FB,
∴∠CFD=∠BFD,
∵∠BFD=∠AFE,
∴∠AFE=∠CFD.
(2)①作点P关于GN的对称点P′,连接P′M交GN于Q,连接PQ,点Q即为所求.
理由:∵GN垂直平分PP′,
∴QP′=QP,∠KQP′=∠KQP,
∵∠GQM=∠KQP′,
∴∠GQM=∠PQK,
∴点P即为所求.
②结论:Q是GN的中点.
理由:设PP′交GN于K.
∵∠G=60°,∠GMN=90°,
∴∠N=30°,
∵PK⊥KN,
∴PK=KP′PN,
∴PP′=PN=PM,
∴∠P′=∠PMP′,
∵∠NPK=∠P′+∠PMP′=60°,
∴∠PMP′=30°,
∴∠N=∠QMN=30°,∠G=∠GMQ=60°,
∴QM=QN,QM=QG,
∴QG=QN,
∴Q是GN的中点.
【点评】本题考查作图﹣复杂作图、线段的垂直平分线的性质、直角三角形斜边中线的性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.
20.(2018 无锡)如图,平面直角坐标系中,已知点B的坐标为(6,4).
(1)请用直尺(不带刻度)和圆规作一条直线AC,它与x轴和y轴的正半轴分别交于点A和点C,且使∠ABC=90°,△ABC与△AOC的面积相等.(作图不必写作法,但要保留作图痕迹.)
(2)问:(1)中这样的直线AC是否唯一?若唯一,请说明理由;若不唯一,请在图中画出所有这样的直线AC,并写出与之对应的函数表达式.
【考点】作图—复杂作图;待定系数法求一次函数解析式.
【专题】作图题.
【答案】见试题解答内容
【分析】(1)①作线段OB的垂直平分线AC,满足条件,②作矩形OA′BC′,直线A′C′,满足条件;
(2)分两种情形分别求解即可解决问题;
【解答】(1)解:如图△ABC即为所求;
(2)解:这样的直线不唯一.
①作线段OB的垂直平分线AC,满足条件,此时直线的解析式为yx.
②作矩形OA′BC′,直线A′C′,满足条件,此时直线A′C′的解析式为yx+4.
【点评】本题考查作图﹣复杂作图,待定系数法等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
