【中考押题预测】2025年中考数学核心考点考前冲刺 代数式(含解析)
文档属性
| 名称 | 【中考押题预测】2025年中考数学核心考点考前冲刺 代数式(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 353.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-10 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
中考数学考前冲刺 代数式
一.选择题(共10小题)
1.(2020秋 安溪县期末)已知a是两位数,b是一位数,把a接写在b的后面,就成为一个三位数.这个三位数可表示成( )
A.10b+a B.ba C.100b+a D.b+10a
2.(2024秋 东城区校级期中)已知代数式x+2y的值是3,则代数式2x+4y+1的值是( )
A.1 B.4 C.7 D.不能确定
3.(2018 临安区)10名学生的平均成绩是x,如果另外5名学生每人得84分,那么整个组的平均成绩是( )分.
A. B. C. D.
4.(2014 十堰)根据如图中箭头的指向规律,从2013到2014再到2015,箭头的方向是以下图示中的( )
A. B. C. D.
5.(2015 日照)观察下列各式及其展开式:
(a+b)2=a2+2ab+b2
(a+b)3=a3+3a2b+3ab2+b3
(a+b)4=a4+4a3b+6a2b2+4ab3+b4
(a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5
…
请你猜想(a+b)10的展开式第三项的系数是( )
A.36 B.45 C.55 D.66
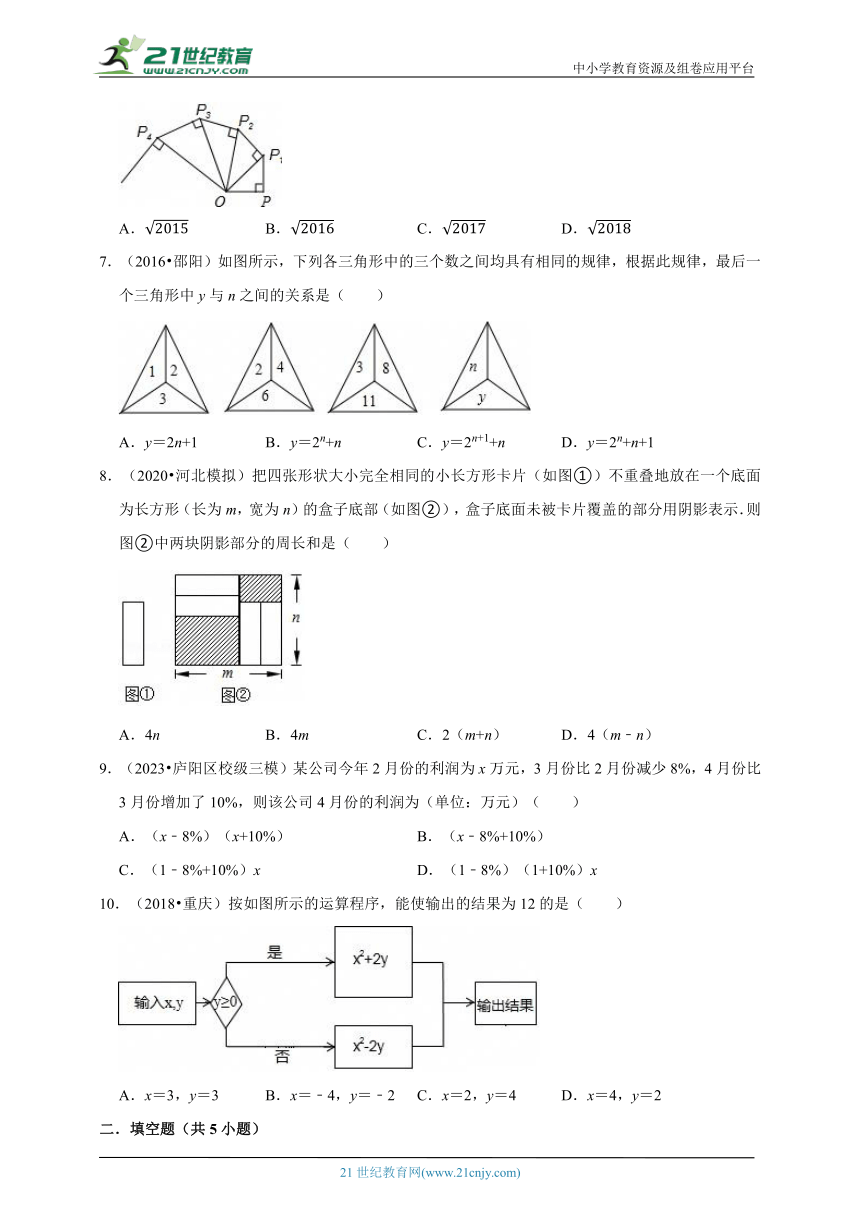
6.(2020秋 金川区校级期末)如图,OP=1,过点P作PP1⊥OP且PP1=1,得OP1;再过点P1作P1P2⊥OP1且P1P2=1,得OP2;又过点P2作P2P3⊥OP2且P2P3=1,得OP3=2…依此法继续作下去,得OP2017=( )
A. B. C. D.
7.(2016 邵阳)如图所示,下列各三角形中的三个数之间均具有相同的规律,根据此规律,最后一个三角形中y与n之间的关系是( )
A.y=2n+1 B.y=2n+n C.y=2n+1+n D.y=2n+n+1
8.(2020 河北模拟)把四张形状大小完全相同的小长方形卡片(如图①)不重叠地放在一个底面为长方形(长为m,宽为n)的盒子底部(如图②),盒子底面未被卡片覆盖的部分用阴影表示.则图②中两块阴影部分的周长和是( )
A.4n B.4m C.2(m+n) D.4(m﹣n)
9.(2023 庐阳区校级三模)某公司今年2月份的利润为x万元,3月份比2月份减少8%,4月份比3月份增加了10%,则该公司4月份的利润为(单位:万元)( )
A.(x﹣8%)(x+10%) B.(x﹣8%+10%)
C.(1﹣8%+10%)x D.(1﹣8%)(1+10%)x
10.(2018 重庆)按如图所示的运算程序,能使输出的结果为12的是( )
A.x=3,y=3 B.x=﹣4,y=﹣2 C.x=2,y=4 D.x=4,y=2
二.填空题(共5小题)
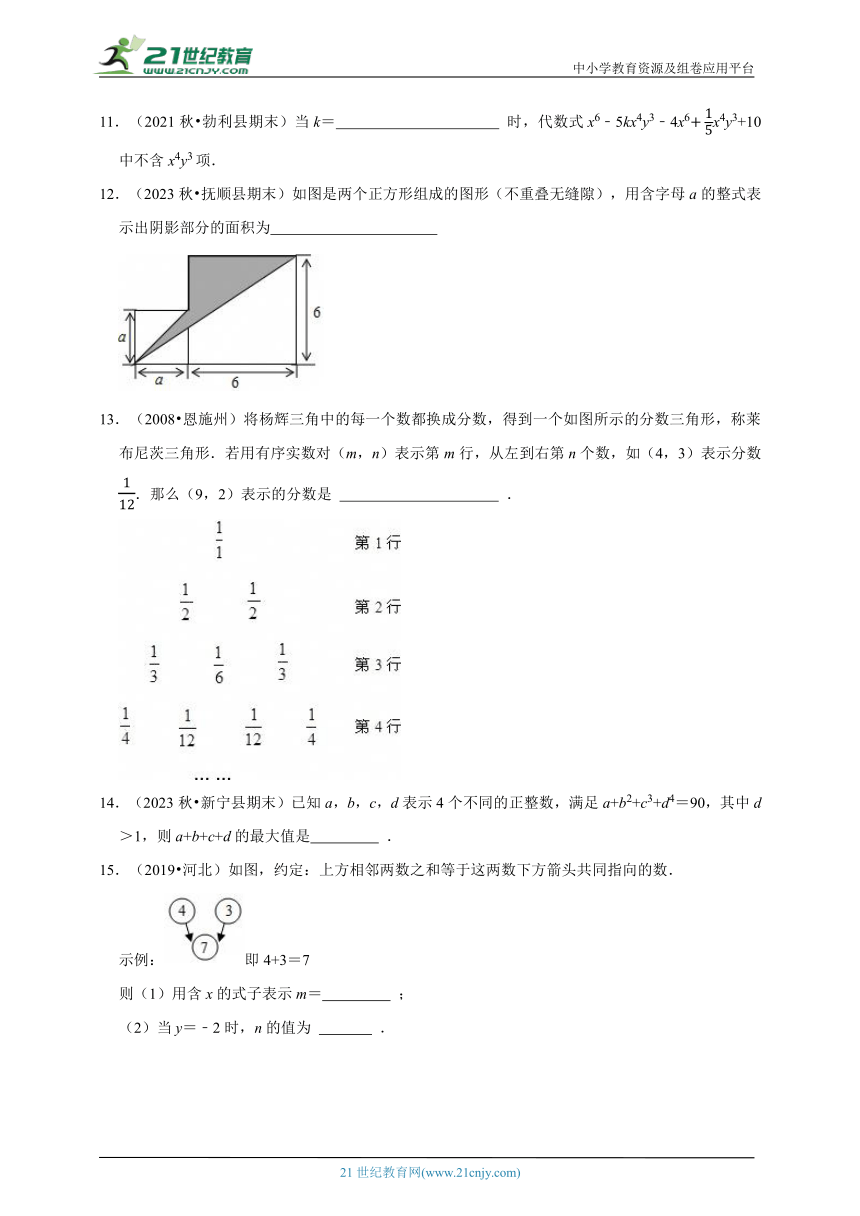
11.(2021秋 勃利县期末)当k= 时,代数式x6﹣5kx4y3﹣4x6x4y3+10中不含x4y3项.
12.(2023秋 抚顺县期末)如图是两个正方形组成的图形(不重叠无缝隙),用含字母a的整式表示出阴影部分的面积为
13.(2008 恩施州)将杨辉三角中的每一个数都换成分数,得到一个如图所示的分数三角形,称莱布尼茨三角形.若用有序实数对(m,n)表示第m行,从左到右第n个数,如(4,3)表示分数.那么(9,2)表示的分数是 .
14.(2023秋 新宁县期末)已知a,b,c,d表示4个不同的正整数,满足a+b2+c3+d4=90,其中d>1,则a+b+c+d的最大值是 .
15.(2019 河北)如图,约定:上方相邻两数之和等于这两数下方箭头共同指向的数.
示例:即4+3=7
则(1)用含x的式子表示m= ;
(2)当y=﹣2时,n的值为 .
三.解答题(共5小题)
16.(2016 邯山区一模)如果单项式5mxay与﹣5nx2a﹣3y是关于x、y的单项式,且它们是同类项.求
(1)(7a﹣22)2013的值;
(2)若5mxay﹣5nx2a﹣3y=0,且xy≠0,求(5m﹣5n)2014的值.
17.(2019秋 长垣市期末)某学校准备印刷一批证书,现有两个印刷厂可供选择:
甲厂收费方式:收制版费1000元,每本印刷费0.5元;
乙厂收费方式:不超过2000本时,每本收印刷费1.5元;超过2000本时,超过部分每本收印刷费0.25元,若该校印制证书x本.
(1)若x 不超过2000时,甲厂的收费为 元,乙厂的收费为 元;
(2)若x 超过2000时,甲厂的收费为 元,乙厂的收费为 元
(3)当印制证书8000本时应该选择哪个印刷厂更节省费用?节省了多少?
(4)请问印刷多少本证书时,甲乙两厂收费相同?
18.(2015 蜀山区自主招生)某商店积压了100件某种商品,为使这批货物尽快脱手,该商店采取了如下销售方案,将价格提高到原来的2.5倍,再作3次降价处理;第一次降价30%,标出“亏本价”;第二次又降价30%,标出“破产价”;第三次再降价30%,标出“跳楼价”.3次降价处理销售结果如下表:
降价次数 一 二 三
销售件数 10 40 一抢而光
(1)跳楼价占原价的百分比是多少?
(2)该商品按新销售方案销售,相比原价全部售完,哪种方案更盈利?
19.(2023秋 纳溪区期末)小明去文具用品商店给同学买某品牌水性笔,已知甲、乙两商店都有该品牌的水性笔且标价都是1.50元/支,但甲、乙两商店的优惠条件却不同.
甲商店:若购买不超过10支,则按标价付款;若一次购10支以上,则超过10支的部分按标价的60%付款.
乙商店:按标价的80%付款.
在水性笔的质量等因素相同的条件下.
(1)设小明要购买的该品牌笔数是x(x>10)支,请用含x的式子分别表示在甲、乙两个商店购买该品牌笔的费用;
(2)若小明要购买该品牌笔30支,你认为在甲、乙两商店中,到哪个商店购买比较省钱?说明理由.
20.(2020秋 济南期末)将7张相同的小长方形纸片(如图1所示)按图2所示的方式不重叠的放在长方形ABCD内,未被覆盖的部分恰好被分割为两个长方形,面积分别为S1和S2.已知小长方形纸片的长为a,宽为b,且a>b.
(1)当a=9,b=3,AD=30时,长方形ABCD的面积是 ,S2﹣S1的值为 .
(2)当AD=40时,请用含a、b的式子表示S2﹣S1的值;
(3)若AB长度为定值,AD变长,将这7张小长方形纸片还按照同样的方式放在新的长方形ABCD内,而S2﹣S1的值总保持不变,则a、b满足的关系是 .
中考数学考前冲刺 代数式
参考答案与试题解析
一.选择题(共10小题)
1.(2020秋 安溪县期末)已知a是两位数,b是一位数,把a接写在b的后面,就成为一个三位数.这个三位数可表示成( )
A.10b+a B.ba C.100b+a D.b+10a
【考点】列代数式.
【答案】C
【分析】b原来的最高位是个位,现在的最高位是百位,扩大了100倍;a不变.
【解答】解:两位数的表示方法:十位数字×10+个位数字;三位数字的表示方法:百位数字×100+十位数字×10+个位数字.
a是两位数,b是一位数,依据题意可得b扩大了100倍,所以这个三位数可表示成100b+a.
故选:C.
【点评】主要考查了三位数的表示方法,该题的易错点是表示百位数字b时忘了a是个2位数,错写成(10b+a).
2.(2024秋 东城区校级期中)已知代数式x+2y的值是3,则代数式2x+4y+1的值是( )
A.1 B.4 C.7 D.不能确定
【考点】代数式求值.
【专题】运算能力.
【答案】C
【分析】把x+2y看作一个整体并把所求代数式整理成已知条件的形式,然后计算即可得解.
【解答】解:∵x+2y=3,
∴2x+4y+1=2(x+2y)+1,
=2×3+1,
=6+1,
=7.
故选:C.
【点评】本题考查了代数式求值,整体思想的利用是解题的关键.
3.(2018 临安区)10名学生的平均成绩是x,如果另外5名学生每人得84分,那么整个组的平均成绩是( )分.
A. B. C. D.
【考点】列代数式.
【答案】B
【分析】整个组的平均成绩=15名学生的总成绩÷15.
【解答】解:先求出这15个人的总成绩10x+5×84=10x+420,再除以15可求得平均值为分.
故选:B.
【点评】此题考查了加权平均数的知识,解题的关键是求的15名学生的总成绩.
4.(2014 十堰)根据如图中箭头的指向规律,从2013到2014再到2015,箭头的方向是以下图示中的( )
A. B. C. D.
【考点】规律型:数字的变化类.
【专题】规律型.
【答案】D
【分析】观察不难发现,每4个数为一个循环组依次循环,用2013除以4,根据商和余数的情况解答即可.
【解答】解:由图可知,每4个数为一个循环组依次循环,2012÷4=503,
即0到2011共2012个数,构成前面503个循环,
∴2012是第504个循环的第1个数,2013是第504个循环组的第2个数,
∴从2013到2014再到2015,箭头的方向是.
故选:D.
【点评】本题是对数字变化规律的考查,仔细观察图形,发现每4个数为一个循环组依次循环是解题的关键.
5.(2015 日照)观察下列各式及其展开式:
(a+b)2=a2+2ab+b2
(a+b)3=a3+3a2b+3ab2+b3
(a+b)4=a4+4a3b+6a2b2+4ab3+b4
(a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5
…
请你猜想(a+b)10的展开式第三项的系数是( )
A.36 B.45 C.55 D.66
【考点】规律型:数字的变化类.
【专题】规律型;运算能力.
【答案】B
【分析】归纳总结,根据杨辉三角的特征得到展开式中第三项系数即可.
【解答】解:(a+b)2=a2+2ab+b2;
(a+b)3=a3+3a2b+3ab2+b3;
(a+b)4=a4+4a3b+6a2b2+4ab3+b4;
(a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5;
(a+b)6=a6+6a5b+15a4b2+20a3b3+15a2b4+6ab5+b6;
(a+b)7=a7+7a6b+21a5b2+35a4b3+35a3b4+21a2b5+7ab6+b7;
第8个式子系数分别为:1,8,28,56,70,56,28,8,1;
第9个式子系数分别为:1,9,36,84,126,126,84,36,9,1;
第10个式子系数分别为:1,10,45,120,210,252,210,120,45,10,1,
则(a+b)10的展开式第三项的系数为45.
故选:B.
【点评】此题考查了完全平方公式,熟练掌握公式是解本题的关键.
6.(2020秋 金川区校级期末)如图,OP=1,过点P作PP1⊥OP且PP1=1,得OP1;再过点P1作P1P2⊥OP1且P1P2=1,得OP2;又过点P2作P2P3⊥OP2且P2P3=1,得OP3=2…依此法继续作下去,得OP2017=( )
A. B. C. D.
【考点】规律型:图形的变化类;勾股定理的应用.
【答案】D
【分析】根据勾股定理分别求出每个直角三角形斜边长,根据结果得出规律,即可得出答案.
【解答】解:∵OP=1,OP1,OP2,OP32,
∴OP4,
…,
OP2017.
故选:D.
【点评】本题考查了勾股定理的应用,注意:在直角三角形中,两直角边的平方和等于斜边的平方,解此题的关键是能根据求出的结果得出规律.
7.(2016 邵阳)如图所示,下列各三角形中的三个数之间均具有相同的规律,根据此规律,最后一个三角形中y与n之间的关系是( )
A.y=2n+1 B.y=2n+n C.y=2n+1+n D.y=2n+n+1
【考点】规律型:数字的变化类.
【答案】B
【分析】由题意可得下边三角形的数字规律为:n+2n,继而求得答案.
【解答】解:∵观察可知:左边三角形的数字规律为:1,2,…,n,
右边三角形的数字规律为:2,22,…,2n,
下边三角形的数字规律为:1+2,2+22,…,n+2n,
∴y=2n+n.
故选:B.
【点评】此题考查了数字规律性问题.注意根据题意找到规律y=2n+n是关键.
8.(2020 河北模拟)把四张形状大小完全相同的小长方形卡片(如图①)不重叠地放在一个底面为长方形(长为m,宽为n)的盒子底部(如图②),盒子底面未被卡片覆盖的部分用阴影表示.则图②中两块阴影部分的周长和是( )
A.4n B.4m C.2(m+n) D.4(m﹣n)
【考点】列代数式.
【答案】A
【分析】本题需先设小长方形卡片的长为a,宽为b,再结合图形得出上面的阴影周长和下面的阴影周长,再把它们加起来即可求出答案.
【解答】解:设小长方形卡片的长为a,宽为b,
∴L上面的阴影=2(n﹣a+m﹣a),
L下面的阴影=2(m﹣2b+n﹣2b),
∴L总的阴影=L上面的阴影+L下面的阴影=2(n﹣a+m﹣a)+2(m﹣2b+n﹣2b)=4m+4n﹣4(a+2b),
又∵a+2b=m,
∴4m+4n﹣4(a+2b),
=4n.
故选:A.
【点评】本题主要考查了整式的加减运算,在解题时要根据题意结合图形得出答案是解题的关键.
9.(2023 庐阳区校级三模)某公司今年2月份的利润为x万元,3月份比2月份减少8%,4月份比3月份增加了10%,则该公司4月份的利润为(单位:万元)( )
A.(x﹣8%)(x+10%) B.(x﹣8%+10%)
C.(1﹣8%+10%)x D.(1﹣8%)(1+10%)x
【考点】列代数式.
【专题】计算题;整式;应用意识.
【答案】D
【分析】首先利用减少率的意义表示出3月份的利润,然后利用增长率的意义表示出4月份的利润.
【解答】解:由题意得3月份的利润为(1﹣8%)x,4月份的利润为(1﹣8%)(1+10%)x.
故选:D.
【点评】本题考查了列代数式,正确理解增长率以及下降率的定义是关键.
10.(2018 重庆)按如图所示的运算程序,能使输出的结果为12的是( )
A.x=3,y=3 B.x=﹣4,y=﹣2 C.x=2,y=4 D.x=4,y=2
【考点】代数式求值.
【专题】计算题;整式.
【答案】C
【分析】根据运算程序,结合输出结果确定的值即可.
【解答】解:A、x=3、y=3时,输出结果为32+2×3=15,不符合题意;
B、x=﹣4、y=﹣2时,输出结果为(﹣4)2﹣2×(﹣2)=20,不符合题意;
C、x=2、y=4时,输出结果为22+2×4=12,符合题意;
D、x=4、y=2时,输出结果为42+2×2=20,不符合题意;
故选:C.
【点评】此题考查了代数式的求值与有理数的混合运算,熟练掌握运算法则是解本题的关键.
二.填空题(共5小题)
11.(2021秋 勃利县期末)当k= 时,代数式x6﹣5kx4y3﹣4x6x4y3+10中不含x4y3项.
【考点】合并同类项.
【答案】见试题解答内容
【分析】根据合并同类项的法则,合并同类项时把系数相加减,字母与字母的指数不变.
【解答】解:代数式x6﹣5kx4y3﹣4x6x4y3+10中不含x4y3项,
即﹣5kx4y3和x4y3合并以后是0,
则得到﹣5k0,
∴k.
答:当k时,代数式x6﹣5kx4y3﹣4x6x4y3+10中不含x4y3项.
【点评】本题就是考查合并同类项的法则,这是一个常见题目类型.
12.(2023秋 抚顺县期末)如图是两个正方形组成的图形(不重叠无缝隙),用含字母a的整式表示出阴影部分的面积为 a2﹣3a+18.
【考点】列代数式.
【专题】整式.
【答案】见试题解答内容
【分析】根据面积的和差:两个正方形的面积和减去两个三角形的面积,可得答案.
【解答】解:阴影部分的面积
=a2+62a2(a+6)×6
=a2+36a2﹣3a﹣18
a2﹣3a+18,
故答案为:a2﹣3a+18.
【点评】本题考查了代数式求值,利用面积的和差得出关系式是解题关键.
13.(2008 恩施州)将杨辉三角中的每一个数都换成分数,得到一个如图所示的分数三角形,称莱布尼茨三角形.若用有序实数对(m,n)表示第m行,从左到右第n个数,如(4,3)表示分数.那么(9,2)表示的分数是 .
【考点】规律型:数字的变化类.
【专题】压轴题;规律型.
【答案】见试题解答内容
【分析】观察图表寻找规律:是第几行就有几个分数;每行每个分数的分子都是1;每行第一个分数的分母为行号,如第n行为,第二个的分母为;每行首尾对称.据此规律解答.
【解答】解:观察图表可知以下规律:是第几行就有几个分数;每行每个分数的分子都是1;每行第一个分数的分母为行号,如第n行为,第二个的分母为;每行首尾对称.
故(9,2)表示第9行,从左到右第2个数,即.故答案填:.
【点评】考查了学生解决实际问题的能力和阅读理解能力,找出本题的数字规律是正确解题的关键.
14.(2023秋 新宁县期末)已知a,b,c,d表示4个不同的正整数,满足a+b2+c3+d4=90,其中d>1,则a+b+c+d的最大值是 70 .
【考点】代数式求值.
【专题】整式.
【答案】70.
【分析】首先根据题意推理出d=2,c=1,b=3,所以a=64,所以求得a+b+c+d最大值为70.
【解答】解:要使a+b+c+d的值最大,
此时d>1,
要使a+b+c+d有最大值,且a+b2+c3+d4=90,
∴b,c,d尽可能取最小,
∴d=2,c=1,b=3,
a=90﹣(b2+c3+d4)=90﹣(9+1+16)=64,
故a+b+c+d的最大值是64+3+2+1=70.
故答案为:70.
【点评】本题考查了代数式求值,根据题意正确推理出a、b、c、d的值是解题的关键.
15.(2019 河北)如图,约定:上方相邻两数之和等于这两数下方箭头共同指向的数.
示例:即4+3=7
则(1)用含x的式子表示m= 3x ;
(2)当y=﹣2时,n的值为 1 .
【考点】代数式求值;列代数式.
【专题】整式.
【答案】见试题解答内容
【分析】(1)根据约定的方法即可求出m;
(2)根据约定的方法即可求出n.
【解答】解:(1)根据约定的方法可得:
m=x+2x=3x;
故答案为:3x;
(2)根据约定的方法即可求出n
x+2x+2x+3=m+n=y.
当y=﹣2时,5x+3=﹣2.
解得x=﹣1.
∴n=2x+3=﹣2+3=1.
故答案为:1.
【点评】本题考查了列代数式和代数式求值,解题的关键是掌握列代数式的约定方法.
三.解答题(共5小题)
16.(2016 邯山区一模)如果单项式5mxay与﹣5nx2a﹣3y是关于x、y的单项式,且它们是同类项.求
(1)(7a﹣22)2013的值;
(2)若5mxay﹣5nx2a﹣3y=0,且xy≠0,求(5m﹣5n)2014的值.
【考点】同类项.
【答案】见试题解答内容
【分析】(1)根据同类项是字母相同且相同字母的指数也相同,可得关于a的方程,解方程,可得答案;
(2)根据合并同类项,系数相加字母部分不变,可得m、n的关系,根据0的任何整数次幂都得零,可得答案.
【解答】解:(1)由单项式5mxay与﹣5nx2a﹣3y是关于x、y的单项式,且它们是同类项,得
a=2a﹣3,
解得a=3,
(7a﹣22)2013=(7×3﹣22)2013=(﹣1)2013=﹣1;
(2)由5mxay﹣5nx2a﹣3y=0,且xy≠0,得
5m﹣5n=0,
解得m=n,
(5m﹣5n)2014=02014=0.
【点评】本题考查了同类项,利用了同类项的定义,负数的奇数次幂是负数,零的任何正数次幂都得零.
17.(2019秋 长垣市期末)某学校准备印刷一批证书,现有两个印刷厂可供选择:
甲厂收费方式:收制版费1000元,每本印刷费0.5元;
乙厂收费方式:不超过2000本时,每本收印刷费1.5元;超过2000本时,超过部分每本收印刷费0.25元,若该校印制证书x本.
(1)若x 不超过2000时,甲厂的收费为 (0.5x+1000) 元,乙厂的收费为 1.5x 元;
(2)若x 超过2000时,甲厂的收费为 (1000+0.5x) 元,乙厂的收费为 (0.25x+2500) 元
(3)当印制证书8000本时应该选择哪个印刷厂更节省费用?节省了多少?
(4)请问印刷多少本证书时,甲乙两厂收费相同?
【考点】列代数式.
【答案】见试题解答内容
【分析】(1)根据印刷费用=数量×单价可分别求得;
(2)根据甲厂印刷费用=数量×单价、乙厂印刷费用=2000×1.5+超出部分的费用可得;
(3)分别计算出x=8000时,甲、乙两厂的费用即可得;
(4)分x≤2000和x>2000分别计算可得.
【解答】解:(1)若x 不超过2000时,甲厂的收费为(1000+0.5x)元,乙厂的收费为(1.5x)元,
故答案为:(0.5x+1000),1.5x;
(2)若x 超过2000时,甲厂的收费为(1000+0.5x)元,乙厂的收费为2000×1.5+0.25(x﹣2000)=0.25x+2500元,
故答案为:(1000+0.5x),(0.25x+2500);
(3)当x=8000时,甲厂费用为1000+0.5×8000=5000元,
乙厂费用为:0.25×8000+2500=4500元,
∴当印制证书8000本时应该选择乙印刷厂更节省费用,节省了500元;
(4)当x≤2000时,1000+0.5x=1.5x,
解得:x=1000;
当x>2000时,1000+0.5x=0.25x+2500,
解得:x=6000;
答:印刷1000或6000本证书时,甲乙两厂收费相同.
【点评】本题主要考查列代数式和方程的应用,理解题意找到相等关系是解题的关键.
18.(2015 蜀山区自主招生)某商店积压了100件某种商品,为使这批货物尽快脱手,该商店采取了如下销售方案,将价格提高到原来的2.5倍,再作3次降价处理;第一次降价30%,标出“亏本价”;第二次又降价30%,标出“破产价”;第三次再降价30%,标出“跳楼价”.3次降价处理销售结果如下表:
降价次数 一 二 三
销售件数 10 40 一抢而光
(1)跳楼价占原价的百分比是多少?
(2)该商品按新销售方案销售,相比原价全部售完,哪种方案更盈利?
【考点】列代数式;代数式求值.
【专题】阅读型;图表型.
【答案】见试题解答内容
【分析】(1)每一次降价的百分数都是相对于前一次降价来说的.题中没有原价,可设原价为1;
(2)每次降价后的价格应找到对应的数量.
【解答】解:(1)设原价为1,则跳楼价为2.5×1×(1﹣30%)×(1﹣30%)×(1﹣30%)=2.5×0.73,
所以跳楼价占原价的百分比为2.5×0.73÷1×100%=85.75%;
(2)原价出售:销售金额=100×1=100,
新价出售:销售金额=2.5×1×0.7×10+2.5×1×0.7×0.7×40+2.5×0.73×50,
=109.375;
∵109.375>100,∴新方案销售更盈利.
【点评】读懂题意,应知道每一次降价的百分数都是相对于前一次降价来说的;为了简便,可设原价为1.
19.(2023秋 纳溪区期末)小明去文具用品商店给同学买某品牌水性笔,已知甲、乙两商店都有该品牌的水性笔且标价都是1.50元/支,但甲、乙两商店的优惠条件却不同.
甲商店:若购买不超过10支,则按标价付款;若一次购10支以上,则超过10支的部分按标价的60%付款.
乙商店:按标价的80%付款.
在水性笔的质量等因素相同的条件下.
(1)设小明要购买的该品牌笔数是x(x>10)支,请用含x的式子分别表示在甲、乙两个商店购买该品牌笔的费用;
(2)若小明要购买该品牌笔30支,你认为在甲、乙两商店中,到哪个商店购买比较省钱?说明理由.
【考点】列代数式.
【答案】见试题解答内容
【分析】(1)先求出甲商店10支水性笔的价钱,然后再求出超过10支的部分的价钱,然后列出代数式;乙商店每支水性笔的价钱是1.5×0.8元,那么x支的价钱是1.5×0.8×x元;
(2)把x=30代入即可得到答案.
【解答】解:(1)在甲商店需要:10×1.5+0.6×1.5×(x﹣10)=0.9x+6(元),
在乙商店需要:1.5×0.8×x=1.2x(元),
(2)当x=30时,0.9x+6=33,1.2x=36,
因为33<36,所以小明要买30支笔应到甲商店买比较省钱.
【点评】本题考查了列代数式,解决问题的关键是读懂题意,找到关键描述语,进而找到所求的量的等量关系.
20.(2020秋 济南期末)将7张相同的小长方形纸片(如图1所示)按图2所示的方式不重叠的放在长方形ABCD内,未被覆盖的部分恰好被分割为两个长方形,面积分别为S1和S2.已知小长方形纸片的长为a,宽为b,且a>b.
(1)当a=9,b=3,AD=30时,长方形ABCD的面积是 630 ,S2﹣S1的值为 ﹣63 .
(2)当AD=40时,请用含a、b的式子表示S2﹣S1的值;
(3)若AB长度为定值,AD变长,将这7张小长方形纸片还按照同样的方式放在新的长方形ABCD内,而S2﹣S1的值总保持不变,则a、b满足的关系是 a=4b .
【考点】代数式求值;列代数式.
【专题】整式.
【答案】见试题解答内容
【分析】(1)根据长方形的面积公式,直接计算即可;求出S1和S2的面积,相减即可;
(2)用含a、b的式子表示出S1和S2的面积,即可求得结论;
(3)用含a、b、AD的式子表示出S2﹣S1,根据S2﹣S1的值总保持不变,即与AD的值无关,整理后,依据AD的系数为0即可得到结果.
【解答】解:(1)长方形ABCD的面积为30×(4×3+9)=630;
S2﹣S1=(30﹣3×3)×9﹣(30﹣9)×4×3=﹣63;
故答案为:630;﹣63;
(2)∵S1=(40﹣a)×4b,S2=(40﹣3b)×a,
∴S2﹣S1=a(40﹣3b)﹣4b(40﹣a)=40a﹣160b+ab;
(3)∵S2﹣S1=a(AD﹣3b)﹣4b(AD﹣a),
整理,得:S2﹣S1=(a﹣4b)AD+ab,
∵若AB长度不变,AD变长,而S2﹣S1的值总保持不变,
∴a﹣4b=0,即a=4b.
即a,b满足的关系是a=4b.
【点评】此题考查了整式的加减以及代数式求值问题,熟练掌握运算法则是解本题的关键.整式加减的应用时:①认真审题,弄清已知和未知的关系;②根据题意列出算式;③计算结果,根据结果解答实际问题.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
中考数学考前冲刺 代数式
一.选择题(共10小题)
1.(2020秋 安溪县期末)已知a是两位数,b是一位数,把a接写在b的后面,就成为一个三位数.这个三位数可表示成( )
A.10b+a B.ba C.100b+a D.b+10a
2.(2024秋 东城区校级期中)已知代数式x+2y的值是3,则代数式2x+4y+1的值是( )
A.1 B.4 C.7 D.不能确定
3.(2018 临安区)10名学生的平均成绩是x,如果另外5名学生每人得84分,那么整个组的平均成绩是( )分.
A. B. C. D.
4.(2014 十堰)根据如图中箭头的指向规律,从2013到2014再到2015,箭头的方向是以下图示中的( )
A. B. C. D.
5.(2015 日照)观察下列各式及其展开式:
(a+b)2=a2+2ab+b2
(a+b)3=a3+3a2b+3ab2+b3
(a+b)4=a4+4a3b+6a2b2+4ab3+b4
(a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5
…
请你猜想(a+b)10的展开式第三项的系数是( )
A.36 B.45 C.55 D.66
6.(2020秋 金川区校级期末)如图,OP=1,过点P作PP1⊥OP且PP1=1,得OP1;再过点P1作P1P2⊥OP1且P1P2=1,得OP2;又过点P2作P2P3⊥OP2且P2P3=1,得OP3=2…依此法继续作下去,得OP2017=( )
A. B. C. D.
7.(2016 邵阳)如图所示,下列各三角形中的三个数之间均具有相同的规律,根据此规律,最后一个三角形中y与n之间的关系是( )
A.y=2n+1 B.y=2n+n C.y=2n+1+n D.y=2n+n+1
8.(2020 河北模拟)把四张形状大小完全相同的小长方形卡片(如图①)不重叠地放在一个底面为长方形(长为m,宽为n)的盒子底部(如图②),盒子底面未被卡片覆盖的部分用阴影表示.则图②中两块阴影部分的周长和是( )
A.4n B.4m C.2(m+n) D.4(m﹣n)
9.(2023 庐阳区校级三模)某公司今年2月份的利润为x万元,3月份比2月份减少8%,4月份比3月份增加了10%,则该公司4月份的利润为(单位:万元)( )
A.(x﹣8%)(x+10%) B.(x﹣8%+10%)
C.(1﹣8%+10%)x D.(1﹣8%)(1+10%)x
10.(2018 重庆)按如图所示的运算程序,能使输出的结果为12的是( )
A.x=3,y=3 B.x=﹣4,y=﹣2 C.x=2,y=4 D.x=4,y=2
二.填空题(共5小题)
11.(2021秋 勃利县期末)当k= 时,代数式x6﹣5kx4y3﹣4x6x4y3+10中不含x4y3项.
12.(2023秋 抚顺县期末)如图是两个正方形组成的图形(不重叠无缝隙),用含字母a的整式表示出阴影部分的面积为
13.(2008 恩施州)将杨辉三角中的每一个数都换成分数,得到一个如图所示的分数三角形,称莱布尼茨三角形.若用有序实数对(m,n)表示第m行,从左到右第n个数,如(4,3)表示分数.那么(9,2)表示的分数是 .
14.(2023秋 新宁县期末)已知a,b,c,d表示4个不同的正整数,满足a+b2+c3+d4=90,其中d>1,则a+b+c+d的最大值是 .
15.(2019 河北)如图,约定:上方相邻两数之和等于这两数下方箭头共同指向的数.
示例:即4+3=7
则(1)用含x的式子表示m= ;
(2)当y=﹣2时,n的值为 .
三.解答题(共5小题)
16.(2016 邯山区一模)如果单项式5mxay与﹣5nx2a﹣3y是关于x、y的单项式,且它们是同类项.求
(1)(7a﹣22)2013的值;
(2)若5mxay﹣5nx2a﹣3y=0,且xy≠0,求(5m﹣5n)2014的值.
17.(2019秋 长垣市期末)某学校准备印刷一批证书,现有两个印刷厂可供选择:
甲厂收费方式:收制版费1000元,每本印刷费0.5元;
乙厂收费方式:不超过2000本时,每本收印刷费1.5元;超过2000本时,超过部分每本收印刷费0.25元,若该校印制证书x本.
(1)若x 不超过2000时,甲厂的收费为 元,乙厂的收费为 元;
(2)若x 超过2000时,甲厂的收费为 元,乙厂的收费为 元
(3)当印制证书8000本时应该选择哪个印刷厂更节省费用?节省了多少?
(4)请问印刷多少本证书时,甲乙两厂收费相同?
18.(2015 蜀山区自主招生)某商店积压了100件某种商品,为使这批货物尽快脱手,该商店采取了如下销售方案,将价格提高到原来的2.5倍,再作3次降价处理;第一次降价30%,标出“亏本价”;第二次又降价30%,标出“破产价”;第三次再降价30%,标出“跳楼价”.3次降价处理销售结果如下表:
降价次数 一 二 三
销售件数 10 40 一抢而光
(1)跳楼价占原价的百分比是多少?
(2)该商品按新销售方案销售,相比原价全部售完,哪种方案更盈利?
19.(2023秋 纳溪区期末)小明去文具用品商店给同学买某品牌水性笔,已知甲、乙两商店都有该品牌的水性笔且标价都是1.50元/支,但甲、乙两商店的优惠条件却不同.
甲商店:若购买不超过10支,则按标价付款;若一次购10支以上,则超过10支的部分按标价的60%付款.
乙商店:按标价的80%付款.
在水性笔的质量等因素相同的条件下.
(1)设小明要购买的该品牌笔数是x(x>10)支,请用含x的式子分别表示在甲、乙两个商店购买该品牌笔的费用;
(2)若小明要购买该品牌笔30支,你认为在甲、乙两商店中,到哪个商店购买比较省钱?说明理由.
20.(2020秋 济南期末)将7张相同的小长方形纸片(如图1所示)按图2所示的方式不重叠的放在长方形ABCD内,未被覆盖的部分恰好被分割为两个长方形,面积分别为S1和S2.已知小长方形纸片的长为a,宽为b,且a>b.
(1)当a=9,b=3,AD=30时,长方形ABCD的面积是 ,S2﹣S1的值为 .
(2)当AD=40时,请用含a、b的式子表示S2﹣S1的值;
(3)若AB长度为定值,AD变长,将这7张小长方形纸片还按照同样的方式放在新的长方形ABCD内,而S2﹣S1的值总保持不变,则a、b满足的关系是 .
中考数学考前冲刺 代数式
参考答案与试题解析
一.选择题(共10小题)
1.(2020秋 安溪县期末)已知a是两位数,b是一位数,把a接写在b的后面,就成为一个三位数.这个三位数可表示成( )
A.10b+a B.ba C.100b+a D.b+10a
【考点】列代数式.
【答案】C
【分析】b原来的最高位是个位,现在的最高位是百位,扩大了100倍;a不变.
【解答】解:两位数的表示方法:十位数字×10+个位数字;三位数字的表示方法:百位数字×100+十位数字×10+个位数字.
a是两位数,b是一位数,依据题意可得b扩大了100倍,所以这个三位数可表示成100b+a.
故选:C.
【点评】主要考查了三位数的表示方法,该题的易错点是表示百位数字b时忘了a是个2位数,错写成(10b+a).
2.(2024秋 东城区校级期中)已知代数式x+2y的值是3,则代数式2x+4y+1的值是( )
A.1 B.4 C.7 D.不能确定
【考点】代数式求值.
【专题】运算能力.
【答案】C
【分析】把x+2y看作一个整体并把所求代数式整理成已知条件的形式,然后计算即可得解.
【解答】解:∵x+2y=3,
∴2x+4y+1=2(x+2y)+1,
=2×3+1,
=6+1,
=7.
故选:C.
【点评】本题考查了代数式求值,整体思想的利用是解题的关键.
3.(2018 临安区)10名学生的平均成绩是x,如果另外5名学生每人得84分,那么整个组的平均成绩是( )分.
A. B. C. D.
【考点】列代数式.
【答案】B
【分析】整个组的平均成绩=15名学生的总成绩÷15.
【解答】解:先求出这15个人的总成绩10x+5×84=10x+420,再除以15可求得平均值为分.
故选:B.
【点评】此题考查了加权平均数的知识,解题的关键是求的15名学生的总成绩.
4.(2014 十堰)根据如图中箭头的指向规律,从2013到2014再到2015,箭头的方向是以下图示中的( )
A. B. C. D.
【考点】规律型:数字的变化类.
【专题】规律型.
【答案】D
【分析】观察不难发现,每4个数为一个循环组依次循环,用2013除以4,根据商和余数的情况解答即可.
【解答】解:由图可知,每4个数为一个循环组依次循环,2012÷4=503,
即0到2011共2012个数,构成前面503个循环,
∴2012是第504个循环的第1个数,2013是第504个循环组的第2个数,
∴从2013到2014再到2015,箭头的方向是.
故选:D.
【点评】本题是对数字变化规律的考查,仔细观察图形,发现每4个数为一个循环组依次循环是解题的关键.
5.(2015 日照)观察下列各式及其展开式:
(a+b)2=a2+2ab+b2
(a+b)3=a3+3a2b+3ab2+b3
(a+b)4=a4+4a3b+6a2b2+4ab3+b4
(a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5
…
请你猜想(a+b)10的展开式第三项的系数是( )
A.36 B.45 C.55 D.66
【考点】规律型:数字的变化类.
【专题】规律型;运算能力.
【答案】B
【分析】归纳总结,根据杨辉三角的特征得到展开式中第三项系数即可.
【解答】解:(a+b)2=a2+2ab+b2;
(a+b)3=a3+3a2b+3ab2+b3;
(a+b)4=a4+4a3b+6a2b2+4ab3+b4;
(a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5;
(a+b)6=a6+6a5b+15a4b2+20a3b3+15a2b4+6ab5+b6;
(a+b)7=a7+7a6b+21a5b2+35a4b3+35a3b4+21a2b5+7ab6+b7;
第8个式子系数分别为:1,8,28,56,70,56,28,8,1;
第9个式子系数分别为:1,9,36,84,126,126,84,36,9,1;
第10个式子系数分别为:1,10,45,120,210,252,210,120,45,10,1,
则(a+b)10的展开式第三项的系数为45.
故选:B.
【点评】此题考查了完全平方公式,熟练掌握公式是解本题的关键.
6.(2020秋 金川区校级期末)如图,OP=1,过点P作PP1⊥OP且PP1=1,得OP1;再过点P1作P1P2⊥OP1且P1P2=1,得OP2;又过点P2作P2P3⊥OP2且P2P3=1,得OP3=2…依此法继续作下去,得OP2017=( )
A. B. C. D.
【考点】规律型:图形的变化类;勾股定理的应用.
【答案】D
【分析】根据勾股定理分别求出每个直角三角形斜边长,根据结果得出规律,即可得出答案.
【解答】解:∵OP=1,OP1,OP2,OP32,
∴OP4,
…,
OP2017.
故选:D.
【点评】本题考查了勾股定理的应用,注意:在直角三角形中,两直角边的平方和等于斜边的平方,解此题的关键是能根据求出的结果得出规律.
7.(2016 邵阳)如图所示,下列各三角形中的三个数之间均具有相同的规律,根据此规律,最后一个三角形中y与n之间的关系是( )
A.y=2n+1 B.y=2n+n C.y=2n+1+n D.y=2n+n+1
【考点】规律型:数字的变化类.
【答案】B
【分析】由题意可得下边三角形的数字规律为:n+2n,继而求得答案.
【解答】解:∵观察可知:左边三角形的数字规律为:1,2,…,n,
右边三角形的数字规律为:2,22,…,2n,
下边三角形的数字规律为:1+2,2+22,…,n+2n,
∴y=2n+n.
故选:B.
【点评】此题考查了数字规律性问题.注意根据题意找到规律y=2n+n是关键.
8.(2020 河北模拟)把四张形状大小完全相同的小长方形卡片(如图①)不重叠地放在一个底面为长方形(长为m,宽为n)的盒子底部(如图②),盒子底面未被卡片覆盖的部分用阴影表示.则图②中两块阴影部分的周长和是( )
A.4n B.4m C.2(m+n) D.4(m﹣n)
【考点】列代数式.
【答案】A
【分析】本题需先设小长方形卡片的长为a,宽为b,再结合图形得出上面的阴影周长和下面的阴影周长,再把它们加起来即可求出答案.
【解答】解:设小长方形卡片的长为a,宽为b,
∴L上面的阴影=2(n﹣a+m﹣a),
L下面的阴影=2(m﹣2b+n﹣2b),
∴L总的阴影=L上面的阴影+L下面的阴影=2(n﹣a+m﹣a)+2(m﹣2b+n﹣2b)=4m+4n﹣4(a+2b),
又∵a+2b=m,
∴4m+4n﹣4(a+2b),
=4n.
故选:A.
【点评】本题主要考查了整式的加减运算,在解题时要根据题意结合图形得出答案是解题的关键.
9.(2023 庐阳区校级三模)某公司今年2月份的利润为x万元,3月份比2月份减少8%,4月份比3月份增加了10%,则该公司4月份的利润为(单位:万元)( )
A.(x﹣8%)(x+10%) B.(x﹣8%+10%)
C.(1﹣8%+10%)x D.(1﹣8%)(1+10%)x
【考点】列代数式.
【专题】计算题;整式;应用意识.
【答案】D
【分析】首先利用减少率的意义表示出3月份的利润,然后利用增长率的意义表示出4月份的利润.
【解答】解:由题意得3月份的利润为(1﹣8%)x,4月份的利润为(1﹣8%)(1+10%)x.
故选:D.
【点评】本题考查了列代数式,正确理解增长率以及下降率的定义是关键.
10.(2018 重庆)按如图所示的运算程序,能使输出的结果为12的是( )
A.x=3,y=3 B.x=﹣4,y=﹣2 C.x=2,y=4 D.x=4,y=2
【考点】代数式求值.
【专题】计算题;整式.
【答案】C
【分析】根据运算程序,结合输出结果确定的值即可.
【解答】解:A、x=3、y=3时,输出结果为32+2×3=15,不符合题意;
B、x=﹣4、y=﹣2时,输出结果为(﹣4)2﹣2×(﹣2)=20,不符合题意;
C、x=2、y=4时,输出结果为22+2×4=12,符合题意;
D、x=4、y=2时,输出结果为42+2×2=20,不符合题意;
故选:C.
【点评】此题考查了代数式的求值与有理数的混合运算,熟练掌握运算法则是解本题的关键.
二.填空题(共5小题)
11.(2021秋 勃利县期末)当k= 时,代数式x6﹣5kx4y3﹣4x6x4y3+10中不含x4y3项.
【考点】合并同类项.
【答案】见试题解答内容
【分析】根据合并同类项的法则,合并同类项时把系数相加减,字母与字母的指数不变.
【解答】解:代数式x6﹣5kx4y3﹣4x6x4y3+10中不含x4y3项,
即﹣5kx4y3和x4y3合并以后是0,
则得到﹣5k0,
∴k.
答:当k时,代数式x6﹣5kx4y3﹣4x6x4y3+10中不含x4y3项.
【点评】本题就是考查合并同类项的法则,这是一个常见题目类型.
12.(2023秋 抚顺县期末)如图是两个正方形组成的图形(不重叠无缝隙),用含字母a的整式表示出阴影部分的面积为 a2﹣3a+18.
【考点】列代数式.
【专题】整式.
【答案】见试题解答内容
【分析】根据面积的和差:两个正方形的面积和减去两个三角形的面积,可得答案.
【解答】解:阴影部分的面积
=a2+62a2(a+6)×6
=a2+36a2﹣3a﹣18
a2﹣3a+18,
故答案为:a2﹣3a+18.
【点评】本题考查了代数式求值,利用面积的和差得出关系式是解题关键.
13.(2008 恩施州)将杨辉三角中的每一个数都换成分数,得到一个如图所示的分数三角形,称莱布尼茨三角形.若用有序实数对(m,n)表示第m行,从左到右第n个数,如(4,3)表示分数.那么(9,2)表示的分数是 .
【考点】规律型:数字的变化类.
【专题】压轴题;规律型.
【答案】见试题解答内容
【分析】观察图表寻找规律:是第几行就有几个分数;每行每个分数的分子都是1;每行第一个分数的分母为行号,如第n行为,第二个的分母为;每行首尾对称.据此规律解答.
【解答】解:观察图表可知以下规律:是第几行就有几个分数;每行每个分数的分子都是1;每行第一个分数的分母为行号,如第n行为,第二个的分母为;每行首尾对称.
故(9,2)表示第9行,从左到右第2个数,即.故答案填:.
【点评】考查了学生解决实际问题的能力和阅读理解能力,找出本题的数字规律是正确解题的关键.
14.(2023秋 新宁县期末)已知a,b,c,d表示4个不同的正整数,满足a+b2+c3+d4=90,其中d>1,则a+b+c+d的最大值是 70 .
【考点】代数式求值.
【专题】整式.
【答案】70.
【分析】首先根据题意推理出d=2,c=1,b=3,所以a=64,所以求得a+b+c+d最大值为70.
【解答】解:要使a+b+c+d的值最大,
此时d>1,
要使a+b+c+d有最大值,且a+b2+c3+d4=90,
∴b,c,d尽可能取最小,
∴d=2,c=1,b=3,
a=90﹣(b2+c3+d4)=90﹣(9+1+16)=64,
故a+b+c+d的最大值是64+3+2+1=70.
故答案为:70.
【点评】本题考查了代数式求值,根据题意正确推理出a、b、c、d的值是解题的关键.
15.(2019 河北)如图,约定:上方相邻两数之和等于这两数下方箭头共同指向的数.
示例:即4+3=7
则(1)用含x的式子表示m= 3x ;
(2)当y=﹣2时,n的值为 1 .
【考点】代数式求值;列代数式.
【专题】整式.
【答案】见试题解答内容
【分析】(1)根据约定的方法即可求出m;
(2)根据约定的方法即可求出n.
【解答】解:(1)根据约定的方法可得:
m=x+2x=3x;
故答案为:3x;
(2)根据约定的方法即可求出n
x+2x+2x+3=m+n=y.
当y=﹣2时,5x+3=﹣2.
解得x=﹣1.
∴n=2x+3=﹣2+3=1.
故答案为:1.
【点评】本题考查了列代数式和代数式求值,解题的关键是掌握列代数式的约定方法.
三.解答题(共5小题)
16.(2016 邯山区一模)如果单项式5mxay与﹣5nx2a﹣3y是关于x、y的单项式,且它们是同类项.求
(1)(7a﹣22)2013的值;
(2)若5mxay﹣5nx2a﹣3y=0,且xy≠0,求(5m﹣5n)2014的值.
【考点】同类项.
【答案】见试题解答内容
【分析】(1)根据同类项是字母相同且相同字母的指数也相同,可得关于a的方程,解方程,可得答案;
(2)根据合并同类项,系数相加字母部分不变,可得m、n的关系,根据0的任何整数次幂都得零,可得答案.
【解答】解:(1)由单项式5mxay与﹣5nx2a﹣3y是关于x、y的单项式,且它们是同类项,得
a=2a﹣3,
解得a=3,
(7a﹣22)2013=(7×3﹣22)2013=(﹣1)2013=﹣1;
(2)由5mxay﹣5nx2a﹣3y=0,且xy≠0,得
5m﹣5n=0,
解得m=n,
(5m﹣5n)2014=02014=0.
【点评】本题考查了同类项,利用了同类项的定义,负数的奇数次幂是负数,零的任何正数次幂都得零.
17.(2019秋 长垣市期末)某学校准备印刷一批证书,现有两个印刷厂可供选择:
甲厂收费方式:收制版费1000元,每本印刷费0.5元;
乙厂收费方式:不超过2000本时,每本收印刷费1.5元;超过2000本时,超过部分每本收印刷费0.25元,若该校印制证书x本.
(1)若x 不超过2000时,甲厂的收费为 (0.5x+1000) 元,乙厂的收费为 1.5x 元;
(2)若x 超过2000时,甲厂的收费为 (1000+0.5x) 元,乙厂的收费为 (0.25x+2500) 元
(3)当印制证书8000本时应该选择哪个印刷厂更节省费用?节省了多少?
(4)请问印刷多少本证书时,甲乙两厂收费相同?
【考点】列代数式.
【答案】见试题解答内容
【分析】(1)根据印刷费用=数量×单价可分别求得;
(2)根据甲厂印刷费用=数量×单价、乙厂印刷费用=2000×1.5+超出部分的费用可得;
(3)分别计算出x=8000时,甲、乙两厂的费用即可得;
(4)分x≤2000和x>2000分别计算可得.
【解答】解:(1)若x 不超过2000时,甲厂的收费为(1000+0.5x)元,乙厂的收费为(1.5x)元,
故答案为:(0.5x+1000),1.5x;
(2)若x 超过2000时,甲厂的收费为(1000+0.5x)元,乙厂的收费为2000×1.5+0.25(x﹣2000)=0.25x+2500元,
故答案为:(1000+0.5x),(0.25x+2500);
(3)当x=8000时,甲厂费用为1000+0.5×8000=5000元,
乙厂费用为:0.25×8000+2500=4500元,
∴当印制证书8000本时应该选择乙印刷厂更节省费用,节省了500元;
(4)当x≤2000时,1000+0.5x=1.5x,
解得:x=1000;
当x>2000时,1000+0.5x=0.25x+2500,
解得:x=6000;
答:印刷1000或6000本证书时,甲乙两厂收费相同.
【点评】本题主要考查列代数式和方程的应用,理解题意找到相等关系是解题的关键.
18.(2015 蜀山区自主招生)某商店积压了100件某种商品,为使这批货物尽快脱手,该商店采取了如下销售方案,将价格提高到原来的2.5倍,再作3次降价处理;第一次降价30%,标出“亏本价”;第二次又降价30%,标出“破产价”;第三次再降价30%,标出“跳楼价”.3次降价处理销售结果如下表:
降价次数 一 二 三
销售件数 10 40 一抢而光
(1)跳楼价占原价的百分比是多少?
(2)该商品按新销售方案销售,相比原价全部售完,哪种方案更盈利?
【考点】列代数式;代数式求值.
【专题】阅读型;图表型.
【答案】见试题解答内容
【分析】(1)每一次降价的百分数都是相对于前一次降价来说的.题中没有原价,可设原价为1;
(2)每次降价后的价格应找到对应的数量.
【解答】解:(1)设原价为1,则跳楼价为2.5×1×(1﹣30%)×(1﹣30%)×(1﹣30%)=2.5×0.73,
所以跳楼价占原价的百分比为2.5×0.73÷1×100%=85.75%;
(2)原价出售:销售金额=100×1=100,
新价出售:销售金额=2.5×1×0.7×10+2.5×1×0.7×0.7×40+2.5×0.73×50,
=109.375;
∵109.375>100,∴新方案销售更盈利.
【点评】读懂题意,应知道每一次降价的百分数都是相对于前一次降价来说的;为了简便,可设原价为1.
19.(2023秋 纳溪区期末)小明去文具用品商店给同学买某品牌水性笔,已知甲、乙两商店都有该品牌的水性笔且标价都是1.50元/支,但甲、乙两商店的优惠条件却不同.
甲商店:若购买不超过10支,则按标价付款;若一次购10支以上,则超过10支的部分按标价的60%付款.
乙商店:按标价的80%付款.
在水性笔的质量等因素相同的条件下.
(1)设小明要购买的该品牌笔数是x(x>10)支,请用含x的式子分别表示在甲、乙两个商店购买该品牌笔的费用;
(2)若小明要购买该品牌笔30支,你认为在甲、乙两商店中,到哪个商店购买比较省钱?说明理由.
【考点】列代数式.
【答案】见试题解答内容
【分析】(1)先求出甲商店10支水性笔的价钱,然后再求出超过10支的部分的价钱,然后列出代数式;乙商店每支水性笔的价钱是1.5×0.8元,那么x支的价钱是1.5×0.8×x元;
(2)把x=30代入即可得到答案.
【解答】解:(1)在甲商店需要:10×1.5+0.6×1.5×(x﹣10)=0.9x+6(元),
在乙商店需要:1.5×0.8×x=1.2x(元),
(2)当x=30时,0.9x+6=33,1.2x=36,
因为33<36,所以小明要买30支笔应到甲商店买比较省钱.
【点评】本题考查了列代数式,解决问题的关键是读懂题意,找到关键描述语,进而找到所求的量的等量关系.
20.(2020秋 济南期末)将7张相同的小长方形纸片(如图1所示)按图2所示的方式不重叠的放在长方形ABCD内,未被覆盖的部分恰好被分割为两个长方形,面积分别为S1和S2.已知小长方形纸片的长为a,宽为b,且a>b.
(1)当a=9,b=3,AD=30时,长方形ABCD的面积是 630 ,S2﹣S1的值为 ﹣63 .
(2)当AD=40时,请用含a、b的式子表示S2﹣S1的值;
(3)若AB长度为定值,AD变长,将这7张小长方形纸片还按照同样的方式放在新的长方形ABCD内,而S2﹣S1的值总保持不变,则a、b满足的关系是 a=4b .
【考点】代数式求值;列代数式.
【专题】整式.
【答案】见试题解答内容
【分析】(1)根据长方形的面积公式,直接计算即可;求出S1和S2的面积,相减即可;
(2)用含a、b的式子表示出S1和S2的面积,即可求得结论;
(3)用含a、b、AD的式子表示出S2﹣S1,根据S2﹣S1的值总保持不变,即与AD的值无关,整理后,依据AD的系数为0即可得到结果.
【解答】解:(1)长方形ABCD的面积为30×(4×3+9)=630;
S2﹣S1=(30﹣3×3)×9﹣(30﹣9)×4×3=﹣63;
故答案为:630;﹣63;
(2)∵S1=(40﹣a)×4b,S2=(40﹣3b)×a,
∴S2﹣S1=a(40﹣3b)﹣4b(40﹣a)=40a﹣160b+ab;
(3)∵S2﹣S1=a(AD﹣3b)﹣4b(AD﹣a),
整理,得:S2﹣S1=(a﹣4b)AD+ab,
∵若AB长度不变,AD变长,而S2﹣S1的值总保持不变,
∴a﹣4b=0,即a=4b.
即a,b满足的关系是a=4b.
【点评】此题考查了整式的加减以及代数式求值问题,熟练掌握运算法则是解本题的关键.整式加减的应用时:①认真审题,弄清已知和未知的关系;②根据题意列出算式;③计算结果,根据结果解答实际问题.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
