人教版高中数学课件 必修一 3.1.2 用二分法求方程的近似解(共25张PPT)
文档属性
| 名称 | 人教版高中数学课件 必修一 3.1.2 用二分法求方程的近似解(共25张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-06-20 18:35:23 | ||
图片预览






文档简介
课件25张PPT。3.1.2 用二分法求方程的
近似解人教A版 高中数学 必修1定理定理回眸知能并重1.复习重温——零点的存在性问题——零点的个数问题思考:如何确定零点的取值?连续不断的一条曲线,有且仅有一个
问题:你会求下列方程的解吗? (1) (3) 2.初步探究解法再现 类型梳理(2)求根公式试根法无法求出精确解探测仪长斧《猫和老鼠》
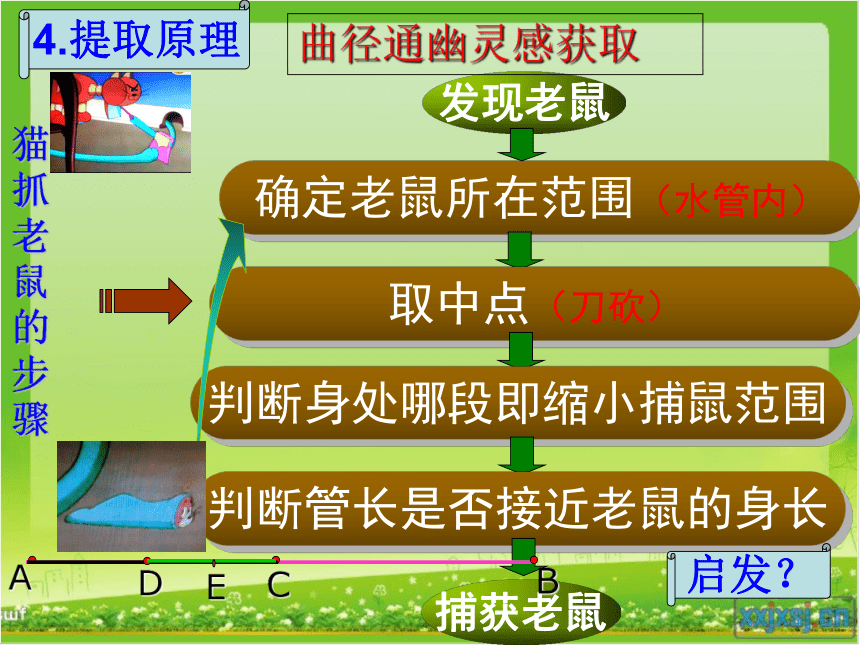
之机器猫节选3.情境再现另辟蹊径策略探求4.提取原理猫抓老鼠的步骤确定老鼠所在范围(水管内)取中点(刀砍)判断身处哪段即缩小捕鼠范围判断管长是否接近老鼠的身长捕获老鼠发现老鼠B启发?曲径通幽灵感获取
?想一想1.确定鼠所在大致范围5.类比迁移一路楼台直达山巅
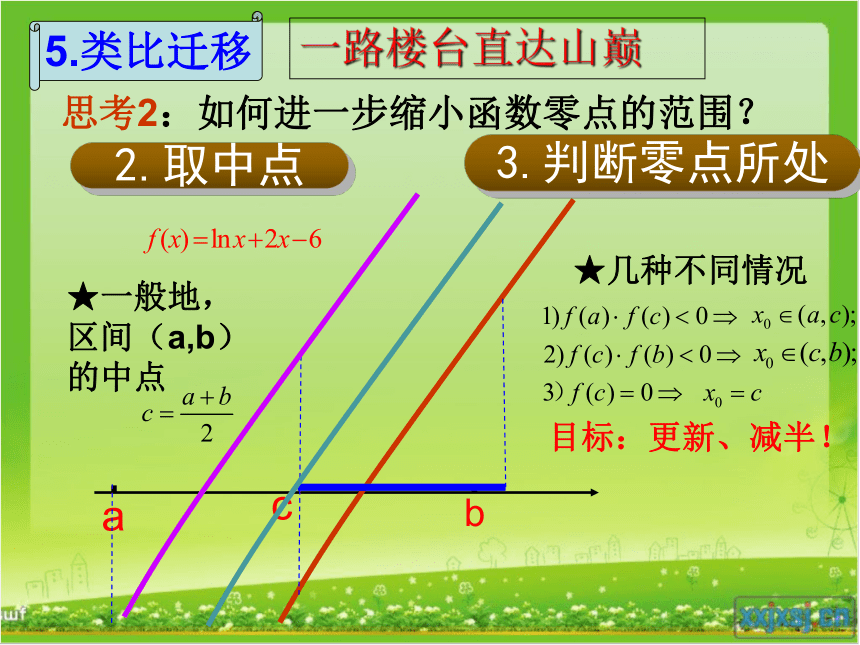
1.确定解所在大致范围5.类比迁移一路楼台直达山巅 思考1:如何确定函数
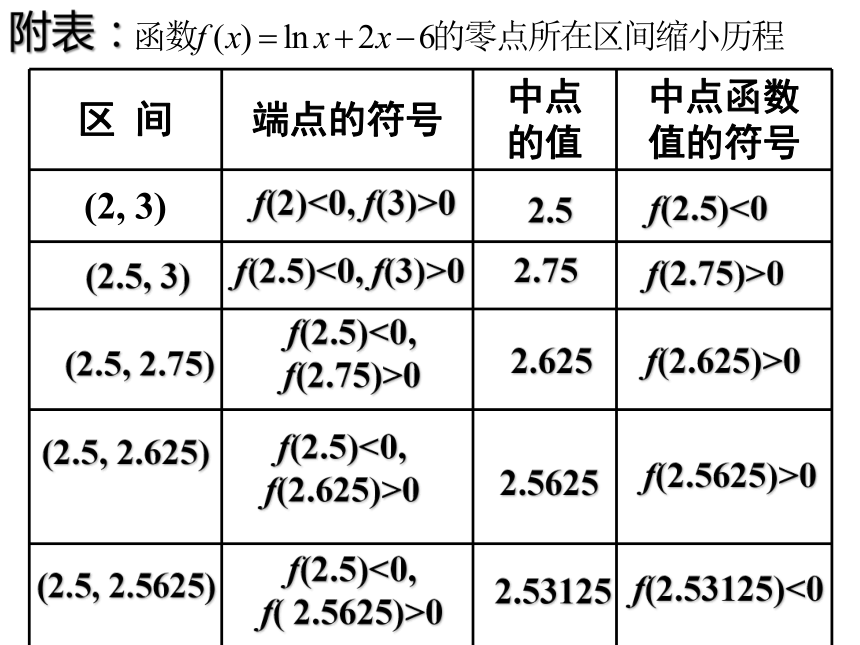
零点所处的初始区间? 思考2:如何进一步缩小函数零点的范围? 2.取中点3.判断零点所处★一般地,区间(a,b)的中点5.类比迁移一路楼台直达山巅★几种不同情况目标:更新、减半!f(2)<0, f(3)>02.5f(2.5)<0(2.5, 3)f(2.5)<0, f(3)>02.75f(2.75)>0(2.5, 2.75)f(2.5)<0,
f(2.75)>02.625f(2.625)>0(2.5, 2.625)f(2.5)<0, f(2.625)>02.5625f(2.5625)>0(2.5, 2.5625)f(2.5)<0,
f( 2.5625)>02.53125f(2.53125)<0附表:附表:思考3:如何设置停止标志?4.判断管长是否接近老鼠的身长ε思考4:停止时,从简洁性的角度,你会选择区间内哪个数作为近似值?可取当前区间(a,b)的端点b。5.类比迁移一路楼台直通山巅例1 根据下表计算函数 在区间(2,3)内精确度为0.01的零点近似值? 解:观察知区间长0.007813<精确度0.01,所以x=2.5390625为函数
f(x)=lnx+2x-6零点的近似值。 取2.539行吗?例1 根据下表计算函数 在区间(2,3)内精确度为0.01的零点近似值? 解:观察知区间长0.007813<精确度0.01,所以x=2.5390625为函数
f(x)=lnx+2x-6零点的近似值。 取得此解共减半
了几次?列式?例1 根据下表计算函数 在区间(2,3)内精确度为0.01的零点近似值? 二分法的定义:想一想?用二分法求函数零点近似值的
步骤是什么?
概念形成算 分判 定6.揭示规律总结归纳显山露水例2、已知函数f(x)的图象如图所示,其中零点的个数与可以用二分法求零点的个数分别为( )A.4,4 B.3,4 C.4,2 D.4,37.概念辨析x2x3x4Cx1重温:二分法求函数零点的条件是什么? 1、函数y=f (x)在[a,b]上连续不断;2、 y=f (x)满足 f (a)f (b)<0.是非曲直感悟真谛变式.若单调函数y=f(x)的一个零点同时在区间(0,16),(0,8),(0,4),(0,2)内, 则下列命题正确的是( )A.函数f(x)在区间(0,1)内有零点;
B.函数f(x)在区间(0,1)或(1,2)内有零点;
C.函数f(x)在区间(2,16)内无零点;
D.函数f(x)在区间(1,16)内无零点;C7.概念辨析是非曲直感悟真谛解:因为f(x)在R内是连续不断的增函数,又因为f(1)·f(2)<0,所以 f(x)= 2x+3x-7有唯一的零点x0∈(1,2).例3.利用计算器,求函数 的零点近似值.(精确度0.1)8.方法体验第二步:用二分法求零点近似值.第一步:确定零点的大致范围.小组合作:一人按计算器,一人记录若“精确到0.1”?第三步:根据精确度要求写出结果.答案为1.4一叶融雪知必躬行变式.函数g(x)=2x+x与h(x)=7-2x的交点横坐标的近似值(精确到0.1)为( )
A. 1.2 B. 1.3 C. 1.4 D. 1.5C例3. 求函数 的零点近似值.(精确度0.1)8.方法体验一叶融雪知必躬行 例4. 在一个风雨交加的夜里,从某水库闸房到防洪指挥部的电话线路发生了故障。这是一条数十公里长的线路,均匀分布着200根电线杆,如何迅速查出故障所在?(将故障点确定在1~2根电线杆附近)
???????
???????9.方法迁移巧用妙施更上层楼200方案一:从第一根电线杆开始,一段段短路测试,最多可能检查200次方案二:采用二分法原理0100150可视为在区间(0,200)上找寻零点,精确度为1建构求零点近似值的模型 例4. 在一个风雨夜,从某水库闸房到防洪指挥部的电话线路发生了故障。这是一条数十公里长的线路,均匀分布着200根电线杆,如何迅速查出故障所在?(将故障点确定在1~2根电线杆附近)
???????
???????x设电杆分布在(1,0),(2,0)……(200,0)需要几次?9.方法迁移巧用妙施更上层楼
转化思想逼近思想数形结合1.定解所在的区间3. 分解所在的区间2.算端点的函数符号用二分法求
方程的近似解算法思想4. 判区间长度是否达到精确度数学
源于生活数学
用于生活10.反思总结联知编网谱写华章布置作业 自我检验 创优练习 28 作业一作业二寻找生活中的实例,用二分法研究(研究性课题) 易水寒江雪敬奉
近似解人教A版 高中数学 必修1定理定理回眸知能并重1.复习重温——零点的存在性问题——零点的个数问题思考:如何确定零点的取值?连续不断的一条曲线,有且仅有一个
问题:你会求下列方程的解吗? (1) (3) 2.初步探究解法再现 类型梳理(2)求根公式试根法无法求出精确解探测仪长斧《猫和老鼠》
之机器猫节选3.情境再现另辟蹊径策略探求4.提取原理猫抓老鼠的步骤确定老鼠所在范围(水管内)取中点(刀砍)判断身处哪段即缩小捕鼠范围判断管长是否接近老鼠的身长捕获老鼠发现老鼠B启发?曲径通幽灵感获取
?想一想1.确定鼠所在大致范围5.类比迁移一路楼台直达山巅
1.确定解所在大致范围5.类比迁移一路楼台直达山巅 思考1:如何确定函数
零点所处的初始区间? 思考2:如何进一步缩小函数零点的范围? 2.取中点3.判断零点所处★一般地,区间(a,b)的中点5.类比迁移一路楼台直达山巅★几种不同情况目标:更新、减半!f(2)<0, f(3)>02.5f(2.5)<0(2.5, 3)f(2.5)<0, f(3)>02.75f(2.75)>0(2.5, 2.75)f(2.5)<0,
f(2.75)>02.625f(2.625)>0(2.5, 2.625)f(2.5)<0, f(2.625)>02.5625f(2.5625)>0(2.5, 2.5625)f(2.5)<0,
f( 2.5625)>02.53125f(2.53125)<0附表:附表:思考3:如何设置停止标志?4.判断管长是否接近老鼠的身长ε思考4:停止时,从简洁性的角度,你会选择区间内哪个数作为近似值?可取当前区间(a,b)的端点b。5.类比迁移一路楼台直通山巅例1 根据下表计算函数 在区间(2,3)内精确度为0.01的零点近似值? 解:观察知区间长0.007813<精确度0.01,所以x=2.5390625为函数
f(x)=lnx+2x-6零点的近似值。 取2.539行吗?例1 根据下表计算函数 在区间(2,3)内精确度为0.01的零点近似值? 解:观察知区间长0.007813<精确度0.01,所以x=2.5390625为函数
f(x)=lnx+2x-6零点的近似值。 取得此解共减半
了几次?列式?例1 根据下表计算函数 在区间(2,3)内精确度为0.01的零点近似值? 二分法的定义:想一想?用二分法求函数零点近似值的
步骤是什么?
概念形成算 分判 定6.揭示规律总结归纳显山露水例2、已知函数f(x)的图象如图所示,其中零点的个数与可以用二分法求零点的个数分别为( )A.4,4 B.3,4 C.4,2 D.4,37.概念辨析x2x3x4Cx1重温:二分法求函数零点的条件是什么? 1、函数y=f (x)在[a,b]上连续不断;2、 y=f (x)满足 f (a)f (b)<0.是非曲直感悟真谛变式.若单调函数y=f(x)的一个零点同时在区间(0,16),(0,8),(0,4),(0,2)内, 则下列命题正确的是( )A.函数f(x)在区间(0,1)内有零点;
B.函数f(x)在区间(0,1)或(1,2)内有零点;
C.函数f(x)在区间(2,16)内无零点;
D.函数f(x)在区间(1,16)内无零点;C7.概念辨析是非曲直感悟真谛解:因为f(x)在R内是连续不断的增函数,又因为f(1)·f(2)<0,所以 f(x)= 2x+3x-7有唯一的零点x0∈(1,2).例3.利用计算器,求函数 的零点近似值.(精确度0.1)8.方法体验第二步:用二分法求零点近似值.第一步:确定零点的大致范围.小组合作:一人按计算器,一人记录若“精确到0.1”?第三步:根据精确度要求写出结果.答案为1.4一叶融雪知必躬行变式.函数g(x)=2x+x与h(x)=7-2x的交点横坐标的近似值(精确到0.1)为( )
A. 1.2 B. 1.3 C. 1.4 D. 1.5C例3. 求函数 的零点近似值.(精确度0.1)8.方法体验一叶融雪知必躬行 例4. 在一个风雨交加的夜里,从某水库闸房到防洪指挥部的电话线路发生了故障。这是一条数十公里长的线路,均匀分布着200根电线杆,如何迅速查出故障所在?(将故障点确定在1~2根电线杆附近)
???????
???????9.方法迁移巧用妙施更上层楼200方案一:从第一根电线杆开始,一段段短路测试,最多可能检查200次方案二:采用二分法原理0100150可视为在区间(0,200)上找寻零点,精确度为1建构求零点近似值的模型 例4. 在一个风雨夜,从某水库闸房到防洪指挥部的电话线路发生了故障。这是一条数十公里长的线路,均匀分布着200根电线杆,如何迅速查出故障所在?(将故障点确定在1~2根电线杆附近)
???????
???????x设电杆分布在(1,0),(2,0)……(200,0)需要几次?9.方法迁移巧用妙施更上层楼
转化思想逼近思想数形结合1.定解所在的区间3. 分解所在的区间2.算端点的函数符号用二分法求
方程的近似解算法思想4. 判区间长度是否达到精确度数学
源于生活数学
用于生活10.反思总结联知编网谱写华章布置作业 自我检验 创优练习 28 作业一作业二寻找生活中的实例,用二分法研究(研究性课题) 易水寒江雪敬奉
