1.1菱形的性质与判定 同步练习(含答案) 2024-2025学年北师大版数学九年级上册
文档属性
| 名称 | 1.1菱形的性质与判定 同步练习(含答案) 2024-2025学年北师大版数学九年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 199.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-10 09:23:30 | ||
图片预览

文档简介
1.1菱形的性质与判定 同步练习 2024-2025学年北师大版数学九年级上册
学校:___________姓名:___________班级:____________
一、选择题
1.菱形具有而一般平行四边形不具有的性质是( )
A. 对边相等 B. 对角相等 C. 对角线互相平分 D. 对角线互相垂直
2.如图,已知四边形的对角线互相垂直,如果适当添加一个条件,就能判定该四边形是菱形,那么这个条件可以是.
A. B.
C. D. ,互相平分
3.一个菱形的两条对角线的长分别是和,则这个菱形的面积为 ( )
A. B. C. D.
4.如图,在菱形中,连接,,若,则的度数为 ( )
A. B. C. D.
5.如图,菱形的顶点坐标为,顶点的坐标为( )
A. B. C. D.
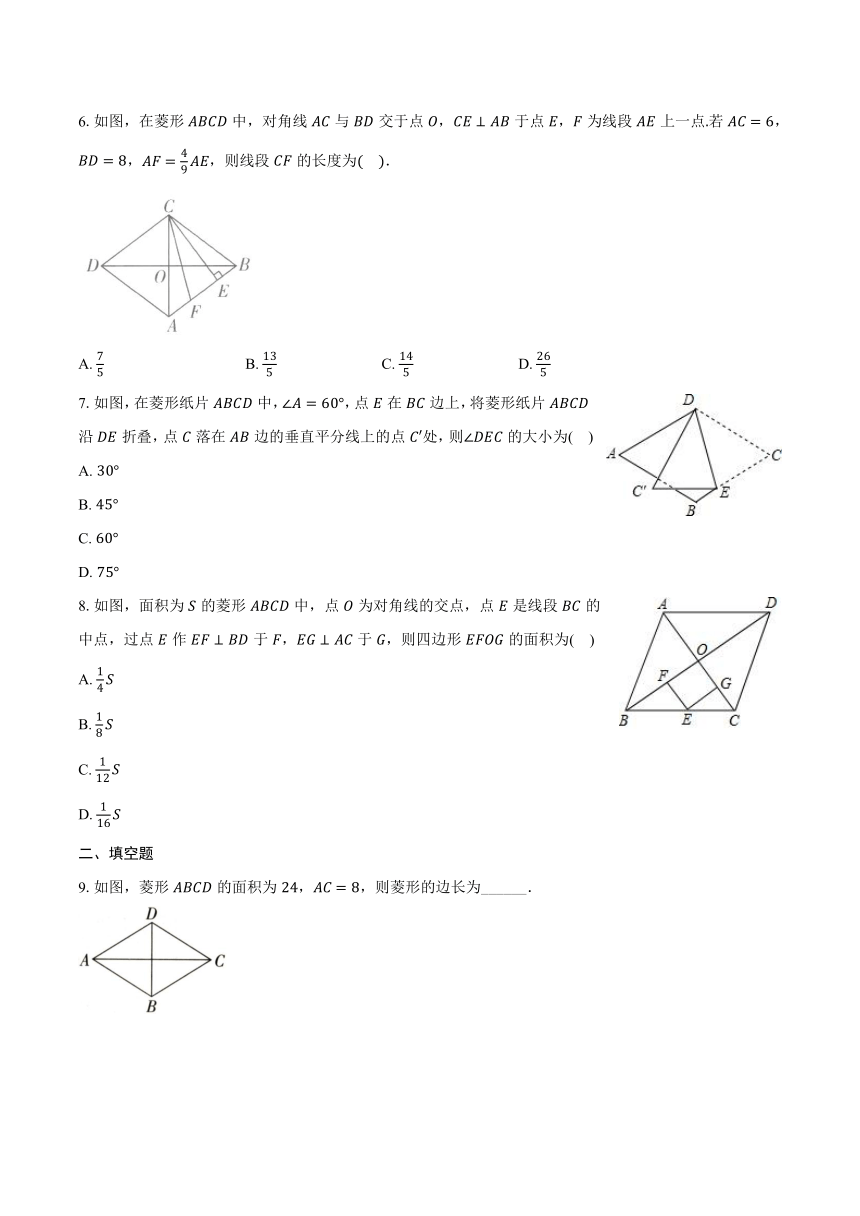
6.如图,在菱形中,对角线与交于点,于点,为线段上一点若,,,则线段的长度为 .
A. B. C. D.
7.如图,在菱形纸片中,,点在边上,将菱形纸片沿折叠,点落在边的垂直平分线上的点处,则的大小为( )
A.
B.
C.
D.
8.如图,面积为的菱形中,点为对角线的交点,点是线段的中点,过点作于,于,则四边形的面积为( )
A.
B.
C.
D.
二、填空题
9.如图,菱形的面积为,,则菱形的边长为______.
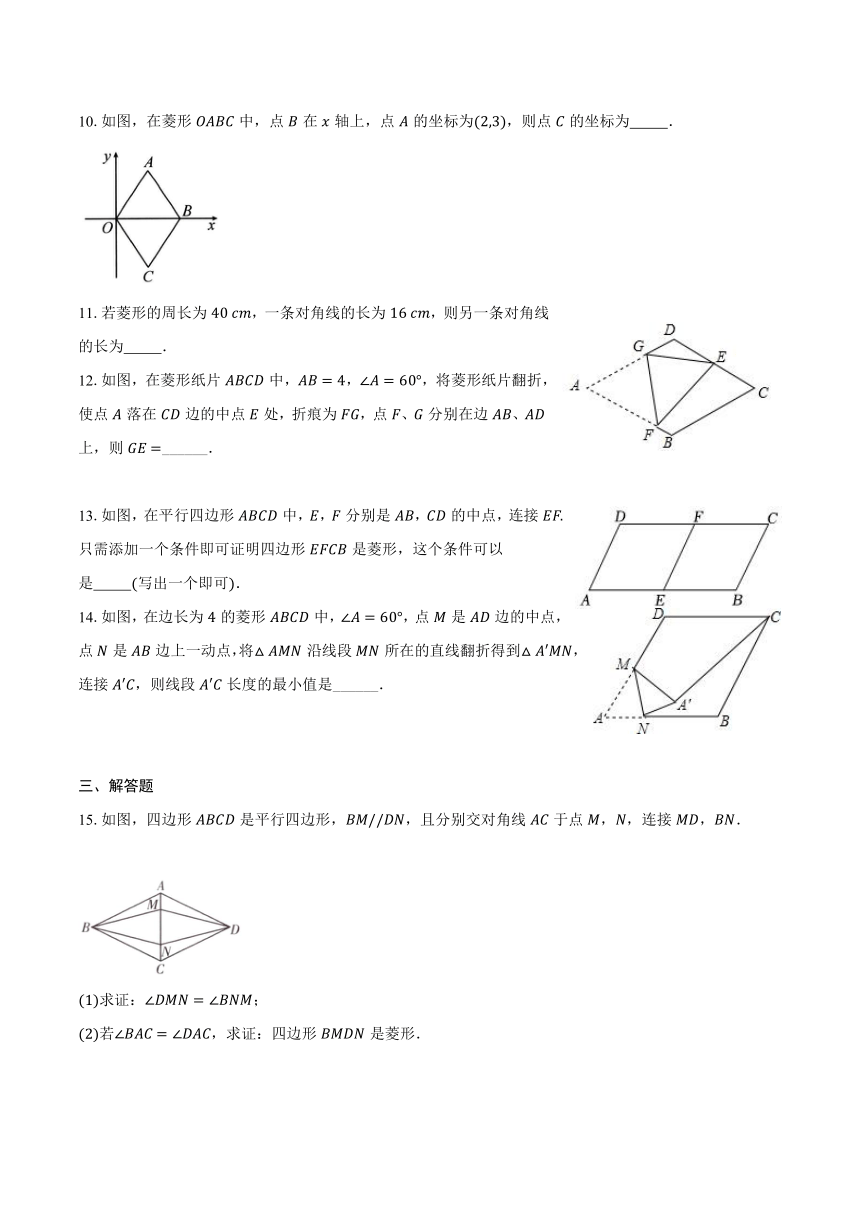
10.如图,在菱形中,点在轴上,点的坐标为,则点的坐标为 .
11.若菱形的周长为,一条对角线的长为,则另一条对角线的长为 .
12.如图,在菱形纸片中,,,将菱形纸片翻折,使点落在边的中点处,折痕为,点、分别在边、上,则______.
13.如图,在平行四边形中,,分别是,的中点,连接只需添加一个条件即可证明四边形是菱形,这个条件可以是 写出一个即可.
14.如图,在边长为的菱形中,,点是边的中点,点是边上一动点,将沿线段所在的直线翻折得到,连接,则线段长度的最小值是______.
三、解答题
15.如图,四边形是平行四边形,,且分别交对角线于点,,连接,.
求证:;
若,求证:四边形是菱形.
16.如图,在 中,点,分别是,的中点,点,在对角线上,且.
求证:≌;
请添加一个条件,使四边形是菱形,并证明.
17.如图,在菱形中,是的中点请仅用无刻度直尺完成下列作图,
在图中,过点作的平行线,与交于点.
在图中,作线段的垂直平分线,垂足为点.
18.如图,在中,已知为边上的中线,以,为邻边作,连接,请你从下面方框中选择一个补充条件,使四边形是菱形.
可选条件:
你选择的补充条件是________;填序号
在的条件下,求证:四边形是菱形.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.答案不唯一
14.
15.【小题】
连接,交于点.
四边形是平行四边形,.
,又,,
,四边形为平行四边形,
,.
【小题】
四边形是平行四边形,
,.
,,
,平行四边形是菱形,
,,平行四边形是菱形.
16.证明:在平行四边形中,,,
,
点,分别是,的中点,
,
在与中,,
解:答案不唯一证明如下:
,
,,
,
,
,
四边形是平行四边形,
四边形是菱形.
17.解:如图中,直线即为所求;
如图中,直线即为所求.
【解析】连接,检验点,作直线交于点,直线即为所求;
连接,交于点,连接交于点,作直线交于点,直线即为所求证明是等边三角形,再根据三条中线交于一点解决问题.
本题考查作图复杂作图,菱形的性质,全等三角形的判定和性质,线段的垂直平分线的性质等知识,解题的关键是理解题意,灵活运用所学知识解决问题.
18.解:或答案不唯一;
选择的补充条件是或答案不唯一;
选,
证明:为边上的中线,
,
在 中,,,
,,
四边形是平行四边形,
,
四边形是菱形.
或选,
证明:为边上的中线,
,
在 中,,,
,,
四边形是平行四边形,
,
四边形是菱形.
学校:___________姓名:___________班级:____________
一、选择题
1.菱形具有而一般平行四边形不具有的性质是( )
A. 对边相等 B. 对角相等 C. 对角线互相平分 D. 对角线互相垂直
2.如图,已知四边形的对角线互相垂直,如果适当添加一个条件,就能判定该四边形是菱形,那么这个条件可以是.
A. B.
C. D. ,互相平分
3.一个菱形的两条对角线的长分别是和,则这个菱形的面积为 ( )
A. B. C. D.
4.如图,在菱形中,连接,,若,则的度数为 ( )
A. B. C. D.
5.如图,菱形的顶点坐标为,顶点的坐标为( )
A. B. C. D.
6.如图,在菱形中,对角线与交于点,于点,为线段上一点若,,,则线段的长度为 .
A. B. C. D.
7.如图,在菱形纸片中,,点在边上,将菱形纸片沿折叠,点落在边的垂直平分线上的点处,则的大小为( )
A.
B.
C.
D.
8.如图,面积为的菱形中,点为对角线的交点,点是线段的中点,过点作于,于,则四边形的面积为( )
A.
B.
C.
D.
二、填空题
9.如图,菱形的面积为,,则菱形的边长为______.
10.如图,在菱形中,点在轴上,点的坐标为,则点的坐标为 .
11.若菱形的周长为,一条对角线的长为,则另一条对角线的长为 .
12.如图,在菱形纸片中,,,将菱形纸片翻折,使点落在边的中点处,折痕为,点、分别在边、上,则______.
13.如图,在平行四边形中,,分别是,的中点,连接只需添加一个条件即可证明四边形是菱形,这个条件可以是 写出一个即可.
14.如图,在边长为的菱形中,,点是边的中点,点是边上一动点,将沿线段所在的直线翻折得到,连接,则线段长度的最小值是______.
三、解答题
15.如图,四边形是平行四边形,,且分别交对角线于点,,连接,.
求证:;
若,求证:四边形是菱形.
16.如图,在 中,点,分别是,的中点,点,在对角线上,且.
求证:≌;
请添加一个条件,使四边形是菱形,并证明.
17.如图,在菱形中,是的中点请仅用无刻度直尺完成下列作图,
在图中,过点作的平行线,与交于点.
在图中,作线段的垂直平分线,垂足为点.
18.如图,在中,已知为边上的中线,以,为邻边作,连接,请你从下面方框中选择一个补充条件,使四边形是菱形.
可选条件:
你选择的补充条件是________;填序号
在的条件下,求证:四边形是菱形.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.答案不唯一
14.
15.【小题】
连接,交于点.
四边形是平行四边形,.
,又,,
,四边形为平行四边形,
,.
【小题】
四边形是平行四边形,
,.
,,
,平行四边形是菱形,
,,平行四边形是菱形.
16.证明:在平行四边形中,,,
,
点,分别是,的中点,
,
在与中,,
解:答案不唯一证明如下:
,
,,
,
,
,
四边形是平行四边形,
四边形是菱形.
17.解:如图中,直线即为所求;
如图中,直线即为所求.
【解析】连接,检验点,作直线交于点,直线即为所求;
连接,交于点,连接交于点,作直线交于点,直线即为所求证明是等边三角形,再根据三条中线交于一点解决问题.
本题考查作图复杂作图,菱形的性质,全等三角形的判定和性质,线段的垂直平分线的性质等知识,解题的关键是理解题意,灵活运用所学知识解决问题.
18.解:或答案不唯一;
选择的补充条件是或答案不唯一;
选,
证明:为边上的中线,
,
在 中,,,
,,
四边形是平行四边形,
,
四边形是菱形.
或选,
证明:为边上的中线,
,
在 中,,,
,,
四边形是平行四边形,
,
四边形是菱形.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
