(期末培优卷)期末核心素养培优卷-2024-2025学年五年级下学期数学苏教版(含解析)
文档属性
| 名称 | (期末培优卷)期末核心素养培优卷-2024-2025学年五年级下学期数学苏教版(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 506.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-10 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
2024-2025学年五年级下学期数学期末核心素养培优卷
考试时间:90分钟;试卷总分:100分;
学校: 班级: 姓名: 成绩:
注意事项:
答题前填写好自己的姓名、班级、考号等信息。
请将答案正确填写在答题区域,注意书写工整,格式正确,卷面整洁。
一、选择题。(每题1分,共8分)
1.同学们去社区做好事,每组6人或9人,都正好不多也不少。去社区做好事的同学至少有( )人。
A.3 B.18 C.54
2.把一张半径4厘米的圆形纸片对折两次,得到一个扇形,这个扇形的周长是( )厘米。
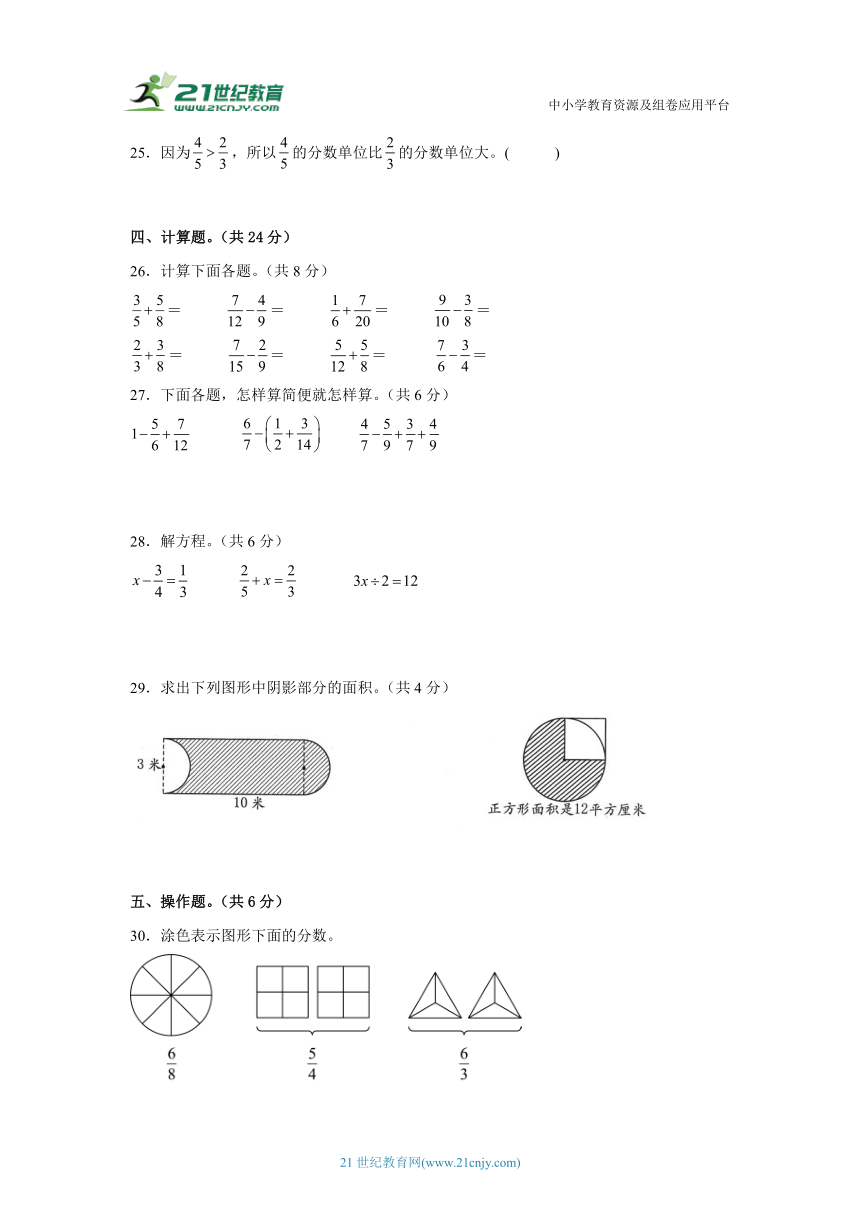
A.π+4 B.π+8 C.2π+4 D.2π+8
3.一根彩带,第一次用去米,第二次用去全长的。两次用去的相比,( )。
A.第一次多 B.第二次多 C.一样多 D.无法确定
4.周长较大的圆的面积( )周长较小的圆的面积。
A.大于 B.小于 C.大于、小于、等于都有可能
5.如图,在直径20厘米的半圆内剪去一个直径10厘米的小圆,剩下部分和剪去部分的面积相比,( )。
A.剩下部分的面积大 B.剪去部分的面积大 C.同样大 D.无法确定
6.a、b是两个相邻自然数(a、b都不为0),a和b的最大公因数是( ),最小公倍数是( )。
A.1;ab B.ab;b C.a;ab D.b;b
7.下面的式子中,( )是方程。
A. B. C.
8.根据甲、乙两人在体育社团连续五次测试得分的统计图(如图)判断,下面结论错误的是( )。
A.两人的得分都呈上升趋势
B.乙的测试得分整体提升得比甲快
C.第二次测试中,甲的得分比乙的得分高13分
D.下次测试中,乙的得分一定比甲高
二、填空题。(每空1分,共27分)
9.用3米长的绳子正好做了2根同样的跳绳。每根跳绳的长度是原来绳长的,每根跳绳长米。
10.白棋每次走4格,黑棋每次走6格。两种棋都能走到的方格有( )个。
11.分数的分母加上12,要使分数的大小不变,分子应加上( );的分子乘4,要使分数的大小不变,分母可以( )。
12.的分数单位是,它有( )个这样的分数单位,再去掉( )个这样的分数单位就是最小的质数。
13.从一个长6分米,宽4分米的长方形木板上锯下一个最大的圆,圆的周长是( )分米,圆的面积是( )平方分米。
14.如图,把一个直径2厘米的圆分成若干等份后拼成了一个近似的长方形,这个近似长方形的周长是( )厘米。
15.甲、乙两人到图书馆去借书,甲每4天去一次,乙每5天去一次,如果7月12日他们两人在图书馆相遇,那么他们下一次同时去图书馆借书是( )月( )日。
16.m、n都是非0自然数,且,m、n的最大公因数是( ),最小公倍数是( )。
17.=( )÷10=40÷( )==( )(填小数)。
18.生活中的数学,110是报警电话,120是急救电话,119是火警电话,12315是消费申诉举报电话。在这些电话号码中,2的倍数有( ),3的倍数有( ),同时是2、3、5的倍数有( )。
19.下图是推导圆面积计算公式的一种方法,把一个草绳编织的圆形茶杯垫片沿半径剪开,打开后得到一个近似的三角形。
仔细观察:三角形的底相当于圆的( ),高相当于圆的( )。如果圆的半径为r,根据三角形的面积=底×高÷2,可以推出圆的面积计算公式为S=( )。
20.一个三位数37□,当它既是2的倍数又是5的倍数时,□里填( )。当它是3的倍数时,□里可以填的数是( )。
三、判断题。(每题1分,共5分)
21.如果a是b的2倍(b≠0),那么a,b的最大公因数是a,最小公倍数是b。( )
22.为了统计商场去年各月电脑的销售数量变化情况,应选用折线统计图。( )
23.圆的直径扩大3倍,它的周长也扩大3倍,面积扩大6倍。( )
24.因为找一个数的因数是一对一对找的,所以一个数的因数有偶数个。( )
25.因为,所以的分数单位比的分数单位大。( )
四、计算题。(共24分)
26.计算下面各题。(共8分)
= = = =
= = = =
27.下面各题,怎样算简便就怎样算。(共6分)
28.解方程。(共6分)
29.求出下列图形中阴影部分的面积。(共4分)
五、操作题。(共6分)
30.涂色表示图形下面的分数。
六、解答题。(每题5分,共30分)
31.学校开展“清廉文化”主题教育活动,四、五年级的同学们一起去参观“史话清廉人物事迹展览”,五年级去的学生人数比四年级多。这两个年级一共去了660人, 是 的1.2倍,两个年级各去了多少人?(请将题中的信息补充完整,再列方程解答)
32.甲乙两地相距300千米,一辆快车和一辆慢车分别从甲、乙两地同时出发,相向而行,1.5小时后相遇。快车每小时行驶105千米。慢车每小时行驶多少千米?(列方程解答)
33.某小区内有一个圆形健身广场,新新和亮亮从起点开始同时反向而行,沿着广场散步,新新每分钟走90米,亮亮每分钟走110米,3分钟后他们俩相遇。这个圆形广场的面积是多少平方米?(本题π取3计算)
34.工地上有两根钢管,一根长36分米,另一根长63分米。因施工需要,把它们都锯成长度相等的小段,每段要尽可能长,且没有剩余。每段钢管长多少分米?一共能锯成多少段?
35.为了庆祝中华人民共和国成立75周年,人民广场用蝴蝶兰和一串红摆成了庆国庆的图案,已知蝴蝶兰的盆数是一串红的3.4倍。蝴蝶兰比一串红多240盆,蝴蝶兰和一串红各有多少盆?(列方程解答)
36.纵桨飞舟,粽叶飘香,赛龙舟是端午佳节的重要组成部分,是中华文化的传承。为弘扬中华传统文化,彰显“水润之城”的城市内涵,6月10日,有38支来自各县区的代表队在市区古黄河金鹰段举办2024宿迁端午龙舟赛。赛道上原来有21个浮漂(首尾各有一个),每两个浮漂之间距离是15米。现在每两个浮漂之间距离改为20米,不需要重新替换的浮漂有多少个?
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案及试题解析
1.B
【分析】根据每组6人或9人,都正好不多也不少,可知去社区做好事的同学数既是6的倍数也是9的倍数,即是6和9的公倍数,要求至少就是求6和9的最小公倍数,据此解答。
【解析】6=2×3
9=3×3
所以6和9的最小公倍数是2×3×3=18。
所以去社区做好事的同学至少有18人。
故答案为:B
2.D
【分析】圆形纸片对折两次,相当于把360°的圆心角平均分成4份,得到的扇形圆心角是360°÷4=90°,半径不变,依旧是圆形纸片的半径4厘米,扇形弧长就是圆周长的;最后扇形的周长就等于弧长加上两条半径长度。
【解析】2π×4÷4=2π
2π+4+4=2π+8
所以这个扇形的周长是(2π+8)厘米。
故答案为:D
3.D
【分析】根据题意可知,绳子的长度不能确定, 假设绳子长1米或绳子长3米,求出两次用去绳子的长度,再进行判断
【解析】假设绳子长1米,第一次用去米,第二次用去全长的,即1÷3=米。
两次用去的长度相等。
假设绳子长3米,第一次用去米,第二次用去全长的,即3÷3=1米。
米<1米
第二次用去的多。
所以绳子的长度不能确定,无法判断两次用去的长短。
故答案为:D
4.A
【分析】假设周长较大的圆的周长是10,周长较小的圆的周长是4,根据圆的周长=2×半径,分别求出较大的圆的半径和较小的圆的半径,再根据圆的面积=×半径的平方,分别求出两个圆的面积,再进行比较即可解答。
【解析】假设周长较大的圆的周长是10,周长较小的圆的周长是4。
10÷÷2
=10÷2
=5
4÷÷2
=4÷2
=2
×=×25=25
×=×4=4
25>4
所以周长较大的圆的面积大于周长较小的圆的面积。
故答案为:A
5.C
【分析】先根据圆的面积=,分别求出半圆的面积和剪去部分小圆的面积,再用半圆的面积减去小圆的面积,求出剩下部分的面积,再比较即可。
【解析】3.14×(20÷2)2÷2
=3.14×102÷2
=3.14×100÷2
=314÷2
=157(平方厘米)
3.14×(10÷2)2
=3.14×52
=3.14×25
=78.5(平方厘米)
157-78.5=78.5(平方厘米)
所以,剩下部分和剪去部分的面积相比,同样大。
故答案为:C
6.A
【分析】a、b是两个相邻自然数,如2和3,它们是互质数;根据“两个数是互质数时,它们的最大公因数是1,最小公倍数是两数的乘积”进行解答。
公因数只有1的两个非零自然数,叫做互质数。
【解析】a、b是两个相邻自然数(a、b都不为0),则a和b是互质数,a和b的最大公因数是(1),最小公倍数是(ab)。
故答案为:A
7.B
【分析】含有未知数的等式是方程,所以方程必须满足两个条件:①含有未知数,②是等式,据此判断即可。
【解析】A.4x>2.8含有未知数,但不是等式,所以它不是方程;
B.x÷y=40含有未知数,且是等式,所以它是方程;
C.35+16=16+35是等式,但不含未知数,所以它不是方程。
故答案为:B
8.D
【分析】复式折线统计图不仅能看清数量的多少,还能通过折线的上升和下降表示2个及以上数量的增减变化情况,折线向上走势越陡成绩增长得越快,折线向上走势越缓成绩增长得越慢,实线表示甲的成绩变化情况,虚线表示乙的成绩变化情况,总体来讲两人的成绩都呈上升趋势,乙的成绩整体比甲的成绩增长得快一些,根据统计图中的数据求出两人在第二次测试中的成绩差,根据折线的走势可以预测下次两人的成绩,但“乙的得分比甲高”并不一定会发生,属于“可能”事件,不能用“一定”描述,据此解答。
【解析】A.观察复式折线统计图可知,两人的得分都呈上升趋势;
B.复式折线统计图中,表示乙的得分情况的折线整体上比表示甲的得分情况的折线更陡一些,所以乙的测试得分整体提升得比甲快;
C.85-72=13(分),所以在第二次测试中,甲的得分比乙的得分高13分;
D.分析可知,下次测试中,乙的得分比甲高属于“可能”事件,不能用“一定”描述,可以说“乙的得分可能比甲高”。
故答案为:D
9.;
【分析】由题意可知,3米长的绳子看作单位“1”,把它平均分成2份,求每份是它的几分之几,用1除以2可解答;求每根跳绳的长度就是把3米长的绳子平均分成2份,求每份的长度,用3除以2计算即可。
【解析】
(米)
用3米长的绳子正好做了2根同样的跳绳。每根跳绳的长度是原来绳长的,每根跳绳长米。
10.2
【分析】由于白棋每次走4格,黑棋每次走6格,由于问两种棋都能走到的方格,就是求4和6的公倍数,先把4和6分解质因数,把公有质因数与独有质因数相乘求出最小公倍数,之后再把最小公倍数分别乘1、2、3、找出31以内的公倍数即可。
【解析】4=2×2
6=2×3
2×2×3=12
12×1=12
12×2=24
所以两种棋都能走到的方格有2个。
11.10 乘4
【分析】分数的基本性质:分数的分子和分母同时乘或除以相同的数(0除外),分数的大小不变。
(1)分数的分母加上12得18,相当于分母乘3,要使分数的大小不变,分子也要乘3,用分子5乘3后再减去5,就是分子应加上的数。
(2)的分子乘4,要使分数的大小不变,分母也要乘4,或用分母6乘4后再减去6,就是分母可以加上的数;
【解析】(1)分母相当于乘:
(6+12)÷6
=18÷6
=3
分子也要乘3或加上:
5×3-5
=15-5
=10
分数的分母加上12,要使分数的大小不变,分子应加上10;
(2)分子乘4,分母也要乘4或加上:
6×4-6
=24-6
=18
的分子乘4,要使分数的大小不变,分母可以乘4(或加上18)。
12.;21;5
【分析】把单位“1”平均分成若干份,表示其中一份的数叫分数单位。
把化成假分数,假分数的分子是几,就有几个这样的分数单位;
最小的质数是2,把2化成分母为8而大小不变的假分数,再看分子与的分子相差几,就是再去掉几个这样的分数单位就是最小的质数。
【解析】=,它有21个;
最小的质数为2,2=,它有16个;
21-16=5,再去掉5个这样的分数单位就是最小的质数。
填空如下:
的分数单位是(),它有(21)个这样的分数单位,再去掉(5)个这样的分数单位就是最小的质数。
13.12.56 12.56
【分析】从一个长方形木板上锯下一个最大的圆,这个圆的直径等于长方形的宽,即圆的直径是4分米。圆的周长=πd,圆的面积=πr2,据此解答。
【解析】这个最大的圆的半径是:4÷2=2(分米)
周长:3.14×4=12.56(分米)
面积:3.14×22
=3.14×4
=12.56(平方分米)
则圆的周长是12.56分米,圆的面积是12.56平方分米。
14.8.28
【分析】根据圆面积公式的推导过程可知,把一个圆剪拼成一个近似长方形,拼成的长方形的长等于圆周长的一半,长方形的宽等于圆的半径,拼成的长方形的周长比圆的周长增加了两条半径的长度(也就是一条直径的长度),根据圆的周长公式:周长=π×直径,代入数据,求出圆的周长,进而求出长方形的周长。
【解析】3.14×2+2
=6.28+2
=8.28(厘米)
这个近似长方形的周长是8.28厘米。
15.8 1
【分析】求两个数的最小公倍数,如果这两个数互质,则这两个数的最小公倍数是这两个数的乘积;根据题意,先求出4和5的最小公倍数,已知7月12日他们两人在图书馆相遇,所以7月12日再加上4和5的最小公倍数,算出来即为两人下次同时去了图书馆的时间,已知7月份有31天,据此推断出具体时间,据此解答。
【解析】4和5的最小公倍数:4×5=20
12+20=32(天)
32-31=1(天)
他们下一次同时去图书馆借书是8月1日。
16.m n
【分析】两个数的公有质因数的连乘积,就是两个数的最大公因数;两个数的公有质因数与每一个数的独有质因数的连乘积,就是两个数的最小公倍数;如果两个数成倍数关系,最大公因数为较小的那个数,最小公倍数为较大的那个数。
【解析】m、n都是非0自然数,m÷n=,
则m=n,n=2m,n÷m=2,n和m成倍数关系,最大公因数是m,最小公倍数是n。
m、n都是非0自然数,且m÷n=,m、n的最大公因数是m,最小公倍数是n。
17.8;50;24;0.8
【分析】根据分数的基本性质,将的分子和分母同时乘2,可得=;将的分子和分母同时乘10,可得=;将的分子和分母同时乘6,可得=;根据分数与除法的关系,可得=8÷10,=40÷50;分数化成小数:用分子除以分母,按照除数是整数的小数除法进行计算,据此可得=0.8。
【解析】根据分析可知,=8÷10=40÷50==0.8。
18.110;120 120;12315 120
【分析】2的倍数特征:个位上的数字是0、2、4、6、8的数是2的倍数。5的倍数特征:个位上的数字是0或5的数是5的倍数。3的倍数的特征:一个数各个数位上的数字的和是3的倍数,这个数就是3的倍数。2,3,5的倍数的特征:个位上的数字是0,各个数位上的数字的和是3的倍数的数。据此解答。
【解析】2的倍数有:110,120;
110;1+1+0=2;2不能被3整除,110不是3的倍数;
120;1+2+0=3;3能被3整除,120是3的倍数;
119;1+1+9=11;11不能被3整除,119不是3的倍数;
12315;1+2+3+1+5=12;12能被3整除,12315是3的倍数;
3的倍数有:120,12315;
同时是2,3,5的倍数有120。
活中的数学,110是报警电话,120是急救电话,119是火警电话,12315是消费申诉举报电话。在这些电话号码中,2的倍数有110,120,3的倍数有120,12315,同时是2、3、5的倍数有120。
19.周长 半径 πr2
【分析】根据题意,把一个草绳编织的圆形茶杯垫片沿半径剪开,打开后得到一个近似的三角形,那么圆的面积等于这个三角形的面积;
从图中可知,三角形的底相当于圆的周长2πr,高相当于圆的半径r;根据三角形的面积=底×高÷2,据此把含有字母的式子代入三角形的面积公式中,推导出圆的面积公式。
【解析】圆的面积=三角形的面积
三角形的面积=底×高÷2
圆的面积=2πr×r÷2=πr2
仔细观察:三角形的底相当于圆的周长,高相当于圆的半径。如果圆的半径为r,根据三角形的面积=底×高÷2,可以推出圆的面积计算公式为S=πr2。
20.0 2、5或8
【分析】2的倍数特征:个位上是0、2、4、6、8的数。
5的倍数特征:个位上是0或5的数。
2、5的倍数特征:个位上是0的数。
3的倍数特征:一个数各位上的数的和是3的倍数,这个数就是3的倍数。
【解析】个位数字是0,这样的数既是2的倍数又是5的倍数,370既是2的倍数又是5的倍数;
3+7+2=12,12是3的倍数,372是3的倍数;
3+7+5=15,15是3的倍数,375是3的倍数;
3+7+8=18,18是3的倍数,378是3的倍数。
一个三位数37□,当它既是2的倍数又是5的倍数时,□里填0。当它是3的倍数时,□里可以填的数是2、5或8。
21.×
【分析】两数成倍数关系,最大公因数是较小数,最小公倍数是较大数,据此分析。
【解析】如果a是b的2倍(b≠0),那么a,b的最大公因数是b,最小公倍数是a,原题说法错误。
故答案为:×
22.√
【分析】条形统计图能清楚地表示出数量的多少;
折线统计图不仅能表示数量的多少,还能表示数量的增减变化情况;
扇形统计图表示部分与整体之间的关系;据此解答。
【解析】为了统计商场去年各月电脑的销售数量变化情况,应选用折线统计图。
原题干说法正确。
故答案为:√
23.×
【分析】设直径为2,扩大后的直径为2×3=6;根据圆的周长公式:周长=π×直径;面积=π×半径2,分别求出原来圆的周长和面积,扩大后圆的周长和面积,再用扩大后圆的周长÷原来圆的周长,扩大后圆的面积÷原来圆的面积,分别求出它的周长扩大到原来的多少倍,面积扩大到原来的多少倍,进而解答。
【解析】设圆的直径为2;扩大后圆的直径为2×3=6。
(π×6)÷(π×2)
=(6π)÷(2π)
=3
[π×(6÷2)2]÷[π×(2÷2)2]
=[π×32]÷[π×12]
=[π×9]÷[π×1]
=9π÷π
=9
圆的直径扩大3倍,它的周长也扩大3倍,面积扩大9倍。
原题干说法错误。
故答案为:×
24.×
【分析】虽然找一个数的因数是一对一对找的,但是这一对有时相同,算一个。比如9的因数有1、3、9三个数,即9的因数的个数不是偶数个。据此判断即可。
【解析】由分析可知:
因为找一个数的因数是一对一对找的,所以一个数的因数有偶数个。此说法错误。
故答案为:×
25.×
【分析】首先分别判断出、的分数单位,然后根据同分子分数大小比较的方法,同分子分数分母小的分数反而大,判断出的分数单位和的分数单位的大小关系即可。
【解析】的分数单位是
的分数单位是
虽然,但是的分数单位比的分数单位小。原题说法错误。
故答案为:×
26.或;;;;
或;;或;
【解析】略
27.;;
【分析】(1)从左往右依次计算;
(2)先算括号里面的加法,再算括号外面的减法;
(3)先交换“”和“”的位置,然后根据减法的性质a-b+c=a-(b-c)把变成,再按顺序计算。
【解析】(1)
(2)
(3)
28.x=;x=;
x=8
【分析】根据等式的性质1,方程两边同时加上;
根据等式的性质1,方程两边同时减去;
方程两边同时乘2,两边再同时除以3。
【解析】x-=
解:x-+=+
x=
x=
+x=
解:+x-=-
x=
x=
3x÷2=12
解:3x÷2×2=12×2
3x=24
3x÷3=24÷3
x=8
29.30平方米;28.26平方厘米
【分析】(1)将图形中右边的半圆移动到左边的空白半圆处,则阴影部分的面积就等于长方形的面积,直接计算长方形的面积即可;
(2)根据正方形的面积是12平方厘米,可知半径的平方等于12平方厘米,然后将半径的平方代入圆的面积公式,然后再乘计算出圆的面积即可。
【解析】(1)10×3=30(平方米)
(2)3.14×12×
=37.68×
=28.26(平方厘米)
30.见详解
【分析】根据分数的意义,分数的分母表示总份数,分子表示所占的份数,据此解答。
【解析】(1)表示将一个圆平均分成8份,涂色部分占其中的6份。如图:
(2)把一个正方形平均分成4份,表示这样的1份是;表示5个,涂色部分占5份。如图:
(3)把一个三角形平均分成3份,表示这样的1份是;表示6个,涂色部分占6份。如图:
31.五年级去的学生人数;四年级去的学生人数;
四年级300人;五年级360人
【分析】因为五年级去的学生人数比四年级多,所以五年级去的人数是四年级去的人数的1.2倍。设四年级去的人数为x人,那么五年级去的人数是1.2x,根据等量关系:五年级去的人数+四年级去的人数=660人,据此列方程解答,求出四年级的人数,再用四年级人数乘1.2得到五年级人数。
【解析】解:设四年级去了x人,则五年级去了1.2x人。
(人)
答:四年级去了300人,五年级去了360人。
32.95千米
【分析】设慢车每小时行驶x千米,快车每小时行驶105千米,1.5小时行驶的距离是(105×1.5)千米,慢车1.5小时行驶的距离是:1.5x千米,两车相遇,它们行驶的距离和正好是甲乙两地的距离,甲乙两地的距离是300千米,列方程:105×1.5+1.5x=300,解方程,即可解答。
【解析】解:设慢车每小时行驶x千米。
105×1.5+1.5x=300
157.5+1.5x=300
1.5x=300-157.5
1.5x=142.5
1.5x÷1.5=142.5÷1.5
x=95
答:慢车每小时行驶95千米。
33.30000平方米
【分析】根据总路程=速度和×相遇时间,求出广场的周长,再根据圆的半径=周长÷圆周率÷2,圆的面积=圆周率×半径的平方,列式解答即可。
【解析】(90+110)×3
=200×3
=600(米)
600÷3÷2=100(米)
3×1002
=3×10000
=30000(平方米)
答:这个圆形广场的面积是30000平方米。
34.9分米;11段
【分析】已知两根钢管要把它们剪成同样长的小段,每段长要尽可能长,且没有剩余,求每段钢管长多少米,就是求36和63的最大公因数;然后分别用36和63除以它们的最大公因数,即可求出两根钢管各自剪成的段数,最后相加即可。
【解析】36=2×2×3×3
63=3×3×7
36和63的最大公因数3×3=9
36÷9+63÷9
=4+7
=11(段)
答:每段钢管长9分米,一共能锯成11段。
35.蝴蝶兰340盆;一串红100盆
【分析】根据题意,设一串红有x盆,则蝴蝶兰有3.4x盆,根据蝴蝶兰比一串红多240盆,列出方程,解方程即可。
【解析】解:设一串红有x盆,则蝴蝶兰有3.4x盆。
3.4x-x=240
2.4x=240
2.4x÷2.4=240÷2.4
x=100
3.4×100=340(盆)
答:蝴蝶兰有340盆,一串红有100盆。
36.6个
【分析】赛道上原来有21个浮漂,首尾各有一个,所以赛道总长是(21-1)个15米,即300米。现在每两个浮漂之间距离改为20米,不需要重新替换的浮漂就是15和20的公倍数,15和20的最小公倍数是60,所以不需要重新替换的浮漂有(300÷60+1)个。
【解析】21-1=20(个)
20×15=300(米)
15=3×5
20=2×2×5
所以15和20的最小公倍数是:5×3×2×2=60
300÷60+1
=5+1
=6(个)
答:不需要重新替换的浮漂有6个。
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
中小学教育资源及组卷应用平台
2024-2025学年五年级下学期数学期末核心素养培优卷
考试时间:90分钟;试卷总分:100分;
学校: 班级: 姓名: 成绩:
注意事项:
答题前填写好自己的姓名、班级、考号等信息。
请将答案正确填写在答题区域,注意书写工整,格式正确,卷面整洁。
一、选择题。(每题1分,共8分)
1.同学们去社区做好事,每组6人或9人,都正好不多也不少。去社区做好事的同学至少有( )人。
A.3 B.18 C.54
2.把一张半径4厘米的圆形纸片对折两次,得到一个扇形,这个扇形的周长是( )厘米。
A.π+4 B.π+8 C.2π+4 D.2π+8
3.一根彩带,第一次用去米,第二次用去全长的。两次用去的相比,( )。
A.第一次多 B.第二次多 C.一样多 D.无法确定
4.周长较大的圆的面积( )周长较小的圆的面积。
A.大于 B.小于 C.大于、小于、等于都有可能
5.如图,在直径20厘米的半圆内剪去一个直径10厘米的小圆,剩下部分和剪去部分的面积相比,( )。
A.剩下部分的面积大 B.剪去部分的面积大 C.同样大 D.无法确定
6.a、b是两个相邻自然数(a、b都不为0),a和b的最大公因数是( ),最小公倍数是( )。
A.1;ab B.ab;b C.a;ab D.b;b
7.下面的式子中,( )是方程。
A. B. C.
8.根据甲、乙两人在体育社团连续五次测试得分的统计图(如图)判断,下面结论错误的是( )。
A.两人的得分都呈上升趋势
B.乙的测试得分整体提升得比甲快
C.第二次测试中,甲的得分比乙的得分高13分
D.下次测试中,乙的得分一定比甲高
二、填空题。(每空1分,共27分)
9.用3米长的绳子正好做了2根同样的跳绳。每根跳绳的长度是原来绳长的,每根跳绳长米。
10.白棋每次走4格,黑棋每次走6格。两种棋都能走到的方格有( )个。
11.分数的分母加上12,要使分数的大小不变,分子应加上( );的分子乘4,要使分数的大小不变,分母可以( )。
12.的分数单位是,它有( )个这样的分数单位,再去掉( )个这样的分数单位就是最小的质数。
13.从一个长6分米,宽4分米的长方形木板上锯下一个最大的圆,圆的周长是( )分米,圆的面积是( )平方分米。
14.如图,把一个直径2厘米的圆分成若干等份后拼成了一个近似的长方形,这个近似长方形的周长是( )厘米。
15.甲、乙两人到图书馆去借书,甲每4天去一次,乙每5天去一次,如果7月12日他们两人在图书馆相遇,那么他们下一次同时去图书馆借书是( )月( )日。
16.m、n都是非0自然数,且,m、n的最大公因数是( ),最小公倍数是( )。
17.=( )÷10=40÷( )==( )(填小数)。
18.生活中的数学,110是报警电话,120是急救电话,119是火警电话,12315是消费申诉举报电话。在这些电话号码中,2的倍数有( ),3的倍数有( ),同时是2、3、5的倍数有( )。
19.下图是推导圆面积计算公式的一种方法,把一个草绳编织的圆形茶杯垫片沿半径剪开,打开后得到一个近似的三角形。
仔细观察:三角形的底相当于圆的( ),高相当于圆的( )。如果圆的半径为r,根据三角形的面积=底×高÷2,可以推出圆的面积计算公式为S=( )。
20.一个三位数37□,当它既是2的倍数又是5的倍数时,□里填( )。当它是3的倍数时,□里可以填的数是( )。
三、判断题。(每题1分,共5分)
21.如果a是b的2倍(b≠0),那么a,b的最大公因数是a,最小公倍数是b。( )
22.为了统计商场去年各月电脑的销售数量变化情况,应选用折线统计图。( )
23.圆的直径扩大3倍,它的周长也扩大3倍,面积扩大6倍。( )
24.因为找一个数的因数是一对一对找的,所以一个数的因数有偶数个。( )
25.因为,所以的分数单位比的分数单位大。( )
四、计算题。(共24分)
26.计算下面各题。(共8分)
= = = =
= = = =
27.下面各题,怎样算简便就怎样算。(共6分)
28.解方程。(共6分)
29.求出下列图形中阴影部分的面积。(共4分)
五、操作题。(共6分)
30.涂色表示图形下面的分数。
六、解答题。(每题5分,共30分)
31.学校开展“清廉文化”主题教育活动,四、五年级的同学们一起去参观“史话清廉人物事迹展览”,五年级去的学生人数比四年级多。这两个年级一共去了660人, 是 的1.2倍,两个年级各去了多少人?(请将题中的信息补充完整,再列方程解答)
32.甲乙两地相距300千米,一辆快车和一辆慢车分别从甲、乙两地同时出发,相向而行,1.5小时后相遇。快车每小时行驶105千米。慢车每小时行驶多少千米?(列方程解答)
33.某小区内有一个圆形健身广场,新新和亮亮从起点开始同时反向而行,沿着广场散步,新新每分钟走90米,亮亮每分钟走110米,3分钟后他们俩相遇。这个圆形广场的面积是多少平方米?(本题π取3计算)
34.工地上有两根钢管,一根长36分米,另一根长63分米。因施工需要,把它们都锯成长度相等的小段,每段要尽可能长,且没有剩余。每段钢管长多少分米?一共能锯成多少段?
35.为了庆祝中华人民共和国成立75周年,人民广场用蝴蝶兰和一串红摆成了庆国庆的图案,已知蝴蝶兰的盆数是一串红的3.4倍。蝴蝶兰比一串红多240盆,蝴蝶兰和一串红各有多少盆?(列方程解答)
36.纵桨飞舟,粽叶飘香,赛龙舟是端午佳节的重要组成部分,是中华文化的传承。为弘扬中华传统文化,彰显“水润之城”的城市内涵,6月10日,有38支来自各县区的代表队在市区古黄河金鹰段举办2024宿迁端午龙舟赛。赛道上原来有21个浮漂(首尾各有一个),每两个浮漂之间距离是15米。现在每两个浮漂之间距离改为20米,不需要重新替换的浮漂有多少个?
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案及试题解析
1.B
【分析】根据每组6人或9人,都正好不多也不少,可知去社区做好事的同学数既是6的倍数也是9的倍数,即是6和9的公倍数,要求至少就是求6和9的最小公倍数,据此解答。
【解析】6=2×3
9=3×3
所以6和9的最小公倍数是2×3×3=18。
所以去社区做好事的同学至少有18人。
故答案为:B
2.D
【分析】圆形纸片对折两次,相当于把360°的圆心角平均分成4份,得到的扇形圆心角是360°÷4=90°,半径不变,依旧是圆形纸片的半径4厘米,扇形弧长就是圆周长的;最后扇形的周长就等于弧长加上两条半径长度。
【解析】2π×4÷4=2π
2π+4+4=2π+8
所以这个扇形的周长是(2π+8)厘米。
故答案为:D
3.D
【分析】根据题意可知,绳子的长度不能确定, 假设绳子长1米或绳子长3米,求出两次用去绳子的长度,再进行判断
【解析】假设绳子长1米,第一次用去米,第二次用去全长的,即1÷3=米。
两次用去的长度相等。
假设绳子长3米,第一次用去米,第二次用去全长的,即3÷3=1米。
米<1米
第二次用去的多。
所以绳子的长度不能确定,无法判断两次用去的长短。
故答案为:D
4.A
【分析】假设周长较大的圆的周长是10,周长较小的圆的周长是4,根据圆的周长=2×半径,分别求出较大的圆的半径和较小的圆的半径,再根据圆的面积=×半径的平方,分别求出两个圆的面积,再进行比较即可解答。
【解析】假设周长较大的圆的周长是10,周长较小的圆的周长是4。
10÷÷2
=10÷2
=5
4÷÷2
=4÷2
=2
×=×25=25
×=×4=4
25>4
所以周长较大的圆的面积大于周长较小的圆的面积。
故答案为:A
5.C
【分析】先根据圆的面积=,分别求出半圆的面积和剪去部分小圆的面积,再用半圆的面积减去小圆的面积,求出剩下部分的面积,再比较即可。
【解析】3.14×(20÷2)2÷2
=3.14×102÷2
=3.14×100÷2
=314÷2
=157(平方厘米)
3.14×(10÷2)2
=3.14×52
=3.14×25
=78.5(平方厘米)
157-78.5=78.5(平方厘米)
所以,剩下部分和剪去部分的面积相比,同样大。
故答案为:C
6.A
【分析】a、b是两个相邻自然数,如2和3,它们是互质数;根据“两个数是互质数时,它们的最大公因数是1,最小公倍数是两数的乘积”进行解答。
公因数只有1的两个非零自然数,叫做互质数。
【解析】a、b是两个相邻自然数(a、b都不为0),则a和b是互质数,a和b的最大公因数是(1),最小公倍数是(ab)。
故答案为:A
7.B
【分析】含有未知数的等式是方程,所以方程必须满足两个条件:①含有未知数,②是等式,据此判断即可。
【解析】A.4x>2.8含有未知数,但不是等式,所以它不是方程;
B.x÷y=40含有未知数,且是等式,所以它是方程;
C.35+16=16+35是等式,但不含未知数,所以它不是方程。
故答案为:B
8.D
【分析】复式折线统计图不仅能看清数量的多少,还能通过折线的上升和下降表示2个及以上数量的增减变化情况,折线向上走势越陡成绩增长得越快,折线向上走势越缓成绩增长得越慢,实线表示甲的成绩变化情况,虚线表示乙的成绩变化情况,总体来讲两人的成绩都呈上升趋势,乙的成绩整体比甲的成绩增长得快一些,根据统计图中的数据求出两人在第二次测试中的成绩差,根据折线的走势可以预测下次两人的成绩,但“乙的得分比甲高”并不一定会发生,属于“可能”事件,不能用“一定”描述,据此解答。
【解析】A.观察复式折线统计图可知,两人的得分都呈上升趋势;
B.复式折线统计图中,表示乙的得分情况的折线整体上比表示甲的得分情况的折线更陡一些,所以乙的测试得分整体提升得比甲快;
C.85-72=13(分),所以在第二次测试中,甲的得分比乙的得分高13分;
D.分析可知,下次测试中,乙的得分比甲高属于“可能”事件,不能用“一定”描述,可以说“乙的得分可能比甲高”。
故答案为:D
9.;
【分析】由题意可知,3米长的绳子看作单位“1”,把它平均分成2份,求每份是它的几分之几,用1除以2可解答;求每根跳绳的长度就是把3米长的绳子平均分成2份,求每份的长度,用3除以2计算即可。
【解析】
(米)
用3米长的绳子正好做了2根同样的跳绳。每根跳绳的长度是原来绳长的,每根跳绳长米。
10.2
【分析】由于白棋每次走4格,黑棋每次走6格,由于问两种棋都能走到的方格,就是求4和6的公倍数,先把4和6分解质因数,把公有质因数与独有质因数相乘求出最小公倍数,之后再把最小公倍数分别乘1、2、3、找出31以内的公倍数即可。
【解析】4=2×2
6=2×3
2×2×3=12
12×1=12
12×2=24
所以两种棋都能走到的方格有2个。
11.10 乘4
【分析】分数的基本性质:分数的分子和分母同时乘或除以相同的数(0除外),分数的大小不变。
(1)分数的分母加上12得18,相当于分母乘3,要使分数的大小不变,分子也要乘3,用分子5乘3后再减去5,就是分子应加上的数。
(2)的分子乘4,要使分数的大小不变,分母也要乘4,或用分母6乘4后再减去6,就是分母可以加上的数;
【解析】(1)分母相当于乘:
(6+12)÷6
=18÷6
=3
分子也要乘3或加上:
5×3-5
=15-5
=10
分数的分母加上12,要使分数的大小不变,分子应加上10;
(2)分子乘4,分母也要乘4或加上:
6×4-6
=24-6
=18
的分子乘4,要使分数的大小不变,分母可以乘4(或加上18)。
12.;21;5
【分析】把单位“1”平均分成若干份,表示其中一份的数叫分数单位。
把化成假分数,假分数的分子是几,就有几个这样的分数单位;
最小的质数是2,把2化成分母为8而大小不变的假分数,再看分子与的分子相差几,就是再去掉几个这样的分数单位就是最小的质数。
【解析】=,它有21个;
最小的质数为2,2=,它有16个;
21-16=5,再去掉5个这样的分数单位就是最小的质数。
填空如下:
的分数单位是(),它有(21)个这样的分数单位,再去掉(5)个这样的分数单位就是最小的质数。
13.12.56 12.56
【分析】从一个长方形木板上锯下一个最大的圆,这个圆的直径等于长方形的宽,即圆的直径是4分米。圆的周长=πd,圆的面积=πr2,据此解答。
【解析】这个最大的圆的半径是:4÷2=2(分米)
周长:3.14×4=12.56(分米)
面积:3.14×22
=3.14×4
=12.56(平方分米)
则圆的周长是12.56分米,圆的面积是12.56平方分米。
14.8.28
【分析】根据圆面积公式的推导过程可知,把一个圆剪拼成一个近似长方形,拼成的长方形的长等于圆周长的一半,长方形的宽等于圆的半径,拼成的长方形的周长比圆的周长增加了两条半径的长度(也就是一条直径的长度),根据圆的周长公式:周长=π×直径,代入数据,求出圆的周长,进而求出长方形的周长。
【解析】3.14×2+2
=6.28+2
=8.28(厘米)
这个近似长方形的周长是8.28厘米。
15.8 1
【分析】求两个数的最小公倍数,如果这两个数互质,则这两个数的最小公倍数是这两个数的乘积;根据题意,先求出4和5的最小公倍数,已知7月12日他们两人在图书馆相遇,所以7月12日再加上4和5的最小公倍数,算出来即为两人下次同时去了图书馆的时间,已知7月份有31天,据此推断出具体时间,据此解答。
【解析】4和5的最小公倍数:4×5=20
12+20=32(天)
32-31=1(天)
他们下一次同时去图书馆借书是8月1日。
16.m n
【分析】两个数的公有质因数的连乘积,就是两个数的最大公因数;两个数的公有质因数与每一个数的独有质因数的连乘积,就是两个数的最小公倍数;如果两个数成倍数关系,最大公因数为较小的那个数,最小公倍数为较大的那个数。
【解析】m、n都是非0自然数,m÷n=,
则m=n,n=2m,n÷m=2,n和m成倍数关系,最大公因数是m,最小公倍数是n。
m、n都是非0自然数,且m÷n=,m、n的最大公因数是m,最小公倍数是n。
17.8;50;24;0.8
【分析】根据分数的基本性质,将的分子和分母同时乘2,可得=;将的分子和分母同时乘10,可得=;将的分子和分母同时乘6,可得=;根据分数与除法的关系,可得=8÷10,=40÷50;分数化成小数:用分子除以分母,按照除数是整数的小数除法进行计算,据此可得=0.8。
【解析】根据分析可知,=8÷10=40÷50==0.8。
18.110;120 120;12315 120
【分析】2的倍数特征:个位上的数字是0、2、4、6、8的数是2的倍数。5的倍数特征:个位上的数字是0或5的数是5的倍数。3的倍数的特征:一个数各个数位上的数字的和是3的倍数,这个数就是3的倍数。2,3,5的倍数的特征:个位上的数字是0,各个数位上的数字的和是3的倍数的数。据此解答。
【解析】2的倍数有:110,120;
110;1+1+0=2;2不能被3整除,110不是3的倍数;
120;1+2+0=3;3能被3整除,120是3的倍数;
119;1+1+9=11;11不能被3整除,119不是3的倍数;
12315;1+2+3+1+5=12;12能被3整除,12315是3的倍数;
3的倍数有:120,12315;
同时是2,3,5的倍数有120。
活中的数学,110是报警电话,120是急救电话,119是火警电话,12315是消费申诉举报电话。在这些电话号码中,2的倍数有110,120,3的倍数有120,12315,同时是2、3、5的倍数有120。
19.周长 半径 πr2
【分析】根据题意,把一个草绳编织的圆形茶杯垫片沿半径剪开,打开后得到一个近似的三角形,那么圆的面积等于这个三角形的面积;
从图中可知,三角形的底相当于圆的周长2πr,高相当于圆的半径r;根据三角形的面积=底×高÷2,据此把含有字母的式子代入三角形的面积公式中,推导出圆的面积公式。
【解析】圆的面积=三角形的面积
三角形的面积=底×高÷2
圆的面积=2πr×r÷2=πr2
仔细观察:三角形的底相当于圆的周长,高相当于圆的半径。如果圆的半径为r,根据三角形的面积=底×高÷2,可以推出圆的面积计算公式为S=πr2。
20.0 2、5或8
【分析】2的倍数特征:个位上是0、2、4、6、8的数。
5的倍数特征:个位上是0或5的数。
2、5的倍数特征:个位上是0的数。
3的倍数特征:一个数各位上的数的和是3的倍数,这个数就是3的倍数。
【解析】个位数字是0,这样的数既是2的倍数又是5的倍数,370既是2的倍数又是5的倍数;
3+7+2=12,12是3的倍数,372是3的倍数;
3+7+5=15,15是3的倍数,375是3的倍数;
3+7+8=18,18是3的倍数,378是3的倍数。
一个三位数37□,当它既是2的倍数又是5的倍数时,□里填0。当它是3的倍数时,□里可以填的数是2、5或8。
21.×
【分析】两数成倍数关系,最大公因数是较小数,最小公倍数是较大数,据此分析。
【解析】如果a是b的2倍(b≠0),那么a,b的最大公因数是b,最小公倍数是a,原题说法错误。
故答案为:×
22.√
【分析】条形统计图能清楚地表示出数量的多少;
折线统计图不仅能表示数量的多少,还能表示数量的增减变化情况;
扇形统计图表示部分与整体之间的关系;据此解答。
【解析】为了统计商场去年各月电脑的销售数量变化情况,应选用折线统计图。
原题干说法正确。
故答案为:√
23.×
【分析】设直径为2,扩大后的直径为2×3=6;根据圆的周长公式:周长=π×直径;面积=π×半径2,分别求出原来圆的周长和面积,扩大后圆的周长和面积,再用扩大后圆的周长÷原来圆的周长,扩大后圆的面积÷原来圆的面积,分别求出它的周长扩大到原来的多少倍,面积扩大到原来的多少倍,进而解答。
【解析】设圆的直径为2;扩大后圆的直径为2×3=6。
(π×6)÷(π×2)
=(6π)÷(2π)
=3
[π×(6÷2)2]÷[π×(2÷2)2]
=[π×32]÷[π×12]
=[π×9]÷[π×1]
=9π÷π
=9
圆的直径扩大3倍,它的周长也扩大3倍,面积扩大9倍。
原题干说法错误。
故答案为:×
24.×
【分析】虽然找一个数的因数是一对一对找的,但是这一对有时相同,算一个。比如9的因数有1、3、9三个数,即9的因数的个数不是偶数个。据此判断即可。
【解析】由分析可知:
因为找一个数的因数是一对一对找的,所以一个数的因数有偶数个。此说法错误。
故答案为:×
25.×
【分析】首先分别判断出、的分数单位,然后根据同分子分数大小比较的方法,同分子分数分母小的分数反而大,判断出的分数单位和的分数单位的大小关系即可。
【解析】的分数单位是
的分数单位是
虽然,但是的分数单位比的分数单位小。原题说法错误。
故答案为:×
26.或;;;;
或;;或;
【解析】略
27.;;
【分析】(1)从左往右依次计算;
(2)先算括号里面的加法,再算括号外面的减法;
(3)先交换“”和“”的位置,然后根据减法的性质a-b+c=a-(b-c)把变成,再按顺序计算。
【解析】(1)
(2)
(3)
28.x=;x=;
x=8
【分析】根据等式的性质1,方程两边同时加上;
根据等式的性质1,方程两边同时减去;
方程两边同时乘2,两边再同时除以3。
【解析】x-=
解:x-+=+
x=
x=
+x=
解:+x-=-
x=
x=
3x÷2=12
解:3x÷2×2=12×2
3x=24
3x÷3=24÷3
x=8
29.30平方米;28.26平方厘米
【分析】(1)将图形中右边的半圆移动到左边的空白半圆处,则阴影部分的面积就等于长方形的面积,直接计算长方形的面积即可;
(2)根据正方形的面积是12平方厘米,可知半径的平方等于12平方厘米,然后将半径的平方代入圆的面积公式,然后再乘计算出圆的面积即可。
【解析】(1)10×3=30(平方米)
(2)3.14×12×
=37.68×
=28.26(平方厘米)
30.见详解
【分析】根据分数的意义,分数的分母表示总份数,分子表示所占的份数,据此解答。
【解析】(1)表示将一个圆平均分成8份,涂色部分占其中的6份。如图:
(2)把一个正方形平均分成4份,表示这样的1份是;表示5个,涂色部分占5份。如图:
(3)把一个三角形平均分成3份,表示这样的1份是;表示6个,涂色部分占6份。如图:
31.五年级去的学生人数;四年级去的学生人数;
四年级300人;五年级360人
【分析】因为五年级去的学生人数比四年级多,所以五年级去的人数是四年级去的人数的1.2倍。设四年级去的人数为x人,那么五年级去的人数是1.2x,根据等量关系:五年级去的人数+四年级去的人数=660人,据此列方程解答,求出四年级的人数,再用四年级人数乘1.2得到五年级人数。
【解析】解:设四年级去了x人,则五年级去了1.2x人。
(人)
答:四年级去了300人,五年级去了360人。
32.95千米
【分析】设慢车每小时行驶x千米,快车每小时行驶105千米,1.5小时行驶的距离是(105×1.5)千米,慢车1.5小时行驶的距离是:1.5x千米,两车相遇,它们行驶的距离和正好是甲乙两地的距离,甲乙两地的距离是300千米,列方程:105×1.5+1.5x=300,解方程,即可解答。
【解析】解:设慢车每小时行驶x千米。
105×1.5+1.5x=300
157.5+1.5x=300
1.5x=300-157.5
1.5x=142.5
1.5x÷1.5=142.5÷1.5
x=95
答:慢车每小时行驶95千米。
33.30000平方米
【分析】根据总路程=速度和×相遇时间,求出广场的周长,再根据圆的半径=周长÷圆周率÷2,圆的面积=圆周率×半径的平方,列式解答即可。
【解析】(90+110)×3
=200×3
=600(米)
600÷3÷2=100(米)
3×1002
=3×10000
=30000(平方米)
答:这个圆形广场的面积是30000平方米。
34.9分米;11段
【分析】已知两根钢管要把它们剪成同样长的小段,每段长要尽可能长,且没有剩余,求每段钢管长多少米,就是求36和63的最大公因数;然后分别用36和63除以它们的最大公因数,即可求出两根钢管各自剪成的段数,最后相加即可。
【解析】36=2×2×3×3
63=3×3×7
36和63的最大公因数3×3=9
36÷9+63÷9
=4+7
=11(段)
答:每段钢管长9分米,一共能锯成11段。
35.蝴蝶兰340盆;一串红100盆
【分析】根据题意,设一串红有x盆,则蝴蝶兰有3.4x盆,根据蝴蝶兰比一串红多240盆,列出方程,解方程即可。
【解析】解:设一串红有x盆,则蝴蝶兰有3.4x盆。
3.4x-x=240
2.4x=240
2.4x÷2.4=240÷2.4
x=100
3.4×100=340(盆)
答:蝴蝶兰有340盆,一串红有100盆。
36.6个
【分析】赛道上原来有21个浮漂,首尾各有一个,所以赛道总长是(21-1)个15米,即300米。现在每两个浮漂之间距离改为20米,不需要重新替换的浮漂就是15和20的公倍数,15和20的最小公倍数是60,所以不需要重新替换的浮漂有(300÷60+1)个。
【解析】21-1=20(个)
20×15=300(米)
15=3×5
20=2×2×5
所以15和20的最小公倍数是:5×3×2×2=60
300÷60+1
=5+1
=6(个)
答:不需要重新替换的浮漂有6个。
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
同课章节目录
