(期末培优卷)期末全真模拟培优卷-2024-2025学年五年级下学期数学苏教版(含解析)
文档属性
| 名称 | (期末培优卷)期末全真模拟培优卷-2024-2025学年五年级下学期数学苏教版(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 519.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-10 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
2024-2025学年五年级下学期数学期末全真模拟培优卷
考试时间:90分钟;试卷总分:100分;
学校: 班级: 姓名: 成绩:
注意事项:
答题前填写好自己的姓名、班级、考号等信息。
请将答案正确填写在答题区域,注意书写工整,格式正确,卷面整洁。
一、选择题。(每题1分,共8分)
1.一个圆的直径扩大到原来的4倍,它的周长和面积分别扩大到原来的多少倍( )。
A.4倍和16倍 B.16倍和4倍 C.4倍和4倍 D.4倍和16倍
2.如果自然数a、b满足b>a>0,那么与相比( )。
A.= B.大 C.大 D.无法确定
3.小明在一条板凳上做摆卡片游戏(如图),他用三种摆法都正好从板凳的一端摆到另一端且无剩余。已知卡片长18厘米,宽12厘米,那么板凳至少长( )厘米。
A.36 B.72 C.90 D.180
4.把10克盐放入100克水中,盐占盐水的( )。
A. B. C. D.
5.用三根同样长的铁丝分别围成一个圆、一个长方形和一个三角形,( )的面积最大。
A.三角形 B.长方形 C.圆
6.一块长方形试验田,周长是180米,长比宽多30米。试验田的长是多少米?设试验田的宽是x米,正确的方程是( )。
A.(30+x+x)×2=180 B.x-30+x=180÷2
C.x+30+x=180 D.x-30+x=180
7.甲和乙参加长跑比赛,路程与时间的关系如图所示。下面描述不正确的是( )。
甲和乙同时出发 B.甲跑的路程多一些
C.甲的平均速度比乙慢 D.乙先到达终点
8.如图,从A点到B点有M、N两条路线,两条路线相比,( )。
A.M路线长 B.N路线长 C.同样长
二、填空题。(每空1分,共25分)
9.在一次综合实践课上,把两根同样长的木料平均锯成9段,小明用了8分钟,小华用了12分钟。小明每分钟锯一根木料的,小华每分钟锯一根木料的,小明所用的时间是小华的。(填最简分数)
10.一批零件有30个,平均分给5人完成,2人完成这批零件的,其中2个零件占零件总个数的。
11.妈妈买回来一些玻璃球,小军6个6个地数,剩1个;5个5个地数,还是剩1个。这些玻璃球至少有( )个。
12.绕一个半径4米的圆形花圃走2圈,一共要走( )米;这个花圃的一半种月季,月季的种植面积是( )平方米。
13.在括号里填“>”“<”或“=”。
( )0.49 ( ) ( ) 400毫升( )升
14.雨水打在水面荡开层层波纹,雨滴落入一个长6米、宽4米的长方形水池中,所形成的最大的整圆波纹的面积是( )平方米。
15.有三张卡片,上面分别写着5、6、7。小红和小明用这三张卡片轮流摆不同的三位数。如果摆出的三位数是奇数就是小红赢,否则小明赢。小红赢的可能性是( ),这样的游戏规则公平吗?( )。
16.小华和小力出同样多的钱合买一箱苹果。结果小华拿了8千克,小力拿了12千克,这样小力就要给小华16元。苹果每千克( )元,这箱苹果共( )元。
17.观察下面三幅点阵图,按照这样的规律画下去,第7幅图中有( )个点,有33个点的图是第( )幅,第n幅图中有( )个点。
18.聪聪和慧慧两家相距1500米,他们相约8:50各自从家向对方家的方向出发,9:02在途中相遇。聪聪的速度为65米/分,慧慧的速度是( )米/分。
19.先把一个圆沿着半径平均分成若干份,然后拼成一个近似的长方形。这个长方形的宽是3厘米,长是( )厘米,原来圆的面积是( )平方厘米。
20.如果a=4b(a、b为非零自然数),那么a和b的最小公倍数是( ),最大公因数是( )。
三、判断题。(每题1分,共5分)
21.相邻两个自然数中一定有一个不是2的倍数。( )
22.圆的半径扩大到原来的2倍,面积也扩大到原来的2倍。( )
23.等式两边同时乘或除以同一个数,所得结果还是等式。( )
24.一个正方形的边长是质数,它的周长一定是合数。( )
25.任何整数都可以和真分数合成带分数。( )
四、计算题。(共26分)
26.直接写出得数。(共8分)
27.怎样简便怎样算。(共8分)
28.解方程。(共6分)
62-x=18
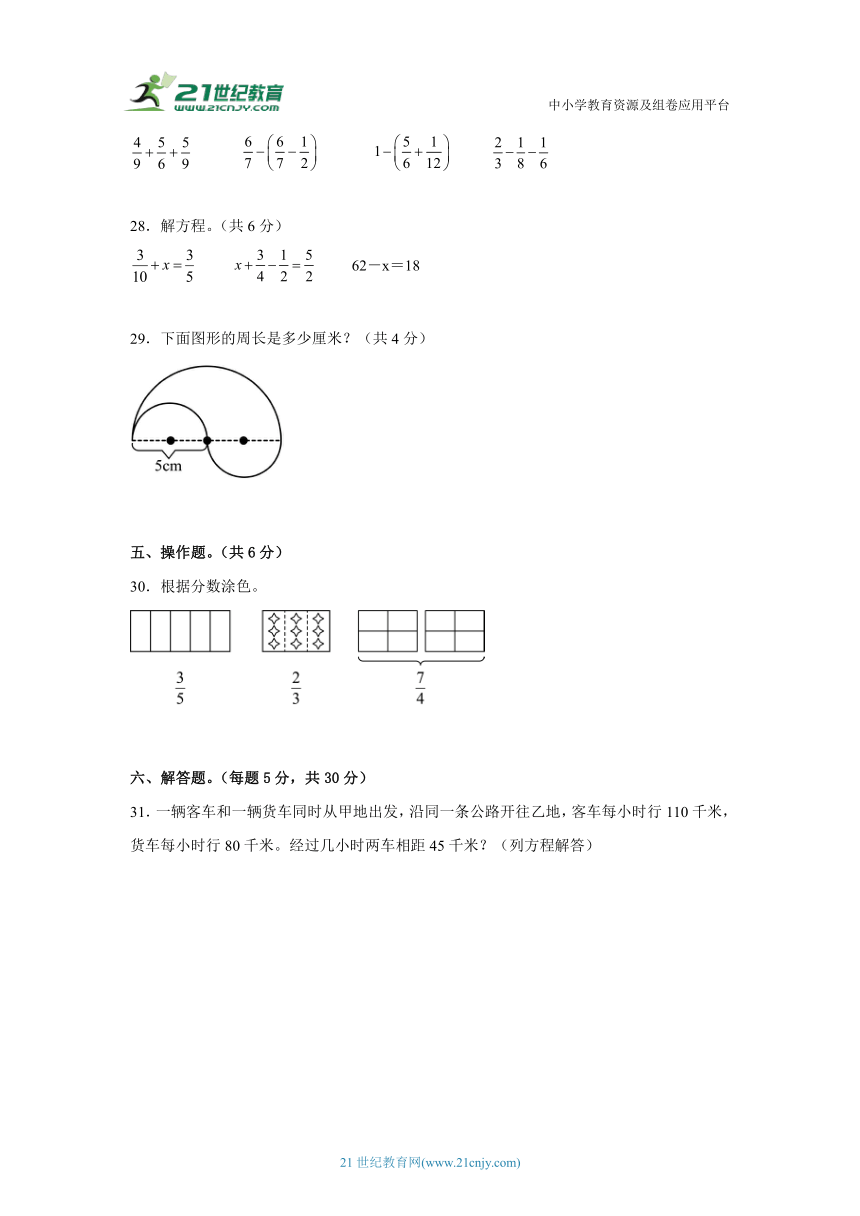
29.下面图形的周长是多少厘米?(共4分)
五、操作题。(共6分)
30.根据分数涂色。
六、解答题。(每题5分,共30分)
31.一辆客车和一辆货车同时从甲地出发,沿同一条公路开往乙地,客车每小时行110千米,货车每小时行80千米。经过几小时两车相距45千米?(列方程解答)
32.丽丽骑自行车绕一个圆形花坛一周,前轮刚好滚动了100圈。已知自行车前轮外直径大约是66厘米,这个圆形花坛的周长大约是多少米?
33.一节课有小时,同学们做实验大约用了全部时间的,老师讲解大约用了全部时间的,其余时间用来讨论和练习。讨论和练习一共用了全部时间的几分之几?
34.某市把每年6月1日定为“全民健身日”。小佳的爸爸和他的同事李叔叔都参加了健身中心的羽毛球锻炼,小佳爸爸每4天去一次,李叔叔每6天去一次。6月1日他们同时在一起打球,6月的哪些天他们还会再次相遇?
35.2024年巴黎奥运会将于7月26日开幕,会上将升起奥运五环旗。奥运五环是由5个相同的圆环套接组成。如图,每个圆环的内外直径分别是10厘米和12厘米,每个相交处的面积大约是4平方厘米。这个奥运五环的面积是多少平方厘米?
36.体育广场是1路和5路公共汽车的起点站,1路车每10分钟发一次车,5路车每15分钟发一次车。这两路公共汽车从早上6:20同时发车后,下一次同时发车是几时几分?(列表并找出答案)
1路车 6:20
5路车 6:20
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案及试题解析
1.A
【分析】圆的周长=圆周率×直径,圆的面积=圆周率×半径的平方,圆的直径扩大到原来的几倍,周长就扩大到原来的几倍,面积扩大到原来的倍数×倍数,据此分析。
【解析】4×4=16
一个圆的直径扩大到原来的4倍,它的周长和面积分别扩大到原来的4倍和16倍。
故答案为:A
2.C
【分析】分子比分母小的分数叫做真分数,真分数的数值小于1;分子比分母大或者分子和分母相等的分数叫做假分数,当分子比分母大时,其值大于1;当分子分母相等时,其值等于1 。
【解析】因为b>a>0,且a、b是自然数:
对于,它是一个真分数,因为分子a小于分母b,所以<1;
对于,它是一个假分数,因为分子b大于分母a,所以>1;
所以<。
故答案为:C
3.D
【分析】三种摆法分别为:卡片的长边(18厘米)沿板凳长度方向;卡片的宽边(12厘米)沿板凳长度方向;卡片的宽边(12厘米)和长边(18厘米)交替沿板凳长度方向直至最后以卡片的长边结束,即以长边和宽边为一组(12+18=30厘米);三种摆法都正好从板凳的一端摆到另一端且无剩余,这意味着板凳的长度是18、12和30的公倍数,要求板凳至少长多少厘米,也就是求18、12和30的最小公倍数,分解质因数求出最小公倍数即可。
【解析】18=2×3×3
12=2×2×3
12+18=30(厘米)
30=2×3×5
所以18、12和30的最小公倍数是:
2×3×3×2×5=180
所以板凳至少长180厘米。
故答案为:D
4.D
【分析】盐水质量=盐质量+水质量,盐占盐水的分数=盐÷盐水,再运用分数基本性质化为最简分数得出答案。
【解析】盐占盐水的:
故答案为:D
5.C
【分析】由题意可知,圆、长方形、三角形的周长都等于铁丝的长度,假设出铁丝的长度。假设三角形为等边三角形,等边三角形的高在直角三角形中,而直角三角形中斜边最长,则等边三角形的高小于边长,根据“”求出三角形的面积;根据铁丝的长度求出长方形长与宽的和,找出符合条件的长和宽,再根据“”求出长方形的面积;根据“”求出圆的半径,再利用“”求出圆的面积,最后比较大小,据此解答。
【解析】假设三根铁丝的长度都是18.84米。
三角形:18.84÷3=6.28(米)
等边三角形的高小于6.28米。
6.28×6.28÷2
=39.4384÷2
=19.7192(平方米)
所以,三角形的面积小于19.7192平方米。
长方形:18.84÷2=9.42(米)
4.72+4.7=9.42(米)
假设长方形的长为4.72米,宽为4.7米。
4.72×4.7=22.184(平方米)
所以,长方形的面积是22.184平方米。
圆:18.84÷3.14÷2
=6÷2
=3(米)
3.14×32
=3.14×9
=28.26(平方米)
所以,圆的面积是28.26平方米。
因为28.26平方米>22.184平方米>19.7192平方米,所以圆的面积>长方形的面积>三角形的面积,即圆的面积最大。
故答案为:C
6.A
【分析】根据长方形的周长计算公式,长方形的周长=(长+宽)×2,设试验田的宽是x米,长比宽多30米,据此用带有x的式子表示长的长度,已知周长是180米,据此列出等式。
【解析】根据分析:设试验田的宽是x米,长是(30+x)米,则列出方程:(30+x+x)×2=180
故答案为:A
7.B
【分析】由图可知,甲和乙参加长跑比赛,他们同时出发,乙在时间1的时候跑到了终点,甲在时间2的时候跑到了终点。他们两人跑的路程相同,乙用的时间更短,所以乙先到达终点。据此解答。
【解析】A.由分析得,甲和乙同时出发。该选项说法正确。
B.由分析得,甲和乙跑的路程相同。该选项说法错误。
C.由分析得,甲乙两人跑的路程相同,乙用的时间更短,甲用的时间更长,所以甲的平均速度比乙慢。该选项说法正确。
D.由分析得,乙先到达终点。该选项说法正确。
故答案为:B
8.C
【分析】设AB的长度是6,M条路线的长度等于直径是6的圆的周长一半;N条路线的长度等于直径是(6÷3)的圆的周长一半×3;根据圆的周长公式:周长=π×半径×2,分别求出M条路线的长度和N条路线的长度,再进行比较,即可解答。
【解析】设AB的长度是6
M条路线的长度:
π×6÷2=3π
N条路线的长度:
6÷3=2
π×2÷2×3
=π×3
=3π
3π=3π,两条路线相比,同样长。
从A点到B点有M、N两条路线,两条路线相比,同样长。
故答案为:C
9.;;
【分析】把整根木料的长度看作单位“1”,根据工作效率=工作总量÷工作时间,用1分别除以小明和小华平均锯成9段用的时间,就是小明、小华分别每分钟锯整根木料的几分之几;用小明用的时间除以小华用的时间求出小明所用的时间是小华的几分之几,结果用最简分数表示;分子和分母只有公因数1,像这样的分数叫作最简分数,
【解析】8÷2=4(分钟)
1÷4=
12÷2=6(分钟)
1÷6=
4÷6=
所以小明每分钟锯整根木料的,小华每分钟锯整根木料的,小明所用的时间是小华的。
10.;
【分析】已知一批零件有30个,平均分给5人完成,求2人完成这批零件的几分之几,相当于求2人完成的占5人完成的几分之几,用2除以5即可。
求2个零件占零件总个数的几分之几,用2除以零件总个数即可。
【解析】2÷5=
2÷30=
2人完成这批零件的,其中2个零件占零件总个数的。
11.31
【分析】6个6个地数,剩1个;5个5个地数,还是剩1个,说明玻璃球的数量至少比5和6的最小公倍数多1,求出5和6的最小公倍数,加1即可。两数互质,最小公倍数是两数的积。
【解析】6×5+1
=30+1
=31(个)
这些玻璃球至少有31个。
12.50.24 25.12
【分析】根据圆的周长=2×圆周率×半径,求出花圃周长,乘2就是走2圈的距离;根据半圆面积=圆周率×半径的平方÷2,即可求出月季的种植面积。
【解析】2×3.14×4×2
=25.12×2
=50.24(米)
3.14×42÷2
=3.14×16÷2
=25.12(平方米)
一共要走50.24米;月季的种植面积是25.12平方米。
13.> = < <
【分析】分数和小数比大小,将分数化成小数再比较,分数化小数,直接用分子÷分母即可;异分母分数比较大小,先通分再比较;最后一空,根据1升=1000毫升,统一单位后再比较。
【解析】=5÷9≈0.56,>0.49;
,=;
、,<;
400毫升=升=升,400毫升<升。
14.12.56
【分析】根据观察可知,所形成的最大的整圆波纹直径相当于长方形水池的宽,即4米,根据圆面积公式:S=πr2,代入数据即可求出所形成的最大的整圆波纹的面积。
【解析】3.14×(4÷2)2
=3.14×22
=3.14×4
=12.56(平方米)
所形成的最大的整圆波纹的面积是12.56平方米。
15. 不公平
【分析】先列出可摆的不同的三位数,再根据奇数:像1,3,5,7不是2的倍数的数叫做奇数。求赢的可能性用赢的次数除以摆出不同三位数的总个数,再比较大小,据此解答。
【解析】用这三张卡片轮流摆出不同三位数有567、576、657、675、756、765,总个数是:3×2×1=6(个)
其中奇数有567、657、675、765,共4个,偶数是2个。
小红赢的可能性是:4÷6=
小明赢的可能性是2÷6=
所以这个游戏规则不公平。
有三张卡片,上面分别写着5、6、7。小红和小明用这三张卡片轮流摆不同的三位数。如果摆出的三位数是奇数就是小红赢,否则小明赢。小红赢的可能性是,这样的游戏规则不公平。
16.8 160
【分析】由题意可知,小华和小力一共买了(8+12)千克苹果,两人出同样多的钱应该拿同样多的千克数,小力要给小华16元说明小力比小华多花(16×2)元,等量关系式:小力花的钱数-小华花的钱数=小力比小华多花的钱数,最后根据“总价=单价×数量”求出这箱苹果的总钱数,据此解答。
【解析】解:设苹果每千克x元。
12x-8x=16×2
4x=32
4x÷4=32÷4
x=8
8×(8+12)
=8×20
=160(元)
所以,苹果每千克8元,这箱苹果共160元。
17.24 10 3n+3
【分析】观察图形可知,第1幅图中有6个点,第2幅图中有(6+3)个点,第3幅图中有(6+3×2)个点,第4幅图中有(6+3×3)个点,依此类推……第n幅图中有[6+3×(n-1)]个点。据此规律解答。
【解析】由分析可知:第n幅图中有:
6+3×(n-1)
=6+3n-3
=(3n+3)(个)
当n=7时,3n+3=3×7+3=21+3=24(个)
3n+3=33
解:3n+3-3=33-3
3n=30
n=30÷3
n=10
所以第7幅图中有24个点,有33个点的图是第10个图形,第n幅图中有(3n+3)个点。
18.60
【分析】用9:02减去8:50求出二人相遇的时间是多少分钟,设慧慧的速度是x米/分,根据路程=速度×时间,分别求出相遇时两人走的路程,根据等量关系:“相遇时聪聪走的路程+慧慧走的路程=1500米”列方程解答即可。
【解析】解:设慧慧的速度是x米/分。
9:02-8:50=12(分)
12x+65×12=1500
12x+780=1500
12x+780-780=1500-780
12x=720
12x÷12=720÷12
x=60
因此,慧慧的速度是60米/分。
19.9.42 28.26
【分析】
如图,把一个圆沿着半径平均分成若干份,然后拼成一个近似的长方形,长方形的面积=圆的面积,长方形的宽=圆的半径,长方形的长=圆周长的一半,根据长方形面积=长×宽,即可推导出圆的面积=圆周率×半径的平方,据此分析。
【解析】3.14×3=9.42(厘米)
9.42×3=28.26(平方厘米)
这个长方形的宽是3厘米,长是9.42厘米,原来圆的面积是28.26平方厘米。
20.a b
【分析】两数成倍数关系,最小公倍数是较大数,最大公因数是较小数,据此分析。
【解析】如果a=4b(a、b为非零自然数),说明a是b的4倍,根据分析,那么a和b的最小公倍数是a,最大公因数是b。
21.√
【分析】自然数按照能否被2整除分为奇数和偶数,相邻的两个自然数必然是一个奇数一个偶数,偶数能被2整除,奇数不能被2整除。据此解答。
【解析】相邻的两个自然数中,一个数是奇数,那么另一个一定是偶数,一个是偶数,那么另一个数是奇数,能被2整除的数是偶数,不能被2整除的数是奇数,所以相邻两个自然数中一定有一个不是2的倍数。
原题说法正确。
故答案为:√
22.×
【分析】假设圆的半径是1厘米,则扩大到原来的2倍是:1×2=2(厘米),根据圆的面积=,分别求出原来圆的面积和半径扩大到原来的2倍后圆的面积,再用半径扩大到原来的2倍后圆的面积除以原来的面积即可解答。
【解析】假设圆的半径是1厘米,则扩大到原来的2倍是:1×2=2(厘米)。
3.14×÷(3.14×)
=3.14×4÷(3.14×1)
=12.56÷3.14
=4
所以圆的半径扩大到原来的2倍,面积扩大到原来的4倍。
原题说法错误。
故答案为:×
23.×
【分析】根据等式的基本性质2:等式的左右两边同时乘(或除以)同一个不为0的数,等式仍然成立。
【解析】等式两边同时乘或除以同一个不为0的数,所得结果还是等式。所以原题说法错误。
故答案为:×
24.√
【分析】根据质数:只有1和它本身两个因数的数叫做质数;合数:除了1和它本身外,还有其他因数的数叫合数;。
【解析】由题意可知,正方形的周长除了1和它本身外,还有4、边长、2、边长的2倍这些因数,所以正方形的周长一定是合数;原题说法正确。
故答案为:√
25.×
【分析】带分数指的是由整数(不包括0)和真分数合成的数,所以带分数都大于1,据此解答。
【解析】整数(0除外)都可以和真分数合成带分数,原说法错误。
故答案为:×
26.;;;
;;;
【解析】略
27.;;
;
【分析】(1)根据加法交换律a+b=b+a,交换和的位置进行简便运算。
(2)根据减法的运算性质a-(b-c)=a-b+c,将算式转化为,进行简便运算。
(3)先计算括号里面的加法,再计算括号外面的减法。
(4)从左往右计算即可。
【解析】(1)
(2)
(3)
(4)
28.x=;x=;x=44
【分析】等式的性质1:等式两边加上或减去同一个数,左右两边仍然相等。等式的性质2:等式两边乘同一个数,或除以同一个不为0的数,左右两边仍然相等。
(1)根据等式的性质1,方程两边同时减去,解出方程;
(2)根据等式的性质1,方程两边同时加上再同时减去,解出方程;
(3)根据等式的性质1和减法的性质,方程转化为x=62-18,解出方程。
【解析】
解:
解:
62-x=18
解:x=62-18
x=44
29.31.4厘米
【分析】观察图形,图形的周长是大半圆弧长加上两个小半圆弧长,根据圆的周长公式,半圆弧的长等于圆周长除以2,代入数据计算。
【解析】2×3.14×5÷2+2×3.14×5÷2
=15.7+15.7
=31.4(厘米)
所以该图形的周长是31.4厘米。
30.见详解
【分析】图形1,根据分数的意义可知,要使涂色部分表示,则将这个图形平均分成5份,其中一份占它的。只需要把其中3份涂色即可。
图形2,根据分数的意义可知,要使涂色部分表示,则将这个图形平均分成3份,其中一份占它的,只需要把其中2份涂色即可。
图形3,根据分数的意义可知,要使涂色部分表示,把其中的大长方形看作单位“1”,平均分成4份,其中的一个大长方形全部涂色,表示,另一个图形涂色其中的3份,表示,两个图形的涂色部分合起来表示,据此涂色。
【解析】如图:
31.1.5小时
【分析】设经过小时两车相距45千米,根据,据此列方程并求解。
【解析】解:设经过小时两车相距45千米。
答:经过1.5小时两车相距45千米。
32.207.24米
【分析】根据圆的周长=圆周率×直径,先求出自行车前轮滚动1圈的距离,再乘滚动圈数,即可求出自行车行驶距离,即花坛的周长,根据1米=100厘米,统一单位即可。
【解析】3.14×66×100
=207.24×100
=20724(厘米)
=207.24(米)
答:这个圆形花坛的周长大约是207.24米。
33.
【分析】把一节课的时间看作单位“1”,根据减法的性质,用“1”减去做实验用了全部时间的,再减去老师讲解用了全部时间的,即是讨论和练习一共用了全部时间的几分之几。
【解析】1--
=1--
=
答:讨论和练习一共用了全部时间的。
34.6月13日和6月25日
【分析】求出两人间隔天数的最小公倍数是两人同时去的间隔天数,根据起点时间+经过时间=终点时间,推算出6月同时去的日期即可。全部公有的质因数和各自独立的质因数,它们连乘的积就是这几个数的最小公倍数。
【解析】4=2×2
6=2×3
2×2×3=12(天)
1+12=13(日)
13+12=25(日)
答:6月13日和6月25日他们还会再次相遇。
35.140.7平方厘米
【分析】用外圆的面积减去内圆的面积(圆环的面积)乘5即是五环的面积,总共相交8次,再减去相交的面积,即是这个图形的面积。其中,圆环的面积S=π(R2-r2),据此解答。
【解析】12÷2=6(厘米)
10÷2=5(厘米)
3.14×(62-52)
=3.14×(36-25)
=3.14×11
=34.54(平方厘米)
34.54×5-4×8
=172.7-32
=140.7(平方厘米)
答:这个奥运五环的面积是140.7平方厘米。
36.列表见详解;6时50分
【分析】根据题意,1路车每10分钟发一次车,5路车每15分钟发一次车,这两路公共汽车从早上6:20同时发车,按时间间隔在表中写出这两路车的发车时刻,即可找出下次同时发车的时刻。
【解析】如下表:
答:下一次同时发车时6时50分。
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
中小学教育资源及组卷应用平台
2024-2025学年五年级下学期数学期末全真模拟培优卷
考试时间:90分钟;试卷总分:100分;
学校: 班级: 姓名: 成绩:
注意事项:
答题前填写好自己的姓名、班级、考号等信息。
请将答案正确填写在答题区域,注意书写工整,格式正确,卷面整洁。
一、选择题。(每题1分,共8分)
1.一个圆的直径扩大到原来的4倍,它的周长和面积分别扩大到原来的多少倍( )。
A.4倍和16倍 B.16倍和4倍 C.4倍和4倍 D.4倍和16倍
2.如果自然数a、b满足b>a>0,那么与相比( )。
A.= B.大 C.大 D.无法确定
3.小明在一条板凳上做摆卡片游戏(如图),他用三种摆法都正好从板凳的一端摆到另一端且无剩余。已知卡片长18厘米,宽12厘米,那么板凳至少长( )厘米。
A.36 B.72 C.90 D.180
4.把10克盐放入100克水中,盐占盐水的( )。
A. B. C. D.
5.用三根同样长的铁丝分别围成一个圆、一个长方形和一个三角形,( )的面积最大。
A.三角形 B.长方形 C.圆
6.一块长方形试验田,周长是180米,长比宽多30米。试验田的长是多少米?设试验田的宽是x米,正确的方程是( )。
A.(30+x+x)×2=180 B.x-30+x=180÷2
C.x+30+x=180 D.x-30+x=180
7.甲和乙参加长跑比赛,路程与时间的关系如图所示。下面描述不正确的是( )。
甲和乙同时出发 B.甲跑的路程多一些
C.甲的平均速度比乙慢 D.乙先到达终点
8.如图,从A点到B点有M、N两条路线,两条路线相比,( )。
A.M路线长 B.N路线长 C.同样长
二、填空题。(每空1分,共25分)
9.在一次综合实践课上,把两根同样长的木料平均锯成9段,小明用了8分钟,小华用了12分钟。小明每分钟锯一根木料的,小华每分钟锯一根木料的,小明所用的时间是小华的。(填最简分数)
10.一批零件有30个,平均分给5人完成,2人完成这批零件的,其中2个零件占零件总个数的。
11.妈妈买回来一些玻璃球,小军6个6个地数,剩1个;5个5个地数,还是剩1个。这些玻璃球至少有( )个。
12.绕一个半径4米的圆形花圃走2圈,一共要走( )米;这个花圃的一半种月季,月季的种植面积是( )平方米。
13.在括号里填“>”“<”或“=”。
( )0.49 ( ) ( ) 400毫升( )升
14.雨水打在水面荡开层层波纹,雨滴落入一个长6米、宽4米的长方形水池中,所形成的最大的整圆波纹的面积是( )平方米。
15.有三张卡片,上面分别写着5、6、7。小红和小明用这三张卡片轮流摆不同的三位数。如果摆出的三位数是奇数就是小红赢,否则小明赢。小红赢的可能性是( ),这样的游戏规则公平吗?( )。
16.小华和小力出同样多的钱合买一箱苹果。结果小华拿了8千克,小力拿了12千克,这样小力就要给小华16元。苹果每千克( )元,这箱苹果共( )元。
17.观察下面三幅点阵图,按照这样的规律画下去,第7幅图中有( )个点,有33个点的图是第( )幅,第n幅图中有( )个点。
18.聪聪和慧慧两家相距1500米,他们相约8:50各自从家向对方家的方向出发,9:02在途中相遇。聪聪的速度为65米/分,慧慧的速度是( )米/分。
19.先把一个圆沿着半径平均分成若干份,然后拼成一个近似的长方形。这个长方形的宽是3厘米,长是( )厘米,原来圆的面积是( )平方厘米。
20.如果a=4b(a、b为非零自然数),那么a和b的最小公倍数是( ),最大公因数是( )。
三、判断题。(每题1分,共5分)
21.相邻两个自然数中一定有一个不是2的倍数。( )
22.圆的半径扩大到原来的2倍,面积也扩大到原来的2倍。( )
23.等式两边同时乘或除以同一个数,所得结果还是等式。( )
24.一个正方形的边长是质数,它的周长一定是合数。( )
25.任何整数都可以和真分数合成带分数。( )
四、计算题。(共26分)
26.直接写出得数。(共8分)
27.怎样简便怎样算。(共8分)
28.解方程。(共6分)
62-x=18
29.下面图形的周长是多少厘米?(共4分)
五、操作题。(共6分)
30.根据分数涂色。
六、解答题。(每题5分,共30分)
31.一辆客车和一辆货车同时从甲地出发,沿同一条公路开往乙地,客车每小时行110千米,货车每小时行80千米。经过几小时两车相距45千米?(列方程解答)
32.丽丽骑自行车绕一个圆形花坛一周,前轮刚好滚动了100圈。已知自行车前轮外直径大约是66厘米,这个圆形花坛的周长大约是多少米?
33.一节课有小时,同学们做实验大约用了全部时间的,老师讲解大约用了全部时间的,其余时间用来讨论和练习。讨论和练习一共用了全部时间的几分之几?
34.某市把每年6月1日定为“全民健身日”。小佳的爸爸和他的同事李叔叔都参加了健身中心的羽毛球锻炼,小佳爸爸每4天去一次,李叔叔每6天去一次。6月1日他们同时在一起打球,6月的哪些天他们还会再次相遇?
35.2024年巴黎奥运会将于7月26日开幕,会上将升起奥运五环旗。奥运五环是由5个相同的圆环套接组成。如图,每个圆环的内外直径分别是10厘米和12厘米,每个相交处的面积大约是4平方厘米。这个奥运五环的面积是多少平方厘米?
36.体育广场是1路和5路公共汽车的起点站,1路车每10分钟发一次车,5路车每15分钟发一次车。这两路公共汽车从早上6:20同时发车后,下一次同时发车是几时几分?(列表并找出答案)
1路车 6:20
5路车 6:20
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案及试题解析
1.A
【分析】圆的周长=圆周率×直径,圆的面积=圆周率×半径的平方,圆的直径扩大到原来的几倍,周长就扩大到原来的几倍,面积扩大到原来的倍数×倍数,据此分析。
【解析】4×4=16
一个圆的直径扩大到原来的4倍,它的周长和面积分别扩大到原来的4倍和16倍。
故答案为:A
2.C
【分析】分子比分母小的分数叫做真分数,真分数的数值小于1;分子比分母大或者分子和分母相等的分数叫做假分数,当分子比分母大时,其值大于1;当分子分母相等时,其值等于1 。
【解析】因为b>a>0,且a、b是自然数:
对于,它是一个真分数,因为分子a小于分母b,所以<1;
对于,它是一个假分数,因为分子b大于分母a,所以>1;
所以<。
故答案为:C
3.D
【分析】三种摆法分别为:卡片的长边(18厘米)沿板凳长度方向;卡片的宽边(12厘米)沿板凳长度方向;卡片的宽边(12厘米)和长边(18厘米)交替沿板凳长度方向直至最后以卡片的长边结束,即以长边和宽边为一组(12+18=30厘米);三种摆法都正好从板凳的一端摆到另一端且无剩余,这意味着板凳的长度是18、12和30的公倍数,要求板凳至少长多少厘米,也就是求18、12和30的最小公倍数,分解质因数求出最小公倍数即可。
【解析】18=2×3×3
12=2×2×3
12+18=30(厘米)
30=2×3×5
所以18、12和30的最小公倍数是:
2×3×3×2×5=180
所以板凳至少长180厘米。
故答案为:D
4.D
【分析】盐水质量=盐质量+水质量,盐占盐水的分数=盐÷盐水,再运用分数基本性质化为最简分数得出答案。
【解析】盐占盐水的:
故答案为:D
5.C
【分析】由题意可知,圆、长方形、三角形的周长都等于铁丝的长度,假设出铁丝的长度。假设三角形为等边三角形,等边三角形的高在直角三角形中,而直角三角形中斜边最长,则等边三角形的高小于边长,根据“”求出三角形的面积;根据铁丝的长度求出长方形长与宽的和,找出符合条件的长和宽,再根据“”求出长方形的面积;根据“”求出圆的半径,再利用“”求出圆的面积,最后比较大小,据此解答。
【解析】假设三根铁丝的长度都是18.84米。
三角形:18.84÷3=6.28(米)
等边三角形的高小于6.28米。
6.28×6.28÷2
=39.4384÷2
=19.7192(平方米)
所以,三角形的面积小于19.7192平方米。
长方形:18.84÷2=9.42(米)
4.72+4.7=9.42(米)
假设长方形的长为4.72米,宽为4.7米。
4.72×4.7=22.184(平方米)
所以,长方形的面积是22.184平方米。
圆:18.84÷3.14÷2
=6÷2
=3(米)
3.14×32
=3.14×9
=28.26(平方米)
所以,圆的面积是28.26平方米。
因为28.26平方米>22.184平方米>19.7192平方米,所以圆的面积>长方形的面积>三角形的面积,即圆的面积最大。
故答案为:C
6.A
【分析】根据长方形的周长计算公式,长方形的周长=(长+宽)×2,设试验田的宽是x米,长比宽多30米,据此用带有x的式子表示长的长度,已知周长是180米,据此列出等式。
【解析】根据分析:设试验田的宽是x米,长是(30+x)米,则列出方程:(30+x+x)×2=180
故答案为:A
7.B
【分析】由图可知,甲和乙参加长跑比赛,他们同时出发,乙在时间1的时候跑到了终点,甲在时间2的时候跑到了终点。他们两人跑的路程相同,乙用的时间更短,所以乙先到达终点。据此解答。
【解析】A.由分析得,甲和乙同时出发。该选项说法正确。
B.由分析得,甲和乙跑的路程相同。该选项说法错误。
C.由分析得,甲乙两人跑的路程相同,乙用的时间更短,甲用的时间更长,所以甲的平均速度比乙慢。该选项说法正确。
D.由分析得,乙先到达终点。该选项说法正确。
故答案为:B
8.C
【分析】设AB的长度是6,M条路线的长度等于直径是6的圆的周长一半;N条路线的长度等于直径是(6÷3)的圆的周长一半×3;根据圆的周长公式:周长=π×半径×2,分别求出M条路线的长度和N条路线的长度,再进行比较,即可解答。
【解析】设AB的长度是6
M条路线的长度:
π×6÷2=3π
N条路线的长度:
6÷3=2
π×2÷2×3
=π×3
=3π
3π=3π,两条路线相比,同样长。
从A点到B点有M、N两条路线,两条路线相比,同样长。
故答案为:C
9.;;
【分析】把整根木料的长度看作单位“1”,根据工作效率=工作总量÷工作时间,用1分别除以小明和小华平均锯成9段用的时间,就是小明、小华分别每分钟锯整根木料的几分之几;用小明用的时间除以小华用的时间求出小明所用的时间是小华的几分之几,结果用最简分数表示;分子和分母只有公因数1,像这样的分数叫作最简分数,
【解析】8÷2=4(分钟)
1÷4=
12÷2=6(分钟)
1÷6=
4÷6=
所以小明每分钟锯整根木料的,小华每分钟锯整根木料的,小明所用的时间是小华的。
10.;
【分析】已知一批零件有30个,平均分给5人完成,求2人完成这批零件的几分之几,相当于求2人完成的占5人完成的几分之几,用2除以5即可。
求2个零件占零件总个数的几分之几,用2除以零件总个数即可。
【解析】2÷5=
2÷30=
2人完成这批零件的,其中2个零件占零件总个数的。
11.31
【分析】6个6个地数,剩1个;5个5个地数,还是剩1个,说明玻璃球的数量至少比5和6的最小公倍数多1,求出5和6的最小公倍数,加1即可。两数互质,最小公倍数是两数的积。
【解析】6×5+1
=30+1
=31(个)
这些玻璃球至少有31个。
12.50.24 25.12
【分析】根据圆的周长=2×圆周率×半径,求出花圃周长,乘2就是走2圈的距离;根据半圆面积=圆周率×半径的平方÷2,即可求出月季的种植面积。
【解析】2×3.14×4×2
=25.12×2
=50.24(米)
3.14×42÷2
=3.14×16÷2
=25.12(平方米)
一共要走50.24米;月季的种植面积是25.12平方米。
13.> = < <
【分析】分数和小数比大小,将分数化成小数再比较,分数化小数,直接用分子÷分母即可;异分母分数比较大小,先通分再比较;最后一空,根据1升=1000毫升,统一单位后再比较。
【解析】=5÷9≈0.56,>0.49;
,=;
、,<;
400毫升=升=升,400毫升<升。
14.12.56
【分析】根据观察可知,所形成的最大的整圆波纹直径相当于长方形水池的宽,即4米,根据圆面积公式:S=πr2,代入数据即可求出所形成的最大的整圆波纹的面积。
【解析】3.14×(4÷2)2
=3.14×22
=3.14×4
=12.56(平方米)
所形成的最大的整圆波纹的面积是12.56平方米。
15. 不公平
【分析】先列出可摆的不同的三位数,再根据奇数:像1,3,5,7不是2的倍数的数叫做奇数。求赢的可能性用赢的次数除以摆出不同三位数的总个数,再比较大小,据此解答。
【解析】用这三张卡片轮流摆出不同三位数有567、576、657、675、756、765,总个数是:3×2×1=6(个)
其中奇数有567、657、675、765,共4个,偶数是2个。
小红赢的可能性是:4÷6=
小明赢的可能性是2÷6=
所以这个游戏规则不公平。
有三张卡片,上面分别写着5、6、7。小红和小明用这三张卡片轮流摆不同的三位数。如果摆出的三位数是奇数就是小红赢,否则小明赢。小红赢的可能性是,这样的游戏规则不公平。
16.8 160
【分析】由题意可知,小华和小力一共买了(8+12)千克苹果,两人出同样多的钱应该拿同样多的千克数,小力要给小华16元说明小力比小华多花(16×2)元,等量关系式:小力花的钱数-小华花的钱数=小力比小华多花的钱数,最后根据“总价=单价×数量”求出这箱苹果的总钱数,据此解答。
【解析】解:设苹果每千克x元。
12x-8x=16×2
4x=32
4x÷4=32÷4
x=8
8×(8+12)
=8×20
=160(元)
所以,苹果每千克8元,这箱苹果共160元。
17.24 10 3n+3
【分析】观察图形可知,第1幅图中有6个点,第2幅图中有(6+3)个点,第3幅图中有(6+3×2)个点,第4幅图中有(6+3×3)个点,依此类推……第n幅图中有[6+3×(n-1)]个点。据此规律解答。
【解析】由分析可知:第n幅图中有:
6+3×(n-1)
=6+3n-3
=(3n+3)(个)
当n=7时,3n+3=3×7+3=21+3=24(个)
3n+3=33
解:3n+3-3=33-3
3n=30
n=30÷3
n=10
所以第7幅图中有24个点,有33个点的图是第10个图形,第n幅图中有(3n+3)个点。
18.60
【分析】用9:02减去8:50求出二人相遇的时间是多少分钟,设慧慧的速度是x米/分,根据路程=速度×时间,分别求出相遇时两人走的路程,根据等量关系:“相遇时聪聪走的路程+慧慧走的路程=1500米”列方程解答即可。
【解析】解:设慧慧的速度是x米/分。
9:02-8:50=12(分)
12x+65×12=1500
12x+780=1500
12x+780-780=1500-780
12x=720
12x÷12=720÷12
x=60
因此,慧慧的速度是60米/分。
19.9.42 28.26
【分析】
如图,把一个圆沿着半径平均分成若干份,然后拼成一个近似的长方形,长方形的面积=圆的面积,长方形的宽=圆的半径,长方形的长=圆周长的一半,根据长方形面积=长×宽,即可推导出圆的面积=圆周率×半径的平方,据此分析。
【解析】3.14×3=9.42(厘米)
9.42×3=28.26(平方厘米)
这个长方形的宽是3厘米,长是9.42厘米,原来圆的面积是28.26平方厘米。
20.a b
【分析】两数成倍数关系,最小公倍数是较大数,最大公因数是较小数,据此分析。
【解析】如果a=4b(a、b为非零自然数),说明a是b的4倍,根据分析,那么a和b的最小公倍数是a,最大公因数是b。
21.√
【分析】自然数按照能否被2整除分为奇数和偶数,相邻的两个自然数必然是一个奇数一个偶数,偶数能被2整除,奇数不能被2整除。据此解答。
【解析】相邻的两个自然数中,一个数是奇数,那么另一个一定是偶数,一个是偶数,那么另一个数是奇数,能被2整除的数是偶数,不能被2整除的数是奇数,所以相邻两个自然数中一定有一个不是2的倍数。
原题说法正确。
故答案为:√
22.×
【分析】假设圆的半径是1厘米,则扩大到原来的2倍是:1×2=2(厘米),根据圆的面积=,分别求出原来圆的面积和半径扩大到原来的2倍后圆的面积,再用半径扩大到原来的2倍后圆的面积除以原来的面积即可解答。
【解析】假设圆的半径是1厘米,则扩大到原来的2倍是:1×2=2(厘米)。
3.14×÷(3.14×)
=3.14×4÷(3.14×1)
=12.56÷3.14
=4
所以圆的半径扩大到原来的2倍,面积扩大到原来的4倍。
原题说法错误。
故答案为:×
23.×
【分析】根据等式的基本性质2:等式的左右两边同时乘(或除以)同一个不为0的数,等式仍然成立。
【解析】等式两边同时乘或除以同一个不为0的数,所得结果还是等式。所以原题说法错误。
故答案为:×
24.√
【分析】根据质数:只有1和它本身两个因数的数叫做质数;合数:除了1和它本身外,还有其他因数的数叫合数;。
【解析】由题意可知,正方形的周长除了1和它本身外,还有4、边长、2、边长的2倍这些因数,所以正方形的周长一定是合数;原题说法正确。
故答案为:√
25.×
【分析】带分数指的是由整数(不包括0)和真分数合成的数,所以带分数都大于1,据此解答。
【解析】整数(0除外)都可以和真分数合成带分数,原说法错误。
故答案为:×
26.;;;
;;;
【解析】略
27.;;
;
【分析】(1)根据加法交换律a+b=b+a,交换和的位置进行简便运算。
(2)根据减法的运算性质a-(b-c)=a-b+c,将算式转化为,进行简便运算。
(3)先计算括号里面的加法,再计算括号外面的减法。
(4)从左往右计算即可。
【解析】(1)
(2)
(3)
(4)
28.x=;x=;x=44
【分析】等式的性质1:等式两边加上或减去同一个数,左右两边仍然相等。等式的性质2:等式两边乘同一个数,或除以同一个不为0的数,左右两边仍然相等。
(1)根据等式的性质1,方程两边同时减去,解出方程;
(2)根据等式的性质1,方程两边同时加上再同时减去,解出方程;
(3)根据等式的性质1和减法的性质,方程转化为x=62-18,解出方程。
【解析】
解:
解:
62-x=18
解:x=62-18
x=44
29.31.4厘米
【分析】观察图形,图形的周长是大半圆弧长加上两个小半圆弧长,根据圆的周长公式,半圆弧的长等于圆周长除以2,代入数据计算。
【解析】2×3.14×5÷2+2×3.14×5÷2
=15.7+15.7
=31.4(厘米)
所以该图形的周长是31.4厘米。
30.见详解
【分析】图形1,根据分数的意义可知,要使涂色部分表示,则将这个图形平均分成5份,其中一份占它的。只需要把其中3份涂色即可。
图形2,根据分数的意义可知,要使涂色部分表示,则将这个图形平均分成3份,其中一份占它的,只需要把其中2份涂色即可。
图形3,根据分数的意义可知,要使涂色部分表示,把其中的大长方形看作单位“1”,平均分成4份,其中的一个大长方形全部涂色,表示,另一个图形涂色其中的3份,表示,两个图形的涂色部分合起来表示,据此涂色。
【解析】如图:
31.1.5小时
【分析】设经过小时两车相距45千米,根据,据此列方程并求解。
【解析】解:设经过小时两车相距45千米。
答:经过1.5小时两车相距45千米。
32.207.24米
【分析】根据圆的周长=圆周率×直径,先求出自行车前轮滚动1圈的距离,再乘滚动圈数,即可求出自行车行驶距离,即花坛的周长,根据1米=100厘米,统一单位即可。
【解析】3.14×66×100
=207.24×100
=20724(厘米)
=207.24(米)
答:这个圆形花坛的周长大约是207.24米。
33.
【分析】把一节课的时间看作单位“1”,根据减法的性质,用“1”减去做实验用了全部时间的,再减去老师讲解用了全部时间的,即是讨论和练习一共用了全部时间的几分之几。
【解析】1--
=1--
=
答:讨论和练习一共用了全部时间的。
34.6月13日和6月25日
【分析】求出两人间隔天数的最小公倍数是两人同时去的间隔天数,根据起点时间+经过时间=终点时间,推算出6月同时去的日期即可。全部公有的质因数和各自独立的质因数,它们连乘的积就是这几个数的最小公倍数。
【解析】4=2×2
6=2×3
2×2×3=12(天)
1+12=13(日)
13+12=25(日)
答:6月13日和6月25日他们还会再次相遇。
35.140.7平方厘米
【分析】用外圆的面积减去内圆的面积(圆环的面积)乘5即是五环的面积,总共相交8次,再减去相交的面积,即是这个图形的面积。其中,圆环的面积S=π(R2-r2),据此解答。
【解析】12÷2=6(厘米)
10÷2=5(厘米)
3.14×(62-52)
=3.14×(36-25)
=3.14×11
=34.54(平方厘米)
34.54×5-4×8
=172.7-32
=140.7(平方厘米)
答:这个奥运五环的面积是140.7平方厘米。
36.列表见详解;6时50分
【分析】根据题意,1路车每10分钟发一次车,5路车每15分钟发一次车,这两路公共汽车从早上6:20同时发车,按时间间隔在表中写出这两路车的发车时刻,即可找出下次同时发车的时刻。
【解析】如下表:
答:下一次同时发车时6时50分。
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
同课章节目录
