(期末培优卷)期末思维提升培优卷-2024-2025学年五年级下学期数学苏教版(含解析)
文档属性
| 名称 | (期末培优卷)期末思维提升培优卷-2024-2025学年五年级下学期数学苏教版(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 532.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-10 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
2024-2025学年五年级下学期数学期末思维提升培优卷
考试时间:90分钟;试卷总分:100分;
学校: 班级: 姓名: 成绩:
注意事项:
答题前填写好自己的姓名、班级、考号等信息。
请将答案正确填写在答题区域,注意书写工整,格式正确,卷面整洁。
一、计算题。(共26分)
1.直接写出得数。(共8分)
2.计算下面各题,能简算的要简算。(共6分)
3.解方程(共6分)
4.求涂色部分的面积。(共6分)
二、填空题。(每空1分,共24分)
5.智能车间可以通过给机械臂输入设定值,让机械臂自动将相同个数的零件装箱打包。一批零件有40个,如果不能每次单个打包,也不能一次全部打包,且最后正好打包完,那么共有( )种设定值。
6.小明把一张圆形纸片对折三次,得到下面的扇形(弧长3.14厘米),这张圆形纸片的半径是( )厘米。
7.的分数单位是( ),有( )个这样的分数单位,再加上( )个这样的单位就是最小质数。它是( )分数,写成带分数形式是( )。
8.=18÷24==3÷( )=( )(填小数)。
9.如果,,那么A和B最大公因数是( ),最小公倍数是( )。
10.将一个圆平均分成若干份,拼成一个近似长方形,拼成的长方形周长比圆的周长多4厘米,原来圆的面积是( )平方厘米。
11.学校买来5箱图书,每箱40本,平均分给五年级8个班。每个班分到箱,3个班分到这批图书的。
12.为了确保通信安全,信息需要加密传输。现规定加密规则:明文(m,n)加密成密文后是(3m+1,mn)。按照这样的加密规则,明文(2,5)加密后是( , ),密文(10,21)的明文是( , )。
13.有一个电子钟,每到整点响铃一次,每过8分钟亮灯一次。如果这个电子钟在中午12时整的时候既响铃又亮灯,那么下一次既响铃又亮灯的时刻是下午( )时。
14.鞋子尺码通常用“码”或“厘米”作单位,它们之间的换算关系是y=2x-10(y表示码数,x表示厘米数)。小芳的脚长22厘米,是( )码,爸爸脚长42码,是( )厘米。
15.一台碾米机30分钟碾米50千克,平均每分钟碾米( )千克,照这样计算,碾米1千克需( )分钟。(填分数)
16.跳绳在中小学成为重要的体育活动项目。体育老师把9米长的绳子平均分成4段,每一段做成一根跳绳。每根跳绳长( )米,每根跳绳占这根绳子总长的( )。
三、选择题。(每题1分,共8分)
17.秦始皇陵兵马俑是世界八大奇迹之一。二号坑第一单元阵心由八路面东的160个蹲跪式弩兵组成,壮壮用下面的方法数这些弩兵俑,不能正好数完的是( )。
A.2个2个地数 B.3个3个地数 C.5个5个地数 D.10个10个地数
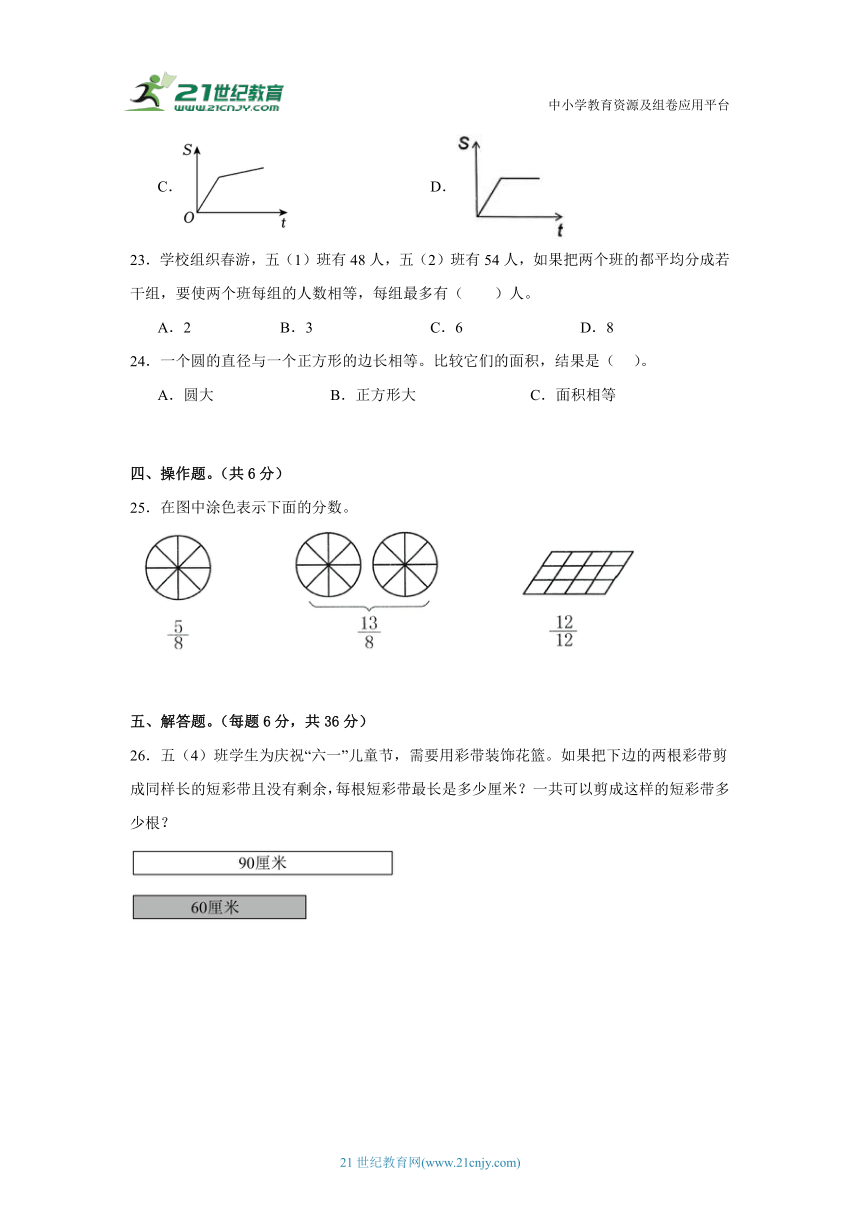
18.如图中,不正确的是( )。
A. B.
C. D.
19.今年3月10日,《中国诗词大会》(第九季)火热开播。王小萌同学想绘制第一季至第九季的收视变化情况,选用( )比较好。
A.统计表 B.条形统计图 C.折线统计图 D.以上都可以
20.为确保信息安全,信息需要加密传输,发送时是:明文→密文(加密过程),接收时是:密文→明文(解密过程)。已知加密规则为:明文m、n对应的密文为3m、2n-1,如果接收到的密文为12、9,那么解密得到的明文应为( )。
A.4、5 B.36、17 C.4、4 D.36、4
21.一根绳子截成两段,第一段占这根绳子的,第二段长米。这两段绳子相比,( )。
A.第一段长 B.第二段长
C.两段一样长 D.无法比较
22.李师傅和王师傅一起修剪一块草坪,两人修剪草坪的速度相同。一开始两人同时修剪,修剪一段时间后,李师傅有事离开,只留下王师傅一人修剪。在下面四幅图中,图( )能表示修剪时间t和修剪面积S之间的关系。
A. B.
C. D.
23.学校组织春游,五(1)班有48人,五(2)班有54人,如果把两个班的都平均分成若干组,要使两个班每组的人数相等,每组最多有( )人。
A.2 B.3 C.6 D.8
24.一个圆的直径与一个正方形的边长相等。比较它们的面积,结果是( )。
A.圆大 B.正方形大 C.面积相等
四、操作题。(共6分)
25.在图中涂色表示下面的分数。
五、解答题。(每题6分,共36分)
26.五(4)班学生为庆祝“六一”儿童节,需要用彩带装饰花篮。如果把下边的两根彩带剪成同样长的短彩带且没有剩余,每根短彩带最长是多少厘米?一共可以剪成这样的短彩带多少根?
27.一张长方形纸长24厘米,宽18厘米,如果剪成大小相同的正方形(正方形边长是整厘米数)且没有剩余,那么正方形的边长最长是多少厘米?当正方形边长最大时,可以剪多少个?(在图中画一画,再列式计算)
28.一节数学课有小时,老师讲解大约用了全部时间的,同学们动手操作、交流大约用了全部时间的,其余时间用来做练习。做练习的时间大约是整节课时间的几分之几?
29.如下图,有一块长12米、宽8米的长方形草地,它的一个角上有一根木桩。如果有一只羊被拴在这根桩上,拴羊的绳子长6米,那么这只羊无法吃到草的草地面积是多少?
30.雯雯家打算给卧室的地面铺正方形地砖,要求只铺一种规格的地砖,且铺得既整齐又没有剩余。地面的形状是一个长42分米、宽36分米的长方形,有几种不同规格的正方形地砖可供雯雯家选择?如果选用最大规格的正方形地砖,那么需要多少块?(只考虑地砖的大小,地砖边长为整分米数)
31.城中公园有一个周长为31.4米的圆形草坪。
(1)现在准备为它安装自动旋转喷灌装置。有射程为5米、10米、20米的三种装置。你认为自动旋转喷灌装置选哪种比较合适?安装在什么地方?写出计算过程和你的想法。
(2)在草坪周围铺设一条宽为1米的水泥路,这条路的面积是多少平方米?
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案及试题解析
1.;2;;;
;;;
【解析】略
2.1;0;(或)
【分析】先观察分数分母,4、6、12的最小公倍数是12,将所有分数通分为分母是12的分数,然后按照从左到右的顺序进行同分母分数的加减运算;
观察式子发现,后面两个分数分母相同,一个数连续减去两个数,等于这个数减去这两个数的和,可先将后面两个分数相加,再用1减去它们的和,这样计算更简便;
观察到式子中和分母相同,根据加法交换律,交换和的位置,先计算+,得到整数1后,再加上,可简化计算过程。
【解析】
=
=
=
=
=
=
=
=
=
=(或)
3.;;
【分析】根据等式的性质解方程。
(1)方程两边同时加上,求出方程的解;
(2)方程两边同时减去,求出方程的解;
(3)方程两边同时减去,求出方程的解。
【解析】(1)
解:
(2)
解:
(3)
解:
4.18.24平方米;3.72平方分米
【分析】
(1)由图可知,正方形的对角线等于圆的直径,正方形的面积等于两个完全相同的等腰直角三角形面积的和,列方程求出圆的半径的平方,再根据“”求出圆的面积,涂色部分的面积=圆的面积-正方形的面积;
(2)由图可知,梯形的上底等于半圆的直径,梯形的高等于半圆的半径,涂色部分的面积=梯形的面积-半圆的面积,据此解答。
【解析】(1)解:设圆的半径为r米。
2r×r××2=32
2r2=32
2r2÷2=32÷2
r2=16
3.14×16=50.24(平方米)
50.24-32=18.24(平方米)
所以,涂色部分的面积是18.24平方米。
(2)4÷2=2(分米)
(4+6)×2÷2-3.14×22×
=10×2÷2-3.14×22×
=10-6.28
=3.72(平方分米)
所以,涂色部分的面积是3.72平方分米。
5.6
【分析】要找出能正好打包完40个零件的设定值,就是找出40的因数,但要去掉1和40这两个不符合条件的因数,据此解答。
【解析】40的因数有:1、2、4、5、8、10、20、40,共8个。
除去1和40,还有2、4、5、8、10、20,共6个。
即共有6种设定值。
6.4
【分析】把一张圆形纸片对折三次,平均分成了(2×2×2)份,扇形弧长×份数=圆的周长,根据圆的半径=周长÷圆周率÷2,列式计算即可。
【解析】2×2×2=8(份)
3.14×8=25.12(厘米)
25.12÷3.14÷2=4(厘米)
这张圆形纸片的半径是4厘米。
7. 7 3 假
【分析】分母是几分数单位就是几分之一,分子是几就有几个这样的分数单位,最小的质数是2,将2化成分母是5的假分数,求出两个分子的差,就是需要加上的分数单位的个数;
分子和分母相等或分子比分母大的分数叫假分数;
假分数化带分数:用分子除以分母。当分子不是分母的整数倍时,能化成带分数,商是带分数的整数部分,余数是分数部分的分子,分母不变。
【解析】2=、10-7=3(个);7÷5=1……2、=
的分数单位是,有7个这样的分数单位,再加上3个这样的单位就是最小质数。它是假分数,写成带分数形式是。
8.48;3;4;0.75
【分析】分数的基本性质:分数的分子和分母同时乘或除以相同的数(0除外),分数的大小不变;
分数与除法的关系:分子相当于被除数,分母相当于除数,分数线相当于除号;
分数化成小数,用分子除以分母即可.
【解析】18÷24===
==
=3÷4=0.75
即=18÷24==3÷4=0.75。
9.2m 56m
【分析】全部公有的质因数(公有质因数)相乘的积就是这两个数的最大公因数。全部公有的质因数和各自独立的质因数,它们连乘的积就是这两个数的最小公倍数。据此
【解析】
=56m
那么A和B最大公因数是2m,最小公倍数是56m。
10./12.56
【分析】把圆沿着它的半径平均分成若干份,然后把它拼成一个近似的长方形,这个长方形的周长比圆的周长增加了两个圆的半径的长度,据此用拼成的长方形周长比圆的周长多4厘米除以2,求出圆的半径,再根据圆的面积=解答即可。
【解析】4÷2=2(厘米)
3.14×
=3.14×4
=12.56(平方厘米)
或=(平方厘米)
所以原来圆的面积是平方厘米或12.56平方厘米。
11.;
【分析】求每班分多少箱,平均分的是具体的数量5箱,求的是具体的数量,用5÷8列式;求3个班分到这批图书的几分之几,把这批图书平均分成8份,求3份占8份的几分之几,用3÷8列式计算。
【解析】5÷8=(箱)
3÷8=
所以每个班分到箱,3个班分到这批图书的。
12.7 10 3 7
【分析】求明文(2,5)加密后的密文,把m=2,n=5代入3m+1和mn计算即可;求密文(10,21)的明文是多少,可得3m+1=10,求出m的值,再把m的值代入mn=21,求出n的值。
【解析】把m=2,n=5代入3m+1和mn,
3×2+1
=6+1
=7
2×5=10
明文(2,5)加密后是(7,10);
3m+1=10
解:3m+1-1=10-1
3m=9
3m÷3=9÷3
m=3
mn=21
解:3n=21
3n÷3=21÷3
n=7
密文(10,21)的明文是(3,7)。
13.2
【分析】已知电子钟,每到整点响铃一次,每过8分钟亮灯一次,也就是每60分钟响铃一次,现在中午12时整的时候既响铃又亮灯,说明下一次同时响铃又亮灯的间隔时间是60分钟和8分钟的最小公倍数,求两个数的最小公倍数,先将这两个数分别分解质因数,最小公倍数是两个数公有的质因数和各自独有的质因数的乘积。再用起始时间加上经过的时间,即可推算出下一次既响铃又亮灯的时刻。
【解析】60=2×2×3×5
8=2×2×2
60和8的最小公倍数是2×2×2×3×5=120
120分钟=2小时
12时+2小时=14时
14时就是下午2时。
下一次既响铃又亮灯的时刻是下午2时。
14.34 26
【分析】把x=22代入y=2x-10,然后求出y的值即可。把y=42代入y=2x-10,然后根据等式的性质1和2解出方程即可。
【解析】把x=22代入y=2x-10,
2×22-10
=44-10
=34(码)
把y=42代入y=2x-10,
2x-10=42
解:2x-10+10=42+10
2x=52
2x÷2=52÷2
x=26
小芳的脚长22厘米,是34码,爸爸脚长42码,是26厘米。
15.
【分析】根据题意,用碾米的质量除以时间,即可求出平均每分钟碾米的质量;用碾米的总时间除以质量,即可求出碾米1千克需要的时间。
【解析】50÷30=(千克)
30÷50=(分钟)
所以,一台碾米机30分钟碾米50千克,平均每分钟碾米千克,照这样计算,碾米1千克需分钟。
16./2.25/
【分析】求每根跳绳的长度,是把9米长的绳子平均分成4段,用这根绳子的长度除以4即可。
把这根绳子的长度看作单位“1”,平均分成4份,求每份占这根绳子的几分之几,用1除以4即可。
【解析】9÷4=(米)
1÷4=
每根跳绳长米,每根跳绳占这根绳子总长的。
17.B
【分析】2的倍数特征:个位上是0、2、4、6、8的数。
3的倍数特征:一个数各个数位上的数的和是3的倍数,这个数就是3的倍数。
5的倍数特征:个位上是0或5的数。
在整数除法中(被除数和除数不为0),如果商是整数且没有余数,我们就说被除数是除数的倍数,除数是被除数的因数。
【解析】A.160的个位上是“0”,160是2的倍数,所以2个2个地数能正好数完;
B.1+6+0=7,7不是3的倍数,则160不是3的倍数,所以3个3个地数不能正好数完;
C.160的个位上是“0”,160是5的倍数,所以5个5个地数能正好数完;
D.160÷10=16,160是10的倍数,所以10个10个地数能正好数完。
故答案为:B
18.C
【分析】A.表示相等关系的式子叫等式。含有未知数的等式叫做方程。据此判断。
B.偶数:像2,4,6,8…都是2的倍数的数叫做偶数。奇数:像1,3,5,7…不是2的倍数的数叫做奇数。据此判断。
C.质数:只有1和它本身两个因数的数叫做质数;合数:除了1和它本身外,还有其他因数的数叫合数。据此判断。
D.真分数:分子比分母小的分数叫做真分数,真分数小于1。假分数:分子比分母大或分子和分母相等的分数叫做假分数,假分数大于或者等于1。据此判断。
【解析】A.据分析可知,方程是等式的一种特殊形式,正确。
B.据分析可知,非0自然数中可分为奇数和偶数,正确。
C.非 0 自然数中包含 1,但 1 既不是质数也不是合数,因此把非 0 自然数直接分成质数和合数并不正确。
D.据分析可知,分数可分为真分数和假分数,正确。
故答案为:C
19.C
【分析】统计表,也就是表格,主要是用来呈现具体的数据值,方便查找和比较单个数据,但对于展示趋势可能不够直观;条形统计图能很容易看出数量的多少,适合比较不同类别的数据大小,但难以清晰体现连续时间上的变化;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况,能直观反映收视率的上升、下降或波动,最适合表现“变化”;据此选择即可。
【解析】根据分析,要展示第一季到第九季的收视变化情况,需要体现数据随时间变化的趋势,选用折线统计图比较好。
故答案为:C
20.A
【分析】如果接收到的密文为12、9,据此可知3m=12,2n-1=9,据此分别求出m和n即可得解。
【解析】3m=12
解:3m÷3=12÷3
m=4
2n-1=9
解:2n-1+1=9+1
2n=10
2n÷2=10÷2
n=5
如果接收到的密文为12、9,那么解密得到的明文应为4、5。
故答案为:A
21.B
【分析】首先明确这根绳子看作单位“1”,已知第一段占这根绳子的。
然后通过计算1-=,得出第二段绳子占这根绳子的比例为,这里是根据整体“1”减去第一段所占比例得到第二段所占比例。
最后比较两段绳子占比大小,因为>,所以第二段绳子占比更大,即第二段绳子长。
【解析】1-
=-
=,因为>,所以第二段绳子长。
故答案为:B
22.C
【分析】分析题目,开始时李师傅和王师傅两人一起修剪,根据修剪总面积=单位时间的修剪面积×修剪时间可知,S随着t的增长而增长较快,即直线比较陡峭;后面李师傅离开后,只剩下王师傅一个人修剪,此时S随着t的增长而增长的较慢,即直线比较平缓,据此解答即可。
【解析】
根据分析可知,能表示修剪时间t和修剪面积S之间的关系。
故答案为:C
23.C
【分析】根据题意,两个班的总人数都平均分成若干组,要使两个班每组的人数相等,那么每组最多的人数就是两班总人数的最大公因数;先把48和54分解质因数,然后把公有的相同质因数乘起来就是它们的最大公因数,据此解答。
【解析】48=2×2×2×2×3
54=2×3×3×3
48和54的最大公因数是:2×3=6
即每组最多有6人。
故答案为:C
24.B
【分析】已知一个圆的直径与一个正方形的边长相等,可以设正方形的边长、圆的直径都等于2;然后根据正方形的面积公式S=a2,圆的面积公式S=πr2,分别求出正方形和圆的面积,再比较大小,得出结论。
【解析】设正方形的边长、圆的直径都等于2;
正方形的面积:2×2=4
圆的面积:
3.14×(2÷2)2
=3.14×12
=3.14×1
=3.14
4>3.14
比较它们的面积,结果是正方形大。
故答案为:B
25.见详解
【分析】分数的意义指的是把单位“1”平均分成若干份,表示其中的1份或几份的数,表示把圆平均分成8份,把其中的5份涂色;=,先把第一个圆全部涂色,第二个圆涂出其中的5份;=1,即把整个图形全部涂色,据此解答。
【解析】=
=1
涂色如下:
26.30厘米;5根
【分析】把90厘米、60厘米长的两根彩带剪成同样长的短彩带且没有剩余,每根短彩带要最长,就是求90和60的最大公因数。
把90、60分解质因数后,把公有的相同质因数乘起来就是最大公因数。
再看90、60里面分别有几个这样的最大公因数,最后相加,即是一共可以剪成这样的短彩带的总根数。
【解析】90=2×3×3×5
60=2×2×3×5
90和60的最大公因数是:2×3×5=30
即每根短彩带最长是30厘米。
90÷30+60÷30
=3+2
=5(根)
答:每根短彩带最长是30厘米,一共可以剪成这样的短彩带5根。
27.12个,图见详解
【分析】由题意可知,正方形的边长为长方形长和宽的公因数,求出24和18的公因数,并找出最大公因数,也就是正方形的最大边长;可以剪最大正方形的个数=(长方形的长÷正方形的最大边长)×(长方形的宽÷正方形的最大边长)。
【解析】画图如下:
24的因数:1,2,3,4,6,8,12,24。
18的因数有:1,2,3,6,9,18。
24和18的公因数有:1,2,3,6。
正方形的最大边长为6厘米。
(24÷6)×(18÷6)
=4×3
=12(个)
答:正方形的边长最长是6厘米,当正方形边长最大时,可以剪12个。
28.
【分析】把一节数学课的时间看作单位“1”,用1减去老师讲解大约用全部时间的分率,减去同学们动手操作、交流大约用了全部时间的分率,即可求出做练习的时间大约是整节课时间的分率,据此解答。
【解析】1--
=-
=-
=
答:做练习的时间大约是整节课时间的。
29.67.74平方米
【分析】在一个角处拴一只羊,那么羊能吃到的范围是以绳子的长度为半径的圆的面积,根据圆的面积公式:S=πr2,长方形的面积:长×宽,把数代入求出两部分的面积,再用长方形的面积减去圆的面积即可求出无法吃到草的草地面积。
【解析】3.14×62÷4
=3.14×36÷4
=28.26(平方米)
12×8-28.26
=96-28.26
=67.74(平方米)
答:这只羊无法吃到草的草地面积是67.74平方米。
30.4;42块
【分析】首先求出42和36的公因数,它们之间有几个公因数就有几种不同规格的正方形地砖可选择;地面是一个长方形,用长和宽分别除以最大公因数,可得长能放的块数和宽能放的块数,最后相乘,就是需要砖的块数。
【解析】42的因数有:1,2,3,6,7,14,21,42
36的因数有:1,2,3,4,6,9,12,18,36
42和36的公因数有:1,2,3,6,有4个公因数。
42和36的最大公因数是:6
42÷6=7(块)
36÷6=6(块)
6×7=42(块)
答:有4种不同规格的正方形地砖可供雯雯家选择。如果选用最大规格的正方形地砖,那么需要42块。
31.(1)见详解;
(2)34.54平方米
【分析】(1)根据圆的特征,安装是圆心的位置比较合适,根据圆的周长公式:C=2πr,那么r=C÷π÷2,据此求出半径,然后与喷灌的射程进行比较即可。
(2)根据环形面积公式:S=π(R2-r2),把数据代入公式解答。
【解析】(1)31.4÷3.14÷2
=10÷2
=5(米)
答:选择射程5米的比较合适,安装是圆心的位置。
(2)5+1=6(米)
3.14×(62-52)
=3.14×(36-25)
=3.14×11
=34.54(平方米)
答:这条路的面积是34.54平方米。
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
中小学教育资源及组卷应用平台
2024-2025学年五年级下学期数学期末思维提升培优卷
考试时间:90分钟;试卷总分:100分;
学校: 班级: 姓名: 成绩:
注意事项:
答题前填写好自己的姓名、班级、考号等信息。
请将答案正确填写在答题区域,注意书写工整,格式正确,卷面整洁。
一、计算题。(共26分)
1.直接写出得数。(共8分)
2.计算下面各题,能简算的要简算。(共6分)
3.解方程(共6分)
4.求涂色部分的面积。(共6分)
二、填空题。(每空1分,共24分)
5.智能车间可以通过给机械臂输入设定值,让机械臂自动将相同个数的零件装箱打包。一批零件有40个,如果不能每次单个打包,也不能一次全部打包,且最后正好打包完,那么共有( )种设定值。
6.小明把一张圆形纸片对折三次,得到下面的扇形(弧长3.14厘米),这张圆形纸片的半径是( )厘米。
7.的分数单位是( ),有( )个这样的分数单位,再加上( )个这样的单位就是最小质数。它是( )分数,写成带分数形式是( )。
8.=18÷24==3÷( )=( )(填小数)。
9.如果,,那么A和B最大公因数是( ),最小公倍数是( )。
10.将一个圆平均分成若干份,拼成一个近似长方形,拼成的长方形周长比圆的周长多4厘米,原来圆的面积是( )平方厘米。
11.学校买来5箱图书,每箱40本,平均分给五年级8个班。每个班分到箱,3个班分到这批图书的。
12.为了确保通信安全,信息需要加密传输。现规定加密规则:明文(m,n)加密成密文后是(3m+1,mn)。按照这样的加密规则,明文(2,5)加密后是( , ),密文(10,21)的明文是( , )。
13.有一个电子钟,每到整点响铃一次,每过8分钟亮灯一次。如果这个电子钟在中午12时整的时候既响铃又亮灯,那么下一次既响铃又亮灯的时刻是下午( )时。
14.鞋子尺码通常用“码”或“厘米”作单位,它们之间的换算关系是y=2x-10(y表示码数,x表示厘米数)。小芳的脚长22厘米,是( )码,爸爸脚长42码,是( )厘米。
15.一台碾米机30分钟碾米50千克,平均每分钟碾米( )千克,照这样计算,碾米1千克需( )分钟。(填分数)
16.跳绳在中小学成为重要的体育活动项目。体育老师把9米长的绳子平均分成4段,每一段做成一根跳绳。每根跳绳长( )米,每根跳绳占这根绳子总长的( )。
三、选择题。(每题1分,共8分)
17.秦始皇陵兵马俑是世界八大奇迹之一。二号坑第一单元阵心由八路面东的160个蹲跪式弩兵组成,壮壮用下面的方法数这些弩兵俑,不能正好数完的是( )。
A.2个2个地数 B.3个3个地数 C.5个5个地数 D.10个10个地数
18.如图中,不正确的是( )。
A. B.
C. D.
19.今年3月10日,《中国诗词大会》(第九季)火热开播。王小萌同学想绘制第一季至第九季的收视变化情况,选用( )比较好。
A.统计表 B.条形统计图 C.折线统计图 D.以上都可以
20.为确保信息安全,信息需要加密传输,发送时是:明文→密文(加密过程),接收时是:密文→明文(解密过程)。已知加密规则为:明文m、n对应的密文为3m、2n-1,如果接收到的密文为12、9,那么解密得到的明文应为( )。
A.4、5 B.36、17 C.4、4 D.36、4
21.一根绳子截成两段,第一段占这根绳子的,第二段长米。这两段绳子相比,( )。
A.第一段长 B.第二段长
C.两段一样长 D.无法比较
22.李师傅和王师傅一起修剪一块草坪,两人修剪草坪的速度相同。一开始两人同时修剪,修剪一段时间后,李师傅有事离开,只留下王师傅一人修剪。在下面四幅图中,图( )能表示修剪时间t和修剪面积S之间的关系。
A. B.
C. D.
23.学校组织春游,五(1)班有48人,五(2)班有54人,如果把两个班的都平均分成若干组,要使两个班每组的人数相等,每组最多有( )人。
A.2 B.3 C.6 D.8
24.一个圆的直径与一个正方形的边长相等。比较它们的面积,结果是( )。
A.圆大 B.正方形大 C.面积相等
四、操作题。(共6分)
25.在图中涂色表示下面的分数。
五、解答题。(每题6分,共36分)
26.五(4)班学生为庆祝“六一”儿童节,需要用彩带装饰花篮。如果把下边的两根彩带剪成同样长的短彩带且没有剩余,每根短彩带最长是多少厘米?一共可以剪成这样的短彩带多少根?
27.一张长方形纸长24厘米,宽18厘米,如果剪成大小相同的正方形(正方形边长是整厘米数)且没有剩余,那么正方形的边长最长是多少厘米?当正方形边长最大时,可以剪多少个?(在图中画一画,再列式计算)
28.一节数学课有小时,老师讲解大约用了全部时间的,同学们动手操作、交流大约用了全部时间的,其余时间用来做练习。做练习的时间大约是整节课时间的几分之几?
29.如下图,有一块长12米、宽8米的长方形草地,它的一个角上有一根木桩。如果有一只羊被拴在这根桩上,拴羊的绳子长6米,那么这只羊无法吃到草的草地面积是多少?
30.雯雯家打算给卧室的地面铺正方形地砖,要求只铺一种规格的地砖,且铺得既整齐又没有剩余。地面的形状是一个长42分米、宽36分米的长方形,有几种不同规格的正方形地砖可供雯雯家选择?如果选用最大规格的正方形地砖,那么需要多少块?(只考虑地砖的大小,地砖边长为整分米数)
31.城中公园有一个周长为31.4米的圆形草坪。
(1)现在准备为它安装自动旋转喷灌装置。有射程为5米、10米、20米的三种装置。你认为自动旋转喷灌装置选哪种比较合适?安装在什么地方?写出计算过程和你的想法。
(2)在草坪周围铺设一条宽为1米的水泥路,这条路的面积是多少平方米?
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案及试题解析
1.;2;;;
;;;
【解析】略
2.1;0;(或)
【分析】先观察分数分母,4、6、12的最小公倍数是12,将所有分数通分为分母是12的分数,然后按照从左到右的顺序进行同分母分数的加减运算;
观察式子发现,后面两个分数分母相同,一个数连续减去两个数,等于这个数减去这两个数的和,可先将后面两个分数相加,再用1减去它们的和,这样计算更简便;
观察到式子中和分母相同,根据加法交换律,交换和的位置,先计算+,得到整数1后,再加上,可简化计算过程。
【解析】
=
=
=
=
=
=
=
=
=
=(或)
3.;;
【分析】根据等式的性质解方程。
(1)方程两边同时加上,求出方程的解;
(2)方程两边同时减去,求出方程的解;
(3)方程两边同时减去,求出方程的解。
【解析】(1)
解:
(2)
解:
(3)
解:
4.18.24平方米;3.72平方分米
【分析】
(1)由图可知,正方形的对角线等于圆的直径,正方形的面积等于两个完全相同的等腰直角三角形面积的和,列方程求出圆的半径的平方,再根据“”求出圆的面积,涂色部分的面积=圆的面积-正方形的面积;
(2)由图可知,梯形的上底等于半圆的直径,梯形的高等于半圆的半径,涂色部分的面积=梯形的面积-半圆的面积,据此解答。
【解析】(1)解:设圆的半径为r米。
2r×r××2=32
2r2=32
2r2÷2=32÷2
r2=16
3.14×16=50.24(平方米)
50.24-32=18.24(平方米)
所以,涂色部分的面积是18.24平方米。
(2)4÷2=2(分米)
(4+6)×2÷2-3.14×22×
=10×2÷2-3.14×22×
=10-6.28
=3.72(平方分米)
所以,涂色部分的面积是3.72平方分米。
5.6
【分析】要找出能正好打包完40个零件的设定值,就是找出40的因数,但要去掉1和40这两个不符合条件的因数,据此解答。
【解析】40的因数有:1、2、4、5、8、10、20、40,共8个。
除去1和40,还有2、4、5、8、10、20,共6个。
即共有6种设定值。
6.4
【分析】把一张圆形纸片对折三次,平均分成了(2×2×2)份,扇形弧长×份数=圆的周长,根据圆的半径=周长÷圆周率÷2,列式计算即可。
【解析】2×2×2=8(份)
3.14×8=25.12(厘米)
25.12÷3.14÷2=4(厘米)
这张圆形纸片的半径是4厘米。
7. 7 3 假
【分析】分母是几分数单位就是几分之一,分子是几就有几个这样的分数单位,最小的质数是2,将2化成分母是5的假分数,求出两个分子的差,就是需要加上的分数单位的个数;
分子和分母相等或分子比分母大的分数叫假分数;
假分数化带分数:用分子除以分母。当分子不是分母的整数倍时,能化成带分数,商是带分数的整数部分,余数是分数部分的分子,分母不变。
【解析】2=、10-7=3(个);7÷5=1……2、=
的分数单位是,有7个这样的分数单位,再加上3个这样的单位就是最小质数。它是假分数,写成带分数形式是。
8.48;3;4;0.75
【分析】分数的基本性质:分数的分子和分母同时乘或除以相同的数(0除外),分数的大小不变;
分数与除法的关系:分子相当于被除数,分母相当于除数,分数线相当于除号;
分数化成小数,用分子除以分母即可.
【解析】18÷24===
==
=3÷4=0.75
即=18÷24==3÷4=0.75。
9.2m 56m
【分析】全部公有的质因数(公有质因数)相乘的积就是这两个数的最大公因数。全部公有的质因数和各自独立的质因数,它们连乘的积就是这两个数的最小公倍数。据此
【解析】
=56m
那么A和B最大公因数是2m,最小公倍数是56m。
10./12.56
【分析】把圆沿着它的半径平均分成若干份,然后把它拼成一个近似的长方形,这个长方形的周长比圆的周长增加了两个圆的半径的长度,据此用拼成的长方形周长比圆的周长多4厘米除以2,求出圆的半径,再根据圆的面积=解答即可。
【解析】4÷2=2(厘米)
3.14×
=3.14×4
=12.56(平方厘米)
或=(平方厘米)
所以原来圆的面积是平方厘米或12.56平方厘米。
11.;
【分析】求每班分多少箱,平均分的是具体的数量5箱,求的是具体的数量,用5÷8列式;求3个班分到这批图书的几分之几,把这批图书平均分成8份,求3份占8份的几分之几,用3÷8列式计算。
【解析】5÷8=(箱)
3÷8=
所以每个班分到箱,3个班分到这批图书的。
12.7 10 3 7
【分析】求明文(2,5)加密后的密文,把m=2,n=5代入3m+1和mn计算即可;求密文(10,21)的明文是多少,可得3m+1=10,求出m的值,再把m的值代入mn=21,求出n的值。
【解析】把m=2,n=5代入3m+1和mn,
3×2+1
=6+1
=7
2×5=10
明文(2,5)加密后是(7,10);
3m+1=10
解:3m+1-1=10-1
3m=9
3m÷3=9÷3
m=3
mn=21
解:3n=21
3n÷3=21÷3
n=7
密文(10,21)的明文是(3,7)。
13.2
【分析】已知电子钟,每到整点响铃一次,每过8分钟亮灯一次,也就是每60分钟响铃一次,现在中午12时整的时候既响铃又亮灯,说明下一次同时响铃又亮灯的间隔时间是60分钟和8分钟的最小公倍数,求两个数的最小公倍数,先将这两个数分别分解质因数,最小公倍数是两个数公有的质因数和各自独有的质因数的乘积。再用起始时间加上经过的时间,即可推算出下一次既响铃又亮灯的时刻。
【解析】60=2×2×3×5
8=2×2×2
60和8的最小公倍数是2×2×2×3×5=120
120分钟=2小时
12时+2小时=14时
14时就是下午2时。
下一次既响铃又亮灯的时刻是下午2时。
14.34 26
【分析】把x=22代入y=2x-10,然后求出y的值即可。把y=42代入y=2x-10,然后根据等式的性质1和2解出方程即可。
【解析】把x=22代入y=2x-10,
2×22-10
=44-10
=34(码)
把y=42代入y=2x-10,
2x-10=42
解:2x-10+10=42+10
2x=52
2x÷2=52÷2
x=26
小芳的脚长22厘米,是34码,爸爸脚长42码,是26厘米。
15.
【分析】根据题意,用碾米的质量除以时间,即可求出平均每分钟碾米的质量;用碾米的总时间除以质量,即可求出碾米1千克需要的时间。
【解析】50÷30=(千克)
30÷50=(分钟)
所以,一台碾米机30分钟碾米50千克,平均每分钟碾米千克,照这样计算,碾米1千克需分钟。
16./2.25/
【分析】求每根跳绳的长度,是把9米长的绳子平均分成4段,用这根绳子的长度除以4即可。
把这根绳子的长度看作单位“1”,平均分成4份,求每份占这根绳子的几分之几,用1除以4即可。
【解析】9÷4=(米)
1÷4=
每根跳绳长米,每根跳绳占这根绳子总长的。
17.B
【分析】2的倍数特征:个位上是0、2、4、6、8的数。
3的倍数特征:一个数各个数位上的数的和是3的倍数,这个数就是3的倍数。
5的倍数特征:个位上是0或5的数。
在整数除法中(被除数和除数不为0),如果商是整数且没有余数,我们就说被除数是除数的倍数,除数是被除数的因数。
【解析】A.160的个位上是“0”,160是2的倍数,所以2个2个地数能正好数完;
B.1+6+0=7,7不是3的倍数,则160不是3的倍数,所以3个3个地数不能正好数完;
C.160的个位上是“0”,160是5的倍数,所以5个5个地数能正好数完;
D.160÷10=16,160是10的倍数,所以10个10个地数能正好数完。
故答案为:B
18.C
【分析】A.表示相等关系的式子叫等式。含有未知数的等式叫做方程。据此判断。
B.偶数:像2,4,6,8…都是2的倍数的数叫做偶数。奇数:像1,3,5,7…不是2的倍数的数叫做奇数。据此判断。
C.质数:只有1和它本身两个因数的数叫做质数;合数:除了1和它本身外,还有其他因数的数叫合数。据此判断。
D.真分数:分子比分母小的分数叫做真分数,真分数小于1。假分数:分子比分母大或分子和分母相等的分数叫做假分数,假分数大于或者等于1。据此判断。
【解析】A.据分析可知,方程是等式的一种特殊形式,正确。
B.据分析可知,非0自然数中可分为奇数和偶数,正确。
C.非 0 自然数中包含 1,但 1 既不是质数也不是合数,因此把非 0 自然数直接分成质数和合数并不正确。
D.据分析可知,分数可分为真分数和假分数,正确。
故答案为:C
19.C
【分析】统计表,也就是表格,主要是用来呈现具体的数据值,方便查找和比较单个数据,但对于展示趋势可能不够直观;条形统计图能很容易看出数量的多少,适合比较不同类别的数据大小,但难以清晰体现连续时间上的变化;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况,能直观反映收视率的上升、下降或波动,最适合表现“变化”;据此选择即可。
【解析】根据分析,要展示第一季到第九季的收视变化情况,需要体现数据随时间变化的趋势,选用折线统计图比较好。
故答案为:C
20.A
【分析】如果接收到的密文为12、9,据此可知3m=12,2n-1=9,据此分别求出m和n即可得解。
【解析】3m=12
解:3m÷3=12÷3
m=4
2n-1=9
解:2n-1+1=9+1
2n=10
2n÷2=10÷2
n=5
如果接收到的密文为12、9,那么解密得到的明文应为4、5。
故答案为:A
21.B
【分析】首先明确这根绳子看作单位“1”,已知第一段占这根绳子的。
然后通过计算1-=,得出第二段绳子占这根绳子的比例为,这里是根据整体“1”减去第一段所占比例得到第二段所占比例。
最后比较两段绳子占比大小,因为>,所以第二段绳子占比更大,即第二段绳子长。
【解析】1-
=-
=,因为>,所以第二段绳子长。
故答案为:B
22.C
【分析】分析题目,开始时李师傅和王师傅两人一起修剪,根据修剪总面积=单位时间的修剪面积×修剪时间可知,S随着t的增长而增长较快,即直线比较陡峭;后面李师傅离开后,只剩下王师傅一个人修剪,此时S随着t的增长而增长的较慢,即直线比较平缓,据此解答即可。
【解析】
根据分析可知,能表示修剪时间t和修剪面积S之间的关系。
故答案为:C
23.C
【分析】根据题意,两个班的总人数都平均分成若干组,要使两个班每组的人数相等,那么每组最多的人数就是两班总人数的最大公因数;先把48和54分解质因数,然后把公有的相同质因数乘起来就是它们的最大公因数,据此解答。
【解析】48=2×2×2×2×3
54=2×3×3×3
48和54的最大公因数是:2×3=6
即每组最多有6人。
故答案为:C
24.B
【分析】已知一个圆的直径与一个正方形的边长相等,可以设正方形的边长、圆的直径都等于2;然后根据正方形的面积公式S=a2,圆的面积公式S=πr2,分别求出正方形和圆的面积,再比较大小,得出结论。
【解析】设正方形的边长、圆的直径都等于2;
正方形的面积:2×2=4
圆的面积:
3.14×(2÷2)2
=3.14×12
=3.14×1
=3.14
4>3.14
比较它们的面积,结果是正方形大。
故答案为:B
25.见详解
【分析】分数的意义指的是把单位“1”平均分成若干份,表示其中的1份或几份的数,表示把圆平均分成8份,把其中的5份涂色;=,先把第一个圆全部涂色,第二个圆涂出其中的5份;=1,即把整个图形全部涂色,据此解答。
【解析】=
=1
涂色如下:
26.30厘米;5根
【分析】把90厘米、60厘米长的两根彩带剪成同样长的短彩带且没有剩余,每根短彩带要最长,就是求90和60的最大公因数。
把90、60分解质因数后,把公有的相同质因数乘起来就是最大公因数。
再看90、60里面分别有几个这样的最大公因数,最后相加,即是一共可以剪成这样的短彩带的总根数。
【解析】90=2×3×3×5
60=2×2×3×5
90和60的最大公因数是:2×3×5=30
即每根短彩带最长是30厘米。
90÷30+60÷30
=3+2
=5(根)
答:每根短彩带最长是30厘米,一共可以剪成这样的短彩带5根。
27.12个,图见详解
【分析】由题意可知,正方形的边长为长方形长和宽的公因数,求出24和18的公因数,并找出最大公因数,也就是正方形的最大边长;可以剪最大正方形的个数=(长方形的长÷正方形的最大边长)×(长方形的宽÷正方形的最大边长)。
【解析】画图如下:
24的因数:1,2,3,4,6,8,12,24。
18的因数有:1,2,3,6,9,18。
24和18的公因数有:1,2,3,6。
正方形的最大边长为6厘米。
(24÷6)×(18÷6)
=4×3
=12(个)
答:正方形的边长最长是6厘米,当正方形边长最大时,可以剪12个。
28.
【分析】把一节数学课的时间看作单位“1”,用1减去老师讲解大约用全部时间的分率,减去同学们动手操作、交流大约用了全部时间的分率,即可求出做练习的时间大约是整节课时间的分率,据此解答。
【解析】1--
=-
=-
=
答:做练习的时间大约是整节课时间的。
29.67.74平方米
【分析】在一个角处拴一只羊,那么羊能吃到的范围是以绳子的长度为半径的圆的面积,根据圆的面积公式:S=πr2,长方形的面积:长×宽,把数代入求出两部分的面积,再用长方形的面积减去圆的面积即可求出无法吃到草的草地面积。
【解析】3.14×62÷4
=3.14×36÷4
=28.26(平方米)
12×8-28.26
=96-28.26
=67.74(平方米)
答:这只羊无法吃到草的草地面积是67.74平方米。
30.4;42块
【分析】首先求出42和36的公因数,它们之间有几个公因数就有几种不同规格的正方形地砖可选择;地面是一个长方形,用长和宽分别除以最大公因数,可得长能放的块数和宽能放的块数,最后相乘,就是需要砖的块数。
【解析】42的因数有:1,2,3,6,7,14,21,42
36的因数有:1,2,3,4,6,9,12,18,36
42和36的公因数有:1,2,3,6,有4个公因数。
42和36的最大公因数是:6
42÷6=7(块)
36÷6=6(块)
6×7=42(块)
答:有4种不同规格的正方形地砖可供雯雯家选择。如果选用最大规格的正方形地砖,那么需要42块。
31.(1)见详解;
(2)34.54平方米
【分析】(1)根据圆的特征,安装是圆心的位置比较合适,根据圆的周长公式:C=2πr,那么r=C÷π÷2,据此求出半径,然后与喷灌的射程进行比较即可。
(2)根据环形面积公式:S=π(R2-r2),把数据代入公式解答。
【解析】(1)31.4÷3.14÷2
=10÷2
=5(米)
答:选择射程5米的比较合适,安装是圆心的位置。
(2)5+1=6(米)
3.14×(62-52)
=3.14×(36-25)
=3.14×11
=34.54(平方米)
答:这条路的面积是34.54平方米。
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
同课章节目录
