(3)勾股定理的应用(含详解)七年级数学北师大版(2024)暑假作业
文档属性
| 名称 | (3)勾股定理的应用(含详解)七年级数学北师大版(2024)暑假作业 |  | |
| 格式 | docx | ||
| 文件大小 | 639.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-10 17:01:04 | ||
图片预览


文档简介
(3)勾股定理的应用——七年级数学北师大版(2024)暑假作业
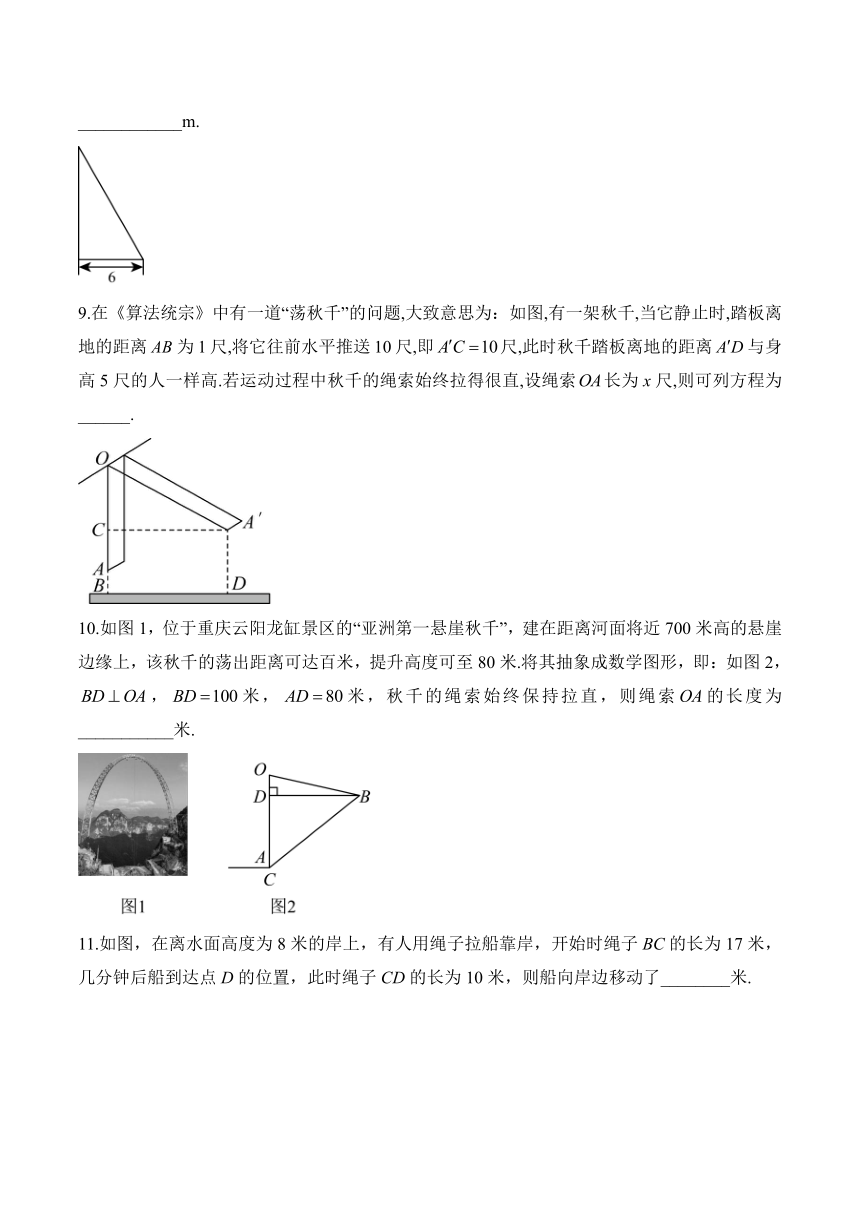
1.如图,有一个水池,水面是一个边长为10尺的正方形,在水池的中央有一根新生的芦苇,它高出水面1尺,如果把这根芦苇垂直拉向岸边,它的顶端恰好到达岸边的水面,则这个水池的深度是( )尺.
A.26 B.24 C.13 D.12
2.如图,在同一水平线上有相距8 m的两棵树AB和CD,其中树AB高8 m,大风将树AB折断,树的顶端B恰好落在AC的中点E处,则树的折断点离地面的高度是( )
A.6 m B.5 m C.4 m D.3 m
3.如图,小亮将升旗的绳子拉到旗杆底端,绳子末端刚好接触到地面,然后将绳子末端拉到距离旗杆8m处,发现此时绳子末端距离地面2m,则旗杆的高度(滑轮上方的部分忽略不计)为( )
A.12m B.13m C.16m D.17m
4.将一支铅笔按如图所示的方式先后放入粗细相同的两个型号圆柱型笔筒,笔筒的高度分别是和,两个铅笔露在笔筒外面的部分分别为和,则铅笔的长是( )
A. B. C. D.
5.用一张纸片剪出一个空洞,空洞由边长分别为a,b的两个正方形和斜边为c的两个直角三角形组成,如图所示,下列表示空洞面积的式子正确的是( )
A. B. C. D.
6.勾股定理是用代数思想解决几何问题最重要的工具,也是数形结合的纽带之一.如图,当秋千静止时,踏板B离地的垂直高度,将它往前推至C处时(即水平距离),踏板离地的垂直高度,它的绳索始终拉直,则绳索的长是( )
A. B. C. D.
7.如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7米,顶端距离地面2.4米,如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面2米,那么小巷的宽度为( )
A.0.7米 B.1.5米 C.2.2米 D.2.4米
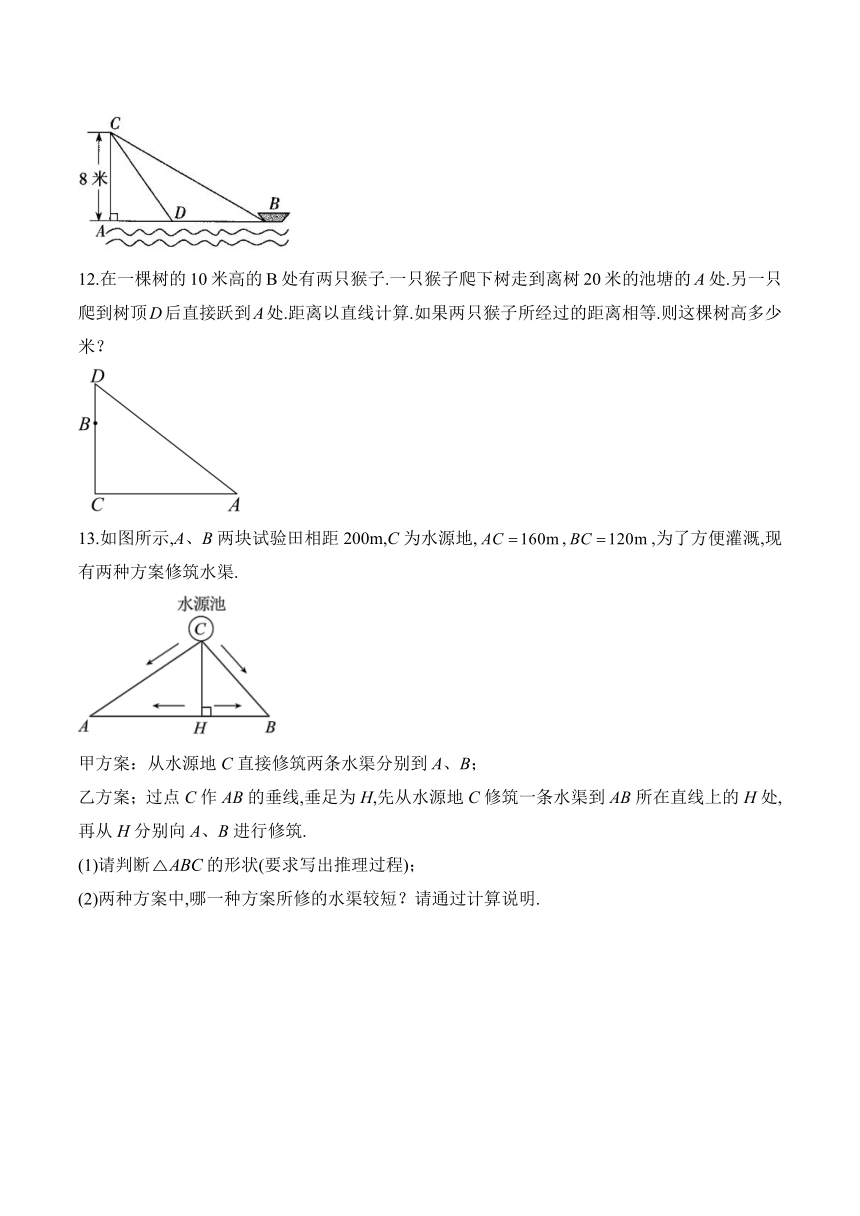
8.如图,小明想知道学校旗杆的高度,他将升旗的绳子拉到旗杆底端,并在绳子上打了一个结,然后将绳子拉到离旗杆底端处,发现此时绳子底端距离打结处,则旗杆的高度为____________m.
9.在《算法统宗》中有一道“荡秋千”的问题,大致意思为:如图,有一架秋千,当它静止时,踏板离地的距离为1尺,将它往前水平推送10尺,即尺,此时秋千踏板离地的距离与身高5尺的人一样高.若运动过程中秋千的绳索始终拉得很直,设绳索长为x尺,则可列方程为______.
10.如图1,位于重庆云阳龙缸景区的“亚洲第一悬崖秋千”,建在距离河面将近700米高的悬崖边缘上,该秋千的荡出距离可达百米,提升高度可至80米.将其抽象成数学图形,即:如图2,,米,米,秋千的绳索始终保持拉直,则绳索的长度为___________米.
11.如图,在离水面高度为8米的岸上,有人用绳子拉船靠岸,开始时绳子BC的长为17米,几分钟后船到达点D的位置,此时绳子CD的长为10米,则船向岸边移动了________米.
12.在一棵树的10米高的B处有两只猴子.一只猴子爬下树走到离树20米的池塘的A处.另一只爬到树顶D后直接跃到A处.距离以直线计算.如果两只猴子所经过的距离相等.则这棵树高多少米?
13.如图所示,A、B两块试验田相距200m,C为水源地,,,为了方便灌溉,现有两种方案修筑水渠.
甲方案:从水源地C直接修筑两条水渠分别到A、B;
乙方案;过点C作AB的垂线,垂足为H,先从水源地C修筑一条水渠到AB所在直线上的H处,再从H分别向A、B进行修筑.
(1)请判断的形状(要求写出推理过程);
(2)两种方案中,哪一种方案所修的水渠较短?请通过计算说明.
答案以及解析
1.答案:D
解析:由题意可知:(尺)
设水深x尺,则芦苇长尺,
由勾股定理得:
解得:,
∴这个水池的深度是12尺.
故选D.
2.答案:D
解析:如图所示:
根据题意可得,,设,则,
在中,
,
即,
解得:,
树的折断点离地面的高度是.
故选:D.
3.答案:D
解析:设旗杆高度为x,则,,,
在中,,即,
解得:,
即旗杆的高度为17米.
故选D.
4.答案:D
解析:设铅笔长度为,
由题意得,,
解得,,
故铅笔的长为;
故选:D.
5.答案:B
解析:观察图形可知:空洞面积为,
故选:B.
6.答案:A
解析:由题意可知,,,,
,
设,则,
由勾股定理得:,
,
解得:,
即绳索的长是,
故:A.
7.答案:C
解析:由题意得.在中,,米,米,.在中,,米,,..,米,(米).故选C.
8.答案:8
解析:设旗杆的高为x米,则绳子长为米,
由勾股定理得:,解得;
即旗杆的高度是8米;
故答案为:8.
9.答案:
解析:根据题意列方程得,
故答案为:.
10.答案:102.5
解析:由题意可知,,
,
,
设米,则米,
在中,由勾股定理得:,
即,
解得:,
即绳索的长度为102.5米,
故答案为:102.5.
11.答案:9
解析:在中,,米,米,,米,米,,米,米,即船向岸边移动了9米,故答案为9.
12.答案:这棵树高15m
解析:如图,根据题意,米,米,
设树的高度为米,因两只猴子所经过的距离相等都为30米.
在中,可有,
∴,
解得.
故这棵树高15m
13.答案:(1)是直角三角形,理由见解析
(2)甲方案所修的水渠较短;理由见解析
解析:(1)是直角三角形;
理由如下:
∴,,
∴,
∴是直角三角形,;
(2)甲方案所修的水渠较短;
理由如下:
∵是直角三角形,
∴的面积,
∴(m),
∵,,
∴,
∴甲方案所修的水渠较短.
1.如图,有一个水池,水面是一个边长为10尺的正方形,在水池的中央有一根新生的芦苇,它高出水面1尺,如果把这根芦苇垂直拉向岸边,它的顶端恰好到达岸边的水面,则这个水池的深度是( )尺.
A.26 B.24 C.13 D.12
2.如图,在同一水平线上有相距8 m的两棵树AB和CD,其中树AB高8 m,大风将树AB折断,树的顶端B恰好落在AC的中点E处,则树的折断点离地面的高度是( )
A.6 m B.5 m C.4 m D.3 m
3.如图,小亮将升旗的绳子拉到旗杆底端,绳子末端刚好接触到地面,然后将绳子末端拉到距离旗杆8m处,发现此时绳子末端距离地面2m,则旗杆的高度(滑轮上方的部分忽略不计)为( )
A.12m B.13m C.16m D.17m
4.将一支铅笔按如图所示的方式先后放入粗细相同的两个型号圆柱型笔筒,笔筒的高度分别是和,两个铅笔露在笔筒外面的部分分别为和,则铅笔的长是( )
A. B. C. D.
5.用一张纸片剪出一个空洞,空洞由边长分别为a,b的两个正方形和斜边为c的两个直角三角形组成,如图所示,下列表示空洞面积的式子正确的是( )
A. B. C. D.
6.勾股定理是用代数思想解决几何问题最重要的工具,也是数形结合的纽带之一.如图,当秋千静止时,踏板B离地的垂直高度,将它往前推至C处时(即水平距离),踏板离地的垂直高度,它的绳索始终拉直,则绳索的长是( )
A. B. C. D.
7.如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7米,顶端距离地面2.4米,如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面2米,那么小巷的宽度为( )
A.0.7米 B.1.5米 C.2.2米 D.2.4米
8.如图,小明想知道学校旗杆的高度,他将升旗的绳子拉到旗杆底端,并在绳子上打了一个结,然后将绳子拉到离旗杆底端处,发现此时绳子底端距离打结处,则旗杆的高度为____________m.
9.在《算法统宗》中有一道“荡秋千”的问题,大致意思为:如图,有一架秋千,当它静止时,踏板离地的距离为1尺,将它往前水平推送10尺,即尺,此时秋千踏板离地的距离与身高5尺的人一样高.若运动过程中秋千的绳索始终拉得很直,设绳索长为x尺,则可列方程为______.
10.如图1,位于重庆云阳龙缸景区的“亚洲第一悬崖秋千”,建在距离河面将近700米高的悬崖边缘上,该秋千的荡出距离可达百米,提升高度可至80米.将其抽象成数学图形,即:如图2,,米,米,秋千的绳索始终保持拉直,则绳索的长度为___________米.
11.如图,在离水面高度为8米的岸上,有人用绳子拉船靠岸,开始时绳子BC的长为17米,几分钟后船到达点D的位置,此时绳子CD的长为10米,则船向岸边移动了________米.
12.在一棵树的10米高的B处有两只猴子.一只猴子爬下树走到离树20米的池塘的A处.另一只爬到树顶D后直接跃到A处.距离以直线计算.如果两只猴子所经过的距离相等.则这棵树高多少米?
13.如图所示,A、B两块试验田相距200m,C为水源地,,,为了方便灌溉,现有两种方案修筑水渠.
甲方案:从水源地C直接修筑两条水渠分别到A、B;
乙方案;过点C作AB的垂线,垂足为H,先从水源地C修筑一条水渠到AB所在直线上的H处,再从H分别向A、B进行修筑.
(1)请判断的形状(要求写出推理过程);
(2)两种方案中,哪一种方案所修的水渠较短?请通过计算说明.
答案以及解析
1.答案:D
解析:由题意可知:(尺)
设水深x尺,则芦苇长尺,
由勾股定理得:
解得:,
∴这个水池的深度是12尺.
故选D.
2.答案:D
解析:如图所示:
根据题意可得,,设,则,
在中,
,
即,
解得:,
树的折断点离地面的高度是.
故选:D.
3.答案:D
解析:设旗杆高度为x,则,,,
在中,,即,
解得:,
即旗杆的高度为17米.
故选D.
4.答案:D
解析:设铅笔长度为,
由题意得,,
解得,,
故铅笔的长为;
故选:D.
5.答案:B
解析:观察图形可知:空洞面积为,
故选:B.
6.答案:A
解析:由题意可知,,,,
,
设,则,
由勾股定理得:,
,
解得:,
即绳索的长是,
故:A.
7.答案:C
解析:由题意得.在中,,米,米,.在中,,米,,..,米,(米).故选C.
8.答案:8
解析:设旗杆的高为x米,则绳子长为米,
由勾股定理得:,解得;
即旗杆的高度是8米;
故答案为:8.
9.答案:
解析:根据题意列方程得,
故答案为:.
10.答案:102.5
解析:由题意可知,,
,
,
设米,则米,
在中,由勾股定理得:,
即,
解得:,
即绳索的长度为102.5米,
故答案为:102.5.
11.答案:9
解析:在中,,米,米,,米,米,,米,米,即船向岸边移动了9米,故答案为9.
12.答案:这棵树高15m
解析:如图,根据题意,米,米,
设树的高度为米,因两只猴子所经过的距离相等都为30米.
在中,可有,
∴,
解得.
故这棵树高15m
13.答案:(1)是直角三角形,理由见解析
(2)甲方案所修的水渠较短;理由见解析
解析:(1)是直角三角形;
理由如下:
∴,,
∴,
∴是直角三角形,;
(2)甲方案所修的水渠较短;
理由如下:
∵是直角三角形,
∴的面积,
∴(m),
∵,,
∴,
∴甲方案所修的水渠较短.
同课章节目录
