(1)探索勾股定理(含详解)七年级数学北师大版(2024)暑假作业
文档属性
| 名称 | (1)探索勾股定理(含详解)七年级数学北师大版(2024)暑假作业 |  | |
| 格式 | docx | ||
| 文件大小 | 529.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-10 17:01:45 | ||
图片预览



文档简介
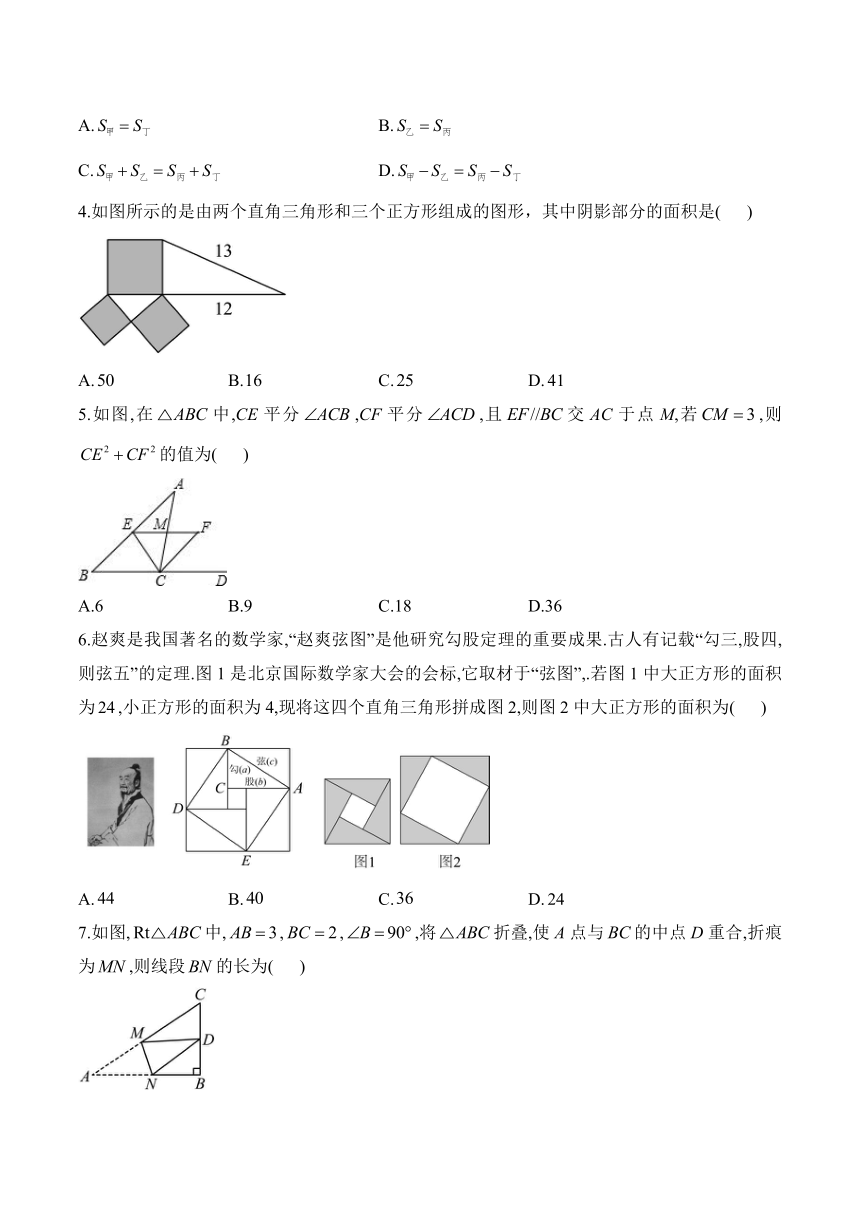
(1)探索勾股定理——七年级数学北师大版(2024)暑假作业
一、知识详解
勾股定理
文字语言 符号语言 图示 变式
直角三角形两直角边的平方和等于斜边的平方 如果直角三角形的两条直角边长分别为,斜边长为,那么.
二、练习
1.如图,正方形内的数字代表所在正方形的面积,则A所在的正方形的面积为( )
A. B.28 C.128 D.100
2.在中,,,则( )
A.9 B.18 C.20 D.24
3.如图,在四边形中,,分别以四边为边向外作正方形甲、乙、丙、丁,若用,,,来表示它们的面积,那么下列结论正确的是( )
A. B.
C. D.
4.如图所示的是由两个直角三角形和三个正方形组成的图形,其中阴影部分的面积是( )
A. B. C. D.
5.如图,在中,CE平分,CF平分,且交AC于点M,若,则的值为( )
A.6 B.9 C.18 D.36
6.赵爽是我国著名的数学家,“赵爽弦图”是他研究勾股定理的重要成果.古人有记载“勾三,股四,则弦五”的定理.图1是北京国际数学家大会的会标,它取材于“弦图”,.若图1中大正方形的面积为,小正方形的面积为4,现将这四个直角三角形拼成图2,则图2中大正方形的面积为( )
A. B. C. D.
7.如图,中,,,,将折叠,使A点与的中点D重合,折痕为,则线段的长为( )
A. B. C. D.
8.在中,,,,对应的边分别为a,b,c,若,则____________.
9.如图是一个长方体盒子,用一根细线绕侧面绑在点A、B处,不计结头,细线最短长度为______.
10.我国是最早了解勾股定理的国家之一,在《周髀算经》中记载了勾股定理的公式与证明,相传是由商高发现,故又称之为“商高定理”.如图所示的“赵爽弦图”是由四个全等直角三角形和中间的小正方形拼成的一个大正方形,若大正方形的面积是25,小正方形的面积是1,直角三角形的两条直角边长分别为m、n,则______.
11.如图是勾股树衍生图案,它由若干个正方形和直角三角形构成,,,,分别表示其对应正方形的面积,若已知上方左右两端的两个正方形的面积分别是64,9,则的值为______
12.数学活动中,小明和同学动手拼图发现:两个边长分别为a、b、c的直角三角形和一个两条直角边都是c的直角三角形,可以拼成如图所示的直角梯形.
(1)请你用两种不同的方法计算这个图形的面积,你能发现a、b、c之间有什么数量关系呢?请证明你的发现.
(2)若这个直角梯形的上下底之差为,高为,请计算一下的面积.
13.如图,将矩形ABCD绕点A顺时针旋转,使点E落在BD上,得到矩形AEFG,EF与AD相交于点H,连接AF.
(1)求证:;
(2)若,,求的长.
答案以及解析
1.答案:D
解析:由勾股定理可知:.
故选:D.
2.答案:B
解析:∵中,,,
∴
故选B.
3.答案:C
解析:连接,
由勾股定理得,
∴甲的面积+乙的面积=丙的面积+丁的面积,即.
故选:C.
4.答案:A
解析:由勾股定理得,大正方形边长的平方,即大正方形面积为25,
∵两个小正方形的边长的平方和等于斜边的平方,
∴两个小正方形的面积和为25,
∴阴影部分的面积为:.
故选:A.
5.答案:D
解析:∵CE平分,CF平分,
∴,,即,
∴为直角三角形,
又∵,CE平分,CF平分,
∴,,
∴,,
由勾股定理可知,
故选D.
6.答案:A
解析:如图,直角三角形的两直角边为a、b,斜边为c,
∵图1中大正方形是由四个全等的直角三角形拼成且大正方形的面积为,
∴,
∵小正方形的面积为4,
∴,
∴,
∵将这四个直角三角形拼成图,
∴图2中最大的正方形的面积为:.
故选:A.
7.答案:A
解析:设,则,
由翻折的性质可知:,
∵点D是的中点,
∴.
在中,由勾股定理可知:,
即,
∴,
∴,
故选:A.
8.答案:18
解析:,,
,
,
故答案为:18.
9.答案:15
解析:如图所示,连接,则即为所求的最短长度;
,,
由勾股定理可得:,
∴;
故答案是15.
10.答案:12
解析:∵大正方形的面积是25,
∴,
∵小正方形的面积是1,
∴,
∴,
∴,
∴,
∴,
故答案为:12.
11.答案:55
解析:建立如图的数据,
由题意得,,,,,,
∴
,
故答案为:55.
12.答案:(1),证明见解析
(2)
解析:(1)利用梯形的面积公式计算为:;
用三个三角形的面积和计算为:,
,整理得;
(2)设上底长为x,则令下底长为,
高为,
,
,,
.
13.答案:(1)证明见解析
(2)
解析:(1)证明:将矩形ABCD绕点A顺时针旋转,使点E落在BD上,得到矩形AEFG,
,,
,,
;
(2),,
,,
,
设,则,,
,,
解得:,.
一、知识详解
勾股定理
文字语言 符号语言 图示 变式
直角三角形两直角边的平方和等于斜边的平方 如果直角三角形的两条直角边长分别为,斜边长为,那么.
二、练习
1.如图,正方形内的数字代表所在正方形的面积,则A所在的正方形的面积为( )
A. B.28 C.128 D.100
2.在中,,,则( )
A.9 B.18 C.20 D.24
3.如图,在四边形中,,分别以四边为边向外作正方形甲、乙、丙、丁,若用,,,来表示它们的面积,那么下列结论正确的是( )
A. B.
C. D.
4.如图所示的是由两个直角三角形和三个正方形组成的图形,其中阴影部分的面积是( )
A. B. C. D.
5.如图,在中,CE平分,CF平分,且交AC于点M,若,则的值为( )
A.6 B.9 C.18 D.36
6.赵爽是我国著名的数学家,“赵爽弦图”是他研究勾股定理的重要成果.古人有记载“勾三,股四,则弦五”的定理.图1是北京国际数学家大会的会标,它取材于“弦图”,.若图1中大正方形的面积为,小正方形的面积为4,现将这四个直角三角形拼成图2,则图2中大正方形的面积为( )
A. B. C. D.
7.如图,中,,,,将折叠,使A点与的中点D重合,折痕为,则线段的长为( )
A. B. C. D.
8.在中,,,,对应的边分别为a,b,c,若,则____________.
9.如图是一个长方体盒子,用一根细线绕侧面绑在点A、B处,不计结头,细线最短长度为______.
10.我国是最早了解勾股定理的国家之一,在《周髀算经》中记载了勾股定理的公式与证明,相传是由商高发现,故又称之为“商高定理”.如图所示的“赵爽弦图”是由四个全等直角三角形和中间的小正方形拼成的一个大正方形,若大正方形的面积是25,小正方形的面积是1,直角三角形的两条直角边长分别为m、n,则______.
11.如图是勾股树衍生图案,它由若干个正方形和直角三角形构成,,,,分别表示其对应正方形的面积,若已知上方左右两端的两个正方形的面积分别是64,9,则的值为______
12.数学活动中,小明和同学动手拼图发现:两个边长分别为a、b、c的直角三角形和一个两条直角边都是c的直角三角形,可以拼成如图所示的直角梯形.
(1)请你用两种不同的方法计算这个图形的面积,你能发现a、b、c之间有什么数量关系呢?请证明你的发现.
(2)若这个直角梯形的上下底之差为,高为,请计算一下的面积.
13.如图,将矩形ABCD绕点A顺时针旋转,使点E落在BD上,得到矩形AEFG,EF与AD相交于点H,连接AF.
(1)求证:;
(2)若,,求的长.
答案以及解析
1.答案:D
解析:由勾股定理可知:.
故选:D.
2.答案:B
解析:∵中,,,
∴
故选B.
3.答案:C
解析:连接,
由勾股定理得,
∴甲的面积+乙的面积=丙的面积+丁的面积,即.
故选:C.
4.答案:A
解析:由勾股定理得,大正方形边长的平方,即大正方形面积为25,
∵两个小正方形的边长的平方和等于斜边的平方,
∴两个小正方形的面积和为25,
∴阴影部分的面积为:.
故选:A.
5.答案:D
解析:∵CE平分,CF平分,
∴,,即,
∴为直角三角形,
又∵,CE平分,CF平分,
∴,,
∴,,
由勾股定理可知,
故选D.
6.答案:A
解析:如图,直角三角形的两直角边为a、b,斜边为c,
∵图1中大正方形是由四个全等的直角三角形拼成且大正方形的面积为,
∴,
∵小正方形的面积为4,
∴,
∴,
∵将这四个直角三角形拼成图,
∴图2中最大的正方形的面积为:.
故选:A.
7.答案:A
解析:设,则,
由翻折的性质可知:,
∵点D是的中点,
∴.
在中,由勾股定理可知:,
即,
∴,
∴,
故选:A.
8.答案:18
解析:,,
,
,
故答案为:18.
9.答案:15
解析:如图所示,连接,则即为所求的最短长度;
,,
由勾股定理可得:,
∴;
故答案是15.
10.答案:12
解析:∵大正方形的面积是25,
∴,
∵小正方形的面积是1,
∴,
∴,
∴,
∴,
∴,
故答案为:12.
11.答案:55
解析:建立如图的数据,
由题意得,,,,,,
∴
,
故答案为:55.
12.答案:(1),证明见解析
(2)
解析:(1)利用梯形的面积公式计算为:;
用三个三角形的面积和计算为:,
,整理得;
(2)设上底长为x,则令下底长为,
高为,
,
,,
.
13.答案:(1)证明见解析
(2)
解析:(1)证明:将矩形ABCD绕点A顺时针旋转,使点E落在BD上,得到矩形AEFG,
,,
,,
;
(2),,
,,
,
设,则,,
,,
解得:,.
同课章节目录
