2025年江苏省中考数学模拟试卷(含详解)
文档属性
| 名称 | 2025年江苏省中考数学模拟试卷(含详解) |

|
|
| 格式 | docx | ||
| 文件大小 | 198.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-10 00:00:00 | ||
图片预览



文档简介
2025年江苏省中考数学模拟试卷
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.下列各数:,,,,其中比小的数是( )
A. B. C. D.
2.年适逢农历乙巳年生肖蛇年,春节期间大街小巷随处可见以灵蛇为意象的创意文案下列年画图案中,是中心对称图形的是( )
A. B.
C. D.
3.下列运算正确的是( )
A. B. C. D.
4.甲、乙两人在篮球社团集训期间进行了次定点投篮测试每次投个,他们命中数的折线统计图如图所示,根据统计图,下列判断不正确的是( )
A. 甲、乙投篮命中数的平均数相同 B. 甲、乙投篮命中数的中位数相同
C. 甲投篮命中数的众数比乙大 D. 甲投篮命中数的方差比乙小
5.如图,已知线段的两个端点坐标分别为,,以原点为位似中心在第一象限内画线段,若,则点的坐标为( )
A.
B.
C.
D.
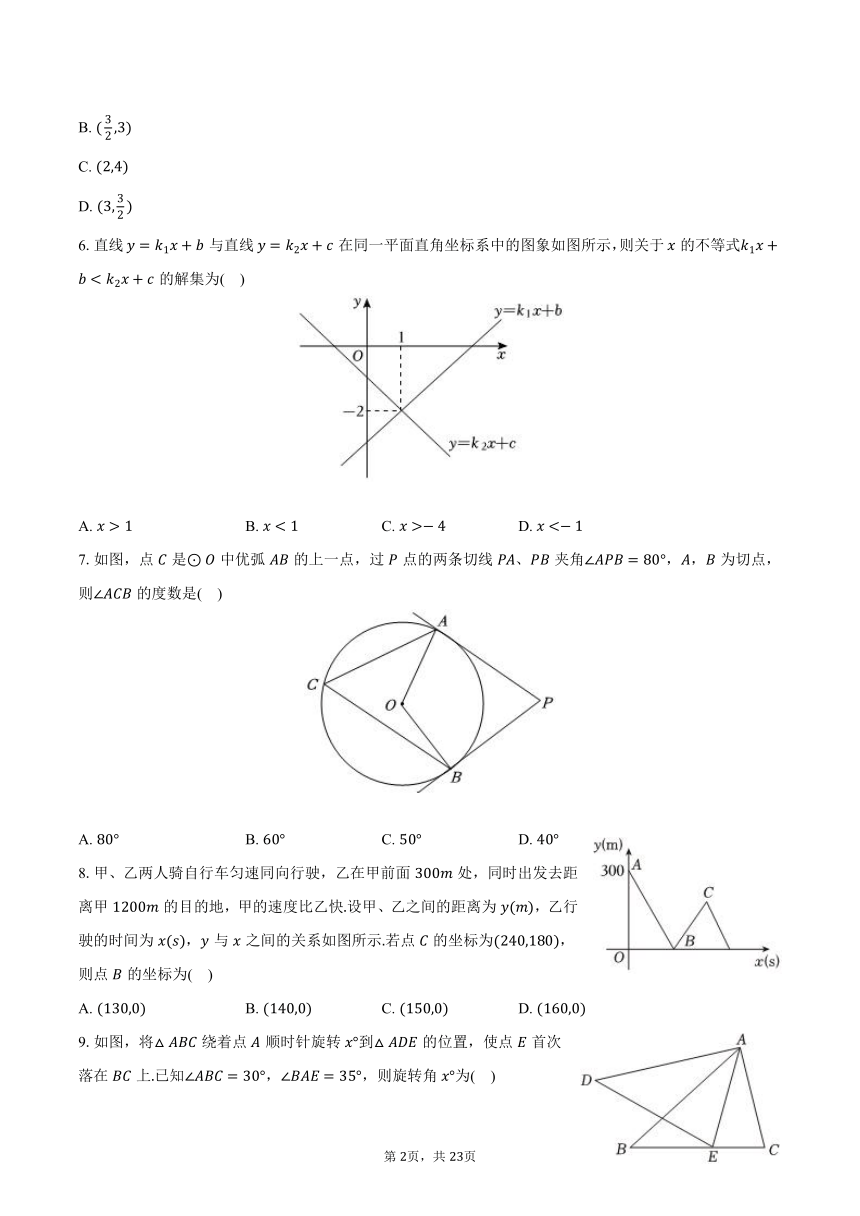
6.直线与直线在同一平面直角坐标系中的图象如图所示,则关于的不等式的解集为( )
A. B. C. D.
7.如图,点是中优弧的上一点,过点的两条切线、夹角,,为切点,则的度数是( )
A. B. C. D.
8.甲、乙两人骑自行车匀速同向行驶,乙在甲前面处,同时出发去距离甲的目的地,甲的速度比乙快设甲、乙之间的距离为,乙行驶的时间为,与之间的关系如图所示若点的坐标为,则点的坐标为( )
A. B. C. D.
9.如图,将绕着点顺时针旋转到的位置,使点首次落在上已知,,则旋转角为( )
A.
B.
C.
D.
10.如图,在中,,分别以点、为圆心,大于的同样长为半径画弧,两弧交于点、,作直线交于点,连接则下列说法中不正确的是( )
A. 是线段的垂直平分线
B.
C.
D.
二、填空题:本题共8小题,每小题3分,共24分。
11.已知,则的平方根为______.
12.要使得式子有意义,则的取值范围是 .
13.已知关于的方程有两个相等的实数根,则______.
14.分式方程的解是______.
15.待定系数法是确定函数解析式的常用方法,也可用于化学方程式的配平以黄铜矿为主要原料的火法炼铜的化学反应方程式为,其中,为常数,则的值为______.
16.如图是一个几何体的三视图图中尺寸单位:,根据图中所示数据,这个几何体的表面积为______.
17.如图,在平面直角坐标系中,已知是等腰直角三角形,,点,分别在轴、轴上,点在函数的图象上若,,则 ______.
18.如图,有一张矩形纸条,,,点在边上,,动点从点向点运动,将四边形沿折叠,点,的对应点分别为点,,线段与边交于点,则的最小值为______,此时点离开初始位置指点从点出发时,点的位置的距离为______.
三、解答题:本题共11小题,共96分。解答应写出文字说明,证明过程或演算步骤。
19.本小题分
计算:.
20.本小题分
分解因式
21.本小题分
先化简,再求值:,其中是从,,中选取的一个合适的数.
22.本小题分
如图,在四边形中,,,.
求证:四边形是矩形;
点是上一点,点是的中点,连接,,,若,,,求的长.
23.本小题分
某商场为了促销举办了摸球得礼金券活动,在一个不透明的盒子里装有个蓝球、个红球和个白球,这个球除颜色不同外其余均相同,将球搅匀.
从盒子里随机摸出一个球是白球的概率是______;
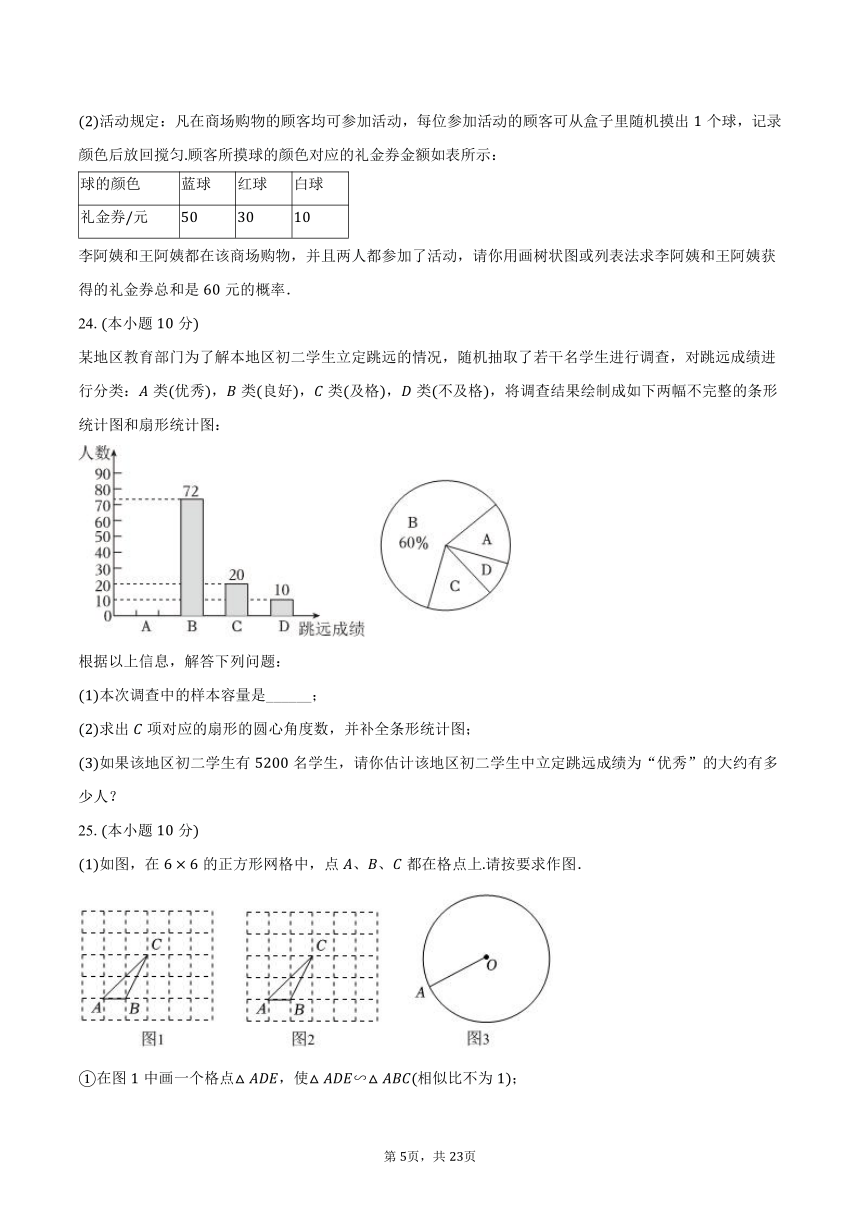
活动规定:凡在商场购物的顾客均可参加活动,每位参加活动的顾客可从盒子里随机摸出个球,记录颜色后放回搅匀顾客所摸球的颜色对应的礼金券金额如表所示:
球的颜色 蓝球 红球 白球
礼金券元
李阿姨和王阿姨都在该商场购物,并且两人都参加了活动,请你用画树状图或列表法求李阿姨和王阿姨获得的礼金券总和是元的概率.
24.本小题分
某地区教育部门为了解本地区初二学生立定跳远的情况,随机抽取了若干名学生进行调查,对跳远成绩进行分类:类优秀,类良好,类及格,类不及格,将调查结果绘制成如下两幅不完整的条形统计图和扇形统计图:
根据以上信息,解答下列问题:
本次调查中的样本容量是______;
求出项对应的扇形的圆心角度数,并补全条形统计图;
如果该地区初二学生有名学生,请你估计该地区初二学生中立定跳远成绩为“优秀”的大约有多少人?
25.本小题分
如图,在的正方形网格中,点、、都在格点上请按要求作图.
在图中画一个格点,使∽相似比不为;
在图中画一条格点线段,交于点,使;
如图,点为上一点.
请用不带刻度的直尺和圆规,在图中作出的内接正方形;保留作图痕迹,不写作法
根据中画出的图形,过圆心作边的垂线,分别交和劣弧于点、,若的半径为,则的长为______.
26.本小题分
如图,是的直径,内接于,取的中点,连接、,过点作,交的延长线于点,且,.
判断与的位置关系,并说明理由;
求的值.
27.本小题分
中国新能源汽车为全球应对气候变化和绿色低碳转型作出了巨大贡献为满足新能源汽车的充电需求,某小区增设了充电站,如图是矩形充电站的平面示意,矩形是其中一个停车位经测量,,,,,是另一个车位的宽,所有车位的长宽相同,按图示并列划定.
根据以上信息回答下列问题:结果保留根号
求的长;
该充电站有个停车位,求的长.
28.本小题分
问题背景:
某数学兴趣小组进行一次数学探究活动:已知两边及一边的对角求作三角形,作出了如下图所示的两个三角形,其中,,,很明显这两个三角形不全等.
探系发现:
探究:如图,在上截取,连接,可证得______,得出,,得出______.
探究:如图,分别过点,作于点,于点,可证出≌,得出,又,证得≌,得出的值.
活动总结:
小组成员感觉本次活动既动手又动脑,收获很大.
探索应用:
处应填写______.
处填______.
如图,菱形中,点为对角线上一点,,求证:.
如图,矩形中,,分别为,上的点,连接,,且,若,求.
29.本小题分
如图,抛物线与轴交于、两点点在点的左侧,与轴交于点,连接、,点为直线上方抛物线上一动点,连接交于点.
求抛物线的函数表达式;
当的值最大时,求点的坐标和的最大值;
若是抛物线上的一点,的内切圆的圆心恰好落在轴上,求点的坐标.
答案和解析
1.【答案】
【解析】,
.
故选:.
2.【答案】
【解析】选项A的图案能找到这样的一个点,使图形绕某一点旋转后与原来的图形重合,所以是中心对称图形;
选项B、、的图案均不能找到这样的一个点,使图形绕某一点旋转后与原来的图形重合,所以不是中心对称图形.
故选:.
3.【答案】
【解析】,故该选项不正确,不符合题意;
B.,故该选项不正确,不符合题意;
C.,故该选项正确,符合题意;
D.,故该选项不正确,不符合题意.
故选:.
4.【答案】
【解析】根据平均数计算方法可得:
,,
选项A正确.不符合题意;
甲、乙投篮命中数的中位数都是,
选项B正确,不符合题意;
甲投篮命中个出现次数最多,共次,
甲命中数的众数是,
乙投篮命中个出现最多,共次,
乙命中数的众数也是,选项C不正确,符合题意;
甲的方差为,乙的方差为,
选项D正确,不符合题意;
故选:.
5.【答案】
【解析】线段的两个端点坐标分别为,,
,
,
::,
线段和线段的位似比为:,
点坐标为,即,
故选:.
6.【答案】
【解析】由图象知:不等式的解集为,
故选:.
7.【答案】
【解析】由题意可得:,,
,
,
.
故选:.
8.【答案】
【解析】点的坐标为,
甲的速度比乙的速度快,
甲追上乙所用时间为,
点的坐标为.
故选:.
由点的坐标求出甲的速度比乙的速度快多少,再由甲追上乙时甲比乙多行驶的路程求出点的横坐标即可.
本题考查一次函数的应用,求出甲的速度比乙的速度快多少是解题的关键.
9.【答案】
【解析】已知,,
,
将绕着点顺时针旋转到的位置,使点首次落在上,
,,
,
,
故选:.
10.【答案】
【解析】由作图可知垂直平分线段,
,故选项A,B正确,不符合题意,
,
,
,故选项D正确,不符合题意,
故选:.
11.【答案】
【解析】由条件可知,
,
的平方根为.
故答案为:.
12.【答案】且
【解析】根据题意可得:,
解得:且,
故答案为:且.
13.【答案】
【解析】由条件可知,
解得:;
故答案为:.
14.【答案】
【解析】两边都乘以得:,
去括号,得:,
移项、合并同类项,得:,
检验:当时,,
原分式方程的解为:,
故答案为:.
15.【答案】
【解析】由原子个数可知,,
由个数知,,
,
,
故答案为:.
16.【答案】
【解析】由主视图和左视图为三角形判断出是锥体,由俯视图是圆形可判断出这个几何体应该是圆锥;
根据三视图知:该圆锥的母线长为,底面半径为,
故表面积
故答案为:.
17.【答案】
【解析】如图,过点作轴,作,
,,
,,
,,
,
,
,
在和中,
,
≌,
,,
设,则,
在中,由勾股定理得:
,
整理得:,
解得:或舍去,
,
点在反比例函数图象上,
,
故答案为:.
18.【答案】
【解析】由折叠的性质得,
,
,
,
,
为等腰三角形;
过作于,如图:
设,则,
设,
,
,,
,
,
,
,
线段与边相交,
,
,
,,
,
,即的最小值为;
故答案为:;
,
最大为;
设,
,,,
,
当点从点出发时
,
,
,
,
即;
的路径长为;
故答案为:.
19.【答案】.
【解析】原式
.
20.【答案】,
,
,
.
21.【答案】,.
【解析】
,
,,
,,
当时,原式.
22.【解析】证明:,,
四边形是平行四边形,
,
平行四边形是矩形;
四边形是矩形,
,
,,,
,
是直角三角形,且,
点是的中点,
.
23.【解析】由题意知,共有种等可能的结果,其中从盒子里随机摸出一个球是白球的结果有种,
从盒子里随机摸出一个球是白球的概率为.
故答案为:.
列表如下:
蓝球 红球 白球 白球
蓝球 蓝球,蓝球 蓝球,红球 蓝球,白球 蓝球,白球
红球 红球,蓝球 红球,红球 红球,白球 红球,白球
白球 白球,蓝球 白球,红球 白球,白球 白球,白球
白球 白球,蓝球 白球,红球 白球,白球 白球,白球
共有种等可能的结果,其中李阿姨和王阿姨获得的礼金券总和是元的结果有:蓝球,白球,蓝球,白球,红球,红球,白球,蓝球,白球,蓝球,共种,
李阿姨和王阿姨获得的礼金券总和是元的概率为.
24.【解析】本次调查的样本容量为人,
故答案为:;
,
项对应的扇形的圆心角的度数为,
人,
补全条形统计图如下:
人,
答:估计该地区初二学生中立定跳远成绩为“优秀”的大约有人.
25.【解析】如图所示,即为所求;
如图所示,线段即为所求;
连接并延长,交于,过点作的垂线,分别交于、,则四边形即为所求;
,分别为的直径,则,相等且互相垂直平分,则四边形是正方形;
四边形是正方形,
,
,
,
,
,
,
故答案为:
26.【解析】是的切线,理由如下,
连接,
由题意可得:,
是的直径,
,
,
,
,
,
又是圆的半径,
是的切线,
连接,设,交于点,
由可得,
则四边形是矩形,
,
,
,
又,
,
∽,
,
,.
,
即,
又,,
∽,
,即,
,
,
,
,,
,
∽,
,
,
,设,,则,
,
,设,则,
,,
,
.
27.【解析】四边形是矩形,
,
在中,,,
,,
四边形是矩形,
,,
,
,
,
,
,
;
在中,,
在中,,
该充电站有个停车位,
,
四边形是矩形,
.
28.【解析】在和中,
,
≌,
故答案为:;
≌,
,
,
,
,
,
故答案为:;
证明:如图,过点作于,于,
则,
四边形是菱形,
,
,
,,
,
在和中,
,
≌,
;
在上截取,如图,
四边形为矩形,
,
,
在和中,
,
≌,
,,
,
,
.
29.【解析】抛物线与轴交于、两点点在点的左侧,将点,点的坐标分别代入得:
,
解得:,
抛物线的函数表达式为;
抛物线与轴交于点,
当时,得:,
,
,
设直线的解析式为,将点,点的坐标分别代入得:
,
解得:,
直线的解析式为,
如图,过点作轴交于点,
设,则,
,
,
∽,
,
当时,取得最大值,此时,;
的内切圆的圆心恰好落在轴上,则轴为的角平分线,
作点关于轴的对称点,则直线与抛物线的交点即为点,如图,
设直线的关系式为,将点、点的坐标分别代入得:
,
解得,
直线的解析式为,
联立得:,
解得或,
点的坐标为.
第1页,共23页
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.下列各数:,,,,其中比小的数是( )
A. B. C. D.
2.年适逢农历乙巳年生肖蛇年,春节期间大街小巷随处可见以灵蛇为意象的创意文案下列年画图案中,是中心对称图形的是( )
A. B.
C. D.
3.下列运算正确的是( )
A. B. C. D.
4.甲、乙两人在篮球社团集训期间进行了次定点投篮测试每次投个,他们命中数的折线统计图如图所示,根据统计图,下列判断不正确的是( )
A. 甲、乙投篮命中数的平均数相同 B. 甲、乙投篮命中数的中位数相同
C. 甲投篮命中数的众数比乙大 D. 甲投篮命中数的方差比乙小
5.如图,已知线段的两个端点坐标分别为,,以原点为位似中心在第一象限内画线段,若,则点的坐标为( )
A.
B.
C.
D.
6.直线与直线在同一平面直角坐标系中的图象如图所示,则关于的不等式的解集为( )
A. B. C. D.
7.如图,点是中优弧的上一点,过点的两条切线、夹角,,为切点,则的度数是( )
A. B. C. D.
8.甲、乙两人骑自行车匀速同向行驶,乙在甲前面处,同时出发去距离甲的目的地,甲的速度比乙快设甲、乙之间的距离为,乙行驶的时间为,与之间的关系如图所示若点的坐标为,则点的坐标为( )
A. B. C. D.
9.如图,将绕着点顺时针旋转到的位置,使点首次落在上已知,,则旋转角为( )
A.
B.
C.
D.
10.如图,在中,,分别以点、为圆心,大于的同样长为半径画弧,两弧交于点、,作直线交于点,连接则下列说法中不正确的是( )
A. 是线段的垂直平分线
B.
C.
D.
二、填空题:本题共8小题,每小题3分,共24分。
11.已知,则的平方根为______.
12.要使得式子有意义,则的取值范围是 .
13.已知关于的方程有两个相等的实数根,则______.
14.分式方程的解是______.
15.待定系数法是确定函数解析式的常用方法,也可用于化学方程式的配平以黄铜矿为主要原料的火法炼铜的化学反应方程式为,其中,为常数,则的值为______.
16.如图是一个几何体的三视图图中尺寸单位:,根据图中所示数据,这个几何体的表面积为______.
17.如图,在平面直角坐标系中,已知是等腰直角三角形,,点,分别在轴、轴上,点在函数的图象上若,,则 ______.
18.如图,有一张矩形纸条,,,点在边上,,动点从点向点运动,将四边形沿折叠,点,的对应点分别为点,,线段与边交于点,则的最小值为______,此时点离开初始位置指点从点出发时,点的位置的距离为______.
三、解答题:本题共11小题,共96分。解答应写出文字说明,证明过程或演算步骤。
19.本小题分
计算:.
20.本小题分
分解因式
21.本小题分
先化简,再求值:,其中是从,,中选取的一个合适的数.
22.本小题分
如图,在四边形中,,,.
求证:四边形是矩形;
点是上一点,点是的中点,连接,,,若,,,求的长.
23.本小题分
某商场为了促销举办了摸球得礼金券活动,在一个不透明的盒子里装有个蓝球、个红球和个白球,这个球除颜色不同外其余均相同,将球搅匀.
从盒子里随机摸出一个球是白球的概率是______;
活动规定:凡在商场购物的顾客均可参加活动,每位参加活动的顾客可从盒子里随机摸出个球,记录颜色后放回搅匀顾客所摸球的颜色对应的礼金券金额如表所示:
球的颜色 蓝球 红球 白球
礼金券元
李阿姨和王阿姨都在该商场购物,并且两人都参加了活动,请你用画树状图或列表法求李阿姨和王阿姨获得的礼金券总和是元的概率.
24.本小题分
某地区教育部门为了解本地区初二学生立定跳远的情况,随机抽取了若干名学生进行调查,对跳远成绩进行分类:类优秀,类良好,类及格,类不及格,将调查结果绘制成如下两幅不完整的条形统计图和扇形统计图:
根据以上信息,解答下列问题:
本次调查中的样本容量是______;
求出项对应的扇形的圆心角度数,并补全条形统计图;
如果该地区初二学生有名学生,请你估计该地区初二学生中立定跳远成绩为“优秀”的大约有多少人?
25.本小题分
如图,在的正方形网格中,点、、都在格点上请按要求作图.
在图中画一个格点,使∽相似比不为;
在图中画一条格点线段,交于点,使;
如图,点为上一点.
请用不带刻度的直尺和圆规,在图中作出的内接正方形;保留作图痕迹,不写作法
根据中画出的图形,过圆心作边的垂线,分别交和劣弧于点、,若的半径为,则的长为______.
26.本小题分
如图,是的直径,内接于,取的中点,连接、,过点作,交的延长线于点,且,.
判断与的位置关系,并说明理由;
求的值.
27.本小题分
中国新能源汽车为全球应对气候变化和绿色低碳转型作出了巨大贡献为满足新能源汽车的充电需求,某小区增设了充电站,如图是矩形充电站的平面示意,矩形是其中一个停车位经测量,,,,,是另一个车位的宽,所有车位的长宽相同,按图示并列划定.
根据以上信息回答下列问题:结果保留根号
求的长;
该充电站有个停车位,求的长.
28.本小题分
问题背景:
某数学兴趣小组进行一次数学探究活动:已知两边及一边的对角求作三角形,作出了如下图所示的两个三角形,其中,,,很明显这两个三角形不全等.
探系发现:
探究:如图,在上截取,连接,可证得______,得出,,得出______.
探究:如图,分别过点,作于点,于点,可证出≌,得出,又,证得≌,得出的值.
活动总结:
小组成员感觉本次活动既动手又动脑,收获很大.
探索应用:
处应填写______.
处填______.
如图,菱形中,点为对角线上一点,,求证:.
如图,矩形中,,分别为,上的点,连接,,且,若,求.
29.本小题分
如图,抛物线与轴交于、两点点在点的左侧,与轴交于点,连接、,点为直线上方抛物线上一动点,连接交于点.
求抛物线的函数表达式;
当的值最大时,求点的坐标和的最大值;
若是抛物线上的一点,的内切圆的圆心恰好落在轴上,求点的坐标.
答案和解析
1.【答案】
【解析】,
.
故选:.
2.【答案】
【解析】选项A的图案能找到这样的一个点,使图形绕某一点旋转后与原来的图形重合,所以是中心对称图形;
选项B、、的图案均不能找到这样的一个点,使图形绕某一点旋转后与原来的图形重合,所以不是中心对称图形.
故选:.
3.【答案】
【解析】,故该选项不正确,不符合题意;
B.,故该选项不正确,不符合题意;
C.,故该选项正确,符合题意;
D.,故该选项不正确,不符合题意.
故选:.
4.【答案】
【解析】根据平均数计算方法可得:
,,
选项A正确.不符合题意;
甲、乙投篮命中数的中位数都是,
选项B正确,不符合题意;
甲投篮命中个出现次数最多,共次,
甲命中数的众数是,
乙投篮命中个出现最多,共次,
乙命中数的众数也是,选项C不正确,符合题意;
甲的方差为,乙的方差为,
选项D正确,不符合题意;
故选:.
5.【答案】
【解析】线段的两个端点坐标分别为,,
,
,
::,
线段和线段的位似比为:,
点坐标为,即,
故选:.
6.【答案】
【解析】由图象知:不等式的解集为,
故选:.
7.【答案】
【解析】由题意可得:,,
,
,
.
故选:.
8.【答案】
【解析】点的坐标为,
甲的速度比乙的速度快,
甲追上乙所用时间为,
点的坐标为.
故选:.
由点的坐标求出甲的速度比乙的速度快多少,再由甲追上乙时甲比乙多行驶的路程求出点的横坐标即可.
本题考查一次函数的应用,求出甲的速度比乙的速度快多少是解题的关键.
9.【答案】
【解析】已知,,
,
将绕着点顺时针旋转到的位置,使点首次落在上,
,,
,
,
故选:.
10.【答案】
【解析】由作图可知垂直平分线段,
,故选项A,B正确,不符合题意,
,
,
,故选项D正确,不符合题意,
故选:.
11.【答案】
【解析】由条件可知,
,
的平方根为.
故答案为:.
12.【答案】且
【解析】根据题意可得:,
解得:且,
故答案为:且.
13.【答案】
【解析】由条件可知,
解得:;
故答案为:.
14.【答案】
【解析】两边都乘以得:,
去括号,得:,
移项、合并同类项,得:,
检验:当时,,
原分式方程的解为:,
故答案为:.
15.【答案】
【解析】由原子个数可知,,
由个数知,,
,
,
故答案为:.
16.【答案】
【解析】由主视图和左视图为三角形判断出是锥体,由俯视图是圆形可判断出这个几何体应该是圆锥;
根据三视图知:该圆锥的母线长为,底面半径为,
故表面积
故答案为:.
17.【答案】
【解析】如图,过点作轴,作,
,,
,,
,,
,
,
,
在和中,
,
≌,
,,
设,则,
在中,由勾股定理得:
,
整理得:,
解得:或舍去,
,
点在反比例函数图象上,
,
故答案为:.
18.【答案】
【解析】由折叠的性质得,
,
,
,
,
为等腰三角形;
过作于,如图:
设,则,
设,
,
,,
,
,
,
,
线段与边相交,
,
,
,,
,
,即的最小值为;
故答案为:;
,
最大为;
设,
,,,
,
当点从点出发时
,
,
,
,
即;
的路径长为;
故答案为:.
19.【答案】.
【解析】原式
.
20.【答案】,
,
,
.
21.【答案】,.
【解析】
,
,,
,,
当时,原式.
22.【解析】证明:,,
四边形是平行四边形,
,
平行四边形是矩形;
四边形是矩形,
,
,,,
,
是直角三角形,且,
点是的中点,
.
23.【解析】由题意知,共有种等可能的结果,其中从盒子里随机摸出一个球是白球的结果有种,
从盒子里随机摸出一个球是白球的概率为.
故答案为:.
列表如下:
蓝球 红球 白球 白球
蓝球 蓝球,蓝球 蓝球,红球 蓝球,白球 蓝球,白球
红球 红球,蓝球 红球,红球 红球,白球 红球,白球
白球 白球,蓝球 白球,红球 白球,白球 白球,白球
白球 白球,蓝球 白球,红球 白球,白球 白球,白球
共有种等可能的结果,其中李阿姨和王阿姨获得的礼金券总和是元的结果有:蓝球,白球,蓝球,白球,红球,红球,白球,蓝球,白球,蓝球,共种,
李阿姨和王阿姨获得的礼金券总和是元的概率为.
24.【解析】本次调查的样本容量为人,
故答案为:;
,
项对应的扇形的圆心角的度数为,
人,
补全条形统计图如下:
人,
答:估计该地区初二学生中立定跳远成绩为“优秀”的大约有人.
25.【解析】如图所示,即为所求;
如图所示,线段即为所求;
连接并延长,交于,过点作的垂线,分别交于、,则四边形即为所求;
,分别为的直径,则,相等且互相垂直平分,则四边形是正方形;
四边形是正方形,
,
,
,
,
,
,
故答案为:
26.【解析】是的切线,理由如下,
连接,
由题意可得:,
是的直径,
,
,
,
,
,
又是圆的半径,
是的切线,
连接,设,交于点,
由可得,
则四边形是矩形,
,
,
,
又,
,
∽,
,
,.
,
即,
又,,
∽,
,即,
,
,
,
,,
,
∽,
,
,
,设,,则,
,
,设,则,
,,
,
.
27.【解析】四边形是矩形,
,
在中,,,
,,
四边形是矩形,
,,
,
,
,
,
,
;
在中,,
在中,,
该充电站有个停车位,
,
四边形是矩形,
.
28.【解析】在和中,
,
≌,
故答案为:;
≌,
,
,
,
,
,
故答案为:;
证明:如图,过点作于,于,
则,
四边形是菱形,
,
,
,,
,
在和中,
,
≌,
;
在上截取,如图,
四边形为矩形,
,
,
在和中,
,
≌,
,,
,
,
.
29.【解析】抛物线与轴交于、两点点在点的左侧,将点,点的坐标分别代入得:
,
解得:,
抛物线的函数表达式为;
抛物线与轴交于点,
当时,得:,
,
,
设直线的解析式为,将点,点的坐标分别代入得:
,
解得:,
直线的解析式为,
如图,过点作轴交于点,
设,则,
,
,
∽,
,
当时,取得最大值,此时,;
的内切圆的圆心恰好落在轴上,则轴为的角平分线,
作点关于轴的对称点,则直线与抛物线的交点即为点,如图,
设直线的关系式为,将点、点的坐标分别代入得:
,
解得,
直线的解析式为,
联立得:,
解得或,
点的坐标为.
第1页,共23页
同课章节目录
