(期末考点培优)专题04 计算题-2024-2025学年六年级数学下册期末复习专项北师大版(含答案解析)
文档属性
| 名称 | (期末考点培优)专题04 计算题-2024-2025学年六年级数学下册期末复习专项北师大版(含答案解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-10 16:40:41 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
2024-2025学年六年级数学下册期末复习专项北师大版
(期末考点培优)专题04 计算题
学校:___________姓名:___________班级:___________考号:___________
1.解方程。
2.解方程或比例。
(1)x-85%x=750 (2)= (3)1.2∶x=5∶1.5
3.计算。
x∶5=0.4∶0.5 23∶x=3∶12 13∶14=15∶x
2÷× 2.25×1.8+12.5×0.18 [1-(+)]×36
4.解方程。
5.解比例。
3.2∶x=0.4∶1.6 x∶25=16∶60
6.解方程。
7.解比例。
8.解比例。
9.解比例方程。
x∶8= 9∶5=4.5∶x ∶∶
10.解比例。
11.解比例。
21∶0.4=∶ = 16∶=5∶0.5
12.解方程或比例。
13.解方程。
2x+0.4=3.2 1.2∶x=0.125∶
14.解比例。
∶x=∶2 0.3∶x=7∶3.5 =4∶9
15.解方程。
0.8∶4=∶8
16.解方程。
3.8x+1.2x=15 3x+4×4.5=24.9
(x+2.5)×4=26 ∶
17.解方程。
6x+7.8=42.9 4.5x-3.8x=14.14
18.解方程。
9x-3.5=14.5
19.解比例。
7∶5=x∶ ∶x=0.2∶51
20.解方程。
0.3x-0.6=1.8 40%x+26=84 12∶x=
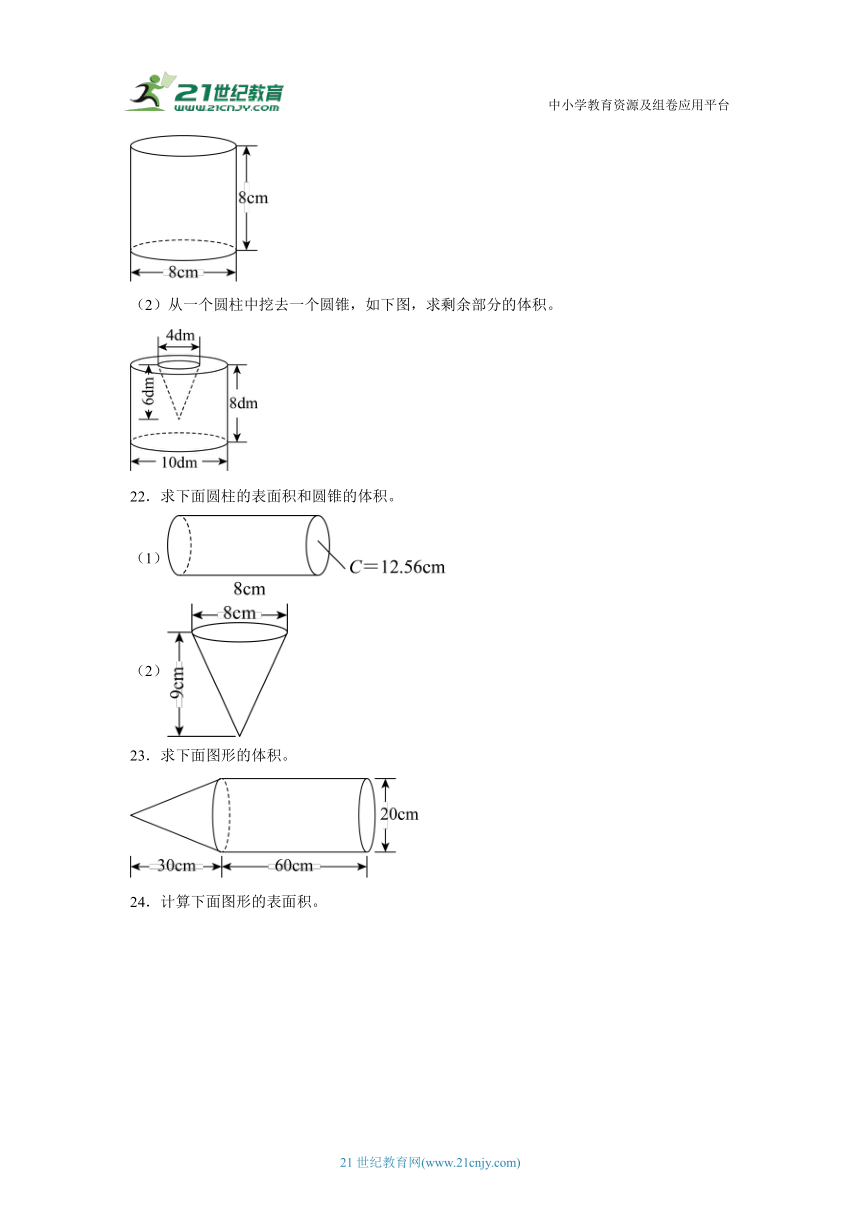
21.(1)计算下面圆柱的表面积。
(2)从一个圆柱中挖去一个圆锥,如下图,求剩余部分的体积。
22.求下面圆柱的表面积和圆锥的体积。
(1)
(2)
23.求下面图形的体积。
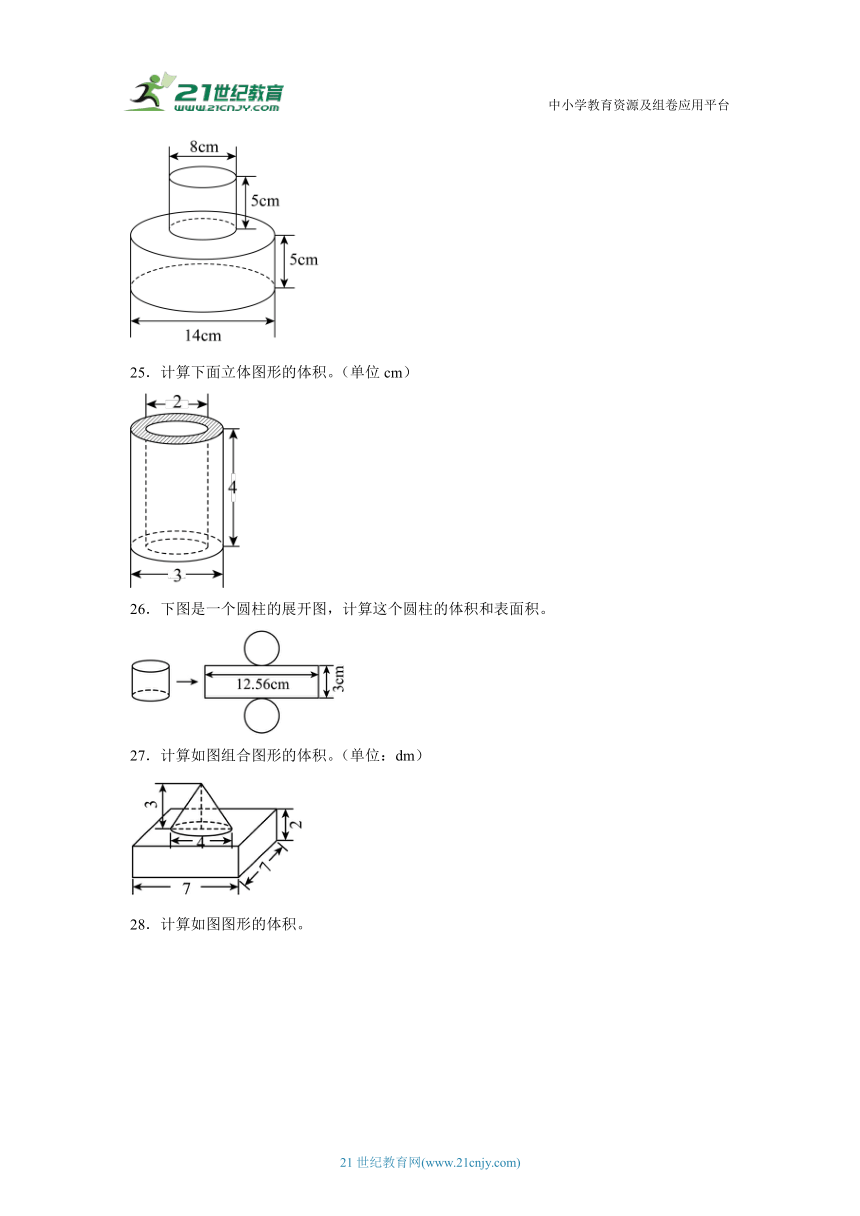
24.计算下面图形的表面积。
25.计算下面立体图形的体积。(单位cm)
26.下图是一个圆柱的展开图,计算这个圆柱的体积和表面积。
27.计算如图组合图形的体积。(单位:dm)
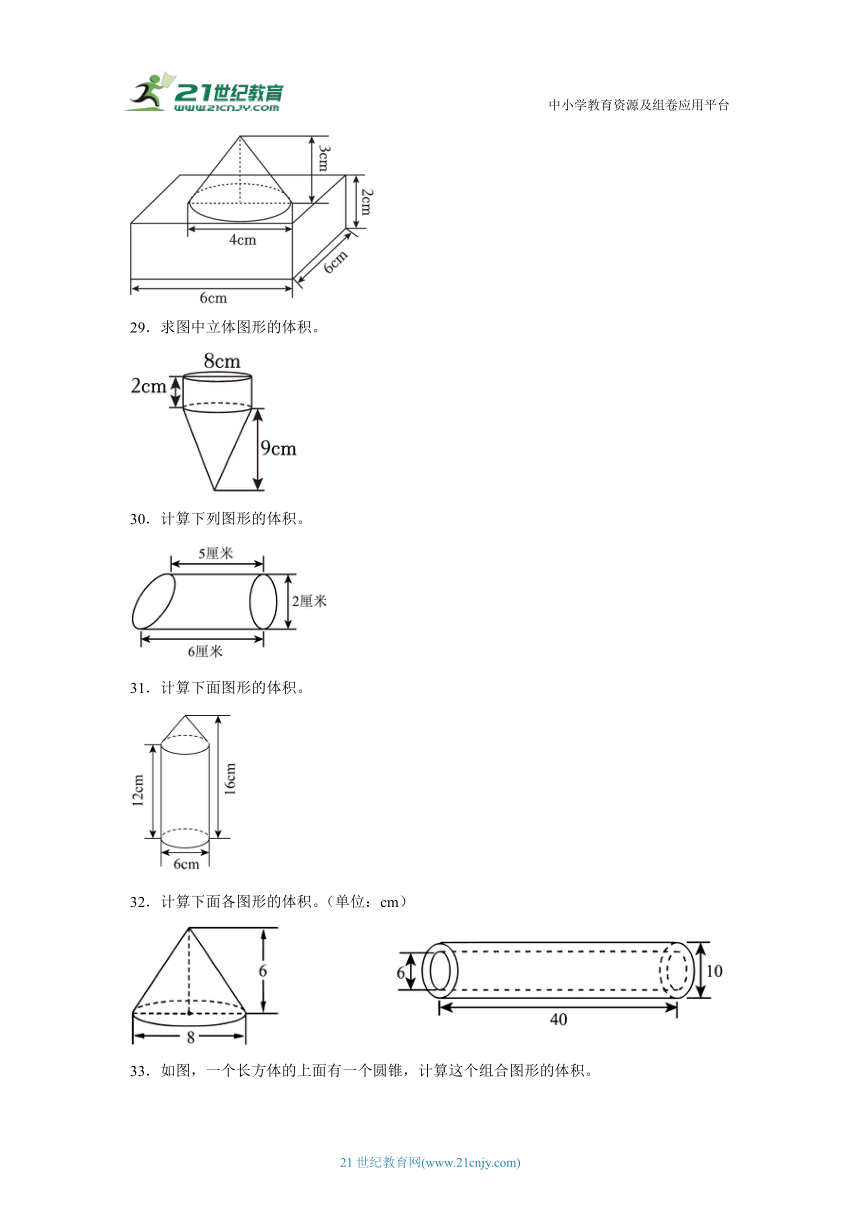
28.计算如图图形的体积。
29.求图中立体图形的体积。
30.计算下列图形的体积。
31.计算下面图形的体积。
32.计算下面各图形的体积。(单位:cm)
33.如图,一个长方体的上面有一个圆锥,计算这个组合图形的体积。
34.求下面两个图形的体积。(单位:cm)
35.求下面几何体的表面积和体积。(单位:厘米)
36.求下列图形的体积。(单位:厘米)
37.计算图形的体积和表面积。
(1)求出图中圆柱的表面积;
(2)求出上图立体图形的体积。
38.求如图物体的体积。
39.求下图中空心圆柱的体积和组合图形的表面积。(单位:厘米)
40.求下面图形的体积。
41.计算下边组合图形的表面积。
42.计算下面图形的体积。
43.求出立体图形的体积。(单位:cm)
44.计算下图的体积。
45.求如图所示图形的体积。(单位∶厘米)
(1)
(2)
46.求下面图形的表面积。(单位:cm)
47.计算下面图形的表面积。
48.计算下面图形(1)的体积与图形(2)的表面积。
(1) (2)
49.计算下面图形的表面积。(单位:cm)
50.计算下左图的表面积和体积,计算下右图的体积。
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案及试题解析
1.;
;
【分析】(1)根据比例的基本性质,将原式变成,再根据等式的性质2,方程两边同时除以,即可求解。
(2)根据等式的性质1,方程两边同时减去7.2,再根据等式的性质2,方程两边同时除以6,即可求解。
(3)根据比例的基本性质,将原式变成,再根据等式的性质2,方程两边同时除以6,即可求解。
(4)先将原式改写成,再根据等式的性质2,方程两边同时乘0.25,即可求解。
【解析】
解:
解:
解:
解:
2.(1)x=5000;(2)x=3;(3)x=0.36
【分析】(1)先将方程左边进行合并,再结合等式的基本性质2,将方程的两边同时除以0.15,从而得出答案;
(2)利用交叉相乘积相等,将比例转化为3x=5×1.2,将方程的两边同时除以3,从而得出答案;
(3)利用比例的基本性质,两内项之积等于两外项之积,将比例转化为5x=1.2×1.5,将方程的两边同时除以5,从而得出答案。
【解析】(1)x-85%x=750
解:x-0.85x=750
0.15x=750
x=750÷0.15
x=5000
(2)=
解:3x=5×1.2
3x=6
x=6÷2
x=3
(3)1.2∶x=5∶1.5
解:5x=1.2×1.5
5x=1.8
x=1.8÷5
x=0.36
3.x=4;x=92;x=
;6.3;6
【分析】x∶5=0.4∶0.5,解比例,原式化为:0.5x=5×0.4,再根据等式的性质2,方程两边同时除以0.5即可。
23∶x=3∶12,解比例,原式化为:3x=23×12,再根据等式的性质2,方程两边同时除以3即可。
13∶14=15∶x,解比例,原式化为:13x=14×15,再根据等式的性质2,方程两边同时除以13即可。
2÷×,先计算除法,再计算乘法;
2.25×1.8+12.5×0.18,把12.5×0.18化为1.25×1.8,原式化为:2.25×1.8+1.25×1.8,再根据乘法分配律的逆运算,原式化为:(2.25+1.25)×1.8,再进行计算。
[1-(+)]×36,先根据减法性质,原式化为:[1--]×36,再根据乘法分配律,原式化为:1×36-×36-×36,再进行计算。
【解析】x∶5=0.4∶0.5
解:0.5x=5×0.4
0.5x=2
0.5x÷0.5=2÷0.5
x=4
23∶x=3∶12
解:3x=23×12
3x=276
3x÷3=276÷3
x=92
13∶14=15∶x
解:13x=14×15
13x=210
13x÷13=210÷13
x=
2÷×
=2××
=×
=
2.25×1.8+12.5×0.18
=2.25×1.8+1.25×1.8
=(2.25+1.25)×1.8
=3.5×1.8
=6.3
[1-(+)]×36
=[1--]×36
=1×36-×36-×36
=36-18-12
=18-12
=6
4.;;
;
【解析】
解:
解:
解:
解:
5.x=12.8;;
【分析】根据比例的基本性质:内项积=外项积,将比例转化为方程0.4x=3.2×1.6,再根据等式的性质2将等式的两边同时除以0.4即可;
根据比例的基本性质,将比例转化为方程60x=25×16,再根据等式的性质2将等式的两边同时除以60即可;
根据比例的基本性质,将比例转化为方程21x=2×7,再根据等式的性质2将等式的两边同时除以21即可;
【解析】3.2∶x=0.4∶1.6
解:0.4x=3.2×1.6
0.4x=5.12
x=5.12÷0.4
x=12.8
x∶25=16∶60
解:60x=25×16
60x=400
x=400÷60
x=
解:21x=2×7
21x=14
x=14÷21
x=
6.;;
【分析】,根据比例的基本性质,先写成的形式,两边同时÷即可;
,根据比例的基本性质,先写成的形式,两边同时÷1.25即可;
,根据比例的基本性质,先写成的形式,两边同时÷3即可。
【解析】
解:
解:
解:
7.;;;
【分析】根据比例的基本性质“两内项之积等于两外项之积”,把比例转化为方程,先计算,然后两边同时除以5即可;
根据比例的基本性质“两内项之积等于两外项之积”,把比例转化为方程,先计算 ,然后两边同时除以8即可;
根据比例的基本性质“两内项之积等于两外项之积”,把比例转化为方程 ,先计算,然后两边同时除以4.5即可;
根据比例的基本性质“两内项之积等于两外项之积”,把比例转化为方程 ,先计算 ,然后两边同时乘7即可;
【解析】
解:
解:
解:
解:
8.;;
【分析】(1)根据比例的基本性质,把等式转化为,先计算等式右边的乘法,再根据等式的基本性质2,等式两边同时除以2,计算即可得解。
(2)根据比例的基本性质,把等式转化为,先计算等式右边的乘法,再根据等式的基本性质2,等式两边同时除以0.25,计算即可得解。
(3)根据比例的基本性质,把等式转化为,先计算等式右边的乘法,再根据等式的基本性质2,等式两边同时除以,计算即可得解。
【解析】(1)
解:
(2)
解:
(3)
解:
9.x=6;x=2.5;
【分析】根据比例的基本性质,先把比例化为方程:4x=8×3,两边再同时除以4;
根据比例的基本性质,先把比例化为方程:9x=5×4.5,两边再同时除以9;
根据比例的基本性质,先把比例化为方程:x=×,两边再同时乘2。
【解析】x∶8=
解:4x=8×3
4x=24
4x÷4=24÷4
x=6
9∶5=4.5∶x
解:9x=5×4.5
9x=22.5
9x÷9=22.5÷9
x=2.5
∶∶
解:x=×
x=
2×x=×2
x=
10.x=6;x=2.5;x=
【分析】根据比例的基本性质,先把比例化为方程:4x=8×3,两边再同时除以4;
根据比例的基本性质,先把比例化为方程:9x=5×4.5,两边再同时除以9;
根据比例的基本性质,先把比例化为方程:x=×,两边再同时乘2。
【解析】
解:4x=8×3
4x=24
4x÷4=24÷4
x=6
9∶5=4.5∶x
解:9x=5×4.5
9x=22.5
9x÷9=22.5÷9
x=2.5
解:x=×
x=
2×x=×2
x=
11.=17.5;=15;=1.6
【分析】(1)先根据比例的基本性质将比例方程改写成0.4=21×,然后方程两边同时除以0.4,求出方程的解;
(2)先根据比例的基本性质将比例方程改写成8=24×5,然后方程两边同时除以8,求出方程的解;
(3)先根据比例的基本性质将比例方程改写成5=16×0.5,然后方程两边同时除以5,求出方程的解。
【解析】(1)21∶0.4=∶
解:0.4=21×
0.4=7
=7÷0.4
=17.5
(2)=
解:8=24×5
8=120
=120÷8
=15
(3)16∶=5∶0.5
解:5=16×0.5
5=8
=8÷5
=1.6
12.;;
【分析】(1)方程两边同时乘20%,求出方程的解;
(2)方程两边先同时减去,再同时除以30%,求出方程的解;
(3)先根据比例的基本性质将比例方程改写成,然后方程两边同时除以1.5,求出方程的解。
【解析】(1)
解:
(2)
解:
(3)
解:
13.x=1.4;x=;x=7.2
【分析】2x+0.4=3.2,根据等式的性质1和2,两边同时-0.4,再同时÷2即可;
,根据等式的性质1和2,两边同时÷2,再同时+1,最后同时÷即可;
1.2∶x=0.125∶,根据比例的基本性质,先写成0.125x=1.2×的形式,两边同时÷0.125即可。
【解析】2x+0.4=3.2
解:2x+0.4-0.4=3.2-0.4
2x=2.8
2x÷2=2.8÷2
x=1.4
解:
x-1=
x-1+1=+1
x=
x=
x=
x=
1.2∶x=0.125∶
解:0.125x=1.2×
0.125x=0.9
0.125x÷0.125=0.9÷0.125
x=7.2
14.x=;x=0.15;x=3.6
【分析】(1)根据比例的基本性质“两内项之积等于两外项之积”可得,先计算出,然后两边同时乘计算出;
(2)根据比例的基本性质“两内项之积等于两外项之积”可得7x=0.3×3.5,先计算出0.3×3.5,然后两边同时除以0.7计算出x;
(3)先把左边分数式的比转化为一般形式的比,根据比例的基本性质“两内项之积等于两外项之积”可得,然后两边同时除以9,计算出。
【解析】(1)
解:
(2)0.3∶x=7∶3.5
解:7x=0.3×3.5
7x=1.05
7x÷7=1.05÷7
x=0.15
(3)
解:
15.=36;=1.6
【分析】(1)先计算等式左边的加法,再根据等式的基本性质2,等式两边同时除以,计算即可得解。
(2)根据比例的基本性质把等式转化为,先计算等式右边的乘法,再根据等式的基本性质2,等式两边同时除以4,计算即可得解。
【解析】
解:
0.8∶4=∶8
解:
16.x=3;x=2.3;
x=4;x=
【分析】根据乘法的分配律,提出x得出5x=15,再根据等式基本性质2将等式的两边同时除以5即可;
先将方程中可以算的先算出,再根据等式基本性质1将等式的两边同时减去18,最后根据等式基本性质2将等式的两边同时除以3即可;
先根据等式基本性质2将等式的两边同时除以4,再根据等式基本性质1将等式的两边同时减去2.5即可;
根据比例性质,外项积等于内项积,得出x=,再根据等式基本性质2将等式的两边同时除以即可。
【解析】3.8x+1.2x=15
5x=15
5x÷5=15÷5
x=3
3x+4×4.5=24.9
3x+18=24.9
3x+18-18=24.9-18
3x=6.9
3x÷3=6.9÷3
x=2.3
(x+2.5)×4=26
(x+2.5)×4÷4=26÷4
x+2.5=6.5
x+2.5-2.5=6.5-2.5
x=4
∶
x=
x=
x=÷
x=
x=
17.x=5.85;x=20.2 ;x=
【分析】(1)先根据等式的基本性质1给方程两边同时减去7.8,再根据等式的基本性质2给方程两边同时除以6即可;
(2)先把方程的左边化简为0.7x,再根据等式的基本性质2给方程两边同时除以0.7即可;
(3)先根据比例的基本性质把方程写成x=×,再根据等式的基本性质2给方程两边同时除以即可。
【解析】6x+7.8=42.9
解:6x+7.8-7.8=42.9-7.8
6x=35.1
6x÷6=35.1÷6
x=5.85
4.5x-3.8x=14.14
解:0.7x=14.14
0.7x÷0.7=14.14÷0.7
x=20.2
∶=x∶
解:x=×
x=
x÷=÷
x=×8
x=
18.x=5;x=2;x=
【分析】(1)根据比例的基本性质,把等式转化为0.6x=1.2×2.5,先计算等式右边的乘,再根据等式的基本性质2,等式两边同时除以0.6,计算即可得解。
(2)根据等式的基本性质1,等式两边同时加3.5,再根据等式的基本性质2,等式两边同时除以9,计算即可得解。
(3)先计算等式左边的加法,再根据等式的基本性质2,等式两边同时除以,计算即可得解。
【解析】
解:0.6x=1.2×2.5
0.6x=3
x=3÷0.6
x=5
9x-3.5=14.5
解:9x-3.5+3.5=14.5+3.5
9x=18
x=18÷9
x=2
解:
x=
x=
x=
x=
19.x=;x=15;x=7;x=
【分析】(1)根据比例的基本性质把等式转化为一般方程,先计算等式右边的乘法,再根据等式的基本性质2,等式两边同时除以5,计算即可得解。
(2)根据比例的基本性质把等式转化为一般方程,先计算等式右边的乘法,再根据等式的基本性质2,等式两边同时除以0.2,计算即可得解。
(3)根据比例的基本性质把等式转化为一般方程,先计算等式右边的乘法,再根据等式的基本性质2,等式两边同时除以0.4,计算即可得解。
(4)根据比例的基本性质把等式转化为一般方程,先计算等式右边的乘法,再根据等式的基本性质2,等式两边同时除以,计算即可得解。
【解析】7∶5=x∶
解:
∶x=0.2∶51
解:
解:
解:
20.x=8;x=145;x=20
【分析】方程两边同时加上0.6,两边再同时除以0.3;
方程两边同时减去26,两边再同时除以40%;
根据比例的基本性质,先把比例化为方程:x=12×,两边再同时乘2。
【解析】0.3x-0.6=1.8
解:0.3x-0.6+0.6=1.8+0.6
0.3x=2.4
0.3x÷0.3=2.4÷0.3
x=8
40%x+26=84
解:40%x+26-26=84-26
40%x=58
40%x÷40%=58÷40%
x=145
12∶x=∶
解:x=12×
x=10
2×x=10×2
x=20
21.(1)301.44cm2
(2)602.88dm3
【分析】(1)圆柱的表面积=底面积×2+侧面积,圆柱的底面积S=πr2,侧面积C=πdh;
(2)剩余部分的体积=圆柱的体积-圆锥的体积,圆柱的体积V=πr2h,圆锥的体积V=πr2h。代入数据计算即可。
【解析】(1)8÷2=4(cm)
3.14×42×2+3.14×8×8
=3.14×16×2+25.12×8
=50.24×2+200.96
=100.48+200.96
=301.44
圆柱的表面积是301.44cm2。
(2)10÷2=5(dm)
4÷2=2(dm)
3.14×52×8-3.14×22×6×
=3.14×25×8-3.14×4×(6×)
=78.5×8-12.56×2
=628-25.12
=602.88(dm3)
剩余部分的体积602.88dm3。
22.(1)125.6cm2;
(2)150.72cm3
【分析】(1)先根据圆的半径=C÷π÷2求出圆柱的底面半径,再根据圆柱的表面积=2πr2+2πrh代入数据列式计算即可;
(2)根据圆锥的体积=π(d÷2)2h代入数据列式计算即可。
【解析】(1)12.56÷3.14÷2
=4÷2
=2(cm)
3.14×22×2+2×2×3.14×8
=3.14×4×2+4×3.14×8
=12.56×2+12.56×8
=25.12+100.48
=125.6(cm2)
圆柱的表面积是125.6cm2。
(2)3.14×(8÷2)2×9×
=3.14×42×9×
=3.14×16×9×
=50.24×9×
=452.16×
=150.72(cm3)
圆锥的体积是150.72cm3。
23.21980
【分析】图形的体积等于底面直径是20cm、高是60cm的圆柱的体积加上底面直径是20cm、高是30cm的圆锥的体积,根据圆柱的体积=×半径的平方×高,圆锥的体积=×半径的平方×高,代入数据计算即可。
【解析】3.14××60+×3.14××30
=3.14××60+×3.14××30
=3.14×100×60+3.14×100×10
=3.14×100×(60+10)
=314×70
=21980()
24.653.12cm2
【分析】据图可知,这个立体图形的表面积等于一个底面直径是14cm高是5cm的圆柱的表面积加上一个底面直径是8cm高是5cm的圆柱的侧面积,据此结合圆柱的表面积=2π(d÷2)2+πdh,圆柱的侧面积=πdh代入数据列式计算即可。
【解析】3.14×(14÷2)2×2+3.14×14×5+3.14×8×5
=3.14×72×2+43.96×5+25.12×5
=3.14×49×2+219.8+125.6
=153.86×2+219.8+125.6
=307.72+219.8+125.6
=653.12(cm2)
图形的表面积是653.12cm2。
25.15.7cm3
【分析】看图可知,图中立体图形的体积=整个大圆柱的体积-中空部分圆柱的体积,圆柱的体积=底面积×高,据此列式计算。
【解析】3÷2=1.5(cm)、2÷2=1(cm)
3.14×1.52×4-3.14×12×4
=3.14×4×(1.52-12)
=12.56×(2.25-1)
=12.56×1.25
=15.7(cm3)
这个立体图形的体积是15.7cm3。
26.体积:37.68立方厘米;表面积:62.8平方厘米
【分析】根据图可知,圆柱的底面周长是12.56厘米,圆柱的高是3厘米;根据圆的周长公式:周长=π×半径×2,半径=周长÷π÷2,代入数据,求出圆柱的底面半径;再根据圆柱的体积公式:体积=底面积×高;表面积公式:表面积=底面积×2+侧面积;代入数据,即可解答。
【解析】12.56÷3.14÷2
=4÷2
=2(厘米)
3.14×22×3
=3.14×4×3
=12.56×3
=37.68(立方厘米)
3.14×22×2+12.56×3
=3.14×4×2+12.56×3
=12.56×2+37.68
=25.12+37.68
=62.8(平方厘米)
圆柱的体积是37.68立方厘米,表面积是62.8平方厘米。
27.110.56dm3
【分析】观察图形可知,组合图形的体积=圆锥的体积+长方体的体积,根据圆锥的体积公式V=πr2h,长方体的体积公式V=abh,代入数据计算求解。
【解析】×3.14×(4÷2)2×3+7×7×2
=×3.14×22×3+7×7×2
=×3.14×4×3+7×7×2
=12.56+98
=110.56(dm3)
组合图形的体积是110.56dm3。
28.84.56
【分析】图形的体积等于长、宽都是6cm,高是2cm的长方体的体积加上底面直径是4cm、高是3cm的圆锥的体积;根据长方体的体积=长×宽×高,圆锥体的体积=×半径的平方,代入数据计算即可。
【解析】6×6×2+×3.14××3
=36×2+(×3)×3.14×
=72+1×3.14×4
=72+12.56
=84.56()
图形的体积是84.56cm3。
29.251.2cm3
【分析】观察图形可知,组合体的体积=圆柱的体积+圆锥的体积,根据圆柱的体积公式V=πr2h,圆锥的体积公式V=πr2h,代入数据计算即可求解。
【解析】3.14×(8÷2)2×2+×3.14×(8÷2)2×9
=3.14×42×2+×3.14×42×9
=3.14×16×2+×3.14×16×9
=100.48+150.72
=251.2(cm3)
组合体的体积是251.2cm3。
30.17.27立方厘米
【分析】观察可知,两个相同的图形可拼成一个底面直径是2厘米,高是厘米的圆柱,根据半径=直径÷2,圆柱的体积公式,代入数据计算圆柱体积,再除以2,即可得解。
【解析】
(立方厘米)
31.
【分析】由图可知,图形的体积等于圆柱体积加圆锥的体积,根据圆柱的体积=πr2h,圆锥的体积=πr2h,代入数据解答即可。
【解析】
=3.14×32×12+×3.14×32×(16-12)
=3.14×9×12+×3.14×9×4
=339.12+37.68
图形的体积是376.8。
32.圆锥100.48cm3;圆柱2009.6cm3
【分析】(1)从图中可知,圆锥的底面直径是8cm,高是6cm,根据圆锥的体积公式V=πr2h,代入数据计算求解;
(2)从图中可知,圆柱的底面是一个圆环,根据圆环的面积公式S环=π(R2-r2)求出圆柱的底面积;再根据圆柱的体积公式V=Sh,代入数据计算求解。
【解析】(1)×3.14×(8÷2)2×6
=×3.14×42×6
=×3.14×16×6
=100.48(cm3)
圆锥的体积是100.48cm3。
(2)3.14×[(10÷2)2-(6÷2)2]×40
=3.14×[52-32]×40
=3.14×[25-9]×40
=3.14×16×40
=2009.6(cm3)
圆柱的体积是2009.6cm3。
33.102.28m3
【分析】长方体体积=长×宽×高,圆锥体积=×底面积×高,由此先分别求出长方体和圆锥的体积,再相加求出组合体的体积。
【解析】8×6×2+×3.14×(2÷2)2×6
=96+×3.14×12×6
=96+×3.14×1×6
=96+6.28
=102.28(m3)
34.1130.4cm3,29.4375cm3
【分析】图形是一半的圆柱,则图形的体积=圆柱形的体积=,将数据带入公式计算即可;
根据圆锥的体积=,将数据带入公式计算即可。
【解析】
(cm3)
则图形的体积是1130.4cm3。
(cm3)
圆锥的体积是29.4375cm3。
35.339.12平方厘米;398.78立方厘米
【分析】虽然上面的圆柱挡住了下面大的圆柱的底面的一部分,但是通过平移可以将上面的圆柱的底面平移到下面圆柱的底面,最后立体图形的表面积=大圆柱的表面积+小圆柱的侧面积。圆柱的侧面积:S=Ch=πdh,圆柱的表面积:S=2πr2+πdh。立体图形的体积等于两个圆柱体积之和,圆柱的体积:V=Sh=πr2h。据此解答。
【解析】(10÷2)2×3.14×2+10×3.14×4+6×3.14×3
=52×3.14×2+125.6+56.52
=25×2×3.14+125.6+56.52
=157+125.6+56.52
=339.12(平方厘米)
这个几何体的表面积是339.12平方厘米。
(6÷2)2×3.14×3+(10÷2)2×3.14×4
=32×3.14×3+52×3.14×4
=9×3.14×3+25×3.14×4
=84.78+314
=398.78(立方厘米)
这个几何体的体积是398.78立方厘米。
36.159.48立方厘米
【分析】题干中的图形是正方体减去圆锥的体积,正方体的棱长为6厘米,圆锥的底面直径为6厘米,正方体体积=棱长×棱长×棱长,圆锥体积=,图形的体积=正方体体积-圆锥体积,据此可计算得出答案。
【解析】图形的体积为:
(立方厘米)
37.(1)50.24m2;(2)41.448m3
【分析】(1)图中圆柱的表面积等于圆柱的侧面积加上一个圆柱的底面积,圆柱的侧面积=底面周长×高,圆柱的底面积=πr2,代入相应数值计算;
(2)该立体图形的体积等于圆锥的体积加上圆柱的体积,圆锥的体积=×底面积×高,圆柱的体积=底面积×高,其中圆锥的底面积和圆柱的底面积相等,代入相应数值计算即可解答。
【解析】(1)3.14×4×3+3.14×(4÷2)2
=37.68+3.14×4
=37.68+12.56
=50.24(m2)
因此图中圆柱的表面积是50.24m2。
(2)
(m3)
因此上图立体图形的体积是41.448m3。
38.7822.5立方厘米
【分析】观察图形可知,这个图形的体积等于长30厘米,宽20厘米,高15厘米的长方体的体积减去底面直径为10厘米,高30厘米的圆柱体积的一半,据此利用长方体和圆柱体的体积公式计算即可解答。
【解析】
物体的体积是7822.5立方厘米。
39.空心圆柱的体积:306.15立方厘米;组合图形的表面积:517.6平方厘米
【分析】空心圆柱的体积=底面直径是8厘米,高是10厘米的圆柱的体积-底面直径是5厘米,高是10厘米的圆柱的体积,根据圆柱的体积公式:体积=底面积×高,代入数据,即可求出空心圆柱的体积;
组合图形的表面积=长是12厘米,宽是5厘米,高是8厘米的长方体的表面积+底面直径是4厘米,高是10厘米的圆柱的侧面积;根据长方体表面积公式:表面积=(长×宽+长×高+宽×高)×2,圆柱侧面积公式:侧面积=底面周长×高,代入数据,即可解答。
【解析】空心圆柱的体积:
3.14×(8÷2)2×10-3.14×(5÷2)2×10
=3.14×42×10-3.14×2.52×10
=3.14×16×10-3.14×6.25×10
=50.24×10-19.625×10
=502.4-196.25
=306.15(立方厘米)
空心圆柱的体积是306.15立方厘米。
组合图形的表面积:
(12×5+12×8+5×8)×2+3.14×4×10
=(60+96+40)×2+12.56×10
=(156+40)×2+125.6
=196×2+125.6
=392+125.6
=517.6(平方厘米)
组合图形的表面积是517.6平方厘米。
40.109.9cm3
【分析】观察图形可知,体积=底面直径是4cm,高是5cm的圆柱的体积+底面直径是6cm,高是5cm的圆锥的体积,根据圆柱的体积公式:体积=底面积×高;圆锥的体积公式:体积=底面积×高×,代入数据,即可解答。
【解析】3.14×(4÷2)2×5+3.14×(6÷2)2×5×
=3.14×22×5+3.14×32×5×
=3.14×4×5+3.14×9×5×
=12.56×5+28.26×5×
=62.8+141.3×
=62.8+47.1
=109.9(cm3)
图形的体积是109.9cm3。
41.252.8平方分米
【分析】通过观察图形发现,上面的圆柱与下面的长方体粘合在一起,所以上面的圆柱只求它的侧面积,下面的长方体求出它的表面积,然后合并起来即可,根据圆柱的侧面积公式:
,长方体的表面积公式:S=(ab+ah+bh)×2,把数据代入公式解答。
【解析】
(平方分米)
组合图形的表面积是252.8平方分米。
42.89.12dm3
【分析】根据图可知,这个组合体下面是一个棱长为4dm的正方体,上面是圆柱的一半,圆柱的底面直径是4dm,高是4dm,根据正方体的体积:棱长×棱长×棱长,圆柱的体积:πr2h,把数代入即可求解,求出圆柱的体积再除以2即可求出上面半圆柱的体积。
【解析】4×4×4+3.14×(4÷2)2×4÷2
=64+3.14×4×4÷2
=64+25.12
=89.12(dm3)
这个组合体的体积是89.12dm3。
43.13256cm3
【分析】根据对图片的分析,该立体图形体积为下面的长方体加上上面的圆柱体的体积之和。
长方体体积公式:V=长×宽×高,圆柱体积公式为:V=r2h,将数据代入求解即可。
【解析】由分析可得:
长方体体积为:
40×30×10
=1200×10
=12000(cm3)
圆柱底面半径为:8÷2=4(cm)
圆柱体积为:
3.14×42×25
=3.14×16×25
=50.24×25
=1256(cm3)
立体图形的体积为:12000+1256=13256(cm3)
44.75.36cm3
【分析】体积=底面半径是(4÷2)cm,高是8cm的圆柱的体积-底面积半径是(4÷2)cm,高是6cm的圆锥的体积,根据圆柱的体积公式:体积=底面积×高;圆锥的体积公式:体积=底面积×高×,代入数据,即可解答。
【解析】3.14×(4÷2)2×8-3.14×(4÷2)2×6×
=3.14×22×8-3.14×22×6×
=3.14×4×8-3.14×4×6×
=12.56×8-12.56×6×
=100.48-75.36×
=100.48-25.12
=75.36(cm3)
45.(1)15.7立方厘米;(2)301.44立方厘米
【分析】(1)体积=底面半径是(3÷2)厘米,高是4厘米的圆柱的体积-底面半径是(2÷2)厘米,高是4厘米的圆柱的体积,根据圆柱的体积公式:体积=底面积×高,代入数据,即可解答。
(2)体积=底面半径是662厘米,高是8厘米的圆锥的体积,根据圆锥的体积公式:体积=底面积×高×,代入数据,即可解答。
【解析】(1)3.14×(3÷2)2×4-3.14×(2÷2)2×4
=3.14×1.52×4-3.14×12×4
=3.14×2.25×4-3.14×4
=7.065×4-12.56
=28.26-12.56
=15.7(立方厘米)
(2)3.14×62×8×
=3.14×36×8×
=113.04×8×
=904.32×
=301.44(立方厘米)
46.394.8cm2
【分析】观察图形可知,组合体的表面积=长是8cm,宽是15cm,高是2cm的长方体的表面积+底面半径是4cm的圆柱的侧面积;根据长方体表面积公式:表面积=(长×宽+长×高+宽×高)×2,圆柱的侧面积公式:侧面积=底面周长×高,代入数据,即可解答。
【解析】(8×15+8×2+15×2)×2+3.14×4×5
=(120+16+30)×2+12.56×5
=(136+30)×2+62.8
=166×2+62.8
=332+62.8
=394.8(cm2)
47.376.8cm2
【分析】由于大小两个圆柱结合在一起,所以它的表面积等于小圆柱的侧面积加上大圆柱的表面积,根据圆柱的侧面积公式:S=Ch,圆柱的表面积=侧面积+底面积×2;把数据代入公式解答。
【解析】3.14×4×5+3.14×10×5+3.14×(10÷2)2×2
=12.56×5+31.4×5+3.14×52×2
=62.8+157+3.14×25×2
=62.8+157+3.14×50
=62.8+157+157
=219.8+157
=376.8(cm2)
这个图形的表面积是376.8cm2。
48.(1);(2)
【分析】(1)根据图示,图形(1)的体积等于圆柱体积加圆锥的体积,据此解答即可;
(2)图形(2)表面积等于正方体的表面积加圆柱的侧面积,据此解答即可。
【解析】(1)
=3.14×108+×3.14×36
图形(1)的体积是376.8,
(2)
图形(2)的表面积是5770。
49.cm2
【分析】由于上面的圆柱与下面的圆柱体组合在一起,所以上面的圆柱只求侧面积,下面圆柱体求表面积,然后求和就是这个图形的表面积。根据圆柱的侧面积公式:S=Ch,圆柱的表面积=侧面积+底面积×2,把数据代入公式解答即可。
【解析】
它的表面积是。
50.表面积是514.96平方厘米,体积是766.16立方厘米;
体积是84.56立方厘米。
【分析】(1)运用圆柱的表面积公式S=d×h+2r2求出大圆柱表面积,再加上小圆柱的侧面积即可,根据圆柱的体积公式:V=r2h求出组合图形的体积。
(2)圆锥的体积公式:V=r2h,V=abc把数据代入公式求出它们的体积和即可。
【解析】12÷2=6(厘米)
8÷2=4(厘米)
表面积:
3.14×12×5+3.14×62×2+3.14×8×4
=3.14×60+3.14×72+3.14×32
=3.14×(60+72+32)
=3.14×164
=514.96(平方厘米)
体积:3.14×62×5+3.14×42×4
=3.14×180+3.14×64
=3.14×(180+64)
=3.14×244
=766.16(立方厘米)
表面积是514.96平方厘米,体积是766.16立方厘米。
(2)6×6×2+3.14×(4÷2)2×3×
=72+3.14×4
=72+12.56
=84.56(立方厘米)
体积是84.56立方厘米。
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
中小学教育资源及组卷应用平台
2024-2025学年六年级数学下册期末复习专项北师大版
(期末考点培优)专题04 计算题
学校:___________姓名:___________班级:___________考号:___________
1.解方程。
2.解方程或比例。
(1)x-85%x=750 (2)= (3)1.2∶x=5∶1.5
3.计算。
x∶5=0.4∶0.5 23∶x=3∶12 13∶14=15∶x
2÷× 2.25×1.8+12.5×0.18 [1-(+)]×36
4.解方程。
5.解比例。
3.2∶x=0.4∶1.6 x∶25=16∶60
6.解方程。
7.解比例。
8.解比例。
9.解比例方程。
x∶8= 9∶5=4.5∶x ∶∶
10.解比例。
11.解比例。
21∶0.4=∶ = 16∶=5∶0.5
12.解方程或比例。
13.解方程。
2x+0.4=3.2 1.2∶x=0.125∶
14.解比例。
∶x=∶2 0.3∶x=7∶3.5 =4∶9
15.解方程。
0.8∶4=∶8
16.解方程。
3.8x+1.2x=15 3x+4×4.5=24.9
(x+2.5)×4=26 ∶
17.解方程。
6x+7.8=42.9 4.5x-3.8x=14.14
18.解方程。
9x-3.5=14.5
19.解比例。
7∶5=x∶ ∶x=0.2∶51
20.解方程。
0.3x-0.6=1.8 40%x+26=84 12∶x=
21.(1)计算下面圆柱的表面积。
(2)从一个圆柱中挖去一个圆锥,如下图,求剩余部分的体积。
22.求下面圆柱的表面积和圆锥的体积。
(1)
(2)
23.求下面图形的体积。
24.计算下面图形的表面积。
25.计算下面立体图形的体积。(单位cm)
26.下图是一个圆柱的展开图,计算这个圆柱的体积和表面积。
27.计算如图组合图形的体积。(单位:dm)
28.计算如图图形的体积。
29.求图中立体图形的体积。
30.计算下列图形的体积。
31.计算下面图形的体积。
32.计算下面各图形的体积。(单位:cm)
33.如图,一个长方体的上面有一个圆锥,计算这个组合图形的体积。
34.求下面两个图形的体积。(单位:cm)
35.求下面几何体的表面积和体积。(单位:厘米)
36.求下列图形的体积。(单位:厘米)
37.计算图形的体积和表面积。
(1)求出图中圆柱的表面积;
(2)求出上图立体图形的体积。
38.求如图物体的体积。
39.求下图中空心圆柱的体积和组合图形的表面积。(单位:厘米)
40.求下面图形的体积。
41.计算下边组合图形的表面积。
42.计算下面图形的体积。
43.求出立体图形的体积。(单位:cm)
44.计算下图的体积。
45.求如图所示图形的体积。(单位∶厘米)
(1)
(2)
46.求下面图形的表面积。(单位:cm)
47.计算下面图形的表面积。
48.计算下面图形(1)的体积与图形(2)的表面积。
(1) (2)
49.计算下面图形的表面积。(单位:cm)
50.计算下左图的表面积和体积,计算下右图的体积。
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案及试题解析
1.;
;
【分析】(1)根据比例的基本性质,将原式变成,再根据等式的性质2,方程两边同时除以,即可求解。
(2)根据等式的性质1,方程两边同时减去7.2,再根据等式的性质2,方程两边同时除以6,即可求解。
(3)根据比例的基本性质,将原式变成,再根据等式的性质2,方程两边同时除以6,即可求解。
(4)先将原式改写成,再根据等式的性质2,方程两边同时乘0.25,即可求解。
【解析】
解:
解:
解:
解:
2.(1)x=5000;(2)x=3;(3)x=0.36
【分析】(1)先将方程左边进行合并,再结合等式的基本性质2,将方程的两边同时除以0.15,从而得出答案;
(2)利用交叉相乘积相等,将比例转化为3x=5×1.2,将方程的两边同时除以3,从而得出答案;
(3)利用比例的基本性质,两内项之积等于两外项之积,将比例转化为5x=1.2×1.5,将方程的两边同时除以5,从而得出答案。
【解析】(1)x-85%x=750
解:x-0.85x=750
0.15x=750
x=750÷0.15
x=5000
(2)=
解:3x=5×1.2
3x=6
x=6÷2
x=3
(3)1.2∶x=5∶1.5
解:5x=1.2×1.5
5x=1.8
x=1.8÷5
x=0.36
3.x=4;x=92;x=
;6.3;6
【分析】x∶5=0.4∶0.5,解比例,原式化为:0.5x=5×0.4,再根据等式的性质2,方程两边同时除以0.5即可。
23∶x=3∶12,解比例,原式化为:3x=23×12,再根据等式的性质2,方程两边同时除以3即可。
13∶14=15∶x,解比例,原式化为:13x=14×15,再根据等式的性质2,方程两边同时除以13即可。
2÷×,先计算除法,再计算乘法;
2.25×1.8+12.5×0.18,把12.5×0.18化为1.25×1.8,原式化为:2.25×1.8+1.25×1.8,再根据乘法分配律的逆运算,原式化为:(2.25+1.25)×1.8,再进行计算。
[1-(+)]×36,先根据减法性质,原式化为:[1--]×36,再根据乘法分配律,原式化为:1×36-×36-×36,再进行计算。
【解析】x∶5=0.4∶0.5
解:0.5x=5×0.4
0.5x=2
0.5x÷0.5=2÷0.5
x=4
23∶x=3∶12
解:3x=23×12
3x=276
3x÷3=276÷3
x=92
13∶14=15∶x
解:13x=14×15
13x=210
13x÷13=210÷13
x=
2÷×
=2××
=×
=
2.25×1.8+12.5×0.18
=2.25×1.8+1.25×1.8
=(2.25+1.25)×1.8
=3.5×1.8
=6.3
[1-(+)]×36
=[1--]×36
=1×36-×36-×36
=36-18-12
=18-12
=6
4.;;
;
【解析】
解:
解:
解:
解:
5.x=12.8;;
【分析】根据比例的基本性质:内项积=外项积,将比例转化为方程0.4x=3.2×1.6,再根据等式的性质2将等式的两边同时除以0.4即可;
根据比例的基本性质,将比例转化为方程60x=25×16,再根据等式的性质2将等式的两边同时除以60即可;
根据比例的基本性质,将比例转化为方程21x=2×7,再根据等式的性质2将等式的两边同时除以21即可;
【解析】3.2∶x=0.4∶1.6
解:0.4x=3.2×1.6
0.4x=5.12
x=5.12÷0.4
x=12.8
x∶25=16∶60
解:60x=25×16
60x=400
x=400÷60
x=
解:21x=2×7
21x=14
x=14÷21
x=
6.;;
【分析】,根据比例的基本性质,先写成的形式,两边同时÷即可;
,根据比例的基本性质,先写成的形式,两边同时÷1.25即可;
,根据比例的基本性质,先写成的形式,两边同时÷3即可。
【解析】
解:
解:
解:
7.;;;
【分析】根据比例的基本性质“两内项之积等于两外项之积”,把比例转化为方程,先计算,然后两边同时除以5即可;
根据比例的基本性质“两内项之积等于两外项之积”,把比例转化为方程,先计算 ,然后两边同时除以8即可;
根据比例的基本性质“两内项之积等于两外项之积”,把比例转化为方程 ,先计算,然后两边同时除以4.5即可;
根据比例的基本性质“两内项之积等于两外项之积”,把比例转化为方程 ,先计算 ,然后两边同时乘7即可;
【解析】
解:
解:
解:
解:
8.;;
【分析】(1)根据比例的基本性质,把等式转化为,先计算等式右边的乘法,再根据等式的基本性质2,等式两边同时除以2,计算即可得解。
(2)根据比例的基本性质,把等式转化为,先计算等式右边的乘法,再根据等式的基本性质2,等式两边同时除以0.25,计算即可得解。
(3)根据比例的基本性质,把等式转化为,先计算等式右边的乘法,再根据等式的基本性质2,等式两边同时除以,计算即可得解。
【解析】(1)
解:
(2)
解:
(3)
解:
9.x=6;x=2.5;
【分析】根据比例的基本性质,先把比例化为方程:4x=8×3,两边再同时除以4;
根据比例的基本性质,先把比例化为方程:9x=5×4.5,两边再同时除以9;
根据比例的基本性质,先把比例化为方程:x=×,两边再同时乘2。
【解析】x∶8=
解:4x=8×3
4x=24
4x÷4=24÷4
x=6
9∶5=4.5∶x
解:9x=5×4.5
9x=22.5
9x÷9=22.5÷9
x=2.5
∶∶
解:x=×
x=
2×x=×2
x=
10.x=6;x=2.5;x=
【分析】根据比例的基本性质,先把比例化为方程:4x=8×3,两边再同时除以4;
根据比例的基本性质,先把比例化为方程:9x=5×4.5,两边再同时除以9;
根据比例的基本性质,先把比例化为方程:x=×,两边再同时乘2。
【解析】
解:4x=8×3
4x=24
4x÷4=24÷4
x=6
9∶5=4.5∶x
解:9x=5×4.5
9x=22.5
9x÷9=22.5÷9
x=2.5
解:x=×
x=
2×x=×2
x=
11.=17.5;=15;=1.6
【分析】(1)先根据比例的基本性质将比例方程改写成0.4=21×,然后方程两边同时除以0.4,求出方程的解;
(2)先根据比例的基本性质将比例方程改写成8=24×5,然后方程两边同时除以8,求出方程的解;
(3)先根据比例的基本性质将比例方程改写成5=16×0.5,然后方程两边同时除以5,求出方程的解。
【解析】(1)21∶0.4=∶
解:0.4=21×
0.4=7
=7÷0.4
=17.5
(2)=
解:8=24×5
8=120
=120÷8
=15
(3)16∶=5∶0.5
解:5=16×0.5
5=8
=8÷5
=1.6
12.;;
【分析】(1)方程两边同时乘20%,求出方程的解;
(2)方程两边先同时减去,再同时除以30%,求出方程的解;
(3)先根据比例的基本性质将比例方程改写成,然后方程两边同时除以1.5,求出方程的解。
【解析】(1)
解:
(2)
解:
(3)
解:
13.x=1.4;x=;x=7.2
【分析】2x+0.4=3.2,根据等式的性质1和2,两边同时-0.4,再同时÷2即可;
,根据等式的性质1和2,两边同时÷2,再同时+1,最后同时÷即可;
1.2∶x=0.125∶,根据比例的基本性质,先写成0.125x=1.2×的形式,两边同时÷0.125即可。
【解析】2x+0.4=3.2
解:2x+0.4-0.4=3.2-0.4
2x=2.8
2x÷2=2.8÷2
x=1.4
解:
x-1=
x-1+1=+1
x=
x=
x=
x=
1.2∶x=0.125∶
解:0.125x=1.2×
0.125x=0.9
0.125x÷0.125=0.9÷0.125
x=7.2
14.x=;x=0.15;x=3.6
【分析】(1)根据比例的基本性质“两内项之积等于两外项之积”可得,先计算出,然后两边同时乘计算出;
(2)根据比例的基本性质“两内项之积等于两外项之积”可得7x=0.3×3.5,先计算出0.3×3.5,然后两边同时除以0.7计算出x;
(3)先把左边分数式的比转化为一般形式的比,根据比例的基本性质“两内项之积等于两外项之积”可得,然后两边同时除以9,计算出。
【解析】(1)
解:
(2)0.3∶x=7∶3.5
解:7x=0.3×3.5
7x=1.05
7x÷7=1.05÷7
x=0.15
(3)
解:
15.=36;=1.6
【分析】(1)先计算等式左边的加法,再根据等式的基本性质2,等式两边同时除以,计算即可得解。
(2)根据比例的基本性质把等式转化为,先计算等式右边的乘法,再根据等式的基本性质2,等式两边同时除以4,计算即可得解。
【解析】
解:
0.8∶4=∶8
解:
16.x=3;x=2.3;
x=4;x=
【分析】根据乘法的分配律,提出x得出5x=15,再根据等式基本性质2将等式的两边同时除以5即可;
先将方程中可以算的先算出,再根据等式基本性质1将等式的两边同时减去18,最后根据等式基本性质2将等式的两边同时除以3即可;
先根据等式基本性质2将等式的两边同时除以4,再根据等式基本性质1将等式的两边同时减去2.5即可;
根据比例性质,外项积等于内项积,得出x=,再根据等式基本性质2将等式的两边同时除以即可。
【解析】3.8x+1.2x=15
5x=15
5x÷5=15÷5
x=3
3x+4×4.5=24.9
3x+18=24.9
3x+18-18=24.9-18
3x=6.9
3x÷3=6.9÷3
x=2.3
(x+2.5)×4=26
(x+2.5)×4÷4=26÷4
x+2.5=6.5
x+2.5-2.5=6.5-2.5
x=4
∶
x=
x=
x=÷
x=
x=
17.x=5.85;x=20.2 ;x=
【分析】(1)先根据等式的基本性质1给方程两边同时减去7.8,再根据等式的基本性质2给方程两边同时除以6即可;
(2)先把方程的左边化简为0.7x,再根据等式的基本性质2给方程两边同时除以0.7即可;
(3)先根据比例的基本性质把方程写成x=×,再根据等式的基本性质2给方程两边同时除以即可。
【解析】6x+7.8=42.9
解:6x+7.8-7.8=42.9-7.8
6x=35.1
6x÷6=35.1÷6
x=5.85
4.5x-3.8x=14.14
解:0.7x=14.14
0.7x÷0.7=14.14÷0.7
x=20.2
∶=x∶
解:x=×
x=
x÷=÷
x=×8
x=
18.x=5;x=2;x=
【分析】(1)根据比例的基本性质,把等式转化为0.6x=1.2×2.5,先计算等式右边的乘,再根据等式的基本性质2,等式两边同时除以0.6,计算即可得解。
(2)根据等式的基本性质1,等式两边同时加3.5,再根据等式的基本性质2,等式两边同时除以9,计算即可得解。
(3)先计算等式左边的加法,再根据等式的基本性质2,等式两边同时除以,计算即可得解。
【解析】
解:0.6x=1.2×2.5
0.6x=3
x=3÷0.6
x=5
9x-3.5=14.5
解:9x-3.5+3.5=14.5+3.5
9x=18
x=18÷9
x=2
解:
x=
x=
x=
x=
19.x=;x=15;x=7;x=
【分析】(1)根据比例的基本性质把等式转化为一般方程,先计算等式右边的乘法,再根据等式的基本性质2,等式两边同时除以5,计算即可得解。
(2)根据比例的基本性质把等式转化为一般方程,先计算等式右边的乘法,再根据等式的基本性质2,等式两边同时除以0.2,计算即可得解。
(3)根据比例的基本性质把等式转化为一般方程,先计算等式右边的乘法,再根据等式的基本性质2,等式两边同时除以0.4,计算即可得解。
(4)根据比例的基本性质把等式转化为一般方程,先计算等式右边的乘法,再根据等式的基本性质2,等式两边同时除以,计算即可得解。
【解析】7∶5=x∶
解:
∶x=0.2∶51
解:
解:
解:
20.x=8;x=145;x=20
【分析】方程两边同时加上0.6,两边再同时除以0.3;
方程两边同时减去26,两边再同时除以40%;
根据比例的基本性质,先把比例化为方程:x=12×,两边再同时乘2。
【解析】0.3x-0.6=1.8
解:0.3x-0.6+0.6=1.8+0.6
0.3x=2.4
0.3x÷0.3=2.4÷0.3
x=8
40%x+26=84
解:40%x+26-26=84-26
40%x=58
40%x÷40%=58÷40%
x=145
12∶x=∶
解:x=12×
x=10
2×x=10×2
x=20
21.(1)301.44cm2
(2)602.88dm3
【分析】(1)圆柱的表面积=底面积×2+侧面积,圆柱的底面积S=πr2,侧面积C=πdh;
(2)剩余部分的体积=圆柱的体积-圆锥的体积,圆柱的体积V=πr2h,圆锥的体积V=πr2h。代入数据计算即可。
【解析】(1)8÷2=4(cm)
3.14×42×2+3.14×8×8
=3.14×16×2+25.12×8
=50.24×2+200.96
=100.48+200.96
=301.44
圆柱的表面积是301.44cm2。
(2)10÷2=5(dm)
4÷2=2(dm)
3.14×52×8-3.14×22×6×
=3.14×25×8-3.14×4×(6×)
=78.5×8-12.56×2
=628-25.12
=602.88(dm3)
剩余部分的体积602.88dm3。
22.(1)125.6cm2;
(2)150.72cm3
【分析】(1)先根据圆的半径=C÷π÷2求出圆柱的底面半径,再根据圆柱的表面积=2πr2+2πrh代入数据列式计算即可;
(2)根据圆锥的体积=π(d÷2)2h代入数据列式计算即可。
【解析】(1)12.56÷3.14÷2
=4÷2
=2(cm)
3.14×22×2+2×2×3.14×8
=3.14×4×2+4×3.14×8
=12.56×2+12.56×8
=25.12+100.48
=125.6(cm2)
圆柱的表面积是125.6cm2。
(2)3.14×(8÷2)2×9×
=3.14×42×9×
=3.14×16×9×
=50.24×9×
=452.16×
=150.72(cm3)
圆锥的体积是150.72cm3。
23.21980
【分析】图形的体积等于底面直径是20cm、高是60cm的圆柱的体积加上底面直径是20cm、高是30cm的圆锥的体积,根据圆柱的体积=×半径的平方×高,圆锥的体积=×半径的平方×高,代入数据计算即可。
【解析】3.14××60+×3.14××30
=3.14××60+×3.14××30
=3.14×100×60+3.14×100×10
=3.14×100×(60+10)
=314×70
=21980()
24.653.12cm2
【分析】据图可知,这个立体图形的表面积等于一个底面直径是14cm高是5cm的圆柱的表面积加上一个底面直径是8cm高是5cm的圆柱的侧面积,据此结合圆柱的表面积=2π(d÷2)2+πdh,圆柱的侧面积=πdh代入数据列式计算即可。
【解析】3.14×(14÷2)2×2+3.14×14×5+3.14×8×5
=3.14×72×2+43.96×5+25.12×5
=3.14×49×2+219.8+125.6
=153.86×2+219.8+125.6
=307.72+219.8+125.6
=653.12(cm2)
图形的表面积是653.12cm2。
25.15.7cm3
【分析】看图可知,图中立体图形的体积=整个大圆柱的体积-中空部分圆柱的体积,圆柱的体积=底面积×高,据此列式计算。
【解析】3÷2=1.5(cm)、2÷2=1(cm)
3.14×1.52×4-3.14×12×4
=3.14×4×(1.52-12)
=12.56×(2.25-1)
=12.56×1.25
=15.7(cm3)
这个立体图形的体积是15.7cm3。
26.体积:37.68立方厘米;表面积:62.8平方厘米
【分析】根据图可知,圆柱的底面周长是12.56厘米,圆柱的高是3厘米;根据圆的周长公式:周长=π×半径×2,半径=周长÷π÷2,代入数据,求出圆柱的底面半径;再根据圆柱的体积公式:体积=底面积×高;表面积公式:表面积=底面积×2+侧面积;代入数据,即可解答。
【解析】12.56÷3.14÷2
=4÷2
=2(厘米)
3.14×22×3
=3.14×4×3
=12.56×3
=37.68(立方厘米)
3.14×22×2+12.56×3
=3.14×4×2+12.56×3
=12.56×2+37.68
=25.12+37.68
=62.8(平方厘米)
圆柱的体积是37.68立方厘米,表面积是62.8平方厘米。
27.110.56dm3
【分析】观察图形可知,组合图形的体积=圆锥的体积+长方体的体积,根据圆锥的体积公式V=πr2h,长方体的体积公式V=abh,代入数据计算求解。
【解析】×3.14×(4÷2)2×3+7×7×2
=×3.14×22×3+7×7×2
=×3.14×4×3+7×7×2
=12.56+98
=110.56(dm3)
组合图形的体积是110.56dm3。
28.84.56
【分析】图形的体积等于长、宽都是6cm,高是2cm的长方体的体积加上底面直径是4cm、高是3cm的圆锥的体积;根据长方体的体积=长×宽×高,圆锥体的体积=×半径的平方,代入数据计算即可。
【解析】6×6×2+×3.14××3
=36×2+(×3)×3.14×
=72+1×3.14×4
=72+12.56
=84.56()
图形的体积是84.56cm3。
29.251.2cm3
【分析】观察图形可知,组合体的体积=圆柱的体积+圆锥的体积,根据圆柱的体积公式V=πr2h,圆锥的体积公式V=πr2h,代入数据计算即可求解。
【解析】3.14×(8÷2)2×2+×3.14×(8÷2)2×9
=3.14×42×2+×3.14×42×9
=3.14×16×2+×3.14×16×9
=100.48+150.72
=251.2(cm3)
组合体的体积是251.2cm3。
30.17.27立方厘米
【分析】观察可知,两个相同的图形可拼成一个底面直径是2厘米,高是厘米的圆柱,根据半径=直径÷2,圆柱的体积公式,代入数据计算圆柱体积,再除以2,即可得解。
【解析】
(立方厘米)
31.
【分析】由图可知,图形的体积等于圆柱体积加圆锥的体积,根据圆柱的体积=πr2h,圆锥的体积=πr2h,代入数据解答即可。
【解析】
=3.14×32×12+×3.14×32×(16-12)
=3.14×9×12+×3.14×9×4
=339.12+37.68
图形的体积是376.8。
32.圆锥100.48cm3;圆柱2009.6cm3
【分析】(1)从图中可知,圆锥的底面直径是8cm,高是6cm,根据圆锥的体积公式V=πr2h,代入数据计算求解;
(2)从图中可知,圆柱的底面是一个圆环,根据圆环的面积公式S环=π(R2-r2)求出圆柱的底面积;再根据圆柱的体积公式V=Sh,代入数据计算求解。
【解析】(1)×3.14×(8÷2)2×6
=×3.14×42×6
=×3.14×16×6
=100.48(cm3)
圆锥的体积是100.48cm3。
(2)3.14×[(10÷2)2-(6÷2)2]×40
=3.14×[52-32]×40
=3.14×[25-9]×40
=3.14×16×40
=2009.6(cm3)
圆柱的体积是2009.6cm3。
33.102.28m3
【分析】长方体体积=长×宽×高,圆锥体积=×底面积×高,由此先分别求出长方体和圆锥的体积,再相加求出组合体的体积。
【解析】8×6×2+×3.14×(2÷2)2×6
=96+×3.14×12×6
=96+×3.14×1×6
=96+6.28
=102.28(m3)
34.1130.4cm3,29.4375cm3
【分析】图形是一半的圆柱,则图形的体积=圆柱形的体积=,将数据带入公式计算即可;
根据圆锥的体积=,将数据带入公式计算即可。
【解析】
(cm3)
则图形的体积是1130.4cm3。
(cm3)
圆锥的体积是29.4375cm3。
35.339.12平方厘米;398.78立方厘米
【分析】虽然上面的圆柱挡住了下面大的圆柱的底面的一部分,但是通过平移可以将上面的圆柱的底面平移到下面圆柱的底面,最后立体图形的表面积=大圆柱的表面积+小圆柱的侧面积。圆柱的侧面积:S=Ch=πdh,圆柱的表面积:S=2πr2+πdh。立体图形的体积等于两个圆柱体积之和,圆柱的体积:V=Sh=πr2h。据此解答。
【解析】(10÷2)2×3.14×2+10×3.14×4+6×3.14×3
=52×3.14×2+125.6+56.52
=25×2×3.14+125.6+56.52
=157+125.6+56.52
=339.12(平方厘米)
这个几何体的表面积是339.12平方厘米。
(6÷2)2×3.14×3+(10÷2)2×3.14×4
=32×3.14×3+52×3.14×4
=9×3.14×3+25×3.14×4
=84.78+314
=398.78(立方厘米)
这个几何体的体积是398.78立方厘米。
36.159.48立方厘米
【分析】题干中的图形是正方体减去圆锥的体积,正方体的棱长为6厘米,圆锥的底面直径为6厘米,正方体体积=棱长×棱长×棱长,圆锥体积=,图形的体积=正方体体积-圆锥体积,据此可计算得出答案。
【解析】图形的体积为:
(立方厘米)
37.(1)50.24m2;(2)41.448m3
【分析】(1)图中圆柱的表面积等于圆柱的侧面积加上一个圆柱的底面积,圆柱的侧面积=底面周长×高,圆柱的底面积=πr2,代入相应数值计算;
(2)该立体图形的体积等于圆锥的体积加上圆柱的体积,圆锥的体积=×底面积×高,圆柱的体积=底面积×高,其中圆锥的底面积和圆柱的底面积相等,代入相应数值计算即可解答。
【解析】(1)3.14×4×3+3.14×(4÷2)2
=37.68+3.14×4
=37.68+12.56
=50.24(m2)
因此图中圆柱的表面积是50.24m2。
(2)
(m3)
因此上图立体图形的体积是41.448m3。
38.7822.5立方厘米
【分析】观察图形可知,这个图形的体积等于长30厘米,宽20厘米,高15厘米的长方体的体积减去底面直径为10厘米,高30厘米的圆柱体积的一半,据此利用长方体和圆柱体的体积公式计算即可解答。
【解析】
物体的体积是7822.5立方厘米。
39.空心圆柱的体积:306.15立方厘米;组合图形的表面积:517.6平方厘米
【分析】空心圆柱的体积=底面直径是8厘米,高是10厘米的圆柱的体积-底面直径是5厘米,高是10厘米的圆柱的体积,根据圆柱的体积公式:体积=底面积×高,代入数据,即可求出空心圆柱的体积;
组合图形的表面积=长是12厘米,宽是5厘米,高是8厘米的长方体的表面积+底面直径是4厘米,高是10厘米的圆柱的侧面积;根据长方体表面积公式:表面积=(长×宽+长×高+宽×高)×2,圆柱侧面积公式:侧面积=底面周长×高,代入数据,即可解答。
【解析】空心圆柱的体积:
3.14×(8÷2)2×10-3.14×(5÷2)2×10
=3.14×42×10-3.14×2.52×10
=3.14×16×10-3.14×6.25×10
=50.24×10-19.625×10
=502.4-196.25
=306.15(立方厘米)
空心圆柱的体积是306.15立方厘米。
组合图形的表面积:
(12×5+12×8+5×8)×2+3.14×4×10
=(60+96+40)×2+12.56×10
=(156+40)×2+125.6
=196×2+125.6
=392+125.6
=517.6(平方厘米)
组合图形的表面积是517.6平方厘米。
40.109.9cm3
【分析】观察图形可知,体积=底面直径是4cm,高是5cm的圆柱的体积+底面直径是6cm,高是5cm的圆锥的体积,根据圆柱的体积公式:体积=底面积×高;圆锥的体积公式:体积=底面积×高×,代入数据,即可解答。
【解析】3.14×(4÷2)2×5+3.14×(6÷2)2×5×
=3.14×22×5+3.14×32×5×
=3.14×4×5+3.14×9×5×
=12.56×5+28.26×5×
=62.8+141.3×
=62.8+47.1
=109.9(cm3)
图形的体积是109.9cm3。
41.252.8平方分米
【分析】通过观察图形发现,上面的圆柱与下面的长方体粘合在一起,所以上面的圆柱只求它的侧面积,下面的长方体求出它的表面积,然后合并起来即可,根据圆柱的侧面积公式:
,长方体的表面积公式:S=(ab+ah+bh)×2,把数据代入公式解答。
【解析】
(平方分米)
组合图形的表面积是252.8平方分米。
42.89.12dm3
【分析】根据图可知,这个组合体下面是一个棱长为4dm的正方体,上面是圆柱的一半,圆柱的底面直径是4dm,高是4dm,根据正方体的体积:棱长×棱长×棱长,圆柱的体积:πr2h,把数代入即可求解,求出圆柱的体积再除以2即可求出上面半圆柱的体积。
【解析】4×4×4+3.14×(4÷2)2×4÷2
=64+3.14×4×4÷2
=64+25.12
=89.12(dm3)
这个组合体的体积是89.12dm3。
43.13256cm3
【分析】根据对图片的分析,该立体图形体积为下面的长方体加上上面的圆柱体的体积之和。
长方体体积公式:V=长×宽×高,圆柱体积公式为:V=r2h,将数据代入求解即可。
【解析】由分析可得:
长方体体积为:
40×30×10
=1200×10
=12000(cm3)
圆柱底面半径为:8÷2=4(cm)
圆柱体积为:
3.14×42×25
=3.14×16×25
=50.24×25
=1256(cm3)
立体图形的体积为:12000+1256=13256(cm3)
44.75.36cm3
【分析】体积=底面半径是(4÷2)cm,高是8cm的圆柱的体积-底面积半径是(4÷2)cm,高是6cm的圆锥的体积,根据圆柱的体积公式:体积=底面积×高;圆锥的体积公式:体积=底面积×高×,代入数据,即可解答。
【解析】3.14×(4÷2)2×8-3.14×(4÷2)2×6×
=3.14×22×8-3.14×22×6×
=3.14×4×8-3.14×4×6×
=12.56×8-12.56×6×
=100.48-75.36×
=100.48-25.12
=75.36(cm3)
45.(1)15.7立方厘米;(2)301.44立方厘米
【分析】(1)体积=底面半径是(3÷2)厘米,高是4厘米的圆柱的体积-底面半径是(2÷2)厘米,高是4厘米的圆柱的体积,根据圆柱的体积公式:体积=底面积×高,代入数据,即可解答。
(2)体积=底面半径是662厘米,高是8厘米的圆锥的体积,根据圆锥的体积公式:体积=底面积×高×,代入数据,即可解答。
【解析】(1)3.14×(3÷2)2×4-3.14×(2÷2)2×4
=3.14×1.52×4-3.14×12×4
=3.14×2.25×4-3.14×4
=7.065×4-12.56
=28.26-12.56
=15.7(立方厘米)
(2)3.14×62×8×
=3.14×36×8×
=113.04×8×
=904.32×
=301.44(立方厘米)
46.394.8cm2
【分析】观察图形可知,组合体的表面积=长是8cm,宽是15cm,高是2cm的长方体的表面积+底面半径是4cm的圆柱的侧面积;根据长方体表面积公式:表面积=(长×宽+长×高+宽×高)×2,圆柱的侧面积公式:侧面积=底面周长×高,代入数据,即可解答。
【解析】(8×15+8×2+15×2)×2+3.14×4×5
=(120+16+30)×2+12.56×5
=(136+30)×2+62.8
=166×2+62.8
=332+62.8
=394.8(cm2)
47.376.8cm2
【分析】由于大小两个圆柱结合在一起,所以它的表面积等于小圆柱的侧面积加上大圆柱的表面积,根据圆柱的侧面积公式:S=Ch,圆柱的表面积=侧面积+底面积×2;把数据代入公式解答。
【解析】3.14×4×5+3.14×10×5+3.14×(10÷2)2×2
=12.56×5+31.4×5+3.14×52×2
=62.8+157+3.14×25×2
=62.8+157+3.14×50
=62.8+157+157
=219.8+157
=376.8(cm2)
这个图形的表面积是376.8cm2。
48.(1);(2)
【分析】(1)根据图示,图形(1)的体积等于圆柱体积加圆锥的体积,据此解答即可;
(2)图形(2)表面积等于正方体的表面积加圆柱的侧面积,据此解答即可。
【解析】(1)
=3.14×108+×3.14×36
图形(1)的体积是376.8,
(2)
图形(2)的表面积是5770。
49.cm2
【分析】由于上面的圆柱与下面的圆柱体组合在一起,所以上面的圆柱只求侧面积,下面圆柱体求表面积,然后求和就是这个图形的表面积。根据圆柱的侧面积公式:S=Ch,圆柱的表面积=侧面积+底面积×2,把数据代入公式解答即可。
【解析】
它的表面积是。
50.表面积是514.96平方厘米,体积是766.16立方厘米;
体积是84.56立方厘米。
【分析】(1)运用圆柱的表面积公式S=d×h+2r2求出大圆柱表面积,再加上小圆柱的侧面积即可,根据圆柱的体积公式:V=r2h求出组合图形的体积。
(2)圆锥的体积公式:V=r2h,V=abc把数据代入公式求出它们的体积和即可。
【解析】12÷2=6(厘米)
8÷2=4(厘米)
表面积:
3.14×12×5+3.14×62×2+3.14×8×4
=3.14×60+3.14×72+3.14×32
=3.14×(60+72+32)
=3.14×164
=514.96(平方厘米)
体积:3.14×62×5+3.14×42×4
=3.14×180+3.14×64
=3.14×(180+64)
=3.14×244
=766.16(立方厘米)
表面积是514.96平方厘米,体积是766.16立方厘米。
(2)6×6×2+3.14×(4÷2)2×3×
=72+3.14×4
=72+12.56
=84.56(立方厘米)
体积是84.56立方厘米。
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
同课章节目录
