(期末考点培优)专题05 操作题-2024-2025学年六年级数学下册期末复习专项北师大版(含答案解析)
文档属性
| 名称 | (期末考点培优)专题05 操作题-2024-2025学年六年级数学下册期末复习专项北师大版(含答案解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-10 16:42:27 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
2024-2025学年六年级数学下册期末复习专项北师大版
(期末考点培优)专题05 操作题
学校:___________姓名:___________班级:___________考号:___________
1.下图是学校劳动实践基地示意图(每个小方格的边长表示1米),图中的点P是一个射程为5米的浇灌水龙头位置。
(1)请画出水龙头浇灌范围。
(2)学校原来计划在图中①号三角形区域种西红柿,现在需要把它按2∶1放大,且在水龙头的浇灌范围内,请画出放大后的西红柿种植区域。
2.如下图,要在张家村和李家村之间修建一个垃圾综合处理站,经过环保部门的监测和选址,确定从垃圾综合处理站到两个村庄的距离皆为3千米。请你在下图中画出垃圾综合处理站的具体位置。(请保留作图痕迹)
3.画一画。
(1)画出图形D绕点O逆时针旋转90°后的图形E。
(2)将图形D放大,使新图形与原图形对应线段长的比为2∶1。
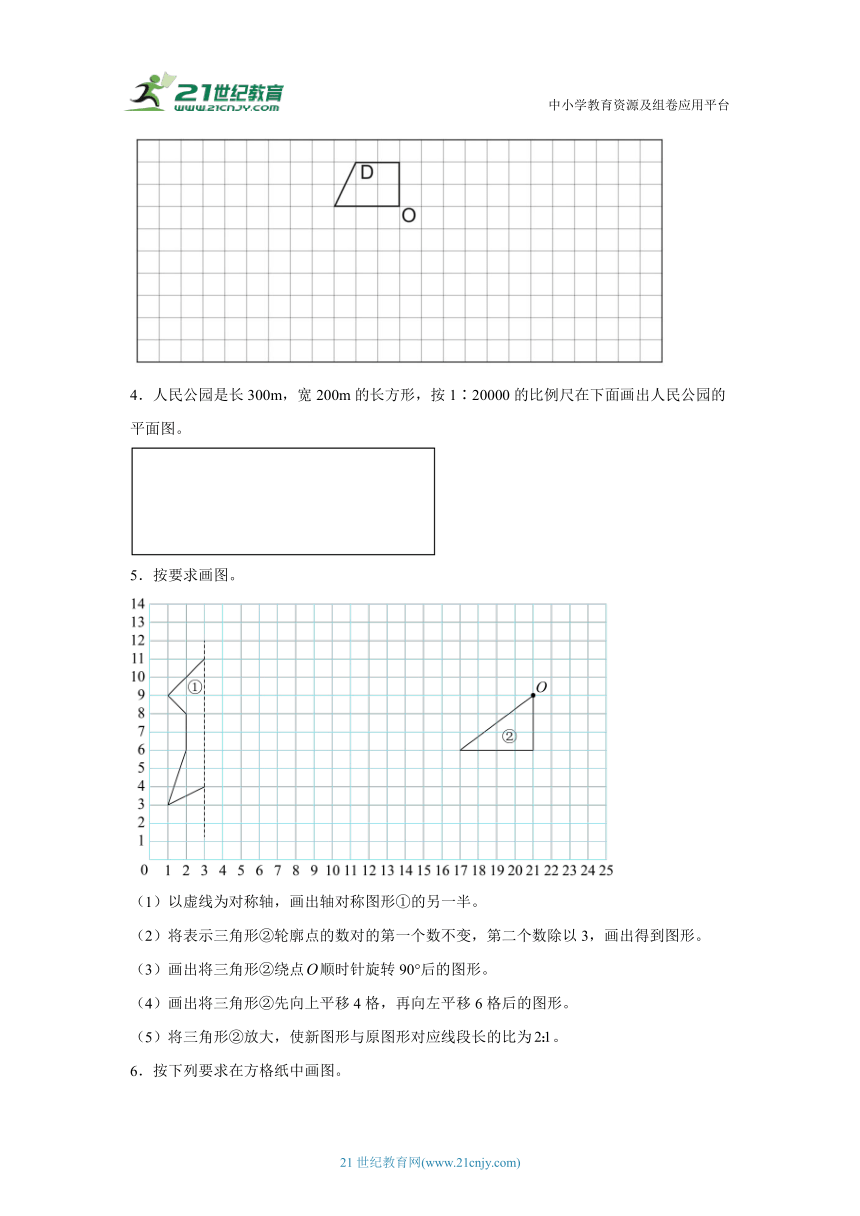
4.人民公园是长300m,宽200m的长方形,按1∶20000的比例尺在下面画出人民公园的平面图。
5.按要求画图。
(1)以虚线为对称轴,画出轴对称图形①的另一半。
(2)将表示三角形②轮廓点的数对的第一个数不变,第二个数除以3,画出得到图形。
(3)画出将三角形②绕点顺时针旋转90°后的图形。
(4)画出将三角形②先向上平移4格,再向左平移6格后的图形。
(5)将三角形②放大,使新图形与原图形对应线段长的比为。
6.按下列要求在方格纸中画图。
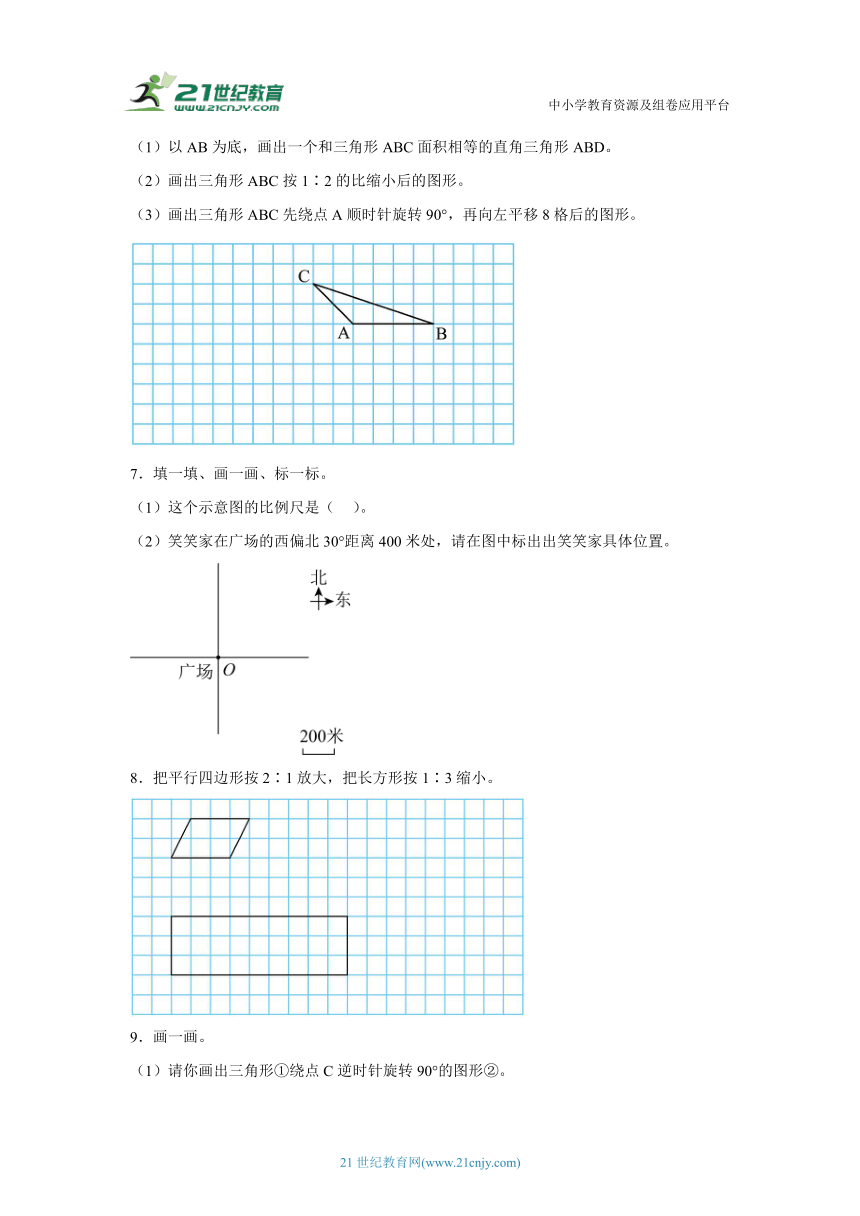
(1)以AB为底,画出一个和三角形ABC面积相等的直角三角形ABD。
(2)画出三角形ABC按1∶2的比缩小后的图形。
(3)画出三角形ABC先绕点A顺时针旋转90°,再向左平移8格后的图形。
7.填一填、画一画、标一标。
(1)这个示意图的比例尺是( )。
(2)笑笑家在广场的西偏北30°距离400米处,请在图中标出出笑笑家具体位置。
8.把平行四边形按2∶1放大,把长方形按1∶3缩小。
9.画一画。
(1)请你画出三角形①绕点C逆时针旋转90°的图形②。
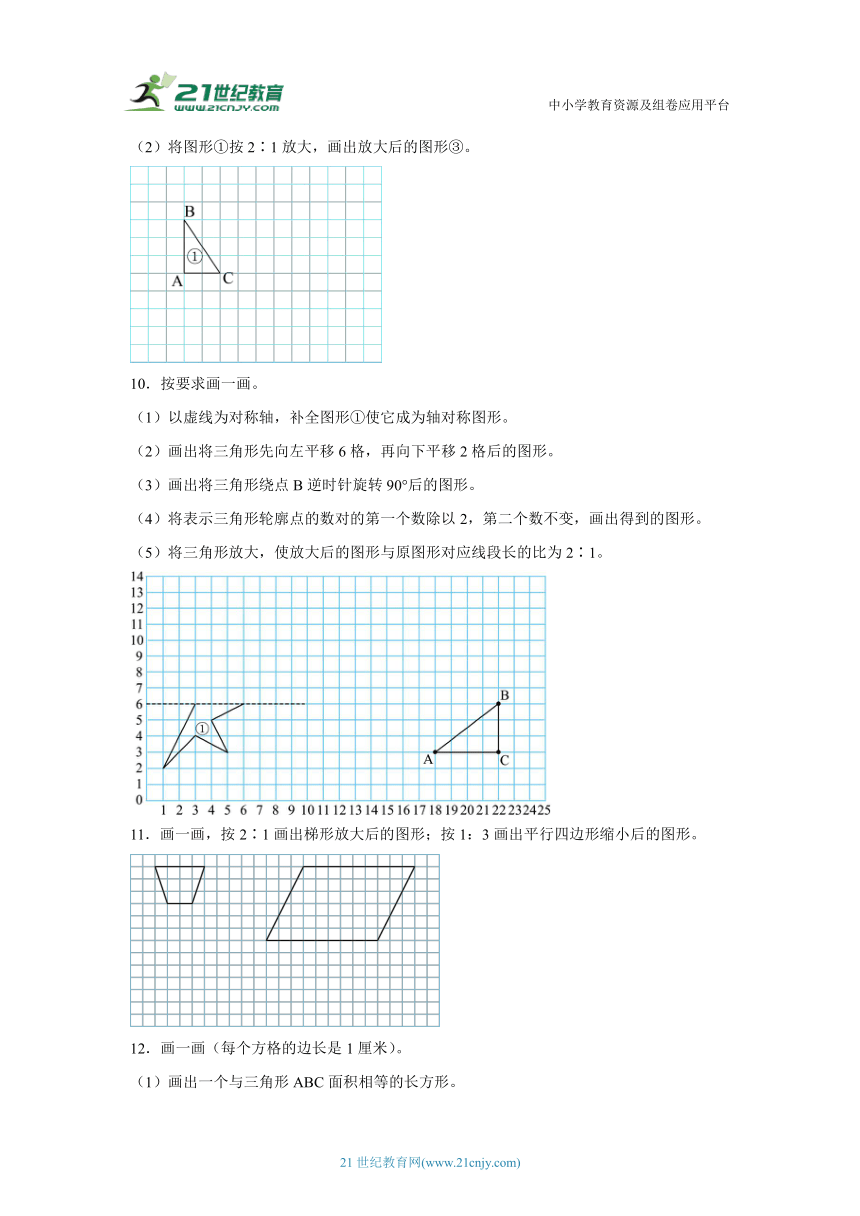
(2)将图形①按2∶1放大,画出放大后的图形③。
10.按要求画一画。
(1)以虚线为对称轴,补全图形①使它成为轴对称图形。
(2)画出将三角形先向左平移6格,再向下平移2格后的图形。
(3)画出将三角形绕点B逆时针旋转90°后的图形。
(4)将表示三角形轮廓点的数对的第一个数除以2,第二个数不变,画出得到的图形。
(5)将三角形放大,使放大后的图形与原图形对应线段长的比为2∶1。
11.画一画,按2∶1画出梯形放大后的图形;按1:3画出平行四边形缩小后的图形。
12.画一画(每个方格的边长是1厘米)。
(1)画出一个与三角形ABC面积相等的长方形。
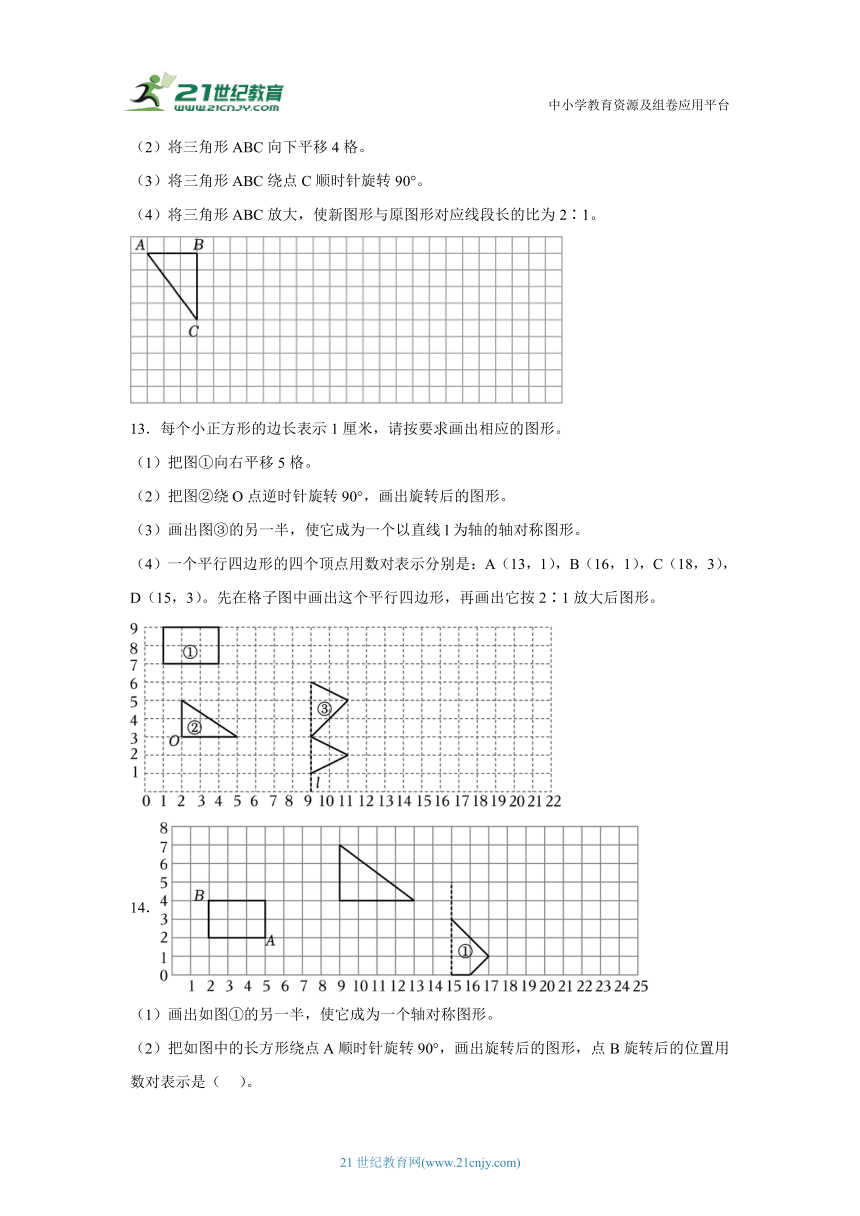
(2)将三角形ABC向下平移4格。
(3)将三角形ABC绕点C顺时针旋转90°。
(4)将三角形ABC放大,使新图形与原图形对应线段长的比为2∶1。
13.每个小正方形的边长表示1厘米,请按要求画出相应的图形。
(1)把图①向右平移5格。
(2)把图②绕O点逆时针旋转90°,画出旋转后的图形。
(3)画出图③的另一半,使它成为一个以直线l为轴的轴对称图形。
(4)一个平行四边形的四个顶点用数对表示分别是:A(13,1),B(16,1),C(18,3),D(15,3)。先在格子图中画出这个平行四边形,再画出它按2∶1放大后图形。
14.
(1)画出如图①的另一半,使它成为一个轴对称图形。
(2)把如图中的长方形绕点A顺时针旋转90°,画出旋转后的图形,点B旋转后的位置用数对表示是( )。
(3)将三角形向右平移8格,画出平移后的图形,如果按2∶1的比放大这个三角形,放大后的三角形面积是原来的( )倍。
15.在团结村南偏西30°方向、距离团结村1000米的地方有一个桃园;在团结村北偏西60°方向、距离团结村800米的地方有一个梨园,请在图上画出桃园和梨园的位置。
16.按要求画图。
(1)在上图中画出图形A关于直线a的对称图形。
(2)把图形B绕点O顺时针旋转90°后的图形画在图中。
(3)把图形C按2∶1的比放大后的图形画在图中。
17.按要求画图。
(1)把图中的长方形绕A点顺时针旋转90°,画出旋转后的图形。旋转后,B点的位置用数对表示是 。
(2)按1∶2的比画出三角形缩小后的图形。缩小后的三角形的面积是原来的。
(3)如果1个小方格表示1平方厘米,在上面的方格纸上设计一个面积是10平方厘米的轴对称图形,并画出对称轴。(画一条即可)
18.按要求填一填,画一画。
(1)如果梯形顶点A的位置用数对表示为(2,1),那么顶点C用数对表示为 。
(2)把梯形绕点B顺时针旋转90°,画出旋转后的图形。
(3)把原来的梯形按2∶1放大,请在空白处画出放大后的梯形。
19.想一想,画一画,算一算。
(1)如图,在长5厘米,宽4厘米的长方形内画一条线段,把长方形分割成一个最大的等腰直角三角形和一个梯形。
(2)梯形的面积是( )平方厘米。
(3)以等腰直角三角形的一条直角边为轴旋转一周后形成的立体图形是( ),这个立体图形的体积是( )立方厘米(保留整数)。
20.按要求画一画。
(1)画出下图中的直角三角形绕O点顺时针旋转90°后的图形B。
(2)以直线n为对称轴,作图形B的轴对称图形,得到图形C。
21.按要求填空,并在方格纸上画出图形。(每个小正方形的边长表示1厘米)。
(1)画出图形1向左平移6格后的图形。
(2)按2∶1的比画出图形2放大后的图形。
(3)点O的位置用数对表示是 。
在平面图中,如果以点O为观测点,点B在点O的 偏 °方向 厘米处。
(4)将图形1绕右下角的顶点顺时针旋转90°并画出来。
22.操作。
(1)画出三角形ABC绕A点逆时针旋转90°后的图形。
(2)画出三角形ABC以1∶2的比例缩小后的图形。
23.画一画。(用直尺和铅笔作图)
(1)将图形A绕点O逆时针旋转90°,得到图形B。
(2)将图形B向右平移6格,得到图形C。
24.(1)以MN为对称轴,画出图形A的轴对称图形B。
(2)将图形B绕O点顺时针旋转,得到图形C。
(3)将图形C向右平移4格后,得到图形D。
25.按要求在下面方格纸上画图。画出下面的图形按2∶1放大后的图形。
26.小风绘制了以实验小学为观测点的平面图。(图上每段表示1cm)
(1)某书店距实验小学的实际距离为400m,请计算出这幅图的比例尺(写出计算过程),并在下图的方框里用线段比例尺表示出来。
(2)实验中学在实验小学东偏北30°方向600m处,在图中用“☆”画出实验中学的位置。
27.
(1)把圆向右平移4格,画出平移后的图形。
(2)把长方形绕点按逆时针方向旋转90度,画出旋转后的图形B。
(3)以虚线为对称轴,作平行四边形的轴对称图形,得到图形C。
(4)将图形C放大,使放大后的图形与原图形对应线段长的比为2∶1。
28.想一想,在方格中画一画。
(1)观察如图,点O所在的位置是( )。
(2)将图形A以点O为中心顺时针旋转90度,得到图形B。
(3)以直线l为对称轴画出图形A的轴对称图形,得到图形C。
(4)画出图形A按2∶1的比放大后的图形D。
29.按要求画图形或填空(如图)。
(1)画出图A向右平移4格,再向下平移5格后得到的图形A′。
(2)画出图B绕点O顺时针旋转90°后得到的图形B′。
(3)画出图形C放大后的图形C′,使新图形与原图形对应线段长的比为2∶1。
(4)画一个面积是6平方厘米的轴对称图形(图上一个方格表示1平方厘米),并画出一条对称轴。
30.根据要求,画一画。
(1)先画出图形A关于直线l的对称图形B;
(2)画出图形A绕点O逆时针旋转90°后所得到的图形C;
(3)画出图形C向上平移3格后所得到的图形D。
31.如图是某校附近的平面图,请你按要求画图。
(1)图书馆在学校的( )面大约( )千米处。
(2)教育局位于学校北偏西40°方向1200米处,请用“ ”在图中标出其大概位置。
(3)在学校正北方向1500米处有一条人民路与工业路平行,请在图中表示出来。
32.按要求在下面的方格中画图。
(1)将图形A向右平移5格,得到图形B。
(2)将图形A绕点O逆时针旋转90°得到图形C。
(3)将图形A按1∶2缩小,得到图形D。
33.画一画,填一填。
(1)以直线MN为对称轴作图形A的轴对称图形,得到图形B。
(2)将图形A绕点O顺时针旋转90°得到图形C。
(3)图中圆心的位置用数对表示是 。
(4)画出圆向右平移4格后的图形D。
34.在方格纸上按要求画图并填空。
(1)在直角三角形ABC中,顶点B的位置用数对表示为 。
(2)以直线l为对称轴,画出三角形ABC的对称图形。
(3)把三角形ABC绕点A顺时针旋转90°,画出旋转后的图形。
(4)画出将三角形ABC平移,使点A的对应点在数对(5,1)位置的图形。
35.按要求画一画。
(1)以虚线为对称轴,画出轴对称图形①的另一半。
(2)画出图形②向左平移5格后的图形。
(3)画出图形③绕点按顺时针方向旋转后的图形。
(4)画出图形④按1∶2缩小后的图形。
36.按要求画一画。
(1)画出图形A先绕点O顺时针旋转90°,再向右平移4格后得到的图形B。
(2)画出图形A按1∶2的比缩小后的图形C。
(3)以直线MN为对称轴,画出图形A的轴对称图形D。
37.小红和小华合作绘制的学校周边的平面图(如图),小华家在学校的东偏北30度600米处,小红家在西偏南45度700米处。请根据比例尺在图上帮小红和小华画出他们家的距离,并用“△”标示出他们家的位置。
38.按要求画图。
(1)在下面方格中,画出2∶1放大的图形。
(2)以放大后三角形的一直角边为直径,画一个圆。
(3)如果上图中的小方格的边长表示1厘米,那么圆的面积是( )平方厘米。(π=3.14)
39.一艘海警船(点A处)接收到一渔船发出的求助信息为:雷达显示,你们(海警船)在我们渔船西偏南30°方向上,因我船故障无法行驶,请求帮助。海警船回复:好的,我们已收到你们的信息,现距离你们3千米,请耐心等待。
请根据以上对话信息,画出目前海警船与渔船的位置关系图,比例尺1∶150000。
40.按要求在方格纸上画图。
(1)将图形A绕O点逆时针旋转90°得到图形B。
(2)以直线L为对称轴作图形A的轴对称图形C,再将图形C向右平移4格得到图形D。
(3)画出图形E按2∶1放大后的图形F。
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案及试题解析
1.见详解
【分析】(1)水龙头浇灌的范围相当于一个以点P为圆心,以半径为5米所画的圆,据此画出一个圆,这个圆就是水龙头浇灌的范围。
(2)把三角形区域按2∶1放大,即三角形的底和高都扩大到原来的2倍,先计算出按2∶1放大后的三角形的底和高,再在水龙头的浇灌范围内画出放大后的三角形。
【解析】三角形放大后的底:4×2=8(米)
三角形放大后的高:2×2=4(米)
(1)(2)如图所示:(圆P是水龙头的浇灌范围,图②是放大后的西红柿种植区域)
2.见详解
【分析】从垃圾综合处理站到两个村庄的距离皆为3千米,即垃圾综合处理站位于以张家村该点为圆心,半径为3千米的圆上;也位于以李家村为圆心,半径为3千米的圆上,两圆的交点即为垃圾综合处理站。
图中的线段比例尺表示图上1厘米相当于实际距离1千米,那么实际距离3千米在图中即是3厘米,据此作图。
【解析】图中AB点均可为垃圾综合处理站的具体位置,作图如下:
3.见详解
【分析】(1)根据旋转的特征,将图形D绕点O逆时针旋转90°,点O位置不变,其余各部分均绕此点按相同方向旋转相同度数,即可画出旋转后的图形E。
(2)图形D按2∶1放大,即原来图形D的上底、下底、高都乘2,就是放大后梯形的上底、下底和高,据此画出放大后的图形。
【解析】(1)画出将图形D绕点O逆时针旋转90°后的图形E,如下图。
(2)放大后梯形的上底:2×2=4
放大后梯形的下底:3×2=6
放大后梯形的高:2×2=4
画一个上底为4、下底为6、高为4的梯形,如下图。
4.见详解
【分析】这个长方形的长和宽的实际长度,以及比例尺已知,1m=100cm,将实际长度的单位换算成单位“cm”,依据“图上距离=实际距离×比例尺”即可求出这个长方形的操场的长和宽的图上距离,进而就可以画出这个长方形的平面图。
【解析】300m=30000cm
200m=20000cm
30000×=1.5(cm)
20000×=1(cm)
如图:
5.(1)(2)(3)(4)(5)见详解
【分析】(1)根据轴对称图形的意义:对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴的另一边画出图形①的关键对称点,依次连接即可。
(2)根据数对表示位置的方法:第一个数字表示列,第二个数字表示行,据此把图②的各个顶点用数对表示出来,再把第二个数除以3,求出三角形三个顶点的数对,再画出图形。
(3)根据旋转的特征,三角形②绕点O顺时针旋转90°后,点O的位置不动,其余各部分均绕此点按相同方向旋转相同的度数,得到旋转后的图形。
(4)根据平移的特征,把三角形②的各个顶点分别向上平移4格,再向左平移6格,依次连接,即可得到平移后的图形。
(5)根据图形放大的特征:把三角形②的各个边扩大到原来的2倍,画出放大后的图形即可。
【解析】(1)图如下:
(2)三角形②的三个点的数对为:(17,6),(21,6),(21,9);第二个数除以3后,三个点的数对为:(17,2),(21,2),(21,3);图如下:
(3)图如下:
(4)图如下:
(5)底:4×2=8(格);高:3×2=6(格);图如下(位置不唯一):
6.见详解
【分析】(1)假设每个小方格的边长为1,三角形ABC的底为4,高为2,画一个和三角形ABC等底等高的直角三角形即可;
(2)由图可知,AB是4,缩小后AB的长度为4×=2,AB对应的高为2,缩小后AB对应的高为2×=1,根据原图形画出缩小后的图形;
(3)根据题目要求确定旋转中心(点A)、旋转方向(顺时针)、旋转角度(90°),分析所作图形,找出构成图形的关键边,按一定的方向和角度分别找出各关键边的对应边,最后依次连接组成封闭图形;找出构成图形的关键点,确定平移方向(向左)和平移距离(8格),由平移的距离确定关键点平移后的对应点的位置,依次连接各对应点,据此作图。
【解析】作图如下:
7.(1)1∶20000
(2)作图见详解
【分析】(1)比例尺是表示图上一条线段的长度与地面相应线段的实际长度之比,由图可知,图上1厘米相当于实际200米,先将200米换算单位为厘米,再根据:比例尺=图上距离∶实际距离解答;
(2)先根据图上距离=实际距离×比例尺,用400米乘比例尺,求出图上距离;再根据在地图上按照“上北下南,左西右东”确定方向,找到笑笑家在广场的西偏北30°,画出线段标注名称即可。
【解析】(1)200米=20000厘米
1厘米∶20000厘米=1∶20000
所以,这个示意图的比例尺是1∶20000。
(2)400米=40000厘米
40000×=2(厘米)
作图如下:
8.见详解
【分析】把平行四边形按2∶1扩大,即平行四边形的每一条边扩大到原来的2倍,原平行四边形的底和高分别乘2,得出扩大后平行四边形的底和高,据此画出扩大后的图形。
把长方形按1∶3缩小,即长方形的每一条边缩小到原来的,原长方形的长和宽分别除以3,得出缩小后长方形的长和宽,据此画出缩小后的图形。
【解析】据分析作图如下:
9.见详解
【分析】(1)画出三角形①绕点C逆时针旋转90°的图形②:首先明确旋转的三要素:旋转中心、旋转方向和旋转角度,本题中旋转中心是点C,旋转方向是逆时针,旋转角度是90°;对于三角形的每个顶点,以点C为中心进行操作,过点C作垂直于对应顶点与点C连线的直线,根据逆时针方向和90°的角度确定顶点旋转后的位置,比如点A,连接AC,过点C作AC的垂线,沿逆时针方向在垂线上截取与AC长度相等的线段,得到点A旋转后的位置,同样的方法找到点B旋转后的位置,最后把旋转后的点连接起来得到旋转后的三角形②。
(2)将图形①按2∶1放大,画出放大后的图形③:按2∶1放大意味着图形的每条边都要放大到原来的2倍。分别测量三角形①三条边的长度,将每条边的长度乘2 ,画出放大后的三角形③。
【解析】(1)、(2)作图如下:
10.见详解
【分析】(1)根据轴对称图形的画法,以虚线为对称轴,在上方画出其另一半即可;
(2)根据平移的方法,将三角形先向左平移6格,再向下平移2格,注意平移不改变图形的形状和大小;
(3)根据旋转,将三角形ABC绕B点逆时针旋转90°,只需将BC和BA分别绕B点逆时针旋转90°,再连接即可;
(4)轮廓点的数对的第一个数除以2,第二个数不变,只需将其三个顶点进行移动,A点(18,3),处理后变成(9,3);B点(22,6)处理后变成(11,6);C点(22,3),处理后变成(11,3),在图中分别找到处理后的点,连接即可;
(5)按照2∶1放大,则AC放大2倍后长8格,BC放大2倍后长6格,然后连接即可得到放大后的图形。
【解析】
11.见详解
【分析】按2∶1画出梯形放大后的图形,即梯形的形状不变,各边都扩大到原来的2倍,原来的梯形的上底是4格,放大后是4×2=8格,原来梯形的下底是2格,放大后是2×2=4格,原来的高是3格,放大后是3×2=6格,据此画出放大后的梯形;
按1:3画出平行四边形缩小后的图形,即平行四边形的各边都缩小到原来的,平行四边形原来的底边是9格,缩小后是9÷3=3格,平行四边形原来的高是6格,缩小后是6÷3=2格,据此画图即可。
【解析】如图:
12.图见详解
【分析】(1)根据三角形的面积=底×高÷2,求出三角形ABC的面积;要画一个与三角形ABC面积相等的长方形,根据长方形的面积=长×宽,得出长方形的长、宽,据此画出这个长方形。
(2)根据平移的特征,将三角形ABC的各顶点分别向下平移4格,依次连接即可得到平移后的图形。
(3)根据旋转的特征,将三角形ABC绕点C顺时针旋转90°,点C位置不变,其余各部分均绕此点按相同方向旋转相同度数,即可画出旋转后的图形。
(4)将三角形ABC按2∶1放大,则原来三角形的底和高都乘2,即是放大后三角形的底和高,据此画出放大后的三角形。
【解析】(1)3×4÷2=6(平方厘米)
因为6=3×2,可以画一个长为3厘米、宽为2厘米的长方形,如下图。
(2)画三角形ABC向下平移4格后的图形,如下图。
(3)画三角形ABC绕点C顺时针旋转90°后的图形,如下图。
(4)放大后三角形的底是:3×2=6(厘米)
放大后三角形的底是:4×2=8(厘米)
画一个底为6厘米、高为8厘米的三角形。
如下图:
(长方形画法不唯一)
13.见详解
【分析】(1)根据平移的特征,将图①的各顶点分别向右平移5格,依次连接即可得到平移后的图形。
(2)根据旋转的特征,将图②绕O点逆时针旋转90°,点O位置不变,其余各部分均绕此点按相同方向旋转相同度数,即可画出旋转后的图形。
(3)根据轴对称图形的特征,对称点到对称轴的距离相等,找到图③的各顶点关于对称轴l的对称点后,依次连接各点得到轴对称图形。
(4)用数对表示位置的方法:数对的第一个数字表示列,第二个数字表示行;据此先在图中标出四个顶点的位置,再依次连接画出这个平行四边形。
把平行四边形按2∶1放大,则平行四边形的底和高都乘2,即是放大后平行四边形的底和高,据此画出放大后的平行四边形。
【解析】(1)平移后的图形,见图④;
(2)旋转后的图形,见图⑤;
(3)补全轴对称的图形,见图⑥;
(4)平行四边形ABCD,见图⑦;
3×2=6
2×2=4
放大后的平行四边形,见图⑧。
14.(1)图见详解
(2)图见详解;(7,5)
(3)图见详解;4
【分析】(1)先确定对称轴(图中的虚线),依据轴对称图形性质,对称点到对称轴距离相等且在对称轴两侧,找出图形①各关键点关于对称轴的对称点,再依次连接这些对称点,即可画出另一半,使其成为轴对称图形。
(2)以点A为旋转中心,将长方形的四条边顺时针旋转90°,通过数方格确定旋转后各边的位置,画出旋转后的长方形;用数对表示位置时先数列再数行,画出旋转后的长方形观察可知点B旋转后的位置在第7列,第5行,所以用数对表示是(7,5)。
(3)将三角形的三个顶点分别向右平移8格,再依次连接这三个平移后的顶点,得到平移后的图形;如果按2∶1的比放大这个三角形,即每条边的长度都扩大到原来的2倍,原来三角形的底是4,扩大到原来的2倍是4×2=8,原来的高是3,扩大到原来的2倍是3×2=6,面积是8×6÷2=24,原来三角形面积是4×3÷2=6,用扩大后的面积除以扩大前的面积即可。
【解析】(1)画出图①的另一半,使它成为一个轴对称图形,如下图。
(2)观察旋转后图形发现,点B旋转后的位置在第7列,第5行,所以用数对表示是(7,5);
作图如下:
(3)4×3÷2
=12÷2
=6
(4×2)×(3×2)÷2
=8×6÷2
=48÷2
=24
24÷6=4
所以放大后的三角形面积是原来的4倍。
作图如下:
15.见详解
【分析】桃园:已知实际距离1000米,因为1米=100厘米,所以1000米=100000厘米,根据“图上距离=实际距离×比例尺”,比例尺为1∶40000,则桃园图上距离为100000×=2.5厘米;用量角器以团结村为顶点,向南偏西30°方向画射线,在射线上从团结村开始量取2.5厘米的长度确定桃园位置。
梨园:已知实际距离800米,800米=80000厘米,同理,梨园图上距离为80000×=2厘米 ;用量角器以团结村为顶点,向北偏西60°方向画射线,在射线上从团结村开始量取2厘米的长度确定梨园位置。
【解析】作图如下:
16.(1)见解答
(2)见解答
(3)见解答
【分析】(1)根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴的左边画出图A的关键对称点,依次连接即可;
(2)根据旋转的特征,图形B绕点O顺时针旋转90°后,点O的位置不动,其余各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图形;
(3)根据图形放大与缩小的意义,把图形C各对应边均放大到原来的2倍即可。
【解析】(1)如下图所示:
(2)如下图所示:
(3)如下图所示:
17.(1)作图见详解;(7,6)
(2)作图见详解;
(3)见详解
【分析】(1)作旋转一定角度后的图形步骤:根据题目要求,确定旋转中心、旋转方向和旋转角;分析所作图形,找出构成图形的关键点;找出关键点的对应点:按一定的方向和角度分别作出各关键点的对应点;作出新图形,顺次连接作出的各点即可。用数对表示位置时,通常把竖排叫列,横排叫行。一般情况下,确定第几列时从左往右数,确定第几行时从前往后数。表示列的数在前,表示行的数在后,中间用逗号“,”隔开,数对加上小括号。
(2)把图形按照1∶n缩小,就是将图形的每一条边缩小到原来的,缩小后图形与原图形对应边长的比是1∶n。三角形面积=底×高÷2,据此分别计算出缩小前后的面积,将原来的面积看作单位“1”,缩小后的面积÷原来的面积=缩小后的三角形的面积是原来的几分之几。
(3)长方形面积=长×宽,据此确定长方形的长和宽,画出一个面积是10平方厘米的长方形。画对称轴的步骤:找出轴对称图形的任意一组对称点;连结对称点;画出对称点所连线段的垂直平分线,就可以得到该图形的对称轴。
【解析】(1)作图如下:
旋转后,B点的位置用数对表示是(7,6)。
(2)作图如下:
(3×2÷2)÷(6×4÷2)
=3÷12
=
缩小后的三角形的面积是原来的。
(3)
(轴对称图形的画法不唯一)
18.(1)(3,3)
(2)见详解
(3)见详解
【分析】(1)用数对表示位置的方法:数对的第一个数字表示列,第二个数字表示行;结合顶点A用数对表示的位置,用数对表示顶点C的位置。
(2)根据旋转的特征,将梯形绕点B顺时针旋转90°,点B位置不变,其余各部分均绕此点按相同方向旋转相同度数,即可画出旋转后的图形。
(3)把原来的梯形按2∶1放大,即原来梯形的上底、下底、高都乘2,即是放大后梯形的上底、下底和高,据此画出放大后的梯形。
【解析】(1)顶点C在第3列第3行,所以顶点的位置用数对表示为(3,3)。
(2)把梯形绕点B顺时针旋转90°后的图形,如下图。
(3)放大后梯形的上底:1×2=2
放大后梯形的下底:2×2=4
放大后梯形的高:2×2=4
放大后的梯形如下图。
19.(1)见详解
(2)12
(3)圆锥;67
【分析】(1)一个最大的等腰直角三角形的直角边应是长方形的宽,据此画图。
(2)梯形的上底等于长方形的长-长方形的宽,梯形的下底等于长方形的长,梯形的高等于长方形的宽,根据梯形的面积公式:面积=(上底+下底)×高÷2,代入数据,即可解答。
(3)根据圆锥的特征可知,以等腰直角三角形的一条直角边为轴,旋转一周,会形成一个圆锥,圆锥的底面半径等于等腰直角三角形的腰,高等于等腰直角三角形的腰,根据圆锥的体积公式:体积=底面积×高×,代入数据,即可解答。
【解析】(1)如图:
(2)(5-4+5)×4÷2
=(1+5)×4÷2
=6×4÷2
=24÷2
=12(平方厘米)
梯形的面积是12平方厘米。
(3)以等腰直角三角形的一条直角边为轴旋转一周后形成的立体图形是圆锥。
3.14×42×4×
=3.14×16×4×
=50.24×4×
=200.96×
≈67(立方厘米)
以等腰直角三角形的一条直角边为轴旋转一周后形成的立体图形是圆锥,这个立体图形的体积是67立方厘米
20.(1)(2)见详解
【分析】(1)根据旋转的特征,直角三角形绕点O顺时针旋转90°后,点O的位置不动,其余各部分均绕此点按相同方向旋转相同的度数,得到旋转后的图形B。
(2)根据轴对称图形的意义:对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴的另一边画出图形B的关键对称点,依次连接即可。
【解析】(1)如下图:
(2)如下图:
21.((1)(2)(4)图见详解
(3)(15,4);东;北;60;2
【分析】(1)根据平移图形的特征,把梯形1的四个顶点分别向左平移6格,再首尾连接各点,即可得到梯形1向左平移6格的图形;
(2)按2∶1的比例画出三角形放大后的图形,就是把原三角形的三条边分别扩大到原来的2倍,据此画出扩大后的图形即可;
(3)用数对表示位置时,先表示第几列,再表示第几行,据此用数对表示点O的位置即可;并以O点为观测点,根据方向和距离确定B点的位置;
(4)根据旋转的意义,找出图中梯形1的4个关键处,再画出按顺时针方向旋转90度后的形状即可。
【解析】(1)如下图所示:
(2)如下图所示:
(3)点O的位置用数对表示是(15,4),
因为OB=OC=2厘米,∠BOC=60°,如果以点O为观测点,点B在点O的北偏东30°方向2厘米处或东偏北60°方向2厘米处。
(4)如下图所示:
22.(1)(2)见详解
【分析】(1)绕A点逆时针旋转90°,需固定A点,将B、C两点绕A按逆时针转90°,依据网格确定旋转后坐标位置,再连线;
(2)按1∶2比例缩小,要先确定原三角形各边长度,再将边长除以2 ,以某顶点为参照确定新顶点位置,最后连接成缩小后的三角形。
【解析】(1)(2)作图如下:
23.(1)(2)见详解
【分析】(1)明确旋转中心为点O ,旋转方向是逆时针,角度为90°,通过直尺确定图形A各顶点绕点O逆时针旋转90°后的位置,再用铅笔连接各点得到图形B;
(2)确定平移方向为向右,距离是6格,用直尺将图形B的各顶点沿水平方向向右移动6格,最后用铅笔连接各平移后的顶点得到图形C。
【解析】(1)(2)作图如下:
24.见详解
【分析】(1)补全轴对称图形的方法:找出图形的关键点,依据对称轴画出关键点的对称点,再依据图形的形状顺次连接各点,画出最终的轴对称图形。据此先找到对称点,画出两条直的边,再根据画圆的方法画出半圆。
(2)作旋转一定角度后的图形步骤:根据题目要求,确定旋转中心、旋转方向和旋转角;分析所作图形,找出构成图形的关键点;找出关键点的对应点:按一定的方向和角度分别作出各关键点的对应点;作出新图形,顺次连接作出的各点即可。
(3)作平移后的图形步骤:找点-找出构成图形的关键点;定方向、距离-确定平移方向和平移距离;画线-过关键点沿平移方向画出平行线;定点-由平移的距离确定关键点平移后的对应点的位置;连点-连接对应点。
【解析】
25.见详解
【分析】放大后的图形的边长是原图形的2倍,据此作图即可。
【解析】根据要求作图如下:
26.(1)1∶20000;作图见详解
(2)见详解
【分析】(1)图上距离∶实际距离=比例尺,据此写出图上距离与实际距离的比,化简即可得出比例尺,再将数值比例尺改写成线段比例尺,补在图上即可;
(2)弄清要标示的物体在哪个方位上,有多少度,按要求的方位和度数准确画图;注意各场所离中心点的距离,根据要求的比例画出相应的长度。图上距离=实际距离×比例尺。
【解析】(1)2cm∶400m=2cm∶40000cm=(2÷2)∶(40000÷2)=1∶20000
20000cm=200m
这幅图的比例尺是1∶20000。作图如下:
(2)600m=60000cm
60000×=3(cm)
27.见详解
【分析】(1)将O点向右平移4格为O’点,以为圆心1格的长度为半径画一个圆,即可得到平移后的图形;
(2)以点A为旋转中心,按照与时针旋转相反的方向,旋转的角度90度,点A不动,图形的各个部分点A按逆时针方向旋转90°得到图形B;
(3)一个轴对称图形按照对称轴对折能够完全重合,据此找到平行四边形的四个顶点的对称点再顺次连接,得到图形C;
(4)图形C按照2∶1放大,图形C的各边均为原来的2倍,得到放大后的图形。
【解析】由分析可作图:
28.(1)(7,5)
(2)(3)(4)见详解
【分析】(1)用数对表示位置的方法:数对的第一个数字表示列,第二个数字表示行;据此用数对表示点O所在的位置。
(2)根据旋转的特征,将图形A以点O为中心顺时针旋转90度,点O位置不变,其余各部分均绕此点按相同方向旋转相同度数,即可画出旋转后的图形B。
(3)根据轴对称图形的特征,对称点到对称轴的距离相等,找到图形A的各顶点关于对称轴l的对称点后,依次连接各点得到图形A的对称图形C。
(4)图形A按2∶1的比放大,即把图形A的每条边都扩大到原来的2倍,据此画出放大后的图形D。
【解析】(1)观察如图,点O所在的位置是(7,5)。
(2)将图形A以点O为中心顺时针旋转90度,得到图形B,如下图。
(3)以直线l为对称轴画出图形A的轴对称图形,得到图形C,如下图。
(4)放大后三角形的底:2×2=4
放大后三角形的高:3×2=6
则画一个底为4、高为6的三角形D,如下图。
29.(1)(2)(3)(4)见详解
【分析】(1)根据平移的特征,把图A的各顶点分别向右平移4格,再向下平移5格,依次连接即可得到平移后的图形A′。
(2)根据旋转的特征,图B绕点O顺时针旋转90°,点O的位置不动,其余各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图形B′。
(3)根据图形放大与缩小的意义,把图形C的各边均放大到原来的2倍,对应角大小不变,所得到的图形就是原图按2∶1放大后的图形C′。
(4)画一个长3格,宽2格的长方形,再画出一条对称轴即可。(画法不唯一)
【解析】如下图:
(画面积是6平方厘米轴对称图形画法不唯一)
30.(1)、(2)、(3)见详解
【分析】(1)补全轴对称图形的方法:找出图A的关键点,依据对称轴画出关键点的对称点,再依据图形的形状顺次连接各点,画出最终的轴对称图形。
(2)旋转图形的作图方法:根据题目要求确定旋转中心(点O)、旋转方向(逆时针)、旋转角度(90°);分析所作图形,找出构成图形的关键边;按一定的方向和角度分别找出各关键边的对应边;最后依次连接组成封闭图形;
(3)平移图形的作图方法:找出构成图形的关键点;确定平移方向(向上)和平移距离(3格);由平移的距离确定关键点平移后的对应点的位置;依次连接各对应点。
【解析】(1)、(2)、(3)据分析作图如下:
31.(1)东;1.8
(2)图见详解
(3)图见详解
【分析】(1)图中的向上为正北方向,向右为正东方向,图书馆位于学校的正右方向,即正东方向,量得距离为3厘米,则运用实际距离=图上距离÷比例尺,计算可得出答案。
(2)与正北方向向西偏40°,实际距离1200米,图上距离=实际距离×比例尺,可得出教育局所在位置。
(3)图上距离=实际距离×比例尺,得到图上距离为2.5厘米,画出平行线可得出答案。
【解析】(1)图书馆与学校的图上距离为3厘米,则图书馆在学校实际距离:60000×3=180000(厘米),180000厘米=1.8千米,图书馆在学校的东面大约1.8千米。
(2)1200米=120000厘米
120000÷60000=2(厘米),如图:
(3)1500米=150000厘米
150000÷60000=2.5(厘米),如图:
32.(1)(2)(3)图见详解
【分析】(1)找出构成图形的关键点,确定平移方向(向右)和平移距离(5格),由平移的距离确定关键点平移后的对应点的位置,依次连接各对应点。
(2)根据题目要求确定旋转中心(点O)、旋转方向(逆时针)、旋转角度(90°),分析所作图形,找出构成图形的关键边,按一定的方向和角度分别找出各关键边的对应边,最后依次连接组成封闭图形。
(3)把图形按照1∶n缩小,就是将图形的每一条边缩小到原来的,缩小后图形与原图形对应边长的比是1∶n。
【解析】(1)(2)(3)作图如下:
33.(1)见详解
(2)见详解
(3)(4,3)
(4)见详解
【分析】(1)根据轴对称图形的画法,以直线MN为对称轴作图形A的轴对称图形,得到图形B,据此解答即可。
(2)点O不动,根据旋转的方法,将图形A绕点O顺时针旋转90°得到图形C,据此解答即可。
(3)根据数对表示位置的方法,找出圆心在第几列、第几行,图中圆心的位置用数对表示是(4,3),据此解答即可。
(4)根据平移的方法,画出圆向右平移4格后的图形D即可。
【解析】(1)以直线MN为对称轴作图形A的轴对称图形,得到图形B。如图:
(2)将图形A绕点O顺时针旋转90°得到图形C。如图:
(3)圆心在第4列,第3行,所以图中圆心的位置用数对表示是(4,3)。
(4)画出圆向右平移4格后的图形D。如图:
34.(1)(1,8)
(2)见详解
(3)见详解
(4)见详解
【分析】(1)根据用数对表示点的位置的方法,第一个数字表示列数,第二个数字表示行数,据此解答。
(2)画轴对称图形的方法:找出三角形ABC的关键点,依据对称轴画出关键点的对称点,再依据图形的形状顺次连接各点,画出最终的轴对称图形。
(3)旋转图形的作图方法:根据题目要求确定旋转中心(点A)、旋转方向(顺时针)、旋转角度(90°);分析所作图形,找出构成图形的关键边;按一定的方向和角度分别找出各关键边的对应边;最后依次连接组成封闭图形;
(4)先根据数对确定点A的对应点,再根据平移不改变三角形的方向、大小和形状,描出另外两个点,最后依次连接组成封闭图形。
【解析】(1)在直角三角形ABC中,顶点B的位置用数对表示为(1,8)。
(2)以直线l为对称轴,画出三角形ABC的对称图形。如图:
(3)把三角形ABC绕点A顺时针旋转90°,画出旋转后的图形。如图:
(4)画出将三角形ABC平移,使点A的对应点在数对(5,1)位置的图形。如图:
35.见详解
【分析】(1)补全轴对称图形的方法:找出图形的关键点,依据对称轴画出关键点的对称点,再依据图形的形状顺次连接各点,画出最终的轴对称图形。
(2)作平移后的图形步骤:找点-找出构成图形的关键点;定方向、距离-确定平移方向和平移距离;画线-过关键点沿平移方向画出平行线;定点-由平移的距离确定关键点平移后的对应点的位置;连点-连接对应点。
(3)作旋转一定角度后的图形步骤:根据题目要求,确定旋转中心、旋转方向和旋转角;分析所作图形,找出构成图形的关键点;找出关键点的对应点:按一定的方向和角度分别作出各关键点的对应点;作出新图形,顺次连接作出的各点即可。
(4)把图形按照1∶n缩小,就是将图形的每一条边缩小到原来的,缩小后图形与原图形对应边长的比是1∶n。
【解析】
36.(1)(2)(3)见详解
【分析】(1)旋转图形的作图方法:根据题目要求确定旋转中心(点O)、旋转方向(顺时针)、旋转角度(90°);分析所作图形,找出构成图形的关键边;按一定的方向和角度分别找出各关键边的对应边;最后依次连接组成封闭图形;平移图形的作图方法:找出构成图形的关键点;确定平移方向(向右)和平移距离(4格);由平移的距离确定关键点平移后的对应点的位置;依次连接各对应点。
(2)图形A按1∶2的比缩小,则组成图形的每条线段长度为原来的一半,据此作图。
(3)画轴对称图形的方法:找出图形A的关键点,依据对称轴画出关键点的对称点,再依据图形的形状顺次连接各点,画出最终的轴对称图形。
【解析】(1)(2)(3)作图如下:
37.见详解
【分析】根据图示方向的规定可知上北下南,左西右东,又因为图上距离1厘米表示实际距离200米,小华家和小红家分别与学校的实际距离已知,分别用实际距离除以200,可以求出它们之间的图上距离,再根据方向关系,即可在图上标出它们的位置,解答即可。
【解析】(厘米)
(厘米)
据分析作图如下:
38.(1)(2)见详解
(3)12.56
【分析】(1)根据图形放大的意义,把这个三角形两直角边均放大到原来的2倍所得到的图形就是原图形按2∶1放大后的图形。
(2)画圆时,“圆心定位置,半径定大小”,以直角三角形的一条直角边的中点为圆心,圆心到顶点为半径,即可画图。
(3)先计算出圆的半径,根据圆的面积公式:面积=π×半径2,代入数据,即可解答。
【解析】(1)2×2=4(厘米),2×2=4(厘米)
如下图:
(2)如下图:
(位置不唯一)
(3)4÷2=2(厘米)
3.14×22
=3.14×4
=12.56(平方厘米)
如果上图中的小方格的边长表示1厘米,那么圆的面积是12.56平方厘米。
39.见详解
【分析】已知这幅图的比例尺是1∶150000,海警船与渔船实际相距3千米,根据“图上距离=实际距离×比例尺”以及进率“1千米=100000厘米”,求出海警船与渔船的图上距离。
已知海警船在渔船西偏南30°方向上,是以渔船为观测点;图中画出了海警船的位置,如果以海警船为观测点,根据位置的相对性可知,观测点不同,方向相反,夹角的度数相同,距离相同;那么海警船在渔船西偏南30°方向上,也可以说成渔船在海警船东偏北30°方向上,根据方向、角度和距离画出警船与渔船的位置关系图。
【解析】3千米=300000厘米
300000×=2(厘米)
如图:
40.(1)(2)(3)见详解
【分析】(1)根据旋转的特征,图形A绕点O逆时针旋转90°,点O的位置不动,这个图形的各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图形。
(2)根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴(虚线L)的右边画出图形A的关键对称点,依次连接、涂色即可作图形A的轴对称图形C;根据平移的特征,把图形C的各顶点分别向右平移4格,依次连接、涂色即可得到平移后的图形D。
(3)根据图形放大的意义,把图形E的长、宽均放大到原来的2倍所得到的长方形就是原图形按2∶1放大后的图形F。
【解析】根据题意画图如下:
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
中小学教育资源及组卷应用平台
2024-2025学年六年级数学下册期末复习专项北师大版
(期末考点培优)专题05 操作题
学校:___________姓名:___________班级:___________考号:___________
1.下图是学校劳动实践基地示意图(每个小方格的边长表示1米),图中的点P是一个射程为5米的浇灌水龙头位置。
(1)请画出水龙头浇灌范围。
(2)学校原来计划在图中①号三角形区域种西红柿,现在需要把它按2∶1放大,且在水龙头的浇灌范围内,请画出放大后的西红柿种植区域。
2.如下图,要在张家村和李家村之间修建一个垃圾综合处理站,经过环保部门的监测和选址,确定从垃圾综合处理站到两个村庄的距离皆为3千米。请你在下图中画出垃圾综合处理站的具体位置。(请保留作图痕迹)
3.画一画。
(1)画出图形D绕点O逆时针旋转90°后的图形E。
(2)将图形D放大,使新图形与原图形对应线段长的比为2∶1。
4.人民公园是长300m,宽200m的长方形,按1∶20000的比例尺在下面画出人民公园的平面图。
5.按要求画图。
(1)以虚线为对称轴,画出轴对称图形①的另一半。
(2)将表示三角形②轮廓点的数对的第一个数不变,第二个数除以3,画出得到图形。
(3)画出将三角形②绕点顺时针旋转90°后的图形。
(4)画出将三角形②先向上平移4格,再向左平移6格后的图形。
(5)将三角形②放大,使新图形与原图形对应线段长的比为。
6.按下列要求在方格纸中画图。
(1)以AB为底,画出一个和三角形ABC面积相等的直角三角形ABD。
(2)画出三角形ABC按1∶2的比缩小后的图形。
(3)画出三角形ABC先绕点A顺时针旋转90°,再向左平移8格后的图形。
7.填一填、画一画、标一标。
(1)这个示意图的比例尺是( )。
(2)笑笑家在广场的西偏北30°距离400米处,请在图中标出出笑笑家具体位置。
8.把平行四边形按2∶1放大,把长方形按1∶3缩小。
9.画一画。
(1)请你画出三角形①绕点C逆时针旋转90°的图形②。
(2)将图形①按2∶1放大,画出放大后的图形③。
10.按要求画一画。
(1)以虚线为对称轴,补全图形①使它成为轴对称图形。
(2)画出将三角形先向左平移6格,再向下平移2格后的图形。
(3)画出将三角形绕点B逆时针旋转90°后的图形。
(4)将表示三角形轮廓点的数对的第一个数除以2,第二个数不变,画出得到的图形。
(5)将三角形放大,使放大后的图形与原图形对应线段长的比为2∶1。
11.画一画,按2∶1画出梯形放大后的图形;按1:3画出平行四边形缩小后的图形。
12.画一画(每个方格的边长是1厘米)。
(1)画出一个与三角形ABC面积相等的长方形。
(2)将三角形ABC向下平移4格。
(3)将三角形ABC绕点C顺时针旋转90°。
(4)将三角形ABC放大,使新图形与原图形对应线段长的比为2∶1。
13.每个小正方形的边长表示1厘米,请按要求画出相应的图形。
(1)把图①向右平移5格。
(2)把图②绕O点逆时针旋转90°,画出旋转后的图形。
(3)画出图③的另一半,使它成为一个以直线l为轴的轴对称图形。
(4)一个平行四边形的四个顶点用数对表示分别是:A(13,1),B(16,1),C(18,3),D(15,3)。先在格子图中画出这个平行四边形,再画出它按2∶1放大后图形。
14.
(1)画出如图①的另一半,使它成为一个轴对称图形。
(2)把如图中的长方形绕点A顺时针旋转90°,画出旋转后的图形,点B旋转后的位置用数对表示是( )。
(3)将三角形向右平移8格,画出平移后的图形,如果按2∶1的比放大这个三角形,放大后的三角形面积是原来的( )倍。
15.在团结村南偏西30°方向、距离团结村1000米的地方有一个桃园;在团结村北偏西60°方向、距离团结村800米的地方有一个梨园,请在图上画出桃园和梨园的位置。
16.按要求画图。
(1)在上图中画出图形A关于直线a的对称图形。
(2)把图形B绕点O顺时针旋转90°后的图形画在图中。
(3)把图形C按2∶1的比放大后的图形画在图中。
17.按要求画图。
(1)把图中的长方形绕A点顺时针旋转90°,画出旋转后的图形。旋转后,B点的位置用数对表示是 。
(2)按1∶2的比画出三角形缩小后的图形。缩小后的三角形的面积是原来的。
(3)如果1个小方格表示1平方厘米,在上面的方格纸上设计一个面积是10平方厘米的轴对称图形,并画出对称轴。(画一条即可)
18.按要求填一填,画一画。
(1)如果梯形顶点A的位置用数对表示为(2,1),那么顶点C用数对表示为 。
(2)把梯形绕点B顺时针旋转90°,画出旋转后的图形。
(3)把原来的梯形按2∶1放大,请在空白处画出放大后的梯形。
19.想一想,画一画,算一算。
(1)如图,在长5厘米,宽4厘米的长方形内画一条线段,把长方形分割成一个最大的等腰直角三角形和一个梯形。
(2)梯形的面积是( )平方厘米。
(3)以等腰直角三角形的一条直角边为轴旋转一周后形成的立体图形是( ),这个立体图形的体积是( )立方厘米(保留整数)。
20.按要求画一画。
(1)画出下图中的直角三角形绕O点顺时针旋转90°后的图形B。
(2)以直线n为对称轴,作图形B的轴对称图形,得到图形C。
21.按要求填空,并在方格纸上画出图形。(每个小正方形的边长表示1厘米)。
(1)画出图形1向左平移6格后的图形。
(2)按2∶1的比画出图形2放大后的图形。
(3)点O的位置用数对表示是 。
在平面图中,如果以点O为观测点,点B在点O的 偏 °方向 厘米处。
(4)将图形1绕右下角的顶点顺时针旋转90°并画出来。
22.操作。
(1)画出三角形ABC绕A点逆时针旋转90°后的图形。
(2)画出三角形ABC以1∶2的比例缩小后的图形。
23.画一画。(用直尺和铅笔作图)
(1)将图形A绕点O逆时针旋转90°,得到图形B。
(2)将图形B向右平移6格,得到图形C。
24.(1)以MN为对称轴,画出图形A的轴对称图形B。
(2)将图形B绕O点顺时针旋转,得到图形C。
(3)将图形C向右平移4格后,得到图形D。
25.按要求在下面方格纸上画图。画出下面的图形按2∶1放大后的图形。
26.小风绘制了以实验小学为观测点的平面图。(图上每段表示1cm)
(1)某书店距实验小学的实际距离为400m,请计算出这幅图的比例尺(写出计算过程),并在下图的方框里用线段比例尺表示出来。
(2)实验中学在实验小学东偏北30°方向600m处,在图中用“☆”画出实验中学的位置。
27.
(1)把圆向右平移4格,画出平移后的图形。
(2)把长方形绕点按逆时针方向旋转90度,画出旋转后的图形B。
(3)以虚线为对称轴,作平行四边形的轴对称图形,得到图形C。
(4)将图形C放大,使放大后的图形与原图形对应线段长的比为2∶1。
28.想一想,在方格中画一画。
(1)观察如图,点O所在的位置是( )。
(2)将图形A以点O为中心顺时针旋转90度,得到图形B。
(3)以直线l为对称轴画出图形A的轴对称图形,得到图形C。
(4)画出图形A按2∶1的比放大后的图形D。
29.按要求画图形或填空(如图)。
(1)画出图A向右平移4格,再向下平移5格后得到的图形A′。
(2)画出图B绕点O顺时针旋转90°后得到的图形B′。
(3)画出图形C放大后的图形C′,使新图形与原图形对应线段长的比为2∶1。
(4)画一个面积是6平方厘米的轴对称图形(图上一个方格表示1平方厘米),并画出一条对称轴。
30.根据要求,画一画。
(1)先画出图形A关于直线l的对称图形B;
(2)画出图形A绕点O逆时针旋转90°后所得到的图形C;
(3)画出图形C向上平移3格后所得到的图形D。
31.如图是某校附近的平面图,请你按要求画图。
(1)图书馆在学校的( )面大约( )千米处。
(2)教育局位于学校北偏西40°方向1200米处,请用“ ”在图中标出其大概位置。
(3)在学校正北方向1500米处有一条人民路与工业路平行,请在图中表示出来。
32.按要求在下面的方格中画图。
(1)将图形A向右平移5格,得到图形B。
(2)将图形A绕点O逆时针旋转90°得到图形C。
(3)将图形A按1∶2缩小,得到图形D。
33.画一画,填一填。
(1)以直线MN为对称轴作图形A的轴对称图形,得到图形B。
(2)将图形A绕点O顺时针旋转90°得到图形C。
(3)图中圆心的位置用数对表示是 。
(4)画出圆向右平移4格后的图形D。
34.在方格纸上按要求画图并填空。
(1)在直角三角形ABC中,顶点B的位置用数对表示为 。
(2)以直线l为对称轴,画出三角形ABC的对称图形。
(3)把三角形ABC绕点A顺时针旋转90°,画出旋转后的图形。
(4)画出将三角形ABC平移,使点A的对应点在数对(5,1)位置的图形。
35.按要求画一画。
(1)以虚线为对称轴,画出轴对称图形①的另一半。
(2)画出图形②向左平移5格后的图形。
(3)画出图形③绕点按顺时针方向旋转后的图形。
(4)画出图形④按1∶2缩小后的图形。
36.按要求画一画。
(1)画出图形A先绕点O顺时针旋转90°,再向右平移4格后得到的图形B。
(2)画出图形A按1∶2的比缩小后的图形C。
(3)以直线MN为对称轴,画出图形A的轴对称图形D。
37.小红和小华合作绘制的学校周边的平面图(如图),小华家在学校的东偏北30度600米处,小红家在西偏南45度700米处。请根据比例尺在图上帮小红和小华画出他们家的距离,并用“△”标示出他们家的位置。
38.按要求画图。
(1)在下面方格中,画出2∶1放大的图形。
(2)以放大后三角形的一直角边为直径,画一个圆。
(3)如果上图中的小方格的边长表示1厘米,那么圆的面积是( )平方厘米。(π=3.14)
39.一艘海警船(点A处)接收到一渔船发出的求助信息为:雷达显示,你们(海警船)在我们渔船西偏南30°方向上,因我船故障无法行驶,请求帮助。海警船回复:好的,我们已收到你们的信息,现距离你们3千米,请耐心等待。
请根据以上对话信息,画出目前海警船与渔船的位置关系图,比例尺1∶150000。
40.按要求在方格纸上画图。
(1)将图形A绕O点逆时针旋转90°得到图形B。
(2)以直线L为对称轴作图形A的轴对称图形C,再将图形C向右平移4格得到图形D。
(3)画出图形E按2∶1放大后的图形F。
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案及试题解析
1.见详解
【分析】(1)水龙头浇灌的范围相当于一个以点P为圆心,以半径为5米所画的圆,据此画出一个圆,这个圆就是水龙头浇灌的范围。
(2)把三角形区域按2∶1放大,即三角形的底和高都扩大到原来的2倍,先计算出按2∶1放大后的三角形的底和高,再在水龙头的浇灌范围内画出放大后的三角形。
【解析】三角形放大后的底:4×2=8(米)
三角形放大后的高:2×2=4(米)
(1)(2)如图所示:(圆P是水龙头的浇灌范围,图②是放大后的西红柿种植区域)
2.见详解
【分析】从垃圾综合处理站到两个村庄的距离皆为3千米,即垃圾综合处理站位于以张家村该点为圆心,半径为3千米的圆上;也位于以李家村为圆心,半径为3千米的圆上,两圆的交点即为垃圾综合处理站。
图中的线段比例尺表示图上1厘米相当于实际距离1千米,那么实际距离3千米在图中即是3厘米,据此作图。
【解析】图中AB点均可为垃圾综合处理站的具体位置,作图如下:
3.见详解
【分析】(1)根据旋转的特征,将图形D绕点O逆时针旋转90°,点O位置不变,其余各部分均绕此点按相同方向旋转相同度数,即可画出旋转后的图形E。
(2)图形D按2∶1放大,即原来图形D的上底、下底、高都乘2,就是放大后梯形的上底、下底和高,据此画出放大后的图形。
【解析】(1)画出将图形D绕点O逆时针旋转90°后的图形E,如下图。
(2)放大后梯形的上底:2×2=4
放大后梯形的下底:3×2=6
放大后梯形的高:2×2=4
画一个上底为4、下底为6、高为4的梯形,如下图。
4.见详解
【分析】这个长方形的长和宽的实际长度,以及比例尺已知,1m=100cm,将实际长度的单位换算成单位“cm”,依据“图上距离=实际距离×比例尺”即可求出这个长方形的操场的长和宽的图上距离,进而就可以画出这个长方形的平面图。
【解析】300m=30000cm
200m=20000cm
30000×=1.5(cm)
20000×=1(cm)
如图:
5.(1)(2)(3)(4)(5)见详解
【分析】(1)根据轴对称图形的意义:对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴的另一边画出图形①的关键对称点,依次连接即可。
(2)根据数对表示位置的方法:第一个数字表示列,第二个数字表示行,据此把图②的各个顶点用数对表示出来,再把第二个数除以3,求出三角形三个顶点的数对,再画出图形。
(3)根据旋转的特征,三角形②绕点O顺时针旋转90°后,点O的位置不动,其余各部分均绕此点按相同方向旋转相同的度数,得到旋转后的图形。
(4)根据平移的特征,把三角形②的各个顶点分别向上平移4格,再向左平移6格,依次连接,即可得到平移后的图形。
(5)根据图形放大的特征:把三角形②的各个边扩大到原来的2倍,画出放大后的图形即可。
【解析】(1)图如下:
(2)三角形②的三个点的数对为:(17,6),(21,6),(21,9);第二个数除以3后,三个点的数对为:(17,2),(21,2),(21,3);图如下:
(3)图如下:
(4)图如下:
(5)底:4×2=8(格);高:3×2=6(格);图如下(位置不唯一):
6.见详解
【分析】(1)假设每个小方格的边长为1,三角形ABC的底为4,高为2,画一个和三角形ABC等底等高的直角三角形即可;
(2)由图可知,AB是4,缩小后AB的长度为4×=2,AB对应的高为2,缩小后AB对应的高为2×=1,根据原图形画出缩小后的图形;
(3)根据题目要求确定旋转中心(点A)、旋转方向(顺时针)、旋转角度(90°),分析所作图形,找出构成图形的关键边,按一定的方向和角度分别找出各关键边的对应边,最后依次连接组成封闭图形;找出构成图形的关键点,确定平移方向(向左)和平移距离(8格),由平移的距离确定关键点平移后的对应点的位置,依次连接各对应点,据此作图。
【解析】作图如下:
7.(1)1∶20000
(2)作图见详解
【分析】(1)比例尺是表示图上一条线段的长度与地面相应线段的实际长度之比,由图可知,图上1厘米相当于实际200米,先将200米换算单位为厘米,再根据:比例尺=图上距离∶实际距离解答;
(2)先根据图上距离=实际距离×比例尺,用400米乘比例尺,求出图上距离;再根据在地图上按照“上北下南,左西右东”确定方向,找到笑笑家在广场的西偏北30°,画出线段标注名称即可。
【解析】(1)200米=20000厘米
1厘米∶20000厘米=1∶20000
所以,这个示意图的比例尺是1∶20000。
(2)400米=40000厘米
40000×=2(厘米)
作图如下:
8.见详解
【分析】把平行四边形按2∶1扩大,即平行四边形的每一条边扩大到原来的2倍,原平行四边形的底和高分别乘2,得出扩大后平行四边形的底和高,据此画出扩大后的图形。
把长方形按1∶3缩小,即长方形的每一条边缩小到原来的,原长方形的长和宽分别除以3,得出缩小后长方形的长和宽,据此画出缩小后的图形。
【解析】据分析作图如下:
9.见详解
【分析】(1)画出三角形①绕点C逆时针旋转90°的图形②:首先明确旋转的三要素:旋转中心、旋转方向和旋转角度,本题中旋转中心是点C,旋转方向是逆时针,旋转角度是90°;对于三角形的每个顶点,以点C为中心进行操作,过点C作垂直于对应顶点与点C连线的直线,根据逆时针方向和90°的角度确定顶点旋转后的位置,比如点A,连接AC,过点C作AC的垂线,沿逆时针方向在垂线上截取与AC长度相等的线段,得到点A旋转后的位置,同样的方法找到点B旋转后的位置,最后把旋转后的点连接起来得到旋转后的三角形②。
(2)将图形①按2∶1放大,画出放大后的图形③:按2∶1放大意味着图形的每条边都要放大到原来的2倍。分别测量三角形①三条边的长度,将每条边的长度乘2 ,画出放大后的三角形③。
【解析】(1)、(2)作图如下:
10.见详解
【分析】(1)根据轴对称图形的画法,以虚线为对称轴,在上方画出其另一半即可;
(2)根据平移的方法,将三角形先向左平移6格,再向下平移2格,注意平移不改变图形的形状和大小;
(3)根据旋转,将三角形ABC绕B点逆时针旋转90°,只需将BC和BA分别绕B点逆时针旋转90°,再连接即可;
(4)轮廓点的数对的第一个数除以2,第二个数不变,只需将其三个顶点进行移动,A点(18,3),处理后变成(9,3);B点(22,6)处理后变成(11,6);C点(22,3),处理后变成(11,3),在图中分别找到处理后的点,连接即可;
(5)按照2∶1放大,则AC放大2倍后长8格,BC放大2倍后长6格,然后连接即可得到放大后的图形。
【解析】
11.见详解
【分析】按2∶1画出梯形放大后的图形,即梯形的形状不变,各边都扩大到原来的2倍,原来的梯形的上底是4格,放大后是4×2=8格,原来梯形的下底是2格,放大后是2×2=4格,原来的高是3格,放大后是3×2=6格,据此画出放大后的梯形;
按1:3画出平行四边形缩小后的图形,即平行四边形的各边都缩小到原来的,平行四边形原来的底边是9格,缩小后是9÷3=3格,平行四边形原来的高是6格,缩小后是6÷3=2格,据此画图即可。
【解析】如图:
12.图见详解
【分析】(1)根据三角形的面积=底×高÷2,求出三角形ABC的面积;要画一个与三角形ABC面积相等的长方形,根据长方形的面积=长×宽,得出长方形的长、宽,据此画出这个长方形。
(2)根据平移的特征,将三角形ABC的各顶点分别向下平移4格,依次连接即可得到平移后的图形。
(3)根据旋转的特征,将三角形ABC绕点C顺时针旋转90°,点C位置不变,其余各部分均绕此点按相同方向旋转相同度数,即可画出旋转后的图形。
(4)将三角形ABC按2∶1放大,则原来三角形的底和高都乘2,即是放大后三角形的底和高,据此画出放大后的三角形。
【解析】(1)3×4÷2=6(平方厘米)
因为6=3×2,可以画一个长为3厘米、宽为2厘米的长方形,如下图。
(2)画三角形ABC向下平移4格后的图形,如下图。
(3)画三角形ABC绕点C顺时针旋转90°后的图形,如下图。
(4)放大后三角形的底是:3×2=6(厘米)
放大后三角形的底是:4×2=8(厘米)
画一个底为6厘米、高为8厘米的三角形。
如下图:
(长方形画法不唯一)
13.见详解
【分析】(1)根据平移的特征,将图①的各顶点分别向右平移5格,依次连接即可得到平移后的图形。
(2)根据旋转的特征,将图②绕O点逆时针旋转90°,点O位置不变,其余各部分均绕此点按相同方向旋转相同度数,即可画出旋转后的图形。
(3)根据轴对称图形的特征,对称点到对称轴的距离相等,找到图③的各顶点关于对称轴l的对称点后,依次连接各点得到轴对称图形。
(4)用数对表示位置的方法:数对的第一个数字表示列,第二个数字表示行;据此先在图中标出四个顶点的位置,再依次连接画出这个平行四边形。
把平行四边形按2∶1放大,则平行四边形的底和高都乘2,即是放大后平行四边形的底和高,据此画出放大后的平行四边形。
【解析】(1)平移后的图形,见图④;
(2)旋转后的图形,见图⑤;
(3)补全轴对称的图形,见图⑥;
(4)平行四边形ABCD,见图⑦;
3×2=6
2×2=4
放大后的平行四边形,见图⑧。
14.(1)图见详解
(2)图见详解;(7,5)
(3)图见详解;4
【分析】(1)先确定对称轴(图中的虚线),依据轴对称图形性质,对称点到对称轴距离相等且在对称轴两侧,找出图形①各关键点关于对称轴的对称点,再依次连接这些对称点,即可画出另一半,使其成为轴对称图形。
(2)以点A为旋转中心,将长方形的四条边顺时针旋转90°,通过数方格确定旋转后各边的位置,画出旋转后的长方形;用数对表示位置时先数列再数行,画出旋转后的长方形观察可知点B旋转后的位置在第7列,第5行,所以用数对表示是(7,5)。
(3)将三角形的三个顶点分别向右平移8格,再依次连接这三个平移后的顶点,得到平移后的图形;如果按2∶1的比放大这个三角形,即每条边的长度都扩大到原来的2倍,原来三角形的底是4,扩大到原来的2倍是4×2=8,原来的高是3,扩大到原来的2倍是3×2=6,面积是8×6÷2=24,原来三角形面积是4×3÷2=6,用扩大后的面积除以扩大前的面积即可。
【解析】(1)画出图①的另一半,使它成为一个轴对称图形,如下图。
(2)观察旋转后图形发现,点B旋转后的位置在第7列,第5行,所以用数对表示是(7,5);
作图如下:
(3)4×3÷2
=12÷2
=6
(4×2)×(3×2)÷2
=8×6÷2
=48÷2
=24
24÷6=4
所以放大后的三角形面积是原来的4倍。
作图如下:
15.见详解
【分析】桃园:已知实际距离1000米,因为1米=100厘米,所以1000米=100000厘米,根据“图上距离=实际距离×比例尺”,比例尺为1∶40000,则桃园图上距离为100000×=2.5厘米;用量角器以团结村为顶点,向南偏西30°方向画射线,在射线上从团结村开始量取2.5厘米的长度确定桃园位置。
梨园:已知实际距离800米,800米=80000厘米,同理,梨园图上距离为80000×=2厘米 ;用量角器以团结村为顶点,向北偏西60°方向画射线,在射线上从团结村开始量取2厘米的长度确定梨园位置。
【解析】作图如下:
16.(1)见解答
(2)见解答
(3)见解答
【分析】(1)根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴的左边画出图A的关键对称点,依次连接即可;
(2)根据旋转的特征,图形B绕点O顺时针旋转90°后,点O的位置不动,其余各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图形;
(3)根据图形放大与缩小的意义,把图形C各对应边均放大到原来的2倍即可。
【解析】(1)如下图所示:
(2)如下图所示:
(3)如下图所示:
17.(1)作图见详解;(7,6)
(2)作图见详解;
(3)见详解
【分析】(1)作旋转一定角度后的图形步骤:根据题目要求,确定旋转中心、旋转方向和旋转角;分析所作图形,找出构成图形的关键点;找出关键点的对应点:按一定的方向和角度分别作出各关键点的对应点;作出新图形,顺次连接作出的各点即可。用数对表示位置时,通常把竖排叫列,横排叫行。一般情况下,确定第几列时从左往右数,确定第几行时从前往后数。表示列的数在前,表示行的数在后,中间用逗号“,”隔开,数对加上小括号。
(2)把图形按照1∶n缩小,就是将图形的每一条边缩小到原来的,缩小后图形与原图形对应边长的比是1∶n。三角形面积=底×高÷2,据此分别计算出缩小前后的面积,将原来的面积看作单位“1”,缩小后的面积÷原来的面积=缩小后的三角形的面积是原来的几分之几。
(3)长方形面积=长×宽,据此确定长方形的长和宽,画出一个面积是10平方厘米的长方形。画对称轴的步骤:找出轴对称图形的任意一组对称点;连结对称点;画出对称点所连线段的垂直平分线,就可以得到该图形的对称轴。
【解析】(1)作图如下:
旋转后,B点的位置用数对表示是(7,6)。
(2)作图如下:
(3×2÷2)÷(6×4÷2)
=3÷12
=
缩小后的三角形的面积是原来的。
(3)
(轴对称图形的画法不唯一)
18.(1)(3,3)
(2)见详解
(3)见详解
【分析】(1)用数对表示位置的方法:数对的第一个数字表示列,第二个数字表示行;结合顶点A用数对表示的位置,用数对表示顶点C的位置。
(2)根据旋转的特征,将梯形绕点B顺时针旋转90°,点B位置不变,其余各部分均绕此点按相同方向旋转相同度数,即可画出旋转后的图形。
(3)把原来的梯形按2∶1放大,即原来梯形的上底、下底、高都乘2,即是放大后梯形的上底、下底和高,据此画出放大后的梯形。
【解析】(1)顶点C在第3列第3行,所以顶点的位置用数对表示为(3,3)。
(2)把梯形绕点B顺时针旋转90°后的图形,如下图。
(3)放大后梯形的上底:1×2=2
放大后梯形的下底:2×2=4
放大后梯形的高:2×2=4
放大后的梯形如下图。
19.(1)见详解
(2)12
(3)圆锥;67
【分析】(1)一个最大的等腰直角三角形的直角边应是长方形的宽,据此画图。
(2)梯形的上底等于长方形的长-长方形的宽,梯形的下底等于长方形的长,梯形的高等于长方形的宽,根据梯形的面积公式:面积=(上底+下底)×高÷2,代入数据,即可解答。
(3)根据圆锥的特征可知,以等腰直角三角形的一条直角边为轴,旋转一周,会形成一个圆锥,圆锥的底面半径等于等腰直角三角形的腰,高等于等腰直角三角形的腰,根据圆锥的体积公式:体积=底面积×高×,代入数据,即可解答。
【解析】(1)如图:
(2)(5-4+5)×4÷2
=(1+5)×4÷2
=6×4÷2
=24÷2
=12(平方厘米)
梯形的面积是12平方厘米。
(3)以等腰直角三角形的一条直角边为轴旋转一周后形成的立体图形是圆锥。
3.14×42×4×
=3.14×16×4×
=50.24×4×
=200.96×
≈67(立方厘米)
以等腰直角三角形的一条直角边为轴旋转一周后形成的立体图形是圆锥,这个立体图形的体积是67立方厘米
20.(1)(2)见详解
【分析】(1)根据旋转的特征,直角三角形绕点O顺时针旋转90°后,点O的位置不动,其余各部分均绕此点按相同方向旋转相同的度数,得到旋转后的图形B。
(2)根据轴对称图形的意义:对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴的另一边画出图形B的关键对称点,依次连接即可。
【解析】(1)如下图:
(2)如下图:
21.((1)(2)(4)图见详解
(3)(15,4);东;北;60;2
【分析】(1)根据平移图形的特征,把梯形1的四个顶点分别向左平移6格,再首尾连接各点,即可得到梯形1向左平移6格的图形;
(2)按2∶1的比例画出三角形放大后的图形,就是把原三角形的三条边分别扩大到原来的2倍,据此画出扩大后的图形即可;
(3)用数对表示位置时,先表示第几列,再表示第几行,据此用数对表示点O的位置即可;并以O点为观测点,根据方向和距离确定B点的位置;
(4)根据旋转的意义,找出图中梯形1的4个关键处,再画出按顺时针方向旋转90度后的形状即可。
【解析】(1)如下图所示:
(2)如下图所示:
(3)点O的位置用数对表示是(15,4),
因为OB=OC=2厘米,∠BOC=60°,如果以点O为观测点,点B在点O的北偏东30°方向2厘米处或东偏北60°方向2厘米处。
(4)如下图所示:
22.(1)(2)见详解
【分析】(1)绕A点逆时针旋转90°,需固定A点,将B、C两点绕A按逆时针转90°,依据网格确定旋转后坐标位置,再连线;
(2)按1∶2比例缩小,要先确定原三角形各边长度,再将边长除以2 ,以某顶点为参照确定新顶点位置,最后连接成缩小后的三角形。
【解析】(1)(2)作图如下:
23.(1)(2)见详解
【分析】(1)明确旋转中心为点O ,旋转方向是逆时针,角度为90°,通过直尺确定图形A各顶点绕点O逆时针旋转90°后的位置,再用铅笔连接各点得到图形B;
(2)确定平移方向为向右,距离是6格,用直尺将图形B的各顶点沿水平方向向右移动6格,最后用铅笔连接各平移后的顶点得到图形C。
【解析】(1)(2)作图如下:
24.见详解
【分析】(1)补全轴对称图形的方法:找出图形的关键点,依据对称轴画出关键点的对称点,再依据图形的形状顺次连接各点,画出最终的轴对称图形。据此先找到对称点,画出两条直的边,再根据画圆的方法画出半圆。
(2)作旋转一定角度后的图形步骤:根据题目要求,确定旋转中心、旋转方向和旋转角;分析所作图形,找出构成图形的关键点;找出关键点的对应点:按一定的方向和角度分别作出各关键点的对应点;作出新图形,顺次连接作出的各点即可。
(3)作平移后的图形步骤:找点-找出构成图形的关键点;定方向、距离-确定平移方向和平移距离;画线-过关键点沿平移方向画出平行线;定点-由平移的距离确定关键点平移后的对应点的位置;连点-连接对应点。
【解析】
25.见详解
【分析】放大后的图形的边长是原图形的2倍,据此作图即可。
【解析】根据要求作图如下:
26.(1)1∶20000;作图见详解
(2)见详解
【分析】(1)图上距离∶实际距离=比例尺,据此写出图上距离与实际距离的比,化简即可得出比例尺,再将数值比例尺改写成线段比例尺,补在图上即可;
(2)弄清要标示的物体在哪个方位上,有多少度,按要求的方位和度数准确画图;注意各场所离中心点的距离,根据要求的比例画出相应的长度。图上距离=实际距离×比例尺。
【解析】(1)2cm∶400m=2cm∶40000cm=(2÷2)∶(40000÷2)=1∶20000
20000cm=200m
这幅图的比例尺是1∶20000。作图如下:
(2)600m=60000cm
60000×=3(cm)
27.见详解
【分析】(1)将O点向右平移4格为O’点,以为圆心1格的长度为半径画一个圆,即可得到平移后的图形;
(2)以点A为旋转中心,按照与时针旋转相反的方向,旋转的角度90度,点A不动,图形的各个部分点A按逆时针方向旋转90°得到图形B;
(3)一个轴对称图形按照对称轴对折能够完全重合,据此找到平行四边形的四个顶点的对称点再顺次连接,得到图形C;
(4)图形C按照2∶1放大,图形C的各边均为原来的2倍,得到放大后的图形。
【解析】由分析可作图:
28.(1)(7,5)
(2)(3)(4)见详解
【分析】(1)用数对表示位置的方法:数对的第一个数字表示列,第二个数字表示行;据此用数对表示点O所在的位置。
(2)根据旋转的特征,将图形A以点O为中心顺时针旋转90度,点O位置不变,其余各部分均绕此点按相同方向旋转相同度数,即可画出旋转后的图形B。
(3)根据轴对称图形的特征,对称点到对称轴的距离相等,找到图形A的各顶点关于对称轴l的对称点后,依次连接各点得到图形A的对称图形C。
(4)图形A按2∶1的比放大,即把图形A的每条边都扩大到原来的2倍,据此画出放大后的图形D。
【解析】(1)观察如图,点O所在的位置是(7,5)。
(2)将图形A以点O为中心顺时针旋转90度,得到图形B,如下图。
(3)以直线l为对称轴画出图形A的轴对称图形,得到图形C,如下图。
(4)放大后三角形的底:2×2=4
放大后三角形的高:3×2=6
则画一个底为4、高为6的三角形D,如下图。
29.(1)(2)(3)(4)见详解
【分析】(1)根据平移的特征,把图A的各顶点分别向右平移4格,再向下平移5格,依次连接即可得到平移后的图形A′。
(2)根据旋转的特征,图B绕点O顺时针旋转90°,点O的位置不动,其余各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图形B′。
(3)根据图形放大与缩小的意义,把图形C的各边均放大到原来的2倍,对应角大小不变,所得到的图形就是原图按2∶1放大后的图形C′。
(4)画一个长3格,宽2格的长方形,再画出一条对称轴即可。(画法不唯一)
【解析】如下图:
(画面积是6平方厘米轴对称图形画法不唯一)
30.(1)、(2)、(3)见详解
【分析】(1)补全轴对称图形的方法:找出图A的关键点,依据对称轴画出关键点的对称点,再依据图形的形状顺次连接各点,画出最终的轴对称图形。
(2)旋转图形的作图方法:根据题目要求确定旋转中心(点O)、旋转方向(逆时针)、旋转角度(90°);分析所作图形,找出构成图形的关键边;按一定的方向和角度分别找出各关键边的对应边;最后依次连接组成封闭图形;
(3)平移图形的作图方法:找出构成图形的关键点;确定平移方向(向上)和平移距离(3格);由平移的距离确定关键点平移后的对应点的位置;依次连接各对应点。
【解析】(1)、(2)、(3)据分析作图如下:
31.(1)东;1.8
(2)图见详解
(3)图见详解
【分析】(1)图中的向上为正北方向,向右为正东方向,图书馆位于学校的正右方向,即正东方向,量得距离为3厘米,则运用实际距离=图上距离÷比例尺,计算可得出答案。
(2)与正北方向向西偏40°,实际距离1200米,图上距离=实际距离×比例尺,可得出教育局所在位置。
(3)图上距离=实际距离×比例尺,得到图上距离为2.5厘米,画出平行线可得出答案。
【解析】(1)图书馆与学校的图上距离为3厘米,则图书馆在学校实际距离:60000×3=180000(厘米),180000厘米=1.8千米,图书馆在学校的东面大约1.8千米。
(2)1200米=120000厘米
120000÷60000=2(厘米),如图:
(3)1500米=150000厘米
150000÷60000=2.5(厘米),如图:
32.(1)(2)(3)图见详解
【分析】(1)找出构成图形的关键点,确定平移方向(向右)和平移距离(5格),由平移的距离确定关键点平移后的对应点的位置,依次连接各对应点。
(2)根据题目要求确定旋转中心(点O)、旋转方向(逆时针)、旋转角度(90°),分析所作图形,找出构成图形的关键边,按一定的方向和角度分别找出各关键边的对应边,最后依次连接组成封闭图形。
(3)把图形按照1∶n缩小,就是将图形的每一条边缩小到原来的,缩小后图形与原图形对应边长的比是1∶n。
【解析】(1)(2)(3)作图如下:
33.(1)见详解
(2)见详解
(3)(4,3)
(4)见详解
【分析】(1)根据轴对称图形的画法,以直线MN为对称轴作图形A的轴对称图形,得到图形B,据此解答即可。
(2)点O不动,根据旋转的方法,将图形A绕点O顺时针旋转90°得到图形C,据此解答即可。
(3)根据数对表示位置的方法,找出圆心在第几列、第几行,图中圆心的位置用数对表示是(4,3),据此解答即可。
(4)根据平移的方法,画出圆向右平移4格后的图形D即可。
【解析】(1)以直线MN为对称轴作图形A的轴对称图形,得到图形B。如图:
(2)将图形A绕点O顺时针旋转90°得到图形C。如图:
(3)圆心在第4列,第3行,所以图中圆心的位置用数对表示是(4,3)。
(4)画出圆向右平移4格后的图形D。如图:
34.(1)(1,8)
(2)见详解
(3)见详解
(4)见详解
【分析】(1)根据用数对表示点的位置的方法,第一个数字表示列数,第二个数字表示行数,据此解答。
(2)画轴对称图形的方法:找出三角形ABC的关键点,依据对称轴画出关键点的对称点,再依据图形的形状顺次连接各点,画出最终的轴对称图形。
(3)旋转图形的作图方法:根据题目要求确定旋转中心(点A)、旋转方向(顺时针)、旋转角度(90°);分析所作图形,找出构成图形的关键边;按一定的方向和角度分别找出各关键边的对应边;最后依次连接组成封闭图形;
(4)先根据数对确定点A的对应点,再根据平移不改变三角形的方向、大小和形状,描出另外两个点,最后依次连接组成封闭图形。
【解析】(1)在直角三角形ABC中,顶点B的位置用数对表示为(1,8)。
(2)以直线l为对称轴,画出三角形ABC的对称图形。如图:
(3)把三角形ABC绕点A顺时针旋转90°,画出旋转后的图形。如图:
(4)画出将三角形ABC平移,使点A的对应点在数对(5,1)位置的图形。如图:
35.见详解
【分析】(1)补全轴对称图形的方法:找出图形的关键点,依据对称轴画出关键点的对称点,再依据图形的形状顺次连接各点,画出最终的轴对称图形。
(2)作平移后的图形步骤:找点-找出构成图形的关键点;定方向、距离-确定平移方向和平移距离;画线-过关键点沿平移方向画出平行线;定点-由平移的距离确定关键点平移后的对应点的位置;连点-连接对应点。
(3)作旋转一定角度后的图形步骤:根据题目要求,确定旋转中心、旋转方向和旋转角;分析所作图形,找出构成图形的关键点;找出关键点的对应点:按一定的方向和角度分别作出各关键点的对应点;作出新图形,顺次连接作出的各点即可。
(4)把图形按照1∶n缩小,就是将图形的每一条边缩小到原来的,缩小后图形与原图形对应边长的比是1∶n。
【解析】
36.(1)(2)(3)见详解
【分析】(1)旋转图形的作图方法:根据题目要求确定旋转中心(点O)、旋转方向(顺时针)、旋转角度(90°);分析所作图形,找出构成图形的关键边;按一定的方向和角度分别找出各关键边的对应边;最后依次连接组成封闭图形;平移图形的作图方法:找出构成图形的关键点;确定平移方向(向右)和平移距离(4格);由平移的距离确定关键点平移后的对应点的位置;依次连接各对应点。
(2)图形A按1∶2的比缩小,则组成图形的每条线段长度为原来的一半,据此作图。
(3)画轴对称图形的方法:找出图形A的关键点,依据对称轴画出关键点的对称点,再依据图形的形状顺次连接各点,画出最终的轴对称图形。
【解析】(1)(2)(3)作图如下:
37.见详解
【分析】根据图示方向的规定可知上北下南,左西右东,又因为图上距离1厘米表示实际距离200米,小华家和小红家分别与学校的实际距离已知,分别用实际距离除以200,可以求出它们之间的图上距离,再根据方向关系,即可在图上标出它们的位置,解答即可。
【解析】(厘米)
(厘米)
据分析作图如下:
38.(1)(2)见详解
(3)12.56
【分析】(1)根据图形放大的意义,把这个三角形两直角边均放大到原来的2倍所得到的图形就是原图形按2∶1放大后的图形。
(2)画圆时,“圆心定位置,半径定大小”,以直角三角形的一条直角边的中点为圆心,圆心到顶点为半径,即可画图。
(3)先计算出圆的半径,根据圆的面积公式:面积=π×半径2,代入数据,即可解答。
【解析】(1)2×2=4(厘米),2×2=4(厘米)
如下图:
(2)如下图:
(位置不唯一)
(3)4÷2=2(厘米)
3.14×22
=3.14×4
=12.56(平方厘米)
如果上图中的小方格的边长表示1厘米,那么圆的面积是12.56平方厘米。
39.见详解
【分析】已知这幅图的比例尺是1∶150000,海警船与渔船实际相距3千米,根据“图上距离=实际距离×比例尺”以及进率“1千米=100000厘米”,求出海警船与渔船的图上距离。
已知海警船在渔船西偏南30°方向上,是以渔船为观测点;图中画出了海警船的位置,如果以海警船为观测点,根据位置的相对性可知,观测点不同,方向相反,夹角的度数相同,距离相同;那么海警船在渔船西偏南30°方向上,也可以说成渔船在海警船东偏北30°方向上,根据方向、角度和距离画出警船与渔船的位置关系图。
【解析】3千米=300000厘米
300000×=2(厘米)
如图:
40.(1)(2)(3)见详解
【分析】(1)根据旋转的特征,图形A绕点O逆时针旋转90°,点O的位置不动,这个图形的各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图形。
(2)根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴(虚线L)的右边画出图形A的关键对称点,依次连接、涂色即可作图形A的轴对称图形C;根据平移的特征,把图形C的各顶点分别向右平移4格,依次连接、涂色即可得到平移后的图形D。
(3)根据图形放大的意义,把图形E的长、宽均放大到原来的2倍所得到的长方形就是原图形按2∶1放大后的图形F。
【解析】根据题意画图如下:
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
同课章节目录
