情境阅读题型解答题典型考点 押题练 2025年小学小升初数学会考复习备考
文档属性
| 名称 | 情境阅读题型解答题典型考点 押题练 2025年小学小升初数学会考复习备考 |  | |
| 格式 | docx | ||
| 文件大小 | 418.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-10 16:26:40 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
情境阅读题型解答题典型考点 押题练
2025年小学小升初会考复习备考
1.认真阅读下面材料,回答问题。
世界因良渚而震惊,震惊于良渚古城遗址的发现。良渚古城遗址的核心是城址,它的面积约8平方千米,由宫殿区(0.39平方千米)、内城(含宫殿区约2.8平方千米)、外城(约3.51平方千米)呈向心式三重布局组成,古河道贯穿其间。古城的外围水利系统分成谷口高坝、平原低坝和山前长堤的11条人工坝体及天然山体、溢洪道,初步估算,整个水利系统形成面积为13平方千米的水库,库容量超过46000000立方米,是中国迄今发现最早的大型水利工程遗址,也是目前已发现的世界上最早的堤坝系统之一。
(1)宫殿区0.39平方千米可以看成把1平方千米平均分成( )份,表示这样的( )份。
(2)外城3.51平方千米表示( )个0.01平方千米。
(3)0.39平方千米=( )公顷 46000000立方米=( )万立方米
(4)一个两位小数精确到十分位后是2.8,这个两位小数最大和最小分别是几?请在下面的数轴上分别用↑标出这两个小数的位置,并写出这两个小数。
(5)将上面材料中横线上的数改写成用“亿”作单位的数是( )立方米。(结果保留一位小数)
2.估计这篇报道的字数,用文字、图或算式来说明估计的过程与方法,并写出估计结果。
春节被赋予的独特意义又多了一层
春节,这张在全球早已家喻户晓的中国文化名片,本周又添了一个新“头衔”,随着中国申报的“春节——中国人庆祝传统新年的社会实践”12月4日通过评审,列入联合国教科文组织人类非物质文化遗产代表作名录,中国已有44个项目列入联合国“非遗”名录、名册,总数居世界第一。春节申遗成功,不仅是世界拥抱中华文明的又一重要里程碑,也为不同文明间的交流互鉴提供了一个新起点。
春节登上“非遗”名录,可以用“实至名归”来形容,春节是一整套中国民俗文化的集合体,不仅带着满满的国粹范儿,也寄托着中华民族独特的精神情感密码。无论是“爆竹声中一岁除”,还是“总把新桃换旧符”,都充满了辞旧迎新的仪式感。春节对于中国社会、对于全世界非遗保护事业的重要意义之一就在于,它是一个传统文化与社会发展相辅相成的很好案例。正如这次申遗文本中所强调的,“‘过年’为中国人提供了一种认同感和延续性”。围绕着春节,在过去几十年从农业中国向工业中国转变的过程中,中国出现了人类历史上最大规模的周期性迁徙。春节所代表的传统文化,成为中国式现代化的一种内在动力和具体形式。(摘自《环球时报》)
3.某音乐厅的舞台在中间,听众的座位分六个区域排列。如图所示,从里向外分别是第一排到第六排。每个区域的第一排均有10个座位,从第二排起每排比前一排多2个座位。
(1)这间音乐厅的第3排每边有多少个座位?
(2)学校合唱团买下了六个区域第4排的所有座位票,合唱团买了几张票?
4.《礼记》有言:“孟春之月,盛德在木”。清明节与春节、端午节、中秋节并称为中国四大传统节日。清明节,又称踏青节、行清节、三月节、祭祖节等,节期在仲春与暮春之交。清明节源自早期人类的祖先信仰,是中华民族最隆重盛大的祭祖大节。清明节兼具自然与人文两大内涵,既是自然节气点,也是传统节日。扫墓祭祖与踏青郊游是清明节的两大礼俗主题,这两大传统礼俗在中国自古传承,至今不辍。涧小三(8)班的40名同学在清明节举行植树活动,3小时植树240棵,照这样计算,30名同学植480棵树,需要多少小时?
5.阅读材料,解答问题。
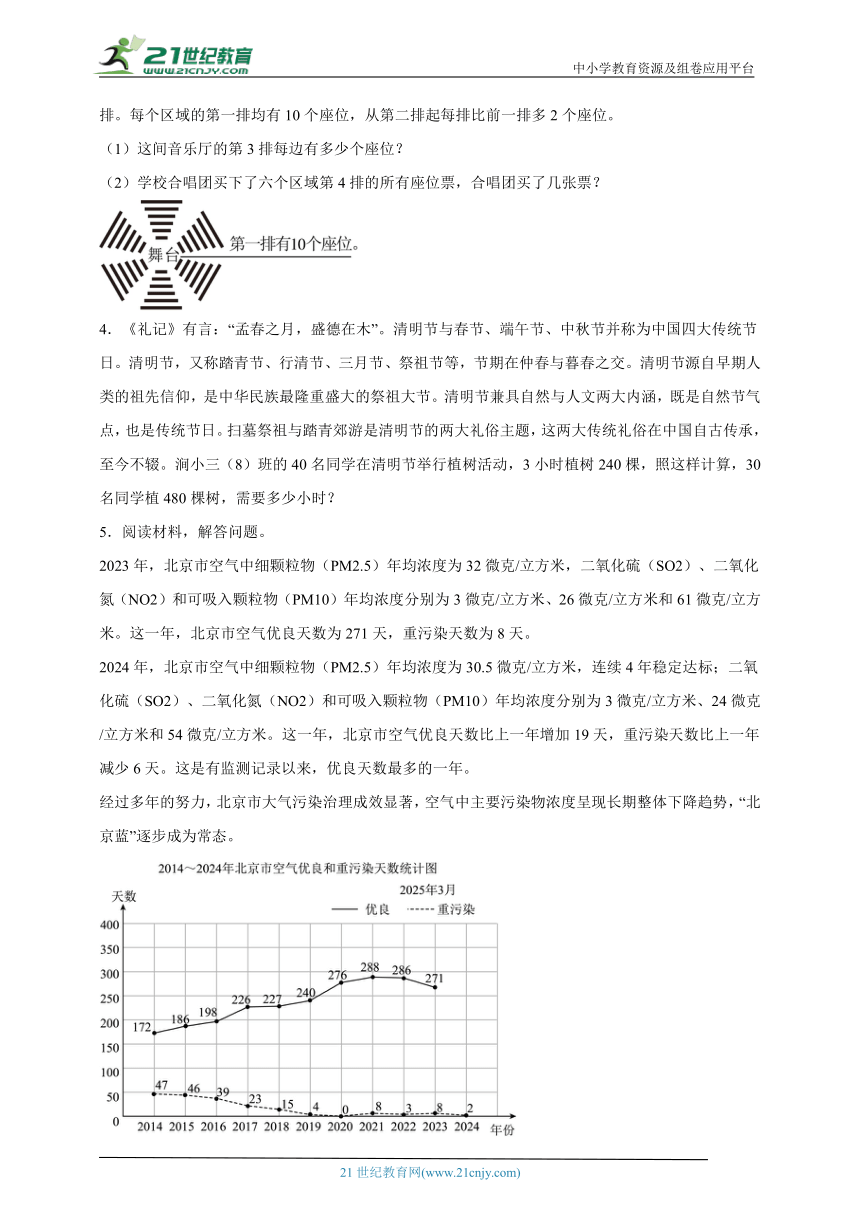
2023年,北京市空气中细颗粒物(PM2.5)年均浓度为32微克/立方米,二氧化硫(SO2)、二氧化氮(NO2)和可吸入颗粒物(PM10)年均浓度分别为3微克/立方米、26微克/立方米和61微克/立方米。这一年,北京市空气优良天数为271天,重污染天数为8天。
2024年,北京市空气中细颗粒物(PM2.5)年均浓度为30.5微克/立方米,连续4年稳定达标;二氧化硫(SO2)、二氧化氮(NO2)和可吸入颗粒物(PM10)年均浓度分别为3微克/立方米、24微克/立方米和54微克/立方米。这一年,北京市空气优良天数比上一年增加19天,重污染天数比上一年减少6天。这是有监测记录以来,优良天数最多的一年。
经过多年的努力,北京市大气污染治理成效显著,空气中主要污染物浓度呈现长期整体下降趋势,“北京蓝”逐步成为常态。
①请把统计图补充完整。
②2023年北京市空气中可吸入颗粒物(PM10)年均浓度是2024年的多少倍?(结果保留两位小数)
③2014~2024年北京市空气优良天数是怎样变化的?重污染天数呢?
④根据阅读材料,请你提出一个数学问题。
6.阅读故事。
高斯是一位伟大的数学家,有“数学王子的美誉”。
小时候,有一次老师让全班同学求算式1+2+3+…+98+99+100的结果。同学们开始认真地计算起来,只有高斯没有动笔,他思考了一会儿后写出了答案:5050,你知道高斯是怎么计算的吗?
高斯告诉大家,他先算1+100=101,2+99=101…这样一共有50个101,因此结果是5050。
计算推导
(1)观察规律,算式1+2+3+…+98+99+100,从第1个数开始,之后每个数都比前一个数多( ),相邻两数的差都( )。高斯求和公式就是为这类题目打造的专用工具。
(2)结合图形推导:将1+2+3+…+98+99+100,看作由若干个小圆堆成如图①的三角形图案,最上面一层有一个圆,以下每层均比上一层多一个圆,一共有100层。再将图①倒置后与原图拼成图②的形状。
计算出小圆的个数是1+2+3+…+98+99+100=(1+100)×100÷2=5050(个)。
得出结论
(1)一组自然数相加,若相邻两数的差都( ),则和=(首数+尾数)×总个数÷2。
(2)高斯的做法利用的运算律是( )。
结论应用:计算1+3+5+…+95+97+99。
7.(如下图)某商家推出一款足球纪念品,并给足球纪念品设计了圆柱形的包装盒,用绸带捆扎进行装饰。
(1)这个包装盒的表面积是多少?
(2)如果绸带打结处正好是底面圆心,打结用去的绸带长30厘米。捆扎这个包装盒至少要用绸带多少厘米?
(3)阅读下面的文本,计算这个足球纪念品的体积?
古希腊著名的数学家阿基米德是历史上杰出的数学家之一,在他众多的科学发现中,他自己最为满意的是“圆柱容球定理”。把一个球正好放在一个圆柱形容器中,球的直径与圆柱的高和底面直径相等,此时球的体积正好是圆柱体积的。
8.变化与不变。
大千世界,到处都在发生着或明显或隐藏的运动与变化。迅速的变化令人目眩神迷,缓慢的变化使人不知不觉。但是,在变化的过程中,常常有相对不变的东西。
数学家的眼光,常常盯住变化中不变的东西。正是这些不变的东西,把变化中的不同镜头联系起来,帮助我们认识变化过程的本质,帮助我们解决各种问题。
我们知道,哥哥长1岁,弟弟也长1岁。两人的年龄都变了,但年龄的差没有变。解有关年龄问题的时候,抓住两个人的年龄差不变这一点,往往可以使问题迎刃而解。
想要求下面图形的周长,最简单的方法就是将线段平移(图),平移后形状变了、面积变大了,但图形的周长没变,抓住这一点,问题就解决了。
“变中有不变”的思想在数学学习中随处可见。请你举一个本学期运用“变中有不变”思想解决问题的例子,并具体说明什么变了、什么没变。
9.数学阅读。
古代有一位公主叫狄多,她的王国发生叛乱后,就逃到了非洲。一天,她向当地的酋长雅布乞求一些土地,雅布酋长不想多给土地,就给了狄多一张犍牛皮,让公主用这张键牛皮圈土地,圈多少就给多少。聪明的公主用这张键牛皮圈得了很多土地,在这片土地上建立了拜萨(意为牛皮)城。
(1)用这张牛皮去覆盖土地,那太少了。把牛皮变成尽可能长,才可以圈出更多的土地。如果你是狄多公主,你准备圈( )形状的土地。
A.正方形 B.长方形 C.圆
(2)如果狄多公主得到的那张键牛皮能变成30000米长的牛皮条,可以圈得多少公项土地?(如果你圈的土地是圆形,取值为)
10.阅读材料。
阿基米德是古希腊伟大的数学家、力学家,他曾说:“给我一个支点,我能撬动地球。”传说,古希腊一位国王让金匠给他制作了一顶纯金王冠。国王怀疑王冠中掺了白银,于是让阿基米德检验一下。阿基米德想了很长时间,也没找到答案。有一天洗澡时,他注意到他的身体在装满水的浴缸里沉下去的时候,有一部分水从浴缸边溢了出来,他突然受到启发,冲进王宫对王说:“我找到方法了!”
阿基米德找到了什么方法?他是怎样试验的?
小辉读了阿基米德的故事后,也想尝试检验奶奶的金手镯是否是纯金的。他查阅资料了解到,黄金饰品按纯度有如下分类:24K、22K、18K、14K、12K、10K等。K指黄金的纯度,即用24份等重的金属熔炼在一起,纯金所占的份数。比如,24K黄金就是24份等重的黄金熔炼在一起;22K黄金就是22份等重的黄金和2份其他金属熔炼在一起……依次类推。请填写下表。(除不尽的,百分号前面保留保留一位小数)
黄金纯度分类 24K金 18K金 14K金 12K金
黄金质量占黄金饰品总质量的百分比
奶奶的金手镯是22K金,质量有72克重,请计算金手镯中含有的黄金质量。
参考答案
1.(1)100;39;
(2)351;
(3)39;4600;
(4)2.84;2.75;在数轴上标数见详解;
(5)0.5;
【分析】(1)0.39是两位小数,写成分数是,是平均分成100份表示这样的39份,据此解答即可;
(2)3.51的计数单位是0.01,去掉3.51即可得到3.51里有几个0.01;
(3)根据1平方千米=100公顷,把0.39平方千米画成公顷为单位即可;
将整万的数改写成用“万”作单位的数,只要省略万位后面的0,并加一个“万”即可;
(4)一个两位小数精确到十分位后是2.8,可以从四舍中找到最大的,从五入中找到最小的;据此解答。
(5)改写成用亿作单位的数,就是在亿位的右下角点上小数点,然后把小数末尾的0去掉,再在数的后面写上亿字;保留一位小数是采用四舍五入的方法,找到小数点后的第二位,看第二位上的数大于等于5向前一位进1,小于5直接舍去。
【详解】(1)求0.39平方千米对应的份数:0.39是两位小数,两位小数表示百分之几,所以0.39平方千米可以看成把1平方千米平均分成100份,0.39里面有39个0.01,就表示这样的39份。
(2)外城3.51平方千米表示351个0.01平方千米。
(3)0.39平方千米=39公顷 46000000立方米=4600万立方米
(4)确定两位小数的最大和最小值并标注:一个两位小数精确到十分位后是2.8,根据“四舍五入”法,如果是“四舍”得到的2.8,那么这个两位小数的个位和十分位是2.8,百分位最大是4,所以这个两位小数最大是2.84;如果是“五入”得到的2.8,那么这个两位小数的个位是2,十分位原来是7,百分位最小是5,所以这个两位小数最小是2.75。在直线上找到对应的位置标注,如答案图所示。
(5)46000000=0.46 亿≈0.5亿
即材料中横线上的数改写成用“亿”作单位的数是0.5立方米。。
2.480个
【分析】根据题意,先数出一共有多少行,再估算每行有多少字,最后相乘即可。一共有8行,每行大约有60个字,即8×60。
【详解】8×60=480(个)
答:这篇报道大概有480个字。
3.(1)14个
(2)96张
【分析】(1)根据题意,第一排均有10个座位,从第二排起每排比前一排多2个座位,用10+2即可求出第二排有多少个座位,用第二排座位的个数再加2即可求出第3排每边有多少个座位。
(2)根据题意,买下了六个区域第4排的所有座位票,先用第三排座位的个数加2求出第四排有多少个座位,再乘6即可求出合唱团买了几张票。
【详解】(1)10+2+2=14(个)
答:这间音乐厅的第3排每边有14个座位。
(2)14+2=16(个)
16×6=96(张)
答:合唱团买了96张票。
4.8小时
【分析】40名同学每小时植树数量为:240 ÷ 3 = 80(棵),每人每小时植树数量为:80 ÷ 40 = 2(棵);每个同学每小时可以植树2棵。计算30名同学每小时的植树数量:30 × 2 = 60 (棵),计算种植480棵所需的时间:时间 = 总植树量 ÷ 每小时植树量 = 480÷ 60 = 8(小时)。
【详解】240÷3÷40
=80÷40
=2(棵)
480÷(30×2)
=480÷60
=8(小时)
答:需要8小时。
5.①见详解
②1.13倍
③见详解
④北京市2022年空气质量优良天数比2020年上涨了多少天?(问题不唯一)10天
【分析】①用271+19,求出优良的天数,将“优良”天数的折线补到290处,即可完成统计图。
②用2023年北京市空气中可吸入颗粒物(PM10)年均浓度÷2024年北京市空气中可吸入颗粒物(PM10)年均浓度,即可解答。
③观察统计图,说出2014~2024年北京市空气优良天数的变化,以及重污染天数的变化。(说法合理即可)
④北京市2022年空气质量优良天数比2020年上涨了多少天?用2022年空气质量优良天数-2020年空气质量优良天数,即可解答(答案不唯一)。
【详解】①271+19=290(天)
如图:
②61÷54≈1.13
答:2023年北京市空气中可吸入颗粒物(PM10)年均浓度是2024年的1.13倍。
③根据统计图可知,2014~2024年,北京市空气优良天数整体呈“逐渐增多”的趋势(从172天增加到290天),中间略有小幅波动;
而重污染天数整体呈“逐渐减少”的趋势(从47天下降到2天),同样有少量上下起伏。
④北京市2022年空气质量优良天数比2020年上涨了多少天?(问题不唯一)
286-276=10(天)
答:北京市2022年空气质量优良天数比2020年上涨了10天。
6.
(1)1;相等
(1)相等
(2)加法交换律和加法结合律
2500
【分析】计算推导:(1)在算式1+2+3+…+98+99+100中,我们通过依次比较相邻两个数的差值来确定规律。用后一个数减去前一个数,如2-1=1 ,3-2=1 ,以此类推,可以发现从第1个数开始,之后每个数都比前一个数多1 ,所以相邻两数的差都相等,差值为1 。
得出结论:(1)通过前面对于1+2+3+…+98+99+100这种有规律的自然数相加算式的分析,我们发现其求和方法是(首数+尾数)×总个数÷2 。这里的规律就是相邻两数的差都相等时,都可以使用这个求和公式。
(2)在高斯的做法里,把1和100组合、2和99组合等。首先,将2和99等数的位置进行交换,这符合加法交换律a+b=b+a ;然后把交换后的数两两结合起来先进行计算,像(1+100) 、(2+99)等,这符合加法结合律(a+b)+c=a+(b+c) 。所以利用的运算律是加法交换律和加法结合律 。
结论应用:对于1+3+5+…+95+97+99,这是一个首项为1 ,末项为99 ,相邻两数差值为2的数列。根据前面得出的结论,当相邻两数差相等时,和=(首数+尾数)×总个数÷2 。这里首数是1 ,尾数是99 ,总个数是50 ,据此代入公式计算。
【详解】计算推导
(1)观察规律,算式1+2+3+…+98+99+100,从第1个数开始,之后每个数都比前一个数多1,相邻两数的差都相等。
得出结论
(1)一组自然数相加,若相邻两数的差都相等,则和=(首数+尾数)×总个数÷2。
(2)高斯的做法利用的运算律是加法交换律和加法结合律。
1+3+5+…+95+97+99
=(1+99)×50÷2
=100×50÷2
=5000÷2
=2500
7.(1)471平方厘米;
(2)110厘米;
(3)立方厘米
【分析】从图中可知,球的直径是(20-10)厘米,圆柱的底面直径和高等于球的直径。
(1)把足球纪念品放入一个圆柱形的包装盒,根据圆柱的表面积S表=S侧+2S底,其中S侧=πdh,S底=πr2,代入数据计算求出包装盒的表面积。
(2)从图中可知,捆扎这个包装盒用绸带的长度=4条圆柱的底面直径+4条圆柱的高+打结用的长度,代入数据计算求解。
(3)根据圆柱的体积(容积)公式V=πr2h,求出圆柱形容器的容积;根据圆柱容球定理可知,此时球的体积正好是圆柱体积的,把圆柱的容积看作单位“1”,单位“1”已知,用圆柱的容积乘,求出这个足球纪念品的体积。
【详解】球的直径、圆柱的底面直径、圆柱的高:20-10=10(厘米)
(1)3.14×10×10+3.14×(10÷2)2×2
=3.14×10×10+3.14×52×2
=3.14×10×10+3.14×25×2
=314+157
=471(平方厘米)
答:这个包装盒的表面积是471平方厘米。
(2)10×4+10×4+30
=40+40+30
=110(厘米)
答:捆扎这个包装盒至少要用绸带110厘米。
(3)3.14×(10÷2)2×10
=3.14×52×10
=3.14×25×10
=785(立方厘米)
785×=(立方厘米)
答:计算这个足球纪念品的体积是立方厘米。
8.见详解
【分析】本学期学习的比的基本性质,运用了“变中有不变”思想,即比的前项和后项,同时乘或除以相同的数(0除外),比值不变,进行说明即可。
【详解】将比的前后项看成份数,根据比的基本性质,2∶3=(2×3)∶(3×3)=6∶9,份数变多了,2+3=5、6+9=15,总份数由原来的5份变成15份,比值没有变,2∶3=2÷3=,还是。
9.(1)C
(2)7500公顷
【分析】(1)周长相等的正方形、长方形、以及圆,圆的面积是最大的。
(2)那张键牛皮能变成30000米长的牛皮条,也就是这个圆的周长是30000米,根据圆的周长=得出圆的半径,再根据圆的面积=代入数据得出面积。注意最后需要换算单位,1公顷=10000平方米,再根据低级单位转化为高级单位除以两个单位之间的进率,得出圈得土地的公顷数。
【详解】(1)周长相等的图形中,圆的面积最大。则如果我是狄多公主,我准备圈圆形状的土地。
故答案为:C
(2)30000÷3÷2
=10000÷2
=5000(米)
3×50002
=3×25000000
=75000000(平方米)
75000000平方米=7500公顷
答:可以圈得7500公项土地。
10.方法见详解;100%;75%;58.3%;50%;66克
【分析】根据故事,阿基米德在洗澡时,看到身体在装满水的浴缸里沉下去的时候,有一部分水从浴缸中溢出,想到通过排水法测量王冠的体积,与纯金的体积比较,从而判断是否掺了其他金属。
已知24K黄金就是24份等重的黄金熔炼在一起;22K黄金就是22份等重的黄金和2份其他金属熔炼在一起……,那么用等重的黄金份数除以24,即可求出黄金质量占黄金饰品总质量的百分比,据此填表。
已知奶奶的金手镯是22K金,质量有72克重,22K的意思是黄金占22份,其它金属占2份,一共是24份;用奶奶金手镯的总质量除以总份数,求出一份数,再用一份数乘黄金占的份数,即是金手镯中含有的黄金质量。
【详解】阿基米德的方法:通过排水法,比较王冠与同质量的纯金排开水的体积,若王冠掺假,其体积会大于同质量的纯金,导致排开水的体积更多,从而发现异常。
24÷24×100%
=1×100%
=100%
18÷24×100%
=0.75×100%
=75%
14÷24×100%
≈0.583×100%
=58.3%
12÷24×100%
=0.50%
=50%
如下表:
黄金纯度分类 24K金 18K金 14K金 12K金
黄金质量占黄金饰品总质量的百分比 100% 75% 58.3% 50%
72÷24×22
=3×22
=66(克)
答:金手镯中含有的黄金质量是66克。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
情境阅读题型解答题典型考点 押题练
2025年小学小升初会考复习备考
1.认真阅读下面材料,回答问题。
世界因良渚而震惊,震惊于良渚古城遗址的发现。良渚古城遗址的核心是城址,它的面积约8平方千米,由宫殿区(0.39平方千米)、内城(含宫殿区约2.8平方千米)、外城(约3.51平方千米)呈向心式三重布局组成,古河道贯穿其间。古城的外围水利系统分成谷口高坝、平原低坝和山前长堤的11条人工坝体及天然山体、溢洪道,初步估算,整个水利系统形成面积为13平方千米的水库,库容量超过46000000立方米,是中国迄今发现最早的大型水利工程遗址,也是目前已发现的世界上最早的堤坝系统之一。
(1)宫殿区0.39平方千米可以看成把1平方千米平均分成( )份,表示这样的( )份。
(2)外城3.51平方千米表示( )个0.01平方千米。
(3)0.39平方千米=( )公顷 46000000立方米=( )万立方米
(4)一个两位小数精确到十分位后是2.8,这个两位小数最大和最小分别是几?请在下面的数轴上分别用↑标出这两个小数的位置,并写出这两个小数。
(5)将上面材料中横线上的数改写成用“亿”作单位的数是( )立方米。(结果保留一位小数)
2.估计这篇报道的字数,用文字、图或算式来说明估计的过程与方法,并写出估计结果。
春节被赋予的独特意义又多了一层
春节,这张在全球早已家喻户晓的中国文化名片,本周又添了一个新“头衔”,随着中国申报的“春节——中国人庆祝传统新年的社会实践”12月4日通过评审,列入联合国教科文组织人类非物质文化遗产代表作名录,中国已有44个项目列入联合国“非遗”名录、名册,总数居世界第一。春节申遗成功,不仅是世界拥抱中华文明的又一重要里程碑,也为不同文明间的交流互鉴提供了一个新起点。
春节登上“非遗”名录,可以用“实至名归”来形容,春节是一整套中国民俗文化的集合体,不仅带着满满的国粹范儿,也寄托着中华民族独特的精神情感密码。无论是“爆竹声中一岁除”,还是“总把新桃换旧符”,都充满了辞旧迎新的仪式感。春节对于中国社会、对于全世界非遗保护事业的重要意义之一就在于,它是一个传统文化与社会发展相辅相成的很好案例。正如这次申遗文本中所强调的,“‘过年’为中国人提供了一种认同感和延续性”。围绕着春节,在过去几十年从农业中国向工业中国转变的过程中,中国出现了人类历史上最大规模的周期性迁徙。春节所代表的传统文化,成为中国式现代化的一种内在动力和具体形式。(摘自《环球时报》)
3.某音乐厅的舞台在中间,听众的座位分六个区域排列。如图所示,从里向外分别是第一排到第六排。每个区域的第一排均有10个座位,从第二排起每排比前一排多2个座位。
(1)这间音乐厅的第3排每边有多少个座位?
(2)学校合唱团买下了六个区域第4排的所有座位票,合唱团买了几张票?
4.《礼记》有言:“孟春之月,盛德在木”。清明节与春节、端午节、中秋节并称为中国四大传统节日。清明节,又称踏青节、行清节、三月节、祭祖节等,节期在仲春与暮春之交。清明节源自早期人类的祖先信仰,是中华民族最隆重盛大的祭祖大节。清明节兼具自然与人文两大内涵,既是自然节气点,也是传统节日。扫墓祭祖与踏青郊游是清明节的两大礼俗主题,这两大传统礼俗在中国自古传承,至今不辍。涧小三(8)班的40名同学在清明节举行植树活动,3小时植树240棵,照这样计算,30名同学植480棵树,需要多少小时?
5.阅读材料,解答问题。
2023年,北京市空气中细颗粒物(PM2.5)年均浓度为32微克/立方米,二氧化硫(SO2)、二氧化氮(NO2)和可吸入颗粒物(PM10)年均浓度分别为3微克/立方米、26微克/立方米和61微克/立方米。这一年,北京市空气优良天数为271天,重污染天数为8天。
2024年,北京市空气中细颗粒物(PM2.5)年均浓度为30.5微克/立方米,连续4年稳定达标;二氧化硫(SO2)、二氧化氮(NO2)和可吸入颗粒物(PM10)年均浓度分别为3微克/立方米、24微克/立方米和54微克/立方米。这一年,北京市空气优良天数比上一年增加19天,重污染天数比上一年减少6天。这是有监测记录以来,优良天数最多的一年。
经过多年的努力,北京市大气污染治理成效显著,空气中主要污染物浓度呈现长期整体下降趋势,“北京蓝”逐步成为常态。
①请把统计图补充完整。
②2023年北京市空气中可吸入颗粒物(PM10)年均浓度是2024年的多少倍?(结果保留两位小数)
③2014~2024年北京市空气优良天数是怎样变化的?重污染天数呢?
④根据阅读材料,请你提出一个数学问题。
6.阅读故事。
高斯是一位伟大的数学家,有“数学王子的美誉”。
小时候,有一次老师让全班同学求算式1+2+3+…+98+99+100的结果。同学们开始认真地计算起来,只有高斯没有动笔,他思考了一会儿后写出了答案:5050,你知道高斯是怎么计算的吗?
高斯告诉大家,他先算1+100=101,2+99=101…这样一共有50个101,因此结果是5050。
计算推导
(1)观察规律,算式1+2+3+…+98+99+100,从第1个数开始,之后每个数都比前一个数多( ),相邻两数的差都( )。高斯求和公式就是为这类题目打造的专用工具。
(2)结合图形推导:将1+2+3+…+98+99+100,看作由若干个小圆堆成如图①的三角形图案,最上面一层有一个圆,以下每层均比上一层多一个圆,一共有100层。再将图①倒置后与原图拼成图②的形状。
计算出小圆的个数是1+2+3+…+98+99+100=(1+100)×100÷2=5050(个)。
得出结论
(1)一组自然数相加,若相邻两数的差都( ),则和=(首数+尾数)×总个数÷2。
(2)高斯的做法利用的运算律是( )。
结论应用:计算1+3+5+…+95+97+99。
7.(如下图)某商家推出一款足球纪念品,并给足球纪念品设计了圆柱形的包装盒,用绸带捆扎进行装饰。
(1)这个包装盒的表面积是多少?
(2)如果绸带打结处正好是底面圆心,打结用去的绸带长30厘米。捆扎这个包装盒至少要用绸带多少厘米?
(3)阅读下面的文本,计算这个足球纪念品的体积?
古希腊著名的数学家阿基米德是历史上杰出的数学家之一,在他众多的科学发现中,他自己最为满意的是“圆柱容球定理”。把一个球正好放在一个圆柱形容器中,球的直径与圆柱的高和底面直径相等,此时球的体积正好是圆柱体积的。
8.变化与不变。
大千世界,到处都在发生着或明显或隐藏的运动与变化。迅速的变化令人目眩神迷,缓慢的变化使人不知不觉。但是,在变化的过程中,常常有相对不变的东西。
数学家的眼光,常常盯住变化中不变的东西。正是这些不变的东西,把变化中的不同镜头联系起来,帮助我们认识变化过程的本质,帮助我们解决各种问题。
我们知道,哥哥长1岁,弟弟也长1岁。两人的年龄都变了,但年龄的差没有变。解有关年龄问题的时候,抓住两个人的年龄差不变这一点,往往可以使问题迎刃而解。
想要求下面图形的周长,最简单的方法就是将线段平移(图),平移后形状变了、面积变大了,但图形的周长没变,抓住这一点,问题就解决了。
“变中有不变”的思想在数学学习中随处可见。请你举一个本学期运用“变中有不变”思想解决问题的例子,并具体说明什么变了、什么没变。
9.数学阅读。
古代有一位公主叫狄多,她的王国发生叛乱后,就逃到了非洲。一天,她向当地的酋长雅布乞求一些土地,雅布酋长不想多给土地,就给了狄多一张犍牛皮,让公主用这张键牛皮圈土地,圈多少就给多少。聪明的公主用这张键牛皮圈得了很多土地,在这片土地上建立了拜萨(意为牛皮)城。
(1)用这张牛皮去覆盖土地,那太少了。把牛皮变成尽可能长,才可以圈出更多的土地。如果你是狄多公主,你准备圈( )形状的土地。
A.正方形 B.长方形 C.圆
(2)如果狄多公主得到的那张键牛皮能变成30000米长的牛皮条,可以圈得多少公项土地?(如果你圈的土地是圆形,取值为)
10.阅读材料。
阿基米德是古希腊伟大的数学家、力学家,他曾说:“给我一个支点,我能撬动地球。”传说,古希腊一位国王让金匠给他制作了一顶纯金王冠。国王怀疑王冠中掺了白银,于是让阿基米德检验一下。阿基米德想了很长时间,也没找到答案。有一天洗澡时,他注意到他的身体在装满水的浴缸里沉下去的时候,有一部分水从浴缸边溢了出来,他突然受到启发,冲进王宫对王说:“我找到方法了!”
阿基米德找到了什么方法?他是怎样试验的?
小辉读了阿基米德的故事后,也想尝试检验奶奶的金手镯是否是纯金的。他查阅资料了解到,黄金饰品按纯度有如下分类:24K、22K、18K、14K、12K、10K等。K指黄金的纯度,即用24份等重的金属熔炼在一起,纯金所占的份数。比如,24K黄金就是24份等重的黄金熔炼在一起;22K黄金就是22份等重的黄金和2份其他金属熔炼在一起……依次类推。请填写下表。(除不尽的,百分号前面保留保留一位小数)
黄金纯度分类 24K金 18K金 14K金 12K金
黄金质量占黄金饰品总质量的百分比
奶奶的金手镯是22K金,质量有72克重,请计算金手镯中含有的黄金质量。
参考答案
1.(1)100;39;
(2)351;
(3)39;4600;
(4)2.84;2.75;在数轴上标数见详解;
(5)0.5;
【分析】(1)0.39是两位小数,写成分数是,是平均分成100份表示这样的39份,据此解答即可;
(2)3.51的计数单位是0.01,去掉3.51即可得到3.51里有几个0.01;
(3)根据1平方千米=100公顷,把0.39平方千米画成公顷为单位即可;
将整万的数改写成用“万”作单位的数,只要省略万位后面的0,并加一个“万”即可;
(4)一个两位小数精确到十分位后是2.8,可以从四舍中找到最大的,从五入中找到最小的;据此解答。
(5)改写成用亿作单位的数,就是在亿位的右下角点上小数点,然后把小数末尾的0去掉,再在数的后面写上亿字;保留一位小数是采用四舍五入的方法,找到小数点后的第二位,看第二位上的数大于等于5向前一位进1,小于5直接舍去。
【详解】(1)求0.39平方千米对应的份数:0.39是两位小数,两位小数表示百分之几,所以0.39平方千米可以看成把1平方千米平均分成100份,0.39里面有39个0.01,就表示这样的39份。
(2)外城3.51平方千米表示351个0.01平方千米。
(3)0.39平方千米=39公顷 46000000立方米=4600万立方米
(4)确定两位小数的最大和最小值并标注:一个两位小数精确到十分位后是2.8,根据“四舍五入”法,如果是“四舍”得到的2.8,那么这个两位小数的个位和十分位是2.8,百分位最大是4,所以这个两位小数最大是2.84;如果是“五入”得到的2.8,那么这个两位小数的个位是2,十分位原来是7,百分位最小是5,所以这个两位小数最小是2.75。在直线上找到对应的位置标注,如答案图所示。
(5)46000000=0.46 亿≈0.5亿
即材料中横线上的数改写成用“亿”作单位的数是0.5立方米。。
2.480个
【分析】根据题意,先数出一共有多少行,再估算每行有多少字,最后相乘即可。一共有8行,每行大约有60个字,即8×60。
【详解】8×60=480(个)
答:这篇报道大概有480个字。
3.(1)14个
(2)96张
【分析】(1)根据题意,第一排均有10个座位,从第二排起每排比前一排多2个座位,用10+2即可求出第二排有多少个座位,用第二排座位的个数再加2即可求出第3排每边有多少个座位。
(2)根据题意,买下了六个区域第4排的所有座位票,先用第三排座位的个数加2求出第四排有多少个座位,再乘6即可求出合唱团买了几张票。
【详解】(1)10+2+2=14(个)
答:这间音乐厅的第3排每边有14个座位。
(2)14+2=16(个)
16×6=96(张)
答:合唱团买了96张票。
4.8小时
【分析】40名同学每小时植树数量为:240 ÷ 3 = 80(棵),每人每小时植树数量为:80 ÷ 40 = 2(棵);每个同学每小时可以植树2棵。计算30名同学每小时的植树数量:30 × 2 = 60 (棵),计算种植480棵所需的时间:时间 = 总植树量 ÷ 每小时植树量 = 480÷ 60 = 8(小时)。
【详解】240÷3÷40
=80÷40
=2(棵)
480÷(30×2)
=480÷60
=8(小时)
答:需要8小时。
5.①见详解
②1.13倍
③见详解
④北京市2022年空气质量优良天数比2020年上涨了多少天?(问题不唯一)10天
【分析】①用271+19,求出优良的天数,将“优良”天数的折线补到290处,即可完成统计图。
②用2023年北京市空气中可吸入颗粒物(PM10)年均浓度÷2024年北京市空气中可吸入颗粒物(PM10)年均浓度,即可解答。
③观察统计图,说出2014~2024年北京市空气优良天数的变化,以及重污染天数的变化。(说法合理即可)
④北京市2022年空气质量优良天数比2020年上涨了多少天?用2022年空气质量优良天数-2020年空气质量优良天数,即可解答(答案不唯一)。
【详解】①271+19=290(天)
如图:
②61÷54≈1.13
答:2023年北京市空气中可吸入颗粒物(PM10)年均浓度是2024年的1.13倍。
③根据统计图可知,2014~2024年,北京市空气优良天数整体呈“逐渐增多”的趋势(从172天增加到290天),中间略有小幅波动;
而重污染天数整体呈“逐渐减少”的趋势(从47天下降到2天),同样有少量上下起伏。
④北京市2022年空气质量优良天数比2020年上涨了多少天?(问题不唯一)
286-276=10(天)
答:北京市2022年空气质量优良天数比2020年上涨了10天。
6.
(1)1;相等
(1)相等
(2)加法交换律和加法结合律
2500
【分析】计算推导:(1)在算式1+2+3+…+98+99+100中,我们通过依次比较相邻两个数的差值来确定规律。用后一个数减去前一个数,如2-1=1 ,3-2=1 ,以此类推,可以发现从第1个数开始,之后每个数都比前一个数多1 ,所以相邻两数的差都相等,差值为1 。
得出结论:(1)通过前面对于1+2+3+…+98+99+100这种有规律的自然数相加算式的分析,我们发现其求和方法是(首数+尾数)×总个数÷2 。这里的规律就是相邻两数的差都相等时,都可以使用这个求和公式。
(2)在高斯的做法里,把1和100组合、2和99组合等。首先,将2和99等数的位置进行交换,这符合加法交换律a+b=b+a ;然后把交换后的数两两结合起来先进行计算,像(1+100) 、(2+99)等,这符合加法结合律(a+b)+c=a+(b+c) 。所以利用的运算律是加法交换律和加法结合律 。
结论应用:对于1+3+5+…+95+97+99,这是一个首项为1 ,末项为99 ,相邻两数差值为2的数列。根据前面得出的结论,当相邻两数差相等时,和=(首数+尾数)×总个数÷2 。这里首数是1 ,尾数是99 ,总个数是50 ,据此代入公式计算。
【详解】计算推导
(1)观察规律,算式1+2+3+…+98+99+100,从第1个数开始,之后每个数都比前一个数多1,相邻两数的差都相等。
得出结论
(1)一组自然数相加,若相邻两数的差都相等,则和=(首数+尾数)×总个数÷2。
(2)高斯的做法利用的运算律是加法交换律和加法结合律。
1+3+5+…+95+97+99
=(1+99)×50÷2
=100×50÷2
=5000÷2
=2500
7.(1)471平方厘米;
(2)110厘米;
(3)立方厘米
【分析】从图中可知,球的直径是(20-10)厘米,圆柱的底面直径和高等于球的直径。
(1)把足球纪念品放入一个圆柱形的包装盒,根据圆柱的表面积S表=S侧+2S底,其中S侧=πdh,S底=πr2,代入数据计算求出包装盒的表面积。
(2)从图中可知,捆扎这个包装盒用绸带的长度=4条圆柱的底面直径+4条圆柱的高+打结用的长度,代入数据计算求解。
(3)根据圆柱的体积(容积)公式V=πr2h,求出圆柱形容器的容积;根据圆柱容球定理可知,此时球的体积正好是圆柱体积的,把圆柱的容积看作单位“1”,单位“1”已知,用圆柱的容积乘,求出这个足球纪念品的体积。
【详解】球的直径、圆柱的底面直径、圆柱的高:20-10=10(厘米)
(1)3.14×10×10+3.14×(10÷2)2×2
=3.14×10×10+3.14×52×2
=3.14×10×10+3.14×25×2
=314+157
=471(平方厘米)
答:这个包装盒的表面积是471平方厘米。
(2)10×4+10×4+30
=40+40+30
=110(厘米)
答:捆扎这个包装盒至少要用绸带110厘米。
(3)3.14×(10÷2)2×10
=3.14×52×10
=3.14×25×10
=785(立方厘米)
785×=(立方厘米)
答:计算这个足球纪念品的体积是立方厘米。
8.见详解
【分析】本学期学习的比的基本性质,运用了“变中有不变”思想,即比的前项和后项,同时乘或除以相同的数(0除外),比值不变,进行说明即可。
【详解】将比的前后项看成份数,根据比的基本性质,2∶3=(2×3)∶(3×3)=6∶9,份数变多了,2+3=5、6+9=15,总份数由原来的5份变成15份,比值没有变,2∶3=2÷3=,还是。
9.(1)C
(2)7500公顷
【分析】(1)周长相等的正方形、长方形、以及圆,圆的面积是最大的。
(2)那张键牛皮能变成30000米长的牛皮条,也就是这个圆的周长是30000米,根据圆的周长=得出圆的半径,再根据圆的面积=代入数据得出面积。注意最后需要换算单位,1公顷=10000平方米,再根据低级单位转化为高级单位除以两个单位之间的进率,得出圈得土地的公顷数。
【详解】(1)周长相等的图形中,圆的面积最大。则如果我是狄多公主,我准备圈圆形状的土地。
故答案为:C
(2)30000÷3÷2
=10000÷2
=5000(米)
3×50002
=3×25000000
=75000000(平方米)
75000000平方米=7500公顷
答:可以圈得7500公项土地。
10.方法见详解;100%;75%;58.3%;50%;66克
【分析】根据故事,阿基米德在洗澡时,看到身体在装满水的浴缸里沉下去的时候,有一部分水从浴缸中溢出,想到通过排水法测量王冠的体积,与纯金的体积比较,从而判断是否掺了其他金属。
已知24K黄金就是24份等重的黄金熔炼在一起;22K黄金就是22份等重的黄金和2份其他金属熔炼在一起……,那么用等重的黄金份数除以24,即可求出黄金质量占黄金饰品总质量的百分比,据此填表。
已知奶奶的金手镯是22K金,质量有72克重,22K的意思是黄金占22份,其它金属占2份,一共是24份;用奶奶金手镯的总质量除以总份数,求出一份数,再用一份数乘黄金占的份数,即是金手镯中含有的黄金质量。
【详解】阿基米德的方法:通过排水法,比较王冠与同质量的纯金排开水的体积,若王冠掺假,其体积会大于同质量的纯金,导致排开水的体积更多,从而发现异常。
24÷24×100%
=1×100%
=100%
18÷24×100%
=0.75×100%
=75%
14÷24×100%
≈0.583×100%
=58.3%
12÷24×100%
=0.50%
=50%
如下表:
黄金纯度分类 24K金 18K金 14K金 12K金
黄金质量占黄金饰品总质量的百分比 100% 75% 58.3% 50%
72÷24×22
=3×22
=66(克)
答:金手镯中含有的黄金质量是66克。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
