华师大版数学八年级下册第十八章第一节18.1平行四边形的性质同步练习
文档属性
| 名称 | 华师大版数学八年级下册第十八章第一节18.1平行四边形的性质同步练习 |
|
|
| 格式 | doc | ||
| 文件大小 | 242.5KB | ||
| 资源类型 | 素材 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-06-23 00:00:00 | ||
图片预览



文档简介
登陆21世纪教育 助您教考全无忧
华师大版数学八年级下册第十八章第一节18.1平行四边形的性质
同步练习
一、选择题
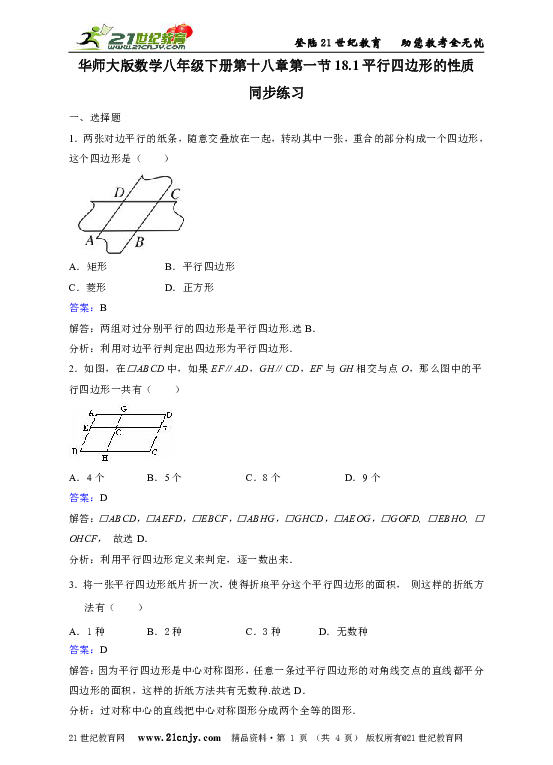
1.两张对边平行的纸条,随意交叠放在一起,转动其中一张,重合的部分构成一个四边形,这个四边形是( )
A.矩形 B.平行四边形
C.菱形 D.正方形
答案:B
解答:两组对过分别平行的四边形是平行四边形.选B.
分析:利用对边平行判定出四边形为平行四边形.
2.如图,在□ABCD中,如果EF∥AD,GH∥CD,EF与GH相交与点O,那么图中的平行四边形一共有( )
A.4个 B.5个 C.8个 D.9个
答案:D
解答:□ABCD,□AEFD,□EBCF,□ABHG,□GHCD,□AEOG,□GOFD, □EBHO, □OHCF, 故选D.
分析:利用平行四边形定义来判定,逐一数出来.
3.将一张平行四边形纸片折一次,使得折痕平分这个平行四边形的面积,则这样的折纸方法有( )
A.1种 B.2种 C.3种 D.无数种
答案:D
解答:因为平行四边形是中心对称图形,任意一条过平行四边形的对角线交点的直线都平分四边形的面积,这样的折纸方法共有无数种.故选D.
分析:过对称中心的直线把中心对称图形分成两个全等的图形.
4.如图,将□ABCD的一边BC延长至点E,若∠A=1100,则∠1=( )
A.1100 B.350 C.700 D.550
答案:C
解答:∵□ABCD中,∠A=1100,∴∠BCD=1100,∴∠1=700.故选C.
分析:利用平行四边形对角相等得出∠BCD的值,再根据邻补角定义得出∠1的值.
5.如图,在□ABCD中,延长AB到点E,使BE=AB,连接DE交BC于点F,则下列结论不一定成立的是( )
A.∠E=∠CDF B.BE=CD
C.∠ADE=∠BFE D.BE=2CF
答案:D
解答:
∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,AB=CD,AD=BC
∴∠E=∠CDF,∠ADE=∠BFE
又∵BE=AB,
∴BE=CD,AD=2BF .
故选D.
分析:利用平行四边形的定义得两组对边互相平行,再根据两直线平行内错角相等得选项A是正确的,根据两直线平行同位角相等得出选项C,利用等量代换得出选项B.
6.如图所示,在□ABCD中,对角线AC,BD交于点O,图中全等三角形有( )
A. 5对 B.4对 C.3对 D.2对
答案:B
解答:△OAB≌△OCD,△OAD≌△OCB ,△ABC≌△CDA ,△ABD≌△CDB,故选B.
分析:利用平行四边形的性质可得.
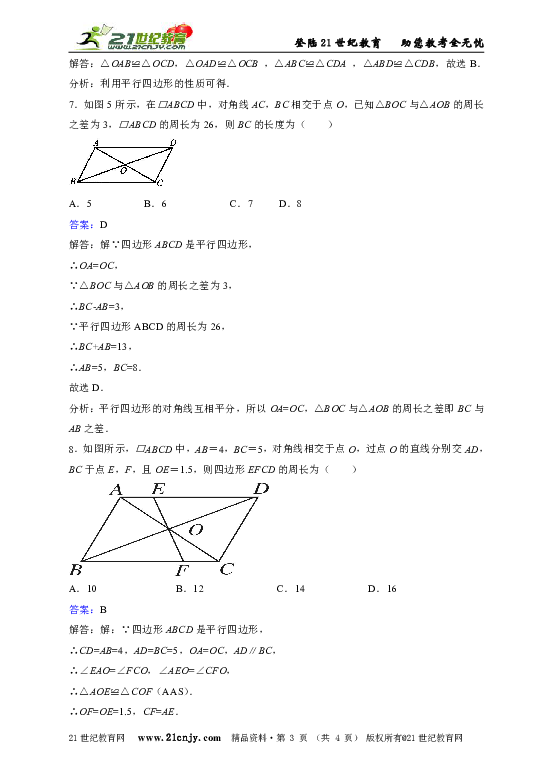
7.如图5所示,在□ABCD中,对角线AC,BC相交于点O,已知△BOC与△AOB的周长之差为3,□ABCD的周长为26,则BC的长度为( )
A.5 B.6 C.7 D.8
答案:D
解答:解∵四边形ABCD是平行四边形,
∴OA=OC,
∵△BOC与△AOB的周长之差为3,
∴BC-AB=3,
∵平行四边形ABCD的周长为26,
∴BC+AB=13,
∴AB=5,BC=8.
故选D.
分析:平行四边形的对角线互相平分,所以OA=OC,△BOC与△AOB的周长之差即BC与AB之差.
8.如图所示,□ABCD中,AB=4,BC=5,对角线相交于点O,过点O的直线分别交AD,BC于点E,F,且OE=1.5,则四边形EFCD的周长为( )
A.10 B.12 C.14 D.16
答案:B
解答:解:∵四边形ABCD是平行四边形,
∴CD=AB=4,AD=BC=5,OA=OC,AD∥BC,
∴∠EAO=∠FCO,∠AEO=∠CFO,
∴△AOE≌△COF(AAS).
∴OF=OE=1.5,CF=AE.
故四边形EFCD的周长为CD+EF+AD=12.
选择B.
分析:先证△AOE≌△COF得AE=CF,从而把四边形的周长转化成EF+AD+CD的值.
9.以A、B、C三点为平行四边形的三个顶点,作形状不同的平行四边形,一共可以作( )
A.0个或3个 B.2个 C.3个 D.4个
答案:A
解答:若是三点在一条直线上,则作0个平行四边形,若是三点不在同一直线上,可作三个平行四边形,故选A.
分析:分情况讨论三点的位置情况.
10.如图,在□ ABCD中,∠B=110°,延长AD至F,延长CD至E,连接EF,∠E+∠F等于( )
A.1100 B.300 C.500 D.700
答案:D
解答:∵□ ABCD中,∠B=110°,
∴∠ADC=1100,
∴∠CDF=700
∴∠E+∠F =∠CDF=700,
故选D.
分析:利用平行四边形的对角相等,邻补角定义,三角形外角性质可求得.
11.如图,在□ABCD中,已知AD=8 cm, AB=6 cm, DE平分∠ADC交BC边于点E,则BE等于( )
A.2cm B.4cm C.6cm D.8cm
答案:A
解答:∵ 四边形ABCD是平行四边形,
∴AD∥BC,
∴∠CED=∠ADE,
∵DE平分∠ADC交BC边于点E,AD=8㎝, AB=6㎝,
∴∠CED=∠CDE,
∴CE=CD=AB=6cm,
∴BE=2㎝,
故选A.
分析:先根据两直线平行,内错角相等和角平分线的定义得到∠CED=∠CDE,再利用等角对等边得到CE=CD,从而求得BE的值.
12.如图,在□ ABCD中,AB=4cm,AD=7cm,∠ABC的平分线交AD于点E,交CD的延长线于点F,则DF=( )
A.3cm B.2cm C.4cm D.3.5cm
答案:A
解答:∵□ ABCD中,AB=4cm,AD=7cm,BF是∠ABC的平分线,
∴∠CBF=∠ABF=∠CFB,
∵AB=4cm,AD=7cm,
∴CF=CB=7cm,CD+AB=4cm,
∴DF=3cm.
故选A.
分析:先用平行四边形的定义得两组对边分别平行,再根据两直线平行,内错角相等和角平分线的定义得到∠CBF=∠CFB,然后根据等角对等边得到CF的长,从而求得DF的长.
13.如图,□ABCD中,对角线AC和BD相交于点O,若AC=8,AB=6,BD=m,那么m的取范围是( )
A.2<m<10 B.2<m<14 C.6<m<8 D.4<m<20
答案:D
解答∵四边形ABCD是平行四边形,AC=8,
∴OA=OC=4
∵AB=6,
∴6-4即:2∴BD的取值范围是4<BD<20,
即:4<m<20.
故选D.
分析:先用平行四边形的性质求出OA的长,然后在三角形OAB中用三角形三边关系确定OB的长,从而确定了BD的长.
14.如图,□ABCD的对角线AC与BD相交于点O,AB⊥AC.若AB=4,AC=6,则BD的长是( )
A.8 B.9 C.10 D.11
答案:C
解答:解:∵□ABCD的对角线AC与BD相交于点O,
∴BO=DO,AO=CO,
∵AB⊥AC,AB=4,AC=6,
∴BO==5,
∴BD=2BO=10,
故选C.
分析:先在直角三角形OAB中计算出OB的长.
15.如图所示,在□ABCD中,对角线AC与BD相交于点O,M,N在对角线AC上,且AM=CN,则BM与DN的关系是( )
A.BM∥DN B.BM∥DN,BM=DN
C.BM=DN D.没有关系
答案:B
解答:解:∵平行四边形ABCD,
∴AD=BC,∠DAC=∠BCA,
∵CM=AC-AM,AN=AC-CN,AM=CN,
∴CM=AN,
∴△AND≌△CMB (SAS),
∴∠AND=∠CMB,BM=DN,
∴BM∥DN.
故选B.
分析:利用平行四边形的性质得出三角形全等的条件.
二、填空题
16.在□ABCD中,AB=6 cm,BC=8 cm,则 ABCD的周长为__ ___cm.
答案:28
解答:∵ 四边形ABCD是平行四边形,
∴AB=CD=6cm,BC=AD=8 cm,
∴AB+BC+CD+AD=28cm.
故填28cm.
分析:利用平行四边形的对边相等求得四条边的长.
17.□ABCD一内角的平分线与边相交并把这条边分成5cm,7cm的两条线段,则□ABCD的周长是 cm.
答案:34cm或38cm
解答:平行四边形由内角的平分线切出的三角形是等腰三角形,所以平行四边形另一条边为7或5㎝,所以周长为(5+7)×2+5×2=34或﹙5+7﹚×2+7×2=38.
分析:平行四边形由内角的平分线切出的三角形是等腰三角形是关键,不注意平行四边形的另一条边有7cm和5cm两种情况.
18.已知点O为□ABCD两对角线的交点,且S△AOB=1,则S□ABCD = .
答案:4
解答:∵O为□ABCD对角线的交点,
∴S△OAB=S△OBC=S△OCD=S△ODA
∵△AOB的面积为1,
∴□ABCD的面积为1×4=4.
故填4.
分析:利用平行四边形的对角线互相平分和三角形的中线平分三角形的面积,可得平行四边形的面积就是一个三角形面积的4倍.
19.如图,□ABCD中,、分别为、边上的点,要使需添加一个条件 .
答案:AF=CE,BE=DF,BF∥CE,∠ABF=∠CDE,∠AFB=∠CED等(答案不唯一)
解答:所添条件AF=CE,∠ABF=∠CDE,∠AFB=∠CED能得△ABF≌△CDE,条件BE=DF,BF∥CE能得四边形BFDE是平行四边形.
分析:所添条件能得△ABF≌△CDE或四边形BFDE是平行四边形.
20.如图,在□ABCD中,BE⊥CD,BF⊥AD,垂足分别为E,F,CE=2,DF=1,∠EBF=600,则□ABCD的周长为 .
答案:20
解答:∵□ABCD中,∠EBF=600,
∴∠D=1200,
∴∠A=∠C=600,
∵CE=2,
∴BC=4,
∴AF=BC-DF=3,
∴AB=6,
∴□ABCD的周长为2(4+6)=20.
故填20.
分析:利用平行四边形的对边相等,对角相等,以及30度直角三角形的性质综合应用.
三、解答题
21.如图,已知□ABCD的对角线AC,BD交于点O,E,F分别是OA,OC的中点.
(1)求证:OE=OF;
答案:证明:∵ 四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵E,F分别是OA,OC的中点,
∴OE= OA,OF= OC,
∴OE=OF;
(2)求证:DE∥BF.
答案:证明:∵在△DEO与△BFO中,
OE=OF,
∠BOE=∠DOF, BO=DO,
∴△BEO≌△DFO(SAS),
∴∠DEO=∠BFO,
∴DE∥BF.
分析:(1)由平行四边形的性质得OA=OC,E,F分别是OA,OC的中点,可得OE=OF;
(2)证△DOE≌△BOF,得∠DEO=∠BFO,得DE∥BF.
22.如图,AD∥BC,AE∥CD,BD平分∠ABC,求证:AB=CE.
.
答案:证明:∵AD∥BC,
∴∠DBC=∠ADB.
又∵BD平分∠ABC,
∴∠ABD=∠DBC,
∴∠ABD=∠ADB,
∴AB=AD.
∵AD∥BC,AE∥CD,
∴四边形ADCE为平行四边形,
∴AD=CE,
∴AB=CE.
分析:先利用等角对等边证得AB=AD,再利用平行四边形的定义证得AD=CE.
23.如图所示,分别过△ABC的顶点A,B,C作对边BC,AC,AB的平行线,交点分别为E,F,D.
(1)请找出图中所有的平行四边形;
答案:解答:□ABCD,□EBCA,□ABFC
(2)求证:2BC=DE.
答案:解答:在□ABCD中,BC=AD,在□EBCA中,BC=AE,
所以,2BC=DE
分析:平行四边形的对边相等是证明线段相等的常用方法.
24.在一次数学探究活动中,小强用两条直线把□ABCD分割成四个部分,使含有一组对顶角的两个图形全等.
(1)根据小强的分割方法,你认为把平行四边形分割成满足以上全等关系的直线共有___________组;
答案:无数
(2)请在下图的三个平行四边形中画出满足小强分割的直线;
答案:解答:如图
(3)由上述实验操作过程,你发现所画的两条直线有什么规律?
答案:解答:两条直线都经过对角线的交点
分析:综合考查平行四边形性质的应用.
25.已知:如图(a),□ABCD的对角线AC、BD相交于点O,EF过点O与AB、CD分别相交于点E、F.求证:OE=OF,AE=CF,BE=DF.
若上图中的条件都不变,将EF转动到图b的位置,那么上述结论是否成立?若将EF向两方延长与平行四边形的两对边的延长线分别相交(图c和图d),结论是否成立,说明你的理由.
答案: 解答:(a)证明:在□ABCD中,AB∥CD,
∴ ∠1=∠2.∠3=∠4.
又 OA=OC(平行四边形的对角线互相平分),
∴ △AOE≌△COF(ASA).
∴ OE=OF,AE=CF(全等三角形对应边相等).
∵ □ABCD,∴ AB=CD(平行四边形对边相等).
∴ AB—AE=CD—CF. 即 BE=FD.
(b) (c) (d)过程参照(a)
分析:这是一道探究发现题型。(a)图的证明利用平行四边形的性质得三角形全等既可,(b)(c)(d)证明可参照(a)的证明,照猫画虎.
A
B
C
D
E
A
B
C
E
D
F
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com 精品资料·第 8 页 (共 11 页) 版权所有@21世纪教育网
华师大版数学八年级下册第十八章第一节18.1平行四边形的性质
同步练习
一、选择题
1.两张对边平行的纸条,随意交叠放在一起,转动其中一张,重合的部分构成一个四边形,这个四边形是( )
A.矩形 B.平行四边形
C.菱形 D.正方形
答案:B
解答:两组对过分别平行的四边形是平行四边形.选B.
分析:利用对边平行判定出四边形为平行四边形.
2.如图,在□ABCD中,如果EF∥AD,GH∥CD,EF与GH相交与点O,那么图中的平行四边形一共有( )
A.4个 B.5个 C.8个 D.9个
答案:D
解答:□ABCD,□AEFD,□EBCF,□ABHG,□GHCD,□AEOG,□GOFD, □EBHO, □OHCF, 故选D.
分析:利用平行四边形定义来判定,逐一数出来.
3.将一张平行四边形纸片折一次,使得折痕平分这个平行四边形的面积,则这样的折纸方法有( )
A.1种 B.2种 C.3种 D.无数种
答案:D
解答:因为平行四边形是中心对称图形,任意一条过平行四边形的对角线交点的直线都平分四边形的面积,这样的折纸方法共有无数种.故选D.
分析:过对称中心的直线把中心对称图形分成两个全等的图形.
4.如图,将□ABCD的一边BC延长至点E,若∠A=1100,则∠1=( )
A.1100 B.350 C.700 D.550
答案:C
解答:∵□ABCD中,∠A=1100,∴∠BCD=1100,∴∠1=700.故选C.
分析:利用平行四边形对角相等得出∠BCD的值,再根据邻补角定义得出∠1的值.
5.如图,在□ABCD中,延长AB到点E,使BE=AB,连接DE交BC于点F,则下列结论不一定成立的是( )
A.∠E=∠CDF B.BE=CD
C.∠ADE=∠BFE D.BE=2CF
答案:D
解答:
∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,AB=CD,AD=BC
∴∠E=∠CDF,∠ADE=∠BFE
又∵BE=AB,
∴BE=CD,AD=2BF .
故选D.
分析:利用平行四边形的定义得两组对边互相平行,再根据两直线平行内错角相等得选项A是正确的,根据两直线平行同位角相等得出选项C,利用等量代换得出选项B.
6.如图所示,在□ABCD中,对角线AC,BD交于点O,图中全等三角形有( )
A. 5对 B.4对 C.3对 D.2对
答案:B
解答:△OAB≌△OCD,△OAD≌△OCB ,△ABC≌△CDA ,△ABD≌△CDB,故选B.
分析:利用平行四边形的性质可得.
7.如图5所示,在□ABCD中,对角线AC,BC相交于点O,已知△BOC与△AOB的周长之差为3,□ABCD的周长为26,则BC的长度为( )
A.5 B.6 C.7 D.8
答案:D
解答:解∵四边形ABCD是平行四边形,
∴OA=OC,
∵△BOC与△AOB的周长之差为3,
∴BC-AB=3,
∵平行四边形ABCD的周长为26,
∴BC+AB=13,
∴AB=5,BC=8.
故选D.
分析:平行四边形的对角线互相平分,所以OA=OC,△BOC与△AOB的周长之差即BC与AB之差.
8.如图所示,□ABCD中,AB=4,BC=5,对角线相交于点O,过点O的直线分别交AD,BC于点E,F,且OE=1.5,则四边形EFCD的周长为( )
A.10 B.12 C.14 D.16
答案:B
解答:解:∵四边形ABCD是平行四边形,
∴CD=AB=4,AD=BC=5,OA=OC,AD∥BC,
∴∠EAO=∠FCO,∠AEO=∠CFO,
∴△AOE≌△COF(AAS).
∴OF=OE=1.5,CF=AE.
故四边形EFCD的周长为CD+EF+AD=12.
选择B.
分析:先证△AOE≌△COF得AE=CF,从而把四边形的周长转化成EF+AD+CD的值.
9.以A、B、C三点为平行四边形的三个顶点,作形状不同的平行四边形,一共可以作( )
A.0个或3个 B.2个 C.3个 D.4个
答案:A
解答:若是三点在一条直线上,则作0个平行四边形,若是三点不在同一直线上,可作三个平行四边形,故选A.
分析:分情况讨论三点的位置情况.
10.如图,在□ ABCD中,∠B=110°,延长AD至F,延长CD至E,连接EF,∠E+∠F等于( )
A.1100 B.300 C.500 D.700
答案:D
解答:∵□ ABCD中,∠B=110°,
∴∠ADC=1100,
∴∠CDF=700
∴∠E+∠F =∠CDF=700,
故选D.
分析:利用平行四边形的对角相等,邻补角定义,三角形外角性质可求得.
11.如图,在□ABCD中,已知AD=8 cm, AB=6 cm, DE平分∠ADC交BC边于点E,则BE等于( )
A.2cm B.4cm C.6cm D.8cm
答案:A
解答:∵ 四边形ABCD是平行四边形,
∴AD∥BC,
∴∠CED=∠ADE,
∵DE平分∠ADC交BC边于点E,AD=8㎝, AB=6㎝,
∴∠CED=∠CDE,
∴CE=CD=AB=6cm,
∴BE=2㎝,
故选A.
分析:先根据两直线平行,内错角相等和角平分线的定义得到∠CED=∠CDE,再利用等角对等边得到CE=CD,从而求得BE的值.
12.如图,在□ ABCD中,AB=4cm,AD=7cm,∠ABC的平分线交AD于点E,交CD的延长线于点F,则DF=( )
A.3cm B.2cm C.4cm D.3.5cm
答案:A
解答:∵□ ABCD中,AB=4cm,AD=7cm,BF是∠ABC的平分线,
∴∠CBF=∠ABF=∠CFB,
∵AB=4cm,AD=7cm,
∴CF=CB=7cm,CD+AB=4cm,
∴DF=3cm.
故选A.
分析:先用平行四边形的定义得两组对边分别平行,再根据两直线平行,内错角相等和角平分线的定义得到∠CBF=∠CFB,然后根据等角对等边得到CF的长,从而求得DF的长.
13.如图,□ABCD中,对角线AC和BD相交于点O,若AC=8,AB=6,BD=m,那么m的取范围是( )
A.2<m<10 B.2<m<14 C.6<m<8 D.4<m<20
答案:D
解答∵四边形ABCD是平行四边形,AC=8,
∴OA=OC=4
∵AB=6,
∴6-4
即:4<m<20.
故选D.
分析:先用平行四边形的性质求出OA的长,然后在三角形OAB中用三角形三边关系确定OB的长,从而确定了BD的长.
14.如图,□ABCD的对角线AC与BD相交于点O,AB⊥AC.若AB=4,AC=6,则BD的长是( )
A.8 B.9 C.10 D.11
答案:C
解答:解:∵□ABCD的对角线AC与BD相交于点O,
∴BO=DO,AO=CO,
∵AB⊥AC,AB=4,AC=6,
∴BO==5,
∴BD=2BO=10,
故选C.
分析:先在直角三角形OAB中计算出OB的长.
15.如图所示,在□ABCD中,对角线AC与BD相交于点O,M,N在对角线AC上,且AM=CN,则BM与DN的关系是( )
A.BM∥DN B.BM∥DN,BM=DN
C.BM=DN D.没有关系
答案:B
解答:解:∵平行四边形ABCD,
∴AD=BC,∠DAC=∠BCA,
∵CM=AC-AM,AN=AC-CN,AM=CN,
∴CM=AN,
∴△AND≌△CMB (SAS),
∴∠AND=∠CMB,BM=DN,
∴BM∥DN.
故选B.
分析:利用平行四边形的性质得出三角形全等的条件.
二、填空题
16.在□ABCD中,AB=6 cm,BC=8 cm,则 ABCD的周长为__ ___cm.
答案:28
解答:∵ 四边形ABCD是平行四边形,
∴AB=CD=6cm,BC=AD=8 cm,
∴AB+BC+CD+AD=28cm.
故填28cm.
分析:利用平行四边形的对边相等求得四条边的长.
17.□ABCD一内角的平分线与边相交并把这条边分成5cm,7cm的两条线段,则□ABCD的周长是 cm.
答案:34cm或38cm
解答:平行四边形由内角的平分线切出的三角形是等腰三角形,所以平行四边形另一条边为7或5㎝,所以周长为(5+7)×2+5×2=34或﹙5+7﹚×2+7×2=38.
分析:平行四边形由内角的平分线切出的三角形是等腰三角形是关键,不注意平行四边形的另一条边有7cm和5cm两种情况.
18.已知点O为□ABCD两对角线的交点,且S△AOB=1,则S□ABCD = .
答案:4
解答:∵O为□ABCD对角线的交点,
∴S△OAB=S△OBC=S△OCD=S△ODA
∵△AOB的面积为1,
∴□ABCD的面积为1×4=4.
故填4.
分析:利用平行四边形的对角线互相平分和三角形的中线平分三角形的面积,可得平行四边形的面积就是一个三角形面积的4倍.
19.如图,□ABCD中,、分别为、边上的点,要使需添加一个条件 .
答案:AF=CE,BE=DF,BF∥CE,∠ABF=∠CDE,∠AFB=∠CED等(答案不唯一)
解答:所添条件AF=CE,∠ABF=∠CDE,∠AFB=∠CED能得△ABF≌△CDE,条件BE=DF,BF∥CE能得四边形BFDE是平行四边形.
分析:所添条件能得△ABF≌△CDE或四边形BFDE是平行四边形.
20.如图,在□ABCD中,BE⊥CD,BF⊥AD,垂足分别为E,F,CE=2,DF=1,∠EBF=600,则□ABCD的周长为 .
答案:20
解答:∵□ABCD中,∠EBF=600,
∴∠D=1200,
∴∠A=∠C=600,
∵CE=2,
∴BC=4,
∴AF=BC-DF=3,
∴AB=6,
∴□ABCD的周长为2(4+6)=20.
故填20.
分析:利用平行四边形的对边相等,对角相等,以及30度直角三角形的性质综合应用.
三、解答题
21.如图,已知□ABCD的对角线AC,BD交于点O,E,F分别是OA,OC的中点.
(1)求证:OE=OF;
答案:证明:∵ 四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵E,F分别是OA,OC的中点,
∴OE= OA,OF= OC,
∴OE=OF;
(2)求证:DE∥BF.
答案:证明:∵在△DEO与△BFO中,
OE=OF,
∠BOE=∠DOF, BO=DO,
∴△BEO≌△DFO(SAS),
∴∠DEO=∠BFO,
∴DE∥BF.
分析:(1)由平行四边形的性质得OA=OC,E,F分别是OA,OC的中点,可得OE=OF;
(2)证△DOE≌△BOF,得∠DEO=∠BFO,得DE∥BF.
22.如图,AD∥BC,AE∥CD,BD平分∠ABC,求证:AB=CE.
.
答案:证明:∵AD∥BC,
∴∠DBC=∠ADB.
又∵BD平分∠ABC,
∴∠ABD=∠DBC,
∴∠ABD=∠ADB,
∴AB=AD.
∵AD∥BC,AE∥CD,
∴四边形ADCE为平行四边形,
∴AD=CE,
∴AB=CE.
分析:先利用等角对等边证得AB=AD,再利用平行四边形的定义证得AD=CE.
23.如图所示,分别过△ABC的顶点A,B,C作对边BC,AC,AB的平行线,交点分别为E,F,D.
(1)请找出图中所有的平行四边形;
答案:解答:□ABCD,□EBCA,□ABFC
(2)求证:2BC=DE.
答案:解答:在□ABCD中,BC=AD,在□EBCA中,BC=AE,
所以,2BC=DE
分析:平行四边形的对边相等是证明线段相等的常用方法.
24.在一次数学探究活动中,小强用两条直线把□ABCD分割成四个部分,使含有一组对顶角的两个图形全等.
(1)根据小强的分割方法,你认为把平行四边形分割成满足以上全等关系的直线共有___________组;
答案:无数
(2)请在下图的三个平行四边形中画出满足小强分割的直线;
答案:解答:如图
(3)由上述实验操作过程,你发现所画的两条直线有什么规律?
答案:解答:两条直线都经过对角线的交点
分析:综合考查平行四边形性质的应用.
25.已知:如图(a),□ABCD的对角线AC、BD相交于点O,EF过点O与AB、CD分别相交于点E、F.求证:OE=OF,AE=CF,BE=DF.
若上图中的条件都不变,将EF转动到图b的位置,那么上述结论是否成立?若将EF向两方延长与平行四边形的两对边的延长线分别相交(图c和图d),结论是否成立,说明你的理由.
答案: 解答:(a)证明:在□ABCD中,AB∥CD,
∴ ∠1=∠2.∠3=∠4.
又 OA=OC(平行四边形的对角线互相平分),
∴ △AOE≌△COF(ASA).
∴ OE=OF,AE=CF(全等三角形对应边相等).
∵ □ABCD,∴ AB=CD(平行四边形对边相等).
∴ AB—AE=CD—CF. 即 BE=FD.
(b) (c) (d)过程参照(a)
分析:这是一道探究发现题型。(a)图的证明利用平行四边形的性质得三角形全等既可,(b)(c)(d)证明可参照(a)的证明,照猫画虎.
A
B
C
D
E
A
B
C
E
D
F
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com 精品资料·第 8 页 (共 11 页) 版权所有@21世纪教育网
