圆柱的体积 圆柱的表面积应用题典型考点 押题练 2025年小学小升初数学会考复习备考
文档属性
| 名称 | 圆柱的体积 圆柱的表面积应用题典型考点 押题练 2025年小学小升初数学会考复习备考 |  | |
| 格式 | docx | ||
| 文件大小 | 359.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-10 16:26:40 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
圆柱的体积 圆柱的表面积应用题典型考点 押题练
2025年小学小升初会考复习备考
1.花瓶是插花的重要一部分,不同的花瓶要选择不同的鲜切花。插花时,如何选对花瓶,主要考虑三要素:口径,高度、体积。花瓶的高度一般约为花束长度的40%至60%,淘气想为朋友们购买下面两种花瓶。
(1)淘气微信钱包里有120元,买了2个长方体花瓶后,剩下的钱能买多少个圆柱花瓶?
(2)将圆柱花瓶中高10厘米的营养液倒入长方体花瓶中,这时营养液的水面高度约是多少厘米?(结果保留一位小数)
2.陀螺是一种传统的儿童玩具,如今它已成为一种体育项目。如图形状的陀螺,上面呈圆柱形,下面呈圆锥形。圆柱的底面半径为4厘米,高5厘米;圆锥部分的高为6厘米。
(1)给陀螺的圆柱形部分涂上红色,圆锥形部分涂上黄色,那么涂红色部分的面积有多大?
(2)这个陀螺的体积是多少立方厘米?
3.早在2000多年前,我国古代劳动人民就会用自己的方法计算各种物体的体积。《九章算术》中记载的圆柱体积的计算方法是“周自相乘,以高乘之,十二而一”,也就是说,用底面周长的平方乘高,再除以12,可以求出圆柱的体积。
(1)如果一个圆柱的底面周长是20厘米,高是10厘米,你能用上面的方法算出这个圆柱的体积吗?(得数保留整立方厘米)
(2)如果用现在的方法计算这个圆柱的体积,计算结果是多少立方厘米?(提示:计算时可以先保留进行约分和计算,最后再用3.14代入,得数保留整立方厘米。)
4.如图,把一个高10厘米的圆柱沿底面直径垂直切成两部分,这两部分的表面积之和比原来增加了200平方厘米,原来圆柱的表面积是多少平方厘米?(结果可用含有的式子表示)
5.有甲、乙两个圆柱,表面积都是90;底面积也相等,每个底面的面积都是15。如果把这两个圆柱接起来,成为一个大圆柱。
(1)这个大圆柱的侧面积是多少cm2?
(2)这个大圆柱的表面积是多少cm2?
6.把一个棱长8厘米的正方体削成一个最大的圆柱,这个圆柱的表面积是多少?
7.阅读并解答。
古希腊的阿基米德是历史上最杰出的数学家之一。按照他生前的遗愿,人们在他的墓碑上刻了一个“圆柱容球”的几何图形。
圆柱容球就是把一个球放在一个圆柱形容器中,盖上盖后,球恰好与圆柱的上、下底面及侧面紧密接触。
当圆柱容球时,球的直径、圆柱的高、圆柱的底面直径都相等,球的表面积正好是圆柱表面积的,球的体积也是圆柱体积的。
(1)当圆柱容球时,如果球的表面积是113.04平方厘米,那么圆柱的表面积是多少?
(2)当圆柱容球时,如果r=3厘米,请求出球的体积。
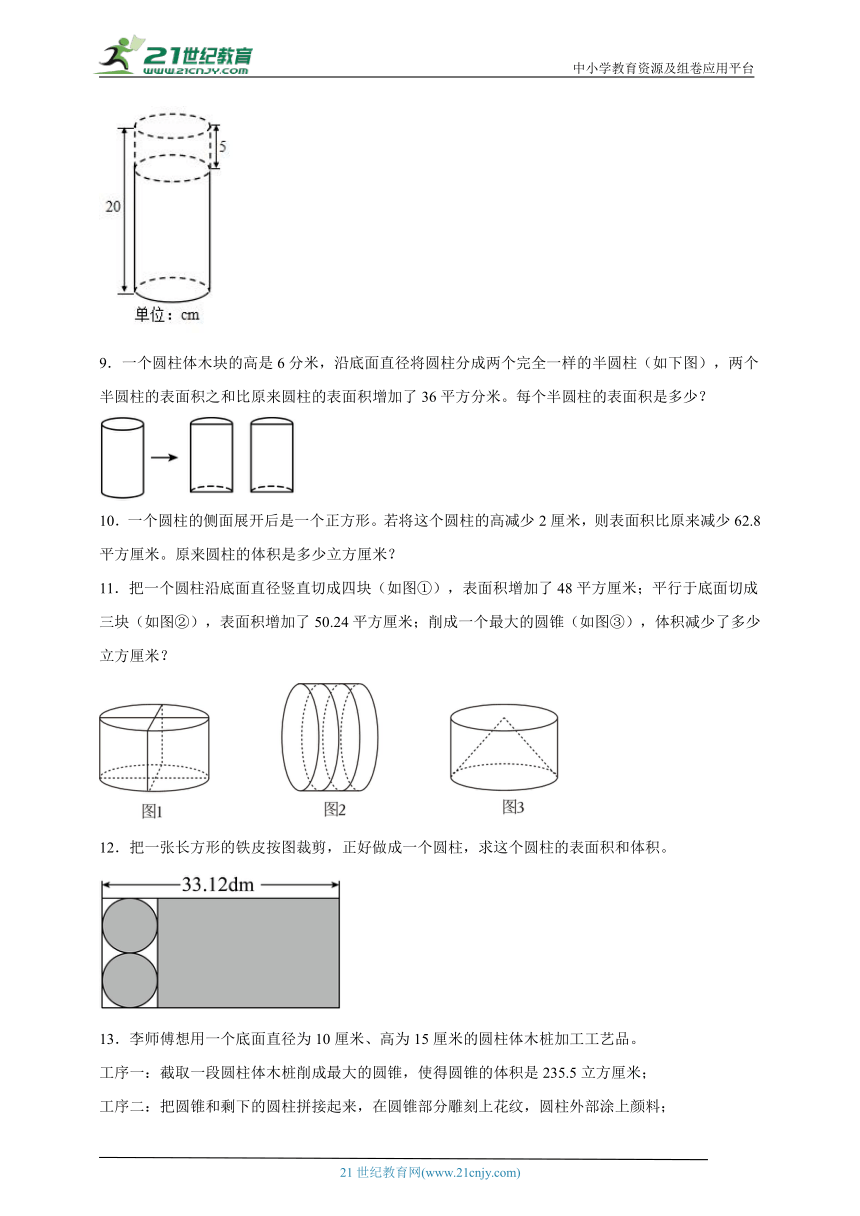
8.如图,一个圆柱体木材被截去5cm后,圆柱的表面积减少了47.1cm2,求原来圆柱体的表面积是多少cm2?
9.一个圆柱体木块的高是6分米,沿底面直径将圆柱分成两个完全一样的半圆柱(如下图),两个半圆柱的表面积之和比原来圆柱的表面积增加了36平方分米。每个半圆柱的表面积是多少?
10.一个圆柱的侧面展开后是一个正方形。若将这个圆柱的高减少2厘米,则表面积比原来减少62.8平方厘米。原来圆柱的体积是多少立方厘米?
11.把一个圆柱沿底面直径竖直切成四块(如图①),表面积增加了48平方厘米;平行于底面切成三块(如图②),表面积增加了50.24平方厘米;削成一个最大的圆锥(如图③),体积减少了多少立方厘米?
12.把一张长方形的铁皮按图裁剪,正好做成一个圆柱,求这个圆柱的表面积和体积。
13.李师傅想用一个底面直径为10厘米、高为15厘米的圆柱体木桩加工工艺品。
工序一:截取一段圆柱体木桩削成最大的圆锥,使得圆锥的体积是235.5立方厘米;
工序二:把圆锥和剩下的圆柱拼接起来,在圆锥部分雕刻上花纹,圆柱外部涂上颜料;
工序三:把做好的工艺品用长方体纸盒进行包装,请你帮李师傅算一算。
(1)截取的木桩有多高?
(2)拼接后,需涂颜料的面积是多少平方厘米?
(3)这个长方体纸盒的体积至少是多少立方厘米?
14.(如下图)某商家推出一款足球纪念品,并给足球纪念品设计了圆柱形的包装盒,用绸带捆扎进行装饰。
(1)这个包装盒的表面积是多少?
(2)如果绸带打结处正好是底面圆心,打结用去的绸带长30厘米。捆扎这个包装盒至少要用绸带多少厘米?
(3)阅读下面的文本,计算这个足球纪念品的体积?
古希腊著名的数学家阿基米德是历史上杰出的数学家之一,在他众多的科学发现中,他自己最为满意的是“圆柱容球定理”。把一个球正好放在一个圆柱形容器中,球的直径与圆柱的高和底面直径相等,此时球的体积正好是圆柱体积的。
15.加工工艺品中的数学问题。
李明同学的爸爸是一个工艺品制作能手,他想把一根底面直径为20厘米、高为40厘米的圆柱形木桩加工成一个工艺品。具体加工步骤如下:
步骤一:截取一段高为9厘米的木桩削成一个最大的圆锥,得到圆锥1。
步骤二:再截取一段圆柱形木桩又削成一个最大的圆锥,使得圆锥的体积是1884立方厘米,得到圆锥2。
步骤三:将截取的圆锥1、圆锥2和剩下部分的圆柱拼接起来(圆柱和圆锥的底面分别拼接),在两个小圆锥上面雕刻花纹装饰,圆柱部分涂上颜料。
步骤四:把做好的工艺品用长方体纸盒进行包装。
请你帮李明爸爸算一算:
(1)圆锥1的体积是多少立方厘米?
(2)圆锥2的高是多少厘米?
(3)用于包装的长方体纸盒体积至少是多少立方厘米?(包装盒厚度忽略不计)
(4)爸爸将这个包装好的工艺品出售后获得的800元现金作为给李明的压岁钱存入银行,存期3年,年利率是。到期后,可以获得本金和利息一共多少元?
参考答案
1.(1)5个;(2)10.5厘米
【分析】(1)根据单价×数量=总价,用26.25×2即可求出2个长方体花瓶的总价,然后用120元减去2个长方体花瓶的总价,即可求出剩余的钱数,然后除以1个圆柱花瓶的单价,即可求出圆柱花瓶的个数。
(2)根据圆柱的体积公式:V=πr2h,代入数据求出水的体积,然后根据长方体的体积=长×宽×高,用水的体积除以长再除以宽,即可求出在长方体花瓶中营养液的水面高度。
【详解】(1)26.25×2=52.5(元)
120-52.5=67.5(元)
67.5÷13.5=5(个)
答:剩下的钱能买5个圆柱花瓶。
(2)3.14×(10÷2)2×10
=3.14×52×10
=3.14×25×10
=785(立方厘米)
785÷15÷5≈10.5(厘米)
答:这时营养液的水面高度约是10.5厘米。
2.(1)175.84平方厘米;(2)351.68立方厘米
【分析】(1)圆柱部分涂红色部分的面积等于圆柱的一个底面积加上圆柱的侧面积,圆柱的底面积=×半径的平方,圆柱的侧面积=2rh,据此代入数据解答。
(2)陀螺的体积等于底面半径为4厘米,高5厘米的圆柱的体积与底面半径为4厘米,高6厘米的圆锥的体积,根据圆柱的体积=h,圆锥的体积=h解答。
【详解】(1)3.14×+2×3.14×4×5
=3.14×16+6.28×4×5
=50.24+25.12×5
=50.24+125.6
=175.84(平方厘米)
答:涂红色部分的面积是175.84平方厘米。
(2)3.14××5+×3.14××6
=3.14×16×5+2×3.14×16
=3.14×80+6.28×16
=251.2+100.48
=351.68(立方厘米)
答:这个陀螺的体积是351.68立方厘米。
3.(1)333立方厘米;
(2)318立方厘米
【分析】(1)由题意可知,圆柱的体积=底面周长×底面周长×高÷12,把题目中的数据代入公式求出结果;
(2)先根据圆柱的底面周长求出圆柱的底面半径,再利用“”求出这个圆柱的体积,据此解答。
【详解】(1)20×20×10÷12
=400×10÷12
=4000÷12
≈333(立方厘米)
答:这个圆柱的体积是333立方厘米。
(2)20÷÷2
=20÷2÷
=10÷
=(厘米)
××10
=××10
=×10
=
≈318(立方厘米)
答:这个圆柱的体积是318立方厘米。
4.150π平方厘米
【分析】“将一个圆柱体沿着底面直径切成两部分,表面积增加了200平方厘米”,就是增加了两个长是圆柱的高,宽是圆柱的底面直径的长方形;据此可求出圆柱的底面直径,然后再根据圆柱的表面积公式进行计算。
【详解】200÷2=100(平方厘米)
100÷10=10(厘米)
π×10×10+π×(10÷2)2×2
=100π+50π
=150π(平方厘米)
答:原来圆柱的表面积是150π平方厘米。
【点睛】本题的关键是理解:“将一个圆柱体沿着底面直径切成两个半圆柱,表面积增加了200平方厘米”,就是增加了两个长是圆柱的高,宽是圆柱的底面直径的长方形的面积。
5.(1)120
(2)150
【分析】(1)用一个圆柱的表面积减去两个底面积就是一个圆柱的侧面积,乘2即可求出大圆柱的侧面积;
(2)用大圆柱的侧面积加上两个底面积就是大圆柱的表面积。
【详解】(1)(90-15×2)×2
=(90-30)×2
=60×2
=120()
答:这个大圆柱的侧面积是120cm2。
(2)120+15×2
=120+30
=150()
答:这个大圆柱的表面积是150cm2。
【点睛】本题考查圆柱的表面积和侧面积,解答本题的关键是掌握圆柱的表面积和侧面积计算公式。
6.301.44平方厘米
【详解】侧面积:8×3.14×8=25.12×8=200.96(平方厘米)
底面积:(平方厘米)
表面积:200.96+50.24×2=200.96+100.48=301.44(平方厘米)
答:这个圆柱的表面积是301.44平方厘米。
【分析】在正方体里削最大的圆柱,那么正方体的棱长就是圆柱的底面直径,也是圆柱的高。已知圆柱的底面直径与高就可以求出圆柱的侧面积、底面积、表面积。
7.(1)169.56平方厘米
(2)113.04立方厘米
【分析】(1)根据当圆柱容球时,球的表面积正好是圆柱表面积的,根据已知一个数的几分之几是多少,求这个数用除法解答,用球的表面积除以就是圆柱的表面积;
(2)当圆柱容球时,球的体积是圆柱体积的,据此先求出圆柱的体积,根据圆柱的体积=h,代入数据计算出圆柱的体积,再根据分数乘法的意义,用圆柱的体积乘就是球的体积。
【详解】(1)113.04
=113.04
=169.56(平方厘米)
答:圆柱的表面积是169.56平方厘米。
(2)3.14×32×(3×2)
=3.14×9×6
=28.26×6
=169.56
=113.04(立方厘米)
答:球的体积是113.04立方厘米。
8.202.53cm2
【分析】通过观察图形可知,把这个圆柱体木材截去5cm,圆柱的表面积减少了47.1cm2,表面积减少的是高5cm的圆柱的侧面积,根据圆柱的侧面积公式:,据此可以求出圆柱的底面周长,再根据圆柱的表面积公式:,把数据代入公式解答。
【详解】47.1÷5=9.42(cm)
9.42×20+3.14×(9.42÷3.14÷2)2×2
=188.4+3.14×2.25×2
=188.4+14.13
=202.53(cm2)
答:原来圆柱体的表面积是202.53cm2。
【点睛】此题主要考查圆柱表面积公式的灵活运用,关键是熟记公式。
9.53.325平方分米
【分析】由题意可知,两个半圆柱的表面积之和比原来圆柱的表面积增加的是长为圆柱的高,宽为圆柱的底面直径的两个长方形的面积之和,用36除以2可得一个长方形的面积,再根据长方形面积公式的逆运算,用面积除以长(圆柱的高)可得圆柱的底面积直径。要求每个半圆柱的表面积,用一个长方形的面积加圆柱侧面积的一半再加圆柱的一个底面积。根据圆柱的侧面积公式、圆的面积公式,代入数据计算即可。
【详解】(平方分米)
(分米)
(平方分米)
答:每个半圆柱的表面积是53.325平方分米。
10.2464.9立方厘米
【分析】如下图:如果圆柱的高减少2厘米,表面积就比原来减少62.8平方厘米,那么表面积减少的是高为2厘米的圆柱的侧面积;圆柱侧面积=底面周长×高,则底面周长=圆柱侧面积÷高,用62.3平方厘米除以2计算出底面周长。
又知:圆的底面周长=2×π×底面半径,进而代入数据计算出圆柱的底面半径。
由题意知:圆柱的侧面展开后是一个正方形,所以圆柱的底面周长和高相等。利用圆柱的体积=底面积×高,计算出圆柱的体积即可。
【详解】圆柱的底面周长(也是原来圆柱的高):62.8÷2=31.4(厘米)
圆柱的底面半径:31.4÷2÷3.14
=15.7÷3.14
=5(厘米)
圆柱的底面积:
=3.14×25
=78.5(平方厘米)
圆柱的体积:78.5×31.4=2464.9(立方厘米)
答:原来圆柱的体积是2464.9立方厘米。
【点睛】圆柱的侧面展开图是一个正方形,说明这个圆柱的底面周长和高相等。
11.25.12立方厘米
【分析】根据图②的切分方法可知,增加的表面积是4个圆柱的底面的面积,先用增加的表面积除以4,求出圆柱的底面积,再根据圆的面积公式S=πr2,求出半径的平方即r2的值,进而推导出圆的半径;
根据图①的切分方法可知,增加的表面积是以圆柱的高的长度为长,底面半径的长度为宽的8个长方形的面积,先用增加的表面积除以8,再除以半径,即可求出圆柱的高;
把这个圆柱削成一个最大的圆锥,则圆柱和圆锥等底等高,根据圆柱的体积公式V=πr2h,圆锥的体积公式V=πr2h,求出圆柱和圆锥的体积,再相减,即是减少的体积。
【详解】底面积:50.24÷4=12.56(平方厘米)
半径的平方:12.56÷3.14=4(平方厘米)
因为4=2×2,所以圆的半径是2厘米;
圆柱的高:48÷8÷2=3(厘米)
减少的体积:
3.14×22×3-×3.14×22×3
=3.14×4×3-×3.14×4×3
=37.68-12.56
=25.12(立方厘米)
答:体积减小了25.12立方厘米。
【点睛】掌握圆柱切割的特点,明确表面积增加的是哪些面的面积,以此为突破口,利用公式求出圆柱的底面半径和高,再根据等底等高的圆柱、圆锥的体积关系求解。
12.502.4平方分米;803.84立方分米
【分析】圆柱侧面沿高展开是个长方形,长方形的长=圆柱底面周长,长方形的宽=圆柱的高,看图可知,圆柱底面周长+底面直径=33.12厘米,即圆周率×底面直径+底面直径=33.12厘米,33.12÷(圆周率+1)=底面直径,底面直径×2=圆柱的高,根据圆柱表面积=底面积×2+侧面积,圆柱体积=底面积×高,列式解答即可。
【详解】33.12÷(3.14+1)
=33.12÷4.14
=8(分米)
8×2=16(分米)
3.14×(8÷2)2×2+3.14×8×16
=3.14×42×2+401.92
=3.14×16×2+401.92
=100.48+401.92
=502.4(平方分米)
3.14×(8÷2)2×16
=3.14×42×16
=3.14×16×16
=803.84(立方分米)
答:这个圆柱的表面积和体积分别是502.4平方分米、803.84立方分米。
【点睛】关键是熟悉圆柱特征,先确定圆柱底面直径和高,掌握并灵活运用圆柱表面积和体积公式。
13.(1)9厘米
(2)266.9平方厘米
(3)1500立方厘米
【分析】(1)截取一段圆柱体木桩削成最大的圆锥,那么圆锥与圆柱等底;根据圆的面积公式S=πr2,求出圆锥的底面积;根据圆锥的体积公式V=Sh可知,圆锥的高h=3V÷S,代入数据计算,即可求出截取木桩的高。
(2)先用原来木桩的高减去圆锥的高,即是剩下圆柱的高;把圆锥和剩下的圆柱拼接起来,在剩下圆柱的外部涂上颜料,那么需涂颜料的面积=圆柱的侧面积+底面积,其中S侧=πdh,代入数据计算即可求解。
(3)把底面直径为10厘米,高为15厘米的木桩工艺品用长方体纸盒进行包装,则这个长方体的长、宽都等于木桩的底面直径,高等于木桩的高;根据长方体的体积=长×宽×高,求出这个长方体纸盒的体积。
【详解】(1)圆锥的底面积:
3.14×(10÷2)2
=3.14×52
=3.14×25
=78.5(平方厘米)
圆锥的高:
235.5×3÷78.5
=706.5÷78.5
=9(厘米)
答:截取的木桩有9厘米高。
(2)3.14×10×(15-9)+78.5
=3.14×10×6+78.5
=188.4+78.5
=266.9(平方厘米)
答:需涂颜料的面积是266.9平方厘米。
(3)10×10×15=1500(立方厘米)
答:这个长方体纸盒的体积至少是1500立方厘米。
14.(1)471平方厘米;
(2)110厘米;
(3)立方厘米
【分析】从图中可知,球的直径是(20-10)厘米,圆柱的底面直径和高等于球的直径。
(1)把足球纪念品放入一个圆柱形的包装盒,根据圆柱的表面积S表=S侧+2S底,其中S侧=πdh,S底=πr2,代入数据计算求出包装盒的表面积。
(2)从图中可知,捆扎这个包装盒用绸带的长度=4条圆柱的底面直径+4条圆柱的高+打结用的长度,代入数据计算求解。
(3)根据圆柱的体积(容积)公式V=πr2h,求出圆柱形容器的容积;根据圆柱容球定理可知,此时球的体积正好是圆柱体积的,把圆柱的容积看作单位“1”,单位“1”已知,用圆柱的容积乘,求出这个足球纪念品的体积。
【详解】球的直径、圆柱的底面直径、圆柱的高:20-10=10(厘米)
(1)3.14×10×10+3.14×(10÷2)2×2
=3.14×10×10+3.14×52×2
=3.14×10×10+3.14×25×2
=314+157
=471(平方厘米)
答:这个包装盒的表面积是471平方厘米。
(2)10×4+10×4+30
=40+40+30
=110(厘米)
答:捆扎这个包装盒至少要用绸带110厘米。
(3)3.14×(10÷2)2×10
=3.14×52×10
=3.14×25×10
=785(立方厘米)
785×=(立方厘米)
答:计算这个足球纪念品的体积是立方厘米。
15.(1)942立方厘米
(2)18厘米
(3)16000立方厘米
(4)863.6元
【分析】(1)由题意可知,这个最大的圆锥1的底面直径是20厘米、高是9厘米,根据圆锥的体积V=,把数据代入即可求解;
(2)已知圆锥的体积V=,则,把数据代入公式即可求解;
(3)由题意可知,长方体的长和宽由圆柱底面直径决定,即20厘米,高度为圆锥1、圆锥2和剩余圆柱的高度之和,即原圆柱体的高40厘米;再根据长方体的体积=长×宽×高求出这个用于包装的长方体纸盒体积至少是多少立方厘米;
(4)根据利息=本金×年利率×存期计算出利息,再加上本金即可求出本金和利息一共多少元。
【详解】(1)×3.14×(20÷2)2×9
=×3.14×102×9
=×9×3.14×100
=3×3.14×100
=9.42×100
=942(立方厘米)
答:圆锥1的体积是942立方厘米。
(2)20÷2=10(厘米)
3×1884÷(3.14×102)
=5652÷(3.14×100)
=5652÷314
=18(厘米)
答:圆锥2的高是18厘米。
(3)20×20×40
=400×40
=16000(立方厘米)
答:用于包装的长方体纸盒体积至少是16000立方厘米。
(4)800××3+800
=800×0.0265×3+800
=21.2×3+800
=63.6+800
=863.6(元)
答:到期后,可以获得本金和利息一共863.6元。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
圆柱的体积 圆柱的表面积应用题典型考点 押题练
2025年小学小升初会考复习备考
1.花瓶是插花的重要一部分,不同的花瓶要选择不同的鲜切花。插花时,如何选对花瓶,主要考虑三要素:口径,高度、体积。花瓶的高度一般约为花束长度的40%至60%,淘气想为朋友们购买下面两种花瓶。
(1)淘气微信钱包里有120元,买了2个长方体花瓶后,剩下的钱能买多少个圆柱花瓶?
(2)将圆柱花瓶中高10厘米的营养液倒入长方体花瓶中,这时营养液的水面高度约是多少厘米?(结果保留一位小数)
2.陀螺是一种传统的儿童玩具,如今它已成为一种体育项目。如图形状的陀螺,上面呈圆柱形,下面呈圆锥形。圆柱的底面半径为4厘米,高5厘米;圆锥部分的高为6厘米。
(1)给陀螺的圆柱形部分涂上红色,圆锥形部分涂上黄色,那么涂红色部分的面积有多大?
(2)这个陀螺的体积是多少立方厘米?
3.早在2000多年前,我国古代劳动人民就会用自己的方法计算各种物体的体积。《九章算术》中记载的圆柱体积的计算方法是“周自相乘,以高乘之,十二而一”,也就是说,用底面周长的平方乘高,再除以12,可以求出圆柱的体积。
(1)如果一个圆柱的底面周长是20厘米,高是10厘米,你能用上面的方法算出这个圆柱的体积吗?(得数保留整立方厘米)
(2)如果用现在的方法计算这个圆柱的体积,计算结果是多少立方厘米?(提示:计算时可以先保留进行约分和计算,最后再用3.14代入,得数保留整立方厘米。)
4.如图,把一个高10厘米的圆柱沿底面直径垂直切成两部分,这两部分的表面积之和比原来增加了200平方厘米,原来圆柱的表面积是多少平方厘米?(结果可用含有的式子表示)
5.有甲、乙两个圆柱,表面积都是90;底面积也相等,每个底面的面积都是15。如果把这两个圆柱接起来,成为一个大圆柱。
(1)这个大圆柱的侧面积是多少cm2?
(2)这个大圆柱的表面积是多少cm2?
6.把一个棱长8厘米的正方体削成一个最大的圆柱,这个圆柱的表面积是多少?
7.阅读并解答。
古希腊的阿基米德是历史上最杰出的数学家之一。按照他生前的遗愿,人们在他的墓碑上刻了一个“圆柱容球”的几何图形。
圆柱容球就是把一个球放在一个圆柱形容器中,盖上盖后,球恰好与圆柱的上、下底面及侧面紧密接触。
当圆柱容球时,球的直径、圆柱的高、圆柱的底面直径都相等,球的表面积正好是圆柱表面积的,球的体积也是圆柱体积的。
(1)当圆柱容球时,如果球的表面积是113.04平方厘米,那么圆柱的表面积是多少?
(2)当圆柱容球时,如果r=3厘米,请求出球的体积。
8.如图,一个圆柱体木材被截去5cm后,圆柱的表面积减少了47.1cm2,求原来圆柱体的表面积是多少cm2?
9.一个圆柱体木块的高是6分米,沿底面直径将圆柱分成两个完全一样的半圆柱(如下图),两个半圆柱的表面积之和比原来圆柱的表面积增加了36平方分米。每个半圆柱的表面积是多少?
10.一个圆柱的侧面展开后是一个正方形。若将这个圆柱的高减少2厘米,则表面积比原来减少62.8平方厘米。原来圆柱的体积是多少立方厘米?
11.把一个圆柱沿底面直径竖直切成四块(如图①),表面积增加了48平方厘米;平行于底面切成三块(如图②),表面积增加了50.24平方厘米;削成一个最大的圆锥(如图③),体积减少了多少立方厘米?
12.把一张长方形的铁皮按图裁剪,正好做成一个圆柱,求这个圆柱的表面积和体积。
13.李师傅想用一个底面直径为10厘米、高为15厘米的圆柱体木桩加工工艺品。
工序一:截取一段圆柱体木桩削成最大的圆锥,使得圆锥的体积是235.5立方厘米;
工序二:把圆锥和剩下的圆柱拼接起来,在圆锥部分雕刻上花纹,圆柱外部涂上颜料;
工序三:把做好的工艺品用长方体纸盒进行包装,请你帮李师傅算一算。
(1)截取的木桩有多高?
(2)拼接后,需涂颜料的面积是多少平方厘米?
(3)这个长方体纸盒的体积至少是多少立方厘米?
14.(如下图)某商家推出一款足球纪念品,并给足球纪念品设计了圆柱形的包装盒,用绸带捆扎进行装饰。
(1)这个包装盒的表面积是多少?
(2)如果绸带打结处正好是底面圆心,打结用去的绸带长30厘米。捆扎这个包装盒至少要用绸带多少厘米?
(3)阅读下面的文本,计算这个足球纪念品的体积?
古希腊著名的数学家阿基米德是历史上杰出的数学家之一,在他众多的科学发现中,他自己最为满意的是“圆柱容球定理”。把一个球正好放在一个圆柱形容器中,球的直径与圆柱的高和底面直径相等,此时球的体积正好是圆柱体积的。
15.加工工艺品中的数学问题。
李明同学的爸爸是一个工艺品制作能手,他想把一根底面直径为20厘米、高为40厘米的圆柱形木桩加工成一个工艺品。具体加工步骤如下:
步骤一:截取一段高为9厘米的木桩削成一个最大的圆锥,得到圆锥1。
步骤二:再截取一段圆柱形木桩又削成一个最大的圆锥,使得圆锥的体积是1884立方厘米,得到圆锥2。
步骤三:将截取的圆锥1、圆锥2和剩下部分的圆柱拼接起来(圆柱和圆锥的底面分别拼接),在两个小圆锥上面雕刻花纹装饰,圆柱部分涂上颜料。
步骤四:把做好的工艺品用长方体纸盒进行包装。
请你帮李明爸爸算一算:
(1)圆锥1的体积是多少立方厘米?
(2)圆锥2的高是多少厘米?
(3)用于包装的长方体纸盒体积至少是多少立方厘米?(包装盒厚度忽略不计)
(4)爸爸将这个包装好的工艺品出售后获得的800元现金作为给李明的压岁钱存入银行,存期3年,年利率是。到期后,可以获得本金和利息一共多少元?
参考答案
1.(1)5个;(2)10.5厘米
【分析】(1)根据单价×数量=总价,用26.25×2即可求出2个长方体花瓶的总价,然后用120元减去2个长方体花瓶的总价,即可求出剩余的钱数,然后除以1个圆柱花瓶的单价,即可求出圆柱花瓶的个数。
(2)根据圆柱的体积公式:V=πr2h,代入数据求出水的体积,然后根据长方体的体积=长×宽×高,用水的体积除以长再除以宽,即可求出在长方体花瓶中营养液的水面高度。
【详解】(1)26.25×2=52.5(元)
120-52.5=67.5(元)
67.5÷13.5=5(个)
答:剩下的钱能买5个圆柱花瓶。
(2)3.14×(10÷2)2×10
=3.14×52×10
=3.14×25×10
=785(立方厘米)
785÷15÷5≈10.5(厘米)
答:这时营养液的水面高度约是10.5厘米。
2.(1)175.84平方厘米;(2)351.68立方厘米
【分析】(1)圆柱部分涂红色部分的面积等于圆柱的一个底面积加上圆柱的侧面积,圆柱的底面积=×半径的平方,圆柱的侧面积=2rh,据此代入数据解答。
(2)陀螺的体积等于底面半径为4厘米,高5厘米的圆柱的体积与底面半径为4厘米,高6厘米的圆锥的体积,根据圆柱的体积=h,圆锥的体积=h解答。
【详解】(1)3.14×+2×3.14×4×5
=3.14×16+6.28×4×5
=50.24+25.12×5
=50.24+125.6
=175.84(平方厘米)
答:涂红色部分的面积是175.84平方厘米。
(2)3.14××5+×3.14××6
=3.14×16×5+2×3.14×16
=3.14×80+6.28×16
=251.2+100.48
=351.68(立方厘米)
答:这个陀螺的体积是351.68立方厘米。
3.(1)333立方厘米;
(2)318立方厘米
【分析】(1)由题意可知,圆柱的体积=底面周长×底面周长×高÷12,把题目中的数据代入公式求出结果;
(2)先根据圆柱的底面周长求出圆柱的底面半径,再利用“”求出这个圆柱的体积,据此解答。
【详解】(1)20×20×10÷12
=400×10÷12
=4000÷12
≈333(立方厘米)
答:这个圆柱的体积是333立方厘米。
(2)20÷÷2
=20÷2÷
=10÷
=(厘米)
××10
=××10
=×10
=
≈318(立方厘米)
答:这个圆柱的体积是318立方厘米。
4.150π平方厘米
【分析】“将一个圆柱体沿着底面直径切成两部分,表面积增加了200平方厘米”,就是增加了两个长是圆柱的高,宽是圆柱的底面直径的长方形;据此可求出圆柱的底面直径,然后再根据圆柱的表面积公式进行计算。
【详解】200÷2=100(平方厘米)
100÷10=10(厘米)
π×10×10+π×(10÷2)2×2
=100π+50π
=150π(平方厘米)
答:原来圆柱的表面积是150π平方厘米。
【点睛】本题的关键是理解:“将一个圆柱体沿着底面直径切成两个半圆柱,表面积增加了200平方厘米”,就是增加了两个长是圆柱的高,宽是圆柱的底面直径的长方形的面积。
5.(1)120
(2)150
【分析】(1)用一个圆柱的表面积减去两个底面积就是一个圆柱的侧面积,乘2即可求出大圆柱的侧面积;
(2)用大圆柱的侧面积加上两个底面积就是大圆柱的表面积。
【详解】(1)(90-15×2)×2
=(90-30)×2
=60×2
=120()
答:这个大圆柱的侧面积是120cm2。
(2)120+15×2
=120+30
=150()
答:这个大圆柱的表面积是150cm2。
【点睛】本题考查圆柱的表面积和侧面积,解答本题的关键是掌握圆柱的表面积和侧面积计算公式。
6.301.44平方厘米
【详解】侧面积:8×3.14×8=25.12×8=200.96(平方厘米)
底面积:(平方厘米)
表面积:200.96+50.24×2=200.96+100.48=301.44(平方厘米)
答:这个圆柱的表面积是301.44平方厘米。
【分析】在正方体里削最大的圆柱,那么正方体的棱长就是圆柱的底面直径,也是圆柱的高。已知圆柱的底面直径与高就可以求出圆柱的侧面积、底面积、表面积。
7.(1)169.56平方厘米
(2)113.04立方厘米
【分析】(1)根据当圆柱容球时,球的表面积正好是圆柱表面积的,根据已知一个数的几分之几是多少,求这个数用除法解答,用球的表面积除以就是圆柱的表面积;
(2)当圆柱容球时,球的体积是圆柱体积的,据此先求出圆柱的体积,根据圆柱的体积=h,代入数据计算出圆柱的体积,再根据分数乘法的意义,用圆柱的体积乘就是球的体积。
【详解】(1)113.04
=113.04
=169.56(平方厘米)
答:圆柱的表面积是169.56平方厘米。
(2)3.14×32×(3×2)
=3.14×9×6
=28.26×6
=169.56
=113.04(立方厘米)
答:球的体积是113.04立方厘米。
8.202.53cm2
【分析】通过观察图形可知,把这个圆柱体木材截去5cm,圆柱的表面积减少了47.1cm2,表面积减少的是高5cm的圆柱的侧面积,根据圆柱的侧面积公式:,据此可以求出圆柱的底面周长,再根据圆柱的表面积公式:,把数据代入公式解答。
【详解】47.1÷5=9.42(cm)
9.42×20+3.14×(9.42÷3.14÷2)2×2
=188.4+3.14×2.25×2
=188.4+14.13
=202.53(cm2)
答:原来圆柱体的表面积是202.53cm2。
【点睛】此题主要考查圆柱表面积公式的灵活运用,关键是熟记公式。
9.53.325平方分米
【分析】由题意可知,两个半圆柱的表面积之和比原来圆柱的表面积增加的是长为圆柱的高,宽为圆柱的底面直径的两个长方形的面积之和,用36除以2可得一个长方形的面积,再根据长方形面积公式的逆运算,用面积除以长(圆柱的高)可得圆柱的底面积直径。要求每个半圆柱的表面积,用一个长方形的面积加圆柱侧面积的一半再加圆柱的一个底面积。根据圆柱的侧面积公式、圆的面积公式,代入数据计算即可。
【详解】(平方分米)
(分米)
(平方分米)
答:每个半圆柱的表面积是53.325平方分米。
10.2464.9立方厘米
【分析】如下图:如果圆柱的高减少2厘米,表面积就比原来减少62.8平方厘米,那么表面积减少的是高为2厘米的圆柱的侧面积;圆柱侧面积=底面周长×高,则底面周长=圆柱侧面积÷高,用62.3平方厘米除以2计算出底面周长。
又知:圆的底面周长=2×π×底面半径,进而代入数据计算出圆柱的底面半径。
由题意知:圆柱的侧面展开后是一个正方形,所以圆柱的底面周长和高相等。利用圆柱的体积=底面积×高,计算出圆柱的体积即可。
【详解】圆柱的底面周长(也是原来圆柱的高):62.8÷2=31.4(厘米)
圆柱的底面半径:31.4÷2÷3.14
=15.7÷3.14
=5(厘米)
圆柱的底面积:
=3.14×25
=78.5(平方厘米)
圆柱的体积:78.5×31.4=2464.9(立方厘米)
答:原来圆柱的体积是2464.9立方厘米。
【点睛】圆柱的侧面展开图是一个正方形,说明这个圆柱的底面周长和高相等。
11.25.12立方厘米
【分析】根据图②的切分方法可知,增加的表面积是4个圆柱的底面的面积,先用增加的表面积除以4,求出圆柱的底面积,再根据圆的面积公式S=πr2,求出半径的平方即r2的值,进而推导出圆的半径;
根据图①的切分方法可知,增加的表面积是以圆柱的高的长度为长,底面半径的长度为宽的8个长方形的面积,先用增加的表面积除以8,再除以半径,即可求出圆柱的高;
把这个圆柱削成一个最大的圆锥,则圆柱和圆锥等底等高,根据圆柱的体积公式V=πr2h,圆锥的体积公式V=πr2h,求出圆柱和圆锥的体积,再相减,即是减少的体积。
【详解】底面积:50.24÷4=12.56(平方厘米)
半径的平方:12.56÷3.14=4(平方厘米)
因为4=2×2,所以圆的半径是2厘米;
圆柱的高:48÷8÷2=3(厘米)
减少的体积:
3.14×22×3-×3.14×22×3
=3.14×4×3-×3.14×4×3
=37.68-12.56
=25.12(立方厘米)
答:体积减小了25.12立方厘米。
【点睛】掌握圆柱切割的特点,明确表面积增加的是哪些面的面积,以此为突破口,利用公式求出圆柱的底面半径和高,再根据等底等高的圆柱、圆锥的体积关系求解。
12.502.4平方分米;803.84立方分米
【分析】圆柱侧面沿高展开是个长方形,长方形的长=圆柱底面周长,长方形的宽=圆柱的高,看图可知,圆柱底面周长+底面直径=33.12厘米,即圆周率×底面直径+底面直径=33.12厘米,33.12÷(圆周率+1)=底面直径,底面直径×2=圆柱的高,根据圆柱表面积=底面积×2+侧面积,圆柱体积=底面积×高,列式解答即可。
【详解】33.12÷(3.14+1)
=33.12÷4.14
=8(分米)
8×2=16(分米)
3.14×(8÷2)2×2+3.14×8×16
=3.14×42×2+401.92
=3.14×16×2+401.92
=100.48+401.92
=502.4(平方分米)
3.14×(8÷2)2×16
=3.14×42×16
=3.14×16×16
=803.84(立方分米)
答:这个圆柱的表面积和体积分别是502.4平方分米、803.84立方分米。
【点睛】关键是熟悉圆柱特征,先确定圆柱底面直径和高,掌握并灵活运用圆柱表面积和体积公式。
13.(1)9厘米
(2)266.9平方厘米
(3)1500立方厘米
【分析】(1)截取一段圆柱体木桩削成最大的圆锥,那么圆锥与圆柱等底;根据圆的面积公式S=πr2,求出圆锥的底面积;根据圆锥的体积公式V=Sh可知,圆锥的高h=3V÷S,代入数据计算,即可求出截取木桩的高。
(2)先用原来木桩的高减去圆锥的高,即是剩下圆柱的高;把圆锥和剩下的圆柱拼接起来,在剩下圆柱的外部涂上颜料,那么需涂颜料的面积=圆柱的侧面积+底面积,其中S侧=πdh,代入数据计算即可求解。
(3)把底面直径为10厘米,高为15厘米的木桩工艺品用长方体纸盒进行包装,则这个长方体的长、宽都等于木桩的底面直径,高等于木桩的高;根据长方体的体积=长×宽×高,求出这个长方体纸盒的体积。
【详解】(1)圆锥的底面积:
3.14×(10÷2)2
=3.14×52
=3.14×25
=78.5(平方厘米)
圆锥的高:
235.5×3÷78.5
=706.5÷78.5
=9(厘米)
答:截取的木桩有9厘米高。
(2)3.14×10×(15-9)+78.5
=3.14×10×6+78.5
=188.4+78.5
=266.9(平方厘米)
答:需涂颜料的面积是266.9平方厘米。
(3)10×10×15=1500(立方厘米)
答:这个长方体纸盒的体积至少是1500立方厘米。
14.(1)471平方厘米;
(2)110厘米;
(3)立方厘米
【分析】从图中可知,球的直径是(20-10)厘米,圆柱的底面直径和高等于球的直径。
(1)把足球纪念品放入一个圆柱形的包装盒,根据圆柱的表面积S表=S侧+2S底,其中S侧=πdh,S底=πr2,代入数据计算求出包装盒的表面积。
(2)从图中可知,捆扎这个包装盒用绸带的长度=4条圆柱的底面直径+4条圆柱的高+打结用的长度,代入数据计算求解。
(3)根据圆柱的体积(容积)公式V=πr2h,求出圆柱形容器的容积;根据圆柱容球定理可知,此时球的体积正好是圆柱体积的,把圆柱的容积看作单位“1”,单位“1”已知,用圆柱的容积乘,求出这个足球纪念品的体积。
【详解】球的直径、圆柱的底面直径、圆柱的高:20-10=10(厘米)
(1)3.14×10×10+3.14×(10÷2)2×2
=3.14×10×10+3.14×52×2
=3.14×10×10+3.14×25×2
=314+157
=471(平方厘米)
答:这个包装盒的表面积是471平方厘米。
(2)10×4+10×4+30
=40+40+30
=110(厘米)
答:捆扎这个包装盒至少要用绸带110厘米。
(3)3.14×(10÷2)2×10
=3.14×52×10
=3.14×25×10
=785(立方厘米)
785×=(立方厘米)
答:计算这个足球纪念品的体积是立方厘米。
15.(1)942立方厘米
(2)18厘米
(3)16000立方厘米
(4)863.6元
【分析】(1)由题意可知,这个最大的圆锥1的底面直径是20厘米、高是9厘米,根据圆锥的体积V=,把数据代入即可求解;
(2)已知圆锥的体积V=,则,把数据代入公式即可求解;
(3)由题意可知,长方体的长和宽由圆柱底面直径决定,即20厘米,高度为圆锥1、圆锥2和剩余圆柱的高度之和,即原圆柱体的高40厘米;再根据长方体的体积=长×宽×高求出这个用于包装的长方体纸盒体积至少是多少立方厘米;
(4)根据利息=本金×年利率×存期计算出利息,再加上本金即可求出本金和利息一共多少元。
【详解】(1)×3.14×(20÷2)2×9
=×3.14×102×9
=×9×3.14×100
=3×3.14×100
=9.42×100
=942(立方厘米)
答:圆锥1的体积是942立方厘米。
(2)20÷2=10(厘米)
3×1884÷(3.14×102)
=5652÷(3.14×100)
=5652÷314
=18(厘米)
答:圆锥2的高是18厘米。
(3)20×20×40
=400×40
=16000(立方厘米)
答:用于包装的长方体纸盒体积至少是16000立方厘米。
(4)800××3+800
=800×0.0265×3+800
=21.2×3+800
=63.6+800
=863.6(元)
答:到期后,可以获得本金和利息一共863.6元。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
