【期末章节复习】立体几何初步-2024-2025学年高一数学下学期苏教版(2019)必修第二册(含解析)
文档属性
| 名称 | 【期末章节复习】立体几何初步-2024-2025学年高一数学下学期苏教版(2019)必修第二册(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-12 23:20:25 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
【期末章节复习】立体几何初步-2024-2025学年高一数学下学期苏教版(2019)必修第二册
一.选择题(共8小题)
1.(2025春 云南期中)下列命题正确的是( )
A.正四棱柱是正方体
B.圆锥的截面是圆
C.一个棱柱至少有5个面
D.正三棱锥的所有面都是全等的等边三角形
2.(2025春 贵州期中)如图,△A′B′C′是利用斜二测画法画出的△ABC的直观图,其中A′C′∥y′轴,A′B′∥x′轴,且A′B′=B′C′=2,则△ABC的边BC=( )
A.2 B.4 C.6 D.
3.(2025春 浙江期中)已知圆锥的轴截面顶角为θ,侧面展开扇形的圆心角为2π﹣θ,则θ为( )
A.锐角 B.直角 C.钝角 D.不存在
4.(2025 冀州区校级模拟)已知圆锥PO的母线长为2,O为底面的圆心,其侧面积等于,则该圆锥的体积为( )
A. B. C.π D.2π
5.(2025 昭通校级模拟)已知某圆台的体积为,其轴截面为梯形ABCD,AB=4,CD=2,则在该圆台的侧距上,从点A到C的最短路径的长度为( )
A.3 B.3 C.6 D.3
6.(2025春 河北期中)已知正方体ABCD﹣A1B1C1D1的棱长为1,则下列说法中正确的是( )
A.若M是C1D1的中点,AM与平面BB1D1D的交点为O,则A1,O,C三点共线
B.以正方体的四个顶点为顶点组成的正四面体的体积为
C.若P是B1D1上的动点,则D,P,B,C1四点共面
D.若Q是AD1上的动点,则A1Q+QB的最小值是
7.(2025春 如皋市月考)在正四棱台ABCD﹣A1B1C1D1中,E,F分别为AD,A1D1的中点,下列各组直线中属于异面直线的是( )
A.AB和C1D1 B.EF和CC1 C.AC和A1C1 D.AC和FC1
8.(2025春 和平区校级期中)宋代瓷器的烧制水平极高,青白釉出自宋代,又称影青瓷.宋蒋祁《陶记》中“江、湖、川、广器尚青白,出于镇之窑者也”,印证了宋人把所说的“影青”瓷器叫做“青白瓷”的史实.图1为宋代的影青瓷花口盏及盏托,我们不妨将该花口盏及盏托看作是两个圆台与一个圆柱的组合体,三个部分的高相同均为6cm,上面的花口盏是底面直径分别为8cm和10cm的圆台,下面的盏托由底面直径8cm的圆柱和底面直径分别为12cm和8cm的圆台组合构成,示意图如图2,则该花口盏及盏托构成的组合体的体积为( )
A.248πcm3 B.274πcm3 C.354πcm3 D.370πcm3
二.多选题(共3小题)
(多选)9.(2025春 陕西校级期中)下列命题中,不正确的有( )
A.有两个面平行,其他各个面都是平行四边形的多面体是棱柱
B.有一个面是平行四边形的棱锥一定是四棱锥
C.过圆锥顶点的所有截面中,轴截面面积最大
D.有两个面互相平行且相似,其他各个面都是梯形的多面体是棱台
(多选)10.(2025春 仙游县期中)如图,正方体ABCD﹣A1B1C1D1的棱长为2,E,F分别是AD,DD1的中点,点P是底面ABCD内一动点,则下列结论正确的为( )
A.过B,E,F三点的平面截正方体所得截面图形是梯形
B.三棱锥C1﹣A1B1P的体积为4
C.三棱锥F﹣ACD的外接球表面积为9π
D.一质点从A点出发沿正方体表面绕行到CC1的中点的最短距离为
(多选)11.(2025春 南海区月考)如图,已知圆台上,下底面的圆心分别为O1,O2,半径分别为2和4,高为,四边形ABCD为圆台O1O2的轴截面,则( )
A.圆台的母线长为6
B.圆台的体积为
C.圆台的侧面积为24π
D.圆台外接球的半径为4
三.填空题(共3小题)
12.(2025 回忆版)一个底面半径为4cm,高为9cm的封闭圆柱形容器(容器壁厚度忽略不计)内有两个半径相等的铁球,则铁球半径的最大值为 cm.
13.(2025春 安康期中)已知正六棱柱ABCDEF﹣A1B1C1D1E1F1的各个顶点都在半径为R的球面上,一个能放进该正六棱柱内部的最大的球的半径为r.若AB=2,则当最小时,该正六棱柱的体积为 .
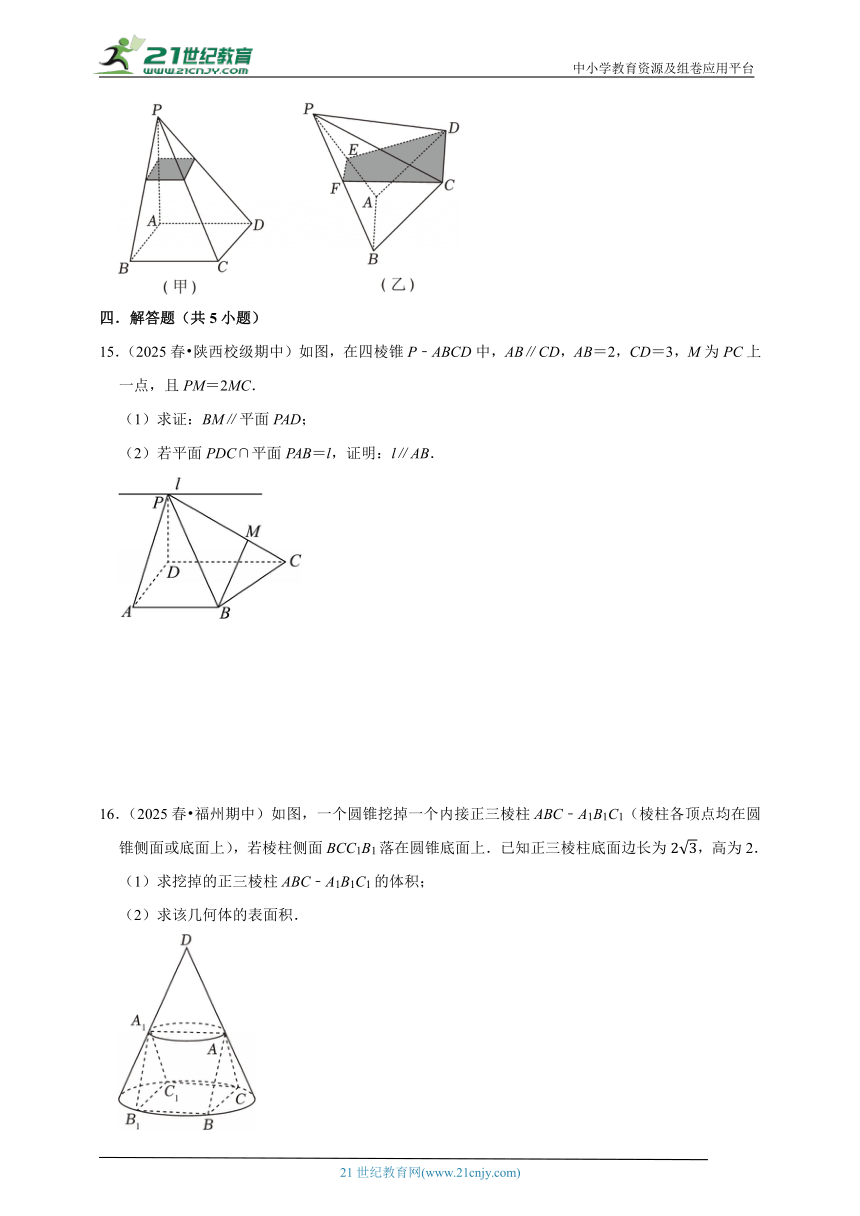
14.(2024秋 上虞区期末)(如图甲)P﹣ABCD是一个水平放置的装有一定量水的四棱锥密闭容器(容器材料厚度不算),底面ABCD为平行四边形.现将容器以棱AB为轴向左侧倾斜(如图乙),这时水面恰好经过CDEF,且E,F分别为棱PA,PB的中点,设棱锥P﹣ABCD的高为2,则图甲中,容器内的水面高度为 .
四.解答题(共5小题)
15.(2025春 陕西校级期中)如图,在四棱锥P﹣ABCD中,AB∥CD,AB=2,CD=3,M为PC上一点,且PM=2MC.
(1)求证:BM∥平面PAD;
(2)若平面PDC∩平面PAB=l,证明:l∥AB.
16.(2025春 福州期中)如图,一个圆锥挖掉一个内接正三棱柱ABC﹣A1B1C1(棱柱各顶点均在圆锥侧面或底面上),若棱柱侧面BCC1B1落在圆锥底面上.已知正三棱柱底面边长为,高为2.
(1)求挖掉的正三棱柱ABC﹣A1B1C1的体积;
(2)求该几何体的表面积.
17.(2025春 永安市期中)如图,正三棱柱ABC﹣A1B1C1中,E,F,G分别是棱AB,BC,B1C1的中点.
(1)判断直线AG与直线EF,直线CG与平面ABB1A1的位置关系;(判断即可,不必说明理由)
(2)求证:B1E∥平面ACG;
(3)在棱CC1上是否存在一点N,使得平面NEF∥平面A1BC1?若存在,请指出点N的位置,并证明;若不存在,请说明理由.
18.(2025春 南海区月考)如图1,内壁光滑且透明的正方体容器ABCD﹣A1B1C1D1内注有一定量的水,已知正方体容器棱长为4.容器厚度不计.当其水平放置时,水面恰好过AA1,BB1,CC1,DD1的中点E,F,G,H.现在固定容器一边BC于水平地面,再将容器倾斜,随着倾斜角度的不同,水面的形状也不同.容器绕BC从图1的放置状态旋转至水面第一次过棱AD的过程中(不包括起始和终止位置),水面与棱AA1,BB1,CC1,DD1分别交于点A2,B2,C2,D2.假设旋转过程中水面始终呈水平状态,不考虑水面的波动.
(1)证明:AA2+BB2是定值;
(2)已知水面A2B2C2D2是矩形面,求水面A2B2C2D2面积的取值范围.
19.(2025春 双阳区校级期中)如图,在四棱锥P﹣ABCD中,四边形ABCD是平行四边形,AC,BD交于点O,点E是棱PB上的一点,且PD∥平面EAC.
(1)求证:点E是PB的中点;
(2)在棱BC上是否存在点G,使得平面EOG∥平面PCD?若存在,请加以证明,并写出的值;若不存在,请说明理由.
【期末章节复习】立体几何初步-2024-2025学年高一数学下学期苏教版(2019)必修第二册
参考答案与试题解析
一.选择题(共8小题)
题号 1 2 3 4 5 6 7 8
答案 C C C C B B D D
二.多选题(共3小题)
题号 9 10 11
答案 ACD ACD BCD
一.选择题(共8小题)
1.(2025春 云南期中)下列命题正确的是( )
A.正四棱柱是正方体
B.圆锥的截面是圆
C.一个棱柱至少有5个面
D.正三棱锥的所有面都是全等的等边三角形
【解答】解:选项A,正四棱柱是底面为正方形,且侧棱垂直于底面的棱柱,但侧棱与底面边长不一定相等,
所以正四棱柱不一定是正方体,故选项A错误;
选项B,圆锥的轴截面是三角形,只有平行于底面的截面才是圆,故选项B错误;
选项C,面数最少的棱柱是三棱柱,共有5个面,所以一个棱柱至少有5个面,故选项C正确;
选项D,正三棱锥的所有侧面都是全等的等腰三角形,底面是等边三角形,故选项D错误.
故选:C.
2.(2025春 贵州期中)如图,△A′B′C′是利用斜二测画法画出的△ABC的直观图,其中A′C′∥y′轴,A′B′∥x′轴,且A′B′=B′C′=2,则△ABC的边BC=( )
A.2 B.4 C.6 D.
【解答】解:根据题意,直观图△A′B′C′中,A′C′∥y′轴,A′B′∥x′轴,且A′B′=B′C′=2,
则A′C′2,
原图中,AC∥y轴,AB∥x轴,AC=4,AB=2,且∠CAB=90°,
故BC6.
故选:C.
3.(2025春 浙江期中)已知圆锥的轴截面顶角为θ,侧面展开扇形的圆心角为2π﹣θ,则θ为( )
A.锐角 B.直角 C.钝角 D.不存在
【解答】解:由题意圆锥的轴截面顶角为θ,侧面展开扇形的圆心角为2π﹣θ,
设圆锥的母线长为l(l>0),则圆锥的底面半径,
侧面展开图的扇形弧长,即圆锥底面的周长C=l(2π﹣θ),
因此,则,
若,则,,显然不满足,故舍去;
若,所以,所以,则,
又,不满足,故舍去;
若,令,,
则f(θ)在上单调递增,又,,
所以存在,使得f(θ0)=0.即在上有解,
符合题意;
综上可得θ为钝角.
故选:C.
4.(2025 冀州区校级模拟)已知圆锥PO的母线长为2,O为底面的圆心,其侧面积等于,则该圆锥的体积为( )
A. B. C.π D.2π
【解答】解:根据题意,设圆锥的底面半径为r,高为h,
由于圆锥PO的母线长为2,O为底面的圆心,其侧面积等于,则有2πr=2π,
解可得r,
则圆锥的高h=1,
故该圆锥的体积Vπr2h=π.
故选:C.
5.(2025 昭通校级模拟)已知某圆台的体积为,其轴截面为梯形ABCD,AB=4,CD=2,则在该圆台的侧距上,从点A到C的最短路径的长度为( )
A.3 B.3 C.6 D.3
【解答】解:由AB=4,CD=2,得圆台的下底面的半径为2,上底面的半径为1,
设圆台的高为h,由圆台的体积为,得,所以,
在梯形ABCD中,则,如图,延长AD,BC,OO1交于点P,
由△PDC∽△PAB,得,所以PC=3,
设该圆台的侧面展开图的圆心角为α,则3α=2π,所以,
连接AC,PC,则从点A到C的最短路径为线段AC,
又PC=3,PA=6,,所以.
故选:B.
6.(2025春 河北期中)已知正方体ABCD﹣A1B1C1D1的棱长为1,则下列说法中正确的是( )
A.若M是C1D1的中点,AM与平面BB1D1D的交点为O,则A1,O,C三点共线
B.以正方体的四个顶点为顶点组成的正四面体的体积为
C.若P是B1D1上的动点,则D,P,B,C1四点共面
D.若Q是AD1上的动点,则A1Q+QB的最小值是
【解答】解:对于A,由题意,连接AD1,BC1,如图,
由于正方体ABCD﹣A1B1C1D1中C1D1∥AB,可得ABC1D1共面,
连接BD1,则AM 平面ABC1D1,
又O∈AM,则O∈平面ABC1D1,
由AM与平面BB1D1D的交点为O,
则O∈平面BB1D1D,可得O∈BD1,即D1,O,B三点共线,
由C1D1∥CD∥AB,M为棱D1C1的中点,
可得D1M∥AB且,
故△OMD1∽△OAB,
于是得,即OB=2OD1,
可得三点D1,O,B共线,且OB=2OD1,
而A1C与BD1交于BD1的中点,
所以三点A1,O,C不共线,故A错误;
对于B,以正方体的四个顶点为顶点组成的正四面体,例如四面体B1﹣D1AC的体积为,故B正确;
对于C,设直线DP与直线BB1相交于点N,直线BC1在平面BB1C1C内,且不过点N,
所以由线线位置关系知,直线DP与BC1是异面直线,故C错误;
对于D,如图,
将平面A1AD1和平面BAD1展开到一个平面上,连接A1B交AD1于点Q,此时A1Q+QB最小,
在△A1AB中,A1A=AB=1,,由余弦定理可知,故D错误.
故选:B.
7.(2025春 如皋市月考)在正四棱台ABCD﹣A1B1C1D1中,E,F分别为AD,A1D1的中点,下列各组直线中属于异面直线的是( )
A.AB和C1D1 B.EF和CC1 C.AC和A1C1 D.AC和FC1
【解答】解:根据题意,依次分析选项:
对于A,AB和C1D1是平行直线,不符合题意;
对于B,EF和CC1是相交直线,不符合题意;
对于C,AC与A1C1是平行直线,不符合题意;
对于D,AC和FC1既不相交也不平行,是异面直线,符合题意.
故选:D.
8.(2025春 和平区校级期中)宋代瓷器的烧制水平极高,青白釉出自宋代,又称影青瓷.宋蒋祁《陶记》中“江、湖、川、广器尚青白,出于镇之窑者也”,印证了宋人把所说的“影青”瓷器叫做“青白瓷”的史实.图1为宋代的影青瓷花口盏及盏托,我们不妨将该花口盏及盏托看作是两个圆台与一个圆柱的组合体,三个部分的高相同均为6cm,上面的花口盏是底面直径分别为8cm和10cm的圆台,下面的盏托由底面直径8cm的圆柱和底面直径分别为12cm和8cm的圆台组合构成,示意图如图2,则该花口盏及盏托构成的组合体的体积为( )
A.248πcm3 B.274πcm3 C.354πcm3 D.370πcm3
【解答】解:由题意花口盏及盏托是两个圆台与一个圆柱的组合体,
三个部分的高相同均为6cm,上面的花口盏是底面直径分别为8cm和10cm的圆台,
下面的盏托由底面直径8cm的圆柱和底面直径分别为12cm和8cm的圆台组合构成,
可得花口盏体积:,
盏托体积:,
所以组合体的体积.
故选:D.
二.多选题(共3小题)
(多选)9.(2025春 陕西校级期中)下列命题中,不正确的有( )
A.有两个面平行,其他各个面都是平行四边形的多面体是棱柱
B.有一个面是平行四边形的棱锥一定是四棱锥
C.过圆锥顶点的所有截面中,轴截面面积最大
D.有两个面互相平行且相似,其他各个面都是梯形的多面体是棱台
【解答】解:对于A,如图所示,
上下底面平行,各个面都是平行四边形,此几何体不是棱柱,故A错误;
对于B,因为棱锥侧面全为三角形,所以若有一个面是平行四边形,则此面为底面,故该棱锥为四棱锥,B正确;
对于C,设圆锥母线长为l,则过圆锥顶点的截面为等腰三角形,且两腰长为l,
设该等腰三角形顶角为θ,则截面三角形面积为,显然当,面积S最大,
故当圆锥的轴截面三角形顶角为钝角时,圆锥的轴截面面积不是最大的,故C错误;
对于D,根据棱台的特征可知,棱台是棱锥被平行于底面的平面截得,侧棱的延长线要交于同一点,
有两个面平行且相似,其他各个面都是梯形的多面体,不能保证侧棱的延长线交于同一点,因此该多面体不一定是棱台,故D错误.
故选:ACD.
(多选)10.(2025春 仙游县期中)如图,正方体ABCD﹣A1B1C1D1的棱长为2,E,F分别是AD,DD1的中点,点P是底面ABCD内一动点,则下列结论正确的为( )
A.过B,E,F三点的平面截正方体所得截面图形是梯形
B.三棱锥C1﹣A1B1P的体积为4
C.三棱锥F﹣ACD的外接球表面积为9π
D.一质点从A点出发沿正方体表面绕行到CC1的中点的最短距离为
【解答】解:对于A,由中位线可得EF∥AD1,在正方体中,AD1∥BC1,所以EF∥BC1,
所以B,C1,E,F四点共面,又因为EF≠BC1,所以截面EBC1F为梯形,故A正确;
对于B,,故B错误;
对于C,三棱锥F﹣ACD的外接球可以补形为长方体外接球,半径,
所以表面积S=4πR2=9π,故C正确;
对于D,记CC1的中点为Q,如图所示,
若正方形BCC1B1沿着BB1展在平面ABB1A1,
在Rt△AC′Q中,AC′=4,C′Q=1.则,
若ABCD沿着CD展开到与平面CDD1C1重合,
在Rt△A′B′Q中,A′B′=2,B′Q=3,则,
综上,一质点从A点出发沿正方体表面绕行到CC1的中点的最短距离为,故D正确.
故选:ACD.
(多选)11.(2025春 南海区月考)如图,已知圆台上,下底面的圆心分别为O1,O2,半径分别为2和4,高为,四边形ABCD为圆台O1O2的轴截面,则( )
A.圆台的母线长为6
B.圆台的体积为
C.圆台的侧面积为24π
D.圆台外接球的半径为4
【解答】解:∵圆台上下底面半径分别为2和4,高为,
则圆台的母线长为l,故A错误;
圆台的体积V,故B正确;
圆台的侧面积S,故C正确;
设圆台外接球球心到上底面的距离为x,可得,解得x,
则球的半径为4,故D正确.
故选:BCD.
三.填空题(共3小题)
12.(2025 回忆版)一个底面半径为4cm,高为9cm的封闭圆柱形容器(容器壁厚度忽略不计)内有两个半径相等的铁球,则铁球半径的最大值为 cm.
【解答】解:若两铁球相切,且下方铁球与底面和侧面均相切,轴截面如图,
则球的半径R=4,此时4R=16>9,故不符合题意;
若两铁球相切,且上方铁球与上底面相切,下方铁球与下底面相切,
两球心均在圆柱上下底面中心连线上,如图,
则铁球半径R满足4R=9,此时R;
若两铁球相切,且上方铁球与上底面相切,下方铁球与下底面相切,
两球心分别在圆柱轴截面对角的角平分线上,轴截面如图,
其中AC为轴截面对角线,O1、O2为两球球心,
分别过O1作AD的平行线,过O2作CD的平行线,两线交于点M,
设铁球半径为R,
则MO1=8﹣2R,O2M=9﹣2R,O1O2=2R,
所以(9﹣2R)2+(8﹣2R)2=4R2,
解得R或R(舍去),
故此时R.
综上,铁球半径的最大值为.
故答案为:.
13.(2025春 安康期中)已知正六棱柱ABCDEF﹣A1B1C1D1E1F1的各个顶点都在半径为R的球面上,一个能放进该正六棱柱内部的最大的球的半径为r.若AB=2,则当最小时,该正六棱柱的体积为 .
【解答】解:设正六边形ABCDEF的中心为点M,则点M与任意一条边均构成等边三角形,
因此点M到各边的距离均为等边三角形的高,为,
不妨设该正六棱柱的高为h,那么有目,r取两者之中的较小者,
易得该正六棱柱的外接球半径为,
当时,,,
当,,,
所以时,取得最小值,
又因为一个等边三角形的面积为,
所以正六边形底面的面积为,
则该正六棱柱的体积为.
故答案为:.
14.(2024秋 上虞区期末)(如图甲)P﹣ABCD是一个水平放置的装有一定量水的四棱锥密闭容器(容器材料厚度不算),底面ABCD为平行四边形.现将容器以棱AB为轴向左侧倾斜(如图乙),这时水面恰好经过CDEF,且E,F分别为棱PA,PB的中点,设棱锥P﹣ABCD的高为2,则图甲中,容器内的水面高度为 2 .
【解答】解:将四棱锥补成平行六面体,如图所示:
设平行四面体的体积为V总,根据E,F分别为棱PA,PB的中点,设棱锥P﹣ABCD高为h,体积为V,
则S四边形BCMQ=4S△BCG,由三棱柱BCG﹣ADE与平行六面体的高相同,得,
根据四棱锥P﹣ABCD与平行六面体底和高均相同,则VV总,即3V=V总,
所以VF﹣BCGVBCG﹣ADE,
则V水VBCG﹣ADEV总3VV,
图甲中上方的小四棱锥高为h1,则,则,
故图甲中的水面高度为(1)h=(1)×2=2.
故答案为:2.
四.解答题(共5小题)
15.(2025春 陕西校级期中)如图,在四棱锥P﹣ABCD中,AB∥CD,AB=2,CD=3,M为PC上一点,且PM=2MC.
(1)求证:BM∥平面PAD;
(2)若平面PDC∩平面PAB=l,证明:l∥AB.
【解答】证明:(1)由题意,在四棱锥P﹣ABCD中,AB∥CD,AB=2,CD=3,PM=2MC.
在PD上取一点N,使得,
由于PM=2MC,因此NM∥CD,且,
由于AB∥CD,AB=2,CD=3,故,
因此NM∥AB且NM=AB,故四边形NMBA为平行四边形,
故BM∥AN,
BM 平面PAD,AN 平面PAD,
故BM∥平面PAD;
(2)证明:由于AB∥CD,AB 平面PCD,CD 平面PCD,
故AB∥平面PCD,
又AB 平面PAB,平面PDC∩平面PAB=l,
所以l∥AB.
16.(2025春 福州期中)如图,一个圆锥挖掉一个内接正三棱柱ABC﹣A1B1C1(棱柱各顶点均在圆锥侧面或底面上),若棱柱侧面BCC1B1落在圆锥底面上.已知正三棱柱底面边长为,高为2.
(1)求挖掉的正三棱柱ABC﹣A1B1C1的体积;
(2)求该几何体的表面积.
【解答】解:(1)∵正三棱柱ABC﹣A1B1C1的底面边长为,高为2,
∴,
∴正三棱柱ABC﹣A1B1C1的体积;
(2)在正三棱柱ABC﹣A1B1C1中,由(1)知,,
,
设圆锥的底面圆圆心为O,则O是矩形BCC1B1的中心,设圆O半径为r,
则,得r=2,
取BC的中点E,连接AE,则AE⊥BC,且AE∥DO,
,OE=1,
于是,解得DO=6,
则圆锥的母线长,
圆锥的底面圆的面积,侧面积,
三棱柱的表面积为,
∴该几何体的表面积为:
.
17.(2025春 永安市期中)如图,正三棱柱ABC﹣A1B1C1中,E,F,G分别是棱AB,BC,B1C1的中点.
(1)判断直线AG与直线EF,直线CG与平面ABB1A1的位置关系;(判断即可,不必说明理由)
(2)求证:B1E∥平面ACG;
(3)在棱CC1上是否存在一点N,使得平面NEF∥平面A1BC1?若存在,请指出点N的位置,并证明;若不存在,请说明理由.
【解答】解:(1)直线AG与直线EF是异面直线,直线CG与平面ABB1A1相交;
(2)证明:取AC的中点为H,连接GH,EH,如图,
∵E、H、G分别是棱AB、AC、A1C1的中点,
∴EH∥BC且,B1G∥BC且,
∴EH∥B1G且EH=B1G,
∴四边形EHGB1是平行四边形,∴EB1∥GH,
∵GH 平面ACG,B1E 平面ACG,∴B1E∥平面ACG;
(3)当点N为棱CC1的中点时,平面NEF∥平面A1BC1.
证明:如图,
∵E,F分别是棱AB,BC的中点,∴EF∥AC
∵AC∥A1C1,∴EF∥A1C1,
∵EF 平面A1BC1,A1C1 平面A1BC1,∴EF∥平面A1BC1,
∵N,F分别是棱CC1,BC的中点,∴NF∥BC1,
∵NF 平面A1BC1,BC1 平面A1BC1,∴NF∥平面A1BC1,
∵EF∩NF=F,∴平面NEF∥平面A1BC1.
18.(2025春 南海区月考)如图1,内壁光滑且透明的正方体容器ABCD﹣A1B1C1D1内注有一定量的水,已知正方体容器棱长为4.容器厚度不计.当其水平放置时,水面恰好过AA1,BB1,CC1,DD1的中点E,F,G,H.现在固定容器一边BC于水平地面,再将容器倾斜,随着倾斜角度的不同,水面的形状也不同.容器绕BC从图1的放置状态旋转至水面第一次过棱AD的过程中(不包括起始和终止位置),水面与棱AA1,BB1,CC1,DD1分别交于点A2,B2,C2,D2.假设旋转过程中水面始终呈水平状态,不考虑水面的波动.
(1)证明:AA2+BB2是定值;
(2)已知水面A2B2C2D2是矩形面,求水面A2B2C2D2面积的取值范围.
【解答】解:(1)证明:因为水的部分在旋转过程中,四棱柱ABFE﹣CDGH的底面积与四棱柱ABB2A2﹣DCC2D2的高为4的棱柱,
因为水的体积为定值,所以ABFE与底面ABB2A2A的面积相等且为定值,而底面梯形ABB2A2的高AB也为定值,
所以底面梯形ABB2A2中,AA2+BB2是定值;
(2)根据题意可得水面A2B2C2D2面积为B2C2×C2D2=4C2D2,
又水的体积为正方体的体积的一半,所以C2D2∈(4,),
所以水面A2B2C2D2面积的取值范围为(16,).
19.(2025春 双阳区校级期中)如图,在四棱锥P﹣ABCD中,四边形ABCD是平行四边形,AC,BD交于点O,点E是棱PB上的一点,且PD∥平面EAC.
(1)求证:点E是PB的中点;
(2)在棱BC上是否存在点G,使得平面EOG∥平面PCD?若存在,请加以证明,并写出的值;若不存在,请说明理由.
【解答】解:(1)证明:在四棱锥P﹣ABCD中,四边形ABCD是平行四边形,
AC,BD交于点O,点E是棱PB上的一点,且PD∥平面EAC,
∵四边形ABCD是平行四边形,∴点O是BD的中点,
∵PD∥平面EAC,平面EAC∩平面PBD=EO,PD 平面PBD,
∴PD∥EO,
∴,∴点E是PB的中点.
(2)存在点G,使得平面EOG∥平面PCD,此时,
∵,∴G为BC中点,
∵点O是BD的中点,∴CD∥GO
又CD 平面PCD,GO 平面PCD,
∴GO∥平面PCD,
由(1)知PD∥EO,同理可得,EO∥平面PCD,
又EO∩GO=O,EO,GO 平面EOG,
∴在棱BC上存在点G,使得平面EOG∥平面PCD,.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
【期末章节复习】立体几何初步-2024-2025学年高一数学下学期苏教版(2019)必修第二册
一.选择题(共8小题)
1.(2025春 云南期中)下列命题正确的是( )
A.正四棱柱是正方体
B.圆锥的截面是圆
C.一个棱柱至少有5个面
D.正三棱锥的所有面都是全等的等边三角形
2.(2025春 贵州期中)如图,△A′B′C′是利用斜二测画法画出的△ABC的直观图,其中A′C′∥y′轴,A′B′∥x′轴,且A′B′=B′C′=2,则△ABC的边BC=( )
A.2 B.4 C.6 D.
3.(2025春 浙江期中)已知圆锥的轴截面顶角为θ,侧面展开扇形的圆心角为2π﹣θ,则θ为( )
A.锐角 B.直角 C.钝角 D.不存在
4.(2025 冀州区校级模拟)已知圆锥PO的母线长为2,O为底面的圆心,其侧面积等于,则该圆锥的体积为( )
A. B. C.π D.2π
5.(2025 昭通校级模拟)已知某圆台的体积为,其轴截面为梯形ABCD,AB=4,CD=2,则在该圆台的侧距上,从点A到C的最短路径的长度为( )
A.3 B.3 C.6 D.3
6.(2025春 河北期中)已知正方体ABCD﹣A1B1C1D1的棱长为1,则下列说法中正确的是( )
A.若M是C1D1的中点,AM与平面BB1D1D的交点为O,则A1,O,C三点共线
B.以正方体的四个顶点为顶点组成的正四面体的体积为
C.若P是B1D1上的动点,则D,P,B,C1四点共面
D.若Q是AD1上的动点,则A1Q+QB的最小值是
7.(2025春 如皋市月考)在正四棱台ABCD﹣A1B1C1D1中,E,F分别为AD,A1D1的中点,下列各组直线中属于异面直线的是( )
A.AB和C1D1 B.EF和CC1 C.AC和A1C1 D.AC和FC1
8.(2025春 和平区校级期中)宋代瓷器的烧制水平极高,青白釉出自宋代,又称影青瓷.宋蒋祁《陶记》中“江、湖、川、广器尚青白,出于镇之窑者也”,印证了宋人把所说的“影青”瓷器叫做“青白瓷”的史实.图1为宋代的影青瓷花口盏及盏托,我们不妨将该花口盏及盏托看作是两个圆台与一个圆柱的组合体,三个部分的高相同均为6cm,上面的花口盏是底面直径分别为8cm和10cm的圆台,下面的盏托由底面直径8cm的圆柱和底面直径分别为12cm和8cm的圆台组合构成,示意图如图2,则该花口盏及盏托构成的组合体的体积为( )
A.248πcm3 B.274πcm3 C.354πcm3 D.370πcm3
二.多选题(共3小题)
(多选)9.(2025春 陕西校级期中)下列命题中,不正确的有( )
A.有两个面平行,其他各个面都是平行四边形的多面体是棱柱
B.有一个面是平行四边形的棱锥一定是四棱锥
C.过圆锥顶点的所有截面中,轴截面面积最大
D.有两个面互相平行且相似,其他各个面都是梯形的多面体是棱台
(多选)10.(2025春 仙游县期中)如图,正方体ABCD﹣A1B1C1D1的棱长为2,E,F分别是AD,DD1的中点,点P是底面ABCD内一动点,则下列结论正确的为( )
A.过B,E,F三点的平面截正方体所得截面图形是梯形
B.三棱锥C1﹣A1B1P的体积为4
C.三棱锥F﹣ACD的外接球表面积为9π
D.一质点从A点出发沿正方体表面绕行到CC1的中点的最短距离为
(多选)11.(2025春 南海区月考)如图,已知圆台上,下底面的圆心分别为O1,O2,半径分别为2和4,高为,四边形ABCD为圆台O1O2的轴截面,则( )
A.圆台的母线长为6
B.圆台的体积为
C.圆台的侧面积为24π
D.圆台外接球的半径为4
三.填空题(共3小题)
12.(2025 回忆版)一个底面半径为4cm,高为9cm的封闭圆柱形容器(容器壁厚度忽略不计)内有两个半径相等的铁球,则铁球半径的最大值为 cm.
13.(2025春 安康期中)已知正六棱柱ABCDEF﹣A1B1C1D1E1F1的各个顶点都在半径为R的球面上,一个能放进该正六棱柱内部的最大的球的半径为r.若AB=2,则当最小时,该正六棱柱的体积为 .
14.(2024秋 上虞区期末)(如图甲)P﹣ABCD是一个水平放置的装有一定量水的四棱锥密闭容器(容器材料厚度不算),底面ABCD为平行四边形.现将容器以棱AB为轴向左侧倾斜(如图乙),这时水面恰好经过CDEF,且E,F分别为棱PA,PB的中点,设棱锥P﹣ABCD的高为2,则图甲中,容器内的水面高度为 .
四.解答题(共5小题)
15.(2025春 陕西校级期中)如图,在四棱锥P﹣ABCD中,AB∥CD,AB=2,CD=3,M为PC上一点,且PM=2MC.
(1)求证:BM∥平面PAD;
(2)若平面PDC∩平面PAB=l,证明:l∥AB.
16.(2025春 福州期中)如图,一个圆锥挖掉一个内接正三棱柱ABC﹣A1B1C1(棱柱各顶点均在圆锥侧面或底面上),若棱柱侧面BCC1B1落在圆锥底面上.已知正三棱柱底面边长为,高为2.
(1)求挖掉的正三棱柱ABC﹣A1B1C1的体积;
(2)求该几何体的表面积.
17.(2025春 永安市期中)如图,正三棱柱ABC﹣A1B1C1中,E,F,G分别是棱AB,BC,B1C1的中点.
(1)判断直线AG与直线EF,直线CG与平面ABB1A1的位置关系;(判断即可,不必说明理由)
(2)求证:B1E∥平面ACG;
(3)在棱CC1上是否存在一点N,使得平面NEF∥平面A1BC1?若存在,请指出点N的位置,并证明;若不存在,请说明理由.
18.(2025春 南海区月考)如图1,内壁光滑且透明的正方体容器ABCD﹣A1B1C1D1内注有一定量的水,已知正方体容器棱长为4.容器厚度不计.当其水平放置时,水面恰好过AA1,BB1,CC1,DD1的中点E,F,G,H.现在固定容器一边BC于水平地面,再将容器倾斜,随着倾斜角度的不同,水面的形状也不同.容器绕BC从图1的放置状态旋转至水面第一次过棱AD的过程中(不包括起始和终止位置),水面与棱AA1,BB1,CC1,DD1分别交于点A2,B2,C2,D2.假设旋转过程中水面始终呈水平状态,不考虑水面的波动.
(1)证明:AA2+BB2是定值;
(2)已知水面A2B2C2D2是矩形面,求水面A2B2C2D2面积的取值范围.
19.(2025春 双阳区校级期中)如图,在四棱锥P﹣ABCD中,四边形ABCD是平行四边形,AC,BD交于点O,点E是棱PB上的一点,且PD∥平面EAC.
(1)求证:点E是PB的中点;
(2)在棱BC上是否存在点G,使得平面EOG∥平面PCD?若存在,请加以证明,并写出的值;若不存在,请说明理由.
【期末章节复习】立体几何初步-2024-2025学年高一数学下学期苏教版(2019)必修第二册
参考答案与试题解析
一.选择题(共8小题)
题号 1 2 3 4 5 6 7 8
答案 C C C C B B D D
二.多选题(共3小题)
题号 9 10 11
答案 ACD ACD BCD
一.选择题(共8小题)
1.(2025春 云南期中)下列命题正确的是( )
A.正四棱柱是正方体
B.圆锥的截面是圆
C.一个棱柱至少有5个面
D.正三棱锥的所有面都是全等的等边三角形
【解答】解:选项A,正四棱柱是底面为正方形,且侧棱垂直于底面的棱柱,但侧棱与底面边长不一定相等,
所以正四棱柱不一定是正方体,故选项A错误;
选项B,圆锥的轴截面是三角形,只有平行于底面的截面才是圆,故选项B错误;
选项C,面数最少的棱柱是三棱柱,共有5个面,所以一个棱柱至少有5个面,故选项C正确;
选项D,正三棱锥的所有侧面都是全等的等腰三角形,底面是等边三角形,故选项D错误.
故选:C.
2.(2025春 贵州期中)如图,△A′B′C′是利用斜二测画法画出的△ABC的直观图,其中A′C′∥y′轴,A′B′∥x′轴,且A′B′=B′C′=2,则△ABC的边BC=( )
A.2 B.4 C.6 D.
【解答】解:根据题意,直观图△A′B′C′中,A′C′∥y′轴,A′B′∥x′轴,且A′B′=B′C′=2,
则A′C′2,
原图中,AC∥y轴,AB∥x轴,AC=4,AB=2,且∠CAB=90°,
故BC6.
故选:C.
3.(2025春 浙江期中)已知圆锥的轴截面顶角为θ,侧面展开扇形的圆心角为2π﹣θ,则θ为( )
A.锐角 B.直角 C.钝角 D.不存在
【解答】解:由题意圆锥的轴截面顶角为θ,侧面展开扇形的圆心角为2π﹣θ,
设圆锥的母线长为l(l>0),则圆锥的底面半径,
侧面展开图的扇形弧长,即圆锥底面的周长C=l(2π﹣θ),
因此,则,
若,则,,显然不满足,故舍去;
若,所以,所以,则,
又,不满足,故舍去;
若,令,,
则f(θ)在上单调递增,又,,
所以存在,使得f(θ0)=0.即在上有解,
符合题意;
综上可得θ为钝角.
故选:C.
4.(2025 冀州区校级模拟)已知圆锥PO的母线长为2,O为底面的圆心,其侧面积等于,则该圆锥的体积为( )
A. B. C.π D.2π
【解答】解:根据题意,设圆锥的底面半径为r,高为h,
由于圆锥PO的母线长为2,O为底面的圆心,其侧面积等于,则有2πr=2π,
解可得r,
则圆锥的高h=1,
故该圆锥的体积Vπr2h=π.
故选:C.
5.(2025 昭通校级模拟)已知某圆台的体积为,其轴截面为梯形ABCD,AB=4,CD=2,则在该圆台的侧距上,从点A到C的最短路径的长度为( )
A.3 B.3 C.6 D.3
【解答】解:由AB=4,CD=2,得圆台的下底面的半径为2,上底面的半径为1,
设圆台的高为h,由圆台的体积为,得,所以,
在梯形ABCD中,则,如图,延长AD,BC,OO1交于点P,
由△PDC∽△PAB,得,所以PC=3,
设该圆台的侧面展开图的圆心角为α,则3α=2π,所以,
连接AC,PC,则从点A到C的最短路径为线段AC,
又PC=3,PA=6,,所以.
故选:B.
6.(2025春 河北期中)已知正方体ABCD﹣A1B1C1D1的棱长为1,则下列说法中正确的是( )
A.若M是C1D1的中点,AM与平面BB1D1D的交点为O,则A1,O,C三点共线
B.以正方体的四个顶点为顶点组成的正四面体的体积为
C.若P是B1D1上的动点,则D,P,B,C1四点共面
D.若Q是AD1上的动点,则A1Q+QB的最小值是
【解答】解:对于A,由题意,连接AD1,BC1,如图,
由于正方体ABCD﹣A1B1C1D1中C1D1∥AB,可得ABC1D1共面,
连接BD1,则AM 平面ABC1D1,
又O∈AM,则O∈平面ABC1D1,
由AM与平面BB1D1D的交点为O,
则O∈平面BB1D1D,可得O∈BD1,即D1,O,B三点共线,
由C1D1∥CD∥AB,M为棱D1C1的中点,
可得D1M∥AB且,
故△OMD1∽△OAB,
于是得,即OB=2OD1,
可得三点D1,O,B共线,且OB=2OD1,
而A1C与BD1交于BD1的中点,
所以三点A1,O,C不共线,故A错误;
对于B,以正方体的四个顶点为顶点组成的正四面体,例如四面体B1﹣D1AC的体积为,故B正确;
对于C,设直线DP与直线BB1相交于点N,直线BC1在平面BB1C1C内,且不过点N,
所以由线线位置关系知,直线DP与BC1是异面直线,故C错误;
对于D,如图,
将平面A1AD1和平面BAD1展开到一个平面上,连接A1B交AD1于点Q,此时A1Q+QB最小,
在△A1AB中,A1A=AB=1,,由余弦定理可知,故D错误.
故选:B.
7.(2025春 如皋市月考)在正四棱台ABCD﹣A1B1C1D1中,E,F分别为AD,A1D1的中点,下列各组直线中属于异面直线的是( )
A.AB和C1D1 B.EF和CC1 C.AC和A1C1 D.AC和FC1
【解答】解:根据题意,依次分析选项:
对于A,AB和C1D1是平行直线,不符合题意;
对于B,EF和CC1是相交直线,不符合题意;
对于C,AC与A1C1是平行直线,不符合题意;
对于D,AC和FC1既不相交也不平行,是异面直线,符合题意.
故选:D.
8.(2025春 和平区校级期中)宋代瓷器的烧制水平极高,青白釉出自宋代,又称影青瓷.宋蒋祁《陶记》中“江、湖、川、广器尚青白,出于镇之窑者也”,印证了宋人把所说的“影青”瓷器叫做“青白瓷”的史实.图1为宋代的影青瓷花口盏及盏托,我们不妨将该花口盏及盏托看作是两个圆台与一个圆柱的组合体,三个部分的高相同均为6cm,上面的花口盏是底面直径分别为8cm和10cm的圆台,下面的盏托由底面直径8cm的圆柱和底面直径分别为12cm和8cm的圆台组合构成,示意图如图2,则该花口盏及盏托构成的组合体的体积为( )
A.248πcm3 B.274πcm3 C.354πcm3 D.370πcm3
【解答】解:由题意花口盏及盏托是两个圆台与一个圆柱的组合体,
三个部分的高相同均为6cm,上面的花口盏是底面直径分别为8cm和10cm的圆台,
下面的盏托由底面直径8cm的圆柱和底面直径分别为12cm和8cm的圆台组合构成,
可得花口盏体积:,
盏托体积:,
所以组合体的体积.
故选:D.
二.多选题(共3小题)
(多选)9.(2025春 陕西校级期中)下列命题中,不正确的有( )
A.有两个面平行,其他各个面都是平行四边形的多面体是棱柱
B.有一个面是平行四边形的棱锥一定是四棱锥
C.过圆锥顶点的所有截面中,轴截面面积最大
D.有两个面互相平行且相似,其他各个面都是梯形的多面体是棱台
【解答】解:对于A,如图所示,
上下底面平行,各个面都是平行四边形,此几何体不是棱柱,故A错误;
对于B,因为棱锥侧面全为三角形,所以若有一个面是平行四边形,则此面为底面,故该棱锥为四棱锥,B正确;
对于C,设圆锥母线长为l,则过圆锥顶点的截面为等腰三角形,且两腰长为l,
设该等腰三角形顶角为θ,则截面三角形面积为,显然当,面积S最大,
故当圆锥的轴截面三角形顶角为钝角时,圆锥的轴截面面积不是最大的,故C错误;
对于D,根据棱台的特征可知,棱台是棱锥被平行于底面的平面截得,侧棱的延长线要交于同一点,
有两个面平行且相似,其他各个面都是梯形的多面体,不能保证侧棱的延长线交于同一点,因此该多面体不一定是棱台,故D错误.
故选:ACD.
(多选)10.(2025春 仙游县期中)如图,正方体ABCD﹣A1B1C1D1的棱长为2,E,F分别是AD,DD1的中点,点P是底面ABCD内一动点,则下列结论正确的为( )
A.过B,E,F三点的平面截正方体所得截面图形是梯形
B.三棱锥C1﹣A1B1P的体积为4
C.三棱锥F﹣ACD的外接球表面积为9π
D.一质点从A点出发沿正方体表面绕行到CC1的中点的最短距离为
【解答】解:对于A,由中位线可得EF∥AD1,在正方体中,AD1∥BC1,所以EF∥BC1,
所以B,C1,E,F四点共面,又因为EF≠BC1,所以截面EBC1F为梯形,故A正确;
对于B,,故B错误;
对于C,三棱锥F﹣ACD的外接球可以补形为长方体外接球,半径,
所以表面积S=4πR2=9π,故C正确;
对于D,记CC1的中点为Q,如图所示,
若正方形BCC1B1沿着BB1展在平面ABB1A1,
在Rt△AC′Q中,AC′=4,C′Q=1.则,
若ABCD沿着CD展开到与平面CDD1C1重合,
在Rt△A′B′Q中,A′B′=2,B′Q=3,则,
综上,一质点从A点出发沿正方体表面绕行到CC1的中点的最短距离为,故D正确.
故选:ACD.
(多选)11.(2025春 南海区月考)如图,已知圆台上,下底面的圆心分别为O1,O2,半径分别为2和4,高为,四边形ABCD为圆台O1O2的轴截面,则( )
A.圆台的母线长为6
B.圆台的体积为
C.圆台的侧面积为24π
D.圆台外接球的半径为4
【解答】解:∵圆台上下底面半径分别为2和4,高为,
则圆台的母线长为l,故A错误;
圆台的体积V,故B正确;
圆台的侧面积S,故C正确;
设圆台外接球球心到上底面的距离为x,可得,解得x,
则球的半径为4,故D正确.
故选:BCD.
三.填空题(共3小题)
12.(2025 回忆版)一个底面半径为4cm,高为9cm的封闭圆柱形容器(容器壁厚度忽略不计)内有两个半径相等的铁球,则铁球半径的最大值为 cm.
【解答】解:若两铁球相切,且下方铁球与底面和侧面均相切,轴截面如图,
则球的半径R=4,此时4R=16>9,故不符合题意;
若两铁球相切,且上方铁球与上底面相切,下方铁球与下底面相切,
两球心均在圆柱上下底面中心连线上,如图,
则铁球半径R满足4R=9,此时R;
若两铁球相切,且上方铁球与上底面相切,下方铁球与下底面相切,
两球心分别在圆柱轴截面对角的角平分线上,轴截面如图,
其中AC为轴截面对角线,O1、O2为两球球心,
分别过O1作AD的平行线,过O2作CD的平行线,两线交于点M,
设铁球半径为R,
则MO1=8﹣2R,O2M=9﹣2R,O1O2=2R,
所以(9﹣2R)2+(8﹣2R)2=4R2,
解得R或R(舍去),
故此时R.
综上,铁球半径的最大值为.
故答案为:.
13.(2025春 安康期中)已知正六棱柱ABCDEF﹣A1B1C1D1E1F1的各个顶点都在半径为R的球面上,一个能放进该正六棱柱内部的最大的球的半径为r.若AB=2,则当最小时,该正六棱柱的体积为 .
【解答】解:设正六边形ABCDEF的中心为点M,则点M与任意一条边均构成等边三角形,
因此点M到各边的距离均为等边三角形的高,为,
不妨设该正六棱柱的高为h,那么有目,r取两者之中的较小者,
易得该正六棱柱的外接球半径为,
当时,,,
当,,,
所以时,取得最小值,
又因为一个等边三角形的面积为,
所以正六边形底面的面积为,
则该正六棱柱的体积为.
故答案为:.
14.(2024秋 上虞区期末)(如图甲)P﹣ABCD是一个水平放置的装有一定量水的四棱锥密闭容器(容器材料厚度不算),底面ABCD为平行四边形.现将容器以棱AB为轴向左侧倾斜(如图乙),这时水面恰好经过CDEF,且E,F分别为棱PA,PB的中点,设棱锥P﹣ABCD的高为2,则图甲中,容器内的水面高度为 2 .
【解答】解:将四棱锥补成平行六面体,如图所示:
设平行四面体的体积为V总,根据E,F分别为棱PA,PB的中点,设棱锥P﹣ABCD高为h,体积为V,
则S四边形BCMQ=4S△BCG,由三棱柱BCG﹣ADE与平行六面体的高相同,得,
根据四棱锥P﹣ABCD与平行六面体底和高均相同,则VV总,即3V=V总,
所以VF﹣BCGVBCG﹣ADE,
则V水VBCG﹣ADEV总3VV,
图甲中上方的小四棱锥高为h1,则,则,
故图甲中的水面高度为(1)h=(1)×2=2.
故答案为:2.
四.解答题(共5小题)
15.(2025春 陕西校级期中)如图,在四棱锥P﹣ABCD中,AB∥CD,AB=2,CD=3,M为PC上一点,且PM=2MC.
(1)求证:BM∥平面PAD;
(2)若平面PDC∩平面PAB=l,证明:l∥AB.
【解答】证明:(1)由题意,在四棱锥P﹣ABCD中,AB∥CD,AB=2,CD=3,PM=2MC.
在PD上取一点N,使得,
由于PM=2MC,因此NM∥CD,且,
由于AB∥CD,AB=2,CD=3,故,
因此NM∥AB且NM=AB,故四边形NMBA为平行四边形,
故BM∥AN,
BM 平面PAD,AN 平面PAD,
故BM∥平面PAD;
(2)证明:由于AB∥CD,AB 平面PCD,CD 平面PCD,
故AB∥平面PCD,
又AB 平面PAB,平面PDC∩平面PAB=l,
所以l∥AB.
16.(2025春 福州期中)如图,一个圆锥挖掉一个内接正三棱柱ABC﹣A1B1C1(棱柱各顶点均在圆锥侧面或底面上),若棱柱侧面BCC1B1落在圆锥底面上.已知正三棱柱底面边长为,高为2.
(1)求挖掉的正三棱柱ABC﹣A1B1C1的体积;
(2)求该几何体的表面积.
【解答】解:(1)∵正三棱柱ABC﹣A1B1C1的底面边长为,高为2,
∴,
∴正三棱柱ABC﹣A1B1C1的体积;
(2)在正三棱柱ABC﹣A1B1C1中,由(1)知,,
,
设圆锥的底面圆圆心为O,则O是矩形BCC1B1的中心,设圆O半径为r,
则,得r=2,
取BC的中点E,连接AE,则AE⊥BC,且AE∥DO,
,OE=1,
于是,解得DO=6,
则圆锥的母线长,
圆锥的底面圆的面积,侧面积,
三棱柱的表面积为,
∴该几何体的表面积为:
.
17.(2025春 永安市期中)如图,正三棱柱ABC﹣A1B1C1中,E,F,G分别是棱AB,BC,B1C1的中点.
(1)判断直线AG与直线EF,直线CG与平面ABB1A1的位置关系;(判断即可,不必说明理由)
(2)求证:B1E∥平面ACG;
(3)在棱CC1上是否存在一点N,使得平面NEF∥平面A1BC1?若存在,请指出点N的位置,并证明;若不存在,请说明理由.
【解答】解:(1)直线AG与直线EF是异面直线,直线CG与平面ABB1A1相交;
(2)证明:取AC的中点为H,连接GH,EH,如图,
∵E、H、G分别是棱AB、AC、A1C1的中点,
∴EH∥BC且,B1G∥BC且,
∴EH∥B1G且EH=B1G,
∴四边形EHGB1是平行四边形,∴EB1∥GH,
∵GH 平面ACG,B1E 平面ACG,∴B1E∥平面ACG;
(3)当点N为棱CC1的中点时,平面NEF∥平面A1BC1.
证明:如图,
∵E,F分别是棱AB,BC的中点,∴EF∥AC
∵AC∥A1C1,∴EF∥A1C1,
∵EF 平面A1BC1,A1C1 平面A1BC1,∴EF∥平面A1BC1,
∵N,F分别是棱CC1,BC的中点,∴NF∥BC1,
∵NF 平面A1BC1,BC1 平面A1BC1,∴NF∥平面A1BC1,
∵EF∩NF=F,∴平面NEF∥平面A1BC1.
18.(2025春 南海区月考)如图1,内壁光滑且透明的正方体容器ABCD﹣A1B1C1D1内注有一定量的水,已知正方体容器棱长为4.容器厚度不计.当其水平放置时,水面恰好过AA1,BB1,CC1,DD1的中点E,F,G,H.现在固定容器一边BC于水平地面,再将容器倾斜,随着倾斜角度的不同,水面的形状也不同.容器绕BC从图1的放置状态旋转至水面第一次过棱AD的过程中(不包括起始和终止位置),水面与棱AA1,BB1,CC1,DD1分别交于点A2,B2,C2,D2.假设旋转过程中水面始终呈水平状态,不考虑水面的波动.
(1)证明:AA2+BB2是定值;
(2)已知水面A2B2C2D2是矩形面,求水面A2B2C2D2面积的取值范围.
【解答】解:(1)证明:因为水的部分在旋转过程中,四棱柱ABFE﹣CDGH的底面积与四棱柱ABB2A2﹣DCC2D2的高为4的棱柱,
因为水的体积为定值,所以ABFE与底面ABB2A2A的面积相等且为定值,而底面梯形ABB2A2的高AB也为定值,
所以底面梯形ABB2A2中,AA2+BB2是定值;
(2)根据题意可得水面A2B2C2D2面积为B2C2×C2D2=4C2D2,
又水的体积为正方体的体积的一半,所以C2D2∈(4,),
所以水面A2B2C2D2面积的取值范围为(16,).
19.(2025春 双阳区校级期中)如图,在四棱锥P﹣ABCD中,四边形ABCD是平行四边形,AC,BD交于点O,点E是棱PB上的一点,且PD∥平面EAC.
(1)求证:点E是PB的中点;
(2)在棱BC上是否存在点G,使得平面EOG∥平面PCD?若存在,请加以证明,并写出的值;若不存在,请说明理由.
【解答】解:(1)证明:在四棱锥P﹣ABCD中,四边形ABCD是平行四边形,
AC,BD交于点O,点E是棱PB上的一点,且PD∥平面EAC,
∵四边形ABCD是平行四边形,∴点O是BD的中点,
∵PD∥平面EAC,平面EAC∩平面PBD=EO,PD 平面PBD,
∴PD∥EO,
∴,∴点E是PB的中点.
(2)存在点G,使得平面EOG∥平面PCD,此时,
∵,∴G为BC中点,
∵点O是BD的中点,∴CD∥GO
又CD 平面PCD,GO 平面PCD,
∴GO∥平面PCD,
由(1)知PD∥EO,同理可得,EO∥平面PCD,
又EO∩GO=O,EO,GO 平面EOG,
∴在棱BC上存在点G,使得平面EOG∥平面PCD,.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
